치주문자
Periodogram신호 처리에서 주기도문은 신호의 스펙트럼 밀도를 추정하는 것이다. 이 용어는 1898년 아서 슈스터에 의해 만들어졌다.[1] 오늘날, 주기각은 더 정교한 방법의 구성요소다(스펙트럼 추정 참조. FIR 필터와 윈도우 기능의 진폭 대 주파수 특성을 검사하는 가장 일반적인 툴이다. FFT 스펙트럼 분석기는 또한 치주문자의 시간 시퀀스로 구현된다.
정의
오늘날 적어도 두 가지 다른 정의가 사용되고 있다.[2] 그 중 하나는 시간 절약과 관련이 있고,[3] 하나는 그렇지 않다.[4] 시간 평균화는 다른 기사(Bartlett의 방법, Welch의 방법)의 청사진이기도 하다. 이 기사는 시간 절약에 관한 것이 아니다. 여기서 관심의 정의는 연속함수 ( t), x의 파워 스펙트럼 밀도가 자동 상관함수의 푸리에 변환이라는 것이다(교차 상관 정리, 스펙트럼 밀도#파워 스펙트럼 밀도, 위너-킨친 정리 참조).
연산

파라미터 T의 값이 충분히 작을 경우, X(f)에 대한 임의의 정확도 근사치를 영역 - 1 < T < 2 {1}{2}{에서 관찰할 수 있다.의 T
이는 x(t)의 0이 아닌 지속시간에 걸친 표본 x(nT)에 의해 정밀하게 결정된다(별도 시간 푸리에 변환 참조).
그리고 파라미터 N의 이 충분히 큰 경우, X1 / ( ) 는 형식 합계를 통해 임의로 가까운 주파수에서 평가할 수 있다.
여기서 k는 정수다. e- {의 주기성을 통해 이산 푸리에 변환의 관점에서 매우 간단하게 작성할 수 있다.
여기서 N}}은(는) 주기적인 합계: x [ ≜m= - x [ - .
0과 N-1 사이의 모든 정수 k에 대해 평가할 때 배열은 다음과 같다.
적용들
FIR 필터나 윈도우 기능의 상세한 특성을 조사하기 위해 주기그램을 사용하는 경우, 파라미터 N을 제로 패딩이라고 하는 x[n] 시퀀스의 0이 아닌 지속시간의 여러 배수로 선택한다(§ 샘플링 the DTFT 참조).[A] 필터 뱅크를 구현하는 데 사용되는 경우, N은 x[n] 시퀀스의 0이 아닌 지속시간에 대한 몇 개의 하위 배이다(§ DTFT 샘플링 참조).
주기그램의 결점 중 하나는 계산에 사용되는 표본의 수가 증가해도 주어진 주파수에서의 분산이 감소하지 않는다는 것이다. 그것은 낮은 신호 대 잡음 비에서 소음 신호 또는 심지어 사인파까지 분석하는데 필요한 평균값을 제공하지 않는다. 윈도우 기능과 필터 임펄스 반응은 소음이 없지만 다른 많은 신호는 보다 정교한 스펙트럼 추정 방법을 필요로 한다. 두 가지 대안 중 하나는 프로세스의 일부로 주기그램을 사용한다.
- 웰치의 방법으로 더 [8]잘 알려진 평균 치주문법은 긴 x[n] 시퀀스를 여러 개의 짧은 시간, 그리고 중복될 수 있는 반복으로 나눈다.[9][10] 창으로 된 각 주기도문을 계산하고 배열 평균, 즉 각 원소가 모든 주기도문의 해당 원소의 평균인 배열을 계산한다. 정지 공정의 경우, 이는 각 원소의 소음 분산을 주기그램 수의 역수와 거의 동일한 인수로 감소시킨다.
- 스무딩은 시간이 아닌 빈도에서 평균화 기법이다. 평활된 주기도문을 스펙트럼 그림이라고도 한다.[11][12]
치주문자 기반 기법은 일부 적용에서 허용되지 않는 작은 편견을 도입한다. 그 밖의 주기그램에 의존하지 않는 기법은 스펙트럼 밀도 추정 기사에 제시되어 있다.
참고 항목
- 일치 필터
- 필터링된 백프로젝션(Radon 변환)
- 웰치의 방법
- 바틀렛의 방법
- 이산 시간 푸리에 변환
- 최소 제곱 스펙트럼 분석, 균등하지 않은 데이터에서 주기그램 계산
- MUltiple SIgnal Classification(MUSIC), 인기 파라메트릭 초해상도 방법
- SAMV
메모들
- ^ N은 Matlab 및 Octave 애플리케이션에서 NFFT로 지정된다.
참조
- ^ Schuster, Arthur (January 1898). "On the investigation of hidden periodicities with application to a supposed 26 day period of meteorological phenomena" (PDF). Terrestrial Magnetism. 3 (1): 13–41. Bibcode:1898TeMag...3...13S. doi:10.1029/TM003i001p00013.
It is convenient to have a word for some representation of a variable quantity which shall correspond to the ‘spectrum’ of a luminous radiation. I propose the word periodogram, and define it more particularly in the following way.
- ^ McSweeney, Laura A. (2004-05-14). "Comparison of periodogram tests". Journal of Statistical Computation and Simulation. online ($50). 76 (4): 357–369. doi:10.1080/10629360500107618.
- ^ "Periodogram—Wolfram Language Documentation".
- ^ a b "Periodogram power spectral density estimate - MATLAB periodogram".
- ^ Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999). Discrete-time signal processing (2nd ed.). Upper Saddle River, N.J.: Prentice Hall. p. 732 (10.55). ISBN 0-13-754920-2. url=https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf
- ^ Rabiner, Lawrence R.; Gold, Bernard (1975). "6.18". Theory and application of digital signal processing. Englewood Cliffs, N.J.: Prentice-Hall. pp. 415. ISBN 0-13-914101-4.
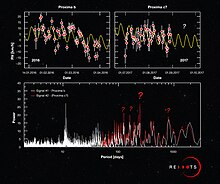
- ^ "Do-it-yourself Science — is Proxima c hiding in this graph?". www.eso.org. Retrieved 11 September 2017.
- ^ 엥겔버그, S.(2008) 디지털 신호 처리: 실험 접근법, 스프링거, 제7장 56호
- ^ Welch, Peter D. (June 1967). "The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms". IEEE Transactions on Audio and Electroacoustics. AU-15 (2): 70–73. Bibcode:1967ITAE...15...70W. doi:10.1109/TAU.1967.1161901.
- ^ "Welch's power spectral density estimate - MATLAB pwelch".
- ^ 스펙트럼 그림, NIST 엔지니어링 통계 핸드북.
- ^ "DATAPLOT Reference Manual" (PDF). NIST.gov. National Institute of Standards and Technology (NIST). 1997-03-11. Retrieved 2019-06-14.
The spectral plot is essentially a “smoothed” periodogram where the smoothing is done in the frequency domain.
추가 읽기
- Box, George E. P.; Jenkins, Gwilym M. (1976). Time series analysis: Forecasting and control. San Francisco: Holden-Day.
- Scargle, J.D. (December 15, 1982). "Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data". Astrophysical Journal, Part 1. 263: 835–853. Bibcode:1982ApJ...263..835S. doi:10.1086/160554.
- Vaughan, Simon; Uttley, Philip (2006). "Detecting X-ray QPOs in active galaxies". Advances in Space Research. 38 (7): 1405–1408. arXiv:astro-ph/0506456. Bibcode:2006AdSpR..38.1405V. doi:10.1016/j.asr.2005.02.064.
 것이다(
것이다(
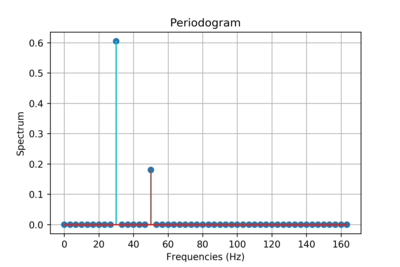
 T
T

![{\displaystyle X_{1/T}\left({\tfrac {k}{NT}}\right)=\sum _{n=-\infty }^{\infty }\underbrace {T\cdot x(nT)} _{x[n]}\cdot e^{-i2\pi {\frac {kn}{N}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42bc1db83e080d742c799757caeedd23f27e85e2)

![{\displaystyle X_{1/T}\left({\tfrac {k}{NT}}\right)=\underbrace {\sum _{n}x_{_{N}}[n]\cdot e^{-i2\pi {\frac {kn}{N}}},} _{DFT}\quad \scriptstyle {{\text{(sum over any }}n{\text{-sequence of length }}N)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ef67a80f0574d2ce253c49d95beadd57939479)

![{\displaystyle x_{_{N}}[n]\ \triangleq \sum _{m=-\infty }^{\infty }x[n-mN].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c541c26e08566dcc09b4e8c877f513c81eeb5cc2)
![{\displaystyle S\left({\tfrac {k}{NT}}\right)=\left|\sum _{n}x_{_{N}}[n]\cdot e^{-i2\pi {\frac {kn}{N}}}\right|^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7818ab0cf4ebd8675f7b053b6a15cf2273c93129)