슬라이드 규칙

슬라이드 규칙은 곱셈, 나눗셈, 지수, 근, 로그 및 삼각법과 같은 수학적 연산을 평가하기 위한 슬라이딩 가능한 눈금자로 구성된 수동 기계 계산기입니다. 가장 간단한 아날로그 컴퓨터 중 하나입니다.^[1][2]

슬라이드 규칙은 다양한 스타일로 존재하며 일반적으로 선형, 원형 또는 원통형으로 나타납니다. 항공 또는 금융과 같은 전문 분야를 위해 제조된 슬라이드 규칙은 일반적으로 해당 분야에 특화된 계산에 도움이 되는 추가 스케일을 특징으로 합니다. 슬라이드 규칙은 응용 프로그램별 계산에 사용되는 노모그램과 밀접한 관련이 있습니다. 이름과 모양이 표준 눈금자와 비슷하지만 슬라이드 규칙은 길이를 측정하거나 직선을 그리는 데 사용되지 않습니다. 또한 주판을 사용하는 것과 같이 일반적으로 다른 방법을 사용하여 수행되는 덧셈이나 뺄셈을 위해 설계되지 않았습니다. 표준 선형 슬라이드 규칙의 최대 정확도는 약 3개의 소수 유효숫자인 반면, 과학적 표기법은 결과의 크기 순서를 추적하는 데 사용됩니다.

영국의 수학자이자 성직자인 윌리엄 오드레드 목사와 다른 사람들은 존 네이피어의 로그에 대한 새로운 연구에 기초하여 17세기에 슬라이드 규칙을 개발했습니다. 종이로 평가하는 것보다 더 빠르고 오류가 적은 계산을 만들었습니다. 과학용 포켓 계산기가 등장하기 전에는 이공계에서 가장 많이 사용되는 계산 도구였습니다.^[3] 슬라이드 규칙의 사용 편의성, 가용성 및 저렴한 비용으로 인해 전자 컴퓨터가 점차 도입되는 1950년대와 1960년대까지 사용이 계속 증가했습니다. 1974년경 휴대용 전자 과학 계산기의 도입으로 슬라이드 규칙은 대부분 쓸모없게 되었고, 대부분의 공급업체는 사업을 중단했습니다.

미국에서는 슬라이드 규칙을 구어체로 슬립스틱이라고 부릅니다.^[4][5]

기본개념

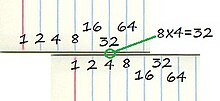
각 눈금자의 눈금에는 다양한 수학 함수의 미리 계산된 출력으로 레이블이 지정된 눈금이 있으며, 각 함수의 입력으로 눈금자의 위치에서 매핑되는 룩업 테이블 역할을 합니다. 미리 계산된 함수를 사용하여 단순 덧셈이나 뺄셈으로 줄일 수 있는 계산은 두 눈금자를 정렬하고 대략적인 결과를 읽음으로써 해결할 수 있습니다.

예를 들어, 로그 눈금자 하나에 곱할 숫자를 다른 눈금자의 시작과 정렬하여 로그를 합할 수 있습니다. 그런 다음 곱의 로그의 법칙을 적용하여 두 숫자의 곱을 읽을 수 있습니다. 더 정교한 슬라이드 규칙은 제곱근, 지수, 로그 및 삼각 함수와 같은 다른 계산을 수행할 수 있습니다.

사용자는 라벨링된 눈금 사이를 정신적으로 보간함으로써 결과에서 소수점의 위치를 추정할 수 있습니다. 과학적 표기법은 더 정확한 계산을 위해 소수점을 추적하는 데 사용됩니다. 계산에서 덧셈과 뺄셈 단계는 일반적으로 슬라이드 규칙이 아닌 정신적으로 또는 종이로 수행됩니다.

구성 요소들

대부분의 슬라이드 규칙은 세 부분으로 구성됩니다.

• 프레임 또는 베이스 – 같은 길이의 스트립 두 개가 간격을 두고 평행하게 고정됩니다.
• 슬라이드 – 프레임과 연동된 중앙 스트립으로 프레임에 대해 길이 방향으로 움직일 수 있습니다.
• 러너 또는 유리 – "커서"라고도 알려진 헤어라인이 있는 외부 슬라이딩 조각.

일부 슬라이드 규칙("이중" 모델)은 규칙과 슬라이드 스트립의 양쪽에 눈금이 있고, 다른 것은 외부 스트립의 한쪽과 슬라이드 스트립의 양쪽에 눈금이 있으며(일반적으로 빼내고 뒤집어서 재삽입할 수 있음), 다른 것은 한쪽에만 눈금이 있습니다("단순" 규칙). 수직 정렬선이 있는 슬라이딩 커서는 서로 인접하지 않거나 양면 모형에서 규칙의 다른 면에 있는 눈금의 해당 점을 찾는 데 사용됩니다. 커서는 척도에 중간 결과를 기록할 수도 있습니다.

수십 년

척도는 10년 단위로 그룹화될 수 있으며, 각 10년은 10의 비율(즉, 10에서ⁿ 10ⁿ⁺¹ 사이의 범위)에 걸쳐 있는 숫자의 범위에 해당합니다. 예를 들어, 1에서 10까지의 범위는 단일 10년이고 10에서 100까지의 범위는 또 다른 10년입니다. 따라서 10년 척도(C 및 D로 명명됨)의 범위는 슬라이드 규칙의 전체 길이에 걸쳐 1에서 10까지인 반면, 10년 척도(A 및 B로 명명됨)의 범위는 슬라이드 규칙의 전체 길이에 걸쳐 1에서 100까지입니다.

작동

로그 눈금

다음 로그 항등식은 곱셈과 나눗셈의 연산을 각각 덧셈과 뺄셈으로 변환합니다.

곱셈

로그 스케일이 2개인 경우 $x$ ${\displaystyle$ x$}$에 대한 하단 스케일의 레이블에서 시작하도록 상단 스케일을 위치시키는 행위는 ${\displaystyle \mathrm{로그}}$⁡(x) ${\displaystyle$\log$($x)}의 거리만큼 상단 로그 스케일을 이동하는 것에 해당합니다. This aligns each top scale's number ${\displaystyle y}$ at offset ${\displaystyle \log(y)}$ with the bottom scale's number at position ${\displaystyle \log(x)+\log(y)}$. Because ${\displaystyle \log(x)+\log(y)=\log(x\times y)}$, $그$ 위치의 맨 아래 눈금 표시는 ${\displaystyle x}$ ×${\displaystyle }$y ${\displaystyle$ x$\times$ y$}$에 해당합니다$.$ 예를 들어 x=2와 y=3의 경우 맨 아래 눈금의 2에서 시작하도록 위쪽 눈금을 지정하면 아래쪽 눈금에서 3×2=6의 곱셈 결과를 읽을 수 있습니다.

위의 예는 10년 이내에 있지만, 사용자는 몇 십 년을 다룰 때 추가적인 제로를 정신적으로 설명해야 합니다. 예를 들어, 7×2=14에 대한 답은 먼저 맨 아래 눈금의 2 위에 시작하도록 맨 위 눈금을 지정한 다음 맨 아래 2 decade 눈금에서 표시 1.4를 읽어 7이 맨 위 눈금에 있는 경우:

그러나 7은 두 번째 수 집합 위에 있으므로 그 수는 10을 곱해야 합니다. 따라서 정답이 직접 1.4를 읽어도 정답은 1.4×10 = 14입니다.

더 큰 숫자를 가진 예를 들어, 88×20을 곱하기 위해 맨 위 눈금은 맨 아래 눈금의 2에서 시작하도록 다시 배치됩니다. 2는 20을 나타내기 때문에 해당 척도의 모든 숫자에 10을 곱합니다. 따라서 두 번째 숫자 집합에 있는 모든 답에 100을 곱합니다. 최상위 척도의 8.8은 88을 나타내기 때문에 답에 추가적으로 10을 곱해야 합니다. 정답은 바로 1.76입니다. 100을 곱한 다음 10을 곱하면 실제 답은 1,760이 나옵니다.

일반적으로 맨 위에 있는 1은 맨 아래에 있는 요인으로 이동되고 다른 요인이 맨 위에 있는 아래에서 답을 읽습니다. 이는 1 표시로부터의 거리가 표시된 값의 로그에 비례하기 때문에 효과가 있습니다.

나누기

아래 그림은 5.5/2의 계산을 보여줍니다. 맨 위 눈금의 2는 맨 아래 눈금의 5.5 위에 놓입니다. 그런 다음 결과 몫인 2.75를 최상위 척도의 1 아래에서 읽을 수 있습니다.

나눗셈을 하는 방법은 여러 가지가 있는데, 여기에 제시된 방법은 최종 결과가 규모를 벗어날 수 없다는 장점이 있습니다. 왜냐하면 어느 한쪽 끝에 1을 사용하는 것을 선택할 수 있기 때문입니다.

식의 분자와 분모에 여러 요인이 포함된 보다 복잡한 계산을 통해 나눗셈과 곱셈을 번갈아 사용하여 눈금의 이동을 최소화할 수 있습니다. 따라서 5.5×3/2는 5.5/2×3으로 계산되며, 결과 8.25는 5.5/2의 중간 결과를 등록할 필요 없이 위 그림의 최상위 척도에서 3 아래에서 읽을 수 있습니다.

기타계량

일부 슬라이드 규칙은 로그 눈금 외에도 다른 보조 눈금에 암호화된 다른 수학 함수를 가지고 있습니다. 가장 일반적인 것은 삼각법, 일반적으로 사인 및 접선, 일반 로그(로그10)(승수 척도의 값 로그를 취하는 경우), 자연 로그(ln) 및 지수(e^x) 척도입니다. 다른 기능은 쌍곡선 함수를 계산하기 위한 척도를 제공합니다. 선형 규칙에서 척도와 레이블은 매우 표준화되어 있으며, 일반적으로 척도가 포함된 항목과^[6] 순서에 따라서만 변동이 발생합니다.

C, D	단일 decade 로그 눈금, 동일한 길이의 단일 섹션, 곱셈과 나눗셈을 위해 함께 사용되며, 일반적으로 그 중 하나는 다른 계산을 위해 다른 눈금과 결합됩니다.
AB	제곱근과 제곱근을 찾는 데 사용되는 두 개의 구간이 각각 C와 D 눈금의 길이의 절반인 10년 로그 눈금
K	세제곱근과 세제곱수를 찾는 데 사용되는 세제곱수는 각각 C와 D 눈금의 길이의 1/3인 세제곱수 척도입니다.
CF, DF	C와 D 눈금의 접힌 버전은 통일성이 아닌 pi(π)에서 시작합니다. 이 두 가지 경우에 편리합니다. 먼저 사용자가 제품이 10에 가까울 것이라고 추측하고 제품이 10보다 약간 작을 것인지 또는 10보다 약간 클 것인지 확신하지 못할 때 접힌 눈금은 눈금에서 벗어날 가능성을 피합니다. 둘째, 시작을 10의 제곱근이 아닌 π으로 함으로써 (이공식에서 일반적으로 사용되는 것처럼) π으로 곱하거나 나누는 것을 단순화합니다.
CI, DI, CIF, DIF	역수를 단순화하기 위해 사용되는, 오른쪽에서 왼쪽으로 실행되는 역수 눈금1 ⁄x) 단계
S	C(또는 D) 척도에서 사인과 코사인을 찾는 데 사용됩니다.
T, T1, T2	C 및 CI(또는 D 및 DI) 눈금에서 접선 및 코탄젠트를 찾는 데 사용됩니다.
R1, R2	제곱근 눈금 – 커서를 R1 또는 R2의 $임의$의 값 r ${\displaystyle r}$로 설정하고, DF 눈금의 커서 ${\displaystyle {아래}^{}}$에서$$πr 2 ${\displaystyle${\$pi$}r^{2}($반지름$ r $displaystyle$ r}의 원 영역)를 찾습니다.
ST, SRT	작은 각도와 도-라디안 변환의 정향 및 접선에 사용됩니다.
Sh, Sh1, Sh2	C(또는 D) 척도에서 쌍곡선 사인을 찾는 데 사용됩니다.
차	C(또는 D) 척도에서 쌍곡선 코사인을 찾는 데 사용됩니다.
그	C(또는 D) 척도에서 쌍곡 접선을 찾는 데 사용됨
L	덧셈, 뺄셈 및 (C 및 D 척도와 함께) 10의 밑수 10 로그 및 거듭제곱을 찾는 데 사용되는 선형 척도
LL0N (or LL/N) and LLN	임의의 기저 및 임의의 지수의 로그 작업을 위해 log-log $folded{\displaystyle {}^{}}$ e${\displaystyle {}^{}}$- ${\displaystyle x^{}}$ ${\$ e$^{-x}}$ 및$$ ${\displaystyle x^{}}$ ${\$ 척도$$. 이러한 유형의 4, 6 또는 8 척도가 일반적으로 표시됩니다.
Ln	자연($기본{\displaystyle }$ ${\displaystyle e$ 로그 및 ${\displaystyle {ex}^{}}$ ${\$를 찾기 위해 C 및 D 눈금과 함께 사용되는 선형 스케일
P	$1{\displaystyle \sqrt{\mathrm{}}}$- ${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{{2\mathrm{}}^{}}}$ ${\$ ~ (1$$) 피타고라스 정리를 풀고 (2) 작은 각도에 대한 코사인을 정확하게 결정합니다 (S척도로)

Kuffel and Esser (K&E) 4181-3 슬라이드 규칙의 앞뒤 눈금

1931년 길슨이 만든 이진 슬라이드 규칙은 분수에 한정된 덧셈과 뺄셈 기능을 수행했습니다.^[7]

뿌리와 힘

단십진법(C와 D), 복십진법(A와 B), 복십진법(K)의 음계가 있습니다. $x{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$ x$^{2}}$를 계산하려면$$예를 들어 D 눈금에서 x를 찾고 A 눈금에서 제곱을 읽습니다. 이 공정을 뒤집으면 제곱근을 찾을 수 있으며, 이와 유사하게 거듭제곱 3, 1/3, 2/3, 3/2를 찾을 수 있습니다. 밑면인 x가 눈금에서 두 곳 이상 발견되면 주의해야 합니다. 예를 들어 A 척도에는 두 개의 9가 있습니다. 9의 제곱근을 찾으려면 첫 번째 것을 사용하고 두 번째 것은 90의 제곱근을 제공합니다.

${\displaystyle {xy}^{}}$ ${\$ 문제의$$ 경우 LL 척도를 사용합니다. LL 눈금이 여러 개 있는 경우 x가 표시된 눈금을 사용합니다. 먼저 C 척도의 가장 왼쪽에 있는 1을 LL 척도의 x와 정렬합니다. 그런 다음 C 눈금에서 y를 구하고 x가 표시된 LL 눈금으로 내려갑니다. 그 눈금은 답을 나타냅니다. y가 "스케일에서 벗어난" 경우 ${\displaystyle x^{}}$ y${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$ ${\$를 찾고 위에서 설명한 대로 A 및 B 눈금을 사용하여 제곱합니다. 또는 C 척도에서 가장 오른쪽에 있는 1을 사용하고 다음으로 높은 LL 척도에서 답을 읽습니다. 예를 들어, C 척도의 맨 오른쪽 1을 LL2 척도의 2로 정렬하고, C 척도의 3을 LL3 척도의 8로 정렬합니다.

C/D 및 A/B 눈금만 있는 슬라이드 규칙을 사용하여 입방근을 추출하려면 B 커서의 1을 A 눈금의 기본 번호와 맞춥니다(A 눈금의 절반 아래와 위쪽을 구분할 때는 항상 주의하십시오). C 커서의 1에 해당하는 D 눈금의 숫자가 B 커서의 숫자와 A 눈금의 기본 숫자에 해당하는 숫자가 될 때까지 슬라이드를 누릅니다(예: A 8, B 2, C 1, D 2; A 27, B 3, C 1, D 3.)

이차방정식의 근

Quadratic equations of the form ${\displaystyle ax^{2}+bx+c=0}$ can be solved by first reducing the equation to the form ${\displaystyle x^{2}-px+q=0}$ (where ${\displaystyle p=-b/a}$ and ${\displaystyle q=c/a}$), 그런 다음 C 척도의 인덱스("1")를 D 척도의$$ $q{\displaystyle }$ ${\displaystyle q}$ 값에 정렬합니다. 그런 다음 CI 및 D 눈금의 숫자가 $p{\displaystyle }$ ${\displaystyle$ p$}$까지 합산되는 위치가 발견될 때까지 규칙을 따라 커서를 이동합니다$.$ 이 두 값은 방정식의 근입니다.

삼각법

S, T 및 ST 척도는 각도에 대한 트리거 함수 및 트리거 함수의 배수에 사용됩니다.

약 5.7 ~ 90도 각도의 경우 S 눈금과 C(또는 D) 눈금을 비교하여 S 눈금을 찾을 수 있습니다. (많은 폐쇄체 규칙에서 S 눈금은 대신 A 및 B 눈금과 관련이 있으며 약 0.57 ~ 90도 각도를 포함합니다. 다음을 적절하게 조정해야 합니다.) S 척도에는 반대 방향으로 실행되는 두 번째 각도 집합(때로는 다른 색)이 있으며 코사인에 사용됩니다. 접선은 T 척도와 45도 미만의 각도에 대한 C(또는 D) 척도를 비교하여 발견됩니다. 45도 이상의 각도의 경우 CI 스케일이 사용됩니다. ${\displaystyle k}$ ${\displaystyle \sin }$ ⁡ x${\displaystyle$k\sin x}와 같은 일반적인 양식은 C 척도 인덱스를 k로 설정하면 S 척도의 x에서 D 척도의 결과로 바로 읽을 수 있습니다. 5.7도 미만의 각도에 대해서는 사인, 접선 및 라디안이 거의 같고 ST 또는 SRT(사인, 라디안 및 접선) 척도에서 발견되거나 57.3도/라디안으로 간단히 나뉩니다. 역삼각함수는 공정을 반대로 함으로써 발견됩니다.

많은 슬라이드 규칙에는 S, T, ST 눈금이 도수와 분으로 표시되어 있습니다(예: 일부 Kuffel 및 Esser 모델(예: Doric duplex 5" 모델), 후기 모델 Teledyne-Post Manheim 유형 규칙). 이른바 데시트리그 모델은 도수의 십진분수를 대신 사용합니다.

로그 및 지수

기본-10 로그와 지수는 선형인 L 척도를 사용하여 구합니다. 일부 슬라이드 규칙에는 베이스 e에 대한 Ln 척도가 있습니다. 다른 기저에 대한 로그는 수의 거듭제곱을 계산하는 절차를 거꾸로 하여 계산할 수 있습니다. 예를 들어 log2 값은 LL2 척도에 2가 있는 C 척도의 맨 왼쪽 또는 맨 오른쪽 1을 일렬로 세우고 해당 LL 척도에서 로그를 계산할 숫자를 찾고 C 척도의 log2 값을 읽음으로써 결정할 수 있습니다.

덧셈과 뺄셈

덧셈과 뺄셈은 일반적으로 슬라이드 규칙에서 수행되지 않지만 다음 두 가지 방법 중 하나를 사용하여 수행할 수 있습니다.^[8]

1. 덧셈과 뺄셈을 나눗셈으로 변환(C와 D 또는 유사한 척도에 필요):
   • 두 변수의 몫 더하기(또는 빼기) 1배의 약수가 그들의 합(또는 차이)과 같다는 항등식을 이용합니다.
     $${\displaystyle {\begin{aligned}\left ({\frac {x}{y}}+1\right)y&=x+y\,{\text{(addition)}},\\\left ({\frac {x}{y}}-1\right)y&=x-y\,{\text{(subt)}}}입니다.\end{align}}}$$

     
   • 이는 GRAPE(Gravity Pipe) 슈퍼컴퓨터나 은닉 마르코프 모델과 같은 특수 컴퓨터 응용 분야에서 로그 수 체계를 갖는 고속 전자 회로에 사용되는 가감법과 유사합니다.
2. 선형 L 척도 사용(일부 모델에서 사용 가능):
   • 커서를 오른쪽(추가용) 또는 왼쪽(감산용)으로 슬라이드하고 슬라이드를 0으로 되돌린 후 결과를 읽을 수 있습니다.

일반화

(거의) 엄격하게 단조로운 척도를 사용하여 한 번의 움직임으로 다른 계산도 할 수 있습니다.^[9][10] 예를 들어, 등식 ${\displaystyle \frac{1}{}}$ x${\displaystyle }$+ ${\displaystyle \frac{1}{}}$ ${\displaystyle y}$ = ${\displaystyle \frac{1}{}}$ ${\$displaystyle {\frac {1}{x}+{\frac {1}{y}}={\frac {1}{z}}(병렬 저항, 고조파 평균 등의 calcul)에 대해 역수 스케일을 사용할 수 있으며, x 2 + y 2 = z 2 {\displaystyle x^{2}+y^{2} = z^{2}}를 푸는 데 2차 스케일을 사용할 수 있습니다.

물리설계

표준 선형 규칙

슬라이드 규칙의 너비는 척도의 공칭 너비로 인용됩니다. 가장 일반적인 "10인치" 모델의 체중계는 미터법 표준으로 만들어졌기 때문에 실제로는 25cm이지만 일부 규칙에서는 결과가 넘쳐날 때 조작을 단순화하기 위해 약간 확장된 체중계를 제공합니다. 포켓 규칙은 일반적으로 5인치(12cm)입니다. 폭이 2-3미터(야드)인 모형은 강의실에 교수 목적으로 걸 수 있도록 제작되었습니다.^[11]

일반적으로 분할은 두 개의 유효숫자의 정밀도로 눈금을 표시하고 사용자는 세 번째 숫자를 추정합니다. 일부 고급 슬라이드 규칙에는 표시를 더 쉽게 볼 수 있는 돋보기 커서가 있습니다. 이러한 커서는 판독의 정확도를 효과적으로 두 배로 높여 10인치 슬라이드 규칙이 20인치 모델과 마찬가지로 작동할 수 있습니다.

그 외에도 다양한 편의점이 개발되었습니다. 삼각형 눈금은 때때로 이중 레이블로 표시되며 검은색과 빨간색으로 상호 보완각이 있는 소위 "Darmstadt" 스타일입니다. 양면 슬라이드 규칙은 종종 뒷면의 눈금 일부를 복제합니다. 스케일은 종종 더 높은 정확도를 얻기 위해 "분할"됩니다.^{[further explanation needed]}

원형 슬라이드 규칙

원형 슬라이드 규칙은 두 가지 기본 유형으로 제공됩니다. 하나는 커서가 두 개이고 다른 하나는 접시와 커서가 하나 있습니다. 듀얼 커서 버전은 다이얼을 중심으로 회전할 때 커서 사이의 일정한 각도를 유지하여 곱셈과 나눗셈을 수행합니다. 1배 커서 버전은 눈금을 적절하게 정렬하여 표준 슬라이드 규칙과 더 유사하게 작동합니다.

원형 슬라이드 규칙의 기본적인 장점은 도구의 가장 넓은 치수가 약 3배(즉, π에 의해) 감소했다는 것입니다. 예를 들어, 10 cm 원형의 경우 최대 정밀도는 31.4 cm 일반 슬라이드 규칙과 거의 같습니다. 또한 순환 슬라이드 규칙을 사용하면 "스케일 외" 계산이 제거됩니다. 왜냐하면 스케일은 "랩"하도록 설계되었기 때문입니다. 결과가 1.0에 가까울 때는 방향을 바꿀 필요가 없기 때문입니다. 규칙은 항상 스케일입니다. 그러나 S, T 및 LL과 같은 비주기적 비 나선 척도의 경우 스케일 폭이 좁아져 끝 마진이 발생할 여지가 있습니다.^[12]

원형 슬라이드 규칙은 기계적으로 더 거칠고 부드럽게 움직이지만 스케일 정렬 정밀도는 중앙 피벗의 중심에 민감합니다. 피벗의 중심에서 1분 0.1mm(0.0039인치) 정도만 벗어나면 0.2mm(0.0079인치) 최악의 경우 정렬 오류가 발생할 수 있습니다. 피벗은 얼굴과 커서가 긁히는 것을 방지합니다. 가장 높은 정확도의 눈금이 외부 링에 배치되어 있습니다. 고급 순환 규칙은 "분할" 척도가 아니라 로그-오브-로그 척도와 같이 더 복잡한 작업을 위해 나선형 척도를 사용합니다. 8인치 프리미엄 원형 규칙 하나에 50인치 나선형 로그 로그 스케일이 있었습니다. 1970년경, B.C.의 저렴한 모델. 보이킨(모델 510)은 50인치 C-D(곱셈)와 로그 눈금을 포함한 20개의 눈금이 특징이었습니다. 로타 룰은 커서에 마찰 브레이크를 장착했습니다.

원형 슬라이드 규칙의 주요 단점은 접시를 따라 도형을 찾기 어렵고 눈금 수가 제한되어 있다는 것입니다. 원형 슬라이드 규칙의 또 다른 단점은 덜 중요한 척도가 중심에 가깝고 정밀도가 낮다는 것입니다. 대부분의 학생들은 선형 슬라이드 규칙에서 슬라이드 규칙 사용을 배웠고, 전환해야 할 이유를 찾지 못했습니다.

전 세계적으로 매일 사용되는 슬라이드 규칙 중 하나는 E6B입니다. 이것은 1930년대에 항공기 조종사들이 추측을 돕기 위해 처음 만들어진 순환 슬라이드 규칙입니다. 프레임에 인쇄된 눈금의 도움으로 시간, 거리, 속도 및 온도 값 변환, 나침반 오류 및 연료 사용량 계산과 같은 기타 작업에도 도움이 됩니다. 소위 "기도 바퀴"는 여전히 비행 상점에서 사용할 수 있으며 여전히 널리 사용되고 있습니다. GPS가 항공 항법을 위한 추측 항법의 사용을 줄이고 휴대용 계산기가 그 기능의 많은 부분을 대체한 반면, E6B는 여전히 기본 또는 백업 장치로 널리 사용되고 있으며 대부분의 비행 학교는 학생들에게 어느 정도의 사용 숙련도를 요구하고 있습니다.

비율 휠은 그래픽 디자인에서 종횡비를 계산하는 데 사용되는 간단한 원형 슬라이드 규칙입니다. 내부 휠과 외부 휠에 원래 크기 값과 원하는 크기 값을 일렬로 배열하면 작은 창에 비율이 백분율로 표시됩니다. 컴퓨터 레이아웃이 등장한 이후로 그렇게 흔하지는 않지만 여전히 만들어지고 사용되고 있습니다.^{[citation needed]}

1952년 스위스 시계 회사인 브라이틀링은 비행 계산에 특화된 원형 슬라이드 규칙이 통합된 조종사 손목시계인 브라이틀링 나비티머를 선보였습니다. 브레이틀링(Breitling)이 "항법 컴퓨터"로 지칭한 Navitimer 순환 규칙은 항공 속도, 상승/하강 속도/시간, 비행 시간, 거리 및 연료 소비 기능과 킬로미터-나티칼 마일 및 갤런-리터 연료량 변환 기능을 포함했습니다.

• 

  주식회사 Concise에서 만든 간단한 원형 슬라이드 규칙, 역, 제곱, 입방 스케일만 있는 일본 도쿄. 반대쪽에는 38미터/제국 변환 인자의 편리한 목록이 있습니다.

• 

  두 바늘이 서로 뭉쳐져 있기 때문에 하나의 커서 슬라이드 규칙으로 작동하는 포켓 워치처럼 구축된 러시아 원형 슬라이드 규칙

• 

  링에 내장된 2축 슬라이드 규칙

• 

  두 개의 커서가 있는 피켓 원형 슬라이드 규칙(4.25인치/10.9cm 너비) 후진에는 추가 눈금과 하나의 커서가 있습니다.

• 

  원형 슬라이드 규칙이 있는 브레이틀링 Navitimer 손목시계

• 

  보이킨 로타 룰 모델 510의 정면

• 

  보이킨 로타 룰 모델 510의 후면

• 

  스페리 4016 포켓 계산기

원통형 슬라이드 규칙

원통형 슬라이드 규칙에는 풀러 계산기, 오티스 킹 및 바이그레이브 슬라이드 규칙과 같은 나선형 눈금이 있는 규칙과 Thacher 및 일부 Loga 모델과 같은 막대가 있는 규칙의 두 가지 주요 유형이 있습니다. 어느 경우든 직선 또는 원형 규칙에 의해 제공되는 것보다 훨씬 더 긴 스케일 및 따라서 잠재적으로 더 큰 정밀도가 장점입니다.

• 

  풀러 계산기, 1928

• 

  오티스 킹 모델 K

• 

  중대한 슬라이드 규칙에 따라

• 

  1890년경 교사 슬라이드 규칙

자재

전통적으로 슬라이드 규칙은 유리와 금속의 커서가 있는 마호가니나 박스우드와 같은 단단한 나무로 만들어졌습니다. 적어도 하나의 고정밀 기구는 강철로 만들어졌습니다.

1895년 일본 회사인 헤미는 셀룰로이드를 입힌 대나무로 슬라이드 룰을 만들기 시작했는데, 이는 차원적으로 안정적이고, 강하고, 자연적으로 스스로 윤활할 수 있는 장점을 가지고 있었습니다. 이러한 대나무 미끄럼틀 규칙은 1933년 9월 스웨덴에서 도입되었으며,^[13] 아마도 독일에서는 조금 더 일찍 도입되었을 것입니다.

비늘은 또한 셀룰로이드 또는 기타 폴리머로 만들어졌거나 알루미늄으로 인쇄되었습니다. 나중에 커서는 아크릴이나 폴리카보네이트, 때로는 테프론 베어링 표면으로 성형되었습니다.

모든 프리미엄 슬라이드 규칙에는 숫자와 눈금이 깊게 새겨진 다음 페인트나 기타 수지로 채워졌습니다. 도장되거나 각인된 슬라이드 규칙은 표식이 마모되거나 화학적으로 손상될 수 있기 때문에 열등한 것으로 간주되었습니다. 그럼에도 불구하고, 미국의 슬라이드 규칙 회사인 피켓은 인쇄된 눈금 규칙만 만들었습니다. 프리미엄 슬라이드 규칙에는 규칙이 실수로 무너지지 않도록 영리한 기계적 캐치, 눈금과 커서가 태블릿 상판에 마찰되지 않도록 보호하는 범퍼 등이 포함되었습니다.

역사

미끄럼틀 규칙은 존 네이피어가 대수의 개념을 발표한 직후인 1620년에서 1630년 사이에 발명되었습니다. 1620년 옥스퍼드의 에드먼드 군터는 단일 로그 눈금을 가진 계산기를 개발했습니다. 추가적인 측정 도구를 사용하면 곱하기와 나누기에 사용할 수 있습니다.^[14] 1622년에 캠브리지의 William Owred는 두 개의 손에 들고 쓰는 Gunter 규칙을 결합하여 인식할 수 있는 현대 슬라이드 규칙인 장치를 만들었습니다.^[15] 우드레드는 한때 그의 제자였던 리처드 들라메인과 윙게이트의 이전 주장과 함께 우선순위에 대한 독설 논란에 휘말리게 되었습니다. 오드레드의 아이디어는 1632년과 1653년에 그의 학생 윌리엄 포스터의 출판물에 발표되었습니다.

1677년에 헨리 코게샬은 코게샬 슬라이드 규칙이라고 불리는 목재 계량을 위한 2피트 접기 규칙을 만들었고, 이는 슬라이드 규칙의 사용을 수학적 탐구를 넘어 확장시켰습니다.

1722년 워너는 2,3십년 눈금을 도입했고, 1755년 에버라드는 반전 눈금을 도입했습니다. 이 모든 눈금을 포함하는 슬라이드 규칙은 보통 "다상" 규칙으로 알려져 있습니다.

1815년에 피터 마크 로젯은 로그의 로그를 나타내는 눈금을 포함하는 로그 슬라이드 규칙을 발명했습니다. 이를 통해 사용자는 근과 지수를 포함하는 계산을 직접 수행할 수 있습니다. 이것은 특히 분수의 거듭제곱에 유용했습니다.

1821년에, Nathaniel Bowditch는 American Practical Navigator에서 "슬라이딩 규칙"을 설명했는데, 이 규칙은 고정된 부분에 척도화된 삼각 함수를 포함하고, 항해 문제를 해결하는 데 사용되는 슬라이더에 일련의 로그사인과 로그탠을 포함합니다.

1845년 글래스고의 폴 카메론(Paul Cameron)은 항해 질문에 대답할 수 있는 항해 슬라이드 규칙을 도입했습니다. 여기에는 태양과 주요 별의 올바른 상승과 하강이 포함됩니다.^[16]

모던폼

슬라이드 규칙의 더 현대적인 형태는 1859년 프랑스 포병 중위 아메데 만하임에 의해 만들어 졌는데, 그는 국가적 명성을 가진 회사에 의해 그의 규칙이 만들어졌고 프랑스 포병대에 의해 채택되었습니다. 만하임의 규칙은 이전의 범용 슬라이드 규칙보다 더 쉽게 사용할 수 있도록 크게 두 가지 수정이 있었습니다. 그런 규칙들은 A, B, C, D의 네 가지 기본 척도를 가지고 있었고, D는 유일한 10년 대수 척도였고, C는 A와 B처럼 20년을 가지고 있었습니다. 대부분의 연산은 A와 B 척도로 이루어졌으며 D는 제곱근과 제곱근을 찾는 데만 사용되었습니다.

만하임은 C 척도를 10년 단위 척도로 변경하고 A와 B 대신 C와 D로 대부분의 연산을 수행했습니다. C와 D 척도는 단 10년이므로 더 정확하게 읽을 수 있으므로 규칙의 결과가 더 정확할 수 있습니다. 또한 그 변화는 더 큰 계산의 일부로 제곱근과 제곱근을 더 쉽게 포함할 수 있게 했습니다. Mannheim의 규칙은 이전의 거의 모든 규칙과 달리 커서가 있으므로 모든 척도를 규칙 너비에 걸쳐 쉽고 정확하게 비교할 수 있습니다. "만하임 규칙"은 19세기 후반의 표준 슬라이드 규칙 배열이 되었고 슬라이드 규칙 시대 내내 일반적인 표준으로 유지되었습니다.

19세기 후반의 엔지니어링 직업의 성장은 슬라이드 규칙의 광범위한 사용을 촉진하여 유럽에서 시작하여 결국 미국에서도 자리를 잡게 되었습니다. 이중 규칙은 1891년 윌리엄 콕스에 의해 발명되었고 뉴욕의 카이펠과 에서 회사에 의해 생산되었습니다.^[17][18]

1881년에 미국 발명가 에드윈 타허는 그의 원통형 규칙을 소개했습니다. 원통형 규칙은 표준 선형 규칙보다 훨씬 더 긴 축척을 가지고 있어서 더 높은 정밀도로, 약 4-5개의 유효숫자로 계산할 수 있었습니다. 그러나, Thacher 규칙은 휴대가 불가능할 뿐만 아니라 꽤 비용이 많이 들기 때문에 기존 슬라이드 규칙보다 훨씬 더 제한된 숫자로 사용되었습니다.

천문학 작업에도 정밀한 계산이 필요했고, 19세기 독일에서는 한 관측소에서 약 2미터 길이의 강철 슬라이드 규칙이 사용되었습니다. 현미경이 부착되어 소수점 6자리까지 정확도를 높였습니다.^{[citation needed]}

1920년대에 소설가이자 기술자인 Nevil Shute 노르웨이(그는 그의 자서전을 슬라이드 룰이라고 불렀습니다)는 1924년부터 Vickers Ltd.의 영국 R100 비행선 설계에 대한 최고 계산원이었습니다. 각각의 가로 프레임에 대한 응력 계산은 2~3개월 동안 풀러의 원통형 슬라이드 규칙을 사용하는 한 쌍의 계산기(사람)에 의한 계산이 필요했습니다. 동시 방정식에는 최대 7개의 알 수 없는 양이 포함되어 있었고, 푸는 데 약 1주일이 걸렸고, 8개의 방사형 와이어 중 어느 것이 느슨한지 추측이 틀리고 느슨하다고 추측된 와이어 중 하나가 느슨하지 않으면 다른 슬랙 와이어 선택으로 반복해야 했습니다. 몇 달 동안의 노력 끝에, "진실은 밝혀지고 (그리고) 거의 종교적인 경험에 가까운 만족감을 만들어냈습니다."^[19]

1950년대와 1960년대에 걸쳐 슬라이드 규칙은 청진기가 의료계와 같은 방식으로 엔지니어 직업의 상징이었습니다.^[20]

Aluminium Pickett 브랜드 슬라이드 규칙은 Project Apollo 우주 임무에서 수행되었습니다. 버즈 올드린이 아폴로 11호를 타고 달에 함께 날아간 N600-ES 모델은 2007년 경매에서 팔렸습니다.^[21] 1970년 아폴로 13호에서 촬영된 N600-ES 모델은 국립항공우주박물관이 소유하고 있습니다.^[22]

일부 공학도들과 엔지니어들은 1970년대 중반까지도 캠퍼스에서 흔히 볼 수 있는 10인치 슬라이드 규칙을 벨트 홀스터에 가지고 다녔습니다. 포켓 디지털 계산기가 등장하기 전까지 학생들은 5인치 포켓 슬라이드 규칙을 가지고 다니면서 집이나 사무실에서^[23] 정밀 작업을 위해 10인치 또는 20인치 규칙을 지킬 수도 있었습니다.

2004년에 교육 연구원 데이비드 B. 셰어와 딘 C. Nataro는 로그를 예측하는 제품을 빠르게 계산하는 알고리즘인 prosthaphaeresis에 기반한 새로운 유형의 슬라이드 규칙을 고안했습니다. 그러나 초기 시제품 이상으로 하나를 구성하는 데는 실질적인 관심이 거의 없었습니다.^[24]

전문계산기

슬라이드 규칙은 종종 정밀도, 증명 계산, 엔지니어링, 내비게이션 등과 같이 사용 분야에 따라 다양한 정도로 전문화되어 왔으며, 일부 슬라이드 규칙은 매우 좁은 응용 분야에 매우 전문화되어 있습니다. 예를 들어, John Rabone & Sons 1892 카탈로그에는 측정으로부터 소의 무게를 추정할 수 있는 장치인 "측정 테이프 및 소 측정기"가 나열되어 있습니다.

사진 응용 프로그램에는 많은 전문 슬라이드 규칙이 있었습니다. 예를 들어, Hurter and Driffield의 액티노그래프는 하루의 시간, 연중 시간 및 위도로부터의 노출을 추정하기 위한 두 개의 슬라이드 박스우드, 황동 및 판지 장치였습니다.

다양한 형태의 엔지니어링, 비즈니스 및 은행을 위한 전문 슬라이드 규칙이 발명되었습니다. 이들은 종종 대출 계산, 최적 구매 수량 또는 특정 공학 방정식과 같은 특수 척도로 직접 표현되는 공통 계산을 가지고 있었습니다. 예를 들어, Fisher Controls 회사는 산업용 유량 제어 밸브의 적절한 크기를 선택하는 데 사용되는 방정식을 해결하는 데 적합한 맞춤형 슬라이드 규칙을 배포했습니다.^[25]

기상 서비스의 기상학자들은 상승하는 수소 또는 헬륨으로 채워진 파일럿 풍선으로부터 위쪽의 풍속을 결정하기 위해 파일럿 풍선 슬라이드 규칙을 사용했습니다.^[26]

E6-B는 조종사와 항해사가 사용하는 원형 슬라이드 규칙입니다.

배란일과 출산력을 추정하는 원형 슬라이드 규칙은 바퀴 계산기로 알려져 있습니다.^[27]

1962년에^[28] 발간된 국방부 간행물에는 원자폭탄의 주어진 수율로부터 폭발 효과, 과압 및 방사선 피폭을 계산하기 위한 특수 목적의 원형 슬라이드 규칙이 악명높게 포함되어 있었습니다.^[29]

• 

  E6-B 항공 컴퓨터

• 

  존 라본 & 선즈 1892년 소 게이지

• 

  허터와 드리필드의 액티노그래프

• 

  1914년에서 1940년 사이에 스위스 육군이 사용한 암호 슬라이드 규칙

• 

  희소 분수 덧셈

거절

슬라이드 규칙의 중요성은 1950년대에는 새롭고 드문 자원인 전자 컴퓨터가 1960년대 기술 종사자들에게 널리 보급되면서 줄어들기 시작했습니다.

슬라이드 규칙에서 벗어난 첫 단계는 상대적으로 저렴한 전자 데스크톱 과학 계산기의 도입이었습니다. 여기에는 1965년에 도입된 ^[30][31]Wang Laboratories LOCI-2와 1968년에 도입된 Hewlett-Packard HP 9100A가 포함됩니다.^[32] 이 두 가지는 모두 프로그래밍이 가능하고 지수 함수와 로그 함수를 제공했습니다. HP에는 삼각 함수(사인, 코사인, 탄젠트)와 쌍곡 삼각 함수도 있었습니다. HP는 시프트 및 가산 연산만을 사용하여 삼각 함수를 계산할 수 ^[33]있는 CORDIC(좌표 회전 디지털 컴퓨터) 알고리즘을 사용했습니다. 이 방법은 훨씬 더 작은 과학적 계산기의 개발을 촉진했습니다.

메인프레임 컴퓨팅과 마찬가지로 이러한 데스크톱 머신의 가용성은 슬라이드 규칙의 유비쿼터스 사용에 큰 영향을 미치지 않았습니다. 1970년대 중반에 저렴한 휴대용 과학 전자 계산기를 사용할 수 있게 될 때까지 이는 급격히 감소했습니다. 주머니 크기의 Hewlett-Packard HP-35 과학 계산기는 이러한 유형의 최초의 휴대용 기기였지만 1972년에 395달러가 들었습니다. 이것은 일부 공학 전문가들에게는 정당한 것이었지만, 대부분의 학생들에게는 너무 비쌌습니다.

1974년경, 저가의 휴대용 전자 과학 계산기는 슬라이드 규칙을 대부분 쓸모없게 만들기 시작했습니다.^{[34][35][36][37]} 1975년까지 기본 4기능 전자계산기는 50달러 미만으로 구입할 수 있었고, 1976년까지 TI-30 과학 계산기는 25달러 미만(129달러 인플레이션 조정)으로 판매되었습니다.

1980년은 텍사스에서 슬라이드 규칙을 사용하는 UIL (University Interscholastic League) 대회의 마지막 해였습니다.^{[citation needed]} UIL은 원래 1910년에 문학 행사를 관리하기 위해 조직되었지만 ^{[citation needed]}학교 스포츠 행사의 관리 기관이 되기도 했습니다.

전자 디지털 계산기와의 비교

그들의 전성기에도 슬라이드 규칙은 일반 대중들에게 결코 인기가 없었습니다.^[38] 덧셈과 뺄셈은 슬라이드 규칙에서 잘 지원되지 않는 연산이며, 슬라이드 규칙에서 계산을 수행하는 것은 계산기보다 느린 경향이 있습니다.^[39] 이로 인해 엔지니어들은 더 정확하지만 복잡한 함수보다 슬라이드 규칙에서 쉬운 연산을 선호하는 수학 방정식을 사용하게 되었습니다. 이러한 근사치는 부정확성과 실수를 초래할 수 있습니다.^[40] 반면, 슬라이드 규칙의 공간적인 수동 조작은 디지털 계산기만 사용한 사람들이 종종 부족한 수치적 관계와 스케일에 대한 직관을 사용자에게 배양합니다.^[41] 슬라이드 규칙은 결과와 함께 계산의 모든 항을 표시하므로 실제로 수행된 계산에 대한 불확실성을 제거합니다. 따라서 전자 계산기에 구현된 역폴란드 표기법(RPN)과 비교되었습니다.^[42]

슬라이드 규칙을 사용하려면 결과에서 소수점 위치를 지정하기 위해 사용자가 답의 크기 순서를 별도로 계산해야 합니다. 예를 들어, 1.5 × 30(45와 같음)은 1500000 × 0.03(45000과 같음)과 동일한 결과를 나타냅니다. 이러한 별도의 계산을 통해 사용자는 단기 메모리의 크기를 추적하고(오류가 발생하기 쉬운), 모든 단계에서 메모를 하거나(거추장스러운) 이유를 기록해야 합니다(다른 계산 요구 사항은 주의를 산만하게 합니다).

슬라이드 규칙의 일반적인 산술 정밀도는 디지털 계산기의 많은 숫자와 비교하여 약 3자리의 유효 숫자입니다. 슬라이드 규칙을 사용할 때 크기 순서가 가장 두드러지기 때문에 사용자가 잘못된 정밀도의 오류를 범할 가능성이 적습니다.

같은 숫자로 곱셈이나 나눗셈을 수행할 때, 어떤 조작도 없이 슬라이드 규칙을 힐끗 보는 것만으로 답을 결정할 수 있는 경우가 많습니다. 이는 백분율을 계산할 때(예: 테스트 점수) 또는 가격을 비교할 때(예: 킬로그램당 달러) 특히 유용할 수 있습니다. 슬라이드 규칙으로 여러 속도-시간-거리 계산을 한 눈에 핸즈프리로 수행할 수 있습니다. 파운드에서 킬로그램까지의 기타 유용한 선형 변환은 규칙에 쉽게 표시할 수 있으며 계산에 직접 사용할 수 있습니다.

슬라이드 규칙은 전적으로 기계적이기 때문에 그리드 전기나 배터리에 의존하지 않습니다. 열이나 사용으로 인해 제대로 구성되지 않았거나 뒤틀린 슬라이드 규칙의 기계적 부정확성은 오류를 초래합니다.

많은 선원들은 전기 고장이나 긴 항로 구간에서 배터리가 고갈될 경우 항해를 위한 백업으로 슬라이드 규칙을 유지하고 있습니다. 슬라이드 규칙은 특히 소형 비행기의 경우 항공에서 여전히 일반적으로 사용됩니다. 그것들은 범용 계산기가 아닌 통합된 특수 목적 및 고가의 비행 컴퓨터로만 대체되고 있습니다. 조종사들이 사용하는 E6B 원형 슬라이드 규칙은 지속적으로 생산되어 왔으며 다양한 모델에서 사용할 수 있습니다. 항공용으로 설계된 일부 손목 시계는 여전히 슬라이드 규칙 눈금이 있어 빠른 계산이 가능합니다. Citizen Skyhawk AT와 Seiko Flight Master SNA411은 두 가지 주목할 만한 예입니다.^[43]

현대적 용도

이 섹션에는 독창적인 연구가 포함되어 있을 수 있습니다. 청구 내용을 확인하고 인라인 인용을 추가하여 개선해 주시기 바랍니다. 원본 연구로만 구성된 문은 제거해야 합니다. (2015년 2월) (본 템플릿 메시지의 제거 방법 및 시기에 대해 알아봅니다.)

21세기에도 실용적인 컴퓨팅 장치로 전자계산기보다 슬라이드 룰을 선호하는 사람들이 있습니다. 다른 사람들은 향수를 불러일으키지 않기 위해 그들의 오래된 슬라이드 규칙을 유지하거나 그것들을 취미로 모읍니다.^[44]

인기 있는 수집형 모델은 Kuffel & Esser Deci-Lon으로, 고급 과학 및 엔지니어링 슬라이드 규칙으로 10인치(25cm) "일반"(Deci-Lon 10)과 5인치 "포켓"(Deci-Lon 5) 변형으로 제공됩니다. 또 다른 소중한 미국 모델은 8인치(20cm) 사이언티픽 인스트루먼트 원형 규칙입니다. 유럽의 규칙 중에서도 수집가들 사이에서는 Faber-Castell의 고급 모델이 가장 인기가 많습니다.

많은 슬라이드 규칙이 시중에 유통되고 있지만 상태가 좋은 표본은 가격이 비싼 경향이 있습니다. 온라인 경매 사이트에서 판매하기 위해 발견된 많은 규칙이 손상되거나 누락된 부분이 있으며 판매자가 관련 정보를 제공하기에 충분하지 않을 수 있습니다. 교체 부품은 부족하고, 고가이며, 일반적으로 개인 수집가의 웹사이트에서 별도 구매만 가능합니다. 1950년경까지의 키펠과 에세르 규칙은 특히 문제가 되는데, 이는 커서의 끝 부분이 셀룰로이드로 만들어져 시간이 지남에 따라 화학적으로 분해되는 경향이 있기 때문입니다. 플라스틱을 보존하는 방법은 일부 오래된 슬라이드 규칙의 열화를 늦추기 위해 사용될 수 있으며, 3D 인쇄는 누락되거나 돌이킬 수 없을 정도로 손상된 커서 부품을 재생하는 데 사용될 수 있습니다.^[45]

새로운 슬라이드 규칙에 대한 소스는 여전히 몇 가지가 있습니다. 1954년 7월 원형 슬라이드 규칙 제조업체로 시작된 도쿄의 간결한 회사는 ^[46]오늘날에도 계속해서 만들고 판매하고 있습니다. 2009년 9월, 온라인 소매업체 ThinkGeek은 "개별적으로 수작업으로 제작된" "성실한 복제품"이라고 설명되는 직선 슬라이드 규칙의 자체 브랜드를 선보였습니다.^[47] 이것들은 2012년에 더 이상 사용할 수 없었습니다.^[48] 또한 Faber-Castell은 2018년 중반까지 웹 스토어를 통해 해외 구매가 가능한 여러 슬라이드 규칙을 인벤토리에 보유하고 있었습니다.^[49] 비율 휠은 여전히 그래픽 디자인에 사용됩니다.

안드로이드 및 iOS 기반 스마트폰 및 태블릿에 다양한 슬라이드 룰 시뮬레이터 앱을 사용할 수 있습니다.

항공에 사용되는 E6B와 포병 포병 포병 포병 포병 포병 포병 포병 포병 포병 포병 포병과 같은 특수 슬라이드 규칙은 더 이상 일상적이지 않지만 여전히 사용되고 있습니다. 이러한 규칙은 교수 및 지도 과정의 일부로 사용됩니다. 학생은 이러한 규칙을 사용하는 방법을 학습할 때 계산의 배경이 되는 원리에 대해 배울 수 있으며, 또한 일반적으로 현대 전자 제품이 사용되지 않을 경우 이러한 도구를 백업으로 사용할 수 있습니다.

컬렉션

매사추세츠주 케임브리지에 있는 MIT 박물관에는 수백 개의 슬라이드 규칙, 노모그램, 기계 계산기 등이 있습니다.^[50] 2005년경 뉴저지주 호보켄에 위치한 슬라이드 규칙 제조업체의 Keuffel and Esser Company 컬렉션이 MIT에 기증되어 기존 보유량을 크게 늘렸습니다.^[51] 컬렉션에서 선택된 품목은 일반적으로 박물관에 전시됩니다.^[52][53]

국제 슬라이드 룰 박물관은 슬라이드 룰과 로그 계산기와 관련된 모든 것에 대해 "세계에서 가장 광범위한 자원"이라고 주장합니다.^[54] 박물관의 웹 페이지에는 슬라이드 규칙과 관련된 광범위한 문헌이 "슬라이드 규칙 라이브러리" 섹션에 포함되어 있습니다.^[55]

참고 항목

• 주판 – 계산 도구
• 컴퓨터(직업) – 전자 컴퓨터가 보급되기 전에 수학적 계산을 수행하는 사람
• 비행 컴퓨터 – 항공에서 사용되는 원형 슬라이드 규칙
• 부동 소수점 – 실수에 대한 컴퓨터 근사값 리디렉션 대상에 대한 짧은 설명을 표시하는 페이지
• 한스 피터 룬 – 독일계 미국인 컴퓨터 과학자
• Nomogram – 아날로그 그래픽 계산기
• 섹터(계측기) – 경첩이 달린 두 개의 눈금자로 구성된 수학계측기
• 슬라이드 계산기 – 기계식 덧셈/ 뺄셈 계산기 - 위키데이터 설명을 폴백으로 표시하는 페이지
• 슬라이드 차트 – 이동 부품(일반적으로 종이)을 포함한 휴대용 장치 참고 또는 계산을 위해 일반적으로 인쇄됨 위키데이터 설명을 폴백으로 표시하는 페이지
• 컴퓨팅 타임라인
• Vernier scale – 정밀도를 높이기 위해 사용되는 측정 장치의 보조 스케일
• 볼륨 – 회전 부품이 있는 종이 구조물은 슬라이드 차트 또는 이동 가능한 책의 하위 클래스로 간주될 수 있습니다.

참고문헌

외부 링크

• 국제 슬라이드 룰 박물관
• 공학 슬라이드 규칙의 역사, 이론 및 사용 - James B 박사. 덴버 대학교 캘버트
• 영국 슬라이드 규칙 서클 홈 페이지 2015-09-28 at the Wayback Machine
• Wouldred Society 슬라이드 규칙 홈 페이지 — 슬라이드 규칙의 보존과 이력을 위한 전용
• Rod Lovett의 슬라이드 규칙 – 검색 시설이 많은 종합 Aristo 사이트
• Derek's virtual slide rule gallery — 이전 슬라이드 규칙의 자바스크립트 시뮬레이션
• "Slide rule" . New International Encyclopedia. 1905.
• "Slide-rule" . Encyclopedia Americana. 1920.
• Reglas de Calculo — 매우 큰 Faber Castell 컬렉션
• 슬라이드 규칙 모음 — 프랑스 슬라이드 규칙(Graphoplex, Tabernier-Gravet 등)
• Eric's 슬라이드 규칙 사이트 — 기록 및 사용
• 슬라이드 규칙 — HP 계산기 박물관의 정보
• 설명, 브랜드 이름별 알파벳순, 이미지 포함(Vintage Tech). 협회)