반로그 그림

과학 및 공학에서 반로그 플롯/그래프 또는 반로그 플롯/그래프는 한 축은 로그 척도로 다른 축은 선형 척도로 가집니다.하나의 변수가 광범위한 값을 포함하는 지수 관계를 가진 데이터에 유용하며, 처음에는 직선처럼 보이지만 실제로는 로그 곡선의 시작 속도가 느리고 변화가 ^[1]처음에 생각했던 것보다 훨씬 크다는 것을 확대하여 시각화할 수 있습니다.

y ${\displaystyle =}$ ${\displaystyle {}^{}}$ a ${\displaystyle a}$ a$$ x \ $displaystyle$ y = \ $displayda$ a$^{\ displayda$ x$}$ $형식$의 모든 방정식은 반비례적으로 플롯될 때 직선을 형성한다. 왜냐하면 양측의 로그를 취하면 다음과 같은 값을 얻을 수 있기 때문이다.

$\displaystyle \log _{a}y=\display x+\log _{a}\displayda.}$

${\displaystyle {\mathrm{이것}}_{}}$은 $기울기$가$$\$displaystyle \gamma$이고 로그가$$\$displaystyle \log$ _${a}\lambda}$인 행입니다${\displaystyle {}_{}}$로그 척도는 일반적으로 10진수로 표시되며, 때로는 2진수로 표시되기도 합니다.

$\displaystyle \log(y)=(\display \log(a)x+\log(\displayda).}$

로그-선형(때로는 로그-린) 그림은 Y 축에 로그 척도가 있고 X 축에 선형 척도가 있습니다. 선형 로그(때로는 선형-로그)는 그 반대입니다.이름은 output-input(y-x)으로 (x, y)와는 반대입니다.

반로그 그림에서 Y축(또는 X축)의 척도 간격은 숫자 자체가 아니라 숫자의 대수에 비례합니다.이는 y 값(또는 x 값)을 로그로 변환하고 데이터를 선형 척도로 표시하는 것과 같습니다.로그-로그 그림에서는 두 축 모두에 대해 로그 척도를 사용하므로 반로그 그림이 아닙니다.

방정식

가로축이 로그(대수 기저값 n)로 스케일링되는 선형 로그 그림 위의 선의 방정식은 다음과 같습니다.

${\displaystyle F(x)=m\log _{n}(x)+b.,}$

로그 축이 로그 스케일(로그 베이스 n)인 로그 선형 플롯의 선에 대한 방정식은 다음과 같습니다.

$\displaystyle \log _{n}(F(x))=display+b}$

$(\displaystyle F(x)=n^{mx+b}=(n^{mx})(n^{b}).}$

반로그 그림에서 함수 찾기

선형 로그 그림

선형 로그 그림에서 F는₀ F(x₀)의 줄임말인 고정점₀(x₀, F)을 선택하고 위의 그래프에서 직선상의 다른 임의의 점(x₁, F₁)을 선택합니다.그래프의 기울기 공식은 다음과 같습니다.

${\displaystyle m=frac {F_{1}-F_{0}}{\log _{n}(x_{1}/x_{0}}}}$

그 결과

${\displaystyle F_{1}-F_{0}=m\log _{n}(x_{1}/x_{0})}$

또는

${\displaystyle F_{1}=m\log _{n}(x_{1}/x_{0})+F_{0}=m\log _{n}(x_{1})-m\log _{n}(x_{0})+F_{0}}$

즉,

즉, F는 x 곱하기 line-log 그래프의 직선 기울기에 상수를 더한 대수에 비례합니다.특히 점(F₀, x₀)과 (F₁, x₁)을 포함하는 선형 로그 그림의 직선은 다음과 같은 함수를 가집니다.

${\displaystyle F(x)=(F_{1}-F_{0}){\left[{\frac {log _{n}(x/x_{0})}{\log _{n}(x_{1}/x_{0}}}}}\light]+F_{0}=(F_{1}-F_{0})\log _{\frac {x_{1}}{x_{0}}{\leftfrac {x}{x_{0}}\right}+F_{0}}$

로그 선형도

로그-선형 그림(Y축의 로그 스케일)에서 F는₀ F(x₀)의 약어인 고정점(x₀, F₀)을 선택하고, 위의 그래프에서 직선상의 어딘가에서 다른 임의의 점(x₁, F₁)을 선택합니다.그래프의 기울기 공식은 다음과 같습니다.

${\displaystyle m=syslog_{n}(F_{1}/F_{0}) {x_{1}-x_{0}}}$

그 결과

$\displaystyle \log _{n}(F_{1}/F_{0})=m(x_{1}-x_{0})}$

n = F라는₁ 점에^log_n(F₁) 유의하십시오.따라서 로그를 반전하여 다음을 찾을 수 있습니다.

${\displaystyle {F_{1}} {F_{0}}=n^{m(x_{1}-x_{0}}}}$

또는

${\displaystyle F_{1}=F_{0}n^{m(x_{1}-x_{0}}}}$

이는 단순히 F₁:가 아니라 임의의 점에 대해 일반화할 수 있습니다.

${\displaystyle F(x)={F_{0}}n^{\left({\frac {x-x_{0}}}\right)\log _{n}(F_{1}/F_{0}}}}}$

실제의 예

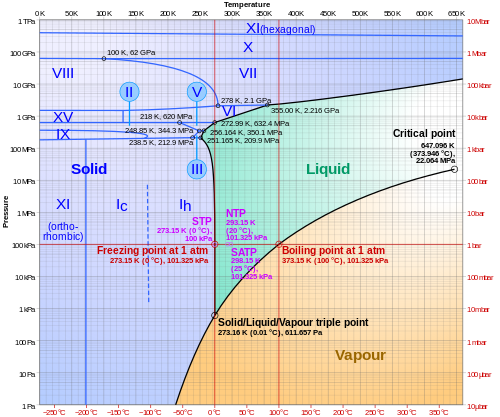
물의 위상도

물리학과 화학에서는 온도에 대한 압력 로그 그래프를 사용하여 다음과 같이 물질의 다양한 위상을 설명할 수 있습니다.

2009년 '독감' 진행

10이 가장 일반적인 베이스이지만 다음 예시와 같이 다른 베이스가 더 적절한 경우가 있습니다.

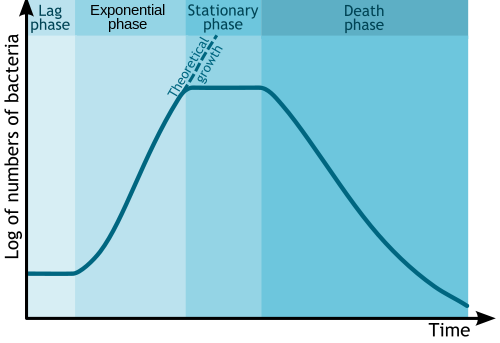
미생물 증식

생물학 및 생물 공학에서, 무성 생식과 영양소 고갈로 인한 미생물 수의 변화는 반로그 플롯에 의해 일반적으로 설명된다.시간은 보통 독립적인 축이며, 박테리아나 다른 미생물의 수나 질량의 대수를 종속 변수로 합니다.이 그래프는 다음과 같이 4개의 서로 다른 위상을 가진 플롯을 형성합니다.

「 」를 참조해 주세요.

• 노모그래프, 더 복잡한 그래프
• 비선형 회귀#비반복 계산 가능한 반로그 형태로 변환하기 위한 변환
• 로그-로그 그림

레퍼런스