데이터 변환(통계)

이 글에는 여러 가지 문제가 있다.이 문제를 개선하거나 대화 페이지에서 토의하십시오.(이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "데이터 변환" 통계 – 뉴스 · 신문 · 책 · 학자 · JSTOR (2014년 9월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) 이 레더 섹션은 대부분의 독자들이 이해하기에는 너무 기술적일 수 있다. 기술 세부 정보를 제거하지 않고 비전문가가 이해할 수 있도록 개선하십시오.(2015년 8월) (이 템플릿 메시지 제거 방법 및 시기 학습) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

통계에서 데이터 변환은 데이터 집합의 각 점에 결정론적 수학적 함수를 적용하는 것이다. 즉, 각 데이터 포인트 z는_i 변환된 값 y_i = f(z_i)로 대체된다. 여기서 f는 함수다.변환은 일반적으로 데이터가 적용될 통계적 추론 절차의 가정을 보다 밀접하게 충족하거나 그래프의 해석성 또는 외관을 개선하기 위해 적용된다.

거의 항상 데이터를 변환하는 데 사용되는 함수는 되돌릴 수 없으며, 일반적으로 연속적이다.변환은 일반적으로 비교 가능한 측정값의 집합에 적용된다.예를 들어, 만약 우리가 사람들의 소득에 관한 데이터를 어떤 통화 단위로 작업하고 있다면, 로그 함수에 의해 각 개인의 소득 가치를 바꾸는 것이 일반적일 것이다.

동기

데이터를 변환하는 방법 또는 변환을 적용해야 하는지에 대한 지침은 수행할 특정 통계 분석에서 도출해야 한다.예를 들어, 모집단 평균에 대해 약 95% 신뢰 구간을 구성하는 간단한 방법은 표본 평균에 표준 오차 단위를 더하거나 빼는 것이다.그러나 여기서 사용되는 상수 인자 2는 정규 분포에 특정하며 표본 평균이 근사적으로 정규 분포를 따르는 경우에만 적용된다.중심 한계 정리는 많은 상황에서 표본 크기가 상당히 크면 표본 평균이 정상적으로 변화한다고 명시한다.그러나 모집단이 상당히 치우쳐 있고 표본 크기가 최대 중간 정도라면 중심 한계 정리에 의해 제공되는 근사치가 불량할 수 있으며, 결과 신뢰 구간이 잘못된 적용 확률을 가질 가능성이 높다.따라서 데이터에 상당한 왜곡이 있다는 증거가 있는 경우 신뢰 구간을 구성하기 전에 데이터를 대칭 분포로^[1] 변환하는 것이 일반적이다.원하는 경우 데이터에 적용된 변환의 역순을 사용하여 신뢰 구간을 원래 척도로 다시 변환할 수 있다.^[2][3]

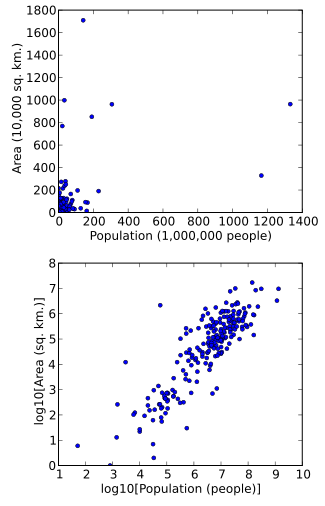
데이터도 쉽게 시각화할 수 있도록 변환할 수 있다.예를 들어, 포인트가 세계의 국가인 산점도를 가지고 있고, 플로팅되고 있는 데이터 값은 각 국가의 토지 면적과 인구라고 가정합시다.만약 플롯이 확인되지 않은 데이터(예: 면적 및 인구 수)를 사용하여 이루어진다면, 대부분의 국가는 그래프의 왼쪽 아래 모서리에 있는 점들의 밀집된 군집으로 플롯될 것이다.매우 큰 영역 및/또는 모집단을 가진 소수의 국가는 그래프의 영역 대부분을 중심으로 얇게 분포될 것이다.단순히 단위(예: 수천 평방 킬로미터 또는 수백만 명의 사람들에게)를 재할인한다고 해서 이것이 바뀌지는 않을 것이다.그러나 영역과 모집단의 로그 변환 후 그래프에서 점들이 더 균일하게 분포될 것이다.

데이터 변환을 적용하는 또 다른 이유는 공식적인 통계 분석이나 시각화를 수행하지 않더라도 해석 가능성을 향상시키기 위함이다.예를 들어, 자동차를 연비 측면에서 비교한다고 가정합시다.이 데이터는 보통 "리터당 킬로미터" 또는 "갤런당 마일"로 제시된다.그러나 한 사람이 다른 차와 비교했을 때 한 해에 얼마나 많은 연료를 추가로 사용할지 평가하는 것이 목표라면, 상호 기능, 킬로미터당 리터, 마일당 갤런을 적용하여 변환된 데이터를 사용하는 것이 더 자연스럽다.

회귀 분석에서

데이터 변환은 원본 데이터가 선형 회귀에 대한 하나 이상의 가정을 위반하는 경우 선형 회귀 분석을 통한 모델링에 적합한 데이터를 만들기 위한 교정 조치로 사용될 수 있다.^[4]예를 들어, 가장 단순한 선형 회귀 모형은 Y의 기대값(예측할 반응 변수)과 각 독립 변수(다른 독립 변수를 고정했을 때) 사이의 선형 관계를 가정한다.선형성이 거의라도 유지되지 못하면 회귀 모형의 독립 변수 또는 종속 변수를 변환하여 선형성을 개선할 수 있는 경우가 있다.^[5]예를 들어 원래 독립 변수의 2차 함수를 추가하면 Y의 기대값과 선형 관계가 형성되어 다항식 회귀 모형, 즉 선형 회귀의 특별한 경우를 초래할 수 있다.

선형 회귀에 대한 또 다른 가정은 균등성, 즉 오류의 분산이 예측 변수의 값에 관계없이 동일해야 한다는 것이다.이러한 가정(즉는 데이터의heteroscedastic은)을 위반하면 Y형태 변화 혼자를 찾고 X(그 예언자라고 변수), Y, 동분산성 가정(직선성 가정 외에)은 변화된 variables[5]과 선형 회귀엘 수 있기 때문에 마찬가지의 변환 가능할 수 있다.be는 이것들에 적용했다.

그러나 데이터 변환의 또 다른 적용은 오류 용어의 정규성 결여 문제를 해결하는 것이다.회귀 모수의 최소 제곱 추정치가 의미 있는 경우에는 일변량 정규성이 필요하지 않다(Gauss-Markov 정리 참조).그러나 변수가 다변량 정규성을 나타내는 경우 신뢰 구간과 가설 검정에서 더 나은 통계 특성을 가질 수 있다.오차항의 분산을 안정화하는 변환(즉, 이단성을 다루는 변환)도 오차항을 근사적으로 정규화하는 데 도움이 되는 경우가 많다.^[5][6]

예

방정식: $[\displaystyle Y=a+bX}$

의미: X의 단위 증가는 Y의 평균 b 단위 증가와 관련이 있다.

방정식: ${\displaystyle \log(Y)=a+bX}$

(방정식의 양쪽을 모두 지수화하는 것에서:${\displaystyle Y}$= ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{}^{}}$ ${\displaystyle b^{}}$ ${\displaystyle X^{}}$ ${\$

의미: X의 단위 증가는 ${\displaystyle \mathrm{로그}}$ ${\displaystyle }$ ${\displaystyle (Y}$ ${\displaystyle )}$ ${\displaystyle \log(Y)}$에서 b 단위의 평균 증가와 관련이 있다$.$ 또는 동등하게, ${\displaystyle Y^{}}$는 e b${\displaystyle {}^{}}${\$displaystyle$ e$^{b}\}$의 곱셈 인수에 의해 평균 증가된다$.$ 예를 들어, 위의 transfo에서 자연 로그 대신 base-10 로그가 사용된 경우.rmation과 동일한 기호(a와 b)가 회귀 계수를 나타내기 위해 사용되며, 그러면 X의 단위가 증가하면 평균적으로 Y의 ${\displaystyle {10b}^{}}$ ${\$배$$ 증가하게 된다.b가 1이었다면 이는 X의 단위 증가에 대한 Y의 10배 증가를 의미한다.

방정식: ${\displaystyle Y=a+b\log(X)}$

의미: X의 k-배 증가량은 평균 $b{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle \mathrm{로그}}$ ${\displaystyle }$( ${\displaystyle k}$) $[\displaystyle b\time \log(k)}$단위 증가와$$ 관련이 있다.예를 들어 위의 변환에서 자연 로그 대신 base-10 로그가 사용되었고 회귀 계수를 나타내기 위해 동일한 기호(a와 b)를 사용한다면, X가 10배 증가하면 $평균{\displaystyle }$ b ${\displaystyle \times }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {10}_{}}$ ${\displaystyle {}_{}}$( ${\displaystyle 10}$)${\displaystyle }$= ${\displaystyle b}$ ${\displaystyle b\time \log _{10}(10)=b}$ 단위가 증가할$$ 것이다.

방정식: ${\displaystyle \log(Y)=a+b\log(X)}$

(방정식의 양쪽을 모두 지수화하는 것에서:${\displaystyle Y}$= ${\displaystyle {}^{}}$ ${\displaystyle {}^{}{}^{}}$ ${\displaystyle b^{}}$ ${\$

의미: X의 k-배 증가량은 $평균적$으로 Y의 k ${\displaystyle b^{}}$ ${\$ k$^{b}$배$$ 증가와 관련이 있다.따라서 X가 두 배로 증가하면 Y가 $2{\displaystyle {\mathrm{}}^{}}$ $displaystyle 2^{b}\!}$의 곱셈 인수에 의해 변경된다$.$^[7]

대안

일반화된 선형 모형(GLM)은 정규 분포 이외의 오차 분포 모델을 갖는 반응 변수를 허용하는 일반 선형 회귀의 유연한 일반화를 제공한다.GLMs는 선형 모델을 링크 함수를 통해 반응 변수와 연관시키고 각 측정값의 분산 크기를 예측값의 함수로 할 수 있도록 한다.^[8][9]

일반적인 경우

로그와 제곱근 변환은 양수 데이터에 일반적으로 사용되며, 0이 아닌 데이터에 대해서는 승수 역(수명) 변환을 사용할 수 있다.전력 변환은 대수, 제곱근, 승법 역수를 특수 사례로 포함하는 비 음수 값 λ에 의해 매개변수화된 변환 계열이다.데이터 변환에 체계적으로 접근하려면 통계적 추정 기법을 사용하여 전력 변환에서 모수 λ을 추정함으로써 주어진 설정에서 대략 가장 적절한 변환을 식별할 수 있다.전력 변환 제품군에는 신분 변환도 포함되므로, 이 접근방식은 변환 없이 데이터를 분석하는 것이 최선인지 여부도 나타낼 수 있다.회귀 분석에서 이 접근법을 Box-Cox 기법이라고 한다.

그 상호 변환, Yeo–Johnson 변환하고, 이러한 역 하이퍼볼릭 사인을 적용하는 정확한 다른 변화 같은 힘의 변환, 의미 있는 긍정적이고 부정적인 values[10](만약 λ은 특이한 정수의 전력 변환이 모든 참된 숫자에 대하가역은)을 포함한다 데이터에 적용될 수 있다..그러나 음수 값과 양의 값이 모두 관측되면, 모든 값에 상수를 추가하여 어떤 전력 변환도 적용할 수 있는 음수가 아닌 데이터 세트를 생성하는 것으로 시작하는 것이 일반적이다.^[3]

데이터 변환이 적용되는 일반적인 상황은 관심 값이 몇 개의 크기 순서에 걸쳐 있는 경우다.많은 물리적, 사회적 현상들이 소득, 종족, 은하수 크기, 강우량 등 그러한 행동을 보이고 있다.전력 변환, 특히 로그는 종종 그러한 데이터에서 대칭을 유도하는 데 사용될 수 있다.로그는 그 결과를 '접은 변화'라는 관점에서 해석하기 쉽기 때문에 종종 선호된다.

로그는 비율에도 유용한 영향을 미친다.비율 X/Y를 사용하여 양수 X와 Y를 비교하는 경우, X < Y는 구간(0,1)에 있는 반면, X > Y는 반선(1,62)에 속하는데, 여기서 1의 비율이 평등에 해당한다.In an analysis where X and Y are treated symmetrically, the log-ratio log(X / Y) is zero in the case of equality, and it has the property that if X is K times greater than Y, the log-ratio is the equidistant from zero as in the situation where Y is K times greater than X (the log-ratios are log(K) and −log(K) in these two situations).

값이 종단점을 포함하지 않고 자연스럽게 0 - 1 범위 내로 제한되는 경우 로짓 변환이 적절할 수 있다. 즉, 로짓 변환은 (-115,610) 범위에서 값을 산출한다.

정규성으로 변환

1. 데이터 세트를 정규 분포를 닮도록 변환하는 것이 항상 필요하거나 바람직한 것은 아니다.그러나 대칭성이나 정규성을 원하는 경우, 전력 변환 중 하나를 통해 유도될 수 있는 경우가 많다.

2. 언어력 함수는 Zipf-Mandelbrot 법칙에 따라 분포한다.이 분포는 극도로 뾰족하고 렙토쿠르틱하며, 이것이 연구자들이 예를 들어 저자 귀속 문제 등을 해결하기 위해 통계에 등을 돌릴 수밖에 없었던 이유다.그럼에도 불구하고 가우스 통계 활용은 데이터 변환을 적용함으로써 완벽하게 가능하다.^[11]

3. 변환 후 정규성이 달성되었는지 여부를 평가하기 위해 표준 정규성 테스트를 사용할 수 있다.그래픽 접근방식은 일반적으로 공식적인 통계적 시험보다 더 유용하므로 정규 분량 그림은 정규 모집단에 대한 데이터 집합의 적합성을 평가하는 데 일반적으로 사용된다.또는 표본의 왜도와 첨도에 기초한 엄지손가락 규칙도 제안되었다.^[12][13]

균등 분포 또는 임의 분포로 변환

만일 우리가 넥타이가 없는 n 값 X₁, ..., X의_n 집합을 관찰한다면(즉, 구별되는 값이 전혀 없다), 우리는_i X를 변환된_i 값 Y = k로 대체할 수 있다. 여기서 k는 모든_i X 값 중에서 k가^th 가장 크도록 정의된다.이를 순위 변환이라고 하며,^[14] 균일한 분포에 완벽하게 맞는 데이터를 생성한다.이 접근방식은 모집단 아날로그가 있다.

확률 적분 변환을 사용하여 X가 임의 변수이고 F가 X의 누적 분포 함수인 경우, F가 변위할 수 없는 한 랜덤 변수 U = F(X)는 단위 간격에 대해 균일한 분포를 따른다 [0,1].

균일한 분포로부터, 우리는 반전 가능한 누적 분포 함수를 가진 어떤 분포로 변환할 수 있다.G가 반전성 누적분포함수이고 U가 균일하게 분포된 랜덤 변수인 경우 랜덤 변수 G⁻¹(U)는 G를 누적분포함수로 한다.

둘을 합치면 X가 임의변수, F가 X의 반전성 누적분포함수, G가 반전성 누적분포함수인 경우 랜덤 변수⁻¹ G(F(X)는 G를 누적분포함수로 한다.

분산 안정화 변환

많은 유형의 통계 데이터는 "변동성-평균 관계"를 나타내며, 이는 기대값이 서로 다른 데이터 값에 대해 변동성이 다르다는 것을 의미한다.예를 들어, 세계의 다른 인구를 비교할 때, 평균 소득과 함께 소득의 분산이 증가하는 경향이 있다.다수의 소지역 단위(예: 미국의 군)를 고려하고 각 카운티 내에서 소득의 평균과 분산을 얻는다면, 평균 소득이 더 높은 카운티도 더 높은 편차를 갖는 것이 일반적이다.

분산 안정화 변환은 평균 대비 분산 관계를 제거하여 분산이 평균에 비례하여 일정하게 되도록 하는 것을 목표로 한다.분산 안정화 변환의 예로는 표본 상관 계수에 대한 Fisher 변환, 포아송 데이터에 대한 제곱근 변환 또는 안스콤브 변환(카운트 데이터), 회귀 분석에 대한 Box-Cox 변환, 비율에 대한 아크사인 제곱근 변환 또는 각도 변환(이항 분포) 등이 있다.데이터). 비례 데이터의 통계 분석에 일반적으로 사용되지만 특히 유형 II 오류 감소로 인해 로지스틱 회귀 분석 또는 로짓 변환이 이항 또는 비이항 비율에 더 적합하기 때문에 아크사인 제곱근 변환은 권장되지 않는다.^[15][3]

다변량 데이터의 변환

일변량 함수는 다변량 데이터에 포인트 방식으로 적용하여 한계 분포를 수정할 수 있다.적절하게 구성된 변환을 사용하여 다변량 분포의 일부 속성을 수정할 수도 있다.예를 들어 시계열 및 기타 유형의 순차적 데이터로 작업할 때 데이터 차이를 통해 스테이션성을 개선하는 것이 일반적이다.랜덤 벡터 X에 의해 생성된 데이터가 공분산 행렬 σ이 있는 관측치의 벡터 X로_i 관측되는 경우 데이터를 장식하는 데 선형 변환을 사용할 수 있다.이를 위해 ch = A'를 표현하는 데 숄스키 분해법을 사용한다.변환된 벡터 Y_i = AX는⁻¹_i 공분산 행렬로 ID 행렬을 가진다.

참고 항목

• 아크신
• 피쳐 엔지니어링
• 로짓
• 비선형 회귀 분석#변환
• Pearson 상관 계수
• 전력 변환(Box-Cox)

참조

외부 링크

• 왜곡된 분포 및 광범위한 분포에 대한 로그 변환 – 로그 및 "서명된 로그" 변환에 대해 논의한다("R을 사용한 실제 데이터 과학"의 한 장).