2차 텐더에 관한 스칼라 , 벡터 , 2차 텐서 의 파생상품은 연속체 역학 에서 상당히 유용하다. 이러한 파생상품은 비선형 탄성 과 가소성 의 이론, 특히 수치 시뮬레이션 을 위한 알고리즘 설계에 사용된다.[1]
방향파생물 은 이러한 파생상품을 체계적으로 찾을 수 있는 방법을 제공한다.[2]
벡터 및 2차 텐더 관련 파생 모델 다양한 상황에 대한 방향파생상품의 정의는 다음과 같다. 파생상품을 취할 수 있을 정도로 기능이 충분히 원활하다고 가정한다.
벡터의 스칼라 가치 함수의 파생 모델 f (v )를 벡터 v 의 실제 가치 있는 함수가 되게 한다.그 다음에 v(또는 v)에 관한 f (v)의 파생상품은 어떤 벡터 u 가 존재하는 그것의 도트 제품을 통해 정의된 벡터 다.
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}} 모든 벡터들을 위해.위의 도트 제품은 스칼라를 산출하며, 만약 u가 단위 벡터라면 u방향 으로 v 에서 f의 방향파생물을 제공한다.
속성:
If f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )+f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mat hbf {v} }+{\frac {\f_{1}:{\reason \mathbf {v}}}{\reason \mathbf {}}\cdot \mathbf {u}}}} If f ( v ) = f 1 ( v ) f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )~f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) f 2 ( v ) + f 1 ( v ) ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathb f {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v} )+f_{1}(\mathbf {v} )~\left({\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} If f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle f(\mathbf {v} )=f_{1}(f_{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ∂ f 2 ∂ v ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~{\frac {\partial f_{2}}{\ 부분 \mathbf{v}}}\cdot \mathbf {u}} 벡터의 벡터 평가함수의 파생상품 f (v )를 벡터 v 의 벡터 값 함수가 되게 한다.그 다음, v (또는 v)에 관한 f(v )의 파생상품은 벡터 u를 포함한 그것의 도트 제품을 통해 정의된 두 번째 순서 텐서 다.
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}} 모든 벡터들을 위해.위의 도트 제품은 벡터를 생성하며, 만약 u 가 단위 벡터라면 방향 u 에서 v 에서 f 의 방향 파생물을 제공한다.
속성:
If f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )+\mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left\frac {f} _{1}{\mathbf {v}}}{1}+{\frac {v}{\mathbf {f} _{2}}:{\mathbf {v}}}\cdot \mathbf {u}}}}}}}}}}}}}}}}}}}} If f ( v ) = f 1 ( v ) × f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )\times \mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) × f 2 ( v ) + f 1 ( v ) × ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)\times \mathbf {f} _{2}(\mathbf {v} )+\mathbf {f} _{1}(\mathbf {v} )\times \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} If f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {f} _{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ⋅ ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} = {\frac {\mathbf {f} _{1}:{1}{1}:{1}\mathbf {f} _{2}}:\cdot \left\frac {\mathbf {f} _{2}}:{\mathbf {v}}}}}\cdot \mathbf {u} \right}}}}}}}} 2차 텐더의 스칼라 평가 함수 파생상품 Let f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} S {\displaystyle {\boldsymbol {S}}} T {\ displaystyle {\boldsymbol{T} 번째 순서 텐서임
∂ f ∂ S : T = D f ( S ) [ T ] = [ d d α f ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} 모든 2차 주문 텐셔너 T {\ displaystyle {\boldsymbol{T}} .
속성:
If f ( S ) = f 1 ( S ) + f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})+f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S + ∂ f 2 ∂ S ) : T {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}:{\partial {\boldsymbol{S}}}+{\frac {\partial f_{2}}{\partial {\boldsymbol{S}}}\right): {\boldsymbol{T}} If f ( S ) = f 1 ( S ) f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})~f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S : T ) f 2 ( S ) + f 1 ( S ) ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbo l {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)~f_{2}({\boldsymbol {S}})+f_{1}({\boldsymbol {S}})~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} If f ( S ) = f 1 ( f 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}(f_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ f 2 ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial f_{2}}}~\l eft({\frac {\partial f_{2}}:{\partial {\boldsymbol{S}}}}}}} 2차 텐더의 텐서 함수 파생상품 Let F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} (또는 {\ displaystyle {\boldsymbol {S S {\ {\boldsymbol {T} 정의 된 네 번째 순서 텐서입니다
∂ F ∂ S : T = D F ( S ) [ T ] = [ d d α F ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} 모든 2차 주문 텐셔너 T {\ displaystyle {\boldsymbol{T}} .
속성:
If F ( S ) = F 1 ( S ) + F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})+{\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S + ∂ F 2 ∂ S ) : T {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}\right): {\boldsymbol{T}} If F ( S ) = F 1 ( S ) ⋅ F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 ( S ) + F 1 ( S ) ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})+{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{ \partial {\boldsymbol{S}}}}\\boldsymbol {T}\오른쪽) If F ( S ) = F 1 ( F 2 ( S ) ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ F ∂ S : T = ∂ F 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\b oldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} If f ( S ) = f 1 ( F 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1 }}{{\partial{\boldsymbol{F}_{2}}:\왼쪽({\frac {\partial {\boldsymbol{F}_{2}}:{\partial {\boldsymbol{S}}}}}}}}}}}}}} 텐서 필드의 그라데이션 임의 상수 벡터 c 방향으로 텐서Tx {\displaystyle boldsymbol {\nabla }{\ boldsymbol {T}} ∇ T {\ { t}}} 같이 .
∇ T ⋅ c = 임이 있는 α → 0 d d α T ( x + α c ) {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} =\lim _{\alpha \rightarrow 0}\quad {\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(\mathbf {x} +\alpha \mathbf {c} )} 순서 n 의 텐서 필드의 구배는 순서 n +1의 텐서 필드다.
데카르트 좌표, 평행 좌표. 참고: 반복 지수를 요약하는 아인슈타인 종합 관례 가 아래에 사용된다. If e 1 , e 2 , e 3 {\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}} Cartesian coordinate system, with coordinates of points denoted by ( x 1 , x 2 , x 3 {\displaystyle x_{1},x_{2},x_{3}} T {\displaystyle {\boldsy mbol {T}
∇ T = ∂ T ∂ x i ⊗ e i {\displaystyle {\boldsymbol {\nabla}{\\boldsymbol{T}}{\partial x_{i}}}\otimes \mathbf {e} _{i}}}}}}{i}}}}}}}}}}}}{\bmathy}}}}}}}}}}}}}}}}}}} 기본 벡터는 데카르트 좌표계에서 다양하지 않기 때문에 스칼라 필드 ϕ{\displaystyle \phi 필드 v, 2차 텐서 필드 S {\ displaystyle{\boldsymbol{S}}}} .
∇ ϕ = ∂ ϕ ∂ x i e i = ϕ , i e i ∇ v = ∂ ( v j e j ) ∂ x i ⊗ e i = ∂ v j ∂ x i e j ⊗ e i = v j , i e j ⊗ e i ∇ S = ∂ ( S j k e j ⊗ e k ) ∂ x i ⊗ e i = ∂ S j k ∂ x i e j ⊗ e k ⊗ e i = S j k , i e j ⊗ e k ⊗ e i {\displaystyle{\begin{정렬}{\boldsymbol{\nabla}}\phi&={\cfrac{\partial \phi}{\partial x_{나는}}}~\mathbf{e}_{나는}=\phi _{,i}~\mathbf{e}_{나는}\\{\boldsymbol{\nabla}}\mathbf{v}&={\cfrac{\partial(v_{j}\mathbf{e}_{j})}{\partial x_{나는}}}\otimes\mathbf{e}_{나는}={\cfrac{\partial v_{j}}{\partial x_{나는}}}{e}_{j}\otimes \mathb ~\mathbf.f{e}_{ i}=v_{j,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\cfrac {\partial (S_{jk}\mathbf {e} _{j}\otimes \mathbf {e} _{k})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial S_{jk}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}= S_{jk,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}\end}}}}}} 곡선 좌표 참고: 반복 지수를 요약하는 아인슈타인 종합 관례 가 아래에 사용된다. If g 1 , g 2 , g 3 {\displaystyle \mathbf {g} ^{1},\mathbf {g} ^{2},\mathbf {g} ^{3}} contravariant basis vectors in a curvilinear coordinate system, with coordinates of points denoted by ( ξ 1 , ξ 2 , ξ 3 {\displaystyle \xi ^{1},\xi ^{2},\xi ^{3}} T {\displaystyle {\boldsymbol {T}
∇ T = ∂ T ∂ ξ i ⊗ g i {\displaystyle {\boldsymbol {\nabla}{\boldsymbol{T}}{\partial \xi ^{i}}\otimes \mathbf {g} ^{i}}}}}{i}}}}}}}}}}}}}}}{\\\\\partmathbmathbf. 이 정의에서 스칼라 필드 grad{\displaystyle \phi }, 및 2차 텐서 필드 {\ displaystyle {\boldsymbol {S}} .
∇ ϕ = ∂ ϕ ∂ ξ i g i ∇ v = ∂ ( v j g j ) ∂ ξ i ⊗ g i = ( ∂ v j ∂ ξ i + v k Γ i k j ) g j ⊗ g i = ( ∂ v j ∂ ξ i − v k Γ i j k ) g j ⊗ g i ∇ S = ∂ ( S j k g j ⊗ g k ) ∂ ξ i ⊗ g i = ( ∂ S j k ∂ ξ i − S l k Γ i j l − S j l Γ i k l ) g j ⊗ g k ⊗ g i {\displaystyle{\begin{정렬}{\boldsymbol{\nabla}}\phi&={\frac{\partial \phi}{\partial\xi ^{나는}}}~\mathbf{g}^{나는}\\{\boldsymbol{\nabla}}\mathbf{v}&={\frac{\partial \left(v^{j}\mathbf{g}_{j}\right)}{\partial\xi ^{나는}}}\mathbf{g}^ᆵ=\left({\frac{\partial v^{j}}{\partial\xi ^{나는}}}+v^{k}~\Gamma_{ik}^{j}\right)~\math \otimes.남자 친구{g}_ {g}^{j}\otimes{g}^{나는}\\{\boldsymbol{\nabla}}{\boldsymbol{S}}및 \mathbf{j}\otimes, ={\frac{\partial \left(S_{jk}~\mathbf{g}^{j}\mathbf{g}^{k}\right \otimes)}{\partial\xi ^{나는}}}(}{\frac{\partial S_{jk}{\mathbf{g}^{나는}=\left \otimes{g}^ᆬ=\left({\frac{\partial v_{j}}{\partial\xi ^{나는}}}-v_{k}~\Gamma_{ij}^{k}\right)~\mathbf \mathbf.\par tial \xi _{i}}}-S_{lk}~\Gamma _{ij}^{l}-S_{jl}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\otimes \mathbf {g} ^{i}\end{aligned}}} 여기서 Christoffel 기호 γ i j k {\ displaystyle \Gamma _{ij}^{k}}}
Γ i j k g k = ∂ g i ∂ ξ j ⟹ Γ i j k = ∂ g i ∂ ξ j ⋅ g k = − g i ⋅ ∂ g k ∂ ξ j {\displaystyle \Gamma _{ij}^{k}~\mathbf {g} _{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\quad \implies \quad \Gamma _{ij}^{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\cdot \mathbf {g} ^{k}=-\mathbf {g} _{i}\cdot {\frac {\partial \mathbf {g} ^{k}}{\partial \xi ^{j}}}} 원통 극좌표 원통형 좌표 에서 구배는 다음과 같이 주어진다.
∇ ϕ = ∂ ϕ ∂ r e r + 1 r ∂ ϕ ∂ θ e θ + ∂ ϕ ∂ z e z ∇ v = ∂ v r ∂ r e r ⊗ e r + ∂ v θ ∂ r e r ⊗ e θ + ∂ v z ∂ r e r ⊗ e z + 1 r ( ∂ v r ∂ θ − v θ ) e θ ⊗ e r + 1 r ( ∂ v θ ∂ θ + v r ) e θ ⊗ e θ + 1 r ∂ v z ∂ θ e θ ⊗ e z + ∂ v r ∂ z e z ⊗ e r + ∂ v θ ∂ z e z ⊗ e θ + ∂ v z ∂ z e z ⊗ e z ∇ S = ∂ S r r ∂ r e r ⊗ e r ⊗ e r + ∂ S r r ∂ z e r ⊗ e r ⊗ e z + 1 r [ ∂ S r r ∂ θ − ( S θ r + S r θ ) ] e r ⊗ e r ⊗ e θ + ∂ S r θ ∂ r e r ⊗ e θ ⊗ e r + ∂ S r θ ∂ z e r ⊗ e θ ⊗ e z + 1 r [ ∂ S r θ ∂ θ + ( S r r − S θ θ ) ] e r ⊗ e θ ⊗ e θ + ∂ S r z ∂ r e r ⊗ e z ⊗ e r + ∂ S r z ∂ z e r ⊗ e z ⊗ e z + 1 r [ ∂ S r z ∂ θ − S θ z ] e r ⊗ e z ⊗ e θ + ∂ S θ r ∂ r e θ ⊗ e r ⊗ e r + ∂ S θ r ∂ z e θ ⊗ e r ⊗ e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e θ ⊗ e r ⊗ e θ + ∂ S θ θ ∂ r e θ ⊗ e θ ⊗ e r + ∂ S θ θ ∂ z e θ ⊗ e θ ⊗ e z + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ ⊗ e θ ⊗ e θ + ∂ S θ z ∂ r e θ ⊗ e z ⊗ e r + ∂ S θ z ∂ z e θ ⊗ e z ⊗ e z + 1 r [ ∂ S θ z ∂ θ + S r z ] e θ ⊗ e z ⊗ e θ + ∂ S z r ∂ r e z ⊗ e r ⊗ e r + ∂ S z r ∂ z e z ⊗ e r ⊗ e z + 1 r [ ∂ S z r ∂ θ − S z θ ] e z ⊗ e r ⊗ e θ + ∂ S z θ ∂ r e z ⊗ e θ ⊗ e r + ∂ S z θ ∂ z e z ⊗ e θ ⊗ e z + 1 r [ ∂ S z θ ∂ θ + S z r ] e z ⊗ e θ ⊗ e θ + ∂ S z z ∂ r e z ⊗ e z ⊗ e r + ∂ S z z ∂ z e z ⊗ e z ⊗ e z + 1 r ∂ S z z ∂ θ e z ⊗ e z ⊗ e θ {\displaystyle{\begin{정렬}{\boldsymbol{\nabla}}\phi ={}\quad&{\frac{\partial \phi}{r\partial}}~\mathbf{e}_{r}+{\frac{1}{r}}~{\frac{\partial \phi}{\theta\partial}}{e}_{\theta}+{\frac{\partial \phi}{z\partial}~\mathbf}~\mathbf{e}_{z}\\{\boldsymbol{\nabla}}\mathbf{v}={}\quad&{\frac{\partial v_{r}}{r\partial}}~\.mathbf{ E}}~\mathbf{e}_{r}\otimes \mathbf{e}_{\theta}+{\frac{\partial v_{z}}{r\partial}}{e}_{r}\otimes \mathbf{e}_{z}\\{}+{}& ~\mathbf,{\frac{1}{r}}{e}_{\theta}\otimes \mathbf{e}_{r}+{\frac{1}\left({\frac{\partial v_{r}}{\partial \theta}}-v_{\theta}\right)~\mathbf\mathbf{e}_{r}+{\frac{\partial v_{\theta}}{r\partial}_{r}\otimes.{r}} \left({\frac{\partial v_{\theta}}{\partial \theta}}+v_{r}\right)~\mathbf{e}_{\theta}\otimes}{e}_{\theta}\otimes \mathbf{e}_{z}\\{}+{}& ~\mathbf,{\frac{\partial v_{r}}{z\partial}}}{\parti{e}_{z}\otimes \mathbf{e}_{r}+{\frac{\partial v_{\theta}~\mathbf{e}_{\theta}+{\frac{1}{r}}{\frac{\partial v_{z}}{\theta\partial}\mathbf.알 z }}{e}_{z}\otimes \mathbf{e}_{\theta}+{\frac{\partial v_{z}}{z\partial}}~\mathbf{e}_{z}\otimes \mathbf{e}_{z}\\{\boldsymbol{\nabla}}{\boldsymbol{S}}={}\quad&{\frac{\partial S_{rr}}{r\partial}}\mathbf{e}_{r}\otimes \mathbf{e}_{r}+{\frac{\partial S_{rr}}{z\partial}}{e}_{r}\otimes ~\mathbf ~\mathbf{e}_{r}\otimes \m ~\mathbf.athb F{e}_{r}\otimes}\left[{\frac{\partial S_{rr}}{\partial \theta}}-(S_{\theta r}+S_{r\theta})\right]~\mathbf,{\frac{\partial S_{r\theta}}{r\partial}}{e}_{r}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{r}+{\frac{\partial S_ ~\mathbf{e}_{z}+{\frac{1}{r}{e}_{r}\otimes \mathbf{e}_{r}\otimes \mathbf{e}_{\theta}\\{}+{}& \mathbf.{r\t 헤타}}{z\partial}};{\frac{\partial S_{rz}}{r\partial}}{e}_{r}\otimes \ma ~\mathbf{e}_{r}\otimes{e}_{\theta}\otimes \mathbf{e}_{z}+{\frac{1}{r}}\left[{\frac{\partial S_{r\theta}}{\partial \theta}}+(S_{rr}-S_{\theta \theta})\right]~\mathbf \mathbf{e}_{r}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{\theta}\\{}+{}& ~\mathbf.thbf {e}_{z}\otimes}}{e}_{r}\otimes \mathbf{e}_{z}\otimes \mathbf{e}_{\theta}\\{}+{}& \left[{\frac{\partial S_{rz}}{\partial \theta}}-S_{\theta z}\right]~\mathbf{e}_{r}\otimes \mathbf{e}_{z}\otimes \mathbf{e}_{z}+{\frac{1}{r}~\mathbf,{\frac{\partial S_{\theta r}}{r\partial}}~\mat{e}_{r}+{\frac{\partial S_{rz}}{z\partial}\mathbf.hbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta}\\{}+{}&,{\frac{\partial S_{\theta \theta}}{r\partial}}~\mathbf{e}_{\theta}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{r}+{\frac{\partial S_{\theta \theta}}{z\partial}}{e}_{\theta}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{z}+{\frac{1}{r}}\left는 경우에는{\frac{\partial S_{\theta \theta}}{\theta\partial}~\mathbf.}+(S _{r\theta}+S_{r\theta})\right]~\mathbf{e}_{\theta}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{\theta}\\{}+{}&,{\frac{\partial S_{\theta z}}{r\partial}}{e}_{\theta}\otimes \mathbf{e}_{z}\otimes \mathbf{e}_{r}+{\frac{\partial S_{\theta z}}{z\partial}}~\mathbf ~\mathbf{e}_{\theta}\otimes \mathbf{e}_{z}\otimes \mathbf{e.}_{ Z}+{\frac{1}{r}}\mathbf{e}_{z}\otimes \mathbf{e}_{\theta}\\{}+{}&,{\frac{\partial S_{zr}}{r\partial}}\mathbf{e}_{r}\otimes \mathbf{e}_{r}+{\frac{\partial S_{zr}}{z\partial}}{e}_{z}\otimes ~\mathbf ~\mathbf \mathbf{e.{e}_{\theta}\otimes{e}_{z}\otimes \left[{\frac{\partial S_{\theta z}}{\partial \theta}}+S_{rz}\right]~\mathbf}_{ R}}\left[{\frac{\partial S_{zr}}{\partial \theta}}-S_{z\theta}\right]~\mathbf{e}_{z}\otimes \mathbf{e}_{r}\otimes{e}_{\theta}\\{}+{}& \mathbf,{\frac{\partial S_{z\theta}}{r\partial}}~\mathbf{e}_{z}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{r}+{\frac{\partial S_{z\theta}}{z\partial}\mathbf{e}_{z}+{\frac{1}{r}\otimes.}~\m Athbf{e}_{z}\otimes{e}_{z}+{\frac{1}{r}}\left[{\frac{\partial S_{z\theta}}{\partial \theta}}+S_{zr}\right]~\mathbf{e}_{z}\otimes \mathbf{e}_{\theta}\otimes \mathbf{e}_{\theta}\\{}+{}&,{\frac{\partial S_{zz}}{r\partial}\mathbf}~\mathbf{e}_{z}\otimes \mathbf{e}_{z}\otimes{e}_{r}+{\frac \mathbf{e}_{\theta}\otimes \mathbf.{\p artial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}} 텐서장 발산 텐서 필드 T x {\displaystyle {\boldsymbol {T}(\mathbf {x} 차이 는 재귀적 관계를 사용하여 정의된다
( ∇ ⋅ T ) ⋅ c = ∇ ⋅ ( c ⋅ T T ) ; ∇ ⋅ v = tr ( ∇ v ) {\displaystyle ({\boldsymbol {\nabla }}\cdot {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot \left(\mathbf {c} \cdot {\boldsymbol {T}}^{\textsf {T}}\right)~;\qquad {\boldsymbol {\nabla }}\cdot \mathbf {v} ={\text{tr}}({\boldsymbol {\nabla }}\mathbf {v} )} 여기서 c 는 임의 상수 벡터, v 는 벡터 필드다. T {\ displaystyle {\boldsymbol {T} n > 1의 텐서 필드인n-1 의 텐서인 것이다.
데카르트 좌표, 평행 좌표. 참고: 반복 지수를 요약하는 아인슈타인 종합 관례 가 아래에 사용된다. 데카르트 좌표계에서는 벡터 필드 v 와 2차 텐서 필드 S {\ displaystyle {\boldsymbol{S}} .
∇ ⋅ v = ∂ v i ∂ x i = v i , i ∇ ⋅ S = ∂ S i k ∂ x i ⋅ e k = S i k , i ⋅ e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &={\frac {\partial v_{i}}{\partial x_{i}}}=v_{i,i}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\frac {\partial S_{ik}}{\partial x_{i}}}\cdot ~\mathbf {e} _{k}=S_{ik,i}\cdot ~\mathbf {e} _{k}\end{aligned}}} 여기서 부분파생상품에 대한 텐서 인덱스 표기법 을 가장 오른쪽 식에 사용한다. 참고:
∇ ⋅ S ≠ ∇ ⋅ S T . {\displaystyle {\boldsymbol {\nabla}\cdot {\boldsymbol {S}\boldsymbol {\nabla}}}\boldsymbol {S}^{\textsf {T}. } 대칭 2차 시제의 경우, 그 차이도 종종 다음과[4]
∇ ⋅ S = ∂ S k i ∂ x i ⋅ e k = S k i , i ⋅ e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\cfrac {\partial S_{ki}}{\partial x_{i}}}\cdot ~\mathbf {e} _{k}=S_{ki,i}\cdot ~\mathbf {e} _{k}\end{aligned}}} 위의 표현식은 데카르트 구성 요소 양식(흔히 div S {\ displaystyle {\boldsymbol {\nabla }}\cdot {\ boldsymbol S}) 사용되기 이러한 정의는 이 글의 나머지 부분과 일치하지 않는다는 점에 유의하십시오(곡선 좌표에 대한 섹션 참조).
차이점은 S displaystyle boldsymbol{S} 이것은 예에 의해 증명된다. 데카르트 좌표계에서 두 번째 순서 텐서(매트릭스) S {\ displaystyle \mathbf {S}은( v {\ displaystyle \mathbf {v} .
∇ ⋅ ( ∇ v ) = ∇ ⋅ ( v i , j e i ⊗ e j ) = v i , j i e i ⋅ e i ⊗ e j = ( ∇ ⋅ v ) , j e j = ∇ ( ∇ ⋅ v ) ∇ ⋅ [ ( ∇ v ) T ] = ∇ ⋅ ( v j , i e i ⊗ e j ) = v j , i i e i ⋅ e i ⊗ e j = ∇ 2 v j e j = ∇ 2 v {\displaystyle{\begin{정렬}{\boldsymbol{\nabla}}\cdot \left({\boldsymbol{\nabla}}\mathbf{v}\right)&, ={\boldsymbol{\nabla}}\cdot \left(v_{i,j}~\mathbf{e}_{나는}_{j}\mathbf{e}\otimes \right)=v_{i,ji}~\mathbf{e}_{나는}\cdot \mathbf{e}_{나는}\otimes 즉{e}_ᆴ=\left({\boldsymbol{\nabla}}\cdot \mathbf{v}\right)_{,j}~\mathbf{e}\mathbf.{j}= {\\cdsymbol {\cdla }\왼쪽 \cdmbol {\cdla }\mathbf {v}\오른쪽) \\{\boldsymbol{\nabla}}\cdot \left[\left({\boldsymbol{\nabla}}\mathbf{v}\right)^{\textsf{T}}\right]&, ={\boldsymbol{\nabla}}\cdot \left(v_{j,i}~\mathbf{e}_{나는}_{j}\mathbf{e}\otimes \right)=v_{j,ii}~\mathbf{e}_{나는}\cdot \mathbf{e}_{나는}\otimes{e}_{j}={\boldsymbol{\nabla}\mathbf}^{2}v_{j}~\mathbf{e}_{j}={\boldsymbol{\nabla}}^{.2}\m atsbf {v} \end{aigned}} 마지막 방정식은 대체 정의/해석과[4]
( ∇ ⋅ ) 알트 ( ∇ v ) = ( ∇ ⋅ ) 알트 ( v i , j e i ⊗ e j ) = v i , j j e i ⊗ e j ⋅ e j = ∇ 2 v i e i = ∇ 2 v {\displaystyle {\begin{aligned}\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left({\boldsymbol {\nabla }}\mathbf {v} \right)=\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,jj}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\cdot \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2 }}v_{i}~\mathbf {e} _{i}={\mathsymbol {\bla }^{2}\mathbf {v}\end{aigned}}}}} 곡선 좌표 참고: 반복 지수를 요약하는 아인슈타인 종합 관례 가 아래에 사용된다. 곡선 좌표에서 벡터 필드 v 와 2차 텐서 필드 {\ displaystyle {\boldsymbol {S}
∇ ⋅ v = ( ∂ v i ∂ ξ i + v k Γ i k i ) ∇ ⋅ S = ( ∂ S i k ∂ ξ i − S l k Γ i i l − S i l Γ i k l ) g k {\displaystyle {\begin{aigned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &=\좌({\cfrac {\partial v^{i}}}}{partial \xi}}}+v^{k}~\Gamma _{i}\i}\rigma) \\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left({\cfrac {\partial S_{ik}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ii}^{l}-S_{il}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{k}\end{aligned}}} 좀 더 일반적으로는
∇ ⋅ S = [ ∂ S i j ∂ q k − Γ k i l S l j − Γ k j l S i l ] g i k b j = [ ∂ S i j ∂ q i + Γ i l i S l j + Γ i l j S i l ] b j = [ ∂ S j i ∂ q i + Γ i l i S j l − Γ i j l S l i ] b j = [ ∂ S i j ∂ q k − Γ i k l S l j + Γ k l j S i l ] g i k b j {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~ S^{lj}+\감마 _{il}^{j}~~ S^{{il}\오른쪽]~\mathbf {b} _{j}\[8pt]&=\왼쪽[{\cfrac {\partial S_{~j}^{i}}}}{\partial q^{i}}}}}}+\감마 _{il}^{i}}}}}. S_{~j}^{l}-\Gamma _{ij}^{l}~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{\partial q^{k}}}-\Gamma _{ik}^{l}~S_{l}^{~j}+\Gamma _{kl}^{j}~ S_{i}^{~l}\오른쪽]~g^{ik}~\mathbf {b} _{j}\end{aigned}}}}
원통 극좌표 원통형 극좌표
∇ ⋅ v = ∂ v r ∂ r + 1 r ( ∂ v θ ∂ θ + v r ) + ∂ v z ∂ z ∇ ⋅ S = ∂ S r r ∂ r e r + ∂ S r θ ∂ r e θ + ∂ S r z ∂ r e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e r + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ + 1 r [ ∂ S θ z ∂ θ + S r z ] e z + ∂ S z r ∂ z e r + ∂ S z θ ∂ z e θ + ∂ S z z ∂ z e z {\displaystyle{\begin{정렬}{\boldsymbol{\nabla}}\cdot\mathbf{v}=\quad&{\frac{\partial v_{r}}{r\partial}}+{\frac{1}{r}}\left({\frac{\partial v_{\theta}}{\partial \theta}}+v_{r}\right)+{\frac{\partial v_{z}}{z\partial}}\\{\boldsymbol{\nabla}}\cdot{\boldsymbol{S}}=\quad&{\frac{\partial S_{rr}}{r\partial}}~\mathbf{e}.{r}+{\fr Ac{\partial S_{r\theta}}{r\partial}}~\mathbf{e}_{\theta}+{\frac{\partial S_{rz}}{r\partial}};{\frac{1}{r}}\left[{\frac{\partial S_{\theta r}}{\partial \theta}}+(S_{rr}-S_{\theta \theta})\right]~\mathbf{e}_{r}+{\frac{1}{r}}\left는 경우{\frac{\partial S_{\theta \theta}}{\theta\partial}}+(S_{r\theta}+S_{\theta{e}_{z}\\{}+{}& ~\mathbf.r}) \right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}} 텐서 필드의 컬 order-n > 1 텐서 필드 Tx {\displaystyle {\boldsymbol {T}(\mathbf {x})} 컬 도 재귀 관계를 사용하여 정의된다
( ∇ × T ) ⋅ c = ∇ × ( c ⋅ T ) ; ( ∇ × v ) ⋅ c = ∇ ⋅ ( v × c ) {\displaystyle ({\boldsymbol {\nabla }}\times {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {T}})~;\qquad ({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )} 여기서 c 는 임의 상수 벡터, v 는 벡터 필드다.
1차 텐서(벡터) 필드의 컬 벡터 필드 v 와 임의 상수 벡터 c 를 고려하십시오. 색인 표기법에서 교차 제품은 다음과 같이 주어진다.
v × c = ε i j k v j c k e i {\displaystyle \mathbf {v} \mathbf {c} =\varepsilon _{ijk}~{j}~{k}~\mathbf {e} _{i}}}} 여기서 ε i j k {\ displaystyle \varepsilon _{ijk} 순열 기호 로서 그러면.
∇ ⋅ ( v × c ) = ε i j k v j , i c k = ( ε i j k v j , i e k ) ⋅ c = ( ∇ × v ) ⋅ c {\displaystyle {\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )=\varepsilon _{ijk}~v_{j,i}~c_{k}=(\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} } 그러므로
∇ × v = ε i j k v j , i e k {\displaystyle {\mathsymbol {\bla }\mathbf {v} =\varepsilon _{ij}~{j}~\mathbf {e} _{k}}}} 2차 텐서 필드의 컬 2차 텐서 S {\ displaystyle {\boldsymbol {S}
c ⋅ S = c m S m j e j {\displaystyle \mathbf {c} \cdot {\boldsymbol {S}=c_{m}~ S_{mj}~\mathbf {e} _{j}} 따라서, 1차 텐서 필드의 컬의 정의를 사용하여,
∇ × ( c ⋅ S ) = ε i j k c m S m j , i e k = ( ε i j k S m j , i e k ⊗ e m ) ⋅ c = ( ∇ × S ) ⋅ c {\displaystyle {\boldsymbol {\nabla}\time(\mathbf {c}\c}\cdot {\boldsymbol {S})=\varepsilon _{ijk}~c_{m}~}~}~ S_{mj,i}~\mathbf {e} _{k}=(\varepsilon _{ijk}). S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e}_{m}\cdot \mathbf {c} =({\boldsymbol {\nabla }}})\cdot \mathbf {c}}}}}} 그러므로, 우리는
∇ × S = ε i j k S m j , i e k ⊗ e m {\displaystyle {\boldsymbol {\nabla }\time {\boldsymbol {S}=\varepsilon _{ijk}~ S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m}} 텐서 필드의 컬링과 관련된 ID 텐서 필드의 컬과 관련하여 가장 일반적으로 사용되는 ID인 T {\ displaystyle {\boldsymbol T} (
∇ × ( ∇ T ) = 0 {\displaystyle {\boldsymbol {\nabla}}\time({\boldsymbol {\nabla}}}{\boldsymbol {T})={\boldsymbol {0}}} 이 신분은 모든 주문의 텐서 분야를 포괄한다. 2차 시제의 중요한 경우, S {\ displaystyle {\boldsymbol{S},
∇ × ( ∇ S ) = 0 ⟹ S m i , j − S m j , i = 0 {\displaystyle {\boldsymbol {\nabla}}\time({\boldsymbol {}}{\boldsymbol {S}}}}={\boldsymbol {0}}\boldsyd\implies \quads_{mi}S_{mj. 2차 텐서 결정요인의 파생상품 2차 주문 텐서 A {\ displaystyle {\boldsymbol{A}}
∂ ∂ A 퇴장시키다 ( A ) = 퇴장시키다 ( A ) [ A − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol{A}}}\det({\boldsymbol{A}})=\det({\boldsymbol {A})~\put[{\boldsymboldmbol{1}^{-1}^{T}}. 정형외과적 기준으로 A {\ displaystyle {\boldsymbol{A}} A 로 쓸 수 있다 이 경우 오른손은 행렬의 공분자에 해당한다.
2차 텐서 불변제 파생상품 2차 시제의 주요 불변제는 다음과 같다.
I 1 ( A ) = tr A I 2 ( A ) = 1 2 [ ( tr A ) 2 − tr A 2 ] I 3 ( A ) = 퇴장시키다 ( A ) {\displaystyle {\reasoned} I_{1}({\boldsymbol{A})&={\text{tr}{\boldsymbol{A}\\ I_{{\boldsymbol{A}}&={\frac {1}{1}:{2}}: 왼쪽[({\text{tr}{\boldsymbol{A}})^{2}-{\text}{{{\boldsymbol}{A}}}{\boldmbmbol}^{2}}\오른쪽]\ \I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}}\ended}}}} A {\ displaystyle {\boldsymbol{A}}
∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = 퇴장시키다 ( A ) [ A − 1 ] T = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle {\begin{aigned}{\frac {\partial I_{1}{1}{1}{\partial {1}\boldsymbol{1}}}}={\partial {\partial I_{partial}{partial}{\partial}}{partial {\bymbolline}}}}}}}}}}}}}}}}}}}}} I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}= I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+ I_{2}~{\boldsymbol {\mathit {1}\오른쪽)^{\textsf {T}\end{aigned}}} 증명 결정요인의 파생어로 우리는 알고 있다. ∂ I 3 ∂ A = 퇴장시키다 ( A ) [ A − 1 ] T . {\displaystyle {{\frac {\partial I_{3}}{\partial {\boldsymbol{A}}}}}}\det({\boldsymbol{A}}}}}})~왼쪽[{\boldsymbol{A}^{-1}^{\textsf{T}}}}}} 다른 두 불변성의 파생상품에 대해서는 특성 방정식으로 돌아가자.
퇴장시키다 ( λ 1 + A ) = λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) . {\displaystyle \det(\lambda ~{\boldsymbol {1}+{\boldsymbol {A})=\lambda ^{3}+ I_{1}({\boldsymbol{A})~\lambda ^{2}+ I_{2}({\boldsymbol{A})~\lambda +I_{3}({\boldsymbol{A})~.} 텐서의 결정요인과 동일한 접근법을 사용하여, 우리는 다음과 같은 것을 보여줄 수 있다.
∂ ∂ A 퇴장시키다 ( λ 1 + A ) = 퇴장시키다 ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.} 이제 왼손은 다음과 같이 확장할 수 있다.
∂ ∂ A 퇴장시키다 ( λ 1 + A ) = ∂ ∂ A [ λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) ] = ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A . {\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+ I_{1}({\boldsymbol{A})~\lambda ^{2}+ I_{2}({\boldsymbol{A})~\lambda +I_{3}({\boldsymbol{A}}}\오른쪽]\ \&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~. \end{정렬}}} 그러므로,
∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A = 퇴장시키다 ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T {\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}} 또는
( λ 1 + A ) T ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = 퇴장시키다 ( λ 1 + A ) 1 . {\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\bo ldsymbol {\mathit{1}~.} 오른쪽을 확장하고 왼쪽의 용어를 분리하면
( λ 1 + A T ) ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 {\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+ I_{1}~\lambda ^{2}+ I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit{1}:{1}:{\boldsymbol {\mathit{1}}}} 또는
[ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ ] 1 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{ligned}\왼쪽[{\frac {\partial I_{1}:{1}{\partial {\\\boldsymbol{A}}}}}*\lambda ^{3}\right. &\left.+{\frac{\partial I_{2}}{\partial{\boldsymbol{A}}}}~\lambda ^{2}+{\frac{\partial I_{3}}{\partial{\boldsymbol{A}}}}~\lambda\right 뻗는다{\boldsymbol{\mathit{1}}}+{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{1}}{\partial{\boldsymbol{A}}}}~\lambda ^{2}+{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{2}}{\partial{\bolds. 임볼{A}}}~\lambda +{\boldsymbol{A}^{{T}}\cdot{\frac{\partial I_{3}}{\partial {\boldsymbol{A}}}}}}}{partial {\bolda ^{3}+} I_{1}~\lambda ^{2}+ I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit{1}}. \end{정렬}}} 만일 우리 0 := 1 displaystyle I_{0}:}을( 4 := displaystyle }= 0}
[ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ + ∂ I 4 ∂ A ] 1 + A T ⋅ ∂ I 0 ∂ A λ 3 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ I 0 λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{ligned}\왼쪽[{\frac {\partial I_{1}:{1}{\partial {\\\boldsymbol{A}}}}}*\lambda ^{3}\right. &\left.+{\frac{\partial I_{2}}{\partial{\boldsymbol{A}}}}~\lambda ^{2}+{\frac{\partial I_{3}}{\partial{\boldsymbol{A}}}}~\lambda +{\frac{\partial I_{4}}{\partial{\boldsymbol{A}}}}\right 뻗는다{\boldsymbol{\mathit{1}}}+{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{0}}{\partial{\boldsymbol{A}}}}~\lambda ^{3}+{\boldsymbol{A}}^{\text. sf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[ I_{0}~\lambda ^{3}+ I_{1}~\lambda ^{2}+ I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit{1}}. \end{정렬}}} λ의 다양한 힘을 담은 용어들을 모아, 우리는
λ 3 ( I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A ) + λ 2 ( I 1 1 − ∂ I 2 ∂ A 1 − A T ⋅ ∂ I 1 ∂ A ) + λ ( I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A ) + ( I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A ) = 0 . {\displaystyle{\begin{정렬}\lambda ^{3}&, \left(I_{0}일 경우~{\boldsymbol{\mathit{1}}}-{\frac{\partial I_{1}}{\partial{\boldsymbol{A}}}}일{\boldsymbol{\mathit{1}}}-{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{0}}{\partial{\boldsymbol{A}}}}\right)+\lambda ^{2}\left(I_{1}~{\boldsymbol{\mathit{1}}}-{\frac{\partial I_{2}}{\partial.{\b Oldsymbol{A}}}}~{\boldsymbol{\mathit{1}}}-{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{1}}{\partial{\boldsymbol{A}}}}\right)+\\&, \qquad\qquad \lambda \left(I_{2}~{\boldsymbol{\mathit{1}}}-{\frac{\partial I_{3}}{\partial{\boldsymbol{A}}}}~{\boldsymbol{\mathit{1}}}-{\boldsymbol{A}}^{\textsf{T}}\cdot{\frac{\partial I_{2.}}{) partial {\boldsymbol {A}}}}\right)+\left(I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right)=0~. \end{정렬}}} 그러면 λ의 차익거래를 발동하면, 우리는
I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A = 0 I 1 1 − ∂ I 2 ∂ A 1 − I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A = 0 I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A = 0 . {\displaystyle {\reasoned} I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}&=0\\ I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=0\\ I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=0~. \end{정렬}}} 라는 뜻을 내포하고 있다.
∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle{\begin{aigned}{\frac {\partial I_{1}{1}:{1}{\partial {\boldsymbol{A}}}&={\boldsymbol {1}\partial I_{1}}}}{\partial {\boldmbol {A}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} I_{1}~{\boldsymbol {\mathit{1}-{\boldsymbol{A}}^{\textsf{T}\\\\prac {\partial I_{3}}{\partial {\boldsymbol{A}}}}&= I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+ I_{2}~{\boldsymbol {\mathit {1}\오른쪽)^{\textsf {T}\end{aigned}}}
2차 아이덴티티 텐서 파생상품 1 {\ displaystyle {\boldsymbol {\mathit{1}} 그런 다음 2차 주문 텐서 {\ displaystyle {\boldsymbol{A}}
∂ 1 ∂ A : T = 0 : T = 0 {\displaystyle {\frac{\partsymbol{\mathit{1}:{1}{{\partial {\boldsymbol{T}}}}={\boldsymbol {0}}:{\boldsymbol{T}}}}}}}}}}}}}}}\boldsymathymaximbol. 1{\ displaystyle {\boldsymbol {\mathit{1}}} A {\ displaystyle {\boldsymbol {A} .
자체와 관련된 2차 텐서의 파생 모델 A {\ displaystyle {\boldsymbol{A}} 그러면.
∂ A ∂ A : T = [ ∂ ∂ α ( A + α T ) ] α = 0 = T = I : T {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}} 그러므로
∂ A ∂ A = I {\displaystyle {\frac {\boldsymbol{A}}{\partial {\boldsymbol{A}}}={\boldsymbol {\mathsf{I}}}}}}}}}}} 여기서 I {\ displaystyle {\boldsymbol {\mathsf{I}}}} 직교 기준과 관련된 색인 표기법
I = δ i k δ j l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsmbol {I}}=\delta _{ik}~\delta _{jl}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{{l}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 이 결과는 다음과 같은 것을 암시한다.
∂ A T ∂ A : T = I T : T = T T {\displaystyle {\frac {\partial {\boldsymbol {A}}^{\textsf {T}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}^{\textsf {T}}:{\boldsymbol {T}}={\boldsymbol {T}}^{\textsf {T}}} 어디에
I T = δ j k δ i l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{\textsf {T}}=\delta _{jk}~\delta _{il}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}} 따라서 텐서 A {\ displaystyle {\boldsymbol {A}}
∂ A ∂ A = I ( s ) = 1 2 ( I + I T ) {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~\left({\boldsymbol {\mathsf {I}}}+{\boldsymbol {\mathsf {I}}}^{\textsf {T}}\right)} 여기서 대칭 4차 순서 ID 텐서는
I ( s ) = 1 2 ( δ i k δ j l + δ i l δ j k ) e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~(\delta _{ik}~\delta _{jl}+\delta _{il}~\delta _{jk})~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}} 2차 텐서 역순의 파생상품 A {\ displaystyle {\boldsymbol {A} T {\ displaystyle {\boldsymbol {T}
∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol{A}}}\왼쪽({\boldsymbol{A}^{1}\right): {\boldsymbol{T}=-{\boldsymbol{A}^{-1}\cdot {\boldsymbol {T}\boldsymbol{A}^{-1}} 직교 기준과 관련된 색인 표기법
∂ A i j − 1 ∂ A k l T k l = − A i k − 1 T k l A l j − 1 ⟹ ∂ A i j − 1 ∂ A k l = − A i k − 1 A l j − 1 {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{ik}^{-1}~T_{kl}~A_{lj}^{-1}\implies {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-A_{ik}^{-1}~A_{lj}^{-1}} 우리는 또한 가지고 있다.
∂ ∂ A ( A − T ) : T = − A − T ⋅ T T ⋅ A − T {\displaystyle {\frac {\partial }{\partial {\boldsymbol{A}}}\왼쪽({\boldsymbol{A}^{-{\textsf{T}}\right): {\boldsymbol{T}=-{\boldsymbol{A}^{-{\textsf{T}}\cdot {\boldsymbol{T}^{\boldsymbol{A}}}}}}}}}}}\cdot {\cdot{-{{\cdextsf{{{{{{\cdextsf}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} 색인 표기법
∂ A j i − 1 ∂ A k l T k l = − A j k − 1 T l k A l i − 1 ⟹ ∂ A j i − 1 ∂ A k l = − A l i − 1 A j k − 1 {\displaystyle {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{jk}^{-1}~T_{lk}~A_{li}^{-1}\implies {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}=-A_{li}^{-1}~A_{jk}^{-1}} 텐서 A {\ displaystyle {\boldsymbol{A}}
∂ A i j − 1 ∂ A k l = − 1 2 ( A i k − 1 A j l − 1 + A i l − 1 A j k − 1 ) {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-{\cfrac {1}{2}}\left(A_{ik}^{-1}~A_{jl}^{-1}+A_{il}^{-1}~A_{jk}^{-1}\right)} 증명 그것을 상기하다. ∂ 1 ∂ A : T = 0 {\displaystyle {\frac {\partial {\boldsymbol {1}:{1}{{\partial {\boldsymbol {A}}}}}, {\boldsymbol {0}}}} A 1 ⋅ A 1 {\ displaystyle {\boldsymbol{A}}^{-1}\cdot{\boldsymbol{A}}={\boldsymbol {\mathit{1}}}}}}}:{\ {
∂ ∂ A ( A − 1 ⋅ A ) : T = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}\왼쪽({\boldsymbol {A}}^{\1}\boldsymbol {A}\right): {\boldsymbol{T}={\boldsymbol {\mathit{0}}}} 두 번째 주문 텐더에 제품 규칙 사용
∂ ∂ S [ F 1 ( S ) ⋅ F 2 ( S ) ] : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 + F 1 ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial}{\partial {\boldsymbol {S}}[{\boldsymbol{F}}}{\boldsymbol{S}}}\cdot {\boldsymbol{F}}}}}}}: {\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} 우리는 얻는다.
∂ ∂ A ( A − 1 ⋅ A ) : T = ( ∂ A − 1 ∂ A : T ) ⋅ A + A − 1 ⋅ ( ∂ A ∂ A : T ) = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol{A}}}}({\boldsymbol{A}}}}}): {\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}+{\boldsymbol {A}}^{-1}\cdot \left({\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)={\boldsymbol {\mathit {0}}}} 또는
( ∂ A − 1 ∂ A : T ) ⋅ A = − A − 1 ⋅ T {\displaystyle \left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}} 그러므로
∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol{A}}}\왼쪽({\boldsymbol{A}^{1}\right): {\boldsymbol{T}=-{\boldsymbol{A}^{-1}\cdot {\boldsymbol {T}\boldsymbol{A}^{-1}}
부품별 통합 도메인 Ω {\displaystyle \Oomega γ {\displaystyle \Gamma} n {\ displaystyle \mathbf n}} 연속체 역학에서 텐서 유도체와 관련된 또 다른 중요한 작업은 부품별 통합이다. 부품별 통합 공식은 다음과 같이 쓸 수 있다.
∫ Ω F ⊗ ∇ G d Ω = ∫ Γ n ⊗ ( F ⊗ G ) d Γ − ∫ Ω G ⊗ ∇ F d Ω {\displaystyle \int _{\Omega }{\boldsymbol {F}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {G}}\,{\rm {d}}\Omega =\int _{\Gamma }\mathbf {n} \otimes ({\boldsymbol {F}}\otimes {\boldsymbol {G}})\,{\rm {d}}\Gamma -\int _{\Omega }{\boldsymbol {G}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {F}}\,{\rm {d}}\Omega } 여기서 F {\ displaystyle {\boldsymbol {F} G {\ displaystyle {\boldsymbol {G} n displaysty mathbf n } . uct 연산자, 그리고 ∇{\ displaystyle {\\symbol {\bla }}} F {\ displaystyle {\boldsymbol{F}} 발산 정리 를 얻는다.
∫ Ω ∇ G d Ω = ∫ Γ n ⊗ G d Γ . {\displaystyle \int_{\Oomega}{\boldsymbol{\nabla}}{\boldsymbol {G}\rm{d}\Oomega =\int_{\Gamma}\mathbf{n}\t}\otimes{\rm {d}\gm}}\gma, \gm, \gm, \gm, \gm, \gm,\gm, \gm, \gm. } 우리는 카트리지수 표기법에서 부분별 통합 공식을 다음과 같이 표현할 수 있다.
∫ Ω F i j k . . . . G l m n . . . , p d Ω = ∫ Γ n p F i j k . . . G l m n . . . d Γ − ∫ Ω G l m n . . . F i j k . . . , p d Ω . {\displaystyle \int _{\Oomega }F_{ijk.... }\,G_{lmn...,p}\,{\rm {d}\\오메가 =\int_{\\\\\\\감마 }n_{p}\,F_{ijk... }\,G_{lmn... }\,{\rm{d}\감마 -\int _{\Oomega }G_{lmn... }\,F_{ijk...,p}\,{\rm {d}\오메가 \, } 텐서 제품 연산이 하나의 인덱스의 수축이고 그라데이션 연산이 다이버전스인 특별 , displaystyle boldsymbol{ displaystyle boldsymbol G}}
∫ Ω F ⋅ ( ∇ ⋅ G ) d Ω = ∫ Γ n ⋅ ( G ⋅ F T ) d Γ − ∫ Ω ( ∇ F ) : G T d Ω . {\displaystyle \int _{\Omega }{\boldsymbol {F}}\cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {G}})\,{\rm {d}}\Omega =\int _{\Gamma }\mathbf {n} \cdot \left({\boldsymbol {G}}\cdot {\boldsymbol {F}}^{\textsf {T}}\right)\,{\rm {d}}\Gamma -\int _{\Omega }({\boldsymbol {\nabla }}{\boldsymbol {F}}):{\boldsymbol {G}}^{\textsf {T}}\,{\rm {d}}\Omega \,. } 색인 표기법
∫ Ω F i j G p j , p d Ω = ∫ Γ n p F i j G p j d Γ − ∫ Ω G p j F i j , p d Ω . {\displaystyle \int _{\Omega }F_{ij}\,G_{pj,p}\,{\rm {d}}\Omega =\int _{\Gamma }n_{p}\,F_{ij}\,G_{pj}\,{\rm {d}}\Gamma -\int _{\Omega }G_{pj}\, F_{ij,p}\,{\rm {d}\오메가 \, } 참고 항목 참조 ^ J. C. 시모와 T. J. R. 1998년 휴즈, 컴퓨터 비탄력성 , 스프링거 ^ J. E. 마스덴과 T. J. R. 휴즈, 2000년 탄력의 수학 재단 도버 ^ Ogden, R. W., 2000, 비선형 탄성 변형 , 도버. ^ a b Hjelmstad, Keith (2004). Fundamentals of Structural Mechanics . Springer Science & Business Media. p. 45. ISBN 9780387233307 ![{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd4359c84cf58e41375f33503df17f688456372)




![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b946f4d0b2712f1f6b890f4b5b45a2bb70b7c7)







![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b97c637955623ac4900c4f80d6ea1bdef354076a)





![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32c53f2457fa27a03ca72cbd48debb1255593088)













![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} &=\left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {T}}(x_{1}+\alpha c_{1},x_{2}+\alpha c_{2},x_{3}+\alpha c_{3})\right|_{\alpha =0}\equiv \left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}~{\boldsymbol {T}}(y_{1},y_{2},y_{3})\right|_{\alpha =0}\\&=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~{\cfrac {\partial y_{1}}{\partial \alpha }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{2}}}~{\cfrac {\partial y_{2}}{\partial \alpha }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~{\cfrac {\partial y_{3}}{\partial \alpha }}\right]_{\alpha =0}=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~c_{3}\right]_{\alpha =0}\\&={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{3}}}~c_{3}\equiv {\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~c_{i}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~(\mathbf {e} _{i}\cdot \mathbf {c} )=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i}\right]\cdot \mathbf {c} \qquad \square \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a0f6d278fcbf035df564ec347a8b535989d49a5)








![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad &{\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dac8a7176f71ff5f55be4fb2abe9bfa6df0eba71)




 정의로
정의로 


![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864380cd0a82178354a80ee58109fc0519c149ba)


![\begin{align}
\boldsymbol{\nabla}\cdot\boldsymbol{S} & = \left[\cfrac{\partial S_{ij}}{\partial q^k} - \Gamma^l_{ki}~S_{lj} - \Gamma^l_{kj}~S_{il}\right]~g^{ik}~\mathbf{b}^j \\[8pt]
& = \left[\cfrac{\partial S^{ij}}{\partial q^i} + \Gamma^i_{il}~S^{lj} + \Gamma^j_{il}~S^{il}\right]~\mathbf{b}_j \\[8pt]
& = \left[\cfrac{\partial S^i_{~j}}{\partial q^i} + \Gamma^i_{il}~S^l_{~j} - \Gamma^l_{ij}~S^i_{~l}\right]~\mathbf{b}^j \\[8pt]
& = \left[\cfrac{\partial S_i^{~j}}{\partial q^k} - \Gamma^l_{ik}~S_l^{~j} + \Gamma^j_{kl}~S_i^{~l}\right]~g^{ik}~\mathbf{b}_j
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85fad1b0228d189867b87f1d770c3968e4394860)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8cd23836a8e6cc12150592c3964d95d6a3f94e9)


 , 다른 말로 Levi-Civita 기호라고 한다.그러면.
, 다른 말로 Levi-Civita 기호라고 한다.그러면.







![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a229cf1ec76d8d0d6c4ebf0e55e24a9289524d0f)

![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}\det({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right|_{\alpha =0}\\&=\left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}\det \left[\alpha ~{\boldsymbol {A}}\left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}\\&=\left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\det \left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a9e26633dd346889937f6b609c79f900050f672)


![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {\rm {d}}{{\rm {d}}\alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\left({\cfrac {1}{\alpha ^{3}}}+I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~{\cfrac {1}{\alpha ^{2}}}+I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~{\cfrac {1}{\alpha }}+I_{3}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right)\right]\right|_{\alpha =0}\\&=\left.\det({\boldsymbol {A}})~{\cfrac {\rm {d}}{{\rm {d}}\alpha }}\left[1+I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha +I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}+I_{3}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{3}\right]\right|_{\alpha =0}\\&=\left.\det({\boldsymbol {A}})~\left[I_{1}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}})+2~I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha +3~I_{3}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}\right]\right|_{\alpha =0}\\&=\det({\boldsymbol {A}})~I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32f6101c7327a2c7f04fd67775072edabd75b498)


![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\det({\boldsymbol {A}})~{\text{tr}}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}:{\boldsymbol {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfbbc8e843ee49828711668186ed4e5faa93384)
![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf1328c61318cc48aa33f6c0b580b55e268f7ebe)
![\begin{align}
I_1(\boldsymbol{A}) & = \text{tr}{\boldsymbol{A}} \\
I_2(\boldsymbol{A}) & = \frac{1}{2} \left[ (\text{tr}{\boldsymbol{A}})^2 - \text{tr}{\boldsymbol{A}^2} \right] \\
I_3(\boldsymbol{A}) & = \det(\boldsymbol{A})
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)
![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19cf1ad5bce9774bf510c8818f4b90e32c4f2640)
![{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9dd4a16751516c5e316be643e40ce0babf1c1df)

![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be1b29969a25190e4efad41db9d76f11e8a8079)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4ad226ea72ae236eaddfe419007ff6de53d55d)
![{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3993a79ec1f95da1b9e188243300861ee7ee2e45)
![{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/782fb846f7870890e72cda9dbeba6e80dfc064b0)
![{\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9d08c98dc866bcc330678342ca3c391da0042a)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6174aae82fa111cbe2235a21c275bb7bc0e243b4)
 ) 정의하고 I
) 정의하고 I 
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8169e3ea8470a718a349e0d8a73e1fb7c162914)



 두 번째 순서로 한다.그런 다음 2차 주문
두 번째 순서로 한다.그런 다음 2차 주문 
![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)

 (는) 네 번째 순서 ID 텐서다.직교 기준과 관련된 색인 표기법
(는) 네 번째 순서 ID 텐서다.직교 기준과 관련된 색인 표기법












![\frac{\partial }{\partial \boldsymbol{S}}[\boldsymbol{F}_1(\boldsymbol{S})\cdot\boldsymbol{F}_2(\boldsymbol{S})]:\boldsymbol{T} =
\left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)\cdot\boldsymbol{F}_2 +
\boldsymbol{F}_1\cdot\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a25e5e0ee3f8a2f287da104d5f72d8342899b9)


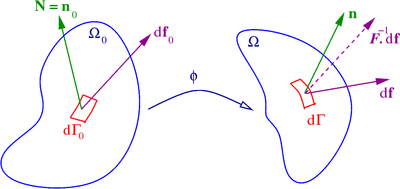



 (와)
(와) 
 텐서 필드가 정의된 도메인의 바깥쪽 정규 단위임
텐서 필드가 정의된 도메인의 바깥쪽 정규 단위임
 (는) 일반화된 그라데이션 연산자다.
(는) 일반화된 그라데이션 연산자다.





