벨의 정리
Bell's theorem벨의 정리는 물리학에서 밀접하게 관련된 여러 결과를 포괄하는 용어로, 측정의 본질에 대한 몇 가지 기본 가정을 고려할 때 양자역학이 국소 숨은 변수 이론과 양립할 수 없다고 결정합니다. 여기서 '로컬'은 입자가 바로 주변 환경에 의해서만 영향을 받을 수 있고, 물리적 장에 의해 매개되는 상호작용은 빛의 속도보다 더 빨리 전파될 수 없다는, 국소성의 원리를 말합니다. "숨은 변수"는 양자 이론에 포함되지는 않지만 실험 결과에 영향을 미치는 양자 입자의 추정 특성입니다. 물리학자 존 스튜어트 벨(John Stewart Bell)의 말에 따르면, 만약 [숨겨진 변수 이론]이 국소적이라면 양자역학과 일치하지 않을 것이고, 양자역학과 일치한다면 국소적이지 않을 것입니다.[1]
이 용어는 여러 가지 다른 유도체에 광범위하게 적용되며, 그 중 첫 번째는 벨에 의해 1964년 "Einstein Podolsky Rosen Paradox"라는 제목의 논문에서 소개되었습니다. 벨의 논문은 1935년 알베르트 아인슈타인, 보리스 포돌스키, 네이선 로젠이 제안한 사고 실험에 대한 응답으로 양자물리학은 "불완전한" 이론이라고 주장했습니다.[2][3] 1935년에 이르러서는 양자물리학의 예측이 확률적이라는 것을 이미 인식하고 있었습니다. 아인슈타인, 포돌스키, 로젠은 양자 상태가 얽히도록 입자 쌍을 준비한 다음 입자를 임의로 큰 거리로 분리하는 시나리오를 제시했습니다. 실험자는 입자 중 하나에 대해 수행할 수 있는 가능한 측정을 선택할 수 있습니다. 그들이 어떤 측정을 선택하고 결과를 얻으면, 다른 입자의 양자 상태는 다른 입자가 아무리 멀리 떨어져 있어도 그 결과에 따라 순간적으로 붕괴되어 새로운 상태가 됩니다. 이것은 첫 번째 입자의 측정도 어떻게든 빛의 속도보다 빠르게 두 번째 입자와 상호 작용했거나 얽힌 입자가 분리되기 전에 최종 양자 상태를 미리 결정하는 일부 측정되지 않은 특성을 가지고 있음을 시사합니다. 따라서 국소성을 가정할 때 양자역학은 입자의 실제 물리적 특성을 완전히 설명할 수 없기 때문에 불완전해야 합니다. 즉, 양자 입자는 전자나 광자와 같이 양자 이론에 포함되지 않은 어떤 속성이나 속성을 지니고 있어야 하며, 양자 이론의 예측에서 불확실성은 나중에 "숨은 변수"라고 불리는 이러한 속성에 대한 무지 또는 알 수 없는 것에 기인할 것입니다.
벨은 양자 얽힘에 대한 분석을 훨씬 더 멀리 수행했습니다. 그는 얽힌 쌍의 분리된 두 입자에 대해 독립적으로 측정을 수행하면 결과가 각 절반 내의 숨겨진 변수에 의존한다는 가정은 두 측정의 결과가 어떻게 상관 관계가 있는지에 대한 수학적 제약을 의미한다고 추론했습니다. 이 제약 조건은 나중에 벨 부등식으로 명명됩니다. 그 후 벨은 양자 물리학이 이 부등식을 위반하는 상관관계를 예측한다는 것을 보여주었습니다. 결과적으로 숨겨진 변수가 양자 물리학의 예측을 설명할 수 있는 유일한 방법은 "비국소적"이라는 것입니다. 즉, 두 입자가 아무리 광범위하게 분리되더라도 순간적으로 상호 작용할 수 있다는 것입니다.[4][5]
그 후 몇 년 동안 벨의 정리에 대한 여러 변형이 제안되었으며, 일반적으로 벨(또는 "벨형") 부등식으로 알려진 다른 밀접하게 관련된 조건을 도입했습니다. 벨의 정리를 시험하기 위해 고안된 최초의 기초적인 실험은 1972년 존 클라우저와 스튜어트 프리드먼에 의해 수행되었습니다.[6] 총칭 벨 테스트(Bell test)로 알려진 보다 발전된 실험들이 그 이후 여러 차례 수행되었습니다. 종종 이러한 실험은 "허점을 좁히는" 목표, 즉 원칙적으로 초기 벨 테스트의 결과의 유효성에 영향을 미칠 수 있는 실험 설계 또는 설정의 개선 문제를 가지고 있었습니다. 현재까지 벨 테스트는 물리적 시스템이 양자역학을 준수하고 벨 부등식을 위반한다는 것을 지속적으로 발견했습니다. 즉, 이러한 실험의 결과는 어떤 국소 숨은 변수 이론과도 양립할 수 없다는 것입니다.[7][8]
상관관계에 대한 벨형 제약을 증명하는 데 필요한 가정의 정확한 특성은 물리학자들과 철학자들에 의해 논의되었습니다. 벨의 정리의 중요성은 의심할 여지가 없지만 양자역학의 해석에 대한 완전한 의미는 여전히 해결되지 않았습니다.
정리
기본적인 아이디어에는 많은 변형이 있는데, 어떤 것은 다른 것보다 더 강한 수학적 가정을 사용합니다.[9] 중요한 것은 벨형 정리가 국소 숨은 변수에 대한 특정 이론을 언급하는 것이 아니라 양자 물리학이 고전적인 자연 그림 뒤에 있는 일반적인 가정을 위반한다는 것을 보여준다는 것입니다. 1964년 벨이 증명한 원래의 정리는 가장 실험하기 적합한 것은 아니며, 나중의 예를 들어 벨형 부등식이라는 장르를 도입하는 것이 편리합니다.[10]
가상의 인물 앨리스와 밥은 넓게 떨어져 있는 장소에 서 있습니다. 그들의 동료 빅터는 한 쌍의 입자를 준비하고 한 쌍은 앨리스에게 보내고 다른 한 쌍은 밥에게 보냅니다. 앨리스는 입자를 받으면 두 가지 가능한 측정 중 하나를 수행하기로 선택합니다(아마도 동전을 뒤집어서 결정할 수 있습니다). Denote these measurements by and . Both and are binary measurements: the result of is either or , 1 에 대해서도 마찬가지입니다 밥은 입자를 받으면 두 개의 측정값 인 B0 {\B_{와 B1 {\B_{를 선택하는데 둘 다 이진법입니다.
각 측정에서 입자가 이미 가지고 있는 속성이 나타난다고 가정합니다. 예를 들어, 앨리스가 를 측정하기로 선택하고+ 의 결과를 얻으면 앨리스가 받은 입자는 0 에 대해+ 의 값을 가지고 있습니다[note 1] 다음 조합을 생각해 보십시오.
Because both and take the values , then either or . In the former case, 0- 1) = {\}-1}=인 반면, 후자의 경우 (a 0 + a ) 0 = 0 {\displaystyle (a_{0}+a_{1}) b{0}=0}입니다. 따라서 위 식의 오른쪽에 있는 용어 중 하나는 사라지고 다른 하나는 ± 2 {\displaystyle \pm 2}입니다. 결과적으로, Victor가 새로운 입자 쌍을 준비하면서 실험을 여러 번 반복하면 모든 실험에서 a 0 + a 1+ - a 1 }b_{1}-a_{1의 평균값이 2보다 작거나 같습니다. Alice와 Bob은 각각 하나의 측정값만 선택할 수 있지만, 기본 속성이 존재한다는 가정 하에 합의 평균값은 각 항의 평균의 합에 불과하기 때문에 이 양을 측정할 수 없습니다. 평균을 나타내는 각도 괄호를 사용하여
양자역학은 다음과 같이 CHSH 부등식을 위반할 수 있습니다. Victor는 Bell 상태로 설명한 큐비트 한 쌍을 준비합니다.
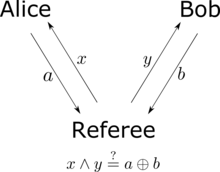
CHSH 부등식은 앨리스와 밥이 자신의 행동을 조정하려고 하는 게임으로도 생각할 수 있습니다.[14][15] Victor는 와 y 의 두 비트를독립적으로 임의로 준비합니다. 그는 Alice에게 비트 를 보내고 Bob에게 y를 보냅니다. Alice와 Bob이 Victor에게 응답 비트 와 b를 반환하면 승리합니다.
벨(1964)
벨의 1964년 논문은 제한된 조건에서 국소 숨은 변수 모델이 양자역학의 예측을 재현할 수 있다고 지적합니다. 그런 다음 그는 이것이 일반적으로 사실일 수 없다는 것을 증명합니다.[3] 벨은 아인슈타인-포돌스키-로젠(EPR) 사고 실험의 데이비드 봄의 세련됨을 고려합니다. 이 시나리오에서는 한 쌍의 입자가 스핀 싱글렛 상태(엉킨 상태의 예)로 묘사되는 방식으로 함께 형성됩니다. 그러면 입자들은 서로 반대 방향으로 떨어져 나갑니다. 각 입자는 서로 다른 방향으로 향할 수 있고+ 및 로 표시되는 두 가지 가능한 결과 중 하나를 보고하는 측정기인 Stern-Gerlach 장치에 의해 측정됩니다 각 측정기의 구성은 단위 벡터로 표시됩니다. 설정 a→ {\ {\ {a 및 b → {\displaystyle {b}}인 두 검출기 간의 상관 관계에 대한 양자역학적 예측은
특히 두 디텍터의 방향이 동일한 경우( → b → {\ a}} = 한 측정 결과는 (a→, →) = - displaystyle P({\vec {a}}, {\vec {a}}) = -1}입니다. 디텍터의 방향이 직교하는 경우( → ⋅ b→ {\ {a}}\cdot {\vec {b}}=0}), 결과는 상관 없으며 P(a →, b → ) = 0 {\displaystyle P({\vec {a}}, {\vec {b})= 0}입니다. 벨은 이러한 특수한 경우가 숨겨진 변수의 관점에서 설명될 수 있다는 것을 예제로 증명한 다음, 중간 각도를 포함하는 모든 범위의 가능성은 설명할 수 없다는 것을 보여줍니다.
벨은 이러한 상관 관계에 대한 로컬 은닉 변수 모델이 일부 은닉 매개 변수λ {\displaystyle\lambda의 가능한 값에 대한 적분으로 설명할 것이라고 가정했습니다.
벨의 1964년 정리는 완벽한 반상관의 가능성을 요구합니다: 첫 번째 검출기의 결과를 알고 두 번째 검출기의 결과에 대한 확률-1 예측을 할 수 있는 능력. 이는 아인슈타인, 포돌스키, 로젠이 1935년 논문에서 소개한 개념인 '실재의 EPR 기준'과 관련이 있습니다. 이 논문은 "만약 시스템을 방해하지 않고, 우리가 물리량의 값을 확실하게 예측할 수 있다면(즉, 통일성과 같은 확률로), 그 양에 상응하는 현실의 요소가 존재할 것입니다."라고 가정합니다.[2]
GHZ–Mermin (1990)
Daniel Greenberger, Michael A. 혼과 안톤 자일링거는 1990년에 4입자 사고 실험을 선보였고, 그 후 데이비드 머민은 3입자만 사용하도록 단순화했습니다.[17][18] 이 사고 실험에서 빅터는 양자 상태에 의해 기술된 세 개의 스핀-1/2 입자 집합을 생성합니다.
Alice, Bob 및 Charlie가 모두σ x \sigma_{x}} 측정을 수행하면 결과의 은 x x x xxc_{x}}가 . 이 값은 에서 추론할 수 있습니다.
이 사고 실험은 CHSH 게임과 같은 정신으로 전통적인 벨 불평등 또는 동등하게 비로컬 게임으로 재구성될 수도 있습니다.[19] 그 안에서 Alice, Bob, Charlie는로부터 x z {\ x, ,를 받고, 항상 짝수 개의 비트, ⊕ y⊕ z=0 {\x\opplusopplus z = 0}을 가지고 a, , a, b, c}를 다시 . a c a가 짝수 개의 입력이 필요할 때 x = = = 0 {\ x = y = z = 0}을 제외한 모든 입력에 대해 홀수 개의 입력이 있으면 게임에서 이깁니다. , ⊕ ⊕ c = ∨ y ∨ z {\display a\opplus b\opplus c= x\lory\lor z}이면 게임에서 승리합니다. 로컬 숨겨진 변수에서 그들이 가질 수 있는 가장 높은 승리 확률은 3/4인 반면 위의 양자 전략을 사용하면 확실하게 승리합니다. 이것은 양자 의사 텔레파시의 한 예입니다.
코헨-스펙커 정리 (1967)
양자 이론에서, 힐베르트 공간에 대한 정규 기저는 그 힐베르트 공간을 갖는 계에서 수행될 수 있는 측정값을 나타냅니다. 기저의 각 벡터는 해당 측정의 가능한 결과를 나타냅니다.[note 2] 숨겨진 변수λ {\displaystyle\lambda }이(가) 존재하므로 λ {\displaystyle \lambda }의값을 알면 측정 결과에 대한 확실성을 의미할 수 있습니다. λ{\lambda 값이 주어지면 각 측정 결과, 즉 힐베르트 공간의 각 벡터는 불가능하거나 보장됩니다. 코헨-스펙커 구성은 다수의 연동 기저로 구성된 벡터의 유한 집합으로, 한 기저에 속하는 것으로 간주될 때 벡터가 항상 불가능하고 다른 기저에 속하는 것으로 간주될 때 보장된다는 속성을 가지고 있습니다. 즉, Kochen-Specker 구성은 변수 λdisplaystyle \lambda}가 측정 결과를 제어할 수 있다고 가정하는 불일치를 보여주는 "컬러링할 수 없는 집합"입니다.
자유의지정리
연동 베이스의 구성을 사용하는 코헨-스펙커 유형의 논법은 벨 유형의 부등식의 기초가 되는 얽힌 쌍을 측정한다는 개념과 결합될 수 있습니다. 이것은 1970년대에 [25]Kochen, Heywood and Redhead,[26][27] Staires, Brown and Svetlichny에 의해 언급되었습니다.[28] EPR이 지적한 바와 같이, 얽힌 쌍의 한쪽에서 측정 결과를 얻는 것은 다른 한쪽에서 해당 측정 결과에 대한 확실성을 의미합니다. "실재의 EPR 기준"은 쌍의 후반부가 방해받지 않았기 때문에 확실성은 그에 속하는 물리적 속성 때문임에 틀림없다고 주장합니다.[29] 즉, 이 기준에 따라 숨겨진 변수λ {\displaystyle\lambda}가 쌍의 아직 측정되지 않은 두 번째 절반 내에 존재해야 합니다. 전반부의 측정값 하나만 고려하면 모순이 발생하지 않습니다. 그러나 관측자가 여러 가능한 측정을 선택하고 해당 측정을 정의하는 벡터가 코헨-스펙커 구성을 형성하면 후반부의 일부 결과가 동시에 불가능하고 보장됩니다.
존 콘웨이와 사이먼 코헨이 자유의지 정리라는 이름으로 그 예를 들어보았을 때, 이러한 유형의 논쟁이 주목을 받았습니다.[30][31][32] 콘웨이-코헨 정리는 얽힌 한 쌍의 쿼트릿과 애셔 페레스가 발견한 코헨-스펙커 구성을 사용합니다.[33]
준고전적 얽힘
벨이 지적한 바와 같이, 양자역학의 일부 예측은 얽힘에서 생성된 상관관계의 특수한 경우를 포함하여 로컬 숨은 변수 모델에서 복제될 수 있습니다. 이 주제는 벨의 정리 이후 몇 년 동안 체계적으로 연구되어 왔습니다. 1989년 라인하르트 베르너는 현재 베르너 상태라고 불리는 것을 소개했는데, 이는 EPR 유형의 상관 관계를 생성하지만 숨겨진 변수 모델도 인정하는 한 쌍의 시스템에 대한 공동 양자 상태입니다.[34] 베르너 상태는 대칭 텐서 곱 형태의 단위에서 불변하는 이분 양자 상태입니다.
2004년 로버트 스페켄스(Robert Spekens)는 국소적이고 이산화된 자유도를 전제로 시작하여 관찰자가 자유도에 대해 얼마나 많이 알 수 있는지를 제한하는 "지식 균형 원리"를 부과하여 숨겨진 변수로 만드는 장난감 모델을 소개했습니다. 기본 변수(온톤 상태)에 대한 허용된 지식 상태(진성 상태)는 양자 상태의 일부 특징을 모방합니다. 장난감 모델의 상관 관계는 일부일처제와 같은 얽힘의 일부 측면을 모방할 수 있지만 구성상 장난감 모델은 벨 부등식을 절대 위반할 수 없습니다.[35][36]
역사
배경
양자역학이 숨은 변수에 의해 '완결'될 수 있느냐는 문제는 양자론의 초기로 거슬러 올라갑니다. 헝가리 태생의 다수학자 존 폰 노이만은 1932년 양자역학 교과서에서 "숨겨진 매개변수"가 있을 수 없다는 증거라고 주장하는 것을 제시했습니다. 폰 노이만의 증명의 타당성과 확정성에 대해서는 한스 라이헨바흐가 의문을 제기했고, 그레테 헤르만이 더 자세히, 그리고 알베르트 아인슈타인이 인쇄한 것은 아니지만 대화에서 의문을 제기했습니다.[note 3] (Simon Kochen과 Ernst Specker는 일찍이 1961년에 폰 노이만의 핵심 가정을 거부했지만, 1967년까지 그것에 대한 비판을 발표하지 않았습니다.)[42]
아인슈타인은 양자역학이 완전한 이론이 될 수 없다고 집요하게 주장했습니다. 그가 선호하는 주장은 지역성의 원리에 의존했습니다.
- 제한된 시간 동안에만 서로 상호작용하는 두 부분계 A와 B로 구성된 기계 시스템을 생각해 보십시오. 상호 작용을 하기 전에 ψ가 작동하도록 합니다. 그러면 슈뢰딩거 방정식은 상호작용이 일어난 후에 ψ 함수를 제공할 것입니다. 이제 측정을 통해 가능한 한 완전히 부분계 A의 물리적 상태를 파악해 보겠습니다. 그런 다음 양자역학을 통해 측정된 측정값과 전체 계의 ψ 함수로부터 부분 계 B의 ψ 함수를 결정할 수 있습니다. 그러나 이 측정은 A의 조건을 지정하는 측정 크기 중 어느 것이 측정되었는지(예: 좌표 또는 운동량)에 따라 달라지는 결과를 제공합니다. 상호작용 후 B의 물리적 조건은 하나뿐이고 B에서 분리된 시스템 A에서 수행하는 특정 측정에 의존하는 것으로 합리적으로 간주될 수 없기 때문에 ψ 기능이 물리적 조건과 명확하게 조정되지 않는다고 결론지을 수 있습니다. 시스템 B의 물리적 조건이 동일한 여러 ψ 함수의 이러한 조정은 ψ 함수가 단위 시스템의 물리적 조건에 대한 (완전한) 설명으로 해석될 수 없음을 다시 보여줍니다.
EPR 사고 실험은 공동파동 함수에 의해 기술된 두 개의 분리된 계 A와 B를 고려할 때도 유사합니다. 그러나, EPR 논문은 B에 대한 측정 결과를 확률 1로 예측할 수 있는 능력은 B 내에 "현실의 요소"가 존재함을 의미하는 것으로 나중에 현실의 EPR 기준으로 알려진 아이디어를 추가합니다.[44]
1951년 데이비드 봄은 EPR 사고 실험의 변형을 제안했는데, 측정은 EPR이 고려하는 위치 및 운동량 측정과 달리 가능한 결과의 이산 범위를 갖습니다.[45] 재작년에, Chien-Shiung Wu와 Irving Shaknov는 얽힌 쌍으로 생성된 광자의 편광을 성공적으로 측정하여 Bohm 버전의 EPR 사고 실험을 실질적으로 가능하게 했습니다.[46]
1940년대 후반, 수학자 조지 매키는 양자 물리학의 기초에 관심을 갖게 되었고, 1957년에 그는 양자역학의 정확한 정의가 되기 위해 취해진 가설들의 목록을 작성했습니다.[47] Mackey는 하나의 공준이 중복된다고 추측했고, 얼마 지나지 않아 Andrew M. Gleason은 그것이 다른 공준으로부터 추론될 수 있다는 것을 증명했습니다.[48][49] 글리슨의 정리는 광범위한 종류의 숨은 변수 이론이 양자역학과 양립할 수 없다는 주장을 제공했습니다.[note 4] 좀 더 구체적으로, 글리슨의 정리는 "비맥락적"인 숨은 변수 모델을 배제합니다. 양자역학에 대한 숨겨진 변수 모델은 글리슨 정리의 의미를 피하기 위해 측정된 시스템에만 속하는 속성이 아니라 측정이 이루어지는 외부 컨텍스트에 의존하는 숨겨진 변수를 포함해야 합니다. 이러한 유형의 의존성은 종종 작위적이거나 바람직하지 않은 것으로 간주됩니다. 일부 환경에서는 특수 상대성 이론과 일치하지 않습니다.[5][51] 코헨-스펙커 정리는 그러한 확률 측정을 정의할 수 없는 광선의 특정 유한 부분 집합을 구성하여 이 문장을 개선합니다.[5][52]
이충다오는 1960년에 벨의 정리를 도출하기에 이르렀습니다. 그는 두 개의 카온이 서로 반대 방향으로 이동하는 사건을 고려했고 숨겨진 변수가 그러한 상황에서 얻을 수 있는 상관 관계를 설명할 수 없다는 결론에 도달했습니다. 그러나 카온이 부패한다는 사실 때문에 복잡한 문제가 발생했고, 그는 벨형 부등식을 추론하는 데까지 나아가지 않았습니다.[note 5]
벨의 출판물들
벨은 그의 정리를 비교적 잘 알려지지 않은 저널에 게재하기로 결정했는데, 그 이유는 페이지 요금이 필요하지 않았기 때문이며, 사실은 그 당시 그곳에서 출판한 저자들에게 돈을 지불했습니다. 그러나 그 저널은 저자들이 배포할 수 있는 기사의 무료 전재를 제공하지 않았기 때문에 벨은 다른 물리학자들에게 보낼 수 있는 사본을 사기 위해 그가 받은 돈을 써야 했습니다.[53] 저널에 인쇄된 기사 자체가 단순히 물리학으로 출판물의 이름을 나열한 반면, 표지에는 영어, 프랑스어 및 러시아어로 기사를 인쇄할 것임을 반영하기 위해 3개 국어 버전의 물리학 피지크 ф изика이 포함되어 있습니다.
1964년의 결과를 증명하기 전에 벨은 또한 코헨-스펙커 정리와 동등한 결과를 증명했습니다. 그러나 이 정리의 출판은 1966년까지 의도치 않게 지연되었습니다.[5][54] 벨은 이 논문에서 숨은 변수 측면에서 양자 현상을 설명하려면 비국소성이 필요하기 때문에 EPR 역설은 "아인슈타인이 가장 좋아하지 않았을 방식으로 해결된다"고 주장했습니다.[54]
실험
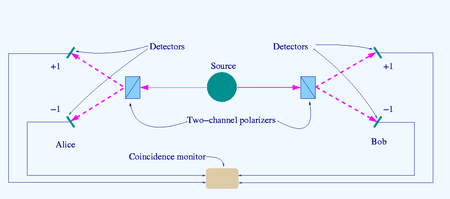
소스 S는 반대 방향으로 전송되는 "광자" 쌍을 생성합니다. 각 광자는 실험자가 방향(a 또는 b)을 설정할 수 있는 2채널 편광기와 마주칩니다. 각 채널에서 발생하는 신호가 감지되고 일치 모니터에 의해 4가지 유형(+, -, +- 및 -+)의 일치가 계산됩니다.
1967년, 특이한 제목의 물리학 피지컬 ф изика은 그 후 벨의 논문을 발견하고 실험실에서 벨 테스트를 수행하는 방법을 고려하기 시작한 존 클라우저의 관심을 끌었습니다. Clauser와 Stuart Freedman은 1972년에 Bell 테스트를 하기 시작했습니다.[56][57] 광자가 소스를 떠나기 전에 디텍터 설정을 선택했기 때문에 이는 제한된 테스트에 불과했습니다. 1982년, Alain Aspect와 공동 연구자들은 이 한계를 제거하기 위해 첫 번째 벨 테스트를 수행했습니다.[58] 이것은 점점 더 엄격해진 벨 테스트의 추세를 시작했습니다. GHZ 사고 실험은 2000년에 광자의 얽힌 삼중항을 사용하여 실제로 구현되었습니다.[59] 2002년까지 학부 실험실 과정에서 CHSH 불평등을 테스트할 수 있었습니다.[60]
Bell 검정에서는 실험 결과의 타당성에 영향을 미치는 실험 설계나 설정의 문제가 있을 수 있습니다. 이러한 문제를 종종 "루프홀"이라고 합니다. 실험의 목적은 자연이 국소적 숨은 변수 이론에 의해 기술될 수 있는지 여부를 테스트하는 것인데, 이는 양자역학의 예측과 모순됩니다.
실제 실험에서 가장 일반적인 허점은 탐지 및 국부적 허점입니다.[61] 검출 루프홀은 실험에서 입자(보통 광자)의 작은 부분이 검출되면 열리게 되는데, 검출된 입자가 대표성이 없는 표본이라고 가정하여 국소 숨은 변수로 데이터를 설명하는 것이 가능합니다. 로컬리티 루프홀은 공간과 같은 분리로 감지가 수행되지 않을 때 열려 상대성과 모순되지 않고 한 측정의 결과가 다른 측정에 영향을 미칠 수 있습니다. 일부 실험에서는 Bell 검정 위반에 대한 로컬-숨겨진 변수 설명을 가능하게 하는 추가 결점이 있을 수 있습니다.[62]
지역성과 탐지 허점이 서로 다른 실험에서 모두 닫혔지만, 오랜 과제는 동일한 실험에서 두 가지를 동시에 닫는 것이었습니다. 이는 2015년 세 번의 실험에서 마침내 이루어졌습니다.[63][64][65][66][67] 이러한 결과에 대해 알랭 애스펙트는 "어떤 실험도... 완전한 허점이 없다고 말할 수 없다"고 썼지만, 그는 실험이 "우리가 포기해야 한다는 마지막 의심을 제거한다"고 말하고, "훨씬 발견되었다", "물리학의 일반적인 추론 방식과는 이질적이다"는 것으로 남아있는 허점의 예를 언급했습니다.[68]
벨 부등식의 위반을 실험적으로 검증하려는 이러한 노력은 나중에 Clauser, Aspect, Anton Zeilinger가 2022년 노벨 물리학상을 수상하는 결과를 가져올 것입니다.[69]
해석
벨의 정리에 대한 반응은 다양하고 다양했습니다. Maximilian Schlosshauer, Johannes Kofler, Zeilinger는 벨 부등식이 "어떻게 우리가 수많은 실험들에 의해 실험된 엄격한 이론적 결과를 가질 수 있는지를 보여주는 훌륭한 예"라고 썼습니다.[70]
코펜하겐 해석
코펜하겐 해석은 주로 닐스 보어와 베르너 하이젠베르크에게 귀속되는 양자역학의 의미에 대한 견해의 모음입니다. 양자역학의 특징은 1925-1927년 동안 양자역학의 발전까지 거슬러 올라가기 때문에 양자역학에 대해 제안된 수많은 해석 중 가장 오래된 것 중 하나이며, 가장 일반적으로 가르치는 것 중 하나로 남아 있습니다.[71] 코펜하겐 해석이 무엇인지에 대한 명확한 역사적 진술은 없습니다. 특히 보어와 하이젠베르크의 견해에는 근본적인 의견 차이가 있었습니다.[72][73][74] 코펜하겐 컬렉션의 일부로 일반적으로 받아들여지는 몇 가지 기본 원칙에는 양자역학이 본질적으로 불확정적이며 Born 규칙을 사용하여 계산된 확률이 있다는 아이디어와 [75]보완성 원칙이 포함됩니다. 특정 속성은 동일한 시스템에 대해 동시에 공동으로 정의될 수 없습니다. 시스템의 특정 속성에 대해 이야기하기 위해서는 특정 실험실 배치의 맥락 내에서 해당 시스템을 고려해야 합니다. 상호 배타적인 실험실 배열에 해당하는 관측 가능한 양을 함께 예측할 수는 없지만 시스템을 특성화하려면 이러한 상호 배타적인 실험을 여러 번 고려해야 합니다.[72] 보어 자신은 EPR "파라독스"가 오류가 있다고 주장하기 위해 보완성을 사용했으며, 위치와 운동량의 측정은 상호 보완적이기 때문에 하나를 측정하는 선택은 다른 하나를 측정할 가능성을 배제한다고 언급했습니다. 결과적으로, 그는 실험 장치의 한 배열에 대해 추론된 사실은 다른 배열에 의해 추론된 사실과 결합될 수 없으며, 따라서 두 번째 입자에 대한 미리 결정된 위치 및 운동량 값의 추론은 타당하지 않다고 주장했습니다.[38]: 194–197 보어는 EPR의 "논증은 양자 기술이 본질적으로 불완전한 것으로 판명된다는 그들의 결론을 정당화하지 못한다"고 결론지었습니다.[76]
코펜하겐형 해석은 일반적으로 벨 불평등의 위반을 반사실적 확정성 또는 "현실주의"라고 불리는 가정을 거부할 근거로 삼는데, 이는 반드시 더 넓은 철학적 의미의 현실주의를 포기하는 것과 같지는 않습니다.[77][78] 예를 들어, Roland Omnès는 숨겨진 변수의 거부를 주장하고 "양자역학은 아마도 그 범위와 성숙도에 대한 어떤 이론이 될 것처럼 현실적일 것입니다."[79]: 531 라고 결론지었습니다. 이는 QB주의뿐만 아니라 일관된 역사(종종 "Copenhagen do right"[80]라고 광고됨)와 같은 코펜하겐 전통에서 유래한 해석에 의해 취해진 경로이기도 합니다.[81]
양자역학에 대한 다세계적 해석
에버렛 해석으로도 알려진 다중세계 해석은 붕괴 없이 양자역학의 단일 부분으로 구성되어 있기 때문에 국부적이고 결정론적입니다. 측정값이 단일 결과를 갖는다는 벨의 암묵적 가정을 위반하므로 벨 부등식을 위반하는 상관 관계를 생성할 수 있습니다. 사실, 벨의 정리는 측정이 단일 결과를 갖는다는 가정으로부터 다세계의 틀에서 증명될 수 있습니다. 따라서 벨 부등식을 위반하면 측정값에 여러 결과가 있음을 보여주는 것으로 해석할 수 있습니다.[82]
벨 상관 관계에 대한 설명은 Alice와 Bob이 측정을 할 때 지역 가지로 나누어진다는 것입니다. 앨리스의 각 사본의 관점에서는 밥이 각기 다른 결과를 경험하는 여러 사본이 있으므로 밥은 확실한 결과를 얻을 수 없으며, 밥의 각 사본의 관점에서도 마찬가지입니다. 그들은 미래의 빛 원뿔이 겹칠 때만 서로 잘 정의된 결과를 얻을 것입니다. 이 시점에서 우리는 벨 상관관계가 존재하기 시작한다고 말할 수 있지만, 그것은 순수하게 국소적인 메커니즘에 의해 생성되었습니다. 따라서 벨 불평등의 위반을 비국소성의 증명으로 해석할 수는 없습니다.[83]
은닉 변수 아이디어의 대부분의 지지자들은 실험이 지역 은닉 변수를 배제했다고 믿습니다.[note 6] 그들은 입자들이 그들의 상태에 대한 정보를 교환하는 비국소 숨은 변수 이론을 통해 벨의 불평등 위반을 설명하면서 지역성을 포기할 준비가 되었습니다. 이것은 우주의 모든 입자가 다른 모든 입자와 순간적으로 정보를 교환할 수 있어야 한다는 양자역학의 봄 해석의 기초입니다. 비국소 은닉 변수 이론의 한 가지 과제는 이러한 순간 통신이 은닉 변수 수준에서 존재할 수 있지만 신호를 보내는 데 사용할 수 없는 이유를 설명하는 것입니다.[86] 2007년의 실험은 보미안 역학 자체는 아니지만 많은 종류의 비보미안 비국소 숨은 변수 이론을 배제했습니다.[87]
시간적으로 앞뒤로 진행하는 파동을 가정하는 거래적 해석 역시 비국소적입니다.[88]
초결정론
벨의 정리를 유도하기 위해 필요한 가정은 숨겨진 변수가 측정 설정과 상관 관계가 없다는 것입니다. 이 가정은 실험자가 설정을 선택할 수 있는 "자유 의지"가 있고, 애초에 과학을 할 필요가 있다는 이유로 정당화되었습니다. 측정의 선택이 측정되는 시스템과 반드시 상관관계가 있는 (가설) 이론을 초결정론이라고 합니다.[61]
결정론적 모델을 지지하는 몇몇 사람들은 국소 숨은 변수를 포기하지 않았습니다. 예를 들어, Gerard't Hooft는 초결정론을 일축할 수 없다고 주장했습니다.[89]
참고 항목
메모들
- ^ 기본 속성에 대한 탐지기의 응답이 결정적이라고 가정하는 편의를 위해 사용합니다. 이 가정을 대체할 수 있습니다. 이는 실험의 모든 관측치에 대한 합동 확률 분포를 가정하는 것과 같습니다.[11][12]
- ^ In more detail, as developed by Paul Dirac,[20] David Hilbert,[21] John von Neumann,[22] and Hermann Weyl,[23] the state of a quantum mechanical system is a vector belonging to a (separable) Hilbert space . Physical quantities of interest — position, momentum, energy, 스핀 - 힐베르트 공간에 작용하는 자기 인접 선형 연산자인 "관측 가능"으로 표시됩니다. 관측치가 측정되면 결과는 Born 규칙에 의해 주어진 확률과 함께 고유값 중 하나가 됩니다. 가장 단순한 경우 고유값η displaystyle \eta}가 비퇴화되고 은⟨ η ψ ⟩ 2{\ \langle \eta \psi \rangle ^{2}, 여기서 η ⟩ {\rangle}은(는) 관련 고유 벡터입니다. 더 일반적으로 고유값은 축퇴되고 확률은⟨ ψP η ψ ⟩ displaystyle \}\psirangle }에 의해 주어집니다 서 P η P_{\eta}}는 해당 고유 공간에 대한 프로젝터입니다. 이 논의의 목적을 위해, 우리는 고유값을 비퇴화적으로 취할 수 있습니다.
- ^ 라이헨바흐와[37] 재머,[38]: 276 머민과 삭을 참조하고,[39] 아인슈타인의 발언은 클라우저와 시모니와[40] 윅을 참조하십시오.[41]: 286
- ^ 결정론적인 숨은 변수 이론은 주어진 결과의 확률이 항상 0 또는 1임을 의미합니다. 예를 들어, 스핀-1 원자에 대한 스턴-게를라흐 측정은 선택한 축을 따라 원자의 각운동량이{\- 및+ 의 세 가지 가능한 값 중 하나라고 보고합니다 결정론적 숨은 변수 이론에서, 측정에서 발견된 결과를 수정하는 기본 물리적 속성이 있습니다. 기본 물리적 속성의 값을 조건으로, 주어진 결과(예:+ 의 결과는 불가능하거나 보장되어야 합니다. 그러나 글리슨의 정리는 어떤 밀도 연산자 ρ {\displaystyle \rho}에 대해 확률 측정도 u →⟨ ρ , u ⟩ {\ u\ \rhou, u\rangle }를 매핑하는 형태를 취해야 한다는 것을 증명하기 때문에 이러한 결정론적 확률 측정이 있을 수 없음을 암시합니다. 이 매핑은 힐베르트 공간의 단위 구에서 연속적이며, 이 단위 구는 연결되어 있으므로 연속적인 확률 측정은 결정론적일 수 없습니다.[50]: §1.3
- ^ 이것은 맥스 재머에 의해 보고되었습니다.[38]: 308 이 씨는 천닝 양과 함께 한 패리티 보존 위반에 대한 예측으로 가장 잘 알려져 있는데, 이 예측은 상을 공동 수상하지 않은 우첸슝에 의해 확인된 후 노벨상을 수상하게 되었습니다.
- ^ E. T. Jaynes는 예외였지만,[84] Jaynes의 주장은 일반적으로 설득력이 있는 것으로 여겨지지 않았습니다.[85]
참고문헌
- ^ Bell, John S. (1987). Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. p. 65. ISBN 9780521368698. OCLC 15053677.
- ^ a b Einstein, A.; Podolsky, B.; Rosen, N. (1935-05-15). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?". Physical Review. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.
- ^ a b Bell, J. S. (1964). "On the Einstein Podolsky Rosen Paradox" (PDF). Physics Physique Физика. 1 (3): 195–200. doi:10.1103/PhysicsPhysiqueFizika.1.195.
- ^ Parker, Sybil B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. p. 542. ISBN 978-0-07-051400-3.
- ^ a b c d Mermin, N. David (July 1993). "Hidden Variables and the Two Theorems of John Bell" (PDF). Reviews of Modern Physics. 65 (3): 803–15. arXiv:1802.10119. Bibcode:1993RvMP...65..803M. doi:10.1103/RevModPhys.65.803. S2CID 119546199.
- ^ "The Nobel Prize in Physics 2022". Nobel Prize (Press release). The Royal Swedish Academy of Sciences. October 4, 2022. Retrieved 6 October 2022.
- ^ The BIG Bell Test Collaboration (9 May 2018). "Challenging local realism with human choices". Nature. 557 (7704): 212–216. arXiv:1805.04431. Bibcode:2018Natur.557..212B. doi:10.1038/s41586-018-0085-3. PMID 29743691. S2CID 13665914.
- ^ Wolchover, Natalie (2017-02-07). "Experiment Reaffirms Quantum Weirdness". Quanta Magazine. Retrieved 2020-02-08.
- ^ a b Shimony, Abner. "Bell's Theorem". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- ^ a b c d Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-1-107-00217-3. OCLC 844974180.
- ^ Fine, Arthur (1982-02-01). "Hidden Variables, Joint Probability, and the Bell Inequalities". Physical Review Letters. 48 (5): 291–295. Bibcode:1982PhRvL..48..291F. doi:10.1103/PhysRevLett.48.291. ISSN 0031-9007.
- ^ Braunstein, Samuel L.; Caves, Carlton M. (August 1990). "Wringing out better Bell inequalities". Annals of Physics. 202 (1): 22–56. Bibcode:1990AnPhy.202...22B. doi:10.1016/0003-4916(90)90339-P.
- ^ Rau, Jochen (2021). Quantum theory : an information processing approach. Oxford University Press. ISBN 978-0-192-65027-6. OCLC 1256446911.
- ^ Cleve, R.; Hoyer, P.; Toner, B.; Watrous, J. (2004). "Consequences and limits of nonlocal strategies". Proceedings. 19th IEEE Annual Conference on Computational Complexity, 2004. IEEE. pp. 236–249. arXiv:quant-ph/0404076. Bibcode:2004quant.ph..4076C. doi:10.1109/CCC.2004.1313847. ISBN 0-7695-2120-7. OCLC 55954993. S2CID 8077237.
- ^ Barnum, H.; Beigi, S.; Boixo, S.; Elliott, M. B.; Wehner, S. (2010-04-06). "Local Quantum Measurement and No-Signaling Imply Quantum Correlations". Physical Review Letters. 104 (14): 140401. arXiv:0910.3952. Bibcode:2010PhRvL.104n0401B. doi:10.1103/PhysRevLett.104.140401. ISSN 0031-9007. PMID 20481921. S2CID 17298392.
- ^ Griffiths, David J. (2005). Introduction to Quantum Mechanics (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC 53926857.
- ^ Greenberger, D.; Horne, M.; Shimony, A.; Zeilinger, A. (1990). "Bell's theorem without inequalities". American Journal of Physics. 58 (12): 1131. Bibcode:1990AmJPh..58.1131G. doi:10.1119/1.16243.
- ^ Mermin, N. David (1990). "Quantum mysteries revisited". American Journal of Physics. 58 (8): 731–734. Bibcode:1990AmJPh..58..731M. doi:10.1119/1.16503.
- ^ Brassard, Gilles; Broadbent, Anne; Tapp, Alain (2005). "Recasting Mermin's multi-player game into the framework of pseudo-telepathy". Quantum Information and Computation. 5 (7): 538–550. arXiv:quant-ph/0408052. Bibcode:2004quant.ph..8052B. doi:10.26421/QIC5.7-2.
- ^ Dirac, Paul Adrien Maurice (1930). The Principles of Quantum Mechanics. Oxford: Clarendon Press.
- ^ Hilbert, David (2009). Sauer, Tilman; Majer, Ulrich (eds.). Lectures on the Foundations of Physics 1915–1927: Relativity, Quantum Theory and Epistemology. Springer. doi:10.1007/b12915. ISBN 978-3-540-20606-4. OCLC 463777694.
- ^ von Neumann, John (1932). Mathematische Grundlagen der Quantenmechanik. Berlin: Springer. 영어 번역:
- ^ Weyl, Hermann (1950) [1931]. The Theory of Groups and Quantum Mechanics. Translated by Robertson, H. P. Dover. ISBN 978-0-486-60269-1. 독일어 번역
- ^ Peres, Asher (1993). Quantum Theory: Concepts and Methods. Kluwer. ISBN 0-7923-2549-4. OCLC 28854083.
- ^ Redhead, Michael; Brown, Harvey (1991-07-01). "Nonlocality in Quantum Mechanics". Proceedings of the Aristotelian Society, Supplementary Volumes. 65 (1): 119–160. doi:10.1093/aristoteliansupp/65.1.119. ISSN 0309-7013. JSTOR 4106773.
A similar approach was arrived at independently by Simon Kochen, although never published (private communication).
- ^ Heywood, Peter; Redhead, Michael L. G. (May 1983). "Nonlocality and the Kochen–Specker paradox". Foundations of Physics. 13 (5): 481–499. Bibcode:1983FoPh...13..481H. doi:10.1007/BF00729511. ISSN 0015-9018. S2CID 120340929.
- ^ Stairs, Allen (December 1983). "Quantum Logic, Realism, and Value Definiteness". Philosophy of Science. 50 (4): 578–602. doi:10.1086/289140. ISSN 0031-8248. S2CID 122885859.
- ^ Brown, H. R.; Svetlichny, G. (November 1990). "Nonlocality and Gleason's lemma. Part I. Deterministic theories". Foundations of Physics. 20 (11): 1379–1387. Bibcode:1990FoPh...20.1379B. doi:10.1007/BF01883492. ISSN 0015-9018. S2CID 122868901.
- ^ Glick, David; Boge, Florian J. (2019-10-22). "Is the Reality Criterion Analytic?". Erkenntnis. 86 (6): 1445–1451. arXiv:1909.11893. Bibcode:2019arXiv190911893G. doi:10.1007/s10670-019-00163-w. ISSN 0165-0106. S2CID 202889160.
- ^ Conway, John; Kochen, Simon (2006). "The Free Will Theorem". Foundations of Physics. 36 (10): 1441. arXiv:quant-ph/0604079. Bibcode:2006FoPh...36.1441C. doi:10.1007/s10701-006-9068-6. S2CID 12999337.
- ^ Rehmeyer, Julie (2008-08-15). "Do subatomic particles have free will?". Science News. Retrieved 2022-04-23.
- ^ Thomas, Rachel (2011-12-27). "John Conway – discovering free will (part I)". Plus Magazine. Retrieved 2022-04-23.
- ^ Conway, John H.; Kochen, Simon (2009). "The strong free will theorem" (PDF). Notices of the AMS. 56 (2): 226–232.
- ^ Werner, Reinhard F. (1989-10-01). "Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model". Physical Review A. 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. ISSN 0556-2791. PMID 9902666.
- ^ Spekkens, Robert W. (2007-03-19). "Evidence for the epistemic view of quantum states: A toy theory". Physical Review A. 75 (3): 032110. arXiv:quant-ph/0401052. Bibcode:2007PhRvA..75c2110S. doi:10.1103/PhysRevA.75.032110. ISSN 1050-2947. S2CID 117284016.
- ^ Catani, Lorenzo; Browne, Dan E. (2017-07-27). "Spekkens' toy model in all dimensions and its relationship with stabiliser quantum mechanics". New Journal of Physics. 19 (7): 073035. Bibcode:2017NJPh...19g3035C. doi:10.1088/1367-2630/aa781c. ISSN 1367-2630. S2CID 119428107.
- ^ Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. p. 14. OCLC 872622725.
- ^ a b c Jammer, Max (1974). The Philosophy of Quantum Mechanics. John Wiley and Sons. ISBN 0-471-43958-4.
- ^ Mermin, N. David; Schack, Rüdiger (2018). "Homer nodded: von Neumann's surprising oversight". Foundations of Physics. 48 (9): 1007–1020. arXiv:1805.10311. Bibcode:2018FoPh...48.1007M. doi:10.1007/s10701-018-0197-5. S2CID 118951033.
- ^ Clauser, J. F.; Shimony, A. (1978). "Bell's theorem: Experimental tests and implications" (PDF). Reports on Progress in Physics. 41 (12): 1881–1927. Bibcode:1978RPPh...41.1881C. CiteSeerX 10.1.1.482.4728. doi:10.1088/0034-4885/41/12/002. S2CID 250885175. Archived (PDF) from the original on 2017-09-23. Retrieved 2017-10-28.
- ^ a b Wick, David (1995). "Bell's Theorem". The Infamous Boundary: Seven Decades of Heresy in Quantum Physics. New York: Springer. pp. 92–100. doi:10.1007/978-1-4612-4030-3_11. ISBN 978-0-387-94726-6.
- ^ Conway, John; Kochen, Simon (2002). "The Geometry of the Quantum Paradoxes". In Bertlmann, Reinhold A.; Zeilinger, Anton (eds.). Quantum [Un]speakables: From Bell to Quantum Information. Berlin: Springer. pp. 257–269. ISBN 3-540-42756-2. OCLC 49404213.
- ^ Einstein, Albert (March 1936). "Physics and reality". Journal of the Franklin Institute. 221 (3): 349–382. Bibcode:1936FrInJ.221..349E. doi:10.1016/S0016-0032(36)91047-5.
- ^ Harrigan, Nicholas; Spekkens, Robert W. (2010). "Einstein, incompleteness, and the epistemic view of quantum states". Foundations of Physics. 40 (2): 125. arXiv:0706.2661. Bibcode:2010FoPh...40..125H. doi:10.1007/s10701-009-9347-0. S2CID 32755624.
- ^ Bohm, David (1989) [1951]. Quantum Theory (Dover reprint ed.). Prentice-Hall. pp. 614–623. ISBN 978-0-486-65969-5. OCLC 1103789975.
- ^ Wu, C.-S.; Shaknov, I. (1950). "The Angular Correlation of Scattered Annihilation Radiation". Physical Review. 77 (1): 136. Bibcode:1950PhRv...77..136W. doi:10.1103/PhysRev.77.136.
- ^ Mackey, George W. (1957). "Quantum Mechanics and Hilbert Space". The American Mathematical Monthly. 64 (8P2): 45–57. doi:10.1080/00029890.1957.11989120. JSTOR 2308516.
- ^ Gleason, Andrew M. (1957). "Measures on the closed subspaces of a Hilbert space". Indiana University Mathematics Journal. 6 (4): 885–893. doi:10.1512/iumj.1957.6.56050. MR 0096113.
- ^ Chernoff, Paul R. "Andy Gleason and Quantum Mechanics" (PDF). Notices of the AMS. 56 (10): 1253–1259.
- ^ Wilce, A. (2017). "Quantum Logic and Probability Theory". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University.
- ^ Shimony, Abner (1984). "Contextual Hidden Variable Theories and Bell's Inequalities". British Journal for the Philosophy of Science. 35 (1): 25–45. doi:10.1093/bjps/35.1.25.
- ^ Peres, Asher (1991). "Two simple proofs of the Kochen-Specker theorem". Journal of Physics A: Mathematical and General. 24 (4): L175–L178. Bibcode:1991JPhA...24L.175P. doi:10.1088/0305-4470/24/4/003. ISSN 0305-4470.
- ^ Whitaker, Andrew (2016). John Stewart Bell and Twentieth Century Physics: Vision and Integrity. Oxford University Press. ISBN 978-0-19-874299-9.
- ^ a b Bell, J. S. (1966). "On the problem of hidden variables in quantum mechanics". Reviews of Modern Physics. 38 (3): 447–452. Bibcode:1966RvMP...38..447B. doi:10.1103/revmodphys.38.447. OSTI 1444158.
- ^ Kaiser, David (2012-01-30). "How the Hippies Saved Physics: Science, Counterculture, and the Quantum Revival [Excerpt]". Scientific American. Retrieved 2020-02-11.
- ^ Freedman, S. J.; Clauser, J. F. (1972). "Experimental test of local hidden-variable theories" (PDF). Physical Review Letters. 28 (938): 938–941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938.
- ^ Freedman, Stuart Jay (1972-05-05). Experimental test of local hidden-variable theories (PDF) (PhD). University of California, Berkeley.
- ^ Aspect, Alain; Dalibard, Jean; Roger, Gérard (1982). "Experimental Test of Bell's Inequalities Using Time-Varying Analyzers". Physical Review Letters. 49 (25): 1804–7. Bibcode:1982PhRvL..49.1804A. doi:10.1103/PhysRevLett.49.1804.
- ^ Pan, Jian-Wei; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. (2000). "Experimental test of quantum nonlocality in three-photon GHZ entanglement". Nature. 403 (6769): 515–519. Bibcode:2000Natur.403..515P. doi:10.1038/35000514. PMID 10676953. S2CID 4309261.
- ^ Dehlinger, Dietrich; Mitchell, M. W. (2002). "Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory". American Journal of Physics. 70 (9): 903–910. arXiv:quant-ph/0205171. Bibcode:2002AmJPh..70..903D. doi:10.1119/1.1498860. S2CID 49487096.
- ^ a b Larsson, Jan-Åke (2014). "Loopholes in Bell inequality tests of local realism". Journal of Physics A: Mathematical and Theoretical. 47 (42): 424003. arXiv:1407.0363. Bibcode:2014JPhA...47P4003L. doi:10.1088/1751-8113/47/42/424003. S2CID 40332044.
- ^ Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Scarani, V.; et al. (2011). "Experimentally faking the violation of Bell's inequalities". Physical Review Letters. 107 (17): 170404. arXiv:1106.3224. Bibcode:2011PhRvL.107q0404G. doi:10.1103/PhysRevLett.107.170404. PMID 22107491. S2CID 16306493.
- ^ Merali, Zeeya (27 August 2015). "Quantum 'spookiness' passes toughest test yet". Nature News. 525 (7567): 14–15. Bibcode:2015Natur.525...14M. doi:10.1038/nature.2015.18255. PMID 26333448. S2CID 4409566.
- ^ Markoff, Jack (21 October 2015). "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real". New York Times. Retrieved 21 October 2015.
- ^ Hensen, B.; et al. (21 October 2015). "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres". Nature. 526 (7575): 682–686. arXiv:1508.05949. Bibcode:2015Natur.526..682H. doi:10.1038/nature15759. PMID 26503041. S2CID 205246446.
- ^ Shalm, L. K.; et al. (16 December 2015). "Strong Loophole-Free Test of Local Realism". Physical Review Letters. 115 (25): 250402. arXiv:1511.03189. Bibcode:2015PhRvL.115y0402S. doi:10.1103/PhysRevLett.115.250402. PMC 5815856. PMID 26722906.
- ^ Giustina, M.; et al. (16 December 2015). "Significant-Loophole-Free Test of Bell's Theorem with Entangled Photons". Physical Review Letters. 115 (25): 250401. arXiv:1511.03190. Bibcode:2015PhRvL.115y0401G. doi:10.1103/PhysRevLett.115.250401. PMID 26722905. S2CID 13789503.
- ^ Aspect, Alain (December 16, 2015). "Closing the Door on Einstein and Bohr's Quantum Debate". Physics. 8: 123. Bibcode:2015PhyOJ...8..123A. doi:10.1103/Physics.8.123.
- ^ Ahlander, Johan; Burger, Ludwig; Pollard, Niklas (2022-10-04). "Nobel physics prize goes to sleuths of 'spooky' quantum science". Reuters. Retrieved 2022-10-04.
- ^ Schlosshauer, Maximilian; Kofler, Johannes; Zeilinger, Anton (2013-01-06). "A Snapshot of Foundational Attitudes Toward Quantum Mechanics". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. doi:10.1016/j.shpsb.2013.04.004. S2CID 55537196.
- ^ Siddiqui, Shabnam; Singh, Chandralekha (2017). "How diverse are physics instructors' attitudes and approaches to teaching undergraduate level quantum mechanics?". European Journal of Physics. 38 (3): 035703. Bibcode:2017EJPh...38c5703S. doi:10.1088/1361-6404/aa6131.
- ^ a b Faye, Jan (2019). "Copenhagen Interpretation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 2019-04-29. Retrieved 2021-09-16.
- ^ Camilleri, K.; Schlosshauer, M. (2015). "Niels Bohr as Philosopher of Experiment: Does Decoherence Theory Challenge Bohr's Doctrine of Classical Concepts?". Studies in History and Philosophy of Modern Physics. 49: 73–83. arXiv:1502.06547. Bibcode:2015SHPMP..49...73C. doi:10.1016/j.shpsb.2015.01.005. S2CID 27697360.
- ^ Peres, Asher (2002). "Popper's experiment and the Copenhagen interpretation". Studies in History and Philosophy of Modern Physics. 33: 23. arXiv:quant-ph/9910078. Bibcode:1999quant.ph.10078P. doi:10.1016/S1355-2198(01)00034-X.
- ^ Bohr, N. (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.Bohr, N. (1928). "The Quantum Postulate and the Recent Development of Atomic Theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.p. 586: "이와 관련하여 [Born]은 파동 함수에 대한 통계적 해석을 얻는 데 성공하여 양자 공준에 필요한 개별 전이 과정의 확률을 계산할 수 있게 되었습니다."
- ^ Bohr, N. (1935-10-13). "Can Quantum-Mechanical Description of Physical Reality be Considered Complete?" (PDF). Physical Review. 48 (8): 696–702. Bibcode:1935PhRv...48..696B. doi:10.1103/PhysRev.48.696. Archived (PDF) from the original on 2020-01-09. Retrieved 2021-09-16.
- ^ Werner, Reinhard F. (2014-10-24). "Comment on 'What Bell did'". Journal of Physics A: Mathematical and Theoretical. 47 (42): 424011. Bibcode:2014JPhA...47P4011W. doi:10.1088/1751-8113/47/42/424011. ISSN 1751-8113. S2CID 122180759.
- ^ Żukowski, Marek (2017). "Bell's Theorem Tells Us Not What Quantum Mechanics is, but What Quantum Mechanics is Not". In Bertlmann, Reinhold; Zeilinger, Anton (eds.). Quantum [Un]Speakables II. The Frontiers Collection. Cham: Springer International Publishing. pp. 175–185. arXiv:1501.05640. doi:10.1007/978-3-319-38987-5_10. ISBN 978-3-319-38985-1. S2CID 119214547.
- ^ Omnès, R. (1994). The Interpretation of Quantum Mechanics. Princeton University Press. ISBN 978-0-691-03669-4. OCLC 439453957.
- ^ Hohenberg, P. C. (2010-10-05). "Colloquium : An introduction to consistent quantum theory". Reviews of Modern Physics. 82 (4): 2835–2844. arXiv:0909.2359. Bibcode:2010RvMP...82.2835H. doi:10.1103/RevModPhys.82.2835. ISSN 0034-6861. S2CID 20551033.
- ^ Healey, Richard (2016). "Quantum-Bayesian and Pragmatist Views of Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 2021-08-17. Retrieved 2021-09-16.
- ^ Deutsch, David; Hayden, Patrick (2000). "Information flow in entangled quantum systems". Proceedings of the Royal Society A. 456 (1999): 1759–1774. arXiv:quant-ph/9906007. Bibcode:2000RSPSA.456.1759D. doi:10.1098/rspa.2000.0585. S2CID 13998168.
- ^ Brown, Harvey R.; Timpson, Christopher G. (2016). "Bell on Bell's Theorem: The Changing Face of Nonlocality". In Bell, Mary; Gao, Shan (eds.). Quantum Nonlocality and Reality: 50 years of Bell's theorem. Cambridge University Press. pp. 91–123. arXiv:1501.03521. doi:10.1017/CBO9781316219393.008. ISBN 9781316219393. S2CID 118686956.
- ^ Jaynes, E. T. (1989). "Clearing up Mysteries — the Original Goal". Maximum Entropy and Bayesian Methods (PDF). pp. 1–27. CiteSeerX 10.1.1.46.1264. doi:10.1007/978-94-015-7860-8_1. ISBN 978-90-481-4044-2. Archived (PDF) from the original on 2011-10-28. Retrieved 2011-10-18.
- ^ Gill, Richard D. (2002). "Time, Finite Statistics, and Bell's Fifth Position". Proceedings of the Conference Foundations of Probability and Physics - 2 : Växjö (Soland), Sweden, June 2-7, 2002. Vol. 5. Växjö University Press. pp. 179–206. arXiv:quant-ph/0301059.
- ^ Wood, Christopher J.; Spekkens, Robert W. (2015-03-03). "The lesson of causal discovery algorithms for quantum correlations: causal explanations of Bell-inequality violations require fine-tuning". New Journal of Physics. 17 (3): 033002. arXiv:1208.4119. Bibcode:2015NJPh...17c3002W. doi:10.1088/1367-2630/17/3/033002. ISSN 1367-2630. S2CID 118518558.
- ^ Gröblacher, Simon; Paterek, Tomasz; Kaltenbaek, Rainer; Brukner, Časlav; Żukowski, Marek; Aspelmeyer, Markus; Zeilinger, Anton (2007). "An experimental test of non-local realism". Nature. 446 (7138): 871–5. arXiv:0704.2529. Bibcode:2007Natur.446..871G. doi:10.1038/nature05677. PMID 17443179. S2CID 4412358.
- ^ Kastner, Ruth E. (May 2010). "The quantum liar experiment in Cramer's transactional interpretation". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 41 (2): 86–92. arXiv:0906.1626. Bibcode:2010SHPMP..41...86K. doi:10.1016/j.shpsb.2010.01.001. S2CID 16242184. Archived from the original on 2018-06-24. Retrieved 2021-09-16.
- ^ 't Hooft, Gerard (2016). The Cellular Automaton Interpretation of Quantum Mechanics. Fundamental Theories of Physics. Vol. 185. Springer. doi:10.1007/978-3-319-41285-6. ISBN 978-3-319-41284-9. OCLC 951761277. S2CID 7779840. Archived from the original on 2021-12-29. Retrieved 2020-08-27.
더보기
다음은 일반 청중을 위한 것입니다.
- Aczel, Amir D. (2001). Entanglement: The greatest mystery in physics. New York: Four Walls Eight Windows.
- Afriat, A.; Selleri, F. (1999). The Einstein, Podolsky and Rosen Paradox. New York and London: Plenum Press.
- Baggott, J. (1992). The Meaning of Quantum Theory. Oxford University Press.
- Gilder, Louisa (2008). The Age of Entanglement: When Quantum Physics Was Reborn. New York: Alfred A. Knopf.
- Greene, Brian (2004). The Fabric of the Cosmos. Vintage. ISBN 0-375-72720-5.
- Mermin, N. David (1981). "Bringing home the atomic world: Quantum mysteries for anybody". American Journal of Physics. 49 (10): 940–943. Bibcode:1981AmJPh..49..940M. doi:10.1119/1.12594. S2CID 122724592.
- Mermin, N. David (April 1985). "Is the moon there when nobody looks? Reality and the quantum theory". Physics Today. 38 (4): 38–47. Bibcode:1985PhT....38d..38M. doi:10.1063/1.880968.
다음은 더 기술적으로 지향적입니다.
- Aspect, A.; et al. (1981). "Experimental Tests of Realistic Local Theories via Bell's Theorem". Phys. Rev. Lett. 47 (7): 460–463. Bibcode:1981PhRvL..47..460A. doi:10.1103/physrevlett.47.460.
- Aspect, A.; et al. (1982). "Experimental Realization of Einstein–Podolsky–Rosen–Bohm Gedankenexperiment: A New Violation of Bell's Inequalities". Phys. Rev. Lett. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/physrevlett.49.91.
- Aspect, A.; Grangier, P. (1985). "About resonant scattering and other hypothetical effects in the Orsay atomic-cascade experiment tests of Bell inequalities: a discussion and some new experimental data". Lettere al Nuovo Cimento. 43 (8): 345–348. doi:10.1007/bf02746964. S2CID 120840672.
- Bell, J. S. (1971). "Introduction to the hidden variable question". Proceedings of the International School of Physics 'Enrico Fermi', Course IL, Foundations of Quantum Mechanics. pp. 171–81.
- Bell, J. S. (2004). "Bertlmann's Socks and the Nature of Reality". Speakable and Unspeakable in Quantum Mechanics. Cambridge University Press. pp. 139–158.
- D'Espagnat, B. (1979). "The Quantum Theory and Reality" (PDF). Scientific American. 241 (5): 158–181. Bibcode:1979SciAm.241e.158D. doi:10.1038/scientificamerican1179-158. Archived (PDF) from the original on 2009-03-27. Retrieved 2009-03-18.
- Fry, E. S.; Walther, T.; Li, S. (1995). "Proposal for a loophole-free test of the Bell inequalities" (PDF). Phys. Rev. A. 52 (6): 4381–4395. Bibcode:1995PhRvA..52.4381F. doi:10.1103/physreva.52.4381. hdl:1969.1/126533. PMID 9912775. Archived from the original on 2021-12-29. Retrieved 2018-03-19.
- Fry, E. S.; Walther, T. (2002). "Atom based tests of the Bell Inequalities — the legacy of John Bell continues". In Bertlmann, R. A.; Zeilinger, A. (eds.). Quantum [Un]speakables. Berlin-Heidelberg-New York: Springer. pp. 103–117.
- Goldstein, Sheldon; et al. (2011). "Bell's theorem". Scholarpedia. 6 (10): 8378. Bibcode:2011SchpJ...6.8378G. doi:10.4249/scholarpedia.8378.
- Griffiths, R. B. (2001). Consistent Quantum Theory. Cambridge University Press. ISBN 978-0-521-80349-6. OCLC 1180958776.
- Hardy, L. (1993). "Nonlocality for 2 particles without inequalities for almost all entangled states". Physical Review Letters. 71 (11): 1665–1668. Bibcode:1993PhRvL..71.1665H. doi:10.1103/physrevlett.71.1665. PMID 10054467. S2CID 11839894.
- Matsukevich, D. N.; Maunz, P.; Moehring, D. L.; Olmschenk, S.; Monroe, C. (2008). "Bell Inequality Violation with Two Remote Atomic Qubits". Phys. Rev. Lett. 100 (15): 150404. arXiv:0801.2184. Bibcode:2008PhRvL.100o0404M. doi:10.1103/physrevlett.100.150404. PMID 18518088. S2CID 11536757.
- Rieffel, Eleanor G.; Polak, Wolfgang H. (4 March 2011). "4.4 EPR Paradox and Bell's Theorem". Quantum Computing: A Gentle Introduction. MIT Press. pp. 60–65. ISBN 978-0-262-01506-6.
- Sulcs, S. (2003). "The Nature of Light and Twentieth Century Experimental Physics". Foundations of Science. 8 (4): 365–391. doi:10.1023/A:1026323203487. S2CID 118769677.
- van Fraassen, B. C. (1991). Quantum Mechanics: An Empiricist View. Clarendon Press. ISBN 978-0-198-24861-3. OCLC 22906474.




 선택하는데
선택하는데

















 y
y 


























