그로버 알고리즘

양자 컴퓨팅에서 양자 검색 알고리즘으로도 알려진 Grover의 알고리즘은 특정 출력 값을 생성하는 블랙박스 함수에 대한 고유 입력을 높은 확률로 찾는 비정형 검색을 위한 양자 알고리즘으로, 함수에 대한 $O{\displaystyle (N)}${\$display O({\sqrt {N}}}$ 평가만$$ 사용하여, 여기서 $N{\displaystyle }$ ${\displaystyle$ N$}$은 함수의 도메인 크기입니다. 그것은 1996년에 Lov Grover에 의해 고안되었습니다.^[1]

고전 계산에서 유사한 문제는 $O{\displaystyle (N)}$ ${\displaystyle$ O$(N)}$ 평가보다$$ 적은 값으로 해결할 수 없습니다(평균적으로 도메인의 절반을 확인해야 올바른 입력을 찾을 수 있기 때문입니다). Charles H. Bennett, Ethan Bernstein, Gilles Brassard 및 Umesh Vazirani는 문제에 대한 양자 솔루션이$$ω(N) ${\displaystyle \Omega({\$sqrt {N}}} 함수를 평가해야 한다는 것을 증명했으며, 따라서 Grover의 알고리즘은 점근적으로 최적입니다. NP-완전 문제에 대한 고전적인 알고리즘은 기하급수적으로 많은 단계를 필요로 하고, Grover의 알고리즘은 구조화되지 않은 검색을 위해 고전적인 솔루션에 비해 기껏해야 2차 속도 향상을 제공하기 때문에, 이는 Grover의 알고리즘 자체가 NP-완전 문제에 대한 다항 시간 해법을 제공하지 않을 것임을 시사합니다(지수 함수의 제곱근이 다항식이 아닌 지수 함수이기 때문).^[3]

고전적인 것에 비해 기하급수적인 속도 향상을 제공할 수 있는 다른 양자 알고리듬과 달리 Grover의 알고리듬은 2차 속도 향상만 제공합니다. 그러나 $N{\displaystyle }$ ${\displaystyle N}$이 큰 경우 2차 속도 증가도 상당하며 Grover의 알고리즘을 적용하여 광범위한 클래스의 알고리즘 속도를 높일 수 있습니다.^[3] Grover의 알고리즘은 128비트 대칭 암호키를 약 2회⁶⁴ 반복으로, 256비트 키를 약 2회¹²⁸ 반복으로 브루트 포스할 수 있습니다. 그러나 Grover의 알고리즘이 기존의 고전적인 알고리즘에 비해 암호화에 대한 위험이 크게 증가하는 경우는 아닐 수 있습니다.^[4]

적용 및 제한 사항

그로버의 알고리즘은 진폭 증폭과 같은 변형과 함께 광범위한 알고리즘의 속도를 높일 수 있습니다.^[5][6][7] 특히, NP-완전 문제에 대한 알고리즘은 일반적으로 서브루틴으로서 철저한 검색을 포함하고 있으며, 이는 Grover의 알고리즘에 의해 속도가 빨라질 수 있습니다.^[6] 3SAT에 대한 현재 최고의 알고리즘이 그러한 예 중 하나입니다. 일반적인 제약 조건 만족 문제는 Grover에서 2차 속도 향상도 볼 수 있습니다.^[8] Grover의 알고리즘은 명시적인 함수(예: 비트 집합이 3SAT 인스턴스를 만족하는지 확인하는 함수)와 함께 적용되기 때문에 이러한 알고리즘은 입력을 오라클 형태로 제공할 필요가 없습니다.

Grover의 알고리즘은 또한 요소의^[9] 구별과 충돌^[10] 문제를 포함하여 양자 쿼리 복잡성의 블랙박스 문제에 대해 입증 가능한 속도 향상을 제공할 수 있습니다.Høyer–Tapp 알고리즘). 이러한 유형의 문제에서는 오라클 함수 f를 데이터베이스로 취급하며, 가능한 한 이 함수에 양자 쿼리를 사용하는 것이 목표입니다.

암호학

그로버의 알고리즘은 본질적으로 함수 반전의 과제를 해결합니다. 대략적으로 양자 컴퓨터에서 평가할 수 있는 $함수$ ${\displaystyle y}$ = f ${\displaystyle (}$x $)$ {\$displaystyle$ y = f (x)}가 있으면, Grover의 알고리즘을 통해 y {\displaystyle y}가 주어졌을 때 x {\displaystyle x}를 계산할 수 있습니다. 결과적으로, Grover의 알고리즘은 충돌 공격 및 사전 이미지 공격을 포함하여 대칭 키 암호화에 대한 다양한 종류의 브루트 포스 공격에 광범위한 점근적 속도 향상을 제공합니다.^[11] 그러나 예를 들어 병렬 rho 알고리즘이 Grover의 알고리즘보다 SHA2에서 충돌을 더 효율적으로 찾을 수 있기 때문에 이것이 반드시 가장 효율적인 알고리즘이라고 할 수는 없습니다.^[12]

한계

Grover의 원래 논문은 이 알고리즘을 데이터베이스 검색 알고리즘이라고 설명했고, 이 설명은 여전히 일반적입니다. 이 비유에서 데이터베이스는 해당 입력으로 색인화된 함수의 모든 출력 테이블입니다. 그러나 이 데이터베이스는 명시적으로 표시되지 않습니다. 대신 오라클은 해당 인덱스로 항목을 평가하기 위해 호출됩니다. 전체 데이터베이스 항목을 항목별로 읽고 이러한 표현으로 변환하는 것은 Grover의 검색보다 훨씬 더 오래 걸릴 수 있습니다. 이러한 효과를 설명하기 위해 Grover의 알고리즘은 방정식을 풀거나 제약 조건을 만족하는 것으로 볼 수 있습니다. 이러한 애플리케이션에서 오라클은 제약 조건을 확인하는 방법이며 검색 알고리즘과 관련이 없습니다. 이러한 분리는 일반적으로 알고리즘 최적화를 방지하는 반면, 기존의 검색 알고리즘은 이러한 최적화에 의존하여 철저한 검색을 피하는 경우가 많습니다.^[13] 다행히 빠른 Grover의 오라클 구현은 많은 제약 조건 만족 및 최적화 문제에 대해 가능합니다.^[14]

Grover의 알고리즘에서 속도 상승을 인스턴스화하는 데 있어 가장 큰 장벽은 달성된 2차 속도 상승이 너무 미미하여 단기 양자 컴퓨터의 큰 오버헤드를 극복할 수 없다는 것입니다.^[15] 그러나 하드웨어 성능이 더 우수한 내결함성 양자 컴퓨터의 후세대에서는 실제 데이터 인스턴스에 대한 이러한 속도 향상을 실현할 수 있을 것입니다.

문제설명

Grover의 알고리즘에 대한 입력으로 함수 $f{\displaystyle :}${ 0${\displaystyle ,}$ ${\displaystyle 1,\dots ,}$ ${\displaystyle \mathrm{N}}$- 1 ${\displaystyle \}}$ →${\displaystyle }${ ${\displaystyle 0,}$ 1 } ${\displaystyle$ f$\$colon$\{$0, 1$,\ldots, N-1\}\ to \{$0,$$1\} 이라고 가정합니다. "unst 구조화된 데이터베이스" 비유에서 도메인은 데이터베이스에 대한 인덱스를 나타내고, x가 가리키는 데이터가 검색 기준을 만족하는 경우에만 f(x) = 1입니다. 또한 하나의 지수만이 f(x) = 1을 만족한다고 가정하고, 이 지수를 ω라고 합니다. 우리의 목표는 ω을 식별하는 것입니다.

우리는 다음과 같이 작용하는 단일 연산자 U의_ω 형태로 서브루틴(때로는 오라클이라고도 함)을 사용하여 f에 액세스할 수 있습니다.

${\displaystyle {\begin{case}U_{\omega } x\rangle =- x\rangle &{\text{for }}x=\omega {\text{, that is, }}f(x)=1,\\U_{\omega } x\rangle = x\rangle &{\text{for }}x\neq \omega {\text{, 즉 }}f(x)=0입니다.\end{case}}}$

이는 $N$ ${\displaystyle N}$차원 상태 $공간$ H ${\$${\displaystyle {displaystyle}_{}}$ ${\mathcal {H}}$을 사용하며$,$ 이 공간은 n =${\displaystyle {}_{}}$⌈${\displaystyle \log }$ 2$$⁡$N$ ⌉ {\$displaystyle$n=\lceil \log _{2}N\rceil} 큐비트를 가진 레지스터에서 제공합니다. 이것은 종종 다음과 같이 쓰입니다.

${\displaystyle U_{\omega } x\rangle = (-1)^{f(x)} x\rangle .}$

Grover의 알고리즘은 U의 O$(N$) {\$display O({\$sqrt {$N$}}} 어플리케이션을${\displaystyle 사용}$하여 1/$2$ 이상의 확률로 ω를 출력합니다. 이 확률은 Grover의 알고리즘을 여러 번 실행하여 임의로 크게 만들 수 있습니다. ω을 찾을 때까지 Grover의 알고리즘을 실행하는 경우 평균 두 번만 실행되므로 예상 애플리케이션 수는 $(N$) {\$displaystyle O({\sqrt {$N$\}\})$입니다.

대체 오라클 정의

이 섹션에서는 위의 오라클 $U$ω {\displaystyle U_${\$omega}}을$($를) ${\displaystyle {오라클}_{}}$ $Uf$ {\$displaystyle$U_{f}}와 비교합니다.

U는_ω 함수 f에 대한 표준 양자 오라클과 다릅니다. 여기서 U로_f 표시되는 이 표준 오라클은 보조 큐비트 시스템을 사용합니다. 그런 다음 작업은 보조 시스템의 f(x) 값으로 조건화된 주 시스템의 반전(NOT 게이트)을 나타냅니다.

${\displaystyle {\begin{case}U_{f} x\rangle y\rangle = x\rangle \negy\rangle & {\text{ for }}x=\omega {\text{, 즉 }}f(x)=1,\U_{f} x\rangley\rangle = x\rangley\rangle & {\text{ for }x\neq \omega {\text{, 즉 }}}f(x)=0,\end{case}}}$

아니면 간단히,

${\displaystyle U_{f} x\rangley\rangle = x\rangley\opplus f(x)\rangle.}$

이러한 오라클은 일반적으로 언컴퓨팅을 사용하여 실현됩니다.

U가 오라클로 주어지면 U를 구현할 수도 있습니다. 보조 큐비트가 상태에 있을 때${\displaystyle }$U는 ${\displaystyle \frac{\sqrt{U}}{}}$이므로 ⟩ = ${\displaystyle 12(0}$ ⟩${\displaystyle }$- $1$ ⟩) = H 1 ⟩ {\$displaystyle -\rangle$ = ${\frac$ {1$}{\sqrt$ {2}}{\big(} 0\rangle - 1\rangle {\big)} = H 1\rangle }:

${\displaystyle {\begin{aligned}U_{f}{\big(} x\rangle \otimes -\rangle {\big)}&={\frac {1}{\sqrt {2}}\left(U_{f} x\rangle 0\rangle -U_{f} x\rangle 1\rangle \right)\\&={\frac {1}{\sqrt {2}}\left(x\rangle f(x)\rangle - x\rangle 1\opplus f(x)\rangle \right)\\&={\begin{case}{\frac {1}{\sqrt {2}}\left (- x\rangle 0\rangle + x\rangle 1\rangle \right)&{\text{if}f(x)=1,\{\frac {1}{\sqrt {2}}\left(x\rangle 0\rangle - x\rangle 1\rangle \right)&{\text{if}f(x)=0\end{case}\&=(U_{\omega } x\rangle)\Otime -\end{aligned}}}$

그래서 어떤 오라클이 주어지든 상관없이 Grover의 알고리즘을 실행할 수 있습니다.^[3] $U$가 주어지면$$⟩ ${\displaystyle$ -$\$rangle } 상태에서 추가 큐비트를 유지하고 U 대신 U를 적용해야 합니다.

알고리즘.

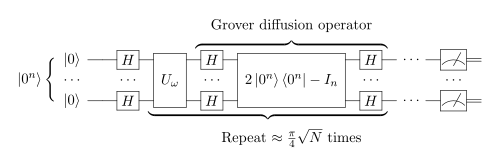
Grover 알고리즘의 단계는 다음과 같습니다.

1. 시스템을 모든 상태에서 균일한 중첩으로 초기화합니다.
   ${\displaystyle s\rangle = {\frac {1}{\sqrt {N}}\sum _{x=0}^{N-1} x\rangle .}$
2. ${\displaystyle \mathrm{다음}}$ "Grover 반복" $r{\displaystyle (}$ N${\displaystyle )}$ ${\style$ r$(N)}$번$$ 수행합니다.
   1. $연산자$ U$$ω {\displaystyle U_${\$omega}} 적용
   2. Grover 확산 연산자 ${\displaystyle {Us}_{}}$ = ${\displaystyle \mathrm{2초}}$⟩ ⟨ - I {\$displaystyle$ U_{s} = 2\lefts\rangle \$lefts\$right -I}
3. 계산 기반에서 결과 양자 상태를 측정합니다.

올바르게 선택된 $r$ ${\displaystyle$ r$}$ 값의 경우$$출력은 ω ⟩ {\$displaystyle$ \$omega$\rangle}이며 확률은 N ≫ 1에 대해 1에 가까워집니다. 분석에 $따르면{\displaystyle }$r${\displaystyle (N}$)$${\$displaystyle$r($N)}$에 대한 이 최종 $값$은${\displaystyle }$r${\displaystyle (N)}$ ≤${\displaystyle }$⌈ π$$4 N ⌉ {\$display$ r(N)\leq {\big \lceil}{\frac {\pi}{4}{\sqrt {N}}{\big \rceil}}을 만족합니다.

이 알고리즘에 대한 단계를 구현하는 것은 큐비트 수에 선형적인 게이트 수를 사용하여 수행할 수 있습니다.^[3] 따라서 이 알고리즘의 게이트 복잡도는 $반복당$ O${\displaystyle (\mathrm{로그}}$ ⁡ ${\displaystyle (N}$) r$($N) {\$display O(\log($N$)$r($N$))}${\displaystyle \mathrm{또는}}$O$로그$⁡ (N) ${\display$O(\log(N))}입니다.

기하학적 정확성 증명

그로버 알고리즘의 양자 상태가 각 단계 후에 2차원의 부분 공간에 머무른다는 것을 관찰하면, 그로버 알고리즘에 대한 기하학적 해석이 있습니다. $평면이$⟩ ${\$$displaystyle$ s$\$rangle }과(와) ω ⟩ {\displaystyle \omega \rangle } 사이에 걸쳐 있다고 생각해 보십시오. 이와 동등하게, 평면은$$ω ⟩ {\$displaystyle$ $\omega \$rangle }과 $수직$ 케트 ⟩ = 1 N - ∑ x ≠ ω {\displaystyle \textstyle s'\$rangle$ = {\frac {1}{\sqrt {N-1}}\sum _{x\n$eq \omega$} x$\rangle$ $\}.$

Grover의 알고리즘은 부분 공간에 있는 $초기$ ${\displaystyle 케트}$ ⟩ {\$displaystyle$ s$\backslash$rangle}로 시작합니다. 연산자 $U$ω {\displaystyle U_${\$omega }는 s' ⟩ ${\$${\displaystyle displaystyle}$s'\$rangle$ } 및 ω ⟩ $\{\backslash$displaystyle \omega \rangle }로$$스팬된 ${\displaystyle 평면}$의 벡터에 대해 ω ⟩${\displaystyle$ \omega \rangle }에${\displaystyle 직교}$하는 초평면에서의 반사입니다. 즉, $S'$⟩ ${\displaystyle$s$\text{'}\backslash$rangle}에 걸쳐 반사되는 역할을 합니다. 이는 U ω${\displaystyle$ U_{\omega }를 Householder reflection의 형태로$$작성하면 확인할 수 있습니다.

${\displaystyle U_{\omega }= I-2 \omega \rangle \ lang \omega .}$

연산자 ${\displaystyle {Us}_{}}$ = ${\displaystyle 2s}$⟩ ⟨ - I {\$displaystyle$ U_{s} = 2s\rangle \ langles - I}는 s ⟩ {\displaystyle s\rangle }를 통한 반사입니다. ${\displaystyle {Us}_{}}$ ${\displaystyle U_{s}}$ 및 $U$ω {\$displaystyle$U_${\$omega}} 연산자는 모두$$평면의 $상태$를 s' ⟩ ${\displaystyle$$'\rangle$ } 및 ω ⟩${\displaystyle$ \omega \rangle }에${\displaystyle 의해}$ 평면의 상태로 전환합니다. 따라서 Grover의 알고리즘은 전체 알고리즘에 대해 이 평면에 머무릅니다.

연산자 ${\displaystyle {}_{}}$가$$ω {\$displaystyle$U_{s})인지 확인하는 것은 간단합니다.각 Grover 반복 단계의 $U_{\omega }}$는 $상태$ ${\displaystyle \frac{\sqrt{벡터}}{}}$를$$$⁡$ ${\displaystyle 1}$ $N$ {\$displaystyle \theta$$=$$2\arcsin${\$tfrac${1$\}\{\backslash$sqrt {N}}}만큼 회전시킵니다. 따라서 충분한 반복으로, $초기$ ${\displaystyle 상태}$ ⟩ {\$displaystyle$ s$\$rangle }에서 원하는 출력 상태 ω ⟩ {\displaystyle \omega \rangle }로 회전할 수 있습니다. 초기 케트는 ω ⟩ {\displaystyle \omega \rangle }와 직교하는 상태에 가깝습니다.

${\displaystyle \langle's\rangle = {\sqrt {\frac {N-1}{N}}}입니다.$

기하학 용어로, s ⟩${\displaystyle$ s\rangle }와 s' ⟩ {\displaystyle s'\rangle $}$ ${\displaystyle 사이}$의 각도 θ / 2 ${\displaystyle \$theta / 2}는 다음과 같습니다.

${\displaystyle \sin {\frac {\theta}{2}}={\frac {1}{\sqrt {N}}}$

상태 벡터가$$ω ⟩ {\$displaystyle$ \$omega$rangle }에 가깝게 통과하면 중지해야 합니다. 이후 반복하면 상태 벡터가$$ω ⟩ {\displaystyle $\omega$\rangle }에서 멀어져서 정답을 얻을 확률이 줄어듭니다. 정답을 측정할 정확한 확률은

${\displaystyle \sin ^{2}\left({\Big(}r+{\frac {1}{2}}{\Big)}\theta \right),}$

여기서 r은 (정수) Grover 반복 횟수입니다. 따라서 최적에 가까운 측정값을 얻을 수 있는 가장 빠른 $시간$은${\displaystyle }$r$$≈ π N / 4 {\$display$ r\approx \pi {\sqrt {N}}/4}입니다.

정확성에 대한 대수적 증명

대수적 해석을 완성하기 위해서, ${\displaystyle {}_{}}$는$$ ω {\$display$ U_${$s}를 반복적으로 적용했을 때 어떤 일이 일어나는지 알아내야 합니다.$U_{\omega$ $\}\}.$ 자연스러운 방법은 행렬의 고유값 분석입니다. 전체 계산 동안 알고리즘의 상태는 $s${\$displaystyle$ s$}$와$$ω {\displaystyle$\$omega}의 선형 조합입니다. 우리는 {s ⟩에 걸쳐$$있는 공간에 $Us {\displaystyle$ U_${$}}와 $U$ω {\display U_{\omega }의 ${\displaystyle {동작}_{}}$을 쓸 수 있습니다.$ω$ ⟩ $}$ ${\$displaystyle \{s\rangle, \omega \rangle \}을(를) 다음과 같이 표시합니다.

${\displaystyle U_{s}:a \omega \rangle + b\rangle \maps to [ \omega \rangle \, s\rangle ]{\begin{bmatrix}-1&0\2/{\sqrt{N}}&1\end{bmatrix}}{\b\end{bmatrix}}}$

${\displaystyle U_{\omega}:a \omega \rangle + b\rangle \maps to [ \omega \rangle \, s\rangle ]{\begin{bmatrix}-1&-2/{\sqrt {N}}\0&1\end{bmatrix}}{\b\end{bmatrix}}$

따라서 기저$${ω ⟩${\displaystyle ,}$ s$$⟩ } {\displaystyle \{ \$omega$ \rangle, s\rangle \}}(전체 공간의 직교하지도 않고 기초도 아님) 액션 U ω {\displaystyle U_{s}$U$$ω$ {\displaystyle U_${\$omega}}를 적용한 후 U {\$displaystyle$U_{s$}}$를 적용한 $U_{\$$omega$$}$는 행렬로 표시됩니다.

${\displaystyle U_{s}U_{\omega }={\begin{bmatrix}-1&0\\2/{\sqrt {N}}&1\end{bmatrix}}{\begin{bmatrix}-1&-2/{\sqrt {N}}\\0&1\end{bmatrix}}={\begin{bmatrix}1&2/{\sqrt {N}}\\-2/{\sqrt {N}}&1-4/N\end{bmatrix}}.}$

이 매트릭스는 아주 편리한 Jordan 형태를 가지고 있습니다. $t$ = ${\displaystyle \arcsin }$⁡ (1 / N ) {\displaystyle t =\arcsin (1 / {\sqrt {N}}}을 정의하면,

$display U_{$$U_{\omega$ }$=$ $M{\$$begin{bmatrix}e^{$2it$}&$0\\0&$e^{-$2it$}\end{bmatrix}}$M^{-1}, 여기서 M $=$ [ - i e - it ] . {\displaystyle M $=$ {\begin{bmatrix}-i&i\\e^{-it}\end{bmatrix}}

행렬의 r번째 거듭제곱(반복에 해당)은 다음과 같습니다.

${\displaystyle (U_{s}U_{\omega })^{r}=M{\begin{bmatrix}e^{2rit}&0\\0&e^{-2rit}\end{bmatrix}}M^{-1}.}$

이 형식을 사용하면 삼각형 항등식을 사용하여 앞 절에서 언급한 반복 후 ω을 관찰할 확률을 계산할 수 있습니다.

${\displaystyle \left {\begin{bmatrix}\langle \omega \rangle &\langle \omega s\rangle \end{bmatrix}}(U_{\omega})^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\right ^{2}=\sin ^{2}\left((2r+1)t\right)}}$

또는 각도 2rt와 -2rt가 가능한 한 멀리 떨어져 $있을$ 때가 ${\displaystyle \mathrm{2rt}}$≈ π /2 {\displaystyle 2rt\approxy \pi /2}에 해당할 때를 구분하는 데 최적에 가까운 시간이라고 합리적으로 상상할 수 있습니다. 또는 $r$ =${\displaystyle }$π / 4 t =$$π / 4 아크신 ⁡ (1 / N) ≈ π N / 4 {\displaystyle r=\pi / 4t=\pi / 4\arcsin(1/{\sqrt {N}})\approx \pi {\sqrt {N}}/4}. 그러면 시스템이 상태가 됩니다.

${\displaystyle [ \omega \rangle \, s\rangle ](U_{s}U_{\omega })^{r}{\begin{bmatrix}0\\1\end{bmatrix}}\approx [ \omega \rangle \, s\rangle]M{\begin{bmatrix}i&0\\0&i\end{bmatrix}}M^{-1}{\begin{bmatrix}0\1\end{bmatrix}}= \omega \rangle {\frac {1}{\cos(t)}- s\rangle {\sin(t)}{cos(t)}}- s\rangle {\cos(t)}}.$

이제 짧은 계산을 통해 관측 결과 O${\displaystyle (1}$ N${\displaystyle )}$ {\$display O\left({\frac${1}{$N}\$right$)\}$ 오류가 있는 정답 ω이 생성됨을 알 수 있습니다.

확장 및 변형

일치하는 항목이 여러개 있음

일치하는 항목이 1개가 아닌 k개 일치하는 항목이 있는 경우 동일한 알고리즘이 작동하지만${\frac{\mathrm{반복}}{}}^{}$횟수는 π 4$($2 {\$textstyle {\$frac {\$pi}{4}}{\left({\frac$ {N}{k$}\$right)^{1$/2}}$ π 4 N/2 $대신 {\textstyle {\frac {\$pi}{4}{N^{1/2}}

k를 알 수 없는 경우 사건을 처리하는 방법은 여러 가지가 있습니다.^[16] 간단한 솔루션은 상수 계수까지 최적으로 수행됩니다. 예를 들어, k = N, N/${\displaystyle 2}$,$N$/4, ... 등 점점 더 작은 k 값에 대해 Grover의 알고리즘을 반복적으로 실행하고, 일치하는 항목이 발견될 때까지 반복 t에 대해 k = N / 2 t {\display k = N/2^{t}를 사용합니다.

충분히 높은 확률로 일부 상수 c에 대해 $반복$ t = ${\displaystyle {\log }_{}}$ ${\displaystyle 2_{}}$⁡ (N / k ) + c {\displaystyle t =\log _{2} (N/k) + c}를 통해 표시된 항목을 찾을 수 있습니다. 따라서 총 반복 횟수는 최대

${\displaystyle {\frac {\pi }{4}}{\Big (}1+{\sqrt {2}}+{\sqrt {4}}+\cdots +{\sqrt {\frac {N}{k2^{c}}}}{\Big )}=O{\big (}{\sqrt {N/k}}{\big )}.}$

k를 알 수 없는 경우의 또 다른 방법은 이전에 양자 계수 알고리즘을 통해 k를 도출하는 것입니다.

$k$ = ${\displaystyle N}$/$$2 {\$displaystyle$ k = N/2}(또는 N = 2 {\displaystyle N = 2}와 함께 실행되는 경우 전통적으로 표시된 상태인 Grover's Algorithm)일 경우 알고리즘은 증폭을 제공하지 않습니다. > / 2 ${\displaystyle$ k > $N/2}$인 경우 k를 증가시키면 해를 구하는 데 필요한 반복 횟수가 증가하기 시작합니다.^[17] ${\displaystyle 반면}$에 k${\displaystyle }$≥ N / 2${\displaystyle$k$\backslash$geq N/2}일 경우 단일 랜덤 입력 선택에 대한 검사 오라클의 고전적인 실행은 올바른 해결책을 제공하지 않을 가능성이 높습니다.

이 알고리즘의 버전은 충돌 문제를 해결하기 위해 사용됩니다.^[18][19]

양자 부분 탐색

Grover와 Radhakrishnan은 2004년에 양자 부분 검색이라는 Grover의 알고리즘을 수정했습니다.^[20] 부분 검색에서는 대상 항목의 정확한 주소를 찾는 데 관심이 없으며 주소의 처음 몇 자리만 있습니다. 마찬가지로 검색 공간을 블록으로 "정크"한 다음 "대상 항목이 어느 블록입니까?"라고 묻는 것을 생각할 수 있습니다. 많은 응용 프로그램에서 이러한 검색은 대상 주소에 원하는 정보가 포함되어 있으면 충분한 정보를 얻을 수 있습니다. 예를 들어, L. K. Grover가 제시한 예를 들어, 학급 순위별로 학생들의 목록이 있다면, 우리는 학생이 하위 25%, 25-50%, 50-75%, 75-100% 백분위수에 속하는지에만 관심을 가질 수 있습니다.

부분 검색을 설명하기 위해 각각 $크기$ ${\displaystyle b}$ = N / K {\displaystyle b$$= N/${\displaystyle K}$}인 $K$ ${\displaystyle K}$ 블록으로 분리된 데이터베이스를 고려합니다. 부분 검색 문제는 더 쉽습니다. 우리가 고전적으로 취할 접근법을 생각해 보십시오. 우리는 임의로 하나의 블록을 선택한 다음 나머지 블록(집합 이론 언어, 보어)을 통해 정상적인 검색을 수행합니다. 목표물을 찾지 못하면 검색하지 않은 블록에 있다는 것을 알게 됩니다. $평균{\displaystyle }$ 반복 횟수가 N${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle$ N$/2}$에서${\displaystyle }$(${\displaystyle N}$- b${\displaystyle }$)${\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle (N-b)/2}$로 떨어집니다$.$

Grover의 알고리즘은$$π 4 N ${\textstyle${\$frac {\pi$}{$4}}{\$sqrt {N}}번 반복해야 합니다. $블록{\displaystyle }$ 수 K ${\displaystyle$ K$}$에 따라 $부분$ 검색이 더 빨라집니다$.$ 부분 검색은 ${\displaystyle {n\mathrm{}}_{}}$ 1 ${\$ 글로벌$$ 반복과 $n{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 로컬$$ 반복을 사용합니다. 글로벌 Grover 연산자는 ${\displaystyle {G1\mathrm{}}_{}}$ ${\$ 로컬$$ Grover 연산자는 ${\displaystyle {G2\mathrm{}}_{}}$ ${\$로 지정됩니다$.$

글로벌 Grover 연산자는 블록에 작용합니다. 기본적으로 다음과 같이 주어집니다.

1. ${\displaystyle {전체\mathrm{}}_{}}$ 데이터베이스에서 j $1{\displaystyle {}_{}}$ ${\$ 표준$$ Grover 반복을 수행합니다.
2. $j{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ 로컬$$ Grover 반복을 수행합니다. 로컬 그로버 반복은 각 블록에 대한 그로버 반복의 직접적인 합입니다.
3. 하나의 표준 Grover 반복을 수행합니다.

$j{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ 및$$ j ${\displaystyle {2\mathrm{}}_{}}$ ${\$의 최적 값은 Grover와 Radhakrishnan의 논문에서 논의됩니다$$. 또한 다양한 수준의 "해상도"에서 연속적인 부분 검색을 적용할 경우 어떤 일이 발생하는지 궁금해 할 수도 있습니다. 이 아이디어는 블라디미르 코레핀(Vladimir Korepin)과 쉬(Xu)에 의해 자세히 연구되었으며, 그는 이것을 이진 양자 탐색이라고 불렀습니다. 그들은 그것이 사실 한 번의 부분 검색을 수행하는 것보다 더 빠르지 않다는 것을 증명했습니다.

최적성

Grover의 알고리즘은 하위 상수 요인까지 최적입니다. 즉, 연산자 U를_ω 사용해야만 데이터베이스에 접근하는 알고리즘은 적어도 Grover의 알고리즘보다 많은 $1{\displaystyle \mathrm{}}$ -${\displaystyle o}$(${\displaystyle 1)}${\$displaystyle 1-o (1)}$ 분수$$ U를_ω 적용해야 합니다.^[21] Grover의 알고리즘을 k개의 일치하는 항목인 π(N/k)/4로 확장하는 것도 최적입니다. 이 결과는 양자 연산의 한계를 이해하는 데 중요합니다.

Grover의 검색 문제가 U의_ω log^c N 응용 프로그램으로 해결될 수 있다면 NP의 문제를 Grover 유형의 검색 문제로 변환함으로써 NP가 BQP에 포함되어 있음을 의미합니다. Grover 알고리즘의 최적성은 양자 컴퓨터가 NP-Complete 문제를 다항식 시간 내에 해결할 수 없으므로 NP가 BQP에 포함되지 않음을 시사합니다.

비로컬 은닉 변수 양자 컴퓨터 클래스는 기껏해야 $N3$ ${\display$ O$({\sqrt[{3}]}{$에서 $N$ ${\displaystyle N}$ 항목 데이터베이스 검색을 구현할 수 있는 것으로 나타났습니다.$N})}$단계입니다$$. 이는 Grover의 알고리즘이 취한 $O{\displaystyle (N)}$ ${\displaystyle$ O$({\sqrt {N}}}$ 단계보다$$ 빠릅니다.^[22]

참고 항목

• 진폭 증폭
• 브래지어–Høyer–Tapp 알고리즘 (충돌 문제 해결을 위한)
• Shor의 알고리즘(인수분해용)
• 양자 보행 탐색

메모들

참고문헌

• 그로버 L.K.: 데이터베이스 검색을 위한 빠른 양자역학 알고리즘, Proceedings, 제28회 컴퓨팅 이론 연례 ACM 심포지엄(1996년 5월) 212페이지
• 그로버 L.K.: 슈뢰딩거 방정식부터 양자검색 알고리즘, American Journal of Physics, 69(7): 769–777, 2001. 알고리즘과 알고리즘의 역사에 대한 교육학적 검토.
• Grover L.K.: 양자전산: 아원자 세계의 이상한 논리가 어떻게 기계가 오늘날 기계보다 수백만 배나 빠른 계산을 가능하게 만들 수 있었을까 The Sciences, 1999년 7월/8월 24-30쪽.
• 닐슨, M.A. 그리고 추앙, I.L. 양자 계산과 양자 정보. 캠브리지 대학 출판부, 2000 6장.
• 퀀텀 폰북이란? Lov Grover, Lucent Technologies

외부 링크

• Davy Wybiral. "Quantum Circuit Simulator". Archived from the original on 2017-01-16. Retrieved 2017-01-13.
• Craig Gidney (2013-03-05). "Grover's Quantum Search Algorithm".
• François Schwarzentruber (2013-05-18). "Grover's algorithm".
• Alexander Prokopenya. "Quantum Circuit Implementing Grover's Search Algorithm". Wolfram Alpha.
• "Quantum computation, theory of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Roberto Maestre (2018-05-11). "Grover's Algorithm implemented in R and C". GitHub.
• Bernhard Ömer. "QCL - A Programming Language for Quantum Computers". Retrieved 2022-04-30. Implemented in /qcl-0.6.4/lib/grover.qcl