일방향 양자 컴퓨터

에 관한 일련의 기사의 일부
양자역학
${\displaystyle i\hbar {\frac t} \psi (t) \rangle = {H} \psi (t) \rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전 역학 구 양자론 브라켓 표기법 해밀턴식 방해다
기초 상보성 데코히렌스 얽힘 에너지 레벨 측정. 비국소성 양자수 주 중첩 대칭 터널링 불확실성 파동 함수 접다
실험 벨 부등식 데이비슨-게르머 더블 슬릿 엘리추르-바이드만 프랑크-헤르츠 레깃-가르그 부등식 마흐-젠더 포퍼 양자 지우개 선택 지연 슈뢰딩거의 고양이 스턴-게라크 휠러의 지연 선택
제제 개요 하이젠베르크 상호 작용 매트릭스 위상 공간 슈뢰딩거 Sum-over-History(경로 적분)
방정식 디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석 개요 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션
상세 토픽 상대론적 양자역학 양자장론 양자정보과학 양자 컴퓨팅 양자 카오스 밀도 매트릭스 산란 이론 양자통계역학 양자 기계 학습
과학자 아하로노프 벨 베테 블래킷 블로치 쾅 보어 태어난 보스 드 브로글리 콤프턴 디락 데이비슨 데비 에렌페스트 아인슈타인 에버렛 폭 페르미 파인만 글라우버 거츠빌러 하이젠베르크 힐베르트 조던 크래머스 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 온네스 플랑크 라비 라만 리드버그 슈뢰딩거 시몬스 솜메르펠트 폰 노이만 와일 빈 위그너 지만 자이링거
v t

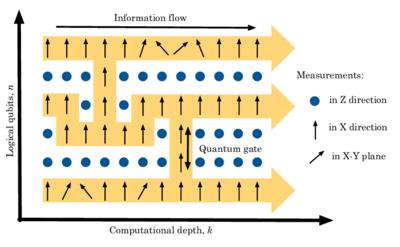
단방향 또는 측정 기반 양자 컴퓨터(MBQC)는 먼저 얽힌 리소스 상태(일반적으로 클러스터 상태 또는 그래프 상태)를 준비한 다음 단일 큐비트 측정을 수행하는 양자 컴퓨팅 방법입니다.측정값에 의해 리소스 상태가 파괴되기 때문에 "단방향"입니다.

각 개별 측정의 결과는 무작위이지만 계산이 항상 성공하는 방식으로 관련이 있습니다.일반적으로 이후 측정을 위한 기준 선택은 이전 측정의 결과에 따라 달라져야 하며, 따라서 모든 측정을 동시에 수행할 수는 없다.

MBQC의 하드웨어 구현은 광자 간의 얽힘 특성 덕분에 주로 광자 장치에 의존합니다.얽힘 및 측정 프로세스는 그래프 도구와 그룹 이론, 특히 스태빌라이저 그룹의 요소에 의해 설명될 수 있습니다.

정의.

양자컴퓨팅의 목적은 양자역학의 특징을 가진 정보이론을 구축하는 데 초점을 맞춘다: 정보의 2진수 단위(비트)를 1 또는 0으로 바꿀 수 있는 대신, 정보의 2진수 단위(쿼트)는 중첩이라고 불리는 현상 덕분에 동시에 0과 1로 바뀔 수 있다.양자 컴퓨팅의 또 다른 주요 기능은 큐비트 ^[4][5][6]간의 얽힘에 의존합니다.^[1][2][3]

양자논리게이트 모델에서는 연산 개시 시에 레지스터라고 불리는 큐비트 세트가 준비되며, 그 후 유니터리 연산자에 의해 반송되는 큐비트 상의 논리연산 세트가 ^[7][8]구현된다.양자회로는 큐비트에 대해 유니터리 변환이 적용되는 큐비트의 레지스터에 의해 형성된다.측정 기반 양자 계산에서는 단일 변환을 통한 논리 연산을 구현하는 대신 입력 큐비트 k$(\$$displaystyle$ k$)$를$보조$ 큐비트 $클러스터$와 결합하여 동일한 연산을 실행하여${\displaystyle }$+${\displaystyle k}$ $=$$$(\$displaystyle$ a$+k$=)의 전체 소스 상태를 형성한다.$n}$ 큐비트를$$ 측정한 다음 ^[9][10]그 중 $(표시 스타일$ m$$$)$을 측정합니다.$나머지{\displaystyle }$ k ${\displaystyle =n}$ -$$m(\$style$ k$=n-m$) 출력 큐비트는 측정된 큐비트와의 얽힘으로 인해 측정의 영향을 받습니다.단방향 컴퓨터는 범용 양자 컴퓨터라는 것이 증명되었는데, 이것은 임의의 수의 큐비트에 ^{[7][11][12][13]}걸쳐 어떤 단일 연산도 재현할 수 있다는 것을 의미한다.

단방향 컴퓨팅

일반적인 절차

측정 기반 양자 컴퓨팅의 표준 과정은 세 단계로 구성됩니다: 큐비트 얽힘, 보조 큐비트 측정 및 출력 수정.^[14][15]첫 번째 단계에서는 소스 상태를 준비하기 위해 큐비트가 얽힌다.두 번째 단계에서는 출력 큐비트 상태에 영향을 주는 앤실라를 측정한다.그러나 양자역학의 ^[15]결정되지 않은 특성으로 인해 측정 출력은 비결정론적 결과입니다. 결정론적 방식으로 계산을 수행하기 위해 부산물이라고 하는 일부 보정 연산자가 도입됩니다.

소스 상태 준비

연산 시작 시 큐비트는 입력 큐비트와 보조 큐비트의 두 가지 범주로 구분할 수 있습니다.입력은 일반적인 ${\displaystyle \delta =}$ ${\displaystyle \alpha \mathrm{}}$ 0${\displaystyle \delta }$ + ${\displaystyle \beta \mathrm{}}$ 1$$δ { $displaystyle \psi \rangle$= \$alpha$0 \$rangle$+ \$langle }$ 상태로$$ 설정된 큐비트를 나타내며, 이에 따라 몇 가지 단일 변환이 수행됩니다.소스 상태를 준비하려면 모든 보조 큐비트를 +$displaystyle +\rangle)$ ^[9][16]상태로$$ 준비해야 합니다.

${\displaystyle +\rangle = tfrac {0\rangle + 1\rangle }{\displayrt {2}},$

${\displaystyle 여기}$서 0$$⟩(\$displaystyle$0\$rangle)$ ${\displaystyle 및}$ 1$${\(\$displaystyle$ 1$\rangle)$은 $클래식{\displaystyle \mathrm{}}$ 0$(\displaystyle$ 0$)$ $및$ 1$(\displaystyle$1) 비트의$$ 양자 부호화입니다.

${\displaystyle 0}$ ${\displaystyle ⟩}$ ${\displaystyle =}$ ( ${\displaystyle \begin{array}{c}1\mathrm{}\end{array}}$ ${\displaystyle \begin{array}{}0\\ \mathrm{}\end{array}}$) 、 ${\displaystyle 1\mathrm{}}$ ${\displaystyle ⟩}$ ${\displaystyle =}$ ( ${\displaystyle \begin{array}{c}0\mathrm{}\\ \end{array}\begin{array}{}1\\ \mathrm{}\end{array}}$ $){$ $displaystyle$0 \ $rangle = displaystyle${ pmatrix }$1$\ \ \ \ \ \ \$end$ { pmatrix$$} ;\ $langle = displaystyle$ {$pmatrix }$0 \ 1 \ 1 \ 1 \ 1 \ 1 \ 1 \ \ \ \ \ }

따라서 n개의$$\$displaystyle$n개의$$ 큐비트를 $가진{\displaystyle }$ 레지스터는 +${\displaystyle {}^n}$n {\$displaystyle +\rangle ^{\otimes$n$\}\}$로 설정됩니다. 그 후 C$$ {\$displaystyle CZ}$ $게이트$ ^[17]조작을 적용하여 2개의 큐비트 간의 얽힘을 수행할 수 있습니다.이러한 2비트 연산자의 행렬 표현은 다음과 같습니다.

$({displaystyle CZ=begin{bmatrix}1&0&0\\0&1&0&0\\0&1&1\end{bmatrix})}$

2개의 큐비트에 $걸친{\displaystyle }$ $(\style CZ$) 게이트의 동작은 다음 시스템으로 설명할 수 있습니다.

${\displaystyle\case}케이스}CZ 0+\rangle = 0+\CZ 0-\rangle = 0-\CZ 1+\rangle = 1-\rangle \\CZ 1-\rangle = 1+\rangle \end {case}$

$C$ Z $게이트$를$$+ ${\$ \ $style$+ \ $rangle$상태의$$ 2개의 Ancillae에 적용할$$ 경우 전체 상태는

$(\displaystyle CZ ++\rangle = specfrac {0+\rangle + 1-\rangle}}{\pecrt {2}}}$

큐빗의 뒤엉킨 쌍으로 바뀝니다.두 개의 앙킬레를 얽을 때, 결과가 동일한 한 어떤 것이 제어 큐비트이고 어떤 것이 목표인지에 대한 중요성은 주어지지 않는다.$마찬가지$로 $(\$style $CZ)$ 게이트는$$ 대각선 형태로 표시되므로 모두 서로 통근하며 어떤 큐비트를 먼저 얽히게 할지는 중요하지 않습니다.광자는 얽힌 물리적 ^[18][19][20]큐비트를 준비하는 가장 일반적인 소스입니다.

큐비트 측정

단일 입자 상태에 대한 측정 프로세스는 관찰 가능한 고유 벡터에 상태를 투영하여 설명할 수 있습니다.예를 ${\displaystyle 들어{}_{}}$ o ${\displaystyle {1\mathrm{}}_{}}$ ${\$ { $displaystyle o$_ { \ $rangle$}및 ${\displaystyle {o\mathrm{}}_{}}$ 2$$display$${ $displaystyle o_{2}\$$rangle$$}$과 ${\displaystyle 같은{}_{}}$ 두 개의 고유 벡터를 가진 $관찰{\displaystyle }$ 가능한$$O$(\$$displaystyle$$$O)를$$ 고려하고,$i-style$을 측정하는 다입자 양자 ${\displaystyle 시스템}$을 취급한다고 가정합니다.ubit by $O{\displaystyle }$ {\$displaystyle$ O$\}$^[16]의 고유 벡터에$$$${\displaystyle $\Psi \rangle}$ 상태를$$ 투영하는 O$${\$displaystyle$ O} 관측 수단:

${\displaystyle {}^{}{\psi \psi }_{}}$=${\displaystyle {}_{}{oi}_{}}$o ${\displaystyle i{}_{}\mathrm{}}$ i o o$idisplay$ i 、 { $displaystyle \Psi$ ' \$rangle = o_{i} \Psi \rangle$}.

${\displaystyle i{}_{}}$ ${\displaystyle$ i$}$ -th$$ qubit의 실제 상태는 ${\displaystyle o_{}}$ ${\$ {\ $now$ now now now now now now now of of of of of of of of of of of of of(양자역학에서는 확률적인) 측정 결과에 따라 ${\displaystyle {o\mathrm{}}_{}}$ 1$$ { $displaystyle o_{1$$}$ $\rangle$ $\}$이 될 수 ${\displaystyle {있습니다\mathrm{}}_{}}$.측정 투영법은 관찰 $가능$한 M${\displaystyle (}$ ${\displaystyle )}$ ) $=$ ${\displaystyle \cos }$ ${\displaystyle (}$ ( ${\displaystyle )}$ )${\displaystyle X}$ + ${\displaystyle \sin }$ ${\displaystyle (}$ (${\displaystyle \theta }$ ) Y$${\$display$ M$(\theta$ )=\$cos(\theta)X+\sin(\theta)Y}$의 고유 상태에 대해 수행할 수 있습니다.

M(θ))못 말리겠고 ⁡(θ)[0110]+죄 ⁡(θ)[0− 나는 나는 0])[0e− 나는 θ eiθ 0]{\displaystyle M(\theta)=\cos(\theta){\begin{bmatrix}0&, 1\\1&, 0\end{bmatrix}}+\sin(\theta){\begin{bmatrix}0&, -i\\i&, 0\end{bmatrix}}={\begin{bmatrix}0&, e^{-i\theta}\\e^{i\theta}.&0\end{bmatrix}}},

$여기$서 X$(\displaystyle$ X$)$와 Y$(\displaystyle$ Y$)$는 Pauli 매트릭스에 속합니다.M${\displaystyle (}$ ${\displaystyle \theta {}_{}}$$)$의 $고유{\displaystyle }$ $벡터$(\$displaystyle$ M(\theta$)$는 ${\displaystyle {\pm }_{}}$ ±${\displaystyle {}_{}=}$ ${\displaystyle 0\mathrm{}}$ ± ${\displaystyle e^{}}$ ${\displaystyle 1{}^{}\mathrm{}}$ 1 ${\$ \ $display$ \$theta$ _ { \ $pm$} \ $rangle = 0$ \ $rangle$\$pm$ e$^{i$\ $theta }$$$1 \ $rangle$ 입니다$.$ ${\displaystyle }$ 에서 쿼트를 측정합니다.${\displaystyle e}$는 ${\displaystyle {+}_{}}$ + ${\$ \ $displaystyle \theta$ _ { + } \ $rangle$} ${\displaystyle 또는}$ ${\displaystyle {-}_{}}$ -${\$ \ $displaystyle \theta$ _ { - } \ $rangle$ $\}$에 투영하는 것을 의미합니다.일방향 양자 컴퓨팅에서는 큐비트가 측정되면 계산 흐름에서 큐비트를 재활용할 수 없습니다.${\displaystyle 따라서{}_{}}$$$${\displaystyle o_{}}$ ${\displaystyle {}_{}{o}_{}{}_{}}$i \ $displaystyle o$_ { i } \ $rangle o _$ { i$$$$} 표기 대신${\displaystyle o_{}}$ i \ $displaystyle o$_ { i$}$ 표기법을$$ $사용$하여 i \ $displaystyle$o _ { i } - th$$ qubit에 대한 투영 측정을 나타내는 것이 일반적입니다.

출력 수정

모든 측정을 수행한 후 시스템은 시스템의 출력 상태를 형성하는 더 적은 수의 큐비트로 감소되었습니다.측정의 확률론적 결과로 인해 시스템은 결정론적 방식으로 설정되지 않습니다. X$(\displaystyle$ X$)$ - $(\displaystyle$ Y$)$ $평면$에서 측정하면 ${\displaystyle 결과}$가$+(\displaystyle \theta$ _${+}\rangle$}) ${\displaystyle 또는}$ （\displaystyle \ta _ta - $ra$$$}) 중 어느 쪽이었는지 여부가 달라질 수 있습니다.$ngle$ 결정론적 계산을 수행하려면 몇 가지 보정이 필요합니다.보정 연산자 또는 부산물 연산자는 모든 측정이 ^[16][21]수행된 후 출력 큐트에 적용됩니다.적용할 수 있는 부산물 사업자다 X{X\displaystyle}과 Z{Z\displaystyle}.[22]은 측정 결과에 따라 부산물 사업자의 출력 상태에 적용할 수 있:j에 대한 X{X\displaystyle}수정{j\displaystyle}-th 이진법, 나의 결과에 따라.asu관찰 가능한$$ M${\displaystyle (}$ $))$을 통해 $i$$({$$displaystyle$ i$}$ - qubit에 대해 수행된 재설정은 ${\displaystyle X_{}^{}}$({$displaystyle X_{j}^s_{i$로 설명할 수 있습니다. 여기서 $측정{\displaystyle {}_{}}$ 결과가 +$display$ $style$$s_{i}$일 경우$$는$0$으로 $설정$됩니다$.$$ystyle \theta$ $_{+}\rangle$ ${\displaystyle 그렇지{}_{}}$ 않으면 1$(\displaystyle 1$$)$이 됩니다${\displaystyle {.}_{}}$첫 번째 경우 수정은 이루어지지 않습니다.첫 번째 경우 X$(\displaystyle$ X$)$ $연산자$는 j$\style$j -$$$qubit$에 구현됩니다.결국 양자역학에서 측정 결과가 결정적이지 않더라도 측정 결과는 보정을 수행하고 결정론적 계산을 수행하기 위해 사용될 수 있다.

CME 패턴

단일 게이트를 구현하기 위해 얽힘, 측정 및 보정 작업을 수행할 수 있습니다.이러한 동작은 회로 내의 모든 로직 게이트에 대해 시간별로 수행될 수 있으며, 오히려 회로 시작 시 모든 얽힘 동작, 중간 시 측정 및 회로 끝 시 보정을 할당하는 패턴으로 수행될 수 있습니다.이러한 계산 패턴을 CME 표준 ^[14][15]패턴이라고 합니다.CME 형식주의에서는$i$와$j{\displaystyle }$($displaystyle$$$j$)$ 큐비트$$ 사이의 얽힘 ${\displaystyle {연산}_{}}$을 $($라고 합니다.X$$-$$ $평면$에서의$$$(\$$displaystyle$$$X$)$ $display$(\displaystyle Y$)$ $bit$(\$display style$ M_{$i}) display$(\displaystyle M_{$i}^{\$theta $\})$ display(\$displaystyle$ X$)$ quit에 $대한{\displaystyle }$ 측정값은 ${\displaystyle {Mi}_{}^{}}$$$${\displaystyle {}_{}^{}}$(\displaystyle M_{i} display$$)로 정의됩니다.$j{\displaystyle }${$displaystyle$ j$}$ 큐비트에$$ 대한 측정은 ${\displaystyle {{}_{}}_{}^{}}$ s$$ {$displaystyle X_{i}^{s_{j$로 설명되며, $여기$서 $s{\displaystyle {}_{}}$ ${\displaystyle j_{}}${$displaystyle$ $s_{j}}$는 ${\displaystyle 결과}$가 ${\displaystyle {+}_{}}$ +${\$ {\$displaystyle$$$$\$$thta$ _$+}$ $상태$일 때$$0으로$$ $설정$됩니다$.$${\displaystyle e{}_{}}$ 결과는 ${\displaystyle {-}_{}}$ -$（$ { $displaystyle \theta$ _ { - } \ $rangle$ 。$Z{\displaystyle }${ \ $displaystyle$ Z$$}부산물에도$$ 동일한 표기가 적용됩니다.

CME 패턴에 따라 계산을 수행할 때 X$(\displaystyle$ X$)$ - $(\displaystyle$ Y$)$의 두 가지 ${\displaystyle {측정값}_{}^{}}$ Mi ${\displaystyle {{1\mathrm{}}_{}}_{}^{}}$1(\$displaystyle M_{i}^{1})$과 ${\displaystyle {Mj}_{}^{}}$ ${\displaystyle {{2\mathrm{}}_{}}_{}^{}}$2(\$displaystyle M_{j}^{\theta _2}})$가 다른 평면에 따라 달라질 수 있습니다.예를 들어$,$ j {\$displaystyle$j} -th$$ qubit의 $측정{\displaystyle }$ 각도 앞에 있는 부호는 i {\$displaystyle$ i$}$ $-th$ qubit에 대한 측정과 관련하여 플립할 수 있습니다. 이 경우 ${\displaystyle {}_{}^{}}$은 [${\displaystyle M_{}^{}}$ ${\displaystyle {{j\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}{}^{}}$ ${\displaystyle {2{}_{}}^{}}$ ] ${\displaystyle s_{}^{}}$ i ${\$ 1 { m ${\displaystyle {{1\mathrm{}}_{}}_{}^{}}$ 1 { $displaystyle$[ $M_j$} { $ta$ _ $ta$_ $ta$_ 2 } } { s } } } { s } } } {s } }${\displaystyle }$} {s } } } {s } } } } $}^{\theta _{$1$\}\}\},$ 따라서 두 측정 작업은 더 이상 서로 이동하지 않습니다.${\displaystyle s_{}}$ i$(\$가 0$(\displaystyle$ 0$)$으로 설정되어 있는 $경우{\displaystyle {}_{}}$ $2{\displaystyle {}_{}}$ 2$(\$$theta$ _${2})$ 기호는$$ 플립되지 않습니다.그렇지 않으면 ${\displaystyle {2\mathrm{}}_{}}$2$(\displaystyle$ $s_{$$i$}$=1$ 각도가${\displaystyle {\theta \mathrm{}}_{}}$ 2$(\$ - ${ta.ta$로 반전됩니다.따라서 ${\displaystyle {}_{}^{}}$ [${\displaystyle {Mj}_{}^{}}$ $]$ i({$displaystyle [M_{$j}^{\$theta$ _${2}})^{s_{$i})는 Mj${\displaystyle {}_{{}^{}}^{}}$- )${\displaystyle {{s_{}}^{}}_{}^{}}$ ${\displaystyle {{i\mathrm{}}_{}}_{}^{}}$ ${\$ 2 { $displaystyle M_{j}^{s_i}\theta_{2$로 고쳐 쓸 수 있습니다.

예:오일러 회전

예시로 ${\displaystyle X}$ ${\displaystyle Z}$ $(\displaystyle XZX)$ 기준에서의$$ 오일러 회전을 고려합니다. 양자 계산의 게이트 모델에서 이러한 연산은 다음과 같이 설명됩니다^[23].

${\displaystyle e^{}}$ i ${\displaystyle r}$ R${\displaystyle {}_{}{X}_{}}$ ( ${\displaystyle )}$ ) ${\displaystyle R_{}{}_{}}$X${\displaystyle {}_{}}$( ${\displaystyle )}$ )$$\ $display$ e^ {$i$ \ $gamma$} R$_$ { $X$} ( \ $phi$) $R$_ { $Z$} ( \ $theta$)$R$_ { $X$} ( \ $lambda$)$$,

$여기$서 ${\displaystyle ,,}$,,$(\display\phi,\theta,\displayda)$는 회전 각도이며,$${\(\$displaystyle\$displayda$)$는 계산과 무관한 글로벌 위상을 정의합니다.이러한 조작을 단방향 컴퓨팅 프레임으로 실행하려면 , 다음의 CME 패턴을 ^[21][24]실장할 수 있습니다.

$displaystyle Z_{$$$$}}X_{3}^{s_{2}+s_$${4}$$}}[M_{4}^{-\phi }]^{s_{1}+s_{3$$}[M_{$3}^{-\$theta }]^{s_{$2}[$M_{$2}^{-\$lambda}]^{s_{$1}$M_{0}E_{4,5}E_{$3,4$}E_{2$,3}$E_{1$$2},$

여기서 입력 상태 ${\displaystyle \psi \mathrm{}}$ ${\displaystyle ⟩}$ $=$ α${\displaystyle }$0 ${\displaystyle 1\mathrm{}}$ + β 1$$ （ \ $displaystyle \psi$ \rangle = \$alpha$0 \$rangle$$$+ \ $display$ 1$}$은 $큐비트{\displaystyle \mathrm{}}$1 {\$displaystyle$ 1$\}$이고, 다른 모든 큐비트는 보조 앙실레이므로$$+ ${\displaystyle ⟩}$ \$displaystyle }$ 상태로$$ 준비해야 합니다.첫 번째 단계에서는 입력 상태 $(\displaystyle \psi \rangle)$가 두 번째 큐비트에 얽히고, 두 번째 큐비트가 세 번째 큐비트에 얽히는 식으로 이어져야 합니다.큐비트 사이의 얽힘 $작업{\displaystyle {}_{}}$ ${\displaystyle {\mathrm{Ei}}_{}}$ j$(\$ij$$})은 C$$Z(\$displaystyle CZ)$ $게이트$에서 수행할 수 있습니다.

두 번째 자리에서는 첫 번째 및 두 번째 큐비트를${\displaystyle M}$ (${\$ ) \ $displaystyle$M ( \ $theta$) 관측$$ $가능$한 고유 상태$$ ( \ displaystyle $\theta \rangle )$에 투영해야 합니다.${\$ {$displaystyle$ \$theta }$가 0인 ${\displaystyle 경우{}_{}}$ ${\displaystyle {\pm }_{}}$ ±${\$ { $displaystyle \$$theta$ _ { \$pm }$ \$rangle$ $}$ 상태는$$$$ {\ ± ${\$ ${\displaystyle 、}$ 즉$,$ X { \ $displaystyle$ X$$}$Pauli$ 연산자의 고유 벡터로 감소합니다.첫 번째 $측정{\displaystyle {}_{}^{}}$ ${\displaystyle {M\mathrm{}}_{}^{}}$ 1 $({$}^{$0})$은 $\mu {\displaystyle }$ ${\displaystyle =}$({$displaystyle \theta =$0) 각도의 $큐비트{\displaystyle \mathrm{}}$1({$displaystyle$1)에서$$ 수행되며, 이는${\displaystyle }$µ $displaystyle \thle$ \$pm})$ 상태로$$ 투영되어야 함을 의미합니다.두 번째 측정${\displaystyle }$[${\displaystyle M_{}^{}}$2 - ${\displaystyle {}_{}^{}{}^{{s\mathrm{}}_{}}}$ 1$${{$displaystyle [M_{2}^{-\lambda}^{$${\displaystyle \mathrm{s\_}}${$1}}$은(는)${\({displaystyle$$$-$\lambda})$ 각도에$$ 대해 수행됩니다. 즉$,{\displaystyle }$ 두 번째 쿼트는 ${\displaystyle 0}$0 ± $1$\$pmangle$에 투영되어야 합니다.단, 이전 측정 결과가 ${\displaystyle -}$ -${\displaystyle }$\ $displaystyle$\$langle -$이면 $\{\backslash {\displaystyle }$ \ $displaystyle$\$lambda$ has of of of of, of of of of of of of of of of of 0${\displaystyle }$+${\displaystyle {}^{}}$ - ${\displaystyle i^{}\mathrm{\lambda }}$1 \ $display$ style \$langle$ 0 + $e$^ { -$i$ \ $lambda }$상태로$$ $투영$됩니다.첫 번째 측정값은${\displaystyle }$θ${\displaystyle }$+ {\$displaystyle \displayle$+ $\}$ 이므로 플립을 수행할 필요가 없습니다.세${\displaystyle }$번째 [${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}{}^{{s\mathrm{}}_{}}}$ 2$${{$displaystyle [M_{3}^{\theta$}}^{$s_{$2} 및$$${\displaystyle }$네 번째 [${\displaystyle {}_{}^{}{}^{}}$]]${\displaystyle {{s\mathrm{}}_{}}^{}}$ 1${\displaystyle {{}_{}}^{}}$+ ${\displaystyle {{}_{}}^{}}$ {$displaystyle [M_{4}^\phi$}^{{1$}+s_$${$3}}}에 대해 동일한 작업을 반복해야 합니다.$}}}$개의$$ 각도와 사인 플립에 따른 측정.${\$ {\$displaystyle \phi }$ $각도$의 부호는 (${\displaystyle {}^{}}$- )의${\displaystyle {{}_{}}^{}}$1 + ${\displaystyle {{s\mathrm{}}_{}}^{}}$3 {{$displaystyle$ ( - )^{$s_{1}+s_{3$으로 설정됩니다.결국 5번째 쿼비트(측정되지 않는 유일한 큐비트)가 출력 상태가 됩니다.

${\displaystyle {마지막}_{}^{}}$으로 Z 5 ${\displaystyle {{s\mathrm{}}_{}}_{}^{}}$ 1${\displaystyle {{}_{}}_{}^{}}$+ ${\displaystyle {{s\mathrm{}}_{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}{}_{}^{}}$ ${\displaystyle {x\mathrm{}}_{}^{}}$ ${\displaystyle {{}_{}}_{}^{}}$ ${\displaystyle {{s\mathrm{}}_{}}_{}^{}}$2 + ${\displaystyle {{s\mathrm{}}_{}}_{}^{}}$4 ({$displaystyle Z_{5}^{1}+s_{3$})가 수정되었습니다.$}}X_{5}^{s_{2}+s_$${4}$$}}}}$은(는) 부산물 운영자를 통해 수행되어야 합니다.예를 들어, 두 번째 및 네 번째 쿼트에 대한 측정값이${\$ + $display$ +${\displaystyle {}_{}}$display ${\displaystyle +{}_{}}$ display + ${\displaystyle {}_{}}$ + $display$\ displaystyle \ $phi$ $_${ +$\}$로 바뀌면 ${\displaystyle {X\mathrm{}}_{}}$ 5$(\$$displaystyle$ $X_$${+})$ $연산자$는 2 $s_2$처럼 $보정$을 수행하지 않습니다.$4}=0$ 입니다.s ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {s\mathrm{}}_{}}$ 4 ${\displaystyle {}_{}}$ { $displaystyle s_{$2}$$$= s_{4$} =$1$} and$$${\displaystyle }$$s{\displaystyle {}_{}}$ s s${\displaystyle {}_{}}$s s s ${\displaystyle {}_{}}$ paul paul paul $paul$ paul paul paul paul paul ${\displaystyle {display\mathrm{}}^{}}$ paul$$、 { $displaystyle$ \$phi$ _ { - { -$$$}$$$$}$ ,,,,,,,,,,, - { - { $displaystyle$ \ $displaystyle$\ s _ { - { - { - { - { -${\displaystyle {}_{}}$} } } }결과에$$$$ 대해 동일한 결과가 유지됩니다.

이러한 예에서 볼 수 있듯이 측정 기반 계산 모델에서는 물리적 입력 큐비트(첫 번째)와 출력 큐비트(세 번째)가 서로 다를 수 있습니다.

양자회로 모델과 MBQC의 등가성

단방향 양자 컴퓨터는 얽힘과 측정을 통해 단일 변환 회로를 구현할 수 있도록 합니다.동시에 모든 양자 회로를 CME 패턴으로 변환할 수 있습니다. 양자 회로를 MBQC 측정 패턴으로 변환하는 기술은 V에 의해 공식화되었습니다.Danos ^[14][15][25]등

이러한 변환은 ${\displaystyle C}$ Z$displaystyle$ $CZ)$ $및$$J$(\theta$$$)$ $연산자$에 의해 구성된 범용 논리 게이트 세트를 사용하여 수행할 수 있습니다. 따라서 어떤 회로도 ${\displaystyle C}$Z(\$displaystyle CZ)$ 및$$$(\displaystyle$ J$(ta)$의 $세트$로 분해할 수 있습니다.${\displaystyle J}$( ${\displaystyle )}$ )$$\ $display J$( \ $theta$)싱글$$ 큐비트 연산자는 $다음$과 같이 정의됩니다.

( ) ( e - ){ $displaystyle$J ( \ $theta$ ) =$flac${ $1$} { \$scap${ $pmatrix }$1 & $e^$ { i \ $theta$} \ $1$& $e^$ { i \ } \ - { $pmatrix$

${\displaystyle J(}$ ${\displaystyle )}$ $)(\style$J(\$theta$)는$$ $다음$과 같이 CME 패턴으로 변환할 수 있습니다.

${\displaystyle J(\theta)=X_{2}M_{1}^{-\theta}E_{1,2}}$

즉${\displaystyle ,}$ ${\displaystyle J}$ ( ${\displaystyle )}$) { $displaystyle$ J ( $\theta )$ $연산자$를 구현하려면 입력 ${\displaystyle 큐비트}$ ${\${ $displaystyle \psi \rangle$}가$$ 안킬라 큐비트${\displaystyle }$+${\$ { $displaystyle$+ \rangle$\}$에 얽혀 있어야$$$$ 합니다.따라서 입력은 X(\$displaystyle$ X$)$ -$$Y(\$displaystyle)$ 평면에서 측정되어야 합니다.출력 큐비트는 $({$ X_${2})$ $부산물$에 의해 보정됩니다.모든 $display)$ {$display$ J$(\theta)$ 게이트가$$ CME 패턴으로 분해되면 전체 계산의 ${\displaystyle {\mathrm{연산}}_{}}$은 E$(\$$display$ $style E_{$ij$$}) $englements{\displaystyle {}_{}^{}}$, ${\displaystyle {{Mi}_{}}_{}^{}}$ - display i$(\$ style $M_{i}^{-\ta_i}$ 측정$$ $및{\displaystyle {}_{}}$(x) 스타일로 구성됩니다.계산 흐름 전체를 CME 패턴으로 이끌기 위해 몇 가지 규칙이 제공됩니다.

표준화

프로세스 시작 시 ${\displaystyle {모든}_{}}$ $(\$ij}) 얽힘을$$ 이동하려면 몇 가지 정류 규칙을 준수해야 합니다.

$({displaystyle E_{ij}Z_{i}^{s}=Z_{i}^{s}E_{ij})$

${\displaystyle E_{i}X_{i}^{s}=X_{i}^{s}Z_{j}^{s}E_{ij}$

$($$A_{k}=A_{k}E_{ij$

얽힘 $연산자{\displaystyle {}_{}}$ $(\$$displaystyle$$E_${ij$$$})$는 Z$(\displaystyle$Z) $Pauli$ 연산자 및 $큐비트{\displaystyle }$ k${\displaystyle (i),}$ j$(\displaystyle$$$k$\neq i,$j$)$로 $동작$하는 다른 ${\displaystyle {연산자}_{}}$ $Ak$(\$displaystyle A_{$k$$})와 $통신하지만$X$($)는 통신하지 않습니다.$style$ i$}$ -th$$ $또는{\displaystyle }$ j$\displaystyle$j -th$$ 큐비트입니다.

파울리 단순화

측정 $연산{\displaystyle {}_{}^{}}$ ${\displaystyle M_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ {\$displaystyle M_{i}^{\theta$}}은$$(는) 다음과 같은 방법으로 보정과 함께 이동합니다.

${\displaystyle M_{i}{\theta}X_{i}^{s}=[M_{i}^{\theta}}^{s}$

$=$$displaystyle M_{i}^{\theta }Z_{i}^{t$$S_{i}^{t}M_{i}^{\theta$

여기서${\displaystyle }$[${\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}{}^{}}$ ${\displaystyle s^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {Mi}_{}^{{}^{}}}$- ) ${\displaystyle {{}^{}}_{}^{}}$ ${\$ { $displaystyle [M_{i}^{\theta$}} $= M_{$i}^{(-)^{$s}\theta$ 이러한 연산은 패턴의 끝에서$$X {\$displaystyle$ X$}$ $보정$을 이동할 때 측정 간에 일부 종속성이 발생함을 의미합니다.${\displaystyle {}_{}^{}}$ t$$\ $displaystyle S_{i}^{t}$ 연산자는$$ $신호{\displaystyle {}_{}^{}}$ 시프트라고 불리며, 이 연산자의 동작은 다음 단락에서 설명합니다.특정$\theta {\displaystyle }$(\$displaystyle \theta)$ 각도에$$ 대해 Pauli 단순화라고 하는 몇 가지 단순화를 도입할 수 있습니다.

${\displaystyle M_{i}^0}X_{i}^{s}=M_{i}^{0}$

${\displaystyle {Mi}_{\pi \mathrm{}}^{}}$ / ${\displaystyle {}_{}^{}{}_{}^{}}$ ${\displaystyle X_{}^{}}$ i ${\displaystyle {}_{}^{}}$ $=$ ${\displaystyle {}_{}^{}}$/ / ${\displaystyle {2\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$s { $displaystyle M_{i}^{\pi /2} X_{i}^{s$}= $M_{i}^{\pi /2}Z_{i}^{s$

신호 이동

신호 이동 $연산자{\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ t$${\$displaystyle S_{i}^{t}}$의 작용은 변환 규칙을 통해 설명할 수 있습니다.

${\displaystyle X_{i}^{s}S_{i}^{t}=S_{i}^{t}X_{i}^{s[(s_{i}+t)/s_{i}}}}$

$=$$]($$S_{i}^{t}Z_{i}^{s[(s_{i}+t)/s_{i$

${\displaystyle s}$[ ( t${\displaystyle }$+ ${\displaystyle {}_{}{i}_{}}$) / ${\displaystyle s_{}}$ i$]$ { $displaystyle$ s [ ($t$ + $s$_ {$i$ ) / $s$_ { $i$} } 조작에$$ $대해{\displaystyle {}_{}}$ 설명해야 합니다$.$${\displaystyle {s\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$+ ${\displaystyle {}_{}{}_{}{2\mathrm{}}_{}}$+${\displaystyle }$. + ${\displaystyle s_{}}$+ . ($$\ $displaystyle$$$$s$_ { 1$$} + $s$_ { 2 + s _ 2$$}$$} 。$+s_{i}+...$${\displaystyle s_{}<img\; alt="\{\backslash displaystyle\; s\_\{1\}+s\_\{2\}+...+s\_\{i\}+...\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/2f546d886d12e2925b01915efda8b547b6a3ab5b"\; style="vertical-align:\; -0.671ex;\; width:20.261ex;\; height:2.343ex;">}$[ (${\displaystyle {}_{}}$ +${\displaystyle {}_{}{s}_{}i{}_{}}$ ) / s$i$]{ $displaystyle s[$( t + s _ { i } / s _$$ { i$$$}$ }$$$.$ . . . . . .$$$s$ +${\displaystyle }$$s$ .${\displaystyle }$$display$ $style$$$s _ {$$i$$$$}으로$치환$하는 것을 의미합니다.$이거$는${\displaystyle {}_{}{}_{}}$${\displaystyle {}_{}}$+${\displaystyle {}_{}{2\mathrm{}}_{}}$+ s + s $+$${\displaystyle s}$가 $.$$+s_{i}+t+...$$\}.$ s$\$$displaystyle$$$$s_{$i$$}가 s$\displaystyle$ s 시퀀스에 표시되지$$ $않으면{\displaystyle {}_{}}$ $대체$되지 않습니다$.$올바른 CME 패턴을 실행하려면 모든 신호 시프트 ${\displaystyle {연산자}_{}^{}}$ ${\displaystyle {}_{}^{}}$ t$\$를 패턴의 끝에 변환해야 합니다.

스태빌라이저 형식주의

대수구조 → 군론 군론
기본 개념 서브그룹 정규 부분군 몫군 (반쪽-)다이렉트 프로덕트 군 동형사상 커널 이미지 직접 합계 화환 제품 간단하죠. 유한한 인피니트 계속되는 곱셈의 첨가물 순환의 아벨리안 이면체 무효 해결 가능한 액션. 군론 용어집 그룹 이론 토픽 목록
유한군 유한단순군분류 순환의 번갈아 거짓말형 산발적인 코시의 정리 라그랑주 정리 시로우 정리 홀의 정리 p그룹 초등 아벨 군 프로베니우스군 슈어 승수 대칭군n S 클라인 4족 V 이면체군n D 사분위수 Q 쌍환기n Dic
개별 그룹 격자 ${\displaystyle \mathbb{}}$($$Z \$displaystyle \mathbb {Z$$$) 자유 그룹 모듈러 그룹 PSL(2,$Z{\displaystyle \mathbb{}}$ \$style \mathbb {Z$ 표시$)$ SL(2,$Z{\displaystyle \mathbb{}}$ \$displaystyle \mathbb {Z$ 산술군 격자 쌍곡선 군
토폴로지 그룹 및 Lie 그룹 솔레노이드 원형 일반 선형 GL(n) 특수 선형 SL(n) 직교 O(n) 유클리드 E(n) 특수 직교 SO(n) 유니터리 U(n) 특수 유니터리 SU(n) 심플렉틱 Sp(n) G2 에프4 E6. E7. E8. 로렌츠 푸앵카레 컨포멀 미분 동형 고리 무한 차원 리 군 O()) SU()) Sp())
대수군 선형 대수군 환원군 아벨 변종 타원 곡선
v t

얽힌 큐비트의 소스 상태를 준비할 때 스태빌라이저 그룹에 의해 그래프 표현이 제공됩니다.는 파울리의 그룹에서 어느 한 사람은 발전기에 의해 설명할 수 있는 스태빌라이저 그룹 Sn{\displaystyle{{S\mathcal}}_{n}}은abelian 서브 그룹 Pn{\displaystyle{{P\mathcal}}_{n}},{±1, 나는±}×{나는, X, Y, Z}⊗ n{\displaystyle\와 같이{\pm 1,\pm i\}\times}.[26][27] stabil \{I,X,Y,Z\}^{\otimes의 스녀}.izer 스톤atte는 n${$$}$ 큐비트스테이트$$$displaystyle\Psi\rangle}$로, 스태빌라이저$$ ^[17]그룹의 $제너레이터$ ${\displaystyle {Si}_{}}$$({$$displaystyle$$S_i})$의 고유스테이트입니다.

${\displaystyle S_{i} \Psi \rangle = \Psi \rangle .}$

Of course, ${\displaystyle S_{i}\in {\mathcal {S}}_{n}\,\forall i}$.

It is therefore possible to define a ${\displaystyle n}$ qubit graph state ${\displaystyle G\rangle }$ as a quantum state associated with a graph, i.e. a set ${\displaystyle G=(V,E)}$ whose vertices ${\displaystyle V}$ correspond to the qubits, while the edges ${\displaystyle E}$ represent the entanglements between the qubits themselves. The vertices can be labelled by a ${\displaystyle i}$ index, while the edges, linking the ${\displaystyle i}$-th vertex to the ${\displaystyle j}$-th one, by two-indices labels, such as ${\displaystyle (i,j)}$.^[28] In the stabilizer formalism, such graph structure can be encoded by the ${\displaystyle K_{i}}$ generators of ${\displaystyle {\mathcal {S}}_{n}}$, defined as^[13][29][30]

${\displaystyle K_{i}=X_{i}\prod _{j\in (i,j)}Z_{j}}$,

where ${\displaystyle {j\in (i,j)}}$ stands for all the ${\displaystyle j}$ qubits neighboring with the ${\displaystyle i}$-th one, i.e. the ${\displaystyle j}$ vertices linked by a ${\displaystyle (i,j)}$ edge with the ${\displaystyle i}$ vertex. Each ${\displaystyle K_{i}}$ generator commute with all the others. A graph composed by ${\displaystyle n}$ vertices can be described by ${\displaystyle n}$ generators from the stabilizer group:

${\displaystyle \langle K_{1},K_{2},...,K_{n}\rangle }$.

While the number of ${\displaystyle X_{i}}$ is fixed for each ${\displaystyle K_{i}}$ generator, the number of ${\displaystyle Z_{j}}$ may differ, with respect to the connections implemented by the edges in the graph.

The Clifford group

The Clifford group ${\displaystyle {\mathcal {C}}_{n}}$ is composed by elements which leave invariant the elements from the Pauli's group ${\displaystyle {\mathcal {P}}_{n}}$:^[17][27][31]

${\displaystyle {\mathcal {C}}_{n}=\{U\in SU(2^{n})\; \;USU^{\dagger }\in {\mathcal {P}}_{n},S\in {\mathcal {P}}_{n}\}}$.

The Clifford group requires three generators, which can be chosen as the Hadamard gate ${\displaystyle H}$ and the phase rotation ${\displaystyle S}$ for the single-qubit gates, and another two-qubits gate from the ${\displaystyle CNOT}$ (controlled NOT gate) or the ${\displaystyle CZ}$ (controlled phase gate):

${\displaystyle H={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}},\quad S={\begin{bmatrix}1&0\\0&i\end{bmatrix}},\quad CNOT={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{bmatrix}}}$.

Consider a state ${\displaystyle G\rangle }$ which is stabilized by a set of stabilizers ${\displaystyle S_{i}}$. Acting via an element ${\displaystyle U}$ from the Clifford group on such state, the following equalities hold:^[27][32]

${\displaystyle U G\rangle =US_{i} G\rangle =US_{i}U^{\dagger }U G\rangle =S'_{i}U G\rangle }$.

Therefore, the ${\displaystyle U}$ operations map the ${\displaystyle G\rangle }$ state to ${\displaystyle U G\rangle }$ and its ${\displaystyle S_{i}}$ stabilizers to ${\displaystyle US_{i}U^{\dagger }}$. Such operation may give rise to different representations for the ${\displaystyle K_{i}}$ generators of the stabilizer group.

The Gottesman–Knill theorem states that, given a set of logic gates from the Clifford group, followed by ${\displaystyle Z}$ measurements, such computation can be efficiently simulated on a classical computer in the strong sense, i.e. a computation which elaborates in a polynomial-time the probability ${\displaystyle P(x)}$ for a given output ${\displaystyle x}$ from the circuit.^{[17][27][33][34][35]}

Hardware and applications

Topological cluster state quantum computer

Measurement-based computation on a periodic 3D lattice cluster state can be used to implement topological quantum error correction.^[36] Topological cluster state computation is closely related to Kitaev's toric code, as the 3D topological cluster state can be constructed and measured over time by a repeated sequence of gates on a 2D array.^[37]

Implementations

One-way quantum computation has been demonstrated by running the 2 qubit Grover's algorithm on a 2x2 cluster state of photons.^[38][39] A linear optics quantum computer based on one-way computation has been proposed.^[40]

Cluster states have also been created in optical lattices,^[41] but were not used for computation as the atom qubits were too close together to measure individually.

AKLT state as a resource

It has been shown that the (spin ${\displaystyle {\tfrac {3}{2}}}$) AKLT state on a 2D honeycomb lattice can be used as a resource for MBQC.^[42][43] More recently it has been shown that a spin-mixture AKLT state can be used as a resource.^[44]

See also

References

General