포스트클래식 물리학의 물리적 상호작용
정력장은 단순한 전기장, 자기장 또는 중력장과 같이 배설 없이 존재하는 장이다. 물리학자들이 산란 계산에 사용하는 가장 일반적인 근사법은 불확실성 원리에 의해 결정되는 짧은 시간 동안만 존재하는 입자인 가상 입자로 매개되는 두 신체 사이의 상호작용에서 발생하는 정적 힘으로 해석할 수 있다.[1] 힘 전달체라고도 알려진 가상 입자는 보손이며 각 힘과 관련된 보손은 서로 다르다.[2]
정적 힘에 대한 가상 입자 설명은 뉴턴의 만유인력의 법칙과 쿨롱의 법칙에서 역제곱 작용과 같은 힘의 공간적 형태를 식별할 수 있다. 또한 그 힘이 같은 몸에 매력적이거나 혐오스러운지 예측할 수 있다.
경로 적분 제형은 힘 전달체를 설명하기 위한 자연 언어다. 이 글은 0번, 1번 및 2번 분야의 힘 전달체를 설명하기 위해 경로 적분 제형을 사용한다. 피온, 광자, 그라비톤은 이러한 각각의 범주에 속한다.
가상 입자 그림의 유효성에는 한계가 있다. 가상 입자 공식은 교호작용이 너무 강하지 않다고 가정하는 근사치인 섭동 이론으로 알려진 방법에서 도출되며, 원자와 같은 결합 상태가 아닌 산란 문제를 위한 것이었다. 낮은 에너지에서 쿼크를 핵으로 결합하는 강한 힘의 경우 섭동 이론은 실험과 일치하는 결과를 산출하는 것으로 나타난 적이 없기 때문에,[3] "강력 매개 입자" 그림의 타당성은 의심스럽다. 마찬가지로 바운드 상태의 경우 방법이 실패한다.[4] 이 경우 물리적 해석을 다시 검토해야 한다. 예를 들어, 원자 물리학의 원자 구조나 양자 화학의 분자 구조 계산은, "강력 매개 입자" 그림을 사용하여, 쉽게 반복될 수 없었다.[citation needed]
비상대적 양자역학에서는 "강력 매개 입자" 그림(FMPP)의 사용이 불필요하며, 결합 상태와 산란 상태를 모두 계산하기 위해 원자물리학과 양자화학에서 주어진 대로 쿨롱의 법칙을 사용한다. 로렌츠 불변성이 보존되는 비주변 상대론적 양자이론은 디락의 방정식에 따르는 기준 전자의 3공간 위치 벡터와 스케일링된 시간에만 의존하는 두 번째 전자의 양자 궤적을 이용하여 쿨롱의 법칙을 4공간 상호작용으로서 평가함으로써 달성할 수 있다. 앙상블에서 각 전자의 양자 궤적은 양자 밀도를 곱한 속도장과 동일하게 설정하고, 속도장의 적분 시간으로부터 위치장을 계산하고, 마지막으로 위치장의 기대값으로부터 양자 궤적을 계산함으로써 각 전자에 대한 디락 전류로부터 유추된다. 양자 궤도는 물론 스핀에 의존하며, 이 이론은 페르미온의 집합에 대해 파울리의 배제 원칙이 지켜지는 것을 확인함으로써 검증될 수 있다.
고전 세력
한 덩어리가 다른 덩어리에 가하는 힘과 한 덩어리가 다른 덩어리에 가하는 힘은 현저하게 유사하다. 둘 다 시체 사이의 거리의 제곱으로 떨어진다. 둘 다 인체의 성질, 중력의 경우 질량, 전기의 경우 전하량에 비례한다.
그들은 또한 현저한 차이를 가지고 있다. 두 덩어리는 서로 끌어당기는 반면, 두 덩어리 같은 전하가 서로 밀어낸다.
두 경우 모두 시체가 먼 거리를 두고 서로 작용하는 것처럼 보인다. 분야라는 개념은 신체들 사이의 상호작용을 중재하기 위해 발명되어 멀리 떨어진 곳에서 행동할 필요가 없게 되었다. 중력은 중력장에 의해 매개되고 쿨롱력은 전자기장에 의해 매개된다.
중력
다른 M {\이(가) 가하는 질량 M에
질량 M에 대한 중력은
대한 중력은

여기서 G는 중력 상수, r은 질량 사이의 거리, 는 질량 에서 m 까지의 단위 벡터다
단위 벡터다

힘은 또한 쓰여질 수 있다.

여기서 ( ) 는 필드 방정식으로 설명하는 중력장이다.
필드 방정식으로 설명하는 중력장이다.

여기서 는 공간의 각 지점에서 질량 밀도다.
공간의 각 지점에서 질량 밀도다.
쿨롱 힘
충전 이(가) 발휘하는 충전 Q Q에 대한
충전 Q Q에 대한 정전기 쿨롱 힘은 (SI 단위)
정전기 쿨롱 힘은 (SI 단위)

여기서 은 진공 허용률, r은 두
진공 허용률, r은 두 전하의 분리, 는 충전 에서
전하의 분리, 는 충전 에서 하는 방향으로의 단위 벡터다
하는 방향으로의 단위 벡터다

쿨롱 힘은 정전기장의 측면에서도 다음과 같이 쓸 수 있다.

어디에

공간 내 각 지점에서 전하 밀도가 됨.
됨.
가상 입자 교환
섭동 이론에서 힘은 가상 입자의 교환에 의해 생성된다. 가상 입자 교환의 역학은 양자 역학의 경로 적분 제형으로 가장 잘 설명된다. 그러나 왜 고전적인 중력과 정전기력이 신체 사이의 거리의 역제곱으로서 떨어져 나가는지 등 경로 통합의 기계에 들어가지 않고도 얻을 수 있는 통찰이 있다.
가상-입자 교환의 경로 통합적 공식화
가상 입자는 진공 상태에 대한 교란으로 생성되며, 가상 입자는 다른 교란으로 인해 진공 상태로 다시 흡수될 때 파괴된다. 그 장애는 가상 입자의 영역과 상호작용하는 신체들 때문이라고 상상된다.
확률 진폭
자연 단위인 = = }을 를) 사용하여 가상 입자의 생성, 전파 및 파괴에 대한 확률 진폭이 다음에 의해 경로 적분 공식에 주어진다.
를) 사용하여 가상 입자의 생성, 전파 및 파괴에 대한 확률 진폭이 다음에 의해 경로 적분 공식에 주어진다.
![Z\equiv \langle 0|\exp \left(-i{\hat H}T\right)|0\rangle =\exp \left(-iET\right)=\int D\varphi \;\exp \left(i{\mathcal {S}}[\varphi ]\right)\;=\exp \left(iW\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/2151b70a2ba29798938e7f517e91c1373a5cd29e)
where  is the Hamiltonian operator,
is the Hamiltonian operator,  is elapsed time,
is elapsed time,  is the energy change due to the disturbance,
is the energy change due to the disturbance,  is the change in action due to the disturbance,
is the change in action due to the disturbance,  is the field of the virtual p기사, 적분은 모든 경로에 걸쳐 있으며, 고전적 작용은 다음에 의해 주어진다.
is the field of the virtual p기사, 적분은 모든 경로에 걸쳐 있으며, 고전적 작용은 다음에 의해 주어진다.
![{\mathcal {S}}[\varphi ]=\int {\mathrm {d}}^{4}x\;{{\mathcal {L}}[\varphi (x)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63813174765f3c2470dbcd12f243413bf2a655a7)
여기서 [( x) 은![{\mathcal {L}}[\varphi (x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2365f42d88d429f1f0f926bfa9bd7deeb8c54db7) (는) 라그랑비아 밀도다.
(는) 라그랑비아 밀도다.
여기서 스페이스타임 메트릭은

경로 적분은 종종 양식으로 변환될 수 있다.
![Z=\int \exp \left[i\int d^{4}x\left({\frac 12}\varphi {\hat O}\varphi +J\varphi \right)\right]D\varphi](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe8b3ee54150e5c533db5c3fbc0bf46a723bae3e)
서 은(는) 및 J displaysty 의 스페이스타임 기능을 가진 차등
displaysty 의 스페이스타임 기능을 가진 차등 연산자다
연산자다 . 논쟁의 첫 번째 용어는 자유 입자를 나타내고, 두 번째 용어는 전하나 질량 같은 외부 근원에서 밭으로 난동을 나타낸다.
. 논쟁의 첫 번째 용어는 자유 입자를 나타내고, 두 번째 용어는 전하나 질량 같은 외부 근원에서 밭으로 난동을 나타낸다.
적분은 쓸 수 있다(양자장 이론의 공통 적분 참조)

어디에

장애로 인한 동작의 변경이며 전파자 - ) 은 (는)
(는)
- D( x- )= 4( - ) )=\ ^{4
 .
.
상호작용 에너지
우리는 두 몸을 나타내는 두 점의 장애가 있고 그 장애가 움직이지 않고 시간에 따라 일정하다고 가정한다. 소란은 기록될 수 있다.



델타 함수가 공간에 있는 경우 는 x→ x →
→  }}에 위치하며 계수 1
}}에 위치하며 계수 1  a}}가 장애의 강점이다
a}}가 장애의 강점이다 .
.
교란의 자기 상호작용을 게을리 하면 W가 된다.
![W\left(J\right)=-\iint d^{4}x\;d^{4}y\;J_{1}\left(x\right){1 \over 2}\left[D\left(x-y\right)+D\left(y-x\right)\right]J_{2}\left(y\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8920a2506fe0de48c5b849d2052b92bc29ab6f09)
쓸 수 있는

여기서 ) 은 (는) 의 푸리에 변환이다.
(는) 의 푸리에 변환이다.
- right
![{1 \over 2}\left[D\left(x-y\right)+D\left(y-x\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/292c9f9aa03864ffaf187c8d724aa2b76ae35a34) .
.
마지막으로, 진공의 정적인 장애에 의한 에너지의 변화는 다음과 같다.
| 
|
이 양이 음수라면 힘은 매력적이다. 만약 그것이 양성이면, 그 힘은 혐오스럽다.
정적이고 움직이지 않으며 상호 작용하는 전류의 예로는 유카와 전위, 진공에서의 쿨롱 전위, 단순한 플라스마 또는 전자 가스에서의 쿨롱 전위 등이 있다.
상호작용 에너지의 표현은 점 입자가 움직이는 상황에 일반화될 수 있지만 빛의 속도에 비해 동작이 느리다. 진공에서의 다윈 상호작용과 플라즈마에서의 다윈 상호작용을 예로 들 수 있다.
마지막으로 교호작용 에너지에 대한 표현은 장애물이 점 입자가 아니라 선상 전하, 전하 튜브 또는 현재 변위일 가능성이 있는 상황에 일반화될 수 있다. 예로는 플라즈마 또는 전자 가스에 내장된 두 개의 라인 전하, 자기장에 내장된 두 개의 전류 루프 사이의 쿨롱 전위, 그리고 단순한 플라즈마 또는 전자 가스에서의 전류 루프 사이의 자기 상호작용 등이 있다. 아래에 나타낸 것과 같이, 충전관 사이의 쿨롱 상호작용에서 볼 수 있듯이, 이러한 더 복잡한 기하학적 구조는 분수 양자 숫자와 같은 이국적인 현상을 초래할 수 있다.
선택한 예제
유카와 씨의 잠재력: 원자핵에서 두 핵 사이의 힘
스핀-0 라그랑지안 밀도[5] 고려
- [【 = [ ( ) - 2 }\
![{\mathcal {L}}[\varphi (x)]={1 \over 2}\left[\left(\partial \varphi \right)^{2}-m^{2}\varphi ^{2}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/41d93ef0316977d86b8996f8f92fdcf9b4dbfe7d)
이 라그랑지아의 운동 방정식은 클라인-고든 방정식이다.
- + m =
 .
.
교란을 추가하면 확률 진폭이
![Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[{1 \over 2}\left(\left(\partial \varphi \right)^{2}-m^{2}\varphi ^{2}\right)+J\varphi \right]\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2546ebbc13d0451682853cc36fd9b1b2a01267a)
부품별로 통합하고 무한대로 경계 항을 무시하면 확률 진폭이 커진다.
- J\varphi ]\
![Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[-{1 \over 2}\varphi \left(\partial ^{2}+m^{2}\right)\varphi +J\varphi \right]\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dea41e0c54b700ba60bb1e7024df724f298571ba)
이 형태의 진폭으로 전파기가 의 해결책임을 알 수 있다.
 .
.
이것으로부터 는 알 수 있다.
- () = 0=- → 2+ 2

정전기 교란으로 인한 에너지가 된다(양자장 이론의 공통 통합 참조).
| 
|
와 함께

매력적이고 다양한 종류의

유카와 교수는 이 장에서 원자핵에 있는 두 핵 사이의 힘을 설명할 것을 제안했다. 그것은 그가 현재 파이온이라고 알려진 입자의 범위와 질량을 모두 예측할 수 있게 해주었고, 이 분야와 연관되어 있었다.
전기 공학
진공 상태의 쿨롱 전위
spin-1 Proca Lagrangian과 교란을[6] 고려하십시오.
![{\mathcal {L}}[\varphi (x)]=-{1 \over 4}F_{{\mu \nu }}F^{{\mu \nu }}+{1 \over 2}m^{2}A_{{\mu }}A^{{\mu }}+A_{{\mu }}J^{{\mu }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591ac6f78391e4d0d1a0b85785580bb271acd6a0)
어디에
- =μA -μA - μA - - }-{\nu

요금이 보전되다
- = }

로렌츠 게이지를 골라서
- =
 .
.
더구나 교란에는 시간과 같은 0밖에 없다고 가정한다. 보통 말로 하면 교란 지점에는 전하가 있지만 전류가 없다는 뜻이다.
시간과 같은 0밖에 없다고 가정한다. 보통 말로 하면 교란 지점에는 전하가 있지만 전류가 없다는 뜻이다.
우리가 유카와 잠재력에서 했던 것과 같은 절차를 따른다면


그 말은

그리고

이것은 생산된다.

타임라이크 전파자를 위해

유카와 사건과는 정반대의 징후가 있는 곳이야
광자 질량이 0인 한계에서 라그랑지안은 전자성을 위해 라그랑지안으로 감소한다.
| 
|
따라서 에너지는 쿨롱 힘에 대한 잠재적 에너지로 감소하고 계수 및  a 2 }}는 전하에 비례한다
a 2 }}는 전하에 비례한다 . 유카와 사건과는 달리 시체처럼 이 정전기 사건에서는 서로 밀어낸다.
. 유카와 사건과는 달리 시체처럼 이 정전기 사건에서는 서로 밀어낸다.
단순한 플라즈마 또는 전자 가스의 쿨롱 전위
플라즈마 파동
플라즈마 파장의 분산 관계는[7]

여기서 은 파형의 각도 주파수,
파형의 각도 주파수,

플라즈마 주파수, 은 전자 전하 크기, 은
전자 전하 크기, 은 전자 질량, T e {\displaystyle 는
전자 질량, T e {\displaystyle 는 전자 온도(볼츠만의 상수)이며 () (\ome 는 자주 발생하는 요인이다
전자 온도(볼츠만의 상수)이며 () (\ome 는 자주 발생하는 요인이다 y 1에서 3까지. 고주파수에서 플라스마 주파수의 순서에 따라 전자 유체의 압축은 부차적 과정이며 )은 3과 같다
y 1에서 3까지. 고주파수에서 플라스마 주파수의 순서에 따라 전자 유체의 압축은 부차적 과정이며 )은 3과 같다 . 저주파에서 압축은 등온 공정이고 ) 은
. 저주파에서 압축은 등온 공정이고 ) 은 1과 같다. 지연 효과는 플라즈마-파장 분산 관계를 얻는 데 있어 간과되어 왔다.
1과 같다. 지연 효과는 플라즈마-파장 분산 관계를 얻는 데 있어 간과되어 왔다.
저주파수의 경우 분산 관계는

어디에

데비 길이의 역인 데비수다. 이것은 전파자가
- ( 0= = =1 k→ 2 + k {\\left2

실제로 지체효과를 소홀히 하지 않으면 산포관계는 다음과 같다.

추측된 전파자를 만들어 내는 거지 이 전파기는 질량이 역데비 길이와 같은 질량인 거대한 쿨롱 전파기와 같다. 그러므로 상호작용 에너지는
| 
|
쿨롱 전위는 데비예 길이의 길이 눈금으로 가려진다.
플라스몬
양자 전자 기체에서는 플라즈마 파동을 플라스몬이라고 한다. 데비 심사는 토마스 심사로 대체된다.항복할[8] 페르미 선별
| 
|
토마스-의 역행에서페르미 스크리닝 길이는

는 페르미 에너지 입니다.
에너지 입니다.

이 표현은 전자 가스의 화학적 전위와 포아송의 방정식에서 파생될 수 있다. 평형에 가까운 전자 가스의 화학적 전위는 일정하며, 다음과 같이 주어진다.

여기서 은(는) 전위(電力)이다 . 페르미 에너지를 밀도 변동에서 첫 번째 순서로 선형화하고 포아송 방정식과 결합하면 선별 길이가 나온다. 힘 전달체는 플라즈마 파형의 양자 버전이다.
. 페르미 에너지를 밀도 변동에서 첫 번째 순서로 선형화하고 포아송 방정식과 결합하면 선별 길이가 나온다. 힘 전달체는 플라즈마 파형의 양자 버전이다.
플라즈마 또는 전자 가스에 포함된 두 개의 라인 전하
전자 가스에 내장된 z 방향으로 축이 있는 전하선을 고려한다.

여기서 은 (는) xy 평면의 충전 라인에서 거리, 는
(는) xy 평면의 충전 라인에서 거리, 는 z 방향의 재료 폭이다. 위첨자 2는 Dirac 델타 함수가 2차원임을 나타낸다. 전파자는
z 방향의 재료 폭이다. 위첨자 2는 Dirac 델타 함수가 2차원임을 나타낸다. 전파자는

여기서 는 역 데비-후켈 선별 길이 또는 역 토마스–페르미 스크리닝 길이.
역 데비-후켈 선별 길이 또는 역 토마스–페르미 스크리닝 길이.
상호작용 에너지는

|
어디에

그리고

besel 함수이며 r 는 두 라인 전하 사이의 거리이다 . 상호 작용 에너지를 얻기 위해 우리는 통합체를 사용했다(양자장 이론의 공통 통합 참조).
. 상호 작용 에너지를 얻기 위해 우리는 통합체를 사용했다(양자장 이론의 공통 통합 참조).

그리고

1의 경우

자기장에 내장된 두 개의 전류 루프 사이의 쿨롱 전위
vortice를 위한 상호작용하는 에너지
우리는 전자 가스에 내장된 자기장을 따라 축이 있는 튜브의 전하 밀도를 고려한다.

여기서 은 (는) 안내 중심으로부터의 거리, 는 자기장 방향의 재료 폭이다
(는) 안내 중심으로부터의 거리, 는 자기장 방향의 재료 폭이다 .
.

여기서 사이클로트론 주파수는 (가우스 단위)

그리고

자기장에 대한 입자의 속도, 그리고 B는 자기장의 크기 입니다. 속도 공식은 자기장 내 전하 입자의 양자 처리에서 란다우 수준 사이의 간격과 동일한 고전적 운동 에너지를 설정함으로써 얻어진다.
이 기하학에서는 상호작용 에너지를 기록할 수 있다.

|
여기서 r 는 현재 루프의 중심과
루프의 중심과

제1종류의 베셀함수다. 상호 작용 에너지를 얻는데 있어서 우리는 통합 에너지를 사용했다.

밀도 섭동에 의한 전기장
평형에 가까운 화학적 전위는 다음과 같다.

여기서- 은(는) 전위에 있는 전자의 전위 에너지이며 , 과
, 과 () N {\ N은
() N {\ N은 각각 정전기 전위가 없는 전자 가스 내의 입자 수입니다.
각각 정전기 전위가 없는 전자 가스 내의 입자 수입니다.
밀도 변동은 그 다음이다.

여기서 은 자기장에 수직인 평면의 재료 영역이다 .
.
포아송 방정식 산출량

어디에

그런 다음 전파자가 된다.

그리고 상호작용 에너지는

|
두 번째 동일성(가우스 단위)에서 우리는 vortices가 동일한 에너지와 전자 전하를 가졌다고 가정한다.
플라스몬과 유사하게 힘 전달체는 자기장에 수직으로 전파되는 종방향 플라즈마 파동인 상부 하이브리드 진동의 양자 버전이다.
각운동량이 있는 전류
델타 함수 전류

그림 1. 값 1의 각운동량 상태에 대한 상호작용 에너지 대 r. The curves are identical to these for any values of  . Lengths are in units are in
. Lengths are in units are in  , and the energy is in units of
, and the energy is in units of  . Here
. Here  의 큰 값에 대한 로컬 미니마가 있다는 점에 유의하십시오
의 큰 값에 대한 로컬 미니마가 있다는 점에 유의하십시오

그림 2. 값 1과 5의 각운동량 상태에 대한 상호작용 에너지 대 r. 
그림 3. 세타의 다양한 값에 대한 상호작용 에너지 대 r. 가장 낮은 에너지는 = 4  = 에 대한 에너지 입니다
= 에 대한 에너지 입니다 표시된 가장 높은 에너지는 = 0 4 4이며
표시된 가장 높은 에너지는 = 0 4 4이며 는 r l mathit{의 단위로 표시된다
는 r l mathit{의 단위로 표시된다
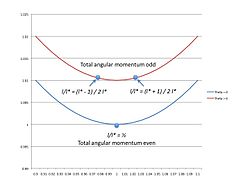
그림 4. 각도 모멘트의 짝수 및 홀수 값에 대한 접지 상태 에너지. 에너지는 수직축에, r은 수평축에 표시된다. When the total angular momentum is even, the energy minimum occurs when  or
or  . When the total angular momentum is odd, there are no integer values of angular 최소한의 에너지에 놓여질 순간 따라서 최소의 양쪽에 놓여 있는 두 개의 주가 있다. Because
. When the total angular momentum is odd, there are no integer values of angular 최소한의 에너지에 놓여질 순간 따라서 최소의 양쪽에 놓여 있는 두 개의 주가 있다. Because  , the total energy is higher than the case when
, the total energy is higher than the case when  for a given value of
for a given value of  .
. 고전 전류와 달리 양자 전류 루프는 주어진 에너지에 대해 Larmor 반경의 다양한 값을 가질 수 있다.[9] 자기장이 존재하는 상태에서 충전된 입자의 에너지 상태인 란다우 레벨은 퇴행성을 곱한다. 전류 루프는 동일한 에너지를 가질 수 있는 전하 입자의 각운동량 상태에 해당한다. 구체적으로 전하 밀도는 반경을 중심으로 정점을 이룬다.

서 l 은 각운동량 양자수 입니다. = 일 때 우리는
각운동량 양자수 입니다. = 일 때 우리는 전자가 라모르 반지름에서 자기장을 공전하는 고전적인 상황을 회복한다. 두 각운동량 나의 만약 전류;0{\displaystyle{\mathit{나는}}_{}^{}>0}과 내가′ ≥ 나는{\displaystyle{\mathit{나는}}^{\prime}\geq{\mathit{나는}}_{}^{}}상호 작용하고, 반지름 r나는{\displaystyle r_{{나는\mathit}}}죄를 밀도 있델타 기능은 interacti으로 추정하고 있다.전기에에너지는
전자가 라모르 반지름에서 자기장을 공전하는 고전적인 상황을 회복한다. 두 각운동량 나의 만약 전류;0{\displaystyle{\mathit{나는}}_{}^{}>0}과 내가′ ≥ 나는{\displaystyle{\mathit{나는}}^{\prime}\geq{\mathit{나는}}_{}^{}}상호 작용하고, 반지름 r나는{\displaystyle r_{{나는\mathit}}}죄를 밀도 있델타 기능은 interacti으로 추정하고 있다.전기에에너지는

|
= = l 의 다양한 에 대한 상호작용 에너지는 그림 에 제시되어 있다
있다 두 가지 다른 값에 대한 에너지는 그림 2에 제시되어 있다.
두 가지 다른 값에 대한 에너지는 그림 2에 제시되어 있다.
콰시파르티클
각운동량의 큰 값의 경우, 에너지는 0과 무한대가 아닌 거리에 국소 미니마를 가질 수 있다. 미니마가 다음 시간에 발생한다는 것을 수치적으로 확인할 수 있다.

이는 r }}}{\mathit에 의해 묶여 분리되는 입자 쌍이 각운동량 + l + {lprimathitprimathit{
각운동량 + l + {lprimathitprimathit{
를 r  로 조정하면 상호작용 에너지가
로 조정하면 상호작용 에너지가

|
어디에

The value of the  at which the energy is minimum,
at which the energy is minimum,  , is independent of the ratio
, is independent of the ratio  . 그러나 최소한 에너지의 가치는 비율에 따라 달라진다. 다음과 같은 경우에 가장 낮은 에너지 최소값이 발생한다.
. 그러나 최소한 에너지의 가치는 비율에 따라 달라진다. 다음과 같은 경우에 가장 낮은 에너지 최소값이 발생한다.

비율이 1과 다를 경우 에너지 최소값이 더 높아진다(그림 3). 따라서 총 운동량의 짝수 값에 대해서는 (그림 4)일 때 가장 낮은 에너지가 발생한다.

또는

총 각도 운동량이 다음과 같이 기록되는 경우

총각운동량이 홀수인 경우, = .{\ 홀수 총각운동량의 최저 에너지 상태가 발생할 수 없음
상태가 발생할 수 없음

또는

그리고

부분 양자 홀 효과의 충만 계수에 대한 직렬로도 나타난다.
파동 함수에 대한 전하 밀도 확산
전하 밀도는 실제로 델타 함수에 집중되지 않는다. 전하가 파동 기능에 퍼진다. 그[10] 경우 전자 밀도는

상호작용 에너지가

|
여기서 은 결합초기하함수 또는 Kummer 함수다. 상호작용 에너지를 얻기 위해 우리는 적분을 사용했다(양자장 이론의 공통적 통합 참조).
결합초기하함수 또는 Kummer 함수다. 상호작용 에너지를 얻기 위해 우리는 적분을 사용했다(양자장 이론의 공통적 통합 참조).

델타 함수 전하와 마찬가지로 에너지가 국소 최소값인 r 의 값은 개별 전류의 각도 모멘텀에 의존하지 않고 총 각도 모멘텀에만 의존한다. 또한 델타 함수 전하와 마찬가지로 각 모멘텀의 비율이 1과 달라짐에 따라 최소 에너지도 증가한다. 그러므로 시리즈는
의 값은 개별 전류의 각도 모멘텀에 의존하지 않고 총 각도 모멘텀에만 의존한다. 또한 델타 함수 전하와 마찬가지로 각 모멘텀의 비율이 1과 달라짐에 따라 최소 에너지도 증가한다. 그러므로 시리즈는

그리고

파장 기능에 의해 전파되는 전하의 경우에도 나타난다.
러플린 파동 기능은 퀘이피사 파동 기능을 위한 안사츠다. 상호작용 에너지의 기대값이 Lauglin 파동 기능보다 더 많이 차지되면, 이러한 시리즈도 보존된다.
자기공명학
진공 상태의 다윈 상호작용
충전된 이동 입자는 다른 충전된 입자의 움직임에 영향을 미치는 자기장을 생성할 수 있다. 이 효과의 정적 버전을 다윈 상호작용이라고 한다. 이를 계산하려면 이동 전하에 의해 생성된 공간의 전류를 고려하십시오.

→ 
이 전류의 푸리에 변환은

전류는 가로 및 세로 부분으로 분해될 수 있다(헬름홀츠 분해 참조).
![{\vec J}_{1}\left({\vec k}\right)=a_{1}\left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{1}\exp \left(i{\vec k}\cdot {\vec x}_{1}\right)+a_{1}\left[{\hat k}{\hat k}\right]\cdot {\vec v}_{1}\exp \left(i{\vec k}\cdot {\vec x}_{1}\right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0d79a6445282ae388d82ee449b22ed22e6d1b1b)
모자는 단위 벡터를 나타낸다. 때문에 마지막 말은 사라진다.

비용 절감의 결과. 여기서 는 정적 힘을 고려하고 있기 때문에 사라진다 .
.
이 형태의 전류로 상호작용의 에너지를 기록할 수 있다.
![E=a_{1}a_{2}\int {d^{3}k \over (2\pi )^{3}}\;\;D\left(k\right)\mid _{{k_{0}=0}}\;{\vec v}_{1}\cdot \left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{2}\;\exp \left(i{\vec k}\cdot \left(x_{1}-x_{2}\right)\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/b31cb210dde9aae552bd4602f092777182990c7b) .
.
프로카 라그랑지아의 전파 방정식은

공간 같은 해결책은

어느 것이 생산되는가
![E=-a_{1}a_{2}\int {d^{3}k \over (2\pi )^{3}}\;\;{{\vec v}_{1}\cdot \left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{2} \over {\vec k}^{2}+m^{2}}\;\exp \left(i{\vec k}\cdot \left(x_{1}-x_{2}\right)\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9871a14a8457fef3cb44a14f461235eaef662678)
평가 대상(양자장 이론의 공통 통합 참조)
![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}e^{{-mr}}\left\{{2 \over \left(mr\right)^{2}}\left(e^{{mr}}-1\right)-{2 \over mr}\right\}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c0e2cb7cceec027934b6da5ac7116cd6fe0ce9)
로 줄어든다.
| ![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe161e44ff7d95dcc83d5a55939ae0f7a09e932)
|
작은 m의 한계에. 상호작용 에너지는 상호작용 라그랑지안의 음이다. 같은 방향으로 이동하는 두 개의 입자에 대해서는 상호작용이 매력적이며, 이는 쿨롱 상호작용과는 정반대다.
혈장 내 다윈 상호작용
플라즈마에서 전자파에 대한 분산 관계는 (= 이다[11]

그 말은

여기서 는 플라즈마 주파수다. 그러므로 상호작용 에너지는
는 플라즈마 주파수다. 그러므로 상호작용 에너지는
| ![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}\;e^{{-\omega _{p}r}}\left\{{2 \over \left(\omega _{p}r\right)^{2}}\left(e^{{\omega _{p}r}}-1\right)-{2 \over \omega _{p}r}\right\}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/11a047fded9d15e84ef56661d2ba389d2eaac59e)
|
단순 플라즈마 또는 전자 가스에서 전류 루프 사이의 자기 상호작용
상호작용 에너지
단순한 플라즈마나 전자 가스에 내장된 자기장에서 회전하는 전류의 관을 생각해 보자. 자기장에 수직인 평면에 있는 전류는 다음과 같이 정의된다.

어디에

및 는 자기장 방향의 단위 벡터다 . 여기서 스타일 는 자기장 방향의 물질의 치수를 나타낸다
. 여기서 스타일 는 자기장 방향의 물질의 치수를 나타낸다 . 파동 벡터에 수직인 횡단 전류가 횡파를 구동한다.
. 파동 벡터에 수직인 횡단 전류가 횡파를 구동한다.
상호작용의 에너지는

여기서 r 는 현재 루프의 중심과
루프의 중심과

제1종류의 베셀함수다. 상호 작용 에너지를 얻기 위해 우리는 통합체를 이용했다.

그리고

양자장 이론의 공통 통합을 참조하십시오.
자기장에 수직인 평면에 국한된 플라스마에서 전류가 비정상적인 파동을 일으킨다.[12] 이 파동은 전자기장을 상호작용하고 수정하는 홀 전류를 생성한다. 비정상적인 파도에 대한 분산은[13]

전파자에게 유리한 점

어디에

다윈 전파자와 유사하게 여기서 상위 하이브리드 주파수는

사이클로트론 주파수는 (가우스 단위)에 의해 주어진다.

및 플라스마 주파수(가우스 단위)

여기서 n은 전자 밀도, e는 전자 전하의 크기, m은 전자 질량이다.
상호작용 에너지는 같은 전류에 대해
| 
|
전류 루프 사이의 작은 거리 제한
전류 루프 사이의 거리가 작은 한계에서,
| 
|
어디에

그리고

그리고 I와 K는 변형된 Besel 함수다. 우리는 두 전류가 동일한 전하와 속도를 가지고 있다고 가정했다.
적분을 활용했다(양자장 이론의 공통 적분 참조)

소형 Mr의 경우 적자가 된다.
![I_{1}\left(mr\right)K_{1}\left(mr\right)\rightarrow {1 \over 2}\left[1-{1 \over 8}\left(mr\right)^{2}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/e390202b2aefd0672891fb96523c9102e6177d08)
라지 Mr의 경우 적분은

양자 홀 효과와의 관계
스크리닝 번호가 기록될 수 있다(가우스 단위)

여기서 은 (는) 미세조정 상수이고 충진 계수는
(는) 미세조정 상수이고 충진 계수는

그리고 N은 물질의 전자수이고 A는 자기장에 수직인 물질의 영역이다. 이 매개변수는 양자 홀 효과와 분수 양자 홀 효과에서 중요하다. 충전 계수는 지상 주 에너지에서 점유된 랜도 주(Landau) 주(州)의 비율이다.
양자 홀 효과에 관심 있는 경우 은(는) 작다 . 이 경우 상호작용 에너지는
. 이 경우 상호작용 에너지는
| ![E=-{E_{0} \over 2}\left[1-{1 \over 8}\mu ^{2}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c296979564d5355f378e0b6dabd44ef0aeeba314)
|
(가우스 단위)

0 채우기 인자에 대한 상호작용 에너지. 우리는 고전적인 운동에너지를 양자 에너지로 설정했다.

중력
중력 교란은 T{\^{\\nu 에 의해 발생한다 따라서 중력장에 대한 라그랑지안은 스핀-2이다. 장애가 없는 경우 스트레스-에너지 텐서의 유일한 구성 요소는 구성
따라서 중력장에 대한 라그랑지안은 스핀-2이다. 장애가 없는 경우 스트레스-에너지 텐서의 유일한 구성 요소는 구성 요소뿐입니다. 만약 우리가 그라비톤에게 약간의 질량을 준 다음 계산이 끝날 때 질량을 0으로 가져가는 것과 같은 수법을 사용한다면 전파자가 된다.
요소뿐입니다. 만약 우리가 그라비톤에게 약간의 질량을 준 다음 계산이 끝날 때 질량을 0으로 가져가는 것과 같은 수법을 사용한다면 전파자가 된다.

그리고
| = - r (- m ) r |
혐오스럽기는커녕 다시 매력적으로 다가온다. 계수는 교란 중량에 비례한다. 작은 그라비톤 질량의 한계에서 우리는 뉴턴 법칙의 역제곱 작용을 회복한다.[14]
그러나 정전기 케이스와 달리 보손의 소량 한계치를 취한다고 해서 정확한 결과가 나오지는 않는다. 좀 더 엄격한 치료는 4/3보다 에너지에서 1의 인자를 산출한다.[15]
참조


 대한
대한 


 필드 방정식으로 설명하는
필드 방정식으로 설명하는 
 공간의 각 지점에서
공간의 각 지점에서 








![Z\equiv \langle 0|\exp \left(-i{\hat H}T\right)|0\rangle =\exp \left(-iET\right)=\int D\varphi \;\exp \left(i{\mathcal {S}}[\varphi ]\right)\;=\exp \left(iW\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/2151b70a2ba29798938e7f517e91c1373a5cd29e)





![{\mathcal {S}}[\varphi ]=\int {\mathrm {d}}^{4}x\;{{\mathcal {L}}[\varphi (x)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63813174765f3c2470dbcd12f243413bf2a655a7)
![{\mathcal {L}}[\varphi (x)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/2365f42d88d429f1f0f926bfa9bd7deeb8c54db7) (는)
(는) 
![Z=\int \exp \left[i\int d^{4}x\left({\frac 12}\varphi {\hat O}\varphi +J\varphi \right)\right]D\varphi](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe8b3ee54150e5c533db5c3fbc0bf46a723bae3e)




 (는)
(는) 







![W\left(J\right)=-\iint d^{4}x\;d^{4}y\;J_{1}\left(x\right){1 \over 2}\left[D\left(x-y\right)+D\left(y-x\right)\right]J_{2}\left(y\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/8920a2506fe0de48c5b849d2052b92bc29ab6f09)

 (는) 의 푸리에 변환이다.
(는) 의 푸리에 변환이다. ![{1 \over 2}\left[D\left(x-y\right)+D\left(y-x\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/292c9f9aa03864ffaf187c8d724aa2b76ae35a34)

![{\mathcal {L}}[\varphi (x)]={1 \over 2}\left[\left(\partial \varphi \right)^{2}-m^{2}\varphi ^{2}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/41d93ef0316977d86b8996f8f92fdcf9b4dbfe7d)

![Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[{1 \over 2}\left(\left(\partial \varphi \right)^{2}-m^{2}\varphi ^{2}\right)+J\varphi \right]\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2546ebbc13d0451682853cc36fd9b1b2a01267a)
![Z=\int D\varphi \;\exp \left\{i\int d^{4}x\;\left[-{1 \over 2}\varphi \left(\partial ^{2}+m^{2}\right)\varphi +J\varphi \right]\right\}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dea41e0c54b700ba60bb1e7024df724f298571ba)





![{\mathcal {L}}[\varphi (x)]=-{1 \over 4}F_{{\mu \nu }}F^{{\mu \nu }}+{1 \over 2}m^{2}A_{{\mu }}A^{{\mu }}+A_{{\mu }}J^{{\mu }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/591ac6f78391e4d0d1a0b85785580bb271acd6a0)












 파형의 각도 주파수,
파형의 각도 주파수, 

 전자
전자 











 z 방향의 재료 폭이다. 위첨자 2는
z 방향의 재료 폭이다. 위첨자 2는 
 역
역 














 ,
,  (
( 각각 정전기 전위가 없는 전자 가스 내의 입자 수입니다.
각각 정전기 전위가 없는 전자 가스 내의 입자 수입니다. 






















 각운동량
각운동량 






















![{\vec J}_{1}\left({\vec k}\right)=a_{1}\left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{1}\exp \left(i{\vec k}\cdot {\vec x}_{1}\right)+a_{1}\left[{\hat k}{\hat k}\right]\cdot {\vec v}_{1}\exp \left(i{\vec k}\cdot {\vec x}_{1}\right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0d79a6445282ae388d82ee449b22ed22e6d1b1b)


![E=a_{1}a_{2}\int {d^{3}k \over (2\pi )^{3}}\;\;D\left(k\right)\mid _{{k_{0}=0}}\;{\vec v}_{1}\cdot \left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{2}\;\exp \left(i{\vec k}\cdot \left(x_{1}-x_{2}\right)\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/b31cb210dde9aae552bd4602f092777182990c7b)


![E=-a_{1}a_{2}\int {d^{3}k \over (2\pi )^{3}}\;\;{{\vec v}_{1}\cdot \left[1-{\hat k}{\hat k}\right]\cdot {\vec v}_{2} \over {\vec k}^{2}+m^{2}}\;\exp \left(i{\vec k}\cdot \left(x_{1}-x_{2}\right)\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9871a14a8457fef3cb44a14f461235eaef662678)
![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}e^{{-mr}}\left\{{2 \over \left(mr\right)^{2}}\left(e^{{mr}}-1\right)-{2 \over mr}\right\}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28c0e2cb7cceec027934b6da5ac7116cd6fe0ce9)
![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe161e44ff7d95dcc83d5a55939ae0f7a09e932)




![E=-{1 \over 2}{a_{1}a_{2} \over 4\pi r}{\vec v}_{1}\cdot \left[1+{{\hat r}}{{\hat r}}\right]\cdot {\vec v}_{2}\;e^{{-\omega _{p}r}}\left\{{2 \over \left(\omega _{p}r\right)^{2}}\left(e^{{\omega _{p}r}}-1\right)-{2 \over \omega _{p}r}\right\}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/11a047fded9d15e84ef56661d2ba389d2eaac59e)
















![I_{1}\left(mr\right)K_{1}\left(mr\right)\rightarrow {1 \over 2}\left[1-{1 \over 8}\left(mr\right)^{2}\right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/e390202b2aefd0672891fb96523c9102e6177d08)


 (는)
(는) 

![E=-{E_{0} \over 2}\left[1-{1 \over 8}\mu ^{2}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c296979564d5355f378e0b6dabd44ef0aeeba314)








