일반 베타 분포

이 기사는 주요 출처에 대한 언급에 너무 많이 의존하고 있다. 이차 또는 3차 소스를 추가하여 개선하십시오.(2013년 4월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

확률과 통계에서 일반화된 베타 분포는^[1] 제한 또는 특수 사례로 명명된 30개 이상의 분포를 포함하여 5개의 모수를 갖는 연속 확률 분포다.그것은 회귀 분석뿐만 아니라 소득분배, 주식수익의 모형화에도 사용되었다.지수 일반화 베타(EGB) 분포는 GB에서 직접 따르며 다른 공통 분포를 일반화한다.

정의

일반화된 베타 랜덤 변수 Y는 다음과 같은 확률밀도함수로 정의된다.

${\displaystyle GB(y;a,b,c,p,q)={\frac { a y^{ap-1}(1-(1-c)(y/b)^{a})^{q-1}}{b^{ap}B(p,q)(1+c(y/b)^{a})^{p+q}}}\quad \quad {\text{ for }}0<y^{a}<{\frac {b^{a}}{1-c}},}$

0.여기서 매개변수는 $0{\displaystyle \mathrm{}}$ ${\displaystyle \le }$ ${\displaystyle c}$ ${\displaystyle \le }$ ${\displaystyle 1}$ ${\displaystyle 0\leq c\leq 1}$ 및$$ $b{\displaystyle }$ ${\displaystyle b$ $p{\displaystyle }$ ${\displaystyle p}$ 및$$$q{\displaystyle }$ ${\displaystyle q}$ 양수를$$ 만족한다.함수 B(p,q)는 베타 함수다.

특성.

순간

h 모멘트는 다음과 같이 표현할 수 있음을 알 수 있다.

${\displaystyle \operatorname {E} _{GB}(Y^{h})={\frac {b^{h}B(p+h/a,q)}{B(p,q)}}{}_{2}F_{1}{\begin{bmatrix}p+h/a,h/a;c\\p+q+h/a;\end{bmatrix}},}$

여기서 ${\displaystyle {}_{\mathrm{}}}$ ${\displaystyle {F\mathrm{}}_{}}$ 1 ${\$}는 초기하계 영상 시리즈(c<1일 경우 모든 h 또는 c=1일 경우 모든 h/a<q에 대해 수렴)를$$ 나타낸다.

관련 분포

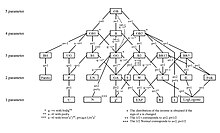
일반화된 베타에는 제한적 또는 특별한 경우로서 많은 분포를 포함한다.위와 같은 GB 분포 트리에 이러한 내용이 설명되어 있다.아래에 열거된 것은 그 세 직계 후손, 즉 하위 가족들이다.

제1종 일반 베타(GB1)

제1종류의 일반화된 베타(beta)는 다음의 pdfdf:

${\displaystyle GB1(y;a,b,p,q)={\frac { a^{ap-1}(1-(y/b)^{a}^{q-1}{b^{ap(p,q)}}}}}}$

$0{\displaystyle }$< < < b$>$ ${\$$displaystyle b$ p ${\displaystyle$ p$},$$q{\displaystyle }$ ${\displaystyle q}$이$($가) 양수인$$ 경우.는 것을 쉽게 증명할 수 있다

${\displaystyle GB1(y;a,b,p,q)=GB(y;a,b,c=0,p,q)}$

GB1의 모멘트는 다음과 같다.

${\displaystyle \operatorname {E} _{GB1}(Y^{h})={\frac {b^{h}B(p+h/a,q)}{B(p,q)}}}$

GB1은 특별한 경우로서 제1종(B1)의 베타, 일반화된 감마(GG) 및 파레토를 포함한다.

${\displaystyle B1(y;b,p,q)=GB1(y;a=1,b,p,q),}$

${\displaystyle GG(y;a,\beta,p)=\lim _{q\to \inflt \infit }GB1(y;a,b=q^{1/a}\beta,p,q),}$

${\displaystyle PARRETO(y;b,p)=GB1(y;a=-1,b,p,q=1)}$

두 번째 종류의 일반 베타(GB2)

GB2는 다음 pdf로 정의된다.

${\displaystyle GB2(y;a,b,p,q)={\frac { a^{ap-1}{b^{b^}B(p,q)(1+(y/b)^{a}^{p+q}}}}}}}}}}}}}}}$

< < ${\displaystyle 0},$ 그 $외$에는 0.는 것을 증명할 수 있다

${\displaystyle GB2(y;a,b,p,q)=GB(y;a,b,c=1,p,q).}$

GB2의 모멘트는 다음과 같다.

${\displaystyle \operatorname {E} _{GB2}(Y^{h})={\frac {b^{h}B(p+h/a,q-h/a)}{B(p,q)}}}$

GB2는 일반화된 베타 프라임(Patil, Boswell, Ratnaparkhi,^[2] 1984)과 변형된 베타(Venter, 1983),^[3] 일반화된 F(Kalfleisch and Fratice, 1980),^[4] Feler-Pareto(Anold,^[5] 1983) 분포의 특별한 경우(μμ0)로도 알려져 있다.The GB2 nests common distributions such as the generalized gamma (GG), Burr type 3, Burr type 12, Dagum, lognormal, Weibull, gamma, Lomax, F statistic, Fisk or Rayleigh, chi-square, half-normal, half-Student's t, exponential, asymmetric log-Laplace, log-Laplace, power function, and the log-logistic.^[6]

베타.

베타 분포(B)는 다음과 같이 정의된다.^[1]

${\displaystyle B(y;b,c,p,q)={\frac {y^{p-1}(1-c)(y/b)^{q-1}{b^{p^{p(p,q)(1+c(y/b))^{p+q}}}}}$

< < /( - ) ${\displaystyle$ 0 $<<b/(1-c)>}$ 및 그 외 0.GB와의 관계는 다음과 같다.

${\displaystyle B(y;b,c,p,q)=GB(y;a=1,b,c,p,q)}$

베타 계열은 제1종과^[7] 제2종(B1과 B2를 베타 프라임이라고도 함)의 베타 계열을 포함하며, 각각 c = 0과 c = 1에 해당한다.

일반 감마

일반화된 감마 분포(GG)는 GB2의 제한 사례다.PDF의 정의는 다음과 같다.^[8]

${\displaystyle GG(y;a,\beta ,p)=\lim _{q\rightarrow \infty }GB2(y,a,b=q^{1/a}\beta ,p,q)={\frac { a y^{ap-1}e^{-(y/\beta )^{a}}}{\beta ^{ap}\Gamma (p)}}}$

$h{\displaystyle }$ [\$displaystyle h}$s$$ moments that dives by.

${\displaystyle \operatorname {E}(Y_{GG}^{h})={\frac {\beta ^{h}\감마(p+h/a)}{\감마(p)}}.}$

앞에서 언급한 바와 같이, GB 분포 가계도는 특수 사례와 제한 사례를 시각적으로 묘사한다(1995년 맥도날드 및 쉬 참조).

파레토

파레토(PA) 분포는 일반화된 감마선의 다음과 같은 제한 사례다.

${\displaystyle PA(y;\beta ,\theta )=\lim _{a\rightarrow -\infty }GG(y;a,\beta ,p=-\theta /a)=\lim _{a\rightarrow -\infty }\left({\frac {\theta y^{-\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{-\theta }(-\theta /a)\Gamma (-\theta /a)}}\right)=}$

${\displaystyle \lim _{a\rightarrow -\infty }\left({\frac {\theta y^{-\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{-\theta }\Gamma (1-\theta /a)}}\right)={\frac {\theta y^{-\theta -1}}{\beta ^{-\theta }}}}$ for $[\displaystyle \property <y}$ 및 $0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$ 이외의$$ 경우.

힘

검정력(P) 분포는 일반화된 감마선의 다음과 같은 제한 사례다.

${\displaystyle P(y;\beta ,\theta )=\lim _{a\rightarrow \infty }GG(y;a=\theta /p,\beta ,p)=\lim _{a\rightarrow \infty }{\frac {\mid {\frac {\theta }{p}} y^{\theta -1}e^{-(y/\beta )^{a}}}{\beta ^{\theta }\Gamma (p)}}=\lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{p\Gamma (p)\beta ^{\theta }}}e^{-(y/\beta )^{a}}=}$

${\displaystyle \lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{\Gamma (p+1)\beta ^{\theta }}}e^{-(y/\beta )^{a}}=\lim _{a\rightarrow \infty }{\frac {\theta y^{\theta -1}}{\Gamma ({\frac {\theta }{a}}+1)\beta ^{\theta }}}e^{-(y/\beta )^{a}}={\frac {\theta y^{\theta -1}}{\beta ^{\theta }}},}$

${\displaystyle \le }$ ${\displaystyle y}$ ${\displaystyle \le }$ ${\displaystyle \beta }$ ${\displaystyle 0\leq y\leq$\ \ $\$ \ } 및 \> 0 ${\displaystyle \theta >0}$에 대한 전원 함수 분포와 동일하다

비대칭 로그-라플라스

비대칭 로그-라플라스 분포(Double Pareto 분포라고도 함)는 다음과 같이 정의된다.^[10]

${\displaystyle ALL(y;b,\lambda _{1},\lambda _{2})=\lim _{a\rightarrow \infty }GB2(y;a,b,p=\lambda _{1}/a,q=\lambda _{2}/a)={\frac {\lambda _{1}\lambda _{2}}{y(\lambda _{1}+\lambda _{2})}}{\begin{cases}({\frac {y}{b}})^{\lambda _{1}}&{\mbox{for }}0<y<b\\({\frac {b}{y}})^{\lambda _{2}}&{\mbox{for }}y\geq b\end{cases}}}$

$여기$서 h ${\displaystyle h}$의 순간은

${\displaystyle \operatorname {E}(Y_{ALL}^{h})={\frac {b^{h}\lambda _{1}\lambda _{1}+h}{2}}:{(\lambda _{1}+h)}.}$

$\lambda {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}인 경우$,$ 이는 log-Laplace 분포와 동일하다.

지수 일반화 베타 분포

Letting ${\displaystyle Y\sim GB(y;a,b,c,p,q)}$, the random variable ${\displaystyle Z=\ln(Y)}$, with re-parametrization, is distributed as an exponential generalized beta (EGB), with the following pdf:

${\displaystyle EGB(z;\delta ,\sigma ,c,p,q)={\frac {e^{p(z-\delta )/\sigma }(1-(1-c)e^{(z-\delta )/\sigma })^{q-1}}{ \sigma B(p,q)(1+ce^{(z-\delta )/\sigma })^{p+q}}}}$

-< - < (1 - ) ${\displaystyle -\inflty <{\frac {z-\fla }}{\ln({\frac{1-c$ 그 외에는 0.EGB는 Gompertz, Gumbel, 극단값 유형 I, 로지스틱, Burr-2, 지수 분포 및 정규 분포의 일반화를 포함한다.

포함된 수치는 EGB와 그것의 특별하고 제한적인 사례 사이의 관계를 보여준다.^[11]

모멘트생성함수

위와 유사한 표기법을 사용하여 EGB의 모멘트 생성 함수는 다음과 같이 표현할 수 있다.

${\displaystyle M_{EGB}(Z)={\frac {e^{\delta t}B(p+t\sigma ,q)}{B(p,q)}}{}_{2}F_{1}{\begin{bmatrix}p+t\sigma ,t\sigma ;c\\p+q+t\sigma ;\end{bmatrix}}.}$

다변량 일반 베타 분포

다변량 일반화된 베타 pdf는 위에 나열된 일변량 분포를 확장한다.For ${\displaystyle n}$ variables ${\displaystyle y=(y_{1},...,y_{n})}$, define ${\displaystyle 1xn}$ parameter vectors by ${\displaystyle a=(a_{1},...,a_{n})}$, ${\displaystyle b=(b_{1},...,b_{n})}$, ${\displaystyle c=}$${\displaystyle c=(c_{1},...,c_{n})}$, and ${\displaystyle p=(p_{1},...,p_{n})}$ where each ${\displaystyle b_{i}}$ and ${\displaystyle p_{i}}$ is positive, and ${\displaystyle 0}$ ${\displaystyle \leq }$ ${\displaystyle$$c_{i$$}}{{$i$\}\}\{\backslash$$displaystyle \leq }$ $1$${\displaystyle \mathrm{}}$ ${\displaystyle 1}$.The parameter ${\displaystyle q}$ is assumed to be positive, and define the function ${\displaystyle B(p_{1},...,p_{n},q)}$ = ${\displaystyle {\frac {\Gamma (p_{1})...$$\감마(p_{n})\감마(q)}{\감마({\$bar$p$}}}}}}$p$ ${\${\$bar{p}}}}$ = $\sum {\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{i}}}$= ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle i_{}}$ ${\$}^{$n}p_{i$

다변량 일반화 베타(${\displaystyle }$ ${\displaystyle G}$ ${\displaystyle B}$ ${\displaystyle MGB$의 pdf는 다음과 같이 작성할 수 있다.

${\displaystyle MGB(y;a,b,p,q,c)={\frac {(\prod _{i=1}^{n} a_{i} y_{i}^{a_{i}p_{i}-1})(1-\sum _{i=1}^{n}(1-c_{i})({\frac {y_{i}}{b_{i}}})^{a_{i}})^{q-1}}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)(1+\sum _{i=1}^{n}c_{i}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}+q}}}}$

어디 0{0\displaystyle}<>{\displaystyle<>}∑ 나는 갈1n(1− c나는)(y는 나는 나는 b)를 명확히 설명{\displaystyle \sum_{i=1}(1-c_{나는})({\frac{y_{나는}}{b_{나는}}})^{a_{나는}}}<0{0\displaystyle}≤{\displaystyle \leq}C.에{\displaystyle<>}1{1\displaystyle} 나는{\dis$playstyle$ c_${$$i}}$<{\$displaystyle$$①$$} {\displaystyle$ 1}과 0 ${\displaystyle$ 0$}$$$${\$$displaystyle y_${i}}일 때 $c{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\${$i{\displaystyle \mathrm{}}$$}$ $$= 1 ${\displaystystystystystysty$ .

일변량 일반화된 베타 분포와 마찬가지로, 다변량 일반화된 베타 분포는 그 계열의 여러 분포를 특별한 경우로 포함한다.모수 벡터에 일정한 제약을 가함으로써 다음과 같은 분포를 쉽게 도출할 수 있다.^[12]

다변량 일반화된 제1종 베타(MGB1)

각 $c{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$이 0과 같을 때 MGB 함수는 다음과 같이 정의되는 제1종(MGB1)의 다변량 일반화 베타(MGB1)로 단순화한다.

${\displaystyle MGB1(y;a,b,p,q)={\frac {(\prod _{i=1}^{n} a_{i} y_{i}^{a_{i}p_{i}-1})(1-\sum _{i=1}^{n}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{q-1}}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)}}}$

여기서 $0{\displaystyle \mathrm{}}$ ${\displaystyle 0}$< ${\$${\displaystyle \underset{}{\overset{}{displaystyle}}}$ $<}$ ${\displaystyle \underset{}{\overset{}{}}}$ i${\displaystyle \underset{}{\overset{}{}}}$= ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{}{\overset{}{}}\frac{{yi}_{}}{}}$) ${\displaystyle {i_{}}^{}}${\$displaystyle$$\$$sum _{i_}{n$}({\$frac {y_}{b_{i}}}}}}}^{a_$${$${\displaystyle \mathrm{}}\}\}\}\}\}\}\}\}\}\}\}\}\}\{\backslash$$displaystyplaystystyplaystyplaystyplaystytimestytytytytytytytype$ $stytype$$st$

다변량 일반화된 두 번째 종류의 베타(MGB2)

각 $c{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$이 1과 동일한 경우, MGB는 두 번째 종류(MGB2)의 다변량 일반화된 베타까지 단순화하며, pdf는 다음과 같이 정의된다.

${\displaystyle MGB2(y;a,b,p,q)={\frac {(\prod _{i=1}^{n} a_{i} y_{i}^{a_{i}p_{i}-1})}{(\prod _{i=1}^{n}b_{i}^{a_{i}p_{i}})B(p_{1},...,p_{n},q)(1+\sum _{i=1}^{n}({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}+q}}}}$

$모든{\displaystyle \mathrm{}}$ $y{\displaystyle {}_{}}$ ${\displaystyle i_{}}$에$$대해 0 {\$displaystyle$ 0$}$$$< {\$displaystyle$ y_{i}}이($가$$)$ {\displaystyle y_$\{$$i$$}$인 경우.

다변량 일반화 감마

The multivariate generalized gamma (MGG) pdf can be derived from the MGB pdf by substituting ${\displaystyle b_{i}}$ = ${\displaystyle \beta _{i}q^{\frac {1}{a_{i}}}}$ and taking the limit as ${\displaystyle q}$ ${\displaystyle \to }$ ${\displaystyle \infty }$, with Stirling's ap다음 함수를 생성하는 감마 함수의 근접:

${\displaystyle MGG(y;a,\beta ,p)=({\frac {(\prod _{i=1}^{n} a_{i} y_{i}^{a_{i}p_{i}-1})}{(\prod _{i=1}^{n}\beta _{i}^{a_{i}p_{i}})\Gamma (p_{i})}})e^{-\sum _{i=1}^{n}({\frac {y_{i}}{\beta _{i}}})^{a_{i}}}=\prod _{i=1}^{n}GG(y_{i};a_{i},\beta _{i},p_{i})}$

이것은 독립적이지만 반드시 동일하게 분포된 일반화된 감마 랜덤 변수의 산물이다.

기타 다변량 분포

유사한 pdfs는 각 pdf 이름 앞에 M을 놓고 일변량 분포의 제약조건과 한계로 나타낸 MGB의 적절한 제한과 특별한 경우를 찾아내는 것만으로 위에 나타낸 패밀리 트리의 다른 변수에 대해 구성할 수 있다.Additional multivariate pdfs in the literature include the Dirichlet distribution (standard form) given by ${\displaystyle MGB1(y;a=1,b=1,p,q)}$, the multivariate inverted beta and inverted Dirichlet (Dirichlet type 2) distribution given by ${\displaystyle MGB2$$(y;a=1,b=1,p,q)}$및 $M{\displaystyle }$ G ${\displaystyle B}$ ${\displaystyle 2(y}$; ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle p,}$ ${\displaystyle \mathrm{q}}$= 1${\displaystyle }$) ${\displaystyle MGB2(y;a,b,p,q=1)$가 제공한 다변량 Burr 분포$.$

한계밀도함수

MGB1과 MGB2의 한계밀도함수는 각각 제1종과 제2종의 일반화된 베타분포로서 다음과 같이 주어진다.

${\displaystyle GB1(y_{i};a_{i},b_{i},p_{i},{\bar {p}}-p_{i}+q)={\frac { a_{i} y_{i}^{a_{i}p_{i}-1}(1-({\frac {y_{i}}{b_{i}}})^{a_{i}})^{{\bar {p}}-p_{i}+q-1}}{b_{i}^{a_{i}p_{i}}B(p_{i},{\bar {p}}-p_{i}+q)}}}$

${\displaystyle GB2(y_{i};a_{i},b_{i},p_{i},q)={\frac { a_{i} y_{i}^{a_{i}p_{i}-1}}{b_{i}^{a_{i}p_{i}}B(p_{i},q)(1+({\frac {y_{i}}{b_{i}}})^{a_{i}})^{p_{i}+q}}}}$

적용들

GB 제품군이 제공하는 유연성은 다음 분포의 모델링에 사용된다.

• 소득분배
• 위험 함수
• 주식 수익률
• 보험 손실

EGB 제품군의 구성원과 관련된 애플리케이션은 다음과 같다.^[1][6]

• 회귀 모형의 부분적 적응적 추정
• 시계열 모델
• (G)ARCH 모델

소득분배

GB2와 그 특별하고 제한적인 몇몇 사례들은 소득분배의 모델로 널리 이용되어 왔다.몇몇 초기 예는 Thurow (1970),^[13][14] Dagum (1977), Singh and Maddala (1976),^[15] 그리고 McDonald (1984)를 참조한다.^[6]개별, 그룹화 또는 최상위 코드화된 데이터를 사용한 최대우도 추정은 이러한 분포로 쉽게 수행된다.

지니지수(G), 피에트라지수(P), 테일지수(T) 등 불평등 척도는 맥도날드와 랜섬(2008)이 제시한 분포변수 측면에서 표현할 수 있다.^[16]

${\displaystyle {\begin{aligned}G=\left({\frac {1}{2\mu }}\right)\operatorname {E} ( Y-X )=\left(P{\frac {1}{2\mu }}\right)\int _{0}^{\infty }\int _{0}^{\infty } x-y f(x)f(y)\,dxdy\\=1-{\frac {\int _{0}^{\infty }(1-F(y))^{2}\,dy}{\int _{0}^{\infit }(1-F(y)\,dy}\\\P=\좌({\frac {1}{2\mu }}\오른쪽)\operatorname {E}(Y-\mu )=\좌({\frac {1}{2\mu }}\int _{0}^{0}}}{\mu f(y)\,dy\\\\\\\\\\\T=\operatorname {E}(\ln(Y/\mu )^{Y/\mu }=\int_{0}^{0}^{\infit }(y/\mu )\ln(y/\mu )f(y)\,dy\end}}}}}$

위험 함수

위험 함수 h(s), 여기서 f(s)는 pdf이고 F(s)는 해당 cdf로 정의된다.

${\displaystyle h(s)={\frac {f}{1-F}}}$

위험 함수는 실업 기간, 제품의 수명 또는 기대 수명 모델링과 같은 많은 응용 분야에서 유용하다.구체적인 예를 들어, 만약 s가 수명을 나타낸다면, h(s)는 개인이 s까지 산다는 것을 고려할 때, s의 사망률이다.인간 사망률 데이터에 대한 위험 함수의 형태는 다음과 같이 나타날 수 있다: 생후 처음 몇 개월 동안 사망률을 감소시킨 다음 비교적 일정한 사망률을 보이고 마지막으로 노년층에서 사망 확률이 증가하는 기간이다.

일반화된 베타 분포의 특별한 경우는 위험 함수의 형상 모형에 더 많은 유연성을 제공하며, 위험 함수의 형상 모형은 "수치" 또는 "수치" 형태를 요구하거나 (I}에 의해 표시됨) 엄격히 증가하거나 (D) 라인을 감소시킬 수 있다.일반화된 감마선은 a>1과 p<1/a의 경우 """자형, a<1과 p>1/a의 경우 "∩"자형, a<1과 p>1/a의 경우 I자형, a<1과 p>1/a의 경우 D자형이다.^[17]이것은 아래 그림에 요약되어 있다.^[18][19]

참조

참고 문헌 목록

• C. Kleiber 및 S. Kotz(2003) 경제 및 보험수리적 과학의 통계적 크기 분포.뉴욕: 와일리
• Johnson, N. L., S. Kotz, N. Balakrishnan(1994) 연속 일변량 분포.제2권, 호보켄, NJ: 와일리-인터사이언스