운동 방정식
Equations of motion| 시리즈의 일부 |
| 고전 역학 |
|---|
물리학에서, 운동 방정식은 물리적 시스템의 움직임을 시간의 [1]함수로 설명하는 방정식이다.보다 구체적으로, 운동 방정식은 물리적 시스템의 동작을 동적 변수의 관점에서 수학적 함수의 집합으로 묘사합니다.이러한 변수는 일반적으로 공간 좌표 및 시간이지만 운동량 성분이 포함될 수 있습니다.가장 일반적인 선택은 물리적 [2]시스템의 편리한 변수가 될 수 있는 일반화 좌표입니다.그 함수는 고전역학에서 유클리드 공간에서 정의되지만 상대성 이론에서는 곡선 공간으로 대체된다.시스템의 역학을 알고 있는 경우, 방정식은 역학의 움직임을 설명하는 미분 방정식의 해입니다.
운동에 대한 두 가지 주요 설명이 있습니다: 역동성과 운동학입니다.모멘타부터 입자의 힘과 에너지가 고려되기 때문에 역학이 일반적입니다.이 경우, 역학이라는 용어는 때때로 시스템이 만족하는 미분 방정식(예: 뉴턴의 제2법칙 또는 오일러-라그랑주 방정식)을 가리키며, 때로는 이러한 방정식에 대한 해들을 가리킵니다.
그러나 운동학은 더 간단하다.대상과 시간의 위치에서 파생된 변수만 관련이 있습니다.일정한 가속의 상황에서 이러한 단순한 운동 방정식은 일반적으로 변위(s), 초기 속도(u), 최종 속도(v), 가속도(a) 및 시간(t)의 운동학적 양의 정의에서 발생하는 SUVAT 방정식이라고 한다.
보통 물리법칙으로 식별되며 [clarification needed]물리량의 정의를 적용하는 미분운동방정식은 문제에 대한 방정식을 설정하는데 사용됩니다.미분방정식을 풀면 임의의 상수를 갖는 일반적인 해, 즉 해군에 대응하는 임의성이 생긴다.상수의 값을 고정하는 초기 값을 설정하면 특정 솔루션을 얻을 수 있습니다.
공식적으로, 일반적으로 아주 식은 개체의 위치 r의 M은 함수를 사용하여 이 말씀 드린다면, 그 속도를 처음 r의 미분, v=.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{.디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}dr/dt), 그리고 그것의 가속도(발음하는 유도 함수., = d2r/dt2), 그리고 시간톤3D의 유클리드 벡터는 전체적으로 굵은 글씨로 표시됩니다.이는 r의 운동방정식이 r의 2차 상미분방정식(ODE)이라고 말하는 것과 같다.
여기서 t는 시간이고, 각 오버닷은 1개의 시간 도함수를 나타냅니다.초기 조건은 t = 0의 상수 값으로 주어진다.
운동 방정식에 대한 해 r(t)는 지정된 초기값으로 t = 0 이후의 모든 시간 t에 대한 시스템을 설명한다.물체의 운동량 p나 각운동량 p와 같은 다른 동적 변수들은 시간 t에서의 물체의 위치가 단연코 가장 원하는 양이지만, 어떤 운동 방정식으로부터 풀어야 할 양으로서 r 대신 사용될 수 있다.
때로는 방정식이 선형이고 정확하게 풀릴 가능성이 더 높습니다.일반적으로 방정식은 비선형이며 정확하게 풀 수 없으므로 다양한 근사치를 사용해야 합니다.비선형 방정식에 대한 해는 시스템이 초기 조건에 얼마나 민감한지에 따라 혼란스러운 동작을 나타낼 수 있습니다.
역사
운동학, 역학, 그리고 우주의 수학적 모형은 우리가 알고 있는 이름 중 일부만 알고 있는 많은 사상가들 덕분에 3천년에 걸쳐 점진적으로 발전했습니다.고대에는 성직자, 점성가, 천문학자들이 일식과 월식, 용기와 태양의 분점과 달의 시기를 예측했다.하지만 그들을 안내할 수 있는 알고리즘 외에는 아무것도 없었습니다.운동 방정식은 이후 천 년 동안 기록되지 않았다.
13세기의 중세 학자들은, 예를 들어 옥스포드와 파리의 비교적 새로운 대학들에서, 지금은 물리학이라고 불리는 새로운 지식 체계를 개발하기 위해 고대 수학자들과 철학자들을 이용했다.
옥스퍼드 대학에서 머튼 대학은 파리 대학의 지식인들과 비슷한 수준의 물리학, 천문학, 수학 등 자연과학에 전념하는 학자들을 보호했다.토마스 브래드워딘은 거리와 속도와 같은 아리스토텔레스적 양을 확장했고, 그 양에 강도와 확장을 부여했다.브래드워딘은 힘, 저항, 거리, 속도, 시간을 포함하는 지수 법칙을 제안했다.니콜라스 오렘은 브래드워딘의 주장을 더욱 확대했다.머튼 학파는 균등하게 가속된 운동을 하는 물체의 운동량이 가속된 운동 중간에 도달한 속도에서 균일한 운동량과 같다는 것을 증명했다.
갈릴레오 이전의 운동학 작가들에게, 작은 시간 간격은 측정할 수 없었기 때문에, 시간과 움직임 사이의 연관성은 불분명했다.그들은 거리를 함수로 시간을 사용했고 자유낙하에서는 더 높은 고도에서 더 빠른 속도를 얻었다.오직 스페인의 신학자인 도밍고 드 소토만이 1545년에 출판된 아리스토텔레스 물리학에 대한 논평에서 속도라는 단어가 사용되지 않은 "균등하게 가속되는" 운동을 시간에 비례한다고 정의한 후, 이러한 운동이 자유롭게 떨어지는 물체와 발사체로 식별될 수 있다고 올바르게 선언했다.그는 이러한 명제를 증명하거나 시간, 속도 및 거리와 관련된 공식을 제안한다.De Soto의 언급은 가속도의 정의(가속도는 시간의 운동 변화율)와 상승 중 가속도가 부정적일 것이라는 관측에 대해 매우 정확하다.
이와 같은 담론은 유럽 전역에 퍼져 갈릴레오 갈릴레이와 다른 사람들의 작품을 형성하고 운동학의 기초를 닦는데 [3]도움을 주었다.갈릴레오는 현재 운동학 방정식의 특별한 경우로 알려진 머튼 법칙을 사용하여 그의 연구에서 방정식 s = 1/2gt를2 기하학적으로 [4]추론했다.
갈릴레오는 발사체의 경로가 포물선이라는 것을 최초로 보여주었다.갈릴레오는 원심력에 대해 이해하고 운동량에 대한 올바른 정의를 내렸다.동력학에서 기본량으로서 운동량을 강조하는 것이 가장 중요하다.그는 속도와 무게의 곱으로 운동량을 측정했다; 질량은 호이겐스와 뉴턴에 의해 개발된 후기 개념이다.단순한 추의 흔들림에서, 갈릴레오는 "원호를 따라 하강할 때 획득되는 모든 운동량은 같은 움직이는 물체가 같은 호를 통해 상승하게 하는 운동량과 같다"고 말한다[5].발사체에 대한 그의 분석은 갈릴레오가 제1법칙과 제2운동법칙을 파악했음을 보여준다.그는 그것들을 일반화하고 지구 중력의 영향을 받지 않는 물체에 적용할 수 있도록 하지 않았다.그 단계는 뉴턴의 공헌이었다.
"관성"이라는 용어는 케플러에 의해 사용되었습니다. 케플러는 그것을 정지 상태의 물체에 적용했습니다. (운동의 제1법칙은 종종 관성의 법칙이라고 불립니다.)
갈릴레오는 아리스토텔레스의 몇 가지 오류를 수정했지만 제3의 운동 법칙인 작용과 반작용의 평등 법칙을 완전히 이해하지 못했다.스테빈과 다른 사람들과 함께 갈릴레오는 정역학에 대해서도 썼다.그는 힘의 평행사변형의 원리를 공식화했지만 그 범위를 완전히 인식하지 못했다.
갈릴레오는 또한 진자의 법칙에 관심이 있었는데, 그의 첫 번째 관찰은 젊은 시절이었다.1583년 피사에 있는 성당에서 기도를 하던 중, 그의 관심은 점등된 거대한 램프의 움직임으로 멈춰졌고 시간을 맞추기 위해 자신의 맥박을 참고했다.그에게 있어서 그 주기는 추의 등시성을 발견하면서 운동이 크게 줄어든 후에도 똑같아 보였다.
나중에 그에 의해 수행된 보다 신중한 실험과 그의 토론에 기술된 바에 따르면, 진동의 주기는 길이의 제곱근에 따라 달라지지만 진자의 질량과 무관하다는 것이 밝혀졌습니다.
그래서 르네 데카르트와 아이작 뉴턴, 고트프리드 라이프니츠 등에 도착했습니다.그리고 현대식으로 인식되기 시작하는 운동 방정식의 진화된 형태입니다.
나중에 운동 방정식은 전기역학에서도 나타났는데, 전기장과 자기장에서 하전된 입자의 운동을 설명할 때 로렌츠 힘은 전기장과 자기장이 의미하는 것의 정의 역할을 하는 일반적인 방정식이다.특수상대성이론과 일반상대성이론의 출현과 함께, 시공간으로의 이론적 수정은 또한 고전적인 운동 방정식이 빛의 유한한 속도와 시공간 곡률을 설명하도록 수정되었다는 것을 의미했다.이 모든 경우에서 미분방정식은 힘과 [6]에너지 변환의 영향을 받아 입자의 궤적을 공간과 시간 좌표로 설명하는 함수의 관점에서 이루어졌다.
그러나 양자역학의 방정식은 양자 상태가 입자의 시공간 좌표를 사용하여 어떻게 유사하게 동작하는지를 기술하는 파동함수의 미분 방정식이기 때문에 "운동의 등식"으로도 간주될 수 있다.물리학의 다른 영역에는 파동, 유체 또는 장으로 간주될 수 있는 물리적 현상의 수집에 대한 운동 방정식의 유사점이 있습니다.
하나의 입자에 대한 운동 방정식
운동량
순간 위치 r = r(t), 시간 t의 순간 값에서의 순간적 의미, 순간 속도 v = v(t) 및 가속도 a = a(t)는 일반적인 좌표 독립적 [7]정의를 갖는다.
속도는 항상 운동 방향을 가리킵니다. 즉, 곡선 경로의 경우 탄젠트 벡터입니다.대략적으로 말하자면, 1차 도함수는 곡선의 접선과 관련이 있습니다.커브 패스의 경우에도 가속도는 패스의 곡률 중심을 향합니다.다시 한 번, 대략적으로 말하자면, 2차 도함수는 곡률과 관련이 있다.
회전 유추는 θ = θ(t), 각속도 = θ(t), 각가속도 α = α(t)이다.
여기서 nθ는 회전축 방향의 단위 벡터이고 θ는 물체가 축을 중심으로 통과하는 각도입니다.
각속도 [8]θ의 일부 축을 중심으로 공전하는 점 모양의 입자에 대해서는 다음과 같은 관계가 성립한다.
여기서 r은 입자의 위치 벡터(회전 축에서 제외)이고 v는 입자의 접선 속도입니다.회전하는 연속체 강체의 경우, 이러한 관계는 강체의 각 점에 대해 유지됩니다.
균일한 가속도
직선에서 일정하거나 균일한 가속도의 입자에 대한 운동 미분 방정식은 간단하다. 즉, 가속도가 일정하기 때문에 물체 위치의 2차 도함수는 일정하다.이 경우의 결과는 다음과 같습니다.
직선으로 일정한 변환 가속
이러한 방정식은 일정한 [9]가속도로 직선으로 3차원으로 선형으로 이동하는 입자에 적용됩니다.위치, 속도 및 가속도는 공선(평행하고 같은 선상에 놓임)이기 때문에 이러한 벡터의 크기만 필요하며, 운동은 직선을 따르기 때문에 문제가 3차원에서 1차원으로 효과적으로 감소합니다.
여기서:
공식 [1]과 [2]는 초기 조건 r(t0) = r0 및 v(t0) = v에0 따라 속도와 [9]가속도의 정의를 통합한 것이다.
규모로는
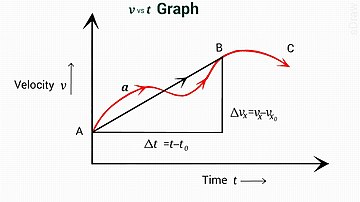
식 [3]은 평균 속도 v + v0/2를 포함한다.직관적으로 속도는 직선적으로 증가하므로 평균속도에 시간을 곱한 값은 v에서0 v로 속도를 증가시키면서 이동한 거리이며, 이는 시간에 대한 속도를 직선 그래프로 그래프로 나타내면 알 수 있다.대수적으로, 이것은 다음에 대해 [1]을 풀면 뒤따른다.
[2]로 대체한다.
그 후, 심플화를 통해
또는 규모에서
[3]부터
[1]의 t를 대체한다.
[3]부터
[2]로 대체:
보통 첫 번째 4개만 필요하고 다섯 번째도 옵션입니다.
여기서 a는 정가속도이며, 물체가 중력의 영향을 받아 이동하는 경우에는 표준 중력 g를 이용한다.각 방정식은 5개의 변수 중 4개를 포함하므로 이 상황에서는 나머지 2개를 계산하기 위해 5개의 변수 중 3개를 아는 것으로 충분합니다.
기초 물리학에서 같은 공식은 종종 다음과 같은 다른 표기로 쓰여진다.
여기서 u는 v를, s는 r - r을0 대체합니다0.이들은 종종 SUVAT 방정식이라고 불리며, 여기서 "SUVAT"는 변수의 약어이다: s = 변위, u = 초기 속도, v = 최종 속도, a = 가속도,[10][11] t = 시간.
모든 방향에서 일정한 선형 가속도
초기 위치, 초기 속도 및 가속도 벡터는 공선일 필요가 없으며 거의 동일한 형태를 취합니다.유일한 차이점은 속도의 제곱 크기에는 점곱이 필요하다는 것입니다.파생은 기본적으로 공선 사례와 동일하다.
토리첼리 방정식 [4]은 다음과 같이 도트 곱의 분포 특성을 사용하여 도출할 수 있다.
적용들
운동학에서 기초적이고 빈번한 예는 발사체와 관련이 있다. 예를 들어 공중에 위로 던지는 공이다.초기 속도 u를 지정하면 공이 떨어지기 전에 얼마나 높이 이동하는지 계산할 수 있다.가속도는 중력 g의 국소 가속도이다.이러한 양은 스칼라로 보이지만 변위, 속도 및 가속의 방향이 중요합니다.그것들은 사실상 단방향 벡터로 간주될 수 있다.지면에서 측정하기 위해 s를 선택하면 중력이 아래로 작용하기 때문에 그에 따른 볼의 가속도가 실제로 -g이어야 합니다.
가장 높은 지점에서는 공이 정지합니다. 따라서 v = 0. 위의 집합에 있는 방정식 [4]을 사용하면 다음과 같이 됩니다.
마이너스 기호를 대체 및 취소하면 다음과 같은 결과가 나타납니다.
일정한 원형 가속도
위의 방정식의 유추는 회전을 위해 쓸 수 있습니다.이 축 벡터는 모두 회전축과 평행해야 하므로 벡터의 크기만 필요합니다.
여기서 α는 일정한 각가속도, α는0 각속도, θ는 초기각속도, θ는 통과각(변위), θ는0 초기각도, t는 초기상태에서 최종상태까지 회전하는 데 걸리는 시간이다.
일반 평면 운동
이것들은 평면에서 경로를 가로지르는 입자에 대한 운동학적 방정식으로, 위치 r = r([12]t)로 설명된다.이들은 단순히 각속도 θ와 각가속도α에 대해 위의 물리량의 정의를 사용한 평면 극좌표 위치 벡터의 시간 미분이다.이것들은 시간에 따라 변하는 순간적인 양이다.
입자의 위치는
여기서 and와r ê는θ 극 단위 벡터이다.시간에 대한 차별화는 속도를 제공한다.
회전으로 인해 방사형 성분 dr/dt 및 추가 성분 rθ가 있습니다.시간과 관련하여 다시 차별화하면 가속도를 얻을 수 있습니다.
이 값은 반경 가속도2 dr/dt2, 구심 가속도 -rθ2, 코리올리 가속도 2µdr/dt 및 각 가속도 rα로 구분됩니다.
이들 방정식에 의해 기술된 특별한 운동 사례는 아래 표에 정성적으로 요약되어 있습니다.두 가지는 이미 위에서 설명한 바와 같이 반경 성분 또는 각도 성분이 0이고 움직임의 비 0 성분이 균일한 가속도를 나타냅니다.
| 동작 상태 | 상수 r | r t의 선형 | t의 r 2차 | r 비선형(t) |
|---|---|---|---|---|
| 상수 » | 문방구 | 균일한 번역(일정한 번역 속도) | 균일한 번역 액셀러레이션 | 불균일한 번역 |
| t의 선형 | 원의 균일한 각도 운동(정각 속도) | 나선형의 일정한 반경 속도에서의 균일한 각도 운동 | 나선형, 일정한 반경 가속도에서의 각도 운동 | 나선형의 다양한 방사형 가속도 각도 운동 |
| θ t의 2차 | 원의 균일한 각도 가속도 | 나선형의 일정한 반경 속도에서의 균일한 각도 가속도 | 나선형의 일정한 반경 가속도에서의 균일한 각도 가속도 | 나선형의 균일한 각도 가속도, 다양한 방사형 가속도 |
| § 비선형(t) | 원의 균일하지 않은 각도 가속도 | 나선형, 일정한 반경 속도에서의 불균일한 각도 가속도 | 나선형의 일정한 반경 가속도에서의 불균일한 각도 가속도 | 나선형의 불균일한 각도 가속도, 다양한 방사형 가속도 |
일반적인 3D 모션
3D 공간에서 대응하는 단위 벡터 êr, êθ 및 ,를φ 갖는 구면 좌표(r, θ, θ), 위치, 속도 및 가속도는 각각 다음과 같이 일반화한다.
상수 θ의 경우 이는 위의 평면 방정식으로 감소합니다.
동적 운동 방정식
뉴턴 역학
개발된 첫 번째 일반 운동 방정식은 뉴턴의 제2 운동 법칙이었다.가장 일반적인 형태에서는 물체의 운동량 변화율 p = p(t) = mv(t)는 [13]물체에 작용하는 힘 F = F(x(t), v(t), t)와 같다.
방정식의 힘은 물체가 행사하는 힘이 아니다.운동량을 질량 곱하기 속도로 대체하면, 법칙은 또한 더 잘 쓰여진다.
뉴턴의 제2법칙은 점 모양의 입자와 강체의 모든 점에 적용된다.또한 변형 가능한 고체나 유체처럼 질량 연속체의 각 점에도 적용되지만, 시스템의 움직임을 고려해야 합니다. 재료 도함수를 참조하십시오.질량이 일정하지 않은 경우에는 질량과 속도에 대한 시간 도함수에 대한 곱셈 법칙을 사용하는 것이 충분하지 않으며, 뉴턴의 제2법칙은 운동량 보존과 일치하는 수정을 필요로 한다. 가변 질량 체계를 참조하십시오.
뉴턴의 운동법칙을 이용해 운동방정식을 벡터 형태로 적는 것은 간단할 수 있지만, 공간 좌표와 시간에 따라 성분이 복잡하게 달라질 수 있어 이를 푸는 것은 쉽지 않다.종종 그 문제에 대해 완전히 풀어야 할 변수들이 과도하게 존재하기 때문에, 뉴턴의 법칙이 항상 시스템의 움직임을 결정하는 가장 효율적인 방법은 아니다.단순한 직사각형 기하학의 경우, 데카르트 좌표에서는 뉴턴의 법칙이 잘 작동하지만, 다른 좌표계에서는 극적으로 복잡해질 수 있습니다.
운동량 형태는 특수 및 일반 상대성 이론과 같은 더 복잡한 시스템에 쉽게 일반화되기 때문에 선호된다(4-운동량 [13]참조).운동량 보존에도 사용할 수 있습니다.하지만, 뉴턴의 법칙은 운동량 보존보다 더 근본적이지 않다. 왜냐하면 뉴턴의 법칙은 단지 물체에 작용하는 0의 결과력이 일정한 운동량을 의미하는 반면, 결과력은 운동량이 일정하지 않다는 사실과 일치하기 때문이다.운동량 보존은 결과력에 영향을 받지 않는 격리된 시스템에 대해 항상 참입니다.
많은 입자의 경우(많은 신체 문제 참조), 다른 입자의[7][14] 영향을 받는 하나의 입자에 대한 운동 방정식은 다음과 같다.
여기서i p는 입자 i의 운동량ij, F는 입자 j에 의한 입자 i에 대한 힘, F는E 시스템의 일부가 아닌 물질에 의한 외부 힘입니다.입자 i는 그 자체에 힘을 가하지 않는다.
오일러의 운동 법칙은 뉴턴의 법칙과 비슷하지만, 그것들은 특히 강체의 움직임에 적용됩니다.뉴턴-울러 방정식은 강체에 작용하는 힘과 토크를 하나의 방정식으로 결합합니다.
뉴턴의 회전 제2법칙은 번역의 [15]경우와 비슷한 형태를 취한다.
차체에 작용하는 토크를 각운동량 L의 변화율과 같게 함으로써 얻을 수 있다.질량 곱하기 가속도와 유사하게, 관성 텐서 I의 모멘트는 회전축에 대한 질량의 분포에 의존하며, 각 가속도는 각 속도의 변화율이다.
이 방정식은 입자와 같은 점이나 강체의 각 점에 적용됩니다.
마찬가지로, 다수의 입자에 대해, 하나의 입자에 대한[16] 운동 방정식은
여기서i L은 입자 i의 각운동량, 입자ij j에 의한 입자 i의 토크, θ는E 결과 외부 토크입니다(계통의 일부가 아닌 물질에 의한).입자 i는 스스로 토크를 가하지 않는다.
적용들
뉴턴의 법칙의 몇 가지 예는[17] 단순한 진자의 운동을 설명하는 것을 포함한다.
감쇠된 정현파 구동 고조파 발진기,
중력에 의한 질량의 움직임을 설명하기 위해 뉴턴의 중력의 법칙을 뉴턴의 제2법칙과 결합할 수 있다.두 가지 예에서 공기 중에 던져진 질량 m의 공(예: 바람)은 저항력 R = R(r, t)의 벡터장으로 설명된다.
여기서 G는 중력 상수, M은 지구의 질량, A = R/m은 위치 r 및 시간 t에서의 기류에 의한 발사체의 가속도이다.
중력으로 인해 서로 상호작용하는 N개의 입자에 대한 전형적인 N-body 문제는 N개의 비선형 결합 2차 ODE 세트이다.
여기서 i = 1, 2, …, N은 각 입자와 관련된 양(질량, 위치 등)을 표시합니다.
해석역학
시스템에 제약이 있는 경우 3D 공간의 세 좌표를 모두 사용할 필요가 없습니다.시스템의 자유도가 N개인 경우 N개의 일반화 좌표 q(t) = [q1(t2), q(t) ... q(t)] 세트를N 사용하여 시스템의 구성을 정의할 수 있습니다.호 길이 또는 각도의 형태를 취할 수 있습니다.이들은 시스템의 움직임을 제한하는 고유 구속조건을 활용하고 좌표의 수를 최소로 줄이기 때문에 움직임을 설명하는 데 상당한 단순화입니다.일반화 좌표의 시간 도함수는 일반화 속도이다.
여기서 라그랑지안은 설정q와 그 시간 변화율 dq/dt(및 시간 t)의 함수입니다.
시스템의 라그랑지안을 설정하고, 그 방정식에 대입하여 편도함수를 평가하여 단순화하면 좌표에서 결합된 N개의 2차 ODE 세트를 얻을 수 있다.
해밀턴이 있는 곳
구성 q 및 켤레 "일반화" 모멘타의 함수입니다.
여기서 θ/timeq = (time/timeq1, θ2/timeq, …, θN/timeq)는 표시된 변수에 대한 편도함수 벡터의 약어 표기법이다(예: 이 분모 표기법에 대한 행렬 미적분 참조), 그리고 시간 t,
시스템의 해밀턴을 설정한 후 방정식에 대입하여 편도함수를 평가하여 단순화하면 좌표i q 및 모멘타i p에서 결합된 2N의 1차 ODE 세트를 얻을 수 있다.
해밀턴-야코비 방정식은[2] 다음과 같다.
어디에
고전 작용이라고도 불리는 해밀턴의 주요 함수는 L의 함수이다.이 경우 모멘타는 다음과 같이 주어진다.
이 방정식은 단순한 일반 형태를 가지고 있지만, 주어진 해밀턴의 경우 실제로는 N + 1 변수에서 단일 1차 비선형 PDE입니다.작용 S는 물리적 시스템의 작용의 미분 가능한 대칭은 에미 노이더에 의한 정리인 상응하는 보존 법칙을 가지고 있기 때문에 기계적 문제 자체를 완전히 해결할 수 없는 경우에도 기계적 시스템에 대한 보존량을 식별할 수 있게 한다.
모든 고전적인 운동 방정식은 해밀턴의 최소 작용 원리로 알려진 변화 원리에서 도출될 수 있다.
시스템이 설정 공간을 통과하는 경로가 액션S가 가장 적은 경로임을 나타냅니다.
전기역학
전기역학에서 전하 q의 하전 입자에 가해지는 힘은 로렌츠 [20]힘입니다.
뉴턴의 제2법칙과 결합하면 입자의 위치에 관한 1차 미분 운동 방정식이 제공됩니다.
또는 그 추진력:
질량 m과 전하 [21]q의 하전 입자에 대해 라그랑지안(및 위의 라그랑지 방정식 적용)을 사용하여 동일한 방정식을 얻을 수 있습니다.
여기서 A와 θ는 전자기 스칼라 및 벡터 전위장입니다.라그랑지안은 추가적인 세부사항을 나타냅니다. 라그랑지안 역학의 표준 운동량은 다음과 같습니다.
단순한 mv 대신에, 하전 입자의 움직임을 암시하는 것은 근본적으로 입자의 질량과 전하로 결정된다.라그랑주 표현식은 힘 방정식을 도출하기 위해 처음 사용되었다.
또는 해밀턴식([19]및 방정식으로 대체):
로런츠 힘 방정식을 도출할 수 있습니다.
일반상대성이론
측지선 운동 방정식
위의 방정식은 평탄한 시공간에서 유효합니다.곡선 시공간에서는 직선이 없기 때문에 일이 수학적으로 더 복잡해진다; 이것은 일반화되어 곡선 시공간(두 점 사이의 가장 짧은 곡선 길이)의 측지학으로 대체된다.미터법 텐서 g가 있는 곡선 다지관의 경우, 미터법은 호 길이의 개념을 제공한다(자세한 내용은 선 요소 참조).차동 호 길이는 다음과 [23]같이 지정됩니다.
측지방정식은 좌표의 2차 미분방정식이다.일반적인 솔루션은 측지학 [24]제품군입니다.
여기서 δ는 두 번째 종류의 크리스토펠 기호로 (좌표계와 관련하여) 메트릭을 포함합니다.
응력-에너지 텐서 T에 의해 제공되는 질량-에너지 분포가 주어졌을 때, 아인슈타인 장 방정식은 메트릭의 비선형 2차 편미분 방정식의 집합이며, 시공간 곡률은 중력장과 동등하다는 것을 의미한다(등가 원리 참조).곡선 시공간에서 떨어지는 질량은 중력장에 떨어지는 질량과 같다. 중력은 가상의 힘이기 때문이다.곡선 시공간에서 한 측지선의 상대 가속도는 측지선 편차 방정식으로 구할 수 있다.
여기서 θα = x2α - x는1α 두 측지학 사이의 분리 벡터이고, D/ds(d/ds뿐만 아니라)는αβγδ 공변 도함수이고, R은 크리스토펠 기호를 포함하는 리만 곡률 텐서이다.즉, 지오데식 편차 방정식은 곡면 시공간에서의 질량에 대한 운동 방정식으로, 전자기장에서의 [25]전하에 대한 로렌츠 힘 방정식과 유사합니다.
평탄한 시공간에서 측정기준은 상수 텐서이므로 크리스토펠 기호는 사라지며 측지방정식은 직선의 해를 갖는다.이것은 또한 질량이 뉴턴의 중력의 법칙에 따라 움직일 때 제한적인 경우이다.
회전하는 물체
일반 상대성 이론에서 회전 운동은 스핀 텐서를 포함한 상대론적 각운동량 텐서에 의해 설명되며, 스핀 텐서는 적절한 시간에 대한 공변 도함수 아래에서 운동 방정식에 들어간다.매티슨-파파페트로우-딕슨 방정식은 중력장 내에서 회전하는 물체의 움직임을 기술합니다.
파도와 필드의 유사점
결합된 상미분방정식의 시스템인 입자역학을 기술하는 운동방정식과 달리 파도와 장의 역학을 지배하는 유사한 방정식은 항상 부분미분방정식이다. 왜냐하면 파도와 장은 공간과 시간의 함수이기 때문이다.특정 솔루션의 경우 초기 조건과 함께 경계 조건을 지정해야 합니다.
때때로 다음과 같은 맥락에서 파장 방정식 또는 장 방정식을 "운동의 등식"이라고도 합니다.
필드 방정식
필드의 공간 의존성과 시간 진화를 설명하는 방정식을 필드 방정식이라고 합니다.여기에는 다음이 포함됩니다.
- 전자기장에 대한 맥스웰의 방정식,
- 뉴턴 중력 또는 정전장 전위에 대한 포아송 방정식
- 아인슈타인 중력장 방정식(뉴턴의 중력의 법칙은 약한 중력장과 낮은 입자 속도에 대한 특별한 경우)
이 용어는 일반적인 용어가 아닙니다.예를 들어 Navier는–스토크스 방정식은 유체의 속도장을 지배하며, 보통 "장 방정식"이라고 부르지 않습니다. 이 맥락에서 그들은 유체의 운동량을 나타내며 대신 "운동 방정식"이라고 불립니다.
파동 방정식
파동 방정식을 파동 방정식이라고 합니다.파동 방정식에 대한 해는 진폭의 시간-진화와 공간 의존성을 제공합니다.경계조건은 솔루션이 이동파를 기술하는지 또는 정지파를 기술하는지 여부를 결정합니다.
고전적인 운동 방정식 및 자기장 방정식으로부터 기계, 중력파, 전자파 방정식을 도출할 수 있습니다.3D의 일반적인 선형파 방정식은 다음과 같습니다.
여기서 X = X(r, t)는 기계적 또는 전자기장 진폭이다.[26]
v는 위상 속도입니다.비선형 방정식은 진폭에 대한 위상 속도의 의존성을 모델링하여 v를 v(X)로 대체합니다.매우 구체적인 용도에 대한 다른 선형 및 비선형 파동 방정식이 있습니다. 예를 들어 Korteweg – de Vries 방정식을 참조하십시오.
양자 이론
양자 이론에서는 파장과 장의 개념이 모두 나타난다.
입자가 파동-입자 이중성에 따라 파동 같은 특성을 갖는 양자역학에서 고전 운동 방정식(뉴턴의 법칙, 오일러-라그랑주 방정식, 해밀턴-야코비 방정식 등)의 유사점은 가장 일반적인 형태의 슈뢰딩거 방정식이다.
여기서 δ는 계의 파동함수이고, δ는 고전역학에서와 같은 함수가 아닌 양자 해밀턴 연산자이며, δ는 플랑크 상수를 2로 나눈 값이다.해밀턴을 설정하고 방정식에 삽입하면 파동방정식이 되는데, 그 해답은 시공간 함수로서의 파동함수이다.슈뢰딩거 방정식 자체는 θ가 0이 되는 한계에서 대응 원리를 고려할 때 해밀턴-야코비 방정식으로 감소한다.
양자 이론의 모든 측면, 상대론적이든 비상대론적이든, 양자 시스템의 시간 진화와 행동을 지배하는 슈뢰딩거 방정식을 대체할 수 있는 다양한 공식들이 있습니다. 예를 들어 다음과 같습니다.
- 하이젠베르크 운동 방정식은 위치, 운동량, 시간의 함수로서 고전 관측 가능성의 시간 진화와 유사하다. 만약 동적 관측 가능 요소를 양자 연산자로 대체하고 고전적 포아송 괄호를 정류자로 대체한다면,
- 위상공간 공식은 고전 해밀턴 역학을 밀접하게 따르고, 위치와 운동량을 동등한 토대 위에 놓는다.
- 파인만 경로 적분 공식은 최소 작용의 원리를 양자 역학과 장 이론으로 확장하고, 해밀턴보다는 라그랑지안의 사용에 중점을 둔다.
「 」를 참조해 주세요.
레퍼런스
- ^ 물리학 백과사전 (제2판), R.G. Lerner, G.L. Trigg, VHC출판사, 1991년, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3.
- ^ a b c d 분석 기계학, L.N. Hand, J.D.Finch, 캠브리지 대학 출판부, 2008, ISBN978-0-521-57572-0
- ^ 브리태니커 수학사 가이드 에디션에릭 그레거슨
- ^ 토론, 갈릴레오
- ^ Galileo Galilei, Henry Crew, Alfonso De Salvio 옮김, 두 개의 새로운 과학에 관한 대화
- ^ Halliday, David; Resnick, Robert; Walker, Jearl (2004-06-16). Fundamentals of Physics (7 Sub ed.). Wiley. ISBN 0-471-23231-9.
- ^ a b 다이내믹스와 상대성, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978-0-470-01460-8
- ^ M.R. Spiegel; S. Lipschutz; D. Spellman (2009). Vector Analysis. Schaum's Outlines (2nd ed.). McGraw Hill. p. 33. ISBN 978-0-07-161545-7.
- ^ a b 물리학의 기본 원리, P.M. 윌란, M.J. 호지슨, 제2판, 1978, John Murray, ISBN 0-7195-3382-1
- ^ Hanrahan, Val; Porkess, R (2003). Additional Mathematics for OCR. London: Hodder & Stoughton. p. 219. ISBN 0-340-86960-7.
- ^ Keith Johnson (2001). Physics for you: revised national curriculum edition for GCSE (4th ed.). Nelson Thornes. p. 135. ISBN 978-0-7487-6236-1.
The 5 symbols are remembered by "suvat". Given any three, the other two can be found.
- ^ 3000 해결된 물리학 문제, 샤움 시리즈, A.Halpern, McGraw Hill, 1988, ISBN 978-07-025734-4
- ^ a b 기계개론, D.Kleppner, R.J. Kolenkow, Cambridge University Press, 2010, 페이지 112, ISBN 978-0-521-19821-9
- ^ 물리학 백과사전 (제2판), R.G. Lerner, G.L. Trigg, VHC 출판사, 1991년, ISBN (VHC Inc.) 0-89573-752-3
- ^ "메트릭스, D.Kleppner 2010"
- ^ 상대성, J.R. Forshaw 2009
- ^ 진동과 파동의 물리학 (제3판), H.J. Pain, John Wiley & Sons, 1983, ISBN 0-471-90182-2
- ^ R. Penrose (2007). The Road to Reality. Vintage books. p. 474. ISBN 978-0-679-77631-4.
- ^ a b c 고전역학 (제2판), T.W.B. 키블, 유럽물리학 시리즈, 1973, ISBN 07-084018-0
- ^ 전자기 (제2판), I.S. Grant, W.R. Phillips, Manchester Physical Series, 2008 ISBN 0-471-92712-0
- ^ Classic Mechanics (제2판), T.W.B. Kibble, 유럽물리학 시리즈, McGraw Hill(영국), 1973, ISBN 0-07-084018-0.
- ^ 미스너, 손, 휠러, 중력
- ^ C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (second ed.). p. 1199. ISBN 0-07-051400-3.
- ^ C.B. Parker (1994). McGraw Hill Encyclopaedia of Physics (second ed.). p. 1200. ISBN 0-07-051400-3.
- ^ J.A. Wheeler; C. Misner; K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 34–35. ISBN 0-7167-0344-0.
- ^ H.D. Young; R.A. Freedman (2008). University Physics (12th ed.). Addison-Wesley (Pearson International). ISBN 978-0-321-50130-1.




![M\left[\mathbf {r} (t),\mathbf {\dot {r}} (t),\mathbf {\ddot {r}} (t),t\right]=0\,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/969c32e88d55826a347715bee49544f4ab6bf67a)





![{\begin{aligned}v&=at+v_{0}\quad [1]\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23303f29ae9db96394ef5a6729cf98d6e9204490)
![{\displaystyle {\begin{aligned}r&=r_{0}+v_{0}t+{\tfrac {1}{2}}{a}t^{2}\quad [2]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a36878090f1271c204f7f623fe0eb5aad6c3b6)
![{\displaystyle {\begin{aligned}r&=r_{0}+{\tfrac {1}{2}}\left(v+v_{0}\right)t\quad [3]\\v^{2}&=v_{0}^{2}+2a\left(r-r_{0}\right)\quad [4]\\r&=r_{0}+vt-{\tfrac {1}{2}}{a}t^{2}\quad [5]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee7762dee82fc5e2f6add29cbdd2d77bb6cb8755)
![{\begin{aligned}\mathbf {v} &=\int \mathbf {a} dt=\mathbf {a} t+\mathbf {v} _{0}\,,\quad [1]\\\mathbf {r} &=\int (\mathbf {a} t+\mathbf {v} _{0})dt={\frac {\mathbf {a} t^{2}}{2}}+\mathbf {v} _{0}t+\mathbf {r} _{0}\,,\quad [2]\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b943e1186a0e4294d3d2f438641386b1ec59f57e)
![{\begin{aligned}v&=at+v_{0}\,,\quad [1]\\r&={\frac {{a}t^{2}}{2}}+v_{0}t+r_{0}\,.\quad [2]\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/317afd1fe00ba07fdc220d0970a7a95cbb7fe843)



![r=r_{0}+\left({\frac {v+v_{0}}{2}}\right)t\quad [3]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c8d0cd441e58cf8f118d4e89eaf8462a45fb02a)

![{\begin{aligned}v&=a\left(r-r_{0}\right)\left({\frac {2}{v+v_{0}}}\right)+v_{0}\\v\left(v+v_{0}\right)&=2a\left(r-r_{0}\right)+v_{0}\left(v+v_{0}\right)\\v^{2}+vv_{0}&=2a\left(r-r_{0}\right)+v_{0}v+v_{0}^{2}\\v^{2}&=v_{0}^{2}+2a\left(r-r_{0}\right)\quad [4]\\\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a107aebb7f3c3f6d35b60ea640f45683fc17d48)

![{\begin{aligned}r&={\frac {{a}t^{2}}{2}}+2r-2r_{0}-vt+r_{0}\\0&={\frac {{a}t^{2}}{2}}+r-r_{0}-vt\\r&=r_{0}+vt-{\frac {{a}t^{2}}{2}}\quad [5]\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc1c05223bd1aed6159f553e238d24b506cb1d79)
![{\displaystyle {\begin{aligned}v&=u+at\quad [1]\\s&=ut+{\tfrac {1}{2}}at^{2}\quad [2]\\s&={\tfrac {1}{2}}(u+v)t\quad [3]\\v^{2}&=u^{2}+2as\quad [4]\\s&=vt-{\tfrac {1}{2}}at^{2}\quad [5]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8876516f71a06f98f87c759f9df9f4100b1e7072)

![{\displaystyle {\begin{aligned}\mathbf {v} &=\mathbf {a} t+\mathbf {v} _{0}\quad [1]\\\mathbf {r} &=\mathbf {r} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}\quad [2]\\\mathbf {r} &=\mathbf {r} _{0}+{\tfrac {1}{2}}\left(\mathbf {v} +\mathbf {v} _{0}\right)t\quad [3]\\v^{2}&=v_{0}^{2}+2\mathbf {a} \cdot \left(\mathbf {r} -\mathbf {r} _{0}\right)\quad [4]\\\mathbf {r} &=\mathbf {r} _{0}+\mathbf {v} t-{\tfrac {1}{2}}\mathbf {a} t^{2}\quad [5]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815d0b024bba8777fc1b0bf021175072d692101d)


























![L=L\left[\mathbf {q} (t),\mathbf {\dot {q}} (t),t\right]\,.](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a30f80cbaa05dc7438902e9efb67fbad8ea096c)

![H=H\left[\mathbf {q} (t),\mathbf {p} (t),t\right]\,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/aecc975922b815e9bb266e1e3158865400b860c7)


![S[\mathbf {q} ,t]=\int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)\,dt\,,](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dde602b4562727a396922b4b680ebe4afdc9828)

















