정재파

물리학에서, 정지파라고도 알려진 정재파는 시간에서는 진동하지만 피크 진폭 프로파일이 공간에서는 움직이지 않는 파동이다.공간의 어느 지점에서나 파동 진동의 피크 진폭은 시간에 따라 일정하며, 파동 전체의 다른 지점에서 발생하는 진동은 위상이 일치합니다.진폭의 절대값이 최소인 위치를 노드라고 하고 진폭의 절대값이 최대인 위치를 안티노드라고 합니다.

서 있는 파도는 1831년 마이클 패러데이에 의해 처음 발견되었다.패러데이는 진동하는 ^[1][2]용기에 담긴 액체 표면에서 정상파를 관찰했다.프란츠 멜데는 1860년 경 "스탠딩 웨이브"(독일어: Stheende Welle 또는 Sthehwelle)라는 용어를 만들었고 진동하는 ^[3][4][5][6]현에 대한 그의 고전적인 실험에서 그 현상을 증명했다.

이 현상은 매체가 파동의 움직임과 반대 방향으로 이동하기 때문에 발생할 수도 있고 반대 방향으로 이동하는 두 개의 파동 사이의 간섭으로 인해 정지된 매체에서 발생할 수도 있습니다.정재파의 가장 일반적인 원인은 공진기의 공진 주파수에서 앞뒤로 반사되는 파동 간 간섭으로 공진기 내부에서 정재파가 발생하는 현상이다.

같은 진폭의 파형이 반대 방향으로 이동하는 경우, 평균적으로 에너지의 순 전파는 없습니다.

이동 매체

첫 번째 유형의 예로는, 특정 기상 조건 하에서 산맥의 풍하에서는 대기 중에 파동이 형성된다.그러한 파도는 종종 글라이더 조종사에 의해 이용된다.

물결과 수력 점프는 또한 소금 스트롬과 같은 급류와 조류에서 형성된다.하천류에서 이를 위한 요건은 물의 관성이 초임계 유속(Froude 수: 1.7~4.5, 4.5를 초과하면 정재파가^[7] 발생함)으로 인해 중력을 초과하는 얕은 깊이의 유수로 장애물에 의해 크게 느려지거나 옆으로 밀리지 않는다.서 있는 강물결은 인기 있는 강 서핑 휴식시간입니다.

마주보는 파도

정재파

정지 매질에서의 정재파.빨간색 점은 파동 노드를 나타냅니다. 반대 방향(빨간색과 파란색)으로 이동하는 두 전파의 합으로 나타나는 정재파(검은색)입니다.

정재파의 전기력 벡터(E)와 자력 벡터(H)이다. 현의 정재파 – 기본 모드와 처음 5개의 고조파.

원형막 위의 정재파, 2차원의 정재파의 예.이것이 기본 모드입니다. 중앙에 2개의 노드선이 교차하는 디스크의 고조파 정재파.

제2종류의 예로서 전송로의 정재파는 서로 반대방향으로 전파하는 같은 주파수의 2개의 파형의 중첩에 의해 전류, 전압 또는 전계강도의 분포가 형성되는 파동이다.이 효과는 전송 라인을 따라 고정된 지점에서 일련의 노드(배치량 제로) 및 안티노드(최대배치량)입니다.이러한 정재파는 전송로의 한쪽 끝에 전파되어 다른 쪽 끝에서 임피던스 미스매치, 즉 단선이나 단락 ^[8]등의 불연속성에 의해 반사될 때 형성될 수 있다.정재파 주파수에서 전력을 전달하지 못하면 일반적으로 감쇠 왜곡이 발생합니다.

실제로, 전송 선로와 다른 구성요소의 손실은 완벽한 반사와 순수한 정재파가 결코 달성되지 않는다는 것을 의미합니다.그 결과 정재파와 진행파의 중첩인 부분 정재파가 된다.파형이 순수 정재파 또는 순수 진행파와 유사한 정도는 정재파비(SWR)^[9]로 측정된다.

또 다른 예는 같은 파동 주기가 반대 방향으로 이동하는 파도에 의해 형성된 외양에서의 정재파이다.이들은 폭풍 중심 부근에서 형성되거나 해안의 팽창 반사에 의해 형성될 수 있으며, 미세 막대와 미세 지진의 근원이다.

수학적 설명

이 절에서는 대표적인 1차원 및 2차원 정재파 사례를 살펴본다.첫째, 무한장 문자열의 예는 반대 방향으로 이동하는 동일한 파동이 어떻게 간섭하여 정재파를 발생시키는지를 보여준다.다음으로 경계조건이 다른 두 개의 유한길이 문자열 예는 경계조건이 정상파를 형성할 수 있는 주파수를 어떻게 제한하는지를 보여준다.다음으로, 파이프 내의 음파의 예는 유사한 경계 조건을 가진 세로파에 동일한 원리를 적용할 수 있는 방법을 보여준다.

정재파는 2차원 또는 3차원 공진기에서도 발생할 수 있다.위의 애니메이션에 나타난 드럼헤드 등의 2차원 막에 정재파가 있으면 노드는 결절선이 되고, 움직임이 없는 표면의 선이 되어 반대 상으로 진동하는 영역을 분리한다.이러한 노드라인 패턴은 클라드니 피규어라고 불립니다.악기 사운드 박스나 마이크로파 공동 공진기와 같은 3차원 공진기에는 노드 표면이 있습니다.이 섹션에는 개념을 고차원으로 확장하는 방법을 설명하기 위해 직사각형 경계가 있는 2차원 정재파 예가 포함되어 있습니다.

무한 길이 스트링의 정재파

시작하려면 x축을 따라 Y 방향으로 가로로 자유롭게 늘어나는 무한 길이의 문자열을 고려합니다.

문자열을 따라 오른쪽으로 이동하는 고조파의 경우, 위치 x 및 시간^[10] t의 함수로서 Y 방향으로 문자열의 변위는 다음과 같습니다.

$\displaystyle y_{\text{R}}(x,t)=y_{\text{max}}\sin \leftpi 2\pi x \over \display\da }-\Omega t\right.}$

왼쪽으로 이동하는 동일한 고조파에 대한 y 방향의 변위는 다음과 같습니다.

$(\displaystyle y_{\text{L}}(x,t)=y_{\text{max}}\sin \leftpi 2\pi x \over \signda }+\Omega t\오른쪽)})$

어디에

• y는_max 각 파형에 대한 문자열 변위의 진폭입니다.
• θ는 각 주파수 또는 등가 주파수 f의 2µ배이다.
• θ는 파장의 파장이다.

동일한 끈에서 동일한 우측 및 좌측 이동 파형의 경우, 끈의 총 변위는_L y와 y의_R 합이다.

$\displaystyle y(x,t)=y_{\text{R}}+y_{\text{L}}=y_{\text{max}}\sin \leftparam2\pi x \over \oper \oper \oper \oper \oper \oper \oper \oper \oper \\oper \oper \oper \oper \oper \oper \oper \\oper t\right)+y_y_{\right}).}$

삼각합계 ${\displaystyle \mathrm{항등성}}$ sin${\displaystyle a}$a + ${\displaystyle \sin b}$ b ${\displaystyle =}$ ${\displaystyle 2}$ ${\displaystyle \sin }$ ${\displaystyle (}$ (${\displaystyle \frac{}{}a\frac{}{}}$ + ${\displaystyle \frac{\mathrm{}}{}}$) ${\displaystyle \cos }$ ${\displaystyle (}$ (${\displaystyle \frac{}{}a\frac{}{}}$ - $b$)$$( \$style$ \ $sin$a + \$sin$b$$=$$2 \ $sin$ \$over$ 2$）$ \ $cos \ left sin$ a $- b$\ $over$ 2$\}$ ) ,

$\displaystyle y(x,t)=2y_{\text{max}}\sin \leftflash2\pi x \over \cos(\cosda }\right)\cos(\mega t).}$

(1)

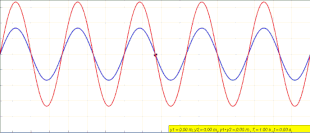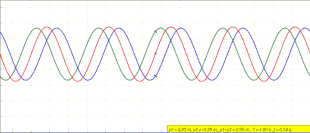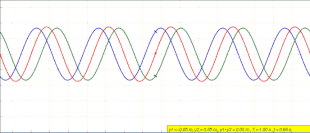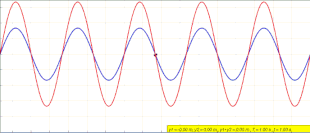
식 (1)은 진행파를 설명하지 않습니다.임의의 위치 x에서 y(x,t)는 ${\displaystyle {\text{2y}}_{}}$ ${\displaystyle \max }$ sin${\displaystyle }$θ (${\displaystyle 2\frac{\mathrm{}}{}}$ ${\displaystyle \frac{\mu }{}}$ x$)\$x \$over \lambda }\right$^[10]로서 x 방향으로 변화하는 진폭으로 시간에 따라 진동합니다.이 기사의 첫머리에 있는 애니메이션은 무슨 일이 일어나고 있는지 묘사하고 있습니다.좌회전하는 푸른 파도와 우회전하는 녹색 파동이 간섭하면서, 그들은 움직이지 않고 제자리에 진동하는 정지하는 붉은 파동을 형성한다.

문자열의 길이는 무한하기 때문에 X축을 따라 어떤 점에서도 변위에 대한 경계 조건이 없습니다.그 결과, 임의의 주파수로 정재파를 형성할 수 있다.

파장의 4분의 1의 배수인 x축 위치에서

$\displaystyle x=\ldots ,-{3\displayda \over 2,\;\displayda \over 2,\;\displayda \over 2,\;\dots }$

진폭은 항상 0입니다.이러한 위치를 노드라고 합니다.1/4 파장의 홀수 배수인 x축 위치에서

${\displaystyle x=\ldots,-{5\displayda \over 4},\;-{\displayda \over 4},\;{3\displayda \over 4},\;{5\dots}$

진폭은 최대이며, 이 정재파 패턴을 생성하기 위해 간섭하는 우파 및 좌파 진폭의 두 배 값이다.이러한 위치를 안티노드라고 합니다.연속된 2개의 노드 또는 안티노드 간의 거리는 파장의 절반인 µ/2입니다.

양끝이 고정된 끈의 정재파

다음으로 끝부분이 x = 0 및 x = L로 고정된 문자열을 고려합니다.현은 이동하는 파도에 의해 늘어나기 때문에 약간의 감쇠가 있지만, 감쇠가 매우 작다고 가정합니다.x = 0 고정 단부에서 일부 주파수 f에서 작은 진폭으로 문자열을 y 방향으로 위아래로 구동하는 사인파 힘이 적용된다고 가정합니다.이 상황에서 구동력은 우측 이동파를 생성합니다.이 파동은 오른쪽 고정단으로부터 반사되어 왼쪽으로 이동하고 왼쪽 고정단으로부터 반사되어 오른쪽으로 되돌아갑니다.최종적으로 무한장 케이스와 같은 좌우 이동파를 가지며, 스트링 내의 감쇠에 의해 방산되는 전력은 구동력에 의해 공급되는 전력과 같아 일정한 진폭을 갖는 정상 상태에 도달한다.

식 (1)은 여전히 이 문자열에 형성될 수 있는 정재파 패턴을 설명하지만, 이제 식 (1)은 문자열이 x = L에 고정되고 고정 x = 0 끝의 구동력이 작다고 가정하기 때문에 x = 0 및 x = L에서 y = 0인 경계 조건을 따릅니다.양 끝의 y 값을 확인하면

${\displaystyle y(0,t)=0,}$

$\displaystyle y(L,t)=2y_{\text{max}}\sin \leftswar2\pi L \over \signda }\right)\cos(\omega t)=0.}$

이 경계 조건은 Sturm-Liouville 공식의 형태이다.후자의 경계조건은 sin${\displaystyle }$θ ( ${\displaystyle 2\frac{\mathrm{}}{}}$ ${\displaystyle \frac{l}{}}$ L${\displaystyle \frac{}{}}$ ) ${\displaystyle =}$ { $displaystyle \sin \left 2$2 \$pi$L \$over \light$ da }$$= 0$$} 이 주어질 때 ${\displaystyle \mathrm{충족}}$되며, 따라서 경계조건은 정재파의^[11] 파장을 다음과 같이 제한한다.

$\displaystyle \displayda = displayfrac {2L}{n}}$

(2)

${\displaystyle n=1,2,3,\ldots}$

파장은 L과의 관계를 만족시키는 파장이 있을 때만 이 스트링에 정재파를 형성할 수 있다. 만약 파장이 스트링을 따라 속도 v로 이동한다면, 정재파의 주파수는 동등하게 제한된다^[11][12].

${\displaystyle f=flac {v}{\flacda}}=flac {flac}{2L}}}.$

n = 1인 정재파는 기본 주파수로 진동하며, 문자열 길이의 두 배인 파장을 가집니다.정수값 n이 클수록 고조파 또는 오버톤이라고 하는 발진 모드에 해당합니다.스트링 상의 모든 정재파에는 고정 엔드 및 n개의 안티노드를 포함한 n개의 +1 노드가 있습니다.

이 예의 노드를 무한 길이 문자열의 정상파에 대한 노드의 설명과 비교하려면 식 (2)를 다음과 같이 다시 쓸 수 있습니다.

$\displaystyle \displayda = displayfrac {4L}{n}},}$

${\displaystyle n=2,4,6,\ldots}$

이 파장 표현식의 변화에서는 n은 짝수여야 합니다.교차 곱셈을 보면 L은 노드이기 때문에 1/4 파장의 짝수 배수임을 알 수 있습니다.

${\displaystyle L=syslogfrac {n\sysda}{4}}$

${\displaystyle n=2,4,6,\ldots}$

이 예는 공명의 유형을 나타내며, 정상파를 생성하는 주파수를 공명 주파수라고 ^[11][13][14]할 수 있습니다.

한쪽 끝이 고정된 끈의 정재파

다음으로 길이 L의 동일한 문자열을 고려하지만 이번에는 x = 0에서만 고정됩니다.x = L에서 문자열은 y 방향으로 자유롭게 이동할 수 있습니다.예를 들어, 끈은 x = L에서 폴 위아래로 자유롭게 미끄러질 수 있는 링에 묶일 수 있다.스트링은 다시 댐핑이 작으며 x = 0의 작은 구동력에 의해 구동됩니다.

이 경우, 식 (1)은 여전히 문자열에 형성될 수 있는 정재파 패턴을 기술하고 있으며 문자열은 x = 0에서 y = 0의 동일한 경계 조건을 가지고 있습니다.그러나 문자열이 자유롭게 이동할 수 있는 x = L에는 최대 진폭 y의 반노드가 있어야 한다.마찬가지로, "자유단"의 경계 조건은 스투름-리우빌 공식의 형태인 x = L에서 δy/θx = 0이라고 할 수 있다.x = L에서 이 경계 조건 θy/θx = 0에 대한 직관은 "자유 끝"의 움직임이 점의 왼쪽의 움직임을 따를 것이라는 것이다.

식 (1) 검토: x = L의 경우, y의 가장 큰 진폭은 µy/µx = 0일 때 발생합니다.

$\displaystyle \cos \leftswar2\pi L \over \displayda }\right)= 0.}$

이것에 의해, 2개의 고정 단자의 예와는 다른 파장의 세트가 발생합니다.여기서 정재파의 파장은 다음과 같이 제한된다.

$\displaystyle \displayda = displayfrac {4L}{n}},}$

${\displaystyle n=1,3,5,\ldots}$

마찬가지로 주파수는 다음과 같이 제한됩니다.

${\displaystyle f=syslogfrac {syslog}{4L}}}.$

이 예에서는 n은 홀수 값만 받습니다.L은 안티노드이기 때문에 1/4 파장의 홀수배수입니다.따라서 이 예의 기본 모드는 완전한 사인 사이클의 1/4(x = 0에서 0, x = L에서 첫 번째 피크)만 가지며, 첫 번째 고조파는 완전한 사인 사이클의 1/4을 갖습니다.

이 예는 또한 공명의 유형을 나타내며, 정상파를 생성하는 주파수를 공명 주파수라고 합니다.

파이프 내 정재파

길이 L의 파이프에 있는 정재파를 생각해 봅시다.파이프 내부의 공기는 파이프를 통해 오른쪽 또는 왼쪽으로 이동하는 세로 방향 음파의 매개체 역할을 합니다.앞의 예에서 본 스트링의 횡파는 파동방향에 수직방향으로 변위하는 반면 파이프 내의 공기를 통과하는 파동은 압력 및 파동방향에 따른 종방향 변위 측면에서 변화한다.파동은 파이프 세그먼트의 공기를 번갈아 압축 및 확장하여 전파되며, 이 파동은 공기를 정지 위치에서 약간 이동시키고 번갈아 가며 가해지는 고압과 저압에 ^[15]의해 가해지는 힘을 통해 인접 세그먼트로 에너지를 전달합니다.파이프내의 좌우 이동파에 의한 압력 δp의 변화에 대해서, 스트링상의 파형과 유사한 방정식을 쓸 수 있다.

$(\displaystyle \Delta p_{\text{R}}(x,t)=p_{\text{max}}\sin \leftparam2\pi x \over \delta }-\obega t\right)})}$

$(\displaystyle \Delta p_{\text{L}}=p_{\text{max}}\sin \leftparam2\pi x \over \delta }+\Omega t\오른쪽)})$

어디에

• p는_max 압력 진폭 또는 각 파동으로 인한 공기 압력의 최대 증가 또는 감소입니다.
• θ는 각 주파수 또는 등가 주파수 f의 2µ배이다.
• θ는 파장의 파장이다.

동일한 우측 및 좌측 이동파가 파이프를 통과할 경우, 그 결과로 발생하는 중첩은 합계로 설명된다.

$(\displaystyle \Delta p(x,t)=\Delta p_{\text{L}}(x,t)=2p_{\text{max}}\sin \sin \displaystyle \delta p(x,t)\cos(\mega t)\cos(t)\cos(t).}$

압력에 대한 이 공식은 식 (1)과 같은 형태이므로 공간에 고정된 고정 압력파가 형성되고 시간에 따라 진동합니다.

파이프의 끝부분이 닫히면 파이프의 닫힌 끝부분이 공기의 이동을 제한하는 힘을 가하기 때문에 압력이 최대가 됩니다.이것은 압력 반절(폐쇄된 끝 근처의 분자는 움직일 수 없기 때문에 분자 운동을 위한 노드)에 해당합니다.파이프의 끝이 열려 있는 경우 압력 노드(열린 끝 근처의 분자가 자유롭게 ^[16][17]움직일 수 있기 때문에 분자 운동을 위한 반노드)에 해당하는 압력 변화는 매우 작습니다.개방단에서의 압력 노드의 정확한 위치는 실제로 파이프의 개방단부를 약간 초과하기 때문에 공진주파수를 결정하기 위한 파이프의 유효 길이는 물리적 ^[18]길이보다 약간 길다.이 예에서는 이 길이의 차이는 무시됩니다.반사의 관점에서, 열린 끝부분은 파동을 부분적으로 파이프 안으로 반사시켜 에너지를 외부 공기로 방출할 수 있게 합니다.폐단은 파동 전체를 반대 방향으로 반사하는 ^[18][19]것이 이상적입니다.

먼저 열린 파이프(예: 열린 기관 파이프 또는 레코더)를 살펴보겠습니다.압력이 양쪽 개방단부에서 0이어야 할 경우 경계조건은 두 개의 고정단부를 가진 끈과 유사하다.

$\displaystyle \Delta p(0,t)=0,}$

$\displaystyle \Delta p(L,t)=2p_{\text{max}\sin \leftpi L \over \delta }\right)\cos(\obega t)=0,}$

정재파의^[18] 파장이 약할 때만 발생한다.

$\displaystyle \displayda = displayfrac {2L}{n}}$

${\displaystyle n=1,2,3,\ldots,}$

또는^[18][20] 주파수가 동일한 경우

${\displaystyle f=syslogfrac {syslog}{2L}},}$

여기서 v는 소리의 속도입니다.

그런 다음 x = 0에서 열리고(따라서 압력 노드가 있음) x = L에서 닫히고(따라서 압력 반노드가 있음) 파이프를 고려합니다.x = L에서의 압력에 대한 닫힌 "자유단" 경계 조건은 스투름-리우빌 공식의 형태인 δ(Ph)/lhbx = 0이라고 할 수 있다.x = L에서 이 경계 조건 δ(Polmp)/lmpx = 0에 대한 직관은 닫힌 끝의 압력이 왼쪽 지점의 압력을 따른다는 것이다.이 설정의 예로는 병과 클라리넷이 있습니다.이 파이프는 고정 끝만 있는 문자열과 유사한 경계 조건을 가집니다.그것의 정파장은 다음과^[18] 같다.

$\displaystyle \displayda = displayfrac {4L}{n}},}$

${\displaystyle n=1,3,5,\ldots,}$

또는 그에 따라 정상파의 주파수는 다음과 같이 제한된다^[21][20].

${\displaystyle f=syslogfrac {syslog}{4L}}}.$

한쪽 끝이 닫혀 있는 경우 n은 한쪽 끝에만 고정된 문자열의 경우와 마찬가지로 홀수 값만 받습니다.

지금까지 파동은 위치 x와 시간의 함수로서 압력의 관점에서 쓰여져 왔다.또, 압력의 변화에 따라 파이프 세그먼트내의 공기가 x방향으로 약간 전후로 이동해, 파동이 한쪽 또는 양쪽 방향으로 이동하는 공기의 세로방향 변위라고 쓸 수 있다.압력 δp 및 종방향 변위 s의 변화는 다음과 같이 관련된다^[22].

${\displaystyle \Delta p=-\rho v^{2}{\frac {\frac s}{\flac x},$

여기서 θ는 공기의 밀도입니다.세로방향 변위면에서는 공기 이동이 제한되기 때문에 파이프의 폐쇄단부는 노드에 대응하고, 공기가 ^[18][23]자유롭게 이동하기 때문에 개방단부는 안티노드에 대응한다.스프링을 ^[24]따라 전파되는 세로파에서도 비슷하고 시각화하기 쉬운 현상이 발생합니다.

양끝이 닫힌 파이프도 고려할 수 있습니다.이 경우 양끝이 압력 안티노드이거나 동등하게 양끝이 변위 노드가 됩니다.이 예는 정재파 패턴의 양끝이 열려 있는 경우와 유사합니다.단, 정재파 패턴은② X방향에 따른 위상 시프트를 통해 노드 위치 시프트 및 안티 디버전스위치 시프트.예를 들어, 공명하는 가장 긴 파장(기본 모드)은 파이프의 두 배 길이입니다. 단, 파이프의 끝에는 압력 노드 대신 압력 반노드가 있습니다.단부 사이에는 압력 노드가 하나 있습니다.두 개의 닫힌 끝의 경우 파장은 다시 다음과 같이 제한됩니다.

$\displaystyle \displayda = displayfrac {2L}{n}}$

${\displaystyle n=1,2,3,\ldots,}$

빈도는 다시 로 제한됩니다.

${\displaystyle f=syslogfrac {syslog}{2L}}}.$

루벤스 튜브는 두 개의 닫힌 ^[25]끝이 있는 튜브에서 정재파의 압력 변동을 시각화할 수 있는 방법을 제공합니다.

직사각형 경계가 있는 2차원 정재파

다음으로 x방향_x 길이 L과 y방향 길이_y L의 직사각형 경계 내에서 2차원 표면을 따라 이동할 수 있는 횡파를 고려한다.이런 유형의 파도의 예로는 수영장 내의 물결이나 팽팽하게 당겨진 직사각형 시트의 물결 등이 있습니다.파동은 표면을 z 방향으로 이동하며, z = 0은 지표면이 정지되어 있을 때 지표면의 높이로 정의됩니다.

2차원 및 데카르트 좌표에서 파동 방정식은 다음과 같습니다.

${\displaystyle {\frac ^{2}z}\;=\c^{2}\frac {\frac x^{2}z}+{\frac {\frac y^{2}}\right}$

어디에

• z(x,y,t)는 표면의 변위이다.
• c는 파도의 속도입니다.

이 미분 방정식을 풀기 위해, 먼저 푸리에 변환에 대해 풀어봅시다.

$\displaystyle Z(x,y,\obega)=\int _{-\infty }^{\infty }z(x,y,t)e^{-i\obega t}dt.}$

파동 방정식의 푸리에 변환을 취하면

${\displaystyle {\frac ^{2}Z}+{\frac {\partial y^{2}Z}=-{\frac {\frac {{2}}{c^{2}}Z(x,y,\obega})}$

이는 주파수가 고유값에 해당하는 고유값 문제이며, 고유값은 주파수별 모드 또는 고유 함수에 해당합니다.구체적으로, 이것은 헬름홀츠 방정식의 한 형태이며 ^[26]변수 분리를 사용하여 풀 수 있습니다.추정하다

$\displaystyle Z=X(x)Y(y)}$

헬름홀츠 방정식을 Z로 나누면

${\displaystyle {1}{X(x)}{\frac {\partial ^{2}X}+{\frac {1}{Y(y)}}{\frac {\frac {{2}}Y}{\partial y^{2}}+{\frac {\frac {\opega ^{2}}{c^{2}}=0.}$

이것은 두 개의 결합된 상미분 방정식으로 이어집니다.x 항은 다음과 같이 정의할 수 있는 x에 대한 상수입니다.

${\displaystyle {1}{X(x)}{\frac {\partial x^{2}}=(ik_{x})^{2}}$

X(x)에 대한 해결,

${\displaystyle X(x)=A_{k_{x}}e^{ik_{x}x}+B_{k_{x}e^{-ik_{x}x}}e^{-ik_{x}x}}}.$

이 x-의존성은 경계 조건에 의해 결정되는 상수_kx A와_kx B와 함께 사인파(Oiler의 공식 호출)이다.마찬가지로, y항은 다음과 같이 정의할 수 있는 y에 대한 상수입니다.

${\displaystyle {1} {Y(y)}} {\frac {\partial ^2}Y}{\partial y^{2}=(ik_{y})^{2}=k_{x}^2}-{\frac {{obega ^{2}}{c^{2}}}$

따라서 이 파동의 분산 관계는

${\displaystyle \obega = c440rt {k_{x}^{2}+k_{y}^{2}}.}$

y항의 미분 방정식을 풀면

${\displaystyle Y(y)=C_{k_{y}}e^{ik_{y}y}+D_{k_{y}e^{-ik_{y}y}e^{-ik_{y}y}y}.}$

이러한 함수를 곱하여 역 푸리에 변환, z(x,y,t)를 적용하면 각 모드가 x,y 및 t에 대한 사인파 함수의 산물인 모드의 중첩입니다.

$\displaystyle z(x,y,t)\sim e^{\pm ik_{x}e^{\pm ik_{y}y}e^{\pm i\obe t}.}$

정확한 사인파 함수를 결정하는 상수는 경계 조건과 초기 조건에 따라 달라집니다.경계 조건이 어떻게 적용되는지 확인하려면 팽팽하게 당겨진 시트와 같은 예를 검토하십시오. 여기서 z(x,y,t)는 직사각형 경계 주위에 모두 0이어야 합니다.x 의존성의 경우 z(x,y,t)는 y와 t의 모든 값에 대해 x = 0과 x = L에서_x 모두 0이 될 수 있는 방식으로 변화해야 합니다.양 끝에 고정된 끈의 1차원 예시와 같이, 이 경계 조건을 만족시키는 사인파 함수는

${\displaystyle \sin {k_{x}x}}$

k가 한정되어 있다_x

${\displaystyle k_{x}=sqfrac {n\pi}{L_{x}}},\quad n=1,2,3,\display}$

마찬가지로, z(x,y,t)의 y의존성은 y = 0과 y_y = L에서 모두 0이어야 하며, 이는 다음과 같이 충족된다.

$\displaystyle \sin {k_{y}y},\display k_{y}=sqfrac {m\pi}{L_{y}},\quad m=1,2,3,\displays}$

파동수를 이러한 값으로 제한하면 공명하는 주파수도 제한됩니다.

${\displaystyle \mega = c\pi {n} {L_{x}\right} {{2}+\left({\frac {m}} {L_{y}}\right)^{2}}.}$

z(x,y,0)와 그 시간 도함수 θ(x,y,0)에 대한 초기 조건이 선택되고 t-의존성이 코사인 함수이면 이 시스템의 정재파는 다음과 같은 형태를 취한다.

${\displaystyle z(x,y,t)=z_{\text{max}\sin\leftfac {n\pi x}{L_{x}}\right}\sin \leftfac {m\pi y}{\displaystyle}\sinL_{y}}\right)\cos \left(\omega t\right).}$

$\displaystyle n=1,2,3,\displays \module m=1,2,3,\displays }$

따라서 이 고정된 직사각형 경계 내의 정재파는 정수 n과 m에 의해 파라미터화된 특정 공진 주파수에서 시간적으로 진동한다.이들은 시간적으로 진동할 때 이동하지 않으며, 공간 변화는 경계 조건을 만족시키기 위해 x-방향과 y방향 모두에서 사인파적입니다.기본 모드인 n = 1 및 m = 1은 직사각형 중앙에 하나의 반노드가 있습니다.다양한 n과 m은 복잡하지만 예측 가능한 직사각형 내부의 노드 및 ^[27]반노드의 2차원 패턴을 제공합니다.

분산 관계에서 볼 때 특정 상황에서는 x 및 y 의존성에 대해 서로 다른 모양을 가지고 있더라도 서로 다른 모드(즉, n과 m의 다른 조합)가 동일한 주파수로 공명할 수 있습니다.예를 들어, 경계가 정사각형인 경우_x, L_y = L, n = 1 및 m = 7, n = 7 및 m = 1, n = 5 및 m = 5 모드 모두 다음과 같이 공진한다.

${\displaystyle \mega = flac {c\pi}{L_{x}}{\sqrt {50}}.}$

θ가 위의 헬름홀츠 방정식의 고유값을 결정한다는 것을 상기하면, 각 주파수에 대응하는 모드의 수는 주파수의 다수와 고유값으로 관련됩니다.

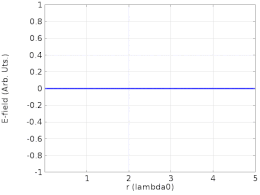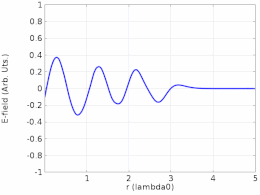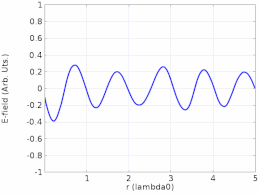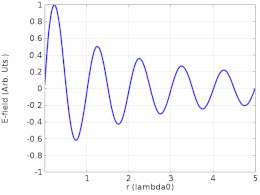
정재파비, 위상 및 에너지 전달

반대 방향으로 움직이는 두 개의 진행파가 동일한 진폭이 아닐 경우, 그것들은 180°의 위상 이탈 지점인 노드에서 완전히 상쇄되지 않으므로 정상파의 진폭이 노드에서 0이 아니라 단지 최소가 된다.정재파비(SWR)는 반노드(최대)에서의 진폭과 노드(최소)에서의 진폭의 비율입니다.순수한 정재파는 SWR이 무한합니다.또한 공간의 모든 지점에 일정한 위상이 있습니다(단, 반주기마다 180° 반전될 수 있습니다).0이 아닌 유한 SWR은 부분적으로 정지하고 부분적으로 이동하는 파형을 나타냅니다.이러한 파형은 이동파 성분과 정지파 성분이라는 두 가지 파형의 중첩으로 분해될 수 있습니다.SWR이 1이면 파형에 정지 성분이 없음을 나타냅니다. 진폭의 비율이 ^[28]1이기 때문에 순수하게 이동 중인 파형입니다.

순수한 정재파는 에너지를 소스에서 ^[29]목적지로 전달하지 않습니다.그러나, 이 파동은 여전히 매질에서 손실될 수 있습니다.이러한 손실은 유한 SWR로 나타나며, 이는 이동파 성분이 손실을 공급하기 위해 소스를 떠난다는 것을 나타냅니다.SWR은 현재 유한하지만 이동 구성요소가 순수하게 손실을 공급하기 때문에 에너지가 목적지에 도달하지 않는 경우가 있습니다.그러나 무손실 매체에서 유한 SWR은 목적지에 대한 에너지의 확실한 전달을 의미합니다.

예

정지된 파도를 이해하기 쉬운 한 가지 예는 두 사람이 줄넘기의 양쪽 끝을 흔드는 것이다.로프가 동시에 흔들리면 로프가 거의 움직이지 않는 정지점(노드)과 로프의 아크가 최대인 점(안티노드)으로 상하로 진동하는 파도의 규칙적인 패턴을 형성할 수 있습니다.

음향 공명

정지파는 현이나 공기 기둥과 같은 물리적 매체에서도 관측된다.매체를 따라 이동하는 모든 파도는 끝에 도달하면 반사됩니다.이러한 효과는 진동 현이나 공기 기둥의 고유 주파수의 다양한 배수로 정상파가 생성되어 고조파를 식별할 수 있는 악기들에서 가장 두드러집니다.노드는 고정 엔드에서 발생하며 안티노드는 오픈 엔드에서 발생합니다.한쪽 끝에만 고정된 경우 홀수 번호의 고조파만 사용할 수 있습니다.파이프의 오픈 엔드에서 안티 노드는 공기와의 접촉에 의해 변경되기 때문에 정확히 엔드에 있지 않기 때문에 엔드 보정이 사용됩니다.문자열의 밀도는 고조파가 생성되는 주파수에 영향을 미칩니다. 밀도가 클수록 주파수는 낮아져야 동일한 고조파의 정상파가 생성됩니다.

가시광선

광도파로나 광공극 등의 광매체에서도 정재파가 관찰된다.레이저에는 파브리-페로 간섭계를 구성하는 한 쌍의 대면 거울 형태의 광학 공동이 사용됩니다.공동 내 이득 매체(예: 결정)는 연속적으로 빛을 방출하고 공동 ^[32]내 빛의 정재파를 들뜨게 합니다.빛의 파장은 매우 짧기 때문에(나노미터, 10미터⁻⁹) 정재파의 크기는 매우 작다.광파를 입상시키는 한 가지 용도는 광학 평면을 사용하여 작은 거리를 측정하는 것입니다.

엑스레이

X선 빔 간의 간섭으로 XSW(^[33]X선 정재파) 필드가 형성될 수 있습니다.X선의 파장이 짧기 때문에(1나노미터 미만) 이 현상은 물질 표면에서 원자 규모의 이벤트를 측정하는 데 이용될 수 있습니다.XSW는 X선 빔이 거의 완벽한 단결정 표면으로부터의 회절 빔 또는 X선 미러로부터의 반사를 간섭하는 영역에서 생성됩니다.결정 지오메트리 또는 X선 파장을 조정함으로써 XSW를 우주공간에서 번역할 수 있으며, 표면 근처의 원자로부터 X선 형광 또는 광전자 수율의 변화를 일으킨다.이러한 변화는 기초 결정 구조나 거울 표면에 상대적인 특정 원자종의 위치를 정확히 파악하기 위해 분석될 수 있다.XSW 방법은 반도체의 ^[34]도판트, ^[35]표면에서의 원자 및 분자 흡착, ^[36]촉매 작용과 관련된 화학적 변환의 원자 규모의 세부 사항을 명확히 하기 위해 사용되어 왔다.

기계파

정재파는 공명을 이용해 고체 매체에 기계적으로 유도할 수 있다.한 가지 이해하기 쉬운 예는 두 사람이 줄넘기의 양쪽 끝을 흔드는 것이다.만약 그것들이 동시에 흔들리면, 로프는 노드나 안티노드와 함께 규칙적인 패턴을 형성하고 정지해 있는 것처럼 보이기 때문에 정재파라는 이름이 붙습니다.마찬가지로 캔틸레버 빔은 베이스 들뜸을 가함으로써 정재파를 가할 수 있다.이 경우 자유단은 빔을 따라 있는 모든 위치에 비해 가장 큰 거리를 가로로 이동합니다.이러한 장치는 파이버의 공명 주파수 또는 위상 변화를 추적하는 센서로 사용할 수 있습니다.하나의 애플리케이션은 치수 도량형 ^[37][38]측정 장치로 사용됩니다.

지진파

지구상의 정지 표면파는 지구의 자유 진동으로 관측된다.

패러데이파

패러데이 파형은 유체역학적 불안정성에 의해 유도되는 공기-액체 계면의 비선형 정재파입니다.마이크로스케일 ^[39]재료를 조립하기 위한 액체 기반 템플릿으로 사용할 수 있습니다.

「 」를 참조해 주세요.

흔든다

일렉트로닉스

메모들

레퍼런스

• Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of Physics (7th ed.). John Wiley & Sons. ISBN 0-471-42959-7.
• Serway, Raymond A.; Faughn, Jerry S. (1992). College Physics (3rd ed.). Saunders College Publishing. ISBN 0-03-076377-0.
• Streets, J. (2010). "Chapter 16 - Superposition and Standing Waves" (PDF). Department of Physics. PHYS122 Fundamentals of Physics II. University of Maryland. Retrieved August 23, 2020.

외부 링크

• Wikimedia Commons의 정재파 관련 매체