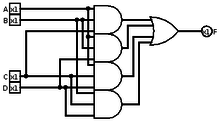
다수 함수
Majority function부울 로직에서 과반수 함수(중위 연산자라고도 함)는 절반 이상의 인수가 false일 때 false로 평가되고 그렇지 않을 경우 true로 평가되는 부울 함수입니다. 즉, 함수의 값은 입력의 과반수 값과 같습니다.참 값을 1로, 거짓 값을 0으로 나타내면 (실제 값) 공식을 사용할 수 있습니다.
공식의 "-1/2"는 인수 n의 수가 짝수일 때 0을 위해 동점을 끊는 역할을 합니다."-1/2"라는 용어를 생략하면, 1을 유리하게 연결 해제하는 함수에 공식을 사용할 수 있습니다.
대부분의 애플리케이션은 입력의 정확히 절반이 0이고 정확히 절반이 1일 때 발생하는 문제에 대처할 필요가 없도록 의도적으로 홀수 개수의 입력을 강제합니다.짝수의 입력에 대해 과반수 함수를 계산하는 소수의 시스템은 종종 "0"에 치우칩니다. 즉, 정확히 절반의 입력이 0일 때 "0"을 생성합니다. 예를 들어, 4입력 과반수 게이트는 [1]입력에 2개 이상의 0이 나타날 때만 출력이 0입니다.일부 시스템에서는 무작위로 [2]동점자가 발생할 수 있습니다.
부울 회로
다수 게이트는 회로의 복잡성 및 부울 회로의 다른 응용 프로그램에서 사용되는 논리 게이트입니다.다수 게이트는 입력의 50% 이상이 참인 경우에만 참을 반환합니다.
예를 들어, 풀 가산기에서 캐리어 출력은 3개의 입력에 과반수 함수를 적용함으로써 구해진다.단, 가산기의 이 부분은 종종 몇 개의 단순한 논리 게이트로 분해된다.
많은 시스템은 트리플 모듈러 용장성을 갖추고 있으며 오류 수정을 구현하기 위해 다수결 로직 디코딩에 다수결 함수를 사용합니다.
회로복잡도의 주요 결과는 대다수의 함수는 지수 이하의 크기의 AC0 회로에 의해 계산될 수 없다고 단언한다.
특성.
임의의 x, y 및 z에 대해 3진수 중앙 연산자 "x, y, z"는 다음 방정식을 만족합니다.
- ⟨x, y, y = y
- ⟨x, y, z = zz, x, y ⟨
- ⟨x, y, z = xx, z, y ⟨
- "x", "w", "y", "w", "z" = "x", "w", "y, w, z"
이것들을 공리로 만족시키는 추상체계는 중앙대수이다.
다수를 위한 단조로운 공식
n = 1의 경우 중위수 연산자는 단항 항등식 연산 x일 뿐입니다.n = 3의 경우 3원 중위수 연산자는 연결 및 분리를 사용하여 xy + yz + zx로 표시할 수 있습니다.이 식은 기호 +가 포함 또는 배타적 또는 배타적으로 해석되는지 여부에 관계없이 동일한 연산을 나타냅니다.
임의의 n의 경우 크기 O(n)의5.3 대다수에 대한 단조 공식이 존재합니다.이는 확률론적 방법을 사용하여 입증된다.따라서 이 공식은 [3]비건설적입니다.
다항식 크기의 대부분에 대한 명시적 공식에 대한 접근법이 존재한다.
- 정렬 네트워크에서 중앙값을 취합니다. 여기서 각 비교 및 스왑 "와이어"는 단순히 OR 게이트와 AND 게이트입니다.AKS(Ajtai-Komlos-Szemerédi) 건설이 그 예입니다.
- 소수점 [4]회로의 출력을 조합합니다.
- 단조로운 [5]공식의 발리안트 증거를 탈단독화하십시오.
메모들
- ^ Peterson, William Wesley; Weldon, E.J. (1972). Error-correcting Codes. MIT Press. ISBN 9780262160391.
- ^ Chaouiya, Claudine; Ourrad, Ouerdia; Lima, Ricardo (July 2013). "Majority Rules with Random Tie-Breaking in Boolean Gene Regulatory Networks". PLOS ONE. Vol. 8, no. 7. Public Library of Science. doi:10.1371/journal.pone.0069626.
- ^ Valiant, Leslie (1984). "Short monotone formulae for the majority function". Journal of Algorithms. 5 (3): 363–366. doi:10.1016/0196-6774(84)90016-6.
- ^ Amano, Kazuyuki (2018). "Depth Two Majority Circuits for Majority and List Expanders". 43rd International Symposium on Mathematical Foundations of Computer Science (MFCS 2018). Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik. 117 (81): 1–13. doi:10.4230/LIPIcs.MFCS.2018.81.
- ^ Hoory, Shlomo; Magen, Avner; Pitassi, Toniann (2006). "Monotone Circuits for the Majority Function". Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques. Lecture Notes in Computer Science. Springer. 4110: 410–425. doi:10.1007/11830924_38. ISBN 978-3-540-38044-3.
레퍼런스
- Knuth, Donald E. (2008). Introduction to combinatorial algorithms and Boolean functions. The Art of Computer Programming. Vol. 4a. Upper Saddle River, NJ: Addison-Wesley. pp. 64–74. ISBN 978-0-321-53496-5.