평균에 대한 회귀

Galton의 실험 설정(그림 8)

통계학에서 평균으로의 회귀(평균으로의 회귀 및 보통으로의 회귀라고도 함)는 랜덤 변수의 한 표본이 극단적일 경우 동일한 랜덤 변수의 다음 표본 추출이 평균에 ^[1]^[2]^[3]더 가까울 수 있다는 사실을 나타내는 개념입니다.또한, 많은 랜덤 변수를 추출하고 가장 극단적인 결과를 의도적으로 추출할 때, 이러한 추출된 변수의 두 번째 표본 추출은 모든 변수의 초기 평균에 가까운 "덜 극단적인" 결과를 낳는다는 사실을 의미한다.

수학적으로 이 "회귀" 효과의 강도는 모든 랜덤 변수가 동일한 분포에서 추출되었는지 여부 또는 각 랜덤 변수에 대한 기본 분포에 진정한 차이가 있는지 여부에 따라 달라집니다.첫 번째 경우에는 "회귀" 효과가 통계적으로 발생할 가능성이 높지만, 두 번째 경우에는 덜 강하거나 전혀 발생하지 않을 수 있다.

따라서 평균에 대한 회귀는 의도적으로 "가장 극단적인" 사건을 선택하는 과학 실험, 데이터 분석 또는 검정을 설계할 때 고려할 수 있는 유용한 개념입니다. 즉, 이러한 사건에 대한 잘못된 결론을 성급히 내리는 것을 피하기 위해 후속 검사가 유용할 수 있습니다. 즉, "진짜" 극단적 사건일 수 있습니다.ly 통계적 잡음으로 인한 무의미한 선택 또는 두 가지 ^[4]사례의 혼합.

개념적인 예

간단한 예: 시험을 보는 학생

한 과목에 대해 100개 항목의 참/거짓 시험을 치르는 한 반의 학생들을 생각해 보세요.모든 학생이 모든 문제에 대해 랜덤으로 선택한다고 가정합니다.그런 다음 각 학생의 점수는 기대 평균이 50인 독립적이고 동일한 분포의 랜덤 변수 집합 중 하나를 실현하는 것입니다.자연히, 어떤 학생들은 50점 이상, 어떤 학생들은 50점 미만 점수를 우연히 받게 될 것이다.상위 10%의 학생들만 선택하고 그들이 다시 모든 항목에서 랜덤으로 선택하는 두 번째 시험을 치른다면, 평균 점수는 다시 50에 가까울 것으로 예상된다.따라서 이 학생들의 평균은 원래 시험을 치른 모든 학생들의 평균으로 "후퇴"할 것이다.학생이 원래 시험에서 어떤 점수를 받든, 두 번째 시험에서 가장 좋은 점수는 50점이다.

시험 문제의 답을 무작위로 고르는 것이 아니라면(예: 학생들이 제공한 답안에 행운(좋은지 나쁜지) 또는 무작위 추측이 포함되지 않은 경우), 모든 학생이 두 번째 테스트에서 원래 테스트에서 채점한 것과 동일한 점수를 받을 것으로 예상되며 평균으로 회귀하는 일은 없습니다.

대부분의 현실적인 상황은 이 두 가지 극단 사이에 있다: 예를 들어, 사람들은 시험 점수를 기술과 행운의 조합으로 생각할 수 있다.이 경우, 평균 이상의 점수를 받은 학생들은 숙련되고 특별히 운이 좋지 않은 학생들과 비숙련되었지만 매우 운이 좋은 학생들로 구성될 것이다.이 서브셋의 재테스트에서, 숙련되지 않은 사람들은 그들의 행운이 반복되지 않을 것이고, 숙련되지 않은 사람들은 불운을 겪을 두 번째 기회를 갖게 될 것이다.따라서 원본을 복제할 수 없더라도 이전에 잘했던 사람들은 2차 시험에서 잘하지 못할 것이다.

다음은 이 두 번째 유형의 평균 회귀 분석의 예입니다.한 반의 학생들이 이틀 연속으로 같은 시험의 두 판을 치른다.첫날 성적이 나쁜 사람은 둘째 날에 점수가 오르고, 첫날 성적이 좋은 사람은 둘째 날에 점수가 떨어지는 경향이 종종 관찰되어 왔다.이러한 현상은 학생들의 점수가 부분적으로 기초적인 능력에 의해 결정되고 부분적으로 우연에 의해 결정되기 때문에 발생한다.첫 번째 시험은 운이 좋고 능력보다 점수가 높은 사람도 있고, 운이 나쁘고 능력보다 점수가 낮은 사람도 있을 것이다.첫 번째 시험에서 운이 좋은 학생들 중 일부는 두 번째 시험에서 다시 운이 좋겠지만, 그들 중 더 많은 학생들은 평균 이하의 점수를 받을 것이다.따라서, 첫 번째 시험에서 운이 좋고 그들의 능력을 과시한 학생은 더 나은 점수보다 두 번째 시험에서 더 나쁜 점수를 받을 가능성이 높다.이와 유사하게, 첫 번째 시험에서 운 나쁘게 능력보다 낮은 점수를 받은 학생들은 두 번째 시험에서 점수가 오르는 경향이 있다.극단적인 사건을 만들어내는 행운의 영향이 클수록, 그 행운이 여러 사건에서 반복될 가능성은 낮아진다.

기타 예

만약 당신이 가장 좋아하는 스포츠 팀이 작년에 우승했다면, 그것은 그들이 다음 시즌에 우승할 가능성에 대해 무엇을 의미할까요?실력(팀 컨디션, 최고 감독 등) 때문인 만큼 내년에도 우승할 가능성이 높다는 신호다.그러나 이것이 행운(약물 스캔들에 휘말린 다른 팀들, 유리한 무승부, 드래프트 선발이 생산적인 것으로 판명된 것 등)에 기인하는 정도가 클수록,^[5] 그들은 내년에 다시 우승할 가능성이 낮아진다.

실적이 변하지 않은 근본적인 이유에도 불구하고, 기업 조직이 매우 수익성이 높은 분기를 가지고 있다면, 다음 ^[6]분기에는 실적이 더 나빠질 가능성이 높습니다.

신인 시즌에 잘 친 야구 선수들은 두 번째인 "소포모어 슬럼프"를 더 잘 할 것 같다.마찬가지로, 평균에 대한 회귀는 스포츠 일러스트레이티드 표지 징크스에 대한 설명입니다. 표지 특징의 결과로 이어지는 특별한 성과 기간에는 더 평범한 성과 기간이 뒤따를 가능성이 높으며, 표지에 나오는 것이 선수의 쇠락을 ^[7]야기한다는 인상을 줍니다.

역사

검출

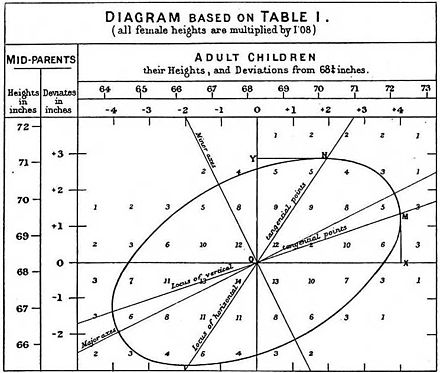
프랜시스 갈튼의 1886년 성인 키와 부모 ^[8]키 사이의 상관관계에 대한 삽화.성인 자녀의 키가 부모보다 평균 키에서 덜 벗어나는 경향이 있다는 관찰은 "평균으로의 회귀"라는 개념을 제시하여 회귀 분석이라는 이름을 얻었다.

퇴행의 개념은 유전학에서 유래했고 19세기 후반 프랜시스 골튼 경이 유전적인 ^[8]지위에서 평범함을 향한 퇴행의 출판을 발표하면서 대중화 되었다.Galton은 부모의 극단적인 특성(예: 키)이 자식에게 완전히 전달되지 않는다는 것을 관찰했다.오히려, 자손의 특성은 평범한 점(그 후 평균으로 식별된 점)으로 퇴보한다.그는 수백 명의 키를 측정함으로써 평균에 대한 회귀를 정량화하고 효과의 크기를 추정할 수 있었다.Galton은 "자녀들의 평균 퇴행은 각각의 중간 부모 편차의 일정한 부분"이라고 썼다.이것은 어떤 특징에 대한 자녀와 부모 사이의 차이가 모집단의 전형적인 사람들로부터의 부모로부터의 편차에 비례한다는 것을 의미한다.만약 그것의 부모가 각각 남성과 여성의 평균보다 2인치 더 크다면, 평균적으로, 그 자손은 부모보다 어떤 요인(오늘날 우리는 1에서 퇴행계수를 뺀 값이라고 부른다)에 의해 2인치씩 더 작을 것이다.Galton은 이 계수를 약 2/3로 추정했다. 즉, 개인의 키는 부모 평균으로부터의 편차의 3분의 2에 해당하는 중간점 부근에서 측정될 것이다.

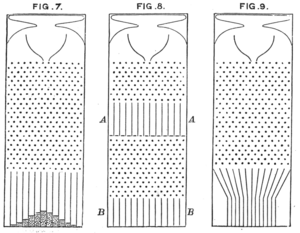
Galton은 또한 입구점 바로 아래에 있는 정규 분포를 형성하기 위해 quincunks에 떨어지는 펠릿의 간단한 예를 사용하여 이러한 결과를^[9] 발표했다.그런 다음 이러한 알갱이는 두 번째 측정에 해당하는 두 번째 갤러리로 방출될 수 있습니다.그리고 나서 Galton은 반대의 질문을 했다: "이 알갱이들은 어디서 왔니?"

그 대답은 '평균 바로 위'가 아니었다.오히려 '평균적으로, 더 가운데쪽으로'는 단순한 이유로, 안쪽으로 ^[10]이동할 수 있는 왼쪽 극단보다 가운데쪽으로 이동할 수 있는 더 많은 알갱이들이 있었다.

용어의 진화하는 사용법

Galton은 다인자 정량적 유전 형질을 유전하는 데 있어 관찰 가능한 사실을 설명하기 위해 "회귀"라는 용어를 만들었다. 즉, 분포의 꼬리에 놓여 있는 부모의 자녀 형질은 종종 분포의 중심인 평균에 더 가까운 경향이 있다는 것이다.그는 이 추세를 계량화했고, 이를 통해 선형 회귀 분석을 발명하여 현대 통계 모델링의 토대를 마련했다.그 이후로, "회귀"라는 용어는 다른 맥락에서 사용되었고, 현대 통계학자들이 유전학 분야에서 골튼의 원래 관찰과는 거의 관련이 없는 표본 편중과 같은 현상을 설명하기 위해 사용될 수 있다.

생물학에서 관찰한 퇴행 현상에 대한 갈튼의 설명은 다음과 같다: "자녀는 부모로부터 부분적으로, 그의 조상으로부터 물려받는다.일반적으로 말하면, 그의 계보가 더 거슬러 올라갈수록, 그의 조상은 더 많아지고 다양해질 것이다.그것은 ^[8]종족 전체로부터 무작위로 채취한 같은 수의 표본과 더 이상 다르지 않을 때까지."Galton의 진술은 유전학에 대한 지식을 고려하여 몇 가지 해명이 필요합니다.아이들은 부모로부터 유전 물질을 받지만, 초기 조상들로부터 물려받은 유전 정보(예: 유전된 특성의 가치)는 부모를 통해 전달될 수 있다(그리고 부모에게 표현되지 않았을 수도 있다).특성의 평균은 랜덤하지 않고 선택 압력에 의해 결정될 수 있지만 평균 주위의 값 분포는 정규 통계 분포를 반영합니다.

Galton에 의해 연구된 모집단 유전 현상은 "평균으로 회귀"하는 특별한 경우이다. 이 용어는 데이터가 평균 주위에 정규 분포를 보이는 많은 통계적 현상을 설명하는 데 종종 사용된다.

중요성

평균에 대한 회귀는 실험 설계에서 중요한 고려 사항입니다.

비슷한 나이의 1,000명의 사람들이 심장 마비를 겪을 위험에 대해 검사받고 점수를 매긴 가정적인 예를 들어보자.통계는 가장 위험성이 큰 것으로 평가된 50명에 대한 개입의 성공 여부를 측정하기 위해 사용될 수 있다.그 개입은 식단, 운동 또는 약물 치료의 변화일 수 있다.개입이 무의미하더라도 평균으로 회귀하기 때문에 검사 그룹은 다음 신체 검사에서 개선을 보일 것으로 기대됩니다.이 효과를 퇴치하는 가장 좋은 방법은 무작위로 그룹을 치료를 받는 치료 그룹과 받지 않는 그룹으로 나누는 것입니다.그러면 치료 그룹이 치료되지 않은 그룹보다 더 나은 경우에만 치료법이 효과적이라고 판단됩니다.

대안으로, 소외된 아이들 집단은 가장 잠재력이 있는 아이들을 식별하기 위해 테스트를 받을 수 있다.상위 1%는 특별 농축 과정, 과외, 상담 및 컴퓨터를 식별하여 제공할 수 있다.비록 이 프로그램이 효과적이라고 해도, 1년 후에 시험을 반복할 때 그들의 평균 점수는 더 낮을 수 있다.하지만, 이러한 상황에서, 특별한 요구가 무시되는 불우한 어린이들로 구성된 통제 그룹을 갖는 것은 비윤리적인 것으로 여겨질 수 있다.수축에 대한 수학적 계산은 이 효과를 조정할 수 있지만 관리 그룹 방법만큼 신뢰할 수는 없습니다(Stein의 예 참조).

그 효과는 또한 일반적인 추론 및 추정에 이용될 수 있다.오늘 전국에서 가장 더운 곳은 내일이 오늘보다 더 서늘할 것 같습니다.지난 3년간 실적이 가장 좋았던 뮤추얼펀드는 향후 3년간 개선보다는 상대적 성과가 감소할 가능성이 높다.올해 가장 성공한 할리우드 배우는 다음 영화에서 더 많은 돈을 벌지 못할 것이다.올스타 브레이크에 의해 가장 높은 타율을 기록한 야구 선수는 시즌 후반기에 더 높은 평균보다 낮은 타율을 가질 가능성이 높다.

오해

평균으로 회귀하는 개념은 매우 쉽게 오용될 수 있다.

위의 학생 테스트 예에서는 두 측정 간에 측정 대상이 변경되지 않았다고 암묵적으로 가정했습니다.그러나 과정이 합격/불합격이고 학생들이 두 테스트에서 모두 70점 이상을 받아야 합격할 수 있다고 가정합니다.그러면 첫 번째 70점 이하의 점수를 받은 학생들은 잘 할 동기가 없을 것이고, 두 번째에는 평균 점수가 더 나빠질 수도 있다.반면 70세가 조금 넘은 학생들은 시험을 보는 동안 공부하고 집중하려는 강한 동기를 갖게 될 것이다.이 경우 70점 이하가 낮아지고 그 이상도 높아집니다.측정 시간 사이의 변화는 평균으로 회귀하는 통계적 경향을 증가시키거나 상쇄하거나 반전시킬 수 있습니다.

평균에 대한 통계적 회귀는 인과적 현상이 아닙니다.첫날 시험에서 가장 낮은 점수를 받은 학생은 그 영향으로 인해 둘째 날에 반드시 점수가 크게 오르지는 않을 것이다.평균적으로, 가장 나쁜 점수를 받은 사람들은 향상되지만, 그것은 가장 나쁜 점수를 받은 사람들이 운이 좋았다기보다는 운이 나빴을 가능성이 높기 때문이다.점수가 무작위로 결정되거나, 점수가 학생의 학업 능력이나 "진정한 가치"로 결정되는 것이 아니라 무작위 변동이나 오차가 있는 한, 그 현상은 영향을 미칠 것이다.이런 점에서 전형적인 실수는 교육에 있었다.좋은 일에 대해 칭찬을 받은 학생들은 다음 측정에서 더 잘하지 못하는 것으로 보여졌고, 나쁜 작업으로 벌을 받은 학생들은 다음 측정에서 더 잘 하는 것으로 보여졌습니다.교육자들은 칭찬을 중단하고 이를 근거로 ^[11]계속 벌을 주기로 결정했다.평균으로의 회귀는 원인과 결과를 기반으로 하는 것이 아니라 평균 주위의 자연 분포에서 랜덤 오차를 기반으로 하기 때문에 이러한 결정은 실수였습니다.

극단적 개별 측정값이 평균으로 회귀하지만 두 번째 측정 표본은 첫 번째 표본보다 평균에 더 가깝지 않습니다.학생들을 다시 생각해 보세요.극단적 개인의 성향이 평균 80을 향해 10% 퇴보한다고 가정하면 첫날 100점을 받은 학생은 둘째 날에 98점을 받고 첫날 70점을 받은 학생은 둘째 날에 71점을 받을 것으로 예상됩니다.이러한 기대는 첫날 점수보다 평균에 가깝다.그러나 둘째 날의 점수는 그들의 기대치에 따라 달라질 것이다; 어떤 것은 더 높고 어떤 것은 더 낮을 것이다.또한 평균에 매우 가깝게 측정하는 개인은 평균에서 멀어질 것으로 예상해야 합니다.효과는 평균에 대한 회귀의 정반대이며, 이를 정확히 상쇄합니다.따라서 극단적 개인의 경우 두 번째 점수가 첫 번째 점수보다 평균에 더 가까울 것으로 예상하지만 모든 개인의 경우 두 측정 집합에서 평균으로부터의 거리 분포가 동일할 것으로 예상합니다.

위의 점과 관련하여 평균에 대한 회귀는 양방향에서 동일하게 잘 작동합니다.우리는 둘째 날에 가장 높은 시험 점수를 받은 학생이 첫째 날에 더 나빴을 것으로 예상한다.그리고 첫째 날 가장 우수한 학생과 둘째 날 가장 우수한 학생을 비교해보면, 같은 사람이든 아니든 간에, 어느 쪽으로든 평균으로 퇴보하는 경향이 있습니다.우리는 두 날의 최고 점수가 평균과 동등하게 멀 것으로 예상한다.

회귀 오류

평균에 대한 회귀 분석을 고려하지 않을 경우 많은 현상이 잘못된 원인에 기인하는 경향이 있습니다.

1933년 출간된 호레이스 세크리스트의 저서 '비즈니스에서의 평범함의 승리'는 통계학 교수가 산더미 같은 자료를 수집해 경쟁력 있는 기업의 수익률이 시간이 지남에 따라 평균에 가까워진다는 것을 증명하는 극단적인 사례다.실제로 이러한 효과는 없다. 수익률의 변동성은 시간이 지남에 따라 거의 일정하다.Secrist는 평균에 대한 일반적인 회귀만을 설명했습니다.화가 난 비평가 해롤드 호텔링은 이 책을 "코끼리들을 열과 열로 배열하고, 그 다음에 수많은 ^[12]다른 동물들에게 같은 일을 함으로써 구구단을 증명하는 것"에 비유했다.

매사추세츠의 표준화된 교육 시험에서 "향상 점수"의 계산과 해석은 아마도 회귀 ^{[citation needed]}오류의 또 다른 예를 제공할 것이다.1999년에 학교에는 개선 목표가 주어졌다.교육부는 각 학교에 대해 1999년과 2000년에 학생들이 달성한 평균 점수 차이를 표로 작성했다.교육부가 정책의 건전성을 확인하는 것으로 받아들인 최악의 학교들은 대부분 목표를 달성했다는 것이 금방 드러났다.하지만, 브룩라인 고등학교와 같이 영연방에서 가장 우수하다고 여겨지는 학교들 중 많은 수가 낙제했다고 또한 지적되었다.통계 및 공공정책과 관련된 많은 사례와 마찬가지로, 이 문제는 논의되고 있지만, "개선점수"는 그 후 몇 년 동안 발표되지 않았고, 그 결과는 평균으로 퇴보한 사례로 보인다.

2002년 노벨 경제학상 수상자인 심리학자 대니얼 카네만은 비난이 성과를 향상시키는 것처럼 보이는 반면 칭찬은 ^[13]역효과를 내는 것처럼 보이는 이유를 평균으로 회귀하는 것이 설명할 수 있다고 지적했다.

나는 비행 교관들에게 기술 습득을 촉진하는 것에 대한 처벌보다 칭찬이 더 효과적이라는 것을 가르치면서 내 경력 중 가장 만족스러운 경험을 했다.열정적인 연설을 마치자 청중 중 가장 노련한 교관 중 한 명이 손을 들어 자신의 짧은 연설을 했다.그것은 긍정적인 강화가 새들에게 좋을지도 모른다는 것을 인정하는 것으로 시작되었지만, 그것은 비행 생도들에게 최적이라는 것을 부정했다.그는 "나는 여러 번 비행 생도들이 곡예 비행을 깔끔하게 수행했다고 칭찬해 왔다. 그리고 일반적으로 그들이 다시 시도하면, 그들은 더 잘하지 못한다"고 말했다.반면에, 저는 종종 생도들에게 나쁜 처신을 한다고 소리쳤는데, 일반적으로 그들은 다음 번에 더 잘합니다.따라서 강화가 효과가 있고 처벌이 효과가 없다고는 말하지 말아주세요.왜냐하면 그 반대이기 때문입니다.이것은 제가 세상에 대한 중요한 진실을 이해한 기쁜 순간이었습니다. 왜냐하면 우리는 다른 사람이 잘하면 보상하고 잘못하면 벌을 주는 경향이 있고, 비열하게 퇴보하는 경향이 있기 때문입니다. 통계적으로 다른 사람에게 보상하면 벌을 받고, 그들을 벌하면 보상을 받는 것은 인간의 조건의 일부이기 때문입니다.저는 즉시 참가자 한 명 한 명이 피드백 없이 자신의 등 뒤에 있는 목표물을 향해 동전 두 개를 던지는 데모를 준비했습니다.목표물과의 거리를 측정하여 첫 번째 시도에서 가장 잘했던 사람들이 두 번째 시도에서 대부분 악화되었고 그 반대도 마찬가지라는 것을 알 수 있었습니다.그러나 나는 이 시위가 평생 동안 비뚤어진 사고에 노출되는 결과를 되돌릴 수 없다는 것을 알고 있었다.

회귀 오류는 롤프 도벨리의 '명확하게 생각하는 기술'에도 설명되어 있다.

영국의 법 집행 정책은 사고 블랙스팟에 정적 또는 이동식 과속 단속 카메라를 가시적으로 설치하는 것을 장려하고 있다.카메라 설치 후 심각한 도로교통사고가 그만큼 줄어든다는 인식에서 정당화됐다.그러나 통계학자들은 구조된 생명에는 순편익이 있지만, 평균 결과에 대한 회귀의 영향을 고려하지 않아 유익성이 ^[14]^[15]^[16]과대포장된다고 지적했다.

통계 분석가들은 스포츠에서 평균으로 회귀하는 효과를 오랫동안 인식해왔다; 그들은 심지어 "소포모어 슬럼프"라는 특별한 이름을 가지고 있다.예를 들어, NBA 덴버 너기츠의 카멜로 앤서니는 2004년에 뛰어난 신인 시즌을 보냈다.2005년 앤서니는 신인 시절부터 숫자가 줄었다.스포츠는 적응과 역조정에 의존하기 때문에 '소포모어 슬럼프'의 원인은 무궁무진하다.스포츠 성적의 평균으로 회귀하는 것은 명백한 "스포츠 일러스트레이티드 커버 징크스"와 "매든 저주"를 설명할 수도 있다.존 홀링거는 평균으로 회귀하는 현상에 대한 대체적인 이름인 "유행 규칙"^{[citation needed]}을 가지고 있는 반면, 빌 제임스는 그것을 "플렉시글라스 원리"^{[citation needed]}라고 부른다.

한 시즌에서 다음 시즌까지 선수들의 경기력 저하를 설명하기 위해 평균으로 회귀하는 것에 대한 통념이 집중되어 왔기 때문에, 그러한 퇴보 또한 경기력 향상의 원인이 될 수 있다는 사실을 간과해 왔다.예를 들어 메이저리그 선수들의 한 시즌 타율을 보면 타율이 평균보다 높았던 선수는 이듬해 평균으로 후퇴하는 반면 평균보다 낮았던 선수는 이듬해 평균으로 ^[17]상승하는 경향이 있다.

기타 통계현상

평균에 대한 회귀 분석에서는 극단적 랜덤 사건에 이어 다음 랜덤 사건도 덜 극단적일 수 있음을 나타냅니다.미래의 사건은 도박꾼의 오류(및 평균의 변종 법칙)에서 가정되지만, 결코 이전 사건을 "보상"하거나 "균등하게" 하지 않는다.마찬가지로, 대수의 법칙은 장기적으로 평균이 기대치를 향할 것이라고 명시하지만 개별 시행에 대해서는 언급하지 않습니다.예를 들어, 페어코인(희귀하고 극단적인 사건)을 10번 돌린 후, 평균으로 회귀하면 다음 번 돌기는 10번 미만일 가능성이 높은 반면, 큰 숫자의 법칙은 장기적으로 이 사건이 평균화될 가능성이 높고, 평균 돌기의 비율은 1/2가 되는 경향이 있습니다.이와는 대조적으로, 도박꾼의 오류는 동전이 이제 균형을 잡기 위해 "유효"하다고 잘못 가정합니다.

반대 효과는 무한대로 향하는 소멸되지 않는 확률 밀도를 가진 분포에서 발생하는 꼬리에 대한 회귀입니다.

데이터 점의 단순 선형 회귀를 위한 정의

이것은 Francis Galton경의 원래 ^[8]용법에 근접하게 따르는 평균으로의 회귀의 정의이다.

데이터 점 {y_i, x_i}이(가) n개 있다고 가정합니다. 여기서 i = 1, 2, ..., n. 회귀선의 방정식, 즉 직선을 구하려고 합니다.

y=\alpha +\display x,,

데이터 포인트에 "최적의" 적합성을 제공합니다.(직선은 특정 데이터 점에 대해 적절한 회귀 곡선이 아닐 수 있습니다.)여기서 "최고"는 선형 회귀 모형의 잔차 제곱 합계를 최소화하는 선과 같은 최소 제곱 접근법과 같습니다.즉, 숫자α와 β는 다음과 같은 최소화 문제를 해결한다.

\min _{\alpha ,\,\beta }Q(\alpha ,\beta )

\min _{\alpha ,\,\beta }Q(\alpha ,\beta )

\min _{\alpha ,\,\beta }Q(\alpha ,\beta )

Q (

\min _{\alpha ,\,\beta }Q(\alpha ,\beta )

β

)

\

displaystyle \min

_

{\alpha,\display }Q(\alpha,\display)}

를 구합니다.

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

서 Q

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

)

\min _{\alpha ,\,\beta }Q(\alpha ,\beta )

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

n

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

(

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

-

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

-

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

x

Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1}^{n}(y_{i}-\alpha -\beta x_{i})^{2}\

= 2 {\

displaystyle

Q(alpha, \

sum

=

2 =

\ sum } _ sum ) _ sum)

^{2}\ }

미적분을 사용하면 목적 함수 Q를 최소화하는 α와 β의 값이 다음과 같은 것을 알 수 있다.

{\displaystyle{\begin{정렬}&.{\hat{\beta}}=ᆮ^ᆯ(x_{나는}-{\bar{x}})(y_{나는}-{\bar{y}})}{\sum_{i=1}(x_{나는}-{\bar{x}})^{2}}}={\frac{{\overline{xy}}-{\bar{)}}{\bar{y}}}{{\overline{x^{2}}}-{\bar{)}}^{2}}}={\frac{\operatorname{Cov}[x, y]}{\operatorname{바르}[)]}}=r_{xy}{\frac{s_{y}}{s_{)}}},\\&,{\hat{\alpha}}){\bar{.y}-{\hat {\bar {x}},\end {aligned}}

여기서_xy r은 x와 y 사이의 표본 상관 계수, s는_x x의 표준 편차, s는_y y의 표준 편차입니다.변수 위의 수평 막대는 해당 변수의 표본 평균을 의미합니다. ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ : x ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ i ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ . ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ { $displaystyle$ { $overline {xy$ } = $tfrac {1}$ { $n}$ \ $textstyle _$ { i ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ = $1$ }^{ $n} x$ _ { $i} y$ _ { i } \ ${\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .$ }

위의 식을 α $^$ { $displaystyle$ ${\hat {\beta }}$ {\ $hat }$ ${\hat {\beta }}$ β ${\hat {\beta }}$ ^ { $displaystyle$ {\hat $}$ 을 ${\hat {\alpha }}$ ${\hat {\beta }}$ $y=\alpha +\beta x,\,$ (를) $y=\alpha +\beta x,\,$ $=$ x로 대체하면 $적합치가 생성$ 됩니다.

(*displaystyle {hat {y}}=***********************************)

그 결과

{{\hat {y}-{\bar {y}}=r_{xy}{\frac {x-{\bar {x}}}{s_{x}}

이는 표준화된 데이터 점의 회귀선에서 r이 수행하는 역할을_xy 나타냅니다.

-1 < r_xy < 1이면 데이터 점이 평균에 대한 회귀를 나타낸다고 할 수 있습니다.즉, 선형 회귀 분석이 표본 상관 계수가 완전하지 않은 데이터 점 집합에 적합한 모형이면 평균에 대한 회귀가 있습니다.예측(또는 적합) 표준화 값 y는 표준화 값 x의 평균보다 평균에 더 가깝습니다.

주변 분포가 동일한 이변량 분포에 대한 정의

제한적 정의

X, X가₂ 평균 μ를 갖는 동일한 주변 분포를 갖는 랜덤 변수라고₁ 가정합니다.이 공식화에서, X와₂ X의₁ 이변량 분포는 만약, 모든 숫자 c > μ에 대하여, 우리가 다음을 가질 경우, 평균에 대한 회귀를 나타낸다고 한다.

μ µ E[X₂₁ X = c] < c,

역부등식이 c < ^[19]^[20]μ일 때 유지된다.

다음은 위의 정의에 대한 비공식적인 설명입니다.위젯 집단을 고려합니다.각 위젯에는 X와₂ X(왼쪽 스팬(X₁)과 오른쪽 스팬₂(X))의₁ 2개의 숫자가 있습니다.모집단에서 X와₂ X의 확률₁ 분포가 동일하고 X와₂ X의 평균이₁ 모두 μ라고 가정합니다.여기서 모집단에서 랜덤 위젯을 가져와 X 값을₁ c로 나타냅니다(c는 μ보다 크거나 같거나 작을 수 있습니다).이 위젯의 X 값은₂ 아직 액세스할 수 없습니다.d는 이 특정 위젯의 예상 X 값을₂ 나타냅니다.(즉, d는 X=c인₁ 모집단에 있는 모든 위젯의 평균₂ X 값을 나타냅니다.)다음 조건에 해당하는 경우:

값 c가 무엇이든 d는 μ와 c 사이에 있다(즉, d는 c보다 μ에 가깝다.

그러면 X와₂ X가 평균에 대한 퇴행을 나타낸다고₁ 할 수 있습니다.

이 정의는 "평균으로 회귀"라는 용어의 골턴의 원래 용법에서 발전한 현재의 일반적인 용법과 밀접하게 일치합니다.한계 분포가 동일한 모든 이변량 분포가 평균에 대한 회귀를 ^[20]나타내지 않는다는 점에서 "제한적"입니다.

정리

랜덤 변수의 쌍(X, Y)이 이변량 정규 분포를 따르는 경우 조건부 평균 E(Y X)는 X의 선형 함수입니다.X와 Y 사이의 상관 계수 r과 X와 Y의 한계 평균 및 분산에 따라 다음과 같은 선형 관계가 결정됩니다.

{E(Y\mid X)-E[Y]}{\sigma _{y}}=r4 frac {X-E[X]}{\sigma _{x}}

여기서 E[X]와 E[Y]는 각각 X와 Y의 기대치이고 θ와_x θ는_y 각각 X와 Y의 표준 편차이다.

따라서 X가 평균보다 t 표준 편차(그리고 t < 0일 때 평균보다 낮은 경우 포함)인 경우 Y의 조건부 기대치는 Y의 평균보다 rt 표준 편차입니다.r ^[21]1 1이므로 Y는 표준 편차의 수로 측정된 X보다 평균에서 멀리 있지 않습니다.

따라서 0µr < 1이면 (X, Y)는 (이 정의에 따라) 평균에 대한 회귀를 나타냅니다.

일반적인 정의

Samuels는 위의 ^[19]평균에 대한 회귀의 보다 제한적인 정의에 대한 대안으로 평균에 대한 회귀에 대한 다음과 같은 정의를 제안했다.

X, X가₂ 평균 μ를 갖는 동일한 주변 분포를 갖는 랜덤 변수라고₁ 가정합니다.이 공식화에서, X와₂ X의₁ 이변량 분포는 만약, 모든 숫자 c에 대하여, 우리가 다음을 가지고 있다면, 평균을 향해 역행하는 것을 나타낸다고 한다.

μ µ E [ X₂ X₁ > c ]< E₁ [ X X₁ > c ],

μ µ E[X₂₁ X < c ]> E[X₁₁ X < c ]

이 정의는 주변 분포가 동일한 모든 이변량 분포가 평균에 대한 회귀를 보인다는 점에서 "일반적"입니다.

재무 사용의 대체 정의

Jeremy Siegel은 "단기적으로는 수익률이 매우 불안정할 수 있지만 장기적으로는 매우 안정적일 수 있다"는 금융 시계열을 설명하기 위해 "Return to the mean"이라는 용어를 사용합니다.보다 양적으로 보면, 평균 연간 수익률의 표준 편차가 보유 기간의 역치보다 빠르게 감소하는 것으로, 그 과정은 랜덤 워크가 아니라, 많은 계절 사업에서와 같이 낮은 수익률의 기간이 체계적으로 뒤따른다는 것을 의미한다.mple을 클릭합니다.^[22]

「」를 참조해 주세요.

레퍼런스

^ Everitt, B. S. (August 12, 2002). The Cambridge Dictionary of Statistics (2 ed.). Cambridge University Press. ISBN 978-0521810999.
^ Upton, Graham; Cook, Ian (21 August 2008). Oxford Dictionary of Statistics. Oxford University Press. ISBN 978-0-19-954145-4.
^ Stigler, Stephen M (1997). "Regression toward the mean, historically considered". Statistical Methods in Medical Research. 6 (2): 103–114. doi:10.1191/096228097676361431. PMID 9261910.
^ Chiolero, A; Paradis, G; Rich, B; Hanley, JA (2013). "Assessing the Relationship between the Baseline Value of a Continuous Variable and Subsequent Change Over Time". Frontiers in Public Health. 1: 29. doi:10.3389/fpubh.2013.00029. PMC 3854983. PMID 24350198.
^ "A statistical review of 'Thinking, Fast and Slow' by Daniel Kahneman". Burns Statistics. November 11, 2013. Retrieved January 1, 2022.
^ "What is regression to the mean? Definition and examples". conceptually.org. Retrieved October 25, 2017.
^ Goldacre, Ben (April 4, 2009). Bad Science. Fourth Estate. p. 39. ISBN 978-0007284870.
^ ^a ^b ^c ^d Galton, F. (1886). "Regression towards mediocrity in hereditary stature". The Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.
^ Galton, Francis (1889). Natural Inheritance. London: Macmillan.
^ Stigler, Stephen M. (June 17, 2010). "Darwin, Galton and the Statistical Enlightenment". Journal of the Royal Statistical Society, Series A. 173 (3): 469–482, 477. doi:10.1111/j.1467-985X.2010.00643.x. ISSN 1467-985X.
^ Kahneman, Daniel (October 1, 2011). Thinking Fast and Slow. Farrar, Straus and Giroux. ISBN 978-0-374-27563-1.
^ Secrist, Horace; Hotelling, Harold; Rorty, M. C.; Gini, Corrada; King, Wilford I. (June 1934). "Open Letters". Journal of the American Statistical Association. 29 (186): 196–205. doi:10.1080/01621459.1934.10502711. JSTOR 2278295.
^ Defulio, Anthony (2012). "Quotation: Kahneman on Contingencies". Journal of the Experimental Analysis of Behavior. 97 (2): 182. doi:10.1901/jeab.2012.97-182. PMC 3292229.
^ Webster, Ben (December 16, 2005). "Speed camera benefits overrated". The Times. Retrieved January 1, 2022.(설명 필요)
^ Mountain, L. (2006). "Safety cameras: Stealth tax or life-savers?". Significance. 3 (3): 111–113. doi:10.1111/j.1740-9713.2006.00179.x.
^ Maher, Mike; Mountain, Linda (2009). "The sensitivity of estimates of regression to the mean". Accident Analysis & Prevention. 41 (4): 861–8. doi:10.1016/j.aap.2009.04.020. PMID 19540977.
^ 예를 들어 네이트 실버, "랜덤니스: 열병을 잡아라!" , 야구 계획서, 2003년 5월 14일 참조.
^ Flyvbjerg, Bent (5 October 2020). "The law of regression to the tail: How to survive Covid-19, the climate crisis, and other disasters". Environmental Science & Policy. 114: 614–618. doi:10.1016/j.envsci.2020.08.013. ISSN 1462-9011. PMC 7533687. PMID 33041651.
^ ^a ^b 를 클릭합니다Samuels, Myra L. (November 1991). "Statistical Reversion Toward the Mean: More Universal than Regression Toward the Mean". The American Statistician. 45 (4): 344–346. doi:10.2307/2684474. JSTOR 2684474..
^ ^a ^b Schmittlein, David C (August 1989). "Surprising Inferences from unsurprising Observations: Do Conditional Expectations really regress to the Mean?". The American Statistician. 43 (3): 176–183. JSTOR 2685070.
^ Chernick, Michael R.; Friis, Robert H. (March 17, 2003). Introductory Biostatistics for the Health Sciences. Wiley-Interscience. p. 272. ISBN 978-0-471-41137-6.
^ Siegel, Jeremy (November 27, 2007). Stocks for the Long Run (4th ed.). McGraw–Hill. pp. 13, 28–29. ISBN 978-0071494700.

추가 정보

J.M. Bland and D.G. Altman (June 1994). "Statistic Notes: Regression towards the mean". British Medical Journal. 308 (6942): 1499. doi:10.1136/bmj.308.6942.1499. PMC 2540330. PMID 8019287. 글에는 골튼의 원본 데이터 다이어그램이 포함되어 있습니다.

Edward J. Dudewicz & Satya N. Mishra (1988). "Section 14.1: Estimation of regression parameters; Linear models". Modern Mathematical Statistics. John Wiley & Sons. ISBN 978-0-471-81472-6.

Francis Galton (1886). "Regression towards mediocrity in hereditary stature" (PDF). The Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.

Donald F. Morrison (1967). "Chapter 3: Samples from the Multivariate Normal Population". Multivariate Statistical Methods. McGraw-Hill. ISBN 978-0-534-38778-5.

Stephen M. Stigler (1999). "Chapter 9". Statistics on the Table. Harvard University Press.

Myra L. Samuels (November 1991). "Statistical Reversion Toward the Mean: More Universal than Regression Toward the Mean". The American Statistician. 45 (4): 344–346. doi:10.2307/2684474. JSTOR 2684474.
스티븐 센.회귀: 오래된 의미의 새로운 양식, The American Statistician, Vol 44, No 2 (1990년 5월), 페이지 181–183.
평균으로의 회귀와 변화의 연구, 심리 속보
평균에 대한 회귀에 대한 비수학적인 설명입니다.
평균에 대한 회귀 시뮬레이션입니다.
아만다 왓스무트, 릴랜드 윌킨슨, 제라드 E. 달랄Galton's Bend: Galton의 가족 신장 회귀 데이터의 발견되지 않은 비선형성 및 Pearson과 Lee의 신장 데이터를 기반으로 한 가능한 설명(Galton의 분석의 현대적 관점)
통계학자에 의해 회귀의 예로 해석된 매사추세츠의 표준화된 시험 점수: sci.stat.edu 및 그 계속에 대한 논의를 참조하십시오.
Gary Smith, What the Luck:일상 생활에서 우연의 놀라운 역할, 뉴욕: 런던, 간과:덕워스.ISBN 978-1-4683-1375-8.

외부 링크

Wikimedia Commons에서의 평균으로의 회귀와 관련된 미디어

[1] Everitt, B. S. (August 12, 2002). The Cambridge Dictionary of Statistics (2 ed.). Cambridge University Press. ISBN 978-0521810999.

[2] Upton, Graham; Cook, Ian (21 August 2008). Oxford Dictionary of Statistics. Oxford University Press. ISBN 978-0-19-954145-4.

[3] Stigler, Stephen M (1997). "Regression toward the mean, historically considered". Statistical Methods in Medical Research. 6 (2): 103–114. doi:10.1191/096228097676361431. PMID 9261910.

[4] Chiolero, A; Paradis, G; Rich, B; Hanley, JA (2013). "Assessing the Relationship between the Baseline Value of a Continuous Variable and Subsequent Change Over Time". Frontiers in Public Health. 1: 29. doi:10.3389/fpubh.2013.00029. PMC 3854983. PMID 24350198.

[5] "A statistical review of 'Thinking, Fast and Slow' by Daniel Kahneman". Burns Statistics. November 11, 2013. Retrieved January 1, 2022.

[6] "What is regression to the mean? Definition and examples". conceptually.org. Retrieved October 25, 2017.

[7] Goldacre, Ben (April 4, 2009). Bad Science. Fourth Estate. p. 39. ISBN 978-0007284870.

[galton1886-8] Galton, F. (1886). "Regression towards mediocrity in hereditary stature". The Journal of the Anthropological Institute of Great Britain and Ireland. 15: 246–263. doi:10.2307/2841583. JSTOR 2841583.

[9] Galton, Francis (1889). Natural Inheritance. London: Macmillan.

[10] Stigler, Stephen M. (June 17, 2010). "Darwin, Galton and the Statistical Enlightenment". Journal of the Royal Statistical Society, Series A. 173 (3): 469–482, 477. doi:10.1111/j.1467-985X.2010.00643.x. ISSN 1467-985X.

[11] Kahneman, Daniel (October 1, 2011). Thinking Fast and Slow. Farrar, Straus and Giroux. ISBN 978-0-374-27563-1.

[12] Secrist, Horace; Hotelling, Harold; Rorty, M. C.; Gini, Corrada; King, Wilford I. (June 1934). "Open Letters". Journal of the American Statistical Association. 29 (186): 196–205. doi:10.1080/01621459.1934.10502711. JSTOR 2278295.

[13] Defulio, Anthony (2012). "Quotation: Kahneman on Contingencies". Journal of the Experimental Analysis of Behavior. 97 (2): 182. doi:10.1901/jeab.2012.97-182. PMC 3292229.

[14] Webster, Ben (December 16, 2005). "Speed camera benefits overrated". The Times. Retrieved January 1, 2022.(설명 필요)

[15] Mountain, L. (2006). "Safety cameras: Stealth tax or life-savers?". Significance. 3 (3): 111–113. doi:10.1111/j.1740-9713.2006.00179.x.

[16] Maher, Mike; Mountain, Linda (2009). "The sensitivity of estimates of regression to the mean". Accident Analysis & Prevention. 41 (4): 861–8. doi:10.1016/j.aap.2009.04.020. PMID 19540977.

[17] 예를 들어 네이트 실버, "랜덤니스: 열병을 잡아라!" , 야구 계획서, 2003년 5월 14일 참조.

[18] Flyvbjerg, Bent (5 October 2020). "The law of regression to the tail: How to survive Covid-19, the climate crisis, and other disasters". Environmental Science & Policy. 114: 614–618. doi:10.1016/j.envsci.2020.08.013. ISSN 1462-9011. PMC 7533687. PMID 33041651.

[Samuels-19] 를 클릭합니다Samuels, Myra L. (November 1991). "Statistical Reversion Toward the Mean: More Universal than Regression Toward the Mean". The American Statistician. 45 (4): 344–346. doi:10.2307/2684474. JSTOR 2684474..

[Schmittlein-20] Schmittlein, David C (August 1989). "Surprising Inferences from unsurprising Observations: Do Conditional Expectations really regress to the Mean?". The American Statistician. 43 (3): 176–183. JSTOR 2685070.

[21] Chernick, Michael R.; Friis, Robert H. (March 17, 2003). Introductory Biostatistics for the Health Sciences. Wiley-Interscience. p. 272. ISBN 978-0-471-41137-6.

[22] Siegel, Jeremy (November 27, 2007). Stocks for the Long Run (4th ed.). McGraw–Hill. pp. 13, 28–29. ISBN 978-0071494700.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[19]

[20]

[21]

[22]

Search

평균에 대한 회귀

네임스페이스

더

목차

개념적인 예

간단한 예: 시험을 보는 학생

기타 예

역사

검출

용어의 진화하는 사용법

중요성

오해

회귀 오류

기타 통계현상

데이터 점의 단순 선형 회귀를 위한 정의

주변 분포가 동일한 이변량 분포에 대한 정의

제한적 정의

정리

일반적인 정의

재무 사용의 대체 정의

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

평균에 대한 회귀

개념적인 예

간단한 예: 시험을 보는 학생

기타 예

역사

검출

용어의 진화하는 사용법

중요성

오해

회귀 오류

기타 통계현상

데이터 점의 단순 선형 회귀를 위한 정의

주변 분포가 동일한 이변량 분포에 대한 정의

제한적 정의

정리

일반적인 정의

재무 사용의 대체 정의

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.