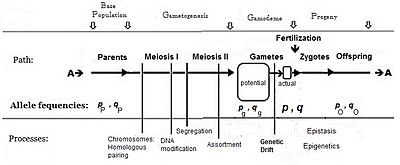
양적 유전학

양적 유전학은 이산적으로 식별 가능한 표현형과 유전자 생성물(예: 눈동자 색 또는 특정 생화학적 존재)이 아닌 지속적으로 변화하는 표현형을 다룬다.

두 가지 모두 유전자의 다른 대립 유전자의 빈도를 사육 개체(가모뎀)에 사용하고, 그것들을 단순한 멘델 유전의 개념과 결합하여 세대와 자손 계통의 유전 패턴을 분석합니다.집단 유전학이 특정 유전자와 그 이후의 대사 산물에 초점을 맞출 수 있는 반면, 양적 유전학은 겉으로 드러나는 표현형에 더 초점을 맞추고, 기초 유전학만을 요약합니다.

표현형 값의 지속적인 분포로 인해, 정량 유전학은 표현형(속성)을 유전자형에 연결하기 위해 다른 많은 통계적 방법(효과 크기, 평균 및 분산 등)을 사용해야 한다.일부 표현형은 컷오프점의 정의 ^[1]^{: 27–69}또는 정량화에 사용되는 메트릭에 따라 이산 범주 또는 연속 표현형으로 분석될 수 있다.멘델은 유명한 ^[2]논문에서 이 문제를 논의해야 했는데, 특히 그의 완두콩이 "줄기의 길이"^[3]^[4]인 "큰/난쟁이" 속성과 관련하여 더욱 그러했다.양적 특성 위치 분석(QTL)^[5]^[6]^[7]은 양적 유전학에 최근 추가된 것으로 분자 유전학과 더 직접적으로 연결됩니다.

유전자 효과

이배체 유기체에서 평균 유전자형 "값"(위치값)은 대립 유전자 "효과"와 우세 효과, 그리고 유전자가 다른 위치(에피스타시스)에서 유전자와 어떻게 상호작용하는가에 의해 정의될 수 있다.양적 유전학의 창시자인 로널드 피셔 경은 ^[8]유전학의 이 분야의 첫 번째 수학을 제안했을 때 이 많은 것을 인지했습니다.

유전자 효과와 표현형 값.

통계학자로서, 그는 유전자 효과를 중심 값으로부터의 이탈로 정의했다. - 이 아이디어를 ^[9]사용하는 평균과 분산과 같은 통계 개념을 사용할 수 있게 했다.그가 선택한 유전자의 중심값은 하나의 궤적에서 대립하는 두 호모 접합체 사이의 중간점이었다.여기에서 "더 큰" 호모 접합 유전자형으로의 편차는 "+a"로 명명될 수 있으며, 따라서 동일한 중간점에서 "더 작은" 호모 접합 유전자형까지 "-a"이다.이것은 위에서 언급한 "알레" 효과입니다.동일한 중간점으로부터의 헤테로 접합자 편차는 ^[10]위에서 언급한 "우위" 효과인 "d"로 명명될 수 있다.이 그림은 아이디어를 묘사하고 있다.그러나 실제로는 표현형을 측정하며, 이 수치는 관찰된 표현형이 유전자 효과와 어떻게 관련되어 있는지를 보여준다.이러한 효과에 대한 공식적인 정의는 이 표현형 ^[11]^[12]초점을 인식한다.인식은 상호작용(즉,^[13] 불일치)으로 통계적으로 접근했지만 후생유전학은 새로운 접근법이 필요할 수 있음을 시사한다.

0<d<a인 경우 우성은 부분적이거나 불완전한 것으로 간주되며, 반면 d=a는 완전 또는 고전적 우성을 나타낸다.이전에는 d>a는 "초과지배"^[14]로 알려져 있었습니다.

멘델의 완두콩 속성 "줄기의 길이"는 우리에게 좋은 ^[3]예를 제공한다.멘델은 키가 큰 진짜 부모들의 줄기 길이는 6-7피트 (180–213cm)이며, 중간값은 198cm (= P1)라고 말했다.키가 작은 부모의 줄기 길이는 0.75 - 1.25피트(23 - 46cm)였고, 둥근 중앙값은 34cm(= P2)였다.이들의 잡종은 길이가 6-7.5피트(180–229cm), 중앙값은 206cm(= F1)였다.P1과 P2의 평균은 116cm로 호모 접합 중간점(mp)의 표현형 값이다.대립 유전자 영향(a)은 [P1-mp] = 82cm = [P2-mp]이다.우위효과(d)는 [F1-mp] = 90cm이다.^[15]이 역사적 예는 표현형 값과 유전자 효과가 어떻게 연관되어 있는지를 명확하게 보여준다.

대립 유전자 및 유전자형 빈도

평균, 분산 및 기타 통계량을 얻으려면 수량과 그 발생이 모두 필요합니다.유전자 효과(위)는 양에 대한 틀을 제공하고 수정 배우자 풀의 대조 대립 유전자의 빈도는 발생에 대한 정보를 제공합니다.

성적 재생산의 분석.

일반적으로 표현형(우성 포함)에서 "더 많은"을 일으키는 대립 유전자의 빈도는 기호 p가 주어지는 반면 대조 대립 유전자의 빈도는 q이다. 대수를 확립할 때 만들어진 초기 가정은 부모 집단이 무한하고 무작위 짝짓기이며, 이는 단순히 유도를 용이하게 하기 위한 것이었다.후속 수학적 발전은 또한 유효 배우자 풀 내의 빈도 분포가 균일하다는 것을 암시했다. 즉, p와 q가 다른 국소 섭동이 없었다.성생식의 도식 분석을 보면 p = p_g = p; 라고 선언하는_P 것과 같으며 ^[14]q에 대해서도 이와 유사하다.이러한 가정에 의존하는 이 짝짓기 시스템은 "판믹시아"로 알려지게 되었다.

판믹시아는 배우자 분포가 제한될 수 있기 때문에,^[16]^{: 152–180}^[17] 예를 들어 분산 제한이나 행동에 의해, 또는 우연한 표본 추출에 의해 실제로 발생하는 경우는 거의 없다(위에서 언급한 국지적 섭동).자연에서 배우자의 엄청난 낭비가 있다는 것은 잘 알려져 있으며, 그래서 다이어그램은 실제 배우자 풀과 별도로 잠재적 배우자 풀을 묘사하고 있다.오직 후자만이 접합자의 최종 주파수를 정합니다: 이것이 진정한 "가모데메"입니다. (가모는 배우자를 의미하고, "데메"는 "인구"를 뜻하는 그리스어에서 유래합니다.)그러나 Fisher의 가정 하에, 가모뎀은 효과적으로 잠재적인 배우자 풀로 확장될 수 있으며, 심지어 부모의 기본 인구('원천' 인구)로도 다시 확장될 수 있다.작은 "실제" 배우자 풀이 큰 "잠재적" 배우자 풀에서 샘플링될 때 발생하는 무작위 샘플링은 유전자 표류라고 알려져 있으며, 이후에 고려된다.

범믹시아는 널리 존재하지는 않지만, 그러한 국지적인 섭동 때문에 일시적인 것일 수도 있지만, 잠재력은 발생한다.예를 들어 교배 후 F1 개체의 무작위 수정에서 파생된 F2가 새로운 잠재적 범혼합 집단의 ^[18]^[19]기원이라는 것이 밝혀졌다.또한 범혼합적 무작위 수정이 지속적으로 일어난다면, 그것은 각각의 연속적인 범혼합적 성생성(Hardy Weinberg 평형)^[13]^{: 34–39}^[20]^[21]^[22]^[23]에 걸쳐 동일한 대립 유전자와 유전자형 빈도를 유지할 것이라는 것이 증명되었다.그러나 유전자 표류가 생식체의 국소 무작위 표본 추출에 의해 시작되자마자, 평형은 중단될 것이다.

무작위 수정

실제 수정 풀 내의 수컷과 암컷 배우자는 일반적으로 대응하는 대립 유전자에 대해 동일한 빈도를 갖는 것으로 간주됩니다.(예외는 고려되었습니다.)즉, A 대립 유전자를 가진 p 수컷 생식체가 같은 대립 유전자를 가진 p 암컷 생식체를 무작위로 수정하면, 결과 접합자는 유전자형 AA를 가지며, 무작위 수정 하에서는 p x p(= p²)의 빈도로 결합이 일어난다.마찬가지로 접합자 aa는 q의² 빈도로 발생할 수 있다.헤테로 접합자(Aa)는 p 수컷(A 대립 유전자)이 q 암컷(알레알레) 생식체를 랜덤하게 수정했을 때 발생할 수 있으며, 그 반대도 마찬가지이다.따라서 헤테로 접합 접합자의 주파수는 2pq이다.^[13]^{: 32}이러한 모집단은 헤테로 접합의 절반을 넘지 않으며, 이 최대값은 p=q=0.5일 때 발생한다.

요약하자면, 무작위 수정 하에서 접합자(유전자형) 주파수는 배우자(알렐) 주파수의 2차 팽창이다 ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ( ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ q ) ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ 2 + ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ q + ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ $=$ 1 { $textstyle (p +$ q )^2} + 2 $p$ = p ^{2 $}$ + 2 = 1 ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ = p^{2} + 2 p q + 2 $q =$ 1 ${\textstyle (p+q)^{2}=p^{2}+2pq+q^{2}=1}$ = 1 . "1" 주파수이다.s는 제안된 프레임워크 내에 있습니다.

"랜덤 수정"과 "판믹시아"는 동의어가 아닙니다.

Mendel의 리서치 크로스– 대조

멘델의 완두콩 실험은 각 ^[3]속성에 대해 "대립" 표현형을 가진 진정한 양육 부모를 확립함으로써 구성되었습니다.이것은 각각의 대립되는 부모가 각각의 대립 유전자에 대해서만 동질성이라는 것을 의미했다.이 예에서 "키 큰 부모 대 왜소"는 p = 1(및 q = 0)인 유전자형 TT이고, 난쟁이 부모는 q = 1(및 p = 0)인 유전자형 tt이다.제어 교잡 후 이들의 하이브리드는 p = q = µ인 Tt가 된다.그러나 이 헤테로 접합체의 빈도 = 1은 인공 십자가의 F1이기 때문에 무작위 ^[24]수정을 통해 발생하지 않았다.F2 생성은 (곤충 오염에 대한 모니터링을 통해) F1의 자연 자가수분에 의해 생성되었으며, 그 결과 p = q = µ이 유지되었다.이러한 F2는 "자생애"라고 불립니다.그러나 유전자형 주파수(0.25T, 0.5T, 0.25Tt)는 무작위 수정과는 매우 다른 결합계를 통해 발생하므로 2차 팽창의 사용은 회피되었다.이것은 원래 동종성 ^[25]반대쪽 부모를 교차시킨 특별한 경우이기 때문에 얻어진 수치들은 무작위 수정의 수치와 동일했다.TT[주파수 0.25]에 대한 T-[주파수 (0.25 + 0.5)]의 우세 때문에 3:1의 비율이 여전히 확보된다는 것을 알 수 있다.

Mendel's와 같은 교배(대부분 호모 접합)가 F1을 생성하기 위해 제어된 방식으로 교배되는 교배는 하이브리드 구조의 특별한 경우이다.F1은 종종 고려 중인 유전자에 대해 "완전히 이형 접합"으로 간주됩니다.그러나 이는 지나치게 단순화된 것으로 일반적으로는 적용되지 않는다. 예를 들어 개별 부모가 동종 접합자가 아닌 경우 또는 모집단이 교잡하여 하이브리드 ^[24]무리를 형성하는 경우이다.종내 잡종(F1)과 F2(둘 다 '자생애'와 '동일애')의 일반적인 특성은 다음 섹션에서 고려된다.

자가 수정 – 대안

완두콩은 자연수분이므로 랜덤 수정 성질을 나타내는 예로서 계속 사용할 수 없습니다.자가수정은 무작위 수정의 주요 대안이며, 특히 식물 내에서 그렇습니다.지구의 대부분의 곡물들은 맥박뿐만 아니라 자연적으로 자가 수분된다.지구상에 있는 수백만 마리의 개체들을 고려해 볼 때, 자기 수정이 최소한 무작위 수정만큼 중요하다는 것은 명백합니다.자가 수정은 생식체의 유전적 기원에 제한적인 독립성이 있을 때마다 발생하는 가장 강도 높은 근친 교배 형태이다.이러한 독립성의 감소는 부모가 이미 혈연관계인 경우 및/또는 생식체 분산에 대한 유전적 표류 또는 기타 공간적 제약으로 인해 발생한다.경로 분석을 통해 이 두 가지가 ^[26]^[27]같은 것과 같다는 것을 알 수 있습니다.이러한 배경에서 발생하는 근친교배계수(종종 F 또는 f로 표시됨)는 어떠한 원인에 의한 근친교배의 효과를 정량화합니다.f에는 몇 가지 정식 정의가 있으며, 이들 중 일부는 이후 섹션에서 다루어진다.그러나 당분간 장기 자가화 종 f = 1. 자연 자가화 개체군은 단일 "순수 라인"이 아니라 그러한 라인의 혼합물이다.이것은 한 번에 하나 이상의 유전자를 고려할 때 특히 명백해진다.따라서 1 또는 0 이외의 대립 유전자 빈도(p 및 q)는 이러한 경우에도 여전히 관련이 있습니다(Mendel Cross 섹션 참조).그러나 유전자형 빈도는 다른 형태를 취합니다.

일반적으로 유전자형 빈도는 AA의 ${\textstyle 2pq(1-f)}$ [ ${\textstyle [p^{2}(1-f)+pf]}$ 2 ${\textstyle [p^{2}(1-f)+pf]}$ ( ${\textstyle [p^{2}(1-f)+pf]}$ - ${\textstyle [p^{2}(1-f)+pf]}$ ) + ${\textstyle [p^{2}(1-f)+pf]}$ f $]$ { $textstyle [p^{2}$ (1 - f) + pf ${\textstyle [p^{2}(1-f)+pf]}$ ${\textstyle 2pq(1-f)}$ { $textstyle 2pq$ ( $1$ - ${\textstyle [q^{2}(1-f)+qf]}$ $)$ ${\textstyle [q^{2}(1-f)+qf]}$ Aa의 경우 ${\textstyle [q^{2}(1-f)+qf]}$ ( ${\textstyle [q^{2}(1-f)+qf]}$ - ${\textstyle [q^{2}(1-f)+qf]}$ f ${\textstyle [q^{2}(1-f)+qf]}$ + ${\textstyle [q^{2}(1-f)+qf]}$ f $}$ { $textstyle$ [ $q$ ^ { $2$ } (1 - f) + ${\textstyle [q^{2}(1-f)+qf]}$ } (1 - f ) ${\textstyle 2pq(1-f)}$ ]가 ${\textstyle [p^{2}(1-f)+pf]}$ ${\textstyle 2pq(1-f)}$ ${\textstyle [p^{2}(1-f)+pf]}$ 된다.

헤테로 접합체의 빈도는 f에 비례하여 감소한다는 점에 유의하십시오.f = 1이면 이 세 가지 주파수는 각각 p, 0 및 q가 됩니다. 반대로 f = 0이면 앞에서 보여 준 랜덤화 2차 확장으로 감소합니다.

모평균

모집단 평균은 중심 기준점을 호모 접합 중간점(mp)에서 성적으로 재생산된 모집단의 평균으로 이동합니다.이는 자연계에 초점을 재배치하는 것뿐만 아니라 통계/생체측정학에서 사용하는 중심 경향의 척도를 사용하는 것도 중요하다.특히,^[9] 이 평균의 제곱은 나중에 유전자형 분산을 구하는 데 사용되는 보정 계수이다.

다양한 d 효과에 대한 p의 모든 값에 대한 모집단 평균입니다.

각 유전자형에 대해 그 대립 유전자 효과는 유전자형 빈도에 의해 곱해지고 생성물은 모델 내의 모든 유전자형에 걸쳐 축적된다.어떤 대수적 단순화는 보통 간결한 결과에 도달하기 위해 뒤따른다.

랜덤 수정 후 평균

AA의 ${\textstyle p^{2}(+)a}$ 는 p ${\textstyle p^{2}(+)a}$ ( ${\textstyle p^{2}(+)a}$ + ) $a,$ Aa의 기여는 p $2$ ( + ${\textstyle p^{2}(+)a}$ ) $a$ $, Aa$ 의 기여는 ${\textstyle 2pqd}$ ${\textstyle 2pqd}$ ${\textstyle 2pqd}$ ${\textstyle q^{2}(-)a}$ d ${\textstyle 2pqd}$ - ) $a$ ${\textstyle q^{2}(-)a}$ 의 기여는 ${\textstyle q^{2}(-)a}$ ${\textstyle a(p^{2}-q^{2})+2pqd}$ 2 ( - ) ${\textstyle q^{2}(-)a}$ 입니다.두 개의 항을 모아서 모든 것을 누적하면 p ${\textstyle a(p^{2}-q^{2})+2pqd}$ ( + ${\textstyle a(p^{2}-q^{2})+2pqd}$ )가 됩니다 ${\textstyle a(p^{2}-q^{2})+2pqd}$ 양이온은 ( ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ - ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ 2) ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ ( ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ - $q$ ) ( ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ + $q ) =$ ( p + q ) = ( ${\textstyle (p^{2}-q^{2})=(p-q)(p+q)}$ ${\textstyle (p+q)=1}$ + $q )$ } ${\textstyle (p+q)=1}$ 1 ${\textstyle (p+q)=1}$ ( $p$ + ${\textstyle (p+q)=1}$ q )을 $호출$ 하여 ${\textstyle (p+q)=1}$ 항을 ( $p$ ${\textstyle (p-q)}$ q $)$ style ( ${\textstyle (p-q)}$ - q ) style로 $줄임$ 으로써 달성된다 $.$

${\textstyle G=a(p-q)+2pqd}$ 간결한 ${\textstyle G=a(p-q)+2pqd}$ 는 G ${\textstyle G=a(p-q)+2pqd}$ ${\textstyle G=a(p-q)+2pqd}$ ( ${\textstyle G=a(p-q)+2pqd}$ p - ${\textstyle G=a(p-q)+2pqd}$ ) + ${\textstyle G=a(p-q)+2pqd}$ ${\textstyle G=a(p-q)+2pqd}$ ${\textstyle G=a(p-q)+2pqd}$ d \ $textstyle$ G = ${\textstyle G=a(p-q)+2pqd}$ a ( $p$ - q ) + 2 $pqd$ 입니다 ${\textstyle G=a(p-q)+2pqd}$ ^[14]

이는 모집단 평균을 호모 접합 중간점으로부터의 "오프셋"으로 정의합니다(호모 a와 d는 해당 중간점으로부터의 편차로 정의됨).그림에서는 약간의 과잉 우위의 경우를 포함하여 d의 여러 값에 대해 p의 모든 값에 걸쳐 G를 나타내고 있습니다.G는 음수인 경우가 많기 때문에 그 자체가 (mp로부터의) 편차임을 강조합니다.

마지막으로 "비정형 공간"에서 실제 모집단 평균을 구하기 위해 중간점 값을 이 오프셋에 추가합니다. ${\textstyle P=G+mp}$ ${\textstyle P=G+mp}$ + ${\textstyle P=G+mp}$ p { $textstyle$ P $= G$ + $mp$

한 ^[28]^{: 103}예는 옥수수의 귀 길이 데이터에서 발생한다.현재 a = 5.45cm, d = 0.12cm [0"이라는 하나의 유전자만 나타낸다고 가정하면 mp = 12.05cm이다.이 예에서 p = 0.6, q = 0.4라고 가정하면 다음과 같습니다.

G = 5.45 (0.6 - 0.4) + (0.48) 0.12 = 1.15 cm (수직)

P = 1.15 + 12.05 = 13.20 cm (표준).

장기 자가 수태 후의 평균

AA의 기여는 ${\textstyle p(+a)}$ p $(+)$ { $textstyle$ p $(+a$ 이며, aa의 기여는 ${\textstyle q(-a)}$ q $)$ { $textstyle$ q(- $a$ 입니다.[주파수에 대해서는 위 참조]이 두 용어를 합치면 매우 간단한 최종 결과를 얻을 수 있습니다.

${\textstyle G_{(f=1)}=a(p-q)}$ ( ${\textstyle G_{(f=1)}=a(p-q)}$ ${\textstyle G_{(f=1)}=a(p-q)}$ ) ${\textstyle G_{(f=1)}=a(p-q)}$ ( $p$ - $q$ ) { ( f ${\textstyle G_{(f=1)}=a(p-q)}$ = ${\textstyle G_{(f=1)}=a(p-q)}$ 1) $= a$ ( p - ${\textstyle G_{(f=1)}=a(p-q)}$ q ) ${\textstyle G_{(f=1)}=a(p-q)}$ 。이전과 ${\textstyle P=G+mp}$ P ${\textstyle P=G+mp}$ + ${\textstyle P=G+mp}$ ( \ $textstyle$ P = ${\textstyle P=G+mp}$ G + $mp$ 。

종종 "G_(f=1)"는 "G₁"로 축약됩니다.

멘델의 완두콩은 대립 유전자 효과와 중간점(앞서 참조)을 제공할 수 있으며, p = 0.6, q = 0.4의 혼합 자가 수분 집단은 예제 빈도를 제공합니다.다음과 같이 됩니다.

G_(f=1) = 82 (0.6 - 0.04) = 59.6 cm (표준)

P_(f=1) = 59.6 + 116 = 175.6 cm (표준)

평균 – 일반화된 수정

일반식은 근친교배계수 f를 포함하며, 그 후 모든 상황을 수용할 수 있다.절차는 앞서 주어진 가중 유전자형 주파수를 사용하여 이전과 정확히 동일합니다.기호로 변환하고 다시 ^[13]정렬한 후:

디스플레이 스타일G_{f}&=a(q-p)+[2pqd-f(2pqd)]\&=a(p-q)+(1-f)2pqd\\&=G_{0}-f\2pqd\end{aligned}}

여기서 G는₀ 앞서 말한 G이다(종종 근친교배는 G보다 G를₀ 선호한다).

옥수수 예가 홀메(좁은 강변 초원)에서 제한되고 f = 0.25까지 부분 근친교배되었다고 가정하면, G의_f 세 번째 버전(위)을 사용한다.

G_0.25 = 1.15 - 0.25 (0.48) 0.12 = 1.14 cm (1.16 cm (160), P_0.25 = 13.14 cm (160)).

이 예에서는 근친교배의 영향이 거의 없으며, 이는 이 속성(d → 0)에 사실상 우위가 없었기 때문에 발생한다.G의 세_f 가지 버전을 모두 조사하면 모집단 평균에 사소한 변화가 생긴다는 것을 알 수 있습니다.그러나 지배력이 두드러지는 곳에는 상당한 변화가 있을 것이다.

유전적 표류

자연 수정 패턴으로 범믹시아가 널리 존재할 가능성을 논할 때 유전적 표류가 도입되었다.[알레알레 및 유전자형 주파수에 대한 섹션을 참조하십시오.여기에서는 잠재적인 생식체 표본 추출에 대해 좀 더 자세히 논의한다.표본 추출에는 각각 A 또는 대립 유전자가 포함될 수 있는 랜덤 배우자 쌍 간의 무작위 수정이 포함됩니다.따라서 표본 추출은 이항 ^[13]^{: 382–395}^[14]^{: 49–63}^[29]^{: 35}^[30]^{: 55}표본 추출입니다.각 표본 "패킷"은 2N 대립 유전자를 포함하며 결과적으로 N개의 접합자("프로게니" 또는 "라인")를 생성합니다.생식기 동안 이 샘플링은 반복 반복되므로 최종 결과는 시료 자손의 혼합이 된다.그 결과 분산 랜덤 수정 $\left(\bigodot \right)$ $\left(\bigodot \right)$ ) ( \ $displaystyle \$ left ( \ $bigodot$ \ $\left(\bigodot \right)$ right )이러한 $\left(\bigodot \right)$ 이벤트와 전체적인 최종 결과를 예시와 함께 조사합니다.

이 예제의 "기본" 대립 유전자의 주파수는 잠재적 양성소이다. A의 주파수는 p_g = 0.75이고, a의 주파수는 q = 0.25이다_g.[그림의 흰색 라벨 '1']실제 5개의 샘플 색소(s = 샘플 수 = 5)를 이 기준에서 2진법으로 추출하고, 각 샘플은 k:(k = 1 ... s)로 순차적으로 지정됩니다(이들은 이전 단락에서 언급한 샘플 "표본"입니다).수정에 관여하는 배우자의 수는 표본마다 다르며, 2N으로_k 표시됩니다(그림의 흰색 레이블 "2").전체적으로 샘플링된 배우자의 총(δ) 수는 52개입니다[그림의 흰색 라벨 "3"].표본마다 크기가 다르기 때문에 전체 결과를 얻을 때 평균(및 기타 통계량)을 얻으려면 가중치가 필요합니다.이것들은 ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ k ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ k ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ / ( ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ k ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ N ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ ) { $textstyle$ \ $amega _$ {k } = ${\textstyle \omega _{k}=2N_{k}/(\sum _{k}^{s}2N_{k})}$ 2 N $_$ { $k$ } / ( \ $sum$ _ ${$ k }^{ $s$ } 2 $N_{k$ 도표의 흰색 라벨 "4"에 표시되어 있습니다.

Genetic Drift 예제 분석.

샘플 색소뎀 – 유전적 표류

이 5개의 이항 표본 추출 이벤트가 완료된 후, 결과물인 실제 양성소 각각은 서로 다른 대립 유전자 주파수 (p와_k_k q)를 포함했다.[그림의 흰색 라벨 '5'에 표시되어 있습니다.]이 결과는 사실 유전적 표류 그 자체입니다.두 표본(k = 1 및 5)이 기본(표준) 색소뎀과 동일한 주파수를 가집니다.또 다른 값(k = 3)은 p와 q의 "치수"를 가진다.표본(k = 2)은 p = 0_k.9, q = 0.1인_k "극한" 경우이며, 나머지 표본(k = 4)은 대립 유전자 빈도에서 "범위의 중간"입니다.이 모든 결과는 이항 표본 추출을 통해 "찬스"에 의해서만 발생합니다.그러나 일어난 후, 그들은 자손들의 모든 하류적인 특성들을 갖추었다.

표본 추출에는 우연이 수반되기 때문에 이러한 표본을 얻을 확률( )이 관심사가 됩니다.이러한 이항 확률은 시작 빈도(p_g 및_g q)와 표본 크기(2N_k)에 따라 달라집니다.그것들은 ^[13]^{: 382–395}^[30]^{: 55}구하기 귀찮지만 꽤 흥미롭다.[그림의 흰색 라벨 "6" 참조]잠재적 유전자 빈도와 동일한 대립 유전자 빈도를 가진 두 검체(k = 1, 5)는 다른 검체보다 발생 빈도가 더 높았다.그러나 표본 크기가 다르기 때문에_k(2N) 이항 확률은 달랐다."추정" 표본(k = 3)은 발생 확률이 매우 낮아서 예상할 수 있는 것을 확인했습니다.그러나 "극한" 대립 유전자 주파수 가모뎀(k = 2)은 "확대"되지 않았고, "범위 중간" 샘플(k=4)은 드물었다.이러한 확률은 이러한 수정의 자손에게도 적용됩니다.

여기서 몇 가지 요약을 시작할 수 있습니다.자손 벌크의 전체 대립 유전자 빈도는 개별 검체의 적절한 빈도에 대한 가중 평균에 의해 공급된다. ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ , p ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ k ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ k { \ $textstyle p _$ { \ $centerdot$ } $=$ \ $sum$ $_$ ${\textstyle p_{\centerdot }=\sum _{k}^{s}\omega _{k}\ p_{k}}$ { k $}^{ s$ } \ ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$ ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$ 、 $k$ 、 k ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$ （ \ $textstyle q$ _ { \ centerdot } = \ $sum _$ { k $}^{$ s } } \ s \ s \ s \ } } ${\textstyle q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ q_{k}}$ 。이 예제의 결과는 p = 0.631_• 및 q = 0.369 [그림의 검은색 레이블 "5"]입니다_•.이러한 값은 시작 값(p_g 및_g q)과는 상당히 다릅니다[흰색 라벨 "1"].샘플 대립 유전자 빈도에는 평균뿐만 아니라 분산도 있습니다.이는 제곱합(SS) 방법을 사용하여 구했다[그림의 검은색 라벨 "5" 오른쪽 참조].[이 차이에 대한 자세한 설명은 아래 광범위한 유전자 표류에 대한 섹션에서 확인할 수 있습니다.]

자손 계통 – 분산

5개의 샘플 자손의 유전자형 빈도는 각각의 대립 유전자 빈도의 통상적인 2차 확장(랜덤 수정)에서 얻을 수 있다.결과는 호모 접합자의 경우 다이어그램의 흰색 레이블 "7"에, 헤테로 접합자의 경우 흰색 레이블 "8"에 표시됩니다.이 방법으로 재배치를 하면 근친교배 수준을 감시할 수 있습니다.이는 총 호모 접합 [(p²_k²_k + q) = (1 - 2pq_k_k)]의 수준을 검사하거나 상보적인 ^[32]헤테로 접합의 수준(2pq_k_k)을 검사하여 수행할 수 있다.대립 유전자 빈도와 관련하여 하나의 샘플이 다른 샘플의 "거울 이미지"임에도 불구하고 샘플 k= 1, 3, 5는 모두 동일한 수준의 헤테로 접합을 보였다는 점에 유의하십시오."극한" 대립 유전자 빈도 사례(k=2)는 모든 검체 중 가장 많은 호모 접합(Homojogisis)을 가졌다."범위의 중간" 사례(k=4)는 호모 접합성이 가장 낮았고(대부분의 헤테로 접합성), 실제로는 각각 0.50으로 동일했다.

전체 요약은 자손 체구에 대한 각 유전자형 빈도의 가중 평균을 구함으로써 지속될 수 있다.따라서 AA의 경우 p ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ 2 $=$ k ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ ${\textstyle p_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ p_{k}^{2}}$ (\ $textstyle$ p_ ${\centerdot}^{2$ }=\ $sum$ _ ${k}^{s$ _ ${k}^2}$ 이고, Aa의 경우 ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ k ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ $\textyle$ ${\textstyle 2p_{\centerdot }q_{\centerdot }=\sum _{k}^{s}\omega _{k}\ 2p_{k}q_{k}}$ 이다.§ ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ $k$ 2 （ \ text $style q$ _ { \ centerdot }^{2} = \ $sum$ _ { $k }^s$ } \ $obega$ _ { $k$ } \ $q$ _ { $k }^$ 2} ${\textstyle q_{\centerdot }^{2}=\sum _{k}^{s}\omega _{k}\ q_{k}^{2}}$ 예시는 호모 접합자의 경우 검은색 라벨 "7"에, 헤테로 접합자의 경우 검은색 라벨 "8"에 제시되어 있습니다.헤테로 접합성 평균은 0.3588이며, 이는 다음 절에서 이 유전적 표류에 따른 근친 교배를 검사하는 데 사용됩니다.

다음 관심의 초점은 분산 그 자체인데, 이것은 자손들의 인구 평균의 "분산"을 의미한다.이들은 흰색 라벨에 제시된 유전자 효과를 사용하여 각 표본 자손에 대해 ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ 로 G k ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ ( ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ - ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ k ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ ) + ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ p ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ ( p $_$ { $k$ } - $q$ _ { k } $= a$ ( p ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ _ { k } - q $_$ { $k$ } $d$ } + 2p_{ $k$ } $d$ 로 ${\textstyle G_{k}=a(p_{k}-q_{k})+2p_{k}q_{k}d}$ . ${\textstyle P_{k}=G_{k}+mp}$ 다음 각 ${\textstyle P_{k}=G_{k}+mp}$ k $=$ ${\textstyle P_{k}=G_{k}+mp}$ k + ${\textstyle P_{k}=G_{k}+mp}$ ${$ $textstyle P_{k$ }= $G_{k}+mp}$ 도 ${\textstyle P_{k}=G_{k}+mp}$ [그림의 흰색 라벨 "10"에서] 구한다."최상의" 라인(k = 2)이 "더 많은" 대립 유전자(A)에 대해 가장 높은 대립 유전자 빈도(호모 접합률도 가장 높음)를 가졌다는 점에 주목하십시오.최악의 자손(k = 3)이 "낮은" 대립 유전자(a)의 빈도가 가장 높았고, 이는 성능 저하의 원인이었다.이 "불량" 선은 "최고" 선보다 호모 접합이 적었고, 두 번째로 좋은 선과 동일한 수준의 호모 접합성을 공유했다(k = 1, 5)."더 많은" 대립 유전자와 "적은" 대립 유전자가 동일한 빈도로 존재하는 자손 계통(k = 4)은 평균이 전체 평균보다 낮았고(다음 단락 참조) 호모 접합성 수준이 가장 낮았다.이러한 결과는 "유전자 풀"에서 가장 널리 퍼져 있는 대립 유전자가 동형 접합의 수준이 아니라 성능을 결정한다는 사실을 보여준다.이항 표본 추출만으로도 이 분산에 영향을 미칩니다.

전체 요약은 이제 G ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ ${\$ ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ k {\ $textstyle$ G_ ${\centerdot$ } = \ $sum _{k}^{s$ }\ $obega _{$ k}\ $g_{$ k ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ } ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ P ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ k $=$ k ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ k ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ k ${\textstyle P_{\centerdot }=\sum _{k}^{s}\omega _{k}\ P_{k}}$ ${\$ $textstyle$ P_ ${\centerdot }{k}_sum$ }를 구함으로써 ${\textstyle G_{\centerdot }=\sum _{k}^{s}\omega _{k}\ G_{k}}$ 을 내릴 수 있다 $.$ P에 대한_• 예제 결과는 36.94입니다(그림에서 검은색 레이블 "10").이것은 나중에 배우자 샘플링을 통해 근친교배 우울증을 전체적으로 정량화하는 데 사용됩니다.[다음 항 참조]단, 일부 "비균형" 자손 평균이 이미 확인되었음을 기억한다(k = 1, 2, 5).이것은 근친교배의 수수께끼입니다.전반적으로 「불황」이 있을 수 있지만, 보통 gamodeme sampling에는 상위 라인이 있습니다.

동등한 분산 후 범믹틱– 근친교배

전체 요약에는 자손 라인(p와_•_• q)의 혼합에서 평균 대립 유전자 빈도가 포함되었다.이것들은 이제 가상의 범믹틱 ^[13]^{: 382–395}^[14]^{: 49–63}^[29]^{: 35}등가물을 구성하는데 사용될 수 있다.이는 배우자 표본 추출에 의한 변화를 평가하기 위한 "참조"로 볼 수 있다.이 예에서는 다이어그램 오른쪽에 이러한 범믹틱을 추가합니다.따라서 AA의 주파수는 (p_•)² = 0.3979입니다.이는 분산된 벌크(검은색 라벨 "7"의 0.4513)에서 발견된 것보다 적습니다.마찬가지로, aa의 경우, (q_•)² = 0.1303 - 자손 벌크(0.130)의 등가 값보다 작다.분명히 유전자 표류는 호모 접합의 전체 수준을 (0.6411 - 0.5342) = 0.1069만큼 증가시켰다.보완적 접근법에서는 헤테로 접합성을 대신 사용할 수 있다.Aa에 대한 범믹틱 당량은 2 p_•_• q = 0.4658로 표본 벌크(0.3588)의 값보다 높다[검은색 라벨 "8"].표본 추출을 통해 헤테로 접합도가 0.1070 감소했는데, 이는 반올림 오류로 인해 이전의 추정치와 크게 다릅니다.

근친교배계수(f)는 자가수정 초기 섹션에서 소개되었다.여기서, 그것에 대한 공식적인 정의는 고려된다: f는 함께 수정하는 두 개의 "같은" 대립 유전자(즉, A와 A, 또는 a와 a)가 공통 조상의 기원이거나, f는 두 개의 상동 대립 유전자가 자기 동질일 확률이다.^[14]^[27]이항 표본 추출에 의해 제한되는 signamy 파트너를 가진 잠재적 gamodeme의 임의의 배우자를 고려합니다.두 번째 배우자가 첫 번째 배우자와 상동성 자기효소가 될 확률은 1/(2N)이며, 이는 양성소 크기의 역수이다.다섯 가지 예제 자손의 경우 이러한 양은 각각 0.1, 0.0833, 0.1, 0.0833 및 0.125이며 가중 평균은 0.0961입니다.전체 이항 분포에 대해 편견이 없는 경우, 이것은 자손 벌크 예의 근친교배 계수이다.그러나 s = 5에 기초한 예는 무한대에 근접하는 표본 번호(s → θ)에 기초한 적절한 전체 이항 분포와 비교할 때 편향될 가능성이 높다.완전 분포에 대한 f의 또 다른 파생된 정의는 f가 동형 접합성의 상승과 같으며, 이는 이형 접합성의 ^[33]하락과 동일하다는 것이다.예를 들어, 이러한 빈도 변화는 각각 0.1069와 0.1070입니다.이 결과는 위의 결과와 다르며, 이 예에서 전체 기본 분포에 대한 편향이 있음을 나타냅니다.예제 자체의 경우 f = 0.1995와 같이_• 후자의 값을 사용하는 것이 더 좋습니다.

등가 범믹틱의 모집단 평균은 [a (p-q_•_•) + 2 pq_•_• d] + mp로 구할 수 있습니다.유전자 효과 예(그림의 흰색 라벨 '9)를 사용하면 평균은 ${\textstyle P_{\centerdot }=}$ ⋅ $=$ {\ $textstyle P_{\centerdot$ } =} 37 ${\textstyle P_{\centerdot }=}$ .87이다.분산 벌크에서 등가 평균은 36.94(검은색 레이블 "10")로, 0.93만큼 눌려 있습니다.이것은 이 유전자 이동으로 인한 근친교배 우울증입니다.그러나 앞서 기술한 바와 같이 세 자손은 우울하지 않았고(k = 1, 2, 5), 범믹틱 당량보다 훨씬 큰 평균을 가졌다.식물 육종업자가 라인 선택 ^[34]프로그램에서 찾는 라인입니다.

광범위한 이항 표본 추출 – 판믹시아는 복원되었습니까?

이항 표본의 수가 많으면(s → ),), p_• → p_g 및_• q_g → q. 이러한 상황에서 판믹시아가 효과적으로 재검출될 수 있는지 여부가 질문될 수 있습니다.그러나 대립 유전자 빈도의 표본 추출은 여전히 발생하였고, 그 결과²_{p, q} ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ →^[35] ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ 로서 ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ q 2 ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ g ${\textstyle \sigma _{p,\ q}^{2}\to {\tfrac {p_{g}q_{g}}{2N}}}$ N $(\$ _ ${p,\q}^{2}\tfrac {p_{g}_{g}}}{2$ }}}{2}}{tfrac {p_p_p_{g}}}입니다. $N$ 이것은 전체 이항 ^[13]^{: 382–395}^[14]^{: 49–63}분포의 분산입니다.또한 "Wahlund 방정식"은 자손 벌크 호모 접합 주파수를 각각의 평균값(p²_• 또는²_• q)과 ^[13]^{: 382–395}θ의²_{p, q} 합으로 구할 수 있음을 나타낸다.마찬가지로 벌크 헤테로 접합자 주파수는 (2p_•_• q)에서 µ의²_{p, q} 2배를 뺀 값이다.이항 표본 추출에서 발생하는 분산이 눈에 띄게 존재합니다.따라서, s → ,, 자손 유전형 빈도가 여전히 호모 접합 증가 및 헤테로 접합 감소를 나타내더라도, 여전히 자손 수단의 분산과 근친교배 및 근친교배 우울증이 존재한다.즉, 범혼합은 유전자 표류(이항 표본 추출)로 인해 한번 상실되면 다시 파악되지 않는다.단, 교배 ^[36]후 알로게임 F2를 통해 새로운 전위 범믹시아를 개시할 수 있다.

지속적인 유전자 이동 – 분산 및 근친교배 증가

유전자 표류에 대한 이전 논의에서는 프로세스의 한 주기(세대)만 조사했습니다.연속된 세대에 걸쳐 샘플링이 계속되면 θ와²_{p, q} f에서 현저한 변화가 발생합니다.또한, "시간"을 추적하려면 또 다른 "지수"가 필요하다. t = 1 ....y 여기서 y = 고려된 "년"(세대)의 수이다.방법론은 종종 이전에 발생한 ^[13]것에 현재의 이항 증가량(δ = "de novo")을 추가하는 것이다.여기서는 전체 이항 분포를 조사합니다.[간단한 예에서 얻을 수 있는 더 이상의 이점은 없습니다]

§ 경유²_p,q 분산

이전에는 이 분산( ))이 다음과 같이 생각되었습니다.

{p,q}^{2}&=p_{g}q_{g}\/\2N\=p_{g}q_{g}\left({\frac {1}{2})N}}\오른쪽)\\&=p_{g}q_{g}\f\&=p_{g}q_{g}\Delta f\\\scriptstyle {재귀 방정식에 사용되는 경우}\end{aligned}}

시간이 지남에 따라 확장하면 첫 번째 사이클의 결과이기도 합니다. ${\textstyle \sigma _{1}^{2}}$ , § 1 ${\textstyle \sigma _{1}^{2}}$ ( $간단하게$ 말하면, \ $sigma \sigma$ _{ $1}^2})$ 도 마찬가지입니다.사이클 2에서는 이 분산이 다시 생성되어 이번에는 de novo 분산(δ ${\textstyle \Delta \sigma ^{2}}$ 2 \ $textstyle$ \ $Delta$ \ $sigma$ ^ {2 $}$ )이 되어, 이미 존재하고 있던 「carry-over」바리안스로 누적됩니다.두 번째 사이클 변동( ${\textstyle \sigma _{2}^{2}}$ 2 ${\textstyle \sigma _{2}^{2}}$ \ $textstyle \sigma$ _ ${2$ 2} )은 이 두 성분의 가중치 합이다. 무게는 de novo의 경우 ${\textstyle 1}$ 1 { $textstyle$ 1 ${\textstyle 1}$ }이고 ${\textstyle 1}$ , ( ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ - ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ N ${\textstyle \left(1-{\tfrac {1}{2N}}\right)}$ ) { $textstyle \left (1$ - { \ $tfrac {1$ } { $2$ ） $N}}\right)$ ${\textstyle \left(1-\Delta f\right)}$ ( ${\textstyle \left(1-\Delta f\right)}$ - ${\textstyle \left(1-\Delta f\right)}$ f ${\textstyle \left(1-\Delta f\right)}$ ) (\ $textstyle \left (1-\Delta$ f $\right))$ 이월 ${\textstyle \left(1-\Delta f\right)}$ ).

따라서,

\displaystyle _{2}^{2}=\left(1\오른쪽)\Delta \delta ^{2}+\left(1-\Delta f\오른쪽)\display_{1}^2}}

(1)

임의의 시간 t로 일반화하기 위한 확장은 대폭 간소화된 ^[13]^{: 328}후 다음과 같이 됩니다.

\displaystyle \delta _{t}^2}=p_{g}q_{g}\left[1-\left(1-\Delta f\right)]^{t}\right]}

(2)

자손의 평균(분산)의 "분산"을 일으킨 것은 대립 유전자 빈도의 변화였기 때문에, 세대별 δ의²_t 변화는 분산 수준의 변화를 나타낸다.

f를 통한 분산

근친교배계수 검사방법은 .과 유사하며, de novo f(δ f) [recall this is 1/(2 N)]와 이월 f에 각각 기존과 동일한 가중치를 사용한다. ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ( ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ) ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ f ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ + ( ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ f ) ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ \ $textstyle f_{2$ } = \ $left$ ( $1$ \ ${\textstyle f_{2}=\left(1\right)\Delta f+\left(1-\Delta f\right)f_{1}}$ ) $\Delta$ f $+\left(1-\Delta$ f $\right) f_{1}.$ 이는 이전 항의 식 (1)과 유사합니다.

무작위 수정의 유전적 표류에서 발생하는 근친교배.

일반적으로 재배열 ^[13]후

{begin {t} f_{t}&=\Delta f+\left(1-\Delta f\right)f_{t-1}\right)+f_{t-1}\end{aligned

왼쪽 그래프는 다양한 실제 양성소 크기(2N)에 대한 유전적 표류에서 발생하는 20세대 이상의 근친교배 수준을 보여준다.

이 일반 방정식의 추가적인 재배열은 몇 가지 흥미로운 관계를 보여준다.

(A) 간략화 ^[13]후 ( ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ t - ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ - ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ ) ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ f ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ f ( ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ - ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ t ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ - ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ ) ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ f ${\textstyle \left(f_{t}-f_{t-1}\right)=\Delta f\left(1-f_{t-1}\right)=\delta f_{t}}$ t \ $textstyle \$ left ( $f$ _ { $t$ } - f $_$ { $t-1$ } \ $right$ ) $=$ $\Delta$ f $\left(1-f_{t-1}\right)=\delta f_{t$ 왼쪽은 현재와 이전 수준의 근친교배 차이, 즉 근친교배의 변화(θf_t)입니다.이 변경 근친교배('f_t')는 첫 번째 사이클(f가 제로인 경우_t-1)에 대해서만 de novo 근친교배('f')와 동일하다는 점에 주의해 주십시오.

(B) 주목되는 항목은 (1-f_t-1)이며, 이는 "비근친교배 지수"이다.그것은 범믹틱 ^[13]^[14]지수로 알려져 있다. ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ t ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ - ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ $=$ ( ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ - ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ - ${\textstyle P_{t-1}=\left(1-f_{t-1}\right)}$ ) { $textstyle$ P_{ $t-1$ } =\ $left(1-f_{t-1}\right$

(C) 범믹틱 ^[13]^[14]지수를 포함한 더욱 유용한 관계가 나타난다.

{begin {aligned}\Delta f&={t-1}}\&=1-{P_{t-1}}{P_{t-1}}\end{aligned}

(D) and와 f 사이에 키링크가 나타난다.일단...^[13]

{\displaystyle\begin{aligned}f_{t}&=1-\left(1-1\Delta f\오른쪽)^{t}\left(1-f_{0}\right)\end{aligned}}

둘째, f = 0이라고₀ 가정할 때, 이 방정식의 오른쪽은 마지막 하위 섹션의 끝에 있는 방정식 (2)의 괄호 안에 있는 섹션으로 감소한다.즉, 처음에 근친교배가 없는 경우

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

t

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

=

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

f

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

{

textstyle

\

timages _

{

t}

= p

_

{

g

}

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

_ {

g

}

f

_ {

{\textstyle \sigma _{t}^{2}=p_{g}q_{g}f_{t}}

timages }

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

{ timages 2

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

_ { t } =

frac2

{

timagesterstyle

f

_ t

} }

{\textstyle f_{t}={\tfrac {\sigma _{t}^{2}}{p_{g}q_{g}}}}

이항 배우자 표본 추출의 pal 관점은 직접적으로 상호 호환된다.

무작위 수정 내에서 자가 생성

교잡 비료에 대한 무작위 수정

무작위 수정에는 자가 수정이 포함된다는 것은 간과하기 쉽다.Sewall Wright는 무작위 수정의 1/N 비율은 실제로 자가 수정 $\left(\bigotimes \right)$ following $)$ 이며, 나머지 (N-1)/N은 교차 수정 $)\$ 이라는 것을 보여주었습니다.경로 분석과 새로운 수정, 단순화를 따라갑니다.근친교배는 ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ $=$ ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ f ( ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ 1 + ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ - ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ ) + ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ - ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ - ${\textstyle f_{t}=\Delta f\left(1+f_{t-1}\right)+{\tfrac {N-1}{N}}f_{t-1}}$ 1 { $textstyle f_{t$ }=\ $Delta$ f $\left(1+f_{t-1}\right)+{\tfrac {N-1}{t-1$ ^[27]^[37] 이전 재배열 결과인 것으로 밝혀졌다. $이들$ 중 두 가지는 잠재적으로 매우 유용했다. 즉, ( ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ f ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ $δ$ f [ ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ + f ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ - ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ ( 2 ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ - 1) $=$ \ $Delta$ f \ $left [ 1$ + f $_$ { t - 1 ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ } \ $left$ ( 1 + f _ { t - 1 $}$ ${\textstyle f_{t}=\Delta f\left[1+f_{t-1}\left(2N-1\right)\right]}$ right ) ; ( ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ ) ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ - ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ ( ${\textstyle f_{t}=\Delta f\left(1-f_{t-1}\right)+f_{t-1}}$ )

자가화(selfing)가 본질적으로 무작위 수정의 일부일 수 있다는 인식은 이전의 무작위 수정 '교배 계수'의 사용에 관한 몇 가지 문제를 야기한다.분명히, 그렇다면, 자기 비호환 메커니즘을 가진 식물, 암수 식물, 양성 동물을 포함한, 자기 수정이 불가능한 어떤 종에게도 부적절하다.라이트의 방정식은 나중에 수정되어 자기 수정 없이 교차 수정만 수반하는 무작위 수정 버전을 제공하게 되었다.이전에 자가화로 인한 1/N 비율은 이전 사이클에서 발생한 이월 유전자 이동 근친 교배를 정의했다.새로운 버전은 다음과 같습니다.^[13]^{: 166}

({displaystyle f_{\mathsf {X}_{t}}=f_{t-1}+\Delta f\left(1+f_{t-2}-2f_{t-1}\right)})

.

오른쪽 그래프는 표준 무작위 수정 RF와 "혼자 교차 수정" CF에 대해 조정된 무작위 수정 간의 차이를 나타냅니다.알 수 있듯이, 작은 gamodeme 샘플 크기에서는 문제가 심각하지 않습니다.

판믹시아는 랜덤 수정의 동의어가 아니라 랜덤 수정과 크로스 수정의 동의어가 아니라는 점에 유의할 필요가 있다.

호모 접합성과 헤테로 접합성

"샘플 가모뎀 – 유전자 표류"에 대한 하위 섹션에서 일련의 배우자 샘플링이 뒤따랐고, 그 결과 헤테로 접합성을 희생하면서 호모 접합성이 증가했다.이러한 관점에서, 호모 접합성의 증가는 배우자 표본 추출에 기인했다.호모 접합의 수준은 호모 접합이 알로 접합으로 발생했는지 또는 자가 접합으로 발생했는지에 따라서도 볼 수 있다.자가효소 대립 유전자는 동일한 대립 유전자의 기원을 가지며, 그 가능성(빈도)은 정의상 근친교배 계수(f)이다.따라서 합체적으로 발생하는 비율은 (1-f)이다.따라서 일반주파수 p로 존재하는 A함유배우자의 경우 자기효율이 있는 배우자의 전체주파수는 (f p)이다.마찬가지로 a-bearing gametes의 경우 자기효율 주파수는 (f ^[38]q)이다.일관성을 확립하려면 유전자형 주파수에 관한 이 두 가지 관점을 연결해야 합니다.

먼저 자동/알로 관점에 이어 알로 접합 성분을 고려합니다.이는 (1-f)의 빈도로 발생하며, 대립 유전자는 무작위 수정 2차 확장에 따라 결합한다.다음과 같이 됩니다.

\displaystyle \left(1-f\right)\left[p_{0}+q_{0}\right]^{2}+q_{2}\right]+left(1-f\right)\left[2p_0}q_{0}\right]

다음으로 자기효율이 높은 컴포넌트를 검토합니다.이들 대립 유전자는 면적유합체이므로 사실상 자기화이며 AA 또는 aa 유전자형을 생성하지만 헤테로 접합체는 생성되지 않는다.따라서 f

{\textstyle fp_{0}}

{\textstyle fp_{0}}

({

textstyle fp_{0

"AA" 호모 접합체와

{\textstyle fq_{0}}

{\textstyle fq_{0}}

0 ({

textstyle fq_{0

"aa" 호모 접합체를

{\textstyle fp_{0}}

한다.이들 2개의 컴포넌트를 합하면 AA 호모자이고트의 경우

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

(

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

- f )

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

+

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

{\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}

left

(

1-f\right) p_

{

0

}^{2

}+fp_

{0

}\right],

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

[

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

(

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

-

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

f )

{\textstyle \left[\left(1-f\right)q_{0}^{2}+fq_{0}\right]}

0

](\styleft - f)

가 됩니다.

{\textstyle \left(1-f\right)2p_{0}q_{0}}

헤테로 접합체의 ^[13]^{: 65}^[14]경우

{\textstyle \left(1-f\right)2p_{0}q_{0}}

0(\

textstyle \left(1-f\right) 2p_{0}q_

이는 "자기 수정 – 대안" 섹션의 앞부분에서 제시된 것과 동일한 방정식이다.헤테로 접합의 감소에 대한 이유는 여기에서 명확하다.헤테로 접합체는 알로 접합체 성분에서만 발생할 수 있으며, 시료 부피의 빈도는 (1-f)에 불과하므로 헤테로 접합체의 빈도를 제어하는 인자여야 한다.

다음으로 샘플링 시점을 재검토한다.이전에 헤테로 접합체의 감소는 f ${\textstyle f\left(2p_{0}q_{0}\right)}$ ( ${\textstyle f\left(2p_{0}q_{0}\right)}$ ${\textstyle f\left(2p_{0}q_{0}\right)}$ ${\textstyle f\left(2p_{0}q_{0}\right)}$ ${\textstyle f\left(2p_{0}q_{0}\right)}$ 0 $){$ f $\left (2p_{0}q_{0}\$ right ${\textstyle f\left(2p_{0}q_{0}\right)}$ 인 것으로 나타났습니다.이러한 감소는 각 호모 접합체에 균등하게 분포되며, 이들의 기본적인 무작위 수정 기대치에 추가됩니다.따라서 유전자형 빈도는 "AA" 호모지고트의 ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ ( ${\textstyle \left(q_{0}^{2}+fp_{0}q_{0}\right)}$ ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ ${\textstyle \left(q_{0}^{2}+fp_{0}q_{0}\right)}$ + ${\textstyle \left(q_{0}^{2}+fp_{0}q_{0}\right)}$ ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ 0 ${\textstyle \left(p_{0}^{2}+fp_{0}q_{0}\right)}$ ) { $textstyle \left (p_{0}^{$ 2} + $fp_{0}\right}$ { $textstyle \left (q_{0}^2}+fp_{0$ }\ $right}입니다$ $tyle 2p_{0}q_{0}-f\left(2p_{0}q_{0}\right)$ 를 ${\textstyle 2p_{0}q_{0}-f\left(2p_{0}q_{0}\right)}$ 지정합니다.

셋째, 이전 두 관점 간의 일관성을 확립할 필요가 있다.헤테로 접합자 주파수는 두 가지 관점에서 동일하다는 것은 단번에 알 수 있다.그러나 이러한 간단한 결과는 호모 접합체에 대해 즉시 명확하지 않다.위의 auto/allo 단락에 있는 AA 호모이지고트의 최종 방정식을 검토하는 것으로 시작합니다 ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ [ ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ ( ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ - ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ ) ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ + ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ 0 ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ ]{ $textstyle \left$ [ \ lef ( $1$ - f \ $right$ ) p $_$ { 0 } + $fp$ _ { $0$ } ${\textstyle \left[\left(1-f\right)p_{0}^{2}+fp_{0}\right]}$ }. 괄호를 확장하고 공통의 두 용어를 사용하여 다시 수집합니다.그 결과 동업-02− f({\textstyle p_{0}(p_{0}일 경우 ^{2}-p_{0}일 경우 \right)}. 다음은 parenthesized"p20",(1-q)를 읽어야에 대한 p, 그 결과가 되고 p 02− f({\textstyle p_{0}[p_{0}일 경우 \left(1-q_{0}일 경우 \right)-p_{0}일 경우 \right]}. .그 대체에 뒤이어, 신호를 다중화하고, 단순화하며, 관찰하는 것은 간단한 문제이다.최종 결과는 ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ 2 ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ + ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ ${\textstyle p_{0}^{2}+fp_{0}q_{0}}$ 0({ $textstyle p_{0}^2)+fp_{0}q_{0$ 이며, 이는 샘플링 단락에서 AA에 대한 정확한 결과이다.따라서 두 가지 관점은 AA 호모 접합에 대해 일치한다.마찬가지로 aa 시점의 일관성도 나타낼 수 있다.두 관점은 유전자형의 모든 클래스에서 일치한다.

확장된 원칙

기타 수정 패턴

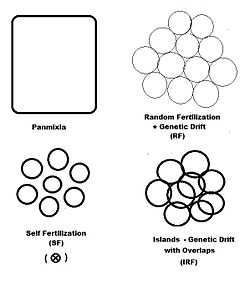
공간 수정 패턴

이전 절에서는 분산 랜덤 수정(유전자 드리프트)을 종합적으로 검토하여 자가수정 및 잡종을 다양한 정도로 검토하였다.왼쪽에 있는 도표는 이 중 처음 두 개의 도표와 또 다른 "공간 기반" 패턴인 섬을 나타내고 있습니다.이것은 분산된 색소(gamodem)를 특징으로 하는 랜덤 수정 패턴으로, 비산포적 랜덤 수정이 발생하는 오버랩(overlap)을 추가한다.섬 패턴에서는, 개개의 gamodeme 사이즈(2N)를 관측할 수 있고, 겹침(m)은 최소한이다.이것은 Sewall Wright의 다양한 가능성 ^[37]중 하나입니다."공간적"에 기초한 수정 패턴 외에도, "유형적" 또는 "관계적" 기준에 기초한 다른 패턴들이 있다.표현형 염기는 (유사 표현형 사이) 구색 수정과 (대립 표현형 사이) 분리 수정이다.관계 패턴에는 자매교차, 사촌교차, 역교차가 포함되며 별도의 섹션에서 고려된다.자기 수정은 공간적 또는 관계적 관점에서 모두 고려될 수 있다.

'섬' 무작위 수정

번식 집단은 표본 ${\textstyle 2N_{k}}$ ${\textstyle 2N_{k}}$ k(\ $textstyle 2N_{k})($ k = 1 ...s)와 비연속 무작위 수정이 발생하는 ${\textstyle m_{k}}$ ${\textstyle m_{k}}$ k $(\$ })의 ${\textstyle m_{k}}$ 겹치는 작은 분산 무작위 수정 색상으로 구성된다. ${\textstyle \left(1-m_{k}\right)}$ 은 ${\textstyle \left(1-m_{k}\right)}$ ( ${\textstyle \left(1-m_{k}\right)}$ - ${\textstyle \left(1-m_{k}\right)}$ m k $){$ $textstyle \left (1$ - $m_{k}\right$ 입니다 ${\textstyle \left(1-m_{k}\right)}$ 대량 집단은 이전 섹션에서 유전자 표류에 대해 그랬던 것처럼 표본 크기, 대립 유전자와 유전자형 빈도 및 자손 평균의 가중 평균으로 구성된다.단, 중복을 위해 각 배우자의 샘플 사이즈를 줄임으로써 ( ${\textstyle \left(1-m_{k}\right)}$ - ${\textstyle \left(1-m_{k}\right)}$ ) ${\textstyle \left(1-m_{k}\right)}$ \ $textstyle \$ left ( 1 - m _ { $k$ } ${\textstyle \left(1-m_{k}\right)}$ $right$ )에 ${\textstyle 2N_{k}}$ ${\textstyle 2N_{k}}$ k ( \ $textstyle 2$ N _ { k } )를 ${\textstyle 2N_{k}}$ 찾을 수 있습니다.

'섬' 무작위 수정

간결하게 하기 위해 첨자가 생략된 상태에서 인수가 계속됩니다. ${\textstyle {\tfrac {1}{2N}}}$ 을 ${\textstyle {\tfrac {1}{2N}}}$ 기억해 주세요{ $textstyle$ { $tfrac$ { 1 } { $2$ $N}}$ 은 ${\textstyle {\tfrac {1}{2N}}}$ 일반적으로 ${\textstyle \Delta f}$ f ${\textstyle$ \ $Delta$ f $}$ 입니다.[여기서 2N은 "섬 조정" 버전이 아니라 이전에 정의된 샘플 크기를 나타냅니다.]

심플화 ^[37]후

^{\mathsf {islands}\Delta f={left(1-m\right)^{2}{2N-m^{2}\left(2N-1\right)}}

m = 0일 때 이 값은 이전 δ f로 감소합니다.이 역수는 위에서 설명한 바와 같이 ( ${\textstyle \left(1-m_{k}\right)}$ - ${\textstyle \left(1-m_{k}\right)}$ k ${\textstyle \left(1-m_{k}\right)}$ ) \ $textstyle \$ left (1 - $m_{k$ }\ ${\textstyle \left(1-m_{k}\right)}$ right ${\textstyle \left(1-m_{k}\right)}$ )에

{\textstyle 2N_{k}}

유효한 ${\textstyle \left(1-m_{k}\right)}$

{\textstyle 2N_{k}}

N

{\textstyle 2N_{k}}

( \

textstyle

2

N

_ {

k

} )"의 추정치를 제공합니다.

이 δf는 또한 이전 근친교배계수로 대체되어 다음과 같은 결과를 얻을 수 있다.

({displaystyle {^{\mathsf {slands}) f_{t}={{\mathsf {islands}}\Delta f_{t}}+\left(1-\{\mathsf {islands}}\right)\{{{\mathsf {t-1}}})\{\mathsf})

여기서 t는 이전과 같이 세대별 인덱스입니다.

효과적인 중첩 비율은 다음과 같이 얻을 ^[37]수 있다.

{\displaystyle m_{t}=1-\left[{\frac {2N\{\mathsf {섬}}\Delta f_{t}}{\left(2N-1\right)\{\mathsf {섬}}\{\mathsf}}}\right]

오른쪽 그래프는 일반 분산 임의 수정(RF)(m=0)의 경우 2N = 50의 양성소 크기에 대한 근친교배와 섬 무작위 수정의 네 가지 중복 수준(m = 0.0625, 0.125, 0.25, 0.5)에 대한 근친교배를 보여준다.중복되는 부분에서의 비분산 무작위 수정으로 인한 근친교배 감소가 실제로 있었다.특히 m → 0.50으로 주목할 만하다.Sewall Wright는 이 값이 이 ^[37]접근방식을 사용하는 데 한계가 되어야 한다고 제안했다.

대립 유전자 교환 – 대립 유전자 치환

유전자 모델은 "입력"과 "출력"의 관점에서 유전 경로를 검사하며, 수정은 하나를 다른 것으로 변환하는 "과정"이다.또 다른 관점에서는 "과정" 자체에 초점을 맞추고 접합자 유전자형을 대립 유전자 교란에서 발생하는 것으로 간주한다.특히, 셔플 중에 하나의 대립 유전자가 다른 대립 유전자에 대해 "치환"된 것처럼 결과를 간주하고, 이러한 관점에서 벗어난 잔류물을 간주한다.이것은 그의 유전자 ^[14]통계를 생성하기 위해 빈도와 효과를 사용하는 것에 더하여 피셔의 ^[8]방법의 필수적인 부분을 형성했다.대립 유전자 치환 대체물의 산술적 도출이 다음에 이루어진다.^[14]^{: 113}

대립 유전자 치환 분석

p gametes (A)와 q gametes (a)로 구성된 "base" gamodeme에서 배우자의 일반적인 무작위 수정이 단일 대립 유전자(A 또는 a, 둘 다 포함)를 포함하는 배우자의 "홍수"로 수정으로 대체된다고 가정하자.접합 결과는 기초적인 "염기" 색소데임에서 대체 대립 유전자를 "치환"한 "홍수" 대립 유전자의 관점에서 해석될 수 있다.이 그림은 이 관점을 따르는 데 도움이 됩니다.상부는 A 치환을, 하부는 치환을 나타내고 있습니다.(그림의 "RF 대립 유전자"는 "기저" 색소단계의 대립 유전자입니다.)

윗부분을 먼저 고려하세요.염기 A는 p의 빈도로 존재하기 때문에 치환기 A는 p의 빈도로 수정하여 a의 대립유전자 효과를 갖는 접합자 AA가 된다.따라서 결과에 대한 기여도는 ${\textstyle \left(p\ a\right)}$ ( ${\textstyle \left(p\ a\right)}$ a ${\textstyle \left(p\ a\right)}$ ) { $textstyle \left(p\a\$ right ${\textstyle \left(p\ a\right)}$ 입니다. 마찬가지로 대체물이 염기 a를 수정하는 경우(q의 빈도와 d의 헤테로 접합자 효과를 갖는 Aa), 기여도는 ${\textstyle \left(q\ d\right)}$ ( ${\textstyle \left(q\ d\right)}$ d $)$ \ $textstyle$ \ $left(q\d\$ right ${\textstyle \left(q\ d\right)}$ 가 됩니다.따라서 A에 의한 치환의 전체적인 결과는 ( ${\textstyle \left(p\ a+q\ d\right)}$ + ${\textstyle \left(p\ a+q\ d\right)}$ d ${\textstyle \left(p\ a+q\ d\right)}$ ) { $textstyle \left(p\a+q\d\$ right ${\textstyle \left(p\ a+q\ d\right)}$ 입니다 ${\textstyle \left(p\ a+q\ d\right)}$ 이것은 현재 모집단 평균(앞부분 참조)을 향해 있습니다. ${\textstyle \left(p\ a+q\ d\right)-G}$ 평균으로부터의 편차로 표현됩니다 ${\textstyle \left(p\ a+q\ d\right)-G}$ ( p ${\textstyle \left(p\ a+q\ d\right)-G}$ + ${\textstyle \left(p\ a+q\ d\right)-G}$ d ${\textstyle \left(p\ a+q\ d\right)-G}$ ) - $G$ \ $textstyle \$ left ( $p$ \ $a +$ q \ $d$ \ $right$ ) - G ${\textstyle \left(p\ a+q\ d\right)-G}$ }

약간의 대수적 단순화 후에, 이것은

\displaystyle _{A}=q\left[a+\left(q-p\right)d\right]

- A의 치환 효과

빈도와 유전자 효과의 차이를 고려하여 그림 하부에 병렬 추론을 적용할 수 있다.그 결과 a의 치환 효과가 나타납니다.

\displaystyle _{a}=-\p\left[a+\left(q-p\right)d\right]

브래킷 내부의 공통 요인은 평균 대립 유전자 치환 ^[14]^{: 113}효과입니다.

\displaystyle \displaystyle = a+\left(q-p\right)d}

보다 직접적인 방법으로 도출할 수도 있지만 결과는 동일합니다.^[39]

후속 섹션에서 이러한 치환 효과는 이러한 새로운 효과(치환 기대)에 의해 예측된 분할(치환 기대)과 이러한 기대와 이전의 유전자 모델 효과 사이의 잔류(치환 편차)로 구성된 유전자 모델 유전자형을 정의하는 데 도움이 된다.기대치는 번식값이라고도 하며 편차는 우세 편차라고도 합니다.

궁극적으로, 치환 기대에서 발생하는 분산은 소위 부가적 유전자 분산())^[14]이²_A 되는 반면, 치환 편차에서 발생하는 분산은 소위 우성 분산(σ²_D)이 된다.이 두 용어 모두 이러한 분산의 진정한 의미를 반영하지 않는 것이 눈에 띈다."유전자 분산"은 가법 유전자 분산보다 덜 의심스럽고, 이 ^[8]^[29]^{: 33}분할에 대한 피셔 자신의 이름과 더 일치한다.우위 편차 분산의 오해의 소지가 적은 이름은 "준우위 분산"이다[자세한 설명은 다음 절 참조].여기서는 후자의 용어를 사용하는 것이 좋습니다.

유전자 효과 재정의

유전자 모델 효과(a, d, -a)는 이전 Alle Substitution 섹션에서 처음 논의된 치환으로부터의 편차를 도출하는 데 곧 중요하다.그러나 그러한 연습에서 유용하게 사용하기 전에 스스로 재정의해야 한다.이들은 먼저 모집단 평균(G)을 중심으로 다시 집중되어야 하며, 다음으로 평균 대립 유전자 치환 효과인 β의 함수로 재배치되어야 한다.

우선 재집중화를 검토한다.AA의 재집중 효과는 a• = a - G이며, 단순화 후 a• = 2q(a-pd)가 된다.Aa에 대한 유사한 효과는 단순화 후 d• = d - G = a(q-p) + d(1-2pq)이다.마지막으로 aa의 재집중 효과는 (-a)• = -2p(a+^[14]^{: 116–119}qd)이다.

둘째, 이러한 재집중 효과의 재배열을 β의 함수로 간주한다."알레 치환" 섹션에서 β = [a +(q-p)d]를 상기하면, 재배열은 = [β -(q-p)d]를 나타낸다.이것을 a•에 대입하여 단순화하면 최종 버전은 a•• = 2q(β-qd)가 된다.마찬가지로 d•는 d• = β(q-p) + 2pqd;가 되고, (-a)•는 (-a)• = -2p(β+pd)^[14]^{: 118}가 된다.

유전자형 대체 – 기대와 편차

접합자 유전자형이 이 모든 제제의 대상이다.호모 접합 유전자형 AA는 A의 두 가지 치환 효과의 결합체이며, 각 성별에서 하나씩이다.따라서_AA 치환 기대치는 β = 2β_A = 2qβ이다(앞 섹션 참조).마찬가지로_Aa Aa의 치환기대는 β_A = β_a + β = (q-p)β이고, aa의 경우_aa β = 2β_a = -2pβ이다.유전자형의 이러한 대체 기대치를 ^[14]^{: 114–116}번식치라고도 한다.

치환 편차는 이러한 기대와 이전 절의 2단계 재정의 후의 유전자 효과 사이의 차이이다.따라서_AA 단순화 후 d = a• - β_AA = -2qd이다².마찬가지로_Aa 단순화 후 d = d• - β_Aa = 2pqd이다.마지막으로_aa 단순화 ^[14]^{: 116–119}후 d = (-a)• - β_aa = -2pd이다².이러한 모든 치환 편차는 궁극적으로 기호로 ["d" + 첨자]를 사용하는 유전자 효과 d의 함수이다.하지만, 그들이 전체 유전자 모델에서 우위(헤테로 접합증)를 설명하는 것으로 간주하는 것은 논리적으로 심각한 비순서이다: 그들은 단지 "d"의 기능일 뿐이고 시스템 내 "d"의 감사가 아니다.대체 예상을 벗어난 결과입니다.

"대체 기대"는 궁극적으로²_A ((일명 "첨가적" 유전자 분산)을 발생시키고, "대체 편차"는 ((일명 "우위적" 유전자 분산)을²_D 발생시킨다.단, 평균 치환 효과(β)에는 "d"도 포함되어 있다는 점에 유의해야 한다(이전 섹션 참조). 이는 우성이 "추가" 분산에도 포함되어 있음을 나타낸다(유래에 대한 유전자형 분산에 대한 다음 섹션 참조).또한 [이전 단락 참조] "대체 편차"는 시스템에서 우세함을 설명하지 않지만 (대체 기대치로부터의 편차일 뿐) 대수적으로 "d"의 함수로 구성된다는 것을 기억한다.이러한 각 분산에 대해 더 적절한 이름은 δ²_B(교배 기대치) 및 δ²_δ(교배 편차) 분산일 수 있습니다.다만, 전술한 바와 같이, 「유전자」(Genic)와 「준지배」(Quasi-Dominance)가 각각 바람직하다.

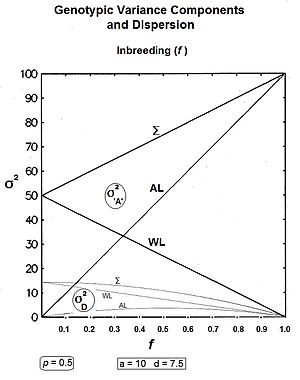
유전자형 분산

유전자형 분산을 정의하고 분할하는 데는 두 가지 주요 접근법이 있다.하나는 유전자 모델 ^[40]효과에 기초하고, 다른 하나는 유전자형 치환^[14] 효과에 기초하며,^[36] 그것들은 서로 대수적으로 상호 변환 가능하다.이 절에서는 근친교배 및 분산의 효과를 제외하고 기본적인 무작위 수정 도출을 고려한다.이것은 나중에 더 일반적인 해결책에 도달하기 위해 다루어집니다.이 단유전학적 치료가 다유전학적 치료로 대체될 때까지, 그리고 후생유전학의 발견에 비추어 서간시스가 해결될 때까지 유전형 분산은 여기서 고려되는 성분만을 가진다.

유전자 모델 어프로치– Mather Jinks Hayman

유전자 모델 효과를 이용한 유전자형 분산 성분.

보정 계수(CF)를 빼서 보정되지 않은 제곱합(USS)을 보정하는 생체 측정 방식을 따르는 것이 편리합니다.USS는 주파수를 통해 모든 효과를 조사했기 때문에 각 유전자형 빈도의 곱과 유전자 효과의 제곱을 합한 값으로 구할 수 있다.이 경우의 CF는 평균 제곱입니다.그 결과 SS가 됩니다.이 역시 주파수를 사용하기 때문에 즉시 ^[9]분산이 됩니다.

${\textstyle {\mathsf {CF}}={\mathsf {G}}^{2}}$ S ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ a ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ + ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ d ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ + ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ 2 ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ( - ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ) ${\textstyle {\mathsf {USS}}=p^{2}a^{2}+2pqd^{2}+q^{2}(-a)^{2}}$ ( \ $textstyle$ { $USS$ } = $p^{2} a^{2$ } + $q^{2}$ ( - $a$ ) ${\textstyle {\mathsf {CF}}={\mathsf {G}}^{2}}$ ${\textstyle {\mathsf {CF}}={\mathsf {G}}^{2}}$ ( \ $textstyle {mathfs$ = $CF}$ ) ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$ ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$ ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$ ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$ - ${\textstyle {\mathsf {SS}}={\mathsf {USS}}-{\mathsf {CF}}}$ F $({$ }} = { $uss}}-{\mathsf {CF}})$

부분 심플화 후

{{displaystyle {text {aligned}\sigma _{G}^{2}+(q-p)4pqad+2pqd^{2}+(2pq)^{2}\&=\sigma _{a}^2}+({\text {weighted-cance})_{d}_{d2}+({d})_ad^{d2}+({d})_d})

마지막 줄은 Mather의 ^[40]^{: 212}^[41]^[42]용어입니다.

단, γ는²_a 호모 접합체 또는 알레산 분산이고, γ는²_d 헤테로 접합체 또는 우성 분산이다.치환 편차 분산(θ²_D)도 존재합니다.(weighted_covariance)_ad^[43]는 여기서 "cov_ad"로 축약됩니다.

이들 성분은 그림에서 p의 모든 값에 걸쳐 표시됩니다.p_ad > 0.5의 경우 cov는 음수입니다.

이들 성분의 대부분은 중심 초점이 호모 접합 중간점(mp)에서 모집단 평균(G)으로 변화함에 따라 영향을 받으며, 호모 접합은 보정 계수의 기초가 된다.COV_ad 및 치환 편차 분산은 이 이동의 산물일 뿐입니다.대립 유전자와 우성 분산은 원래 유전자 모델의 진정한 유전자 분할이며, 유일한 EU 유전자 구성 요소입니다.그 후에도 대립 유전자 분산의 대수식은 G의 존재에 의해 영향을 받는다: mp에서 ^[36]G로의 이동에 의해 영향을 받지 않는 것은 우성 분산(즉 δ²_d)일 뿐이다.이러한 통찰력은 일반적으로 인정받지 못합니다.

[마더 형식] 용어를 더 모으면 1 ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ + ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ δ + ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ 3 + ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ 2 ${\$ $+$ {\ $tfrac$ {1} ${{$ 2}} ${\mathsf$ { $F}$ {\prime} {\ $tf}$ {\mathsf} {\f} {{\ $f}$ {\tf} {\frac} {\f} {\f}이(으)이)이( ${\textstyle {\tfrac {1}{2}}{\mathsf {D}}+{\tfrac {1}{2}}{\mathsf {F}}^{\prime }+{\tfrac {1}{2}}{\mathsf {H}}_{3}+{\tfrac {1}{4}}{\mathsf {H}}_{2}}$ 됩니다. ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ 1 ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ( ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ - ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ) ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ ${\textstyle {\tfrac {1}{2}}{\mathsf {H}}_{3}=(q-p)^{2}{\tfrac {1}{2}}{\mathsf {H}}_{1}=(q-p)^{2}2pqd^{2}}$ 2 { \ $textstyle$ { $tfrac$ { 1 } $_ {$ } = { q - p $}$ = ( q - p )^2 $}$ {\ $tfrac {1}$ {2 $}$ {\ $mathsf {H} _$ { $1 =$ ( q - p) $2p$ q d $}$ $2$ } 이 기능은 나중에 유용합니다.

마지막으로 주어진 재배열 후에 처음 세 항을 함께 결합하고, 추가로 재배열하고, 단순화하면, 그 결과는 피셔 치환 예상의 분산이 된다.

즉, $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ 2 $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ 2 + $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ + $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ $\sigma _{A}^{2}=\sigma _{a}^{2}+{\mathsf {cov}}_{ad}+\sigma _{d}^{2}$ 2 \ $displaystyle \ display$ _ { A }^{2} = \ $sigma$ _ { $a$ }^2 $}$ + { \ $mathsf$ { $cov }$ + { $ad$ } + \ $sigma$ _ { $d$ }^ $2$ }

특히 is이²_A σ이²_a 아닌 것에 주의해 주세요.첫 번째는 대체 기대치 분산이고, 두 번째는 대립 유전자 ^[45]분산입니다.또한 θ²_D(치환-탈이차이)가 θ²_d(우성차이)가 아니라는 점에 유의하고 보정계수에 G를 사용하여 발생한 아티팩트임을 기억한다.[위의 '파란 단락' 참조]이것은 이제 "준지배적" 분산으로 언급될 것이다.

또, θ²_D < θ²_d ("2pq"는 항상 분수)이며, (1) θ²_D = 2pq θ²_d 및 (2) θ²_d = θ²_D / (2pq)라는 점에 주의해 주세요.즉, δ가²_D 모델의 우성 분산을 정량화하지 않는 것이 확인된다.그것을 하는 것은 which입니다²_d.단, 2pq를 이용할 수 있는 경우 우성분산²_D(δ²_d)은 δ에서 쉽게 추정할 수 있다.

그림에서 이러한 결과는 still²_a²_D, and²_d, cov를_ad 누적하여 ,를²_A 얻으면서 still은 분리된 상태로 둘 수 있다.그림에서도 θ < , expected²_D < , , , it²_d 。

전체 결과(Fisher 형식)는 다음과 같습니다.

{\displaystyle {transpired}\sigma _{G}^2}&=2pq\left[a+(q-p)d\right]^{2}+\sigma _{D}^{2}\\\\\sigma _{D}^2\\left[sigma]

Fisherian 구성요소는 방금 도출되었지만, 대체 효과 자체를 통한 파생도 다음 절에서 설명한다.

대립 유전자 치환 접근법– Fisher

대립 유전 치환 효과를 사용하는 유전자형 분산 성분.

대립 유전자 치환에 대한 몇 가지 초기 섹션을 참조하면 두 가지 궁극적인 효과는 유전자형 치환 기대와 유전자형 치환 편차라는 것을 알 수 있다.이러한 각 값은 이미 랜덤 수정 모집단 평균(G)으로부터의 편차로 정의되어 있습니다.따라서 각 유전자형에 대해 주파수의 곱과 해당 효과의 제곱을 구하고 이를 축적하여 직접 SS와 ^[46]θ를² 얻는다.자세한 내용은 다음과 같습니다.

δ = p²_AA² β + 2pq_Aa² β²_aa² + q β로 단순화되며²_A, 이는 δ = 2pqβ로² 유전자²_A 분산이다.

θ = p²_AA² d + 2pq_Aa²_aa² d + q d. 이는 θ²_D = (2pq²)² d로 단순화된다²_D. 즉, 준지배적 분산이다.

이러한 결과가 누적되면 = + 가 됩니다²_G²_A²_D.이러한 컴포넌트는 오른쪽 그래프에 표시됩니다.평균 대립 유전자 치환 효과도 그래프로 나타내지만, 기호는 "β"(여기서 사용되는)가 아니라 "α"(인용에서 흔히 볼 수 있는)이다.

그러나 다시 한 번 이들 컴포넌트의 진정한 의미와 정체성에 대한 이전의 논의를 참조해 주십시오.피셔 자신은 이러한 현대 용어를 자신의 구성요소에 사용하지 않았습니다.그가 "유전자적" 분산이라고 이름 붙인 치환 기대 분산과 "유전자적" 분산 사이의 이름 없는 잔차로 간주한 치환 편차 분산은 단순히 "유전자" 분산과 "유전자" ^[8]^[29]^{: 33}^[47]^[48]분산 사이의 잔차로 간주했다.[이 글에서 사용된 용어와 파생어는 Fisher 자신의 용어와 완전히 일치합니다]기대 변동에 대한 Mather의 용어인 "genic"^[40]은 피셔의 용어에서 파생된 것으로, "genetic"의 사용을 피한다(사용이 너무 일반화되어 현재 상황에서 가치가 없다).그 기원은 현대의 잘못된 용어인 "추가적"과 "지배적" 차이에서 모호하다.

이 대립 유전자 치환 접근방식은 구성 요소를 개별적으로 정의한 후 최종 유전자형 분산을 얻기 위해 합산한 것에 유의하십시오.반대로 유전자 모델 접근방식은 전체 상황(성분 및 전체)을 하나의 운동으로 도출했다.이로 인해 발생하는 상여금은 ①의²_A 실제 구조에 대한 폭로로 ②와 ②의²_d 실제 의미와 상대적 크기(이전²_D 항 참조)였다.또한 "Mather" 분석이 더 유익하고 "Fisher" 분석이 항상 그것으로부터 구성될 수 있다는 것이 명백하다.그러나_ad COV에 대한 정보가 누락되기 때문에 반대의 변환은 불가능합니다.

분산 및 유전자형 분산

유전자 표류에 관한 부분과 근친 교배에 대해 논의하는 다른 부분에서 대립 유전자 주파수 샘플링의 주요 결과는 자손 수단의 분산이었다.이 평균 집합에는 자체 평균이 있으며 분산인 행간 분산도 있습니다.(이것은 대립 유전자의 빈도가 아닌 속성 자체의 변화입니다).다음 세대에 걸쳐 분산이 더욱 심화됨에 따라 이러한 라인 간 분산은 증가할 것으로 예상된다.반대로 호모 접합성이 증가하면 라인 내 분산이 감소할 것으로 예상됩니다.따라서 총 분산이 변화하고 있는지, 변화하고 있다면 어떤 방향으로 변화한다면 어떤 방향으로 변화하고 있는가?지금까지 이러한 문제는 유전자 모델 구성 요소보다는 유전체( )) 및 준지배성( )) 분산의 관점에서 제시되어 왔다.이 작업은 여기서도 실시됩니다.

중요한 개요 방정식은 Sewall ^[13]Wright에서 유래하며, 극단의 가중 평균에 ${\textstyle f}$ 한 근친 $유전형$ 분산의 개요이며, ${\textstyle f}$ 가중치는 근친교배계수 f $\textstyle$ f에 대해 2차이다.이 방정식은 다음과 같습니다.

\displaystyle _{G_{f}^{2}=\left(1-f\right)\sigma _{G_{0}^2}+f\left(1-f\right)\left [G_{0}-G_{1}\right]^{2}+f\sigma _{G_{1}\right}

${\textstyle f}$ 서 ${\textstyle f}$ f { $textstyle$ $f$ $}$ 는 ${\textstyle f}$ 근친교배계수이고, ${\textstyle \sigma _{G_{0}}^{2}}$ G ${\textstyle \sigma _{G_{0}}^{2}}$ ${\textstyle \sigma _{G_{0}}^{2}}$ ${{G_$ ${0$ $}^2$ }는 ${\textstyle \sigma _{G_{0}}^{2}}$ f=0에서의 유전자형 분산이며, ${\textstyle \sigma _{G_{1}}^{2}}$ ${\textstyle \sigma _{G_{1}}^{2}}$ 1 ${\textstyle \sigma _{G_{1}}^{2}}$ {{ $G_{1}^{2}}$ 는 ${\textstyle \sigma _{G_{1}}^{2}}$ f=1, G ${\textstyle G_{0}}$ ${{$ G_0}^{2 $}}$ 은 ${\textstyle G_{0}}$ 모집단의 평균이다.}}은 ${\textstyle G_{1}}$ (는) f=1에서 모집단 평균입니다 $.$

${\textstyle \left(1-f\right)}$ - ${\textstyle \left(1-f\right)}$ ) \ $textstyle \left (1-f\$ right) 성분 ${\textstyle \left(1-f\right)}$ [위 방정식]은 자손 계열 내의 분산 감소를 개략적으로 나타냅니다. ${\textstyle f}$ {\ $textstyle$ f $}$ 구성요소는 자손 계통 간 편차의 증가를 해결합니다. ${\textstyle f\left(1-f\right)}$ 으로 f ${\textstyle f\left(1-f\right)}$ 1 ${\textstyle f\left(1-f\right)}$ - $)$ { $textstyle$ f $\left(1-f\right)}$ ${\textstyle f\left(1-f\right)}$ 이 ${\textstyle f\left(1-f\right)}$ (다음 줄에) 표시되어 준우위차이에 ^[13]대처합니다.^{: 99 & 130} 이러한 컴포넌트는 한층 더 확장될 수 있기 때문에, 한층 더 통찰력을 얻을 수 있습니다.그 결과, 다음과 같이 됩니다.

\displaystyle _{G_{f}^{2}=\left(1-f\right)\left[\sigma _{A_{0}^{2}\right]+f\left(4pq\a^{2}\right)+f\left(1-f\right d2]

첫째²_G(0), § [위 식에서]는 두 개의 하위 성분을 나타내도록 확장되었다["유전자 분산" 섹션 참조].다음으로²_G(1) 4pqa로² 변환되어 다음 항에서 파생됩니다.세 번째 성분의 대체는 모집단 평균의 두 "친교배 극단" 사이의 차이이다[모집단 ^[36]평균 섹션 참조].

유전자형 분산의 분산 및 성분

요약: 라인 내 컴포넌트는 ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ ( ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ ) a ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{A_{0}}^{2}}$ 2 \ $textstyle \$ left ( 1 - f \ $right$ )\ $sigma$ _ { A _ { $0$ }^ $2$ } ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ 및 ( ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ) ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ 2 \ $textstyle \ left$ ( 1 - f \ $right$ )\ ${\textstyle 2f\ \sigma _{a_{0}}^{2}}$ ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ _ { $D$ _ { 0 ${\textstyle \left(1-f\right)\sigma _{D_{0}}^{2}}$ ${\textstyle 2f\ \sigma _{a_{0}}^{2}}$ ;- 。 ${\textstyle \left(f-f^{2}\right)\sigma _{D_{0}}^{2}}$ ) ${\textstyle \left(f-f^{2}\right)\sigma _{D_{0}}^{2}}$ D ${\textstyle \left(f-f^{2}\right)\sigma _{D_{0}}^{2}}$ 2 \ $textstyle \$ left ( f - $f^$ { $2}$ \ right ) \ $sigma _$ { D _ { 0 } 、 { $2$ ^[36]} 。

분산의 개발

재배열은 다음을 제공합니다.

({displaystyle {arget {aligned}\displaystyle _ {A_{inbrid}^2}&= left (1+f\right)^{2}&= {A_{f\right}^2}\left (1+f\right)\end}\sigma _{A_{{f\right}{2}\left}}}}\lected}_{A_{A_{2}}}\right}\lected}\lected}\left}

마지막 줄의 버전에 대해서는 다음 섹션에서 자세히 설명합니다.

유사하게,

{displaystyle {arged}\left(1-f\right)^{2}&={D_{D_{0}^2}+\left(f-f^{2}\right)\sigma_{D_{2\right}\&=\left(1-f^{2\right)_Sigma_Right)_{D_{D_{{{D}_{{{{D}_Right

왼쪽 그래프는 p = 0.5에 대해 f의 모든 값에 걸쳐 세 개의 준분산(준분산)과 세 개의 준분산(준분산)을 보여준다.오른쪽 그래프는 유전자형 분산 분할(각 유전자 분할 및 준 유전자 분할의 합계)이 10세대에 걸쳐 변화하는 것을 보여준다(예: f = 0.10).

첫 번째로, 총 분산에 대한 질문[그래프의 δ]에 대한 답변: 유전자 분산은 근친교배 계수와 선형적으로 상승하여 시작 수준의 두 배에서 최대화된다.준우위 분산은 0에서 끝날 때까지 (1 - f² )의 비율로 감소한다.낮은 수준의 f에서는 감소가 매우 점진적으로 이루어지지만, 높은 수준의 f에 따라 감소가 가속화됩니다.

둘째, 다른 트렌드를 주목하세요.직감적으로, 근친 교배가 계속되면 행내 분산이 제로로 감소합니다.이것은 (양쪽 모두 같은 선형 레이트(1-f))로 보입니다.두 선분산 모두 f = 0.5까지 근친교배, 2f의 속도에서 유전자 분산, (f - f²)의 속도에서 준균형 분산과 함께 증가한다.단, f > 0.5에서는 트렌드가 변화합니다.선간 일반 분산은 총 일반 분산과 같아질 때까지 선형 증가를 계속합니다.그러나 (f - f²)도 f > 0.5일 ^[36]때 감소하기 때문에 중간선 준우위 분산은 0을 향해 감소한다.

§의²_G(1) 파생

f=1일 때 헤테로 접합성은 0이고, 라인 내 분산은 0이며, 따라서 모든 유전자형 분산은 라인 간 분산과 우성 분산 고갈이라는 것을 기억한다.즉, θ는²_G(1) 완전히 근친교배된 선평균 간의 차이이다.이러한 평균(G₁, 실제로)이 G = a(p-q)임을 ["자율화 후 평균" 섹션으로부터] 더 상기한다.p를 (1-q)로 치환하면 G = a (1 - 2q)^[14]^{: 265} = a - 2aq가 된다₁.따라서 실제로는 is이²_G(1) actually입니다²_(a-2aq).일반적으로 차이(x-y)의 분산은 [σ²_x + - - 2²_y cov_xy ^[49]^{: 100}^[50]]입니다.^{: 232} 따라서 δ²_G(1) = [ δ²_a + δ²_2aq - 2 cov_{(a, 2aq)} ]. 그러나 a(알레알레 효과)와 q(알레알레 빈도)는 독립적이므로 이 공분산은 0입니다.또한 a는 한 줄에서 다음 줄까지의 상수이므로 θ도²_a 0이다.또한 2a는 다른 상수(k)이므로 θ는²_2aq θ형이다²_{k X}.일반적으로 분산 is은²_{k X} k .^[50]^{: 232}과²_X 같다². 이 모든 것을 종합하면 σ²_(a-2aq) = (2a)² .이²_q 드러난다. ["계속 유전자 표류" 섹션으로부터 σ²_q = pq f. 이 현재 유도 내에서 f=1이면, 이것은 pq 1이 되고, 이것은 앞의 것으로 치환된다.

최종 결과는 σ²_G(1) = σ²_(a-2aq) = 4a² pq = 2 (2pq² a) = 2 σ²_a 입니다.

f²_G(1) ] = f²_a 2 . ] ] 。[이 마지막 f는 최초의 Sewall Wright 방정식에서 나온 것이다: 위의 두 줄에서 도출된 파생에서 f는 "1"로 방금 설정된 것이 아니다.]

총 분산 유전자 분산 – β²_A(f)_f

이전 섹션에서는 라인 내 유전자 분산은 치환 유래 유전자 분산( ))에²_A 기초하지만 라인 간 유전자 분산은 유전자 모델 알레릭 분산( ).)에²_a 기초한다.이 두 가지를 단순히 더해서 총 유전자 분산을 얻을 수는 없습니다.이 문제를 피하기 위한 한 가지 접근법은 평균 대립 유전자 치환 효과의 도출을 다시 방문하고 분산 효과를 포함하는 버전 (β_f)을 구축하는 것이었다.Crow와 Kimura는 앞에서 설명한 재중심 대립 유전자 효과(a•, d•, (-a)• )를 사용하여 이를 달성했다^[13].그러나, 그 후에 총 제네릭 분산을 약간 낮게 평가한 것이 발견되었고, 새로운 분산 기반 파생이 개선된 ^[36]버전으로 이어졌다.

정제_f 버전은 β = { a² + [ ( 1 - f ) / ( 1 + f ) ]2 ( q - p )ad + [ ( 1 - f ) / ( 1 + f ) ] (q - ²p )d² } 입니다.

따라서, δ²_A(f) = (1 + f ) 2pq_f β는 [(1-f) δ²_A(0) + 2f δ²_a(0) ]와 정확히 일치한다.

전체 및 분할 분산 준지배적 분산

총 유전자 분산은 그 자체의 권리에 내재된 관심사이다.그러나 ^[36]고든이 개선하기 전에는 또 다른 중요한 용도가 있었다."분산"된 준지배력에 대한 현존하는 추정치는 없었다.이는 Sewall Wright의 근친 유전형 분산과 총 "분산" 유전형 분산 사이의 차이로 추정되었다[이전 섹션 참조].그러나 이형 접합성의 감소에도 불구하고 총 준우위성 ^[14]분산이 근친교배 초기에 증가하는 것으로 보였기 때문에 이상 징후가 나타났다.^{: 128} ^{: 266}

이전 하위 섹션의 개선으로 이 이상이 ^[36]수정되었습니다.동시에, 총 준지배적 분산에 대한 직접 해법을 얻었고, 따라서 이전의 "감산" 방법이 필요하지 않았다.또한 준지배적 분산의 라인 간 및 라인 내 분할에 대한 직접 해법도 처음으로 얻었다.[이것들은 "분산 및 유전자형 분산" 섹션에서 제시되었습니다.]

환경차이

환경변화는 표현형 다양성으로 유전학에서 기인할 수 없다.단순하게 들리지만 두 가지를 분리하기 위해 필요한 실험 설계는 매우 세심한 계획이 필요합니다."외부" 환경도 공간 및 시간 구성요소("사이트") 및 "년")로 나눌 수 있으며 "리터" 또는 "가족" 및 "문화" 또는 "역사"와 같은 파티션으로 나눌 수 있습니다.이러한 성분은 연구에 사용된 실제 실험 모델에 매우 의존합니다.이러한 문제는 연구 자체에서 매우 중요하지만, 양적 유전학에 대한 이 기사에서는 이 개요로 충분할 것이다.

단, 요약에는 적절한 장소입니다.

표현형 분산 = 유전자형 분산 + 환경 분산 + 유전자형-환경 상호작용 + 실험 "오류" 분산

즉, θ²_P = θ²_G + θ²_E + θ²_GE + θ²

또는 ²²_P = ²²_A + ²²_D + ²²_I + ²²_E + ²²_GE

유전자형 분산(G)을 "유전자적"(A), "준우위적"(D) 및 "유전자적"(I)^[51] 성분 분산으로 나눈 후.

환경 분산은 "상속성" 및 "상관 속성"과 같은 다른 섹션에 나타납니다.

유전성과 반복성

특성의 유전성은 유전형 분산 또는 유전형 분산의 일부 성분이든 유전형 분산에 기인하는 총(phetotype) 분산의² 비율이다.그것은 표현형 변화가 유전학에 기인하는 정도를 수량화한다: 그러나 정확한 의미는 비율의 ^[52]분자에 사용되는 유전자 분산 분할에 따라 달라진다.유전성에 ^[53]대한 연구 추정치에는 모든 추정 통계량과 마찬가지로 표준 오차가 있습니다.

여기서 분자 분산은 전체 유전자형 분산( ),)이며²_G, 유전율은 "광의" 유전율(H²)로 알려져 있습니다.그것은 속성의 변동성이 유전학 전체에 의해 결정되는 정도를 수량화한다.

디스플레이 스타일H^{2}&=sigma frac {{G}^{2}{\sigma _{P}^{2}\=sigma frac {{A}^{2}+\sigma _{D}^2}{\sigma _{{P}^2}}\\\\&sigma frac {{{{{{\c}^{{{{}}}}

[유전자형 분산 섹션 참조]

분자에 유전자 분산(δ²_A)만 사용되는 경우, 유전율은 "좁은 감각"(h²)이라고 할 수 있다.표현형 분산이 피셔의 대체 기대 분산에 의해 결정되는 정도를 수량화한다.

({displaystyle {displaystyle _{A}^{2}&=sigma _{P}^{2}}\&=sigma frac {{p}^2}+{d}^{2}+cov_{ad}}}{\sigma _{P}^{2}}{\sigma_{{{p}^{}}}}}{\nd}{d}}}}}\sigma_sigma_sigma_sigma_sigma_sigma_sigma_

피셔는 이러한 좁은 의미의 유전성이 "적응"^[29]에 있는 변화 가능성에 초점을 맞춘 자연선택의 결과를 고려하는데 적절할 수 있다고 제안했다.그는 다윈의 진화를 수량화하는 것에 관해 그것을 제안했다.

는 대립 형질 차이(σ 2a)과gene-model[그Genotypic 차이에 섹션을 참조]의(σ 2b) 있eu-genetic 구성 요소는 우성 분산, 그리고 σ 2D(대체 편차 또는"quasi-dominance"분산)과 covad를 동형접 합체 중간점(융점)는 인구 감소로 변경할 예정이다(G)뜻을 되새기면서, 그 볼 수 있다. 진짜이러한 유전성의 의미는 불명확하다. ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ 2 ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ 2 + ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ d ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ P ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ p P 2 ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ （ { $textstyle H _$ { ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ }^{2 $} =$ ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ $tfrac {$ { $a$ }^{2} + \ $time$ _ { d }^2} $}$ {\ e ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ 2 ${\textstyle H_{eu}^{2}={\tfrac {\sigma _{a}^{2}+\sigma _{d}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ 2 ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ 2 $σ$ p ${\textstyle h_{eu}^{2}={\tfrac {\sigma _{a}^{2}}{\sigma _{P}^{2}}}}$ _ { $textstyle }$

좁은 감각의 유전성은 또한 일반적으로 인위적인 선택의 결과를 예측하는 데 사용되어 왔다.그러나 후자의 경우, 전체적인 속성이 변경되고 있기 때문에 넓은 의미의 유전성이 더 적합할 수 있습니다. 즉, 적응 능력뿐만이 아닙니다.일반적으로 선택에서 진보는 유전율이 높을수록 더 빠르다.['선택' 섹션 참조]동물에서 생식 특성의 유전율은 일반적으로 낮은 반면, 질병 저항성과 생산의 유전율은 중간 정도에서 중간 정도이며, 신체 형성의 유전율은 높다.

반복성(r²)은 동일한 주체의 반복 측정 차이에서 기인하는 표현형 분산의 비율이며, 이후 기록에서 발생한다.그것은 특히 장수하는 종에게 사용된다.이 값은 성인의 체질량, 대사율 또는 쓰레기 크기와 같이 생물의 일생 동안 여러 번 나타나는 특징에 대해서만 결정될 수 있습니다.예를 들어, 개인의 출생 질량은 반복 가능성 값을 가지지 않지만, 유전 가능성 값을 가질 것이다.일반적으로 반복성은 유전성의 ^[54]상위 수준을 나타냅니다.

r² = (s²_G + s²_PE/s²_P)

여기서_PE s² = 표현형-환경 상호작용 = 반복성.

그러나 위의 반복성 개념은 측정 간에 반드시 크게 변화하는 특성에는 문제가 있습니다.예를 들어, 출생과 성인기 사이에 많은 유기체에서 체질량이 크게 증가한다.그럼에도 불구하고, 주어진 연령 범위(또는 수명 주기 단계) 내에서 반복적인 조치가 수행될 수 있으며, 반복성은 해당 단계에서 의미가 있을 것이다.

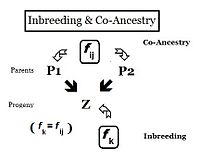
관계

근친교배계수와 동고계수 사이의 연결.

유전의 관점에서 보면, 관계는 하나 이상의 공통 조상으로부터 유전자를 물려받은 개인이다.따라서, 그들의 "관계"는 그들이 공통의 조상으로부터 대립 유전자의 복사본을 물려받았을 확률에 근거해 수량화될 수 있다.이전 섹션에서 근친교배계수는 "두 개의 동일한 대립 유전자(A와 A, 또는 a)가 공통의 기원을 가질 확률" 또는 "두 개의 상동 대립 유전자가 자기효소를 가질 확률"로 정의되었다.이전에는 개인이 두 개의 대립 유전자를 가질 가능성에 중점을 두었고, 그에 따라 계수를 틀화했다.하지만, 개인의 자가효소의 확률은 두 부모 각각이 이 자가효소의 대립 유전자를 가지고 있었을 확률도 분명합니다.이 재초점 형태에서 확률은 두 개인 i와 j(f)에 대한 공동 계수라고 불립니다.이 형태에서, 그것은 두 개인 사이의 관계를 정량화하는 데 사용될 수 있으며, 친족 계수 또는 친족 ^[13]^{: 132–143}계수라고도 알려져 있다.^[14]^{: 82–92}

혈통 분석

설명적인 혈통.

혈통은 개인과 그들의 조상들, 그리고 아마도 그들과 유전적인 유산을 공유하는 그룹의 다른 구성원들 사이의 가족적 연결의 도표이다.그것들은 관계 지도입니다.따라서 혈통을 분석하여 근친교배 및 공동조상의 계수를 밝혀낼 수 있다.이러한 혈통은 사실 경로 분석에서 사용된 경로도의 비공식적인 묘사이며, Sewall Wright가 ^[55]^{: 266–298}근친교배에 대한 연구를 공식화했을 때 발명되었습니다.인접한 도표를 사용하여, 개인 "B"와 "C"가 조상 "A"로부터 자기효소를 받았을 확률은 1/2이다. (2개의 이배체 대립 유전자 중 1개)이것은 이 단계에서 "de novo" 근친교배입니다_Ped.그래서 이 줄여서의 가능성은(데노보 보체 조상은 A의 근친 교배로 곱하),(1− ΔfPed)fA)(1/2)fA 그러나, 다른 유전자,. 이전 세대로부터"캐리 오버"autozygosity 따라서, autozygosity의 B와 C에서 혈통의 bi-furcation에 이어총 발생 가능성은 볼수밖에 없다는 것. 합즉, (1/2) + (1_A/2)f = (1/2) (1+f ) 입니다.이것은 조상 A에서 온 두 개의 무작위 배우자가 자기효소를 가지고 있을 확률로 볼 수 있으며, 그러한 맥락에서 친족 계수 (f_AA)^[13]^{: 132–143}^[14]^{: 82–92}라고 불린다.다음 단락에서 자주 볼 수 있습니다.

"B" 경로를 따라, 모든 자기효소가 각 연속된 부모에게 "전달"될 확률은 각 단계에서 다시 (1/2)("목표" X에 대한 마지막 대립 유전자를 포함)입니다.따라서, 「B 패스」아래로의 전송의 전체적인 확률은 (1/2)³입니다.(1/2)이 상승하는 검정력은 "A와 X 사이의 경로에 있는 중간체의 수", n_B = 3으로 볼 수 있다. 마찬가지로, "C 경로"의_C 경우 n = 2이고 "전달 확률"은 (1/²2)이다.따라서 A에서 X로 자동효율이 전달될 확률은 [f_AA(1/2)^(n_B) (1/2) (1/2)]^(n_C)입니다_X. f = f_PQ = (1/2)^{(n_B + n_C + 1)} (1+f_A ), f = f = 0, f = 0.0156 (1+f )이_AA_A 있다고 가정하면 f = f의_PQ 측정과 관련된 f = 0, f_X = 0.0156 (1/2)가 됩니다.

이 절에서는 (1/2)의 검정력을 사용하여 "자기효소의 확률"을 표현하였다.나중에, 이 방법은 혈통으로 유전되는 조상 유전자 풀의 비율을 나타내기 위해 사용될 것이다.

교차 곱셈 규칙.

교차 곱셈 규칙

형제자매 교배와 유사한 주제에 대한 다음 절에서는 많은 "평균 규칙"이 유용하다.이것들은 경로 ^[55]분석에서 파생됩니다.이 규칙은 적절한 조부모 조합과 부모 조합 간의 교차 공조 평균으로 어떤 공조계수를 얻을 수 있음을 보여준다.그러므로, 인접한 도표를 가리키는 Cross-multiplier 1(fAC, fAD, fBC, fBD)의 fPQ)평균)(1/4)[fAC+fAD+fBC+fBD]=fY. 비슷한 패션에서 fPC,cross-multiplier 2국가=)(1/2)[fAD+fBD]fPD(1/2)[fAC+fBC]—whilecross-multiplier 3개 주. 첫번째 승수로 돌아가서, 지금 것을 볼 수 있다는 것이다.N도(1/2)-LSB- fPC+fPDfPQ. 는 곱셈기 2와 3을 대체한 후 원래 형태로 돌아갑니다.

다음 중 대부분은 조부모세대를 (t-2), 부모세대를 (t-1), 타깃세대를 (t)라고 부릅니다.

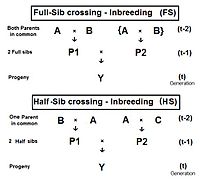
풀시브크로스(FS)

형제 관계에서의 근친 교배

오른쪽 그림은 완전한 형제 교차가 교차 승수 1의 직접적인 적용이며, 개인 P1과 P2가 부모 P1과 P2의 공통, 즉 완전한 형제라는 것을 나타내기 위해 부모 A와 B가 (C와 D 대신) 반복하는 약간의 수정이 있음을 보여준다.개인 Y는 두 형제자매가 교배한 결과입니다.따라서_Y f = f_P1,P2 = (1/4) [ f_AA + 2 f_AB + f_BB ]. f와_BB f는 앞에서 (페디그리 분석에서) 현재 컨텍스트에서 각각 (1/2)[1+f_A_B]와 같은 부모 계수로 정의되었음을_AA 기억하십시오.이 가장으로 조부모 A와 B는 세대(t-2)를 나타낸다는 것을 알아두세요.따라서 어떤 세대에서도 근친교배의 모든 수준이 동일하다고 가정하면 이들 2개의 부모 계수는 각각 (1/2) [1 + f_(t-2) ]를 나타냅니다.

풀시브와 하프시브의 교배와 셀프잉으로부터의 근친교배.

f를 조사합니다_AB.이것도 f 또는_P1_P2 f이며, 그 발생을 나타내는 것입니다.f_(t-1).를 종합하면_t f = (1/4) [1_AA + f + 2_(t-1) f_AB ]= (1/4) [1_(t-2) + f + 2 f ]입니다.이것은 Full-Sib ^[13]^{: 132–143}^[14]^{: 82–92}crossing의 근친교배 계수입니다.왼쪽 그래프는 이 근친교배율이 20세대에 걸쳐 반복되고 있음을 나타내고 있습니다."반복"은 사이클 t 이후의 자손들이 연속적으로 사이클(t+1)을 생성하는 교차 부모가 된다는 것을 의미한다.그래프에는 비교를 위해 무작위 수정 2N=20에 대한 근친교배도 나와 있습니다.자손 Y에 대한 이 근친교배계수는 부모에 대한 공동 조산계수이기도 하며 두 Fill 형제 간의 연관성에 대한 척도이기도 합니다.

하프 시브 크로스(HS)

이복형제 교차의 파생은 완전형제와는 약간 다른 경로를 취한다.다음 그림에서 세대(t-1)의 2개의 하프시브는 공통의 부모인 세대(t-2)의 부모 'A'만을 가집니다.f = f_(P1,P2) = (1/4) [f_AA + f_AC_BA + f + f_BC ]를 나타내는_Y 교차분산 1이 다시 사용됩니다. 이번에는 부모 계수가 1개뿐이지만 (t-2) 수준에서 세 개의 보조분산 계수가 있습니다(그 중 하나는_BC "f"이며 (t-1) 세대에서는 실제 개인을 나타내지 않습니다).전에, 혈통에 관한 계수, 3co-ancestries 각 f(t-1)을 나타낸다. 그 fA 남아 포함한다 이 반형매 근교(HS)20successi에 fY)피트)(1/8)[f(t-2)1++6f(t-1)].[13]:132–143[14]:82–92 그 그래프를 준다 f(t-2), 최종 회동과 용어를 단순화를 나타내면서(1/2)[1+fA] 있다.ve 세대입니다.

자가 수정 근친 교배

또한 이전과 마찬가지로 생성 시(t-1)의 2개의 하프시브의 관련성을 f의 대체_{(P1, P2)} 형태로 정량화합니다.

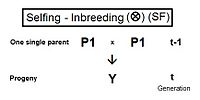
자가 수정(SF)

우측에는 셀프링을 위한 계통도가 있습니다.이것은 매우 간단하기 때문에 교차 곱셈 규칙이 필요하지 않습니다.그것은 근친교배계수와 그 대안인 공동조상계수의 기본적인 병치만을 사용한다.이 경우, 후자 역시 부모 계수가 된다는 것을 인식한다.따라서_Y f = f_{(P1, P1)} = f_t = f = (1/2) [1 + f_(t-1) ].^[13]^{: 132–143}^[14]^{: 82–92} 이는 위의 그래프에서 볼 수 있듯이 모든 유형의 근친교배 속도 중 가장 빠른 속도입니다.자화곡선은 사실 부모 계수의 그래프입니다.

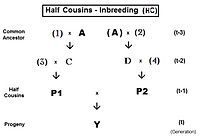
사촌 교배

혈통 분석 일촌

이것들은 ^[13]^{: 132–143}^[14]^{: 82–92}형제자매와 유사한 방법으로 도출된다.종래와 같이 근친교배계수의 공동조상관점은 이들 사촌 표현에서 부모 P1과 P2의 '관련성'을 나타낸다.

First Cousins(FC)의 혈통은 오른쪽에 있습니다.소수 방정식은 f = f_t = f_P1,P2 = (1/4) [f_1D + f₁₂ + f_CD + f_C2 ]입니다_Y.대응하는 근친교배계수로 치환하여 용어를 수집하고 단순화하면 f = (1/4) [3_(t-1) f + (1/4) [2_(t-2) f + f_(t-3) + 1 ]이 됩니다_t.이것은 반복용 버전, 즉 일반적인 패턴을 관찰하기 위한 버전, 컴퓨터 프로그래밍에 사용됩니다.최종 버전은 f = (1/16) [12 f + 2_(t-2) f_(t-1) + f_(t-3) + 1 ]입니다_t.

혈통 분석 2촌

세컨드 커즌(SC) 혈통은 왼쪽에 있습니다.공통 조상과 관련이 없는 혈통의 부모는 문자 대신 숫자로 표시됩니다.여기서, 소수 방정식은 f = f_t_P1,P2 = f = (1/4) [f_3F + f₃₄_EF + f + f_E4 ]이다_Y.적절한 대수를 거쳐 f = (1/4) [3_(t-1) f + (1/4)] [3_(t-2) f + (1/4) [2_(t-3) f_(t-4) + f + 1 ]이 됩니다_t.이것은 반복 버전입니다."최종_t" 버전은 f = (1/64) [48_(t-1)_(t-2) f + 12_(t-3) f + 2_(t-4) f + f + 1 ]

여러 단계의 사촌간 교배에서 근친교배.

완전 사촌 방정식의 패턴을 시각화하려면 f = (1/4)[2_(t-1) f + f_(t-2) + 1 ] 반복 형식으로 다시 쓴 완전 sib 방정식으로 시리즈를 시작합니다_t.이것은 각 사촌 반복 형태에서 마지막 용어의 "필수 계획"이며, 각 사촌 "수준"에서 발생 지수가 "1"씩 증가하는 작은 차이이다.이제 사촌 레벨을 k = 1(친사촌), = 2(친사촌), = 3(친사촌), = 0(친사촌) 등으로 정의합니다.마지막 항은 다음과 같이 쓸 수 있습니다. (1_(t-(1+k))/4) [2 f + f_(t-(2+k)) + 1 ]. 이 마지막 항 앞에 (1/4) [3_(t-j) f + ...] 형식으로 1개 이상의 반복 증분이 쌓입니다.여기서 j는 반복 인덱스이며 필요에 따라 연속 반복에 대해 1 ... k의 값을 취합니다.이 모든 것을 종합하면 풀 시브를 포함한 가능한 모든 수준의 사촌들을 위한 일반적인 공식을 얻을 수 있습니다.k레벨 완전 사촌의 경우, f{_tk} = δ_{j = 1}^k { (1/4) [3_(t-j) f + _j} + (1/4) [2_(t-(1+k))_(t-(2+k)) f + f + 1].반복 시작 시 모든 f는_(t-x) "0"으로 설정되며, 각 f는 세대를 통해 계산될 때 치환된 값을 가진다.오른쪽 그래프는 여러 수준의 완전한 사촌에 대한 연속적인 근친 교배를 보여줍니다.

혈통 분석 반촌

전반부 사촌(FHC)의 경우 혈통은 왼쪽에 있습니다.공통 조상(개별 A)은 1개뿐입니다.또, 2촌에 대해서는, 공통의 조상에 관련하지 않는 부모를 숫자로 표시한다.여기서, 소수 방정식은 f = f_t_P1,P2 = f = (1/4) [f_3D + f₃₄_CD + f + f_C4 ]이다_Y.적절한 대수를 거쳐 f = (1/4) [3_(t-1) f + (1/8) [6_(t-2) f + f_(t-3) + 1 ]이 됩니다_t.이것은 반복 버전입니다."최종" 버전은 f_t = (1/32) [24_(t-1) f + 6 f_(t-2) + f_(t-3) + 1 ]입니다. 반복 알고리즘은 마지막 항이 (1/8) [6_(t-(1+k)) f + f_(t-(2+k)) + 1 ]이라는 점을 제외하면 완전한 사촌 및 완전 자매의 패턴과 기본적으로 이 마지막 항이 반자매 방정식과 유사하다는 점에 유의하십시오.다시 말해, 이복 자매는 "제로 레벨"의 이복 사촌이다.

족보에 대한 관심이 크기 때문인지 사촌간 교배를 인간지향적인 시각으로 보는 경향이 있다.근친 교배를 이끌어내기 위해 혈통을 사용하는 것은 아마도 이러한 "가족사" 관점을 강화시킬 것이다.그러나 이러한 종류의 교잡은 자연 개체군에서도 발생합니다. 특히 정주하고 있거나 계절마다 다시 방문하는 "번식 지역"이 있는 개체군에서도 발생합니다.예를 들어 지배적인 수컷을 가진 하렘의 자손 집단은 특히 "섬" 유형의 유전적 표류뿐만 아니라 자매 교배, 사촌 교배, 역교배의 요소들을 포함할 수 있다.또한 때때로 "아웃크로스"가 혼합에 하이브리드화 요소를 추가합니다.그것은 범믹시아가 아니다.

백크로스(BC)

혈통 분석:백크로스

백크로스: 기본적인 근친교배 수준

A와 R의 하이브리드화에 이어 F1(개별 B)을 원래의 부모(R)에게 크로스백(BC1)하여 BC1 세대(개별 C)를 생성한다.【백크로스 하는 행위나, 백크로스에서 생산되는 세대에는 같은 라벨을 사용하는 것이 일반적입니다.백크로스 동작은 이탤릭체로 나타내고 있습니다.] 부모 R은 반복 부모입니다.두 개의 연속적인 백크로스가 묘사되어 있으며, 개별 D는 BC2 세대이다.이들 세대에는 t개의 지표도 제시되어 있다.이전과 같이 f = f_t = f_CR = f = (1_RB/2_RR) [f + f ]는_D 앞에서 설명한 교차 적층기 2를 사용한다.방금_RB 정의한 f는 (t-1)과 (t-2)의 생성과 관련된 것입니다.단, 전적으로 세대_RB(t-2)에 포함되는 또 다른 f가 있으며, 현재 사용되는 것은 개인 C의 부모 세대(t-1)의 공동 조상으로서이다.이와 같이 C의 근친교배계수이므로 f이다_(t-1).반복되는 부모의 혈통의 나머지 fRR은 계수는(1/2)[1+fR]. 이 모든 것: 옳은 설명할 Backcross 20backcrosses에(고정)근교의 순환 pa.에 세가지 다른 수준의 근교에 피트)(1/2)[(1/2컵용 1+fR]+f(t-1) 뻗는다)(1/4)[1+fR+2f(t-1)]. 그 그래프세내다.

이 루틴은 동물과 식물 사육 프로그램에서 일반적으로 사용됩니다.종종 잡종을 만든 후에(특히 개인이 단수명인 경우), 재발하는 부모는 역교차에서 미래의 재발하는 부모로서의 유지를 위해 별도의 "라인 교배"가 필요하다.이러한 유지는 종의 번식 가능성에 따라 자가 번식, 완전 자웅 또는 반 자웅 교잡, 또는 제한된 무작위 수정 개체군을 통해 이루어질 수 있습니다.물론 f의 증분_R 증가는 백크로스의 f로_t 넘어갑니다.결과는_R f가 처음부터 고정된 수준이 아니기 때문에 이 그래프에 표시된 것보다 점근선까지 올라가는 더 점진적인 곡선이 된다.

조상 유전자의 공헌

"경로 분석" 섹션에서 ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ ( ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ 2 ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ ) ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ \ $textstyle \$ left ( { \ $tfrac {$ 1} {2 $}$ } \ ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ ) $^{n}}$ 는 ${\textstyle \left({\tfrac {1}{2}}\right)^{n}}$ 혈통의 가지 아래 n세대에 걸친 자기효능 대립 유전자 강하 확률을 나타내기 위해 사용되었다.이 공식은 (i) 두 부모가 실질적으로 동등한 상염색체 유전자의 공유를 기여하고 (ii) 접합자와 부모의 "초점" 수준 사이의 각 세대에 대해 연속적인 희석이라는 성적 생식에 의해 부과된 규칙 때문에 생겨났다.이 규칙들은 또한 두 성별의 생식 체계에서 혈통에 대한 다른 관점에도 적용된다.그러한 것 중 하나는 접합자의 유전자형에 포함된 조상 유전자 풀의 비율이다.

따라서 유전자형에서 조상 제네풀의 비율은 다음과 같습니다.

\displaystyle _{n}=\leftfrac {1}{2}}\오른쪽)^{n}}

여기서 n = 접합자와 초점 조상 사이의 성적 생성 횟수.

예를 들어 각 부모는 자녀에게 기여하는 ${\textstyle \left({\tfrac {1}{2}}\right)^{1}}$ genepool ( ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ ${\textstyle \left({\tfrac {1}{2}}\right)^{1}}$ 2 ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ ) ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ $\$ textstyle \ $left$ $({\tfrac {1$ $}{2$ $}}\right$ $)^{1}{$ 1}{1 $}{1}\right}$ 를 ${\textstyle \left({\tfrac {1}{2}}\right)^{1}}$ ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ 정의하고 ${\textstyle \left({\tfrac {1}{2}}\right)^{3}}$ .

접합자의 총 제네풀(δ)은 물론 그 후손에 대한 성적 기여의 합계이다.

{begin{aligned}\Gamma &=\sum _{n}\cisco _{n}\&=\sum _{n=1}^{n}{\left\frac {1}{2}\right}^{n}}\end{aligned}

조상 유전자에 의한 관계

공통 조상의 제네풀의 후손들은 분명히 연관이 있다.이것은 그들의 유전자(알레)가 동일하다고 말하는 것이 아니다. 왜냐하면, 조상의 각 수준에서, 배우자를 생산하는데 있어서 분리 및 분류가 일어났기 때문이다.그러나 그것들은 이러한 감수성과 그 이후의 수정에 이용 가능한 동일한 대립 유전자 풀에서 유래했을 것이다.[이 아이디어는 혈통 분석과 관계 섹션에서 처음 접하게 되었습니다]따라서 가장 가까운 공통 조상 조상 조상 조상 조상 조상 조상 조상 조상 조상 노드(genepool)의 유전자 풀 기여(위 섹션 참조)를 사용하여 이들의 관계를 정의할 수 있습니다.이것은 가족력에서 발견되는 친숙한 "관련성"의 개념과 잘 부합하는 관계의 직관적인 정의로 이어지며, 그러한 계보로부터 발생하는 관계의 복잡한 패턴에 대한 "관련성 정도"의 비교를 가능하게 한다.

(각 개인에게 차례로) 필요한 유일한 수정은 γ이며, "개인의 전체 조상"이 아닌 "공유된 공통 조상"으로 전환되기 때문이다.이를 위해 δ(δ 대신), m = 노드에서 공통 조상 수(즉, m = 1 또는 2에만 해당) 및 "개별 지수" k를 정의한다.다음과 같이 됩니다.

{naligned}\mathrm {P}_{k}&={m=1}{1,2}\\sum _{m=1}{\leftfrac {1}{2}\right)^{n}}\end{aligned}

여기서, 이전과 같이, n = 개인과 조상 노드 사이의 성적 세대 수.

예시는 두 개의 첫 번째 완전한 사촌에 의해 제공됩니다.그들의 가장 가까운 공통 조상은 두 형제 부모를 낳은 조부모이며, 그들은 이 두 조부모를 공통으로 가지고 있다.[이전의 혈통 참조]이 경우 m=2 및 n=2이므로 각각에 대해

{displaystyle {narged}\mathrm {P}_{k}&={m=1}^2}{\\sum _{{2}{{n}\left\frac {1}{2}{right}\&=frac {n}{n}{n}{ned}\&=frac {ned

이 간단한 예에서는 각 사촌은 같은 δ를 가지고 있습니다.

두 번째 예는 두 개의 완전한 사촌간일 수 있지만, 한 개의 (k=1)은 조상 노드(n=3)로 되돌아가는 3세대를 가지고 있고, 다른 한 개의 (k=2)는 두 개의 (n=2)만 있다[즉, 두 번째와 첫 번째 사촌 관계].둘 다 m=2(정사촌 관계)입니다.

{{displaystyle {argined}\mathrm {P}_{1}{{{3}}\\&=\sum _{m=1}{2}{{{{2}\right}{3}}\\&=sum frac {4}{}{end}}\\\\sum fright frac {arg}{{{1}{{{{}}}}}}{{{{}}}}}}}}} 정렬됨

그리고.

{{displaystyle {argined}\mathrm {P}_{2}\sum _{m=1}^{2}{\sum _{m=1}{{2}{{{2}}\right}{2}}\&=sum frac {2}{2}{{{2}}\\\\sum fright}{{\sum frac1}{2}{{{{{{{{}}}}}}}{\sumined}}}}{\sumined}}}{{{{{\sumined}}}}}}

사촌마다 다른 ρ이 있다는 점에 주의해 주세요.

GRC – genepool 관계 계수

모든 쌍별 관계 추정에는 각 개인에 대해 하나의_k Ω이 있습니다. 즉, 이들을 단일 "관계 계수"로 결합하기 위해 평균을 내는 것이 남습니다.각 δ는 전체 genepool의 일부이기 때문에 적절한 평균은 기하 평균입니다. 이 평균은 Genepool 관계 계수, 즉 "GRC"입니다.

첫 번째 예(완전한 첫 번째 예 2개)의 경우 GRC = 0.5이고, 두 번째 예(완전한 첫 번째 및 두 번째 사촌)의 경우 GRC = 0.3536이다.

이러한 모든 관계(GRC)는 경로 ^[55]^{: 214–298}분석 응용 프로그램입니다.다음은 일부 수준의 관계(GRC)에 대한 요약입니다.

GRC	관계 예
1.00	풀 시브스
0.7071	부모 ↔ 자손, 삼촌/이모 ↔ 조카/조카
0.5	친형제; 이복형제; 대부모 ↔ 대손
0.3536	전체 사촌 첫째 ↔ 두 번째, 전체 사촌 {1 제거}
0.25	완전한 2촌;반쪽 1촌;완전한 1촌 {2 제거}
0.1768	전체 첫째 사촌 {3 제거}, 전체 둘째 사촌 {1 제거}
0.125	전체 3촌, 절반 2촌, 전체 1촌 {4 제거}
0.0884	첫 번째 사촌 {5 제거}, 두 번째 사촌 {1 제거}
0.0625	완전한 사촌; 반삼촌

친척간의 유사성

이들은 유전자형 분산과 마찬가지로 유전자 모델("Mather") 접근법 또는 대립 유전자 치환("Fisher") 접근법에 의해 도출될 수 있다.여기서 각 방법은 대체 사례에 대해 시연됩니다.

부모-오프프링 공분산

이러한 값은 자식과 부모 중 하나(PO) 사이의 공분산 또는 자식 간의 공분산과 부모 둘 다(MPO)의 "중간" 값으로 볼 수 있다.

한부모자녀(PO)

이는 대립 유전자 치환 접근법을 사용하여 부모 유전자 효과와 자손 기대치의 절반 사이의 교차 산물의 합으로 도출될 수 있다.두 부모 중 한 명만 고려되고 있다는 사실에 대해 자손들의 기대치의 절반이 설명된다.따라서 적절한 부모 유전자 효과는 유전자형 분산을 조기에 정의하는 데 사용된 2단계 재정의 유전자 효과이다. 즉, aγ = 2q(a - qd) 및 dγ = (q-p)a + 2pqd 및 (-a)γ = -2p(a + pd)이다[제너 효과 재정의 참조].마찬가지로, 대립 유전자 변형 기대치에 대한 적절한 자손 효과는 초기 번식 값의 절반이며, 후자는_AA = 2qa, a_Aa = (q-p)a이며_aa, 또한 = -2pa이다("유전자형 대체 – 기대 및 편차" 섹션 참조).

이러한 효과는 유전자형 평균에서 이미 벗어난 것으로 정의되어 있기 때문에, {genotype-frequency * parent gen-effect * half-breading-value}를 사용한 교차 산물의 합은 어느 한쪽 부모와 그 자손 사이의 대립 유전자 치환 기대 공분산을 즉시 제공한다.용어 및 단순화를 신중하게 수집한 후 cov(PO)_A = pqa² = s²_A .^[13]s가 됩니다.

불행히도, 대립 유전자 치환 제거는 보통 간과되지만, 그럼에도 불구하고 그들은 "존재하는 것을 멈추지는 않았다"!이러한 편차는 d_AA = -2q² d, d_Aa = 2pq d 및 d_aa = -2p² d라는 점에 유의하십시오("유전자형 대체 – 기대 및 편차" 섹션 참조).따라서 {genotype-frequency * parent genet-effect * half-stitution-deviations}를 이용한 교차생성합은 어느 한쪽 부모와 그 자손 사이의 대립 유전자 치환 이탈 공분산도 즉시 제공한다.다시 한 번, 용어와 단순화를 신중하게 수집한 후, cov(PO)_D = 2pqd²²² = ½²_D s가 됩니다.

따라서 우위가 간과되지 않을 때 cov(PO) = cov(PO)_A + cov(PO)_D = ½²_A s + ½²_D s!

중간부모자녀(MPO)

부모 유전자형의 조합이 많기 때문에, 각 부모쌍을 얻는 빈도의 다양성과 함께 고려해야 할 중간 부모 및 자녀 수단이 많이 있다.이 경우 유전자 모델 접근법이 가장 편리하다.따라서 {전체 유전자형 평균}을 보정 계수(CF)로 빼서 모든 제품 {부모-쌍수 *중부모-제네 효과 * 자손-유전자형 평균}²을 사용하여 교차 산물의 미조정 합계(USCP)를 조정한다.모든 다양한 조합을 곱하고, 용어를 신중하게 수집하고, 필요에 따라 단순화하고, 인수화하고, 소거하면 다음과 같이 됩니다.

cov(MPO) = pq [a + (q-p)d ²] = pq² a = µ²_A s이며,^[13] 이 경우 a를 정의하는 데 사용되었기 때문에 우성이 간과되지 않았다.

응용 프로그램(부모 대상)

가장 명백한 적용은 상호 교차가 있든 없든 모든 부모와 그 자손을 포함하는 실험으로, 모든 적절한 평균, 분산 및 공분산을 표준 오류와 함께 추정할 수 있도록 하는 것이 바람직하다.이러한 추정 통계는 유전자 분산을 추정하는 데 사용될 수 있다.두 가지 형태의 (수정된) 상위-상위 공분산 추정치의 두 배 차이는 s의²_D 추정치를 제공하고, 두 배의 cov(MPO) 추정치는²_A s의 추정치를 제공한다.적절한 실험 설계와 ^[9]^[49]^[50]분석을 통해 이러한 유전자 통계의 표준 오차도 얻을 수 있다.이것은 Dialle Analysis로 알려진 실험의 기본 핵심이며, Mather, Jinks 및 Hayman 버전은 다른 섹션에서 설명합니다.

두 번째 응용 프로그램에는 ^[9]^[49]^[58]^[59]미적분의 세로좌표(Y-추정), 도함수(회귀계수) 및 상수(Y-절편)를 통계로부터 추정하는 회귀 분석을 사용하는 것이 포함됩니다.회귀 계수는 적합 곡선과 관측된 데이터(MINRES) 사이의 잔차를 최소화하여 X에서 Y를 예측하는 함수의 변화율을 추정합니다.이러한 함수를 추정하는 대체 방법은 MINRES의 이 기본 요건을 충족하지 않는다.일반적으로 회귀 계수는 행렬식(X)의 분산에 대한 공분산(XY)의 비율로 추정됩니다.실제로 표본 크기는 일반적으로 X와 Y에 대해 동일하기 때문에 SCP(XY) / SS(X)로 쓸 수 있습니다. 여기서 모든 항은 이전에 ^[9]^[58]^[59]정의되었습니다.이 문맥에서 부모는 결정 변수(X)로, 자녀는 결정 변수(Y)로, 회귀 계수는 둘 사이의 기능 관계(θ_PO)로 본다.cov(MPO) = s²_A s를 cov(XY)로²_P, s / 2(중간 부모 두 부모 평균의 분산)를 s로²_X 취하면 v_MPO = [ ½²_A s ] / [ s²_P s ] = h. 다음으로² ^[60]cov(PO) = [ ½²_A s + ½²_D s ]를 coV(SXY)로²_P²_X 사용하고, s / s / s / s / s / s / s로 취한다.

인식의 분석은 이전에 유형²_AA s 및²_AD s 및²_DD s의 상호작용 분산 접근방식을 통해 시도되었다.이것은 인식 분산에 대한 추정자를 제공하기 위한 노력으로 이러한 현재의 공분산들과 통합되었다.그러나 후생유전학의 발견은 이것이 인식증을 정의하는 적절한 방법이 아닐 수 있음을 시사한다.

형제자매의 공유

대립 유전 치환 방법을 사용하여 하프 시브(HS) 간의 공분산을 쉽게 정의할 수 있지만, 다시 한번 지배적 기여는 역사적으로 누락되었다.그러나 중간 부모/상위 공분산과 마찬가지로, 풀 시브(FS) 간의 공분산은 "부모 결합" 접근법을 필요로 하므로 유전자 모델 보정 교차 생성물 방법을 사용해야 하며, 지배적 기여는 역사적으로 간과되지 않았다.유전자 모델 유도의 우수성은 유전자형 분산의 우수성과 마찬가지로 여기에서 명백하다.

같은 공통 부모(HS)의 하프시브(Half-sibs)

사용된 [교배값: 대립 유전자 치환 기대치를 나타내는] 효과가 이미 정의되어 있기 때문에 동일한 공통 부모 그룹에 있는 교차 제품 {Common-parent-breading-value * half-sib의 half-breading-value}의 합계는 필요한 공분산 중 하나를 즉시 제공합니다.유전자형 평균으로부터의 s ["알레 대체 – 기대 및 편차" 섹션 참조]심플화 후.이:)cov(HS)A이 되½pq a2)¼s2A .[13]:132–141[14]:134–147 하지만, 대체 편차도 존재, 정의 합의 cross-products{common-parent 주파수*어떤 다른 반 자매의 그 같은 common-parent-group의 한 반형매*half-substitution-deviation의 half-substitution-deviation},, 결국에:. Cov(HS)D)p2q2 d2)¼ s2D. 더한다.2개의 컴포넌트는 다음과 같습니다.

cov(HS) = cov(HS)_A + cov(HS)_D = ¼²_A s + ¼²_D s.

풀시브(FS)

서론에서 설명한 바와 같이 중간 부모/프로그래니 공분산에 사용되는 방법과 유사한 방법이 사용됩니다.따라서 모든 제품({parent-pair-frequency * farent-genotype-mean}의 제곱)을 사용하는 조정되지 않은 교차 산물(USCP)의 합계는 보정 계수(²CF)로서 {전체 유전자형 평균}을 빼서 조정한다.이 경우 모든 조합을 곱하고, 용어를 신중하게 수집하고, 단순화하고, 인수화하고, 소거하는 작업은 매우 오래 걸립니다.최종적으로는 다음과 같습니다.

cov(FS) = pq² a + p²² q² d = µ²_A s + µ²_D s이며,^[13] 우성은 간과되지 않았다.^{: 132–141}^[14] ^{: 134–147}

응용 프로그램(자매)

유전자 통계학에서 가장 유용한 응용은 0.5sibs 사이의 상관관계입니다.상관 계수(r)는 분산에 대한 공분산의 비율입니다("관련 속성" 섹션 참조).따라서, r_HS = cov(HS) / s²_{all HS together}²_P = [colors²_A s + δ²_D s ] / s = ^[61]h이다². 최대값 사이의 상관관계는_FS r = cov(FS) / s²_{all FS together} = [colors²_A s + δ²_D s ] / s²_P. "근사"라는² 제안은 별로 쓸모가 없다.

물론 형제자매 간의 상관관계는 유전성이나 유전자형 분산을 추정하기 위해 가질 수 있는 효용과는 상당히 별개로 그들 자신의 권리에 내재적인 관심이 있다.

[ cov (FS) - cov (HS) ] = ]s²_A. FS 및 HS 계열로 구성된 실험은 클래스 내 상관관계를 사용하여 실험 분산 구성요소를 이러한 공분류와 동등하게 함으로써 이를 활용할 수 있다(이 배경의 근거는 "클래스 내 상관관계 계수" 섹션 참조).

인식에 관한 이전의 코멘트는 여기에 다시 적용된다["어플리케이션(부모 오프프링)" 섹션 참조].

선택.

기본 원칙

유전적 진전과 선택압력 반복

선택은 속성(phetotype)에 따라 이루어지며, 선택 임계값_P(z)을 초과한 개체는 다음 세대에서 유효한 부모가 됩니다.기준 모집단의 비율은 선택 압력입니다.비율이 작을수록 압력이 강합니다.선택된 그룹(P_s)의 평균은 기준 모집단 평균(P₀)보다 선택 차분(S)이라고 불리는 차이만큼 크다.이 모든 양은 표현형이다.기초 유전자와 "연계"하기 위해 유전율 h를² 사용하여 생체학적 의미에서 결정 계수의 역할을 수행한다.여전히 표현형 측정 단위로 표현되는 예상 유전자 변화는 유전자 발전(δG)이라고 하며, 선택 미분(S)의 곱과 결정 계수(h²)에 의해 얻어진다.자손(P₁)의 기대평균은 기본평균(P₀)에 유전자진보(δG)를 더해 구한다.오른쪽 그래프는 (초기) 유전적 진보를 더 강한 선택 압력(더 작은 확률)으로 어떻게 더 큰지를 보여준다.또한 선택 자체에 의해 표현형 분산과 유전성이 감소하기 때문에 연속적인 선택 주기(같은 선택 압력에서도)의 진행이 어떻게 꾸준히 감소하는지 보여준다.이에 대해서는 잠시 후에 자세히 설명하겠습니다.

따라서 $\Delta G=Sh^{2}$ G $\Delta G=Sh^{2}$ $\Delta G=Sh^{2}$ $\Delta G=Sh^{2}$ $\Delta G=Sh^{2}$ (\ $displaystyle$ \ $Delta$ G = $Sh^ {$ 2} ) $\Delta G=Sh^{2}$ ^[14] $P_{1}=P_{0}+\Delta G$ p $P_{1}=P_{0}+\Delta G$ $P_{1}=P_{0}+\Delta G$ $P_{1}=P_{0}+\Delta G$ $P_{$ 1} = $P_{0}$ + \ $Delta$ G $P_{1}=P_{0}+\Delta G$ ^[14] 입니다.

만약broad-sense 물려 줄 수 있음(H2)의 적절한 사용은 유전자형 분산(σ2G)에 연결하는 협의유 전력(h2)보통, 그것으로써 유전자의 분산(σ2A)으로 거슬러 올라간다. 하지만, 그리고 심지언 대립 유전적[h2eu=(σ2a)/(σ2P)]고려될 수 있(σ2a)에 연결하는 사용된다.[Heritability에 섹션을 참조하십시오.]

선택이 실제로 이루어지기 전에 이러한 개념을 적용하고 대안(예를 들어 선택 임계값의 선택 등)의 결과를 예측하기 위해, 이러한 표현형 통계는 정규 분포의 속성, 특히 분포의 상위 꼬리 자르기 관련 통계와 관련하여 다시 고려된다.이러한 고려사항에서는 이전의 "phenotype" 버전 대신 표준화된 선택 차분(i) 및 표준화된 선택 임계값(z)을 사용한다.표현형 표준 편차(θ_P(0))도 필요하다.이것에 대해서는, 다음의 항에서 설명합니다.

따라서 δG = (i_P )) h이며²,^[14] 여기서 (i σ_P(0)) = S이다.^{: 1710–181}

반복 선택으로 인한 변화

위의 텍스트는 "input"[표현형 분산( ))]이 앞의 ^[14]^{: 1710–181}선택에 의해 감소하기 때문에 연속적인 δG가²_P 감소하는 것에 주목했다.유전율도 저하됩니다.왼쪽 그래프는 동일한 선택 압력이 주장되는 동안 반복 선택 10주기에 걸쳐 이러한 감소가 있음을 보여준다.이 예에서 누적 유전자 발전(δδG)은 6세대에 의해 사실상 점근에 도달했다.이 감소는 부분적으로 정규 분포의 절단 특성에 따라 달라지며, 부분적으로 감수 분열 결정과 함께 유전율에 따라 달라진다(b²).마지막 두 항목은 감수분열 ^[14]중 분리 및 분류에서 발생하는 새로운 변동에 의해 절단이 "오프셋"되는 정도를 정량화한다.^{: 1710–181}^[27] 이는 곧 논의될 것이지만, 여기에서는 분산되지 않은 무작위 수정에 대한 단순화된 결과(f = 0)에 주목한다.

따라서 : σ²_P(1)²_P(0) = [ [ 1 - i ( i - z ) h² h ] (i ( i - z ) = K = 절단계수 및² = h = R = 재생계수^[14]^{: 1710–181}^[27]) can²_P(1)²_P(0) problems = [ [ 1 - K R ]로 표기할 수 있으므로 선택문제의 상세한 분석이 용이하다.

여기서 i와 z는 이미 정의되어 있고, θ는 f=0에 대한 감수분열 결정(b²)이며, 나머지 기호는 유전율이다.이러한 것에 대해서는, 다음의 항에서 자세하게 설명하겠습니다.또한 보다 일반적으로 R = b²² h라는 점에 유의하십시오.일반적인 감수분열 판정(b²)을 사용하면 이전 근친교배 결과를 선택에 포함할 수 있다.표현형 분산 방정식은 다음과 같습니다.

σ²_P(1)²_P(0) = [ [ 1 - i ( i² - z ) b² h ]

선택한 그룹( ) )에²_P(S) 의해 잘린 표현형 분산은 단순히²_P(0) [1 - K]이며, 포함된 유전자 분산은 (h²₀²_P(S) ). )이다.선택이 환경분산을 변화시키지 않았다고 가정할 때 자손의 유전자분산은 θ²_A(1) = ( θ²_P(1) - θ²_E)로 근사할 수 있다. 이로부터 h²₁ = ( θ²_A(1) / θ²_P(1) ).필요에 따라 required과²_G(1)²₁ , 또는 and과²_a(1)²_eu(1) if에 대해서도 같은 견적을 낼 수 있다.

대체 δG

다음의 재배치는, 복수의 어트리뷰트(문자)의 선택을 검토할 경우에 편리합니다.유전성을 분산 성분으로 확장하는 것으로 시작합니다.δG = i_P σ²_A ( σ²_P / ) ). and와_P²_P σ는 부분적으로 취소되어 단독_P σ이 남습니다.다음으로, 유전율 내부의 θ는²_A (θ_A × θ_A)로 확장될 수 있으며, 이는 다음과 같이 이어진다.

선택 차분 및 정규 분포

δG = i_A_A （ σ_P / ） = i_A （ h ）。

δG = i h_G H 또는 δG = i σ_a_eu h로 지정되는 대체 유전율을 사용하여 해당 재측정을 수행할 수 있다.

집단유전학에서의 다유전자적응모델

양적 유전학의 이러한 적응에 대한 전통적인 관점은 선택된 표현형이 시간에 따라 어떻게 변화하는지에 대한 모델을 선택 미분과 유전성의 함수로서 제공한다.그러나 그것은 유전적 세부 사항, 특히 관련된 위치의 수, 그들의 대립 유전자 빈도와 효과 크기, 그리고 선택에 의한 빈도 변화에 대한 통찰력을 제공하지 않는다.반대로, 이것은 집단 유전학 분야에서의 다유전자 적응에^[62] 대한 연구의 초점이다.최근의 연구들은 ^[63]^[64]^[65]키와 같은 특징들이 키에 영향을 미치는 수천 개의 변종에서 작은 대립 유전자 빈도 변화의 결과로 지난 수천 년 동안 인간에서 진화해 왔다는 것을 보여 주었다.

배경

표준화된 선택 – 정규 분포

전체 기준 모집단은 오른쪽의 정규^[59]^{: 78–89} 곡선으로 윤곽을 그립니다.Z축을 따라 최소값부터 최대값까지 속성의 모든 값이 표시되며, 이 축에서 곡선까지의 높이 자체가 아래 축에 있는 값의 빈도입니다."정상" 곡선("공통 경험" 곡선)에 대해 이러한 주파수를 찾는 방정식이 타원에 주어집니다.평균())과 분산(σ²)이 포함되어 있습니다.z축을 따라 무한히 이동하면 인접 값의 주파수를 앞의 값 옆에 "스택"할 수 있으므로 스택 내의 모든 값을 얻을 확률을 나타내는 영역이 축적됩니다.[그게 미적분과의 통합입니다]선택은 선택 임계값(z)에서 곡선의 상단 꼬리 끝까지의 음영 영역에 초점을 맞춘다.이것이 선택압력입니다.선택한 그룹(차세대의 유효한 부모)에는 z부터 ^[66]꼬리의 "끝"까지의 모든 표현형 값이 포함됩니다.선택된 그룹의 평균은 θ이며_s, 이 그룹과 기준 평균(θ)의 차이는 선택 차분(S)을 나타낸다.관심 곡선 구간과 대수의 일부 정렬에 대한 부분 적분을 취함으로써, "대수 미분"이 S = [y (θ / Pro.)]임을 보여줄 수 있다. 여기서 y는 "대수 임계값" z(z의 ^[13]^{: 226–230}좌표)에서의 값의 빈도이다.이 관계를 재정렬하면 S / θ = y / Prob가 나오는데, 왼쪽은 선택 차이를 표준 편차로 나눈 값이다. 즉, 표준화된 선택 미분(i)이다.관계의 오른쪽은 i에 대한 "추정기" 즉, 선택 임계값을 선택 압력으로 나눈 좌표를 제공합니다.정규^[49] 분포의 표를 사용할 수 있지만 i 자체의 표도 사용할 수 있습니다.^[67]^{: 123–124}후자의 참조는 또한 "준무한"을 가정할 수 없는 소규모 모집단(400 이하)^[67]^{: 111–122}에 대해 조정된 i 값을 제공한다(단, 위의 "정규 분포" 개요에서 추정).표준화된 선택 차이(i)는 ^[14]^{: 174, 186}선택 강도라고도 합니다.

마지막으로, 이전 서브섹션에서 서로 다른 용어를 사용하는 교차링크가 유용할 수 있다. ( (여기) = "P₀" (여기), µ_S = "P_S" 및 σ² = "p²_P"이다.

감수분열 결정 – 생식 경로 분석

결정 및 근친교배의 생식계수

성적 재생산의 경로 분석.

감수분열 결정(b²)은 부모가 배우자를 생성하는 세포분열인 감수분열 결정 계수이다.Sewall Wright는 경로 분석이 그림 지향 버전인 표준화된 부분 회귀의 원칙에 따라 성 생식 중 유전자 흐름 경로를 분석하여 전체 ^[27]^[37]결과에 대한 다양한 성분의 "기여력"(결정 계수)을 확립했다.경로 분석에는 편상관 계수뿐만 아니라 편회귀 계수(후자는 경로 계수)도 포함됩니다.화살표 헤드가 1개인 선은 방향 결정 경로이며, 화살표 헤드가 2개인 선은 상관 연결입니다.경로 분석 규칙에 따라 다양한 경로를 추적하는 것은 표준화된 부분 ^[55]회귀의 대수를 에뮬레이트합니다.

왼쪽의 경로도는 성적 재생산의 분석을 나타냅니다.그것의 흥미로운 요소들 중에서, 선택 맥락에서 중요한 것은 감수 분열이다.여기서 분리 및 분류가 발생합니다. 즉, 선택에서 발생하는 표현형 분산의 절단을 부분적으로 개선하는 프로세스입니다.경로 계수 b는 감수 분열 경로입니다.a라는 라벨이 붙은 것이 수정 경로입니다.동일한 부모(g)의 배우자 간 상관관계는 감수성 상관관계이다.같은 세대 내 부모 사이의 값은 r이다_A.서로 다른 부모의 배우자 간(f)은 나중에 근친교배계수로 ^[13]^{: 64}알려지게 되었다.소수점( ' )은 생성(t-1)을 나타내고, 프라이밍되지 않은 것은 생성 t를 나타냅니다.여기에서는 본 분석의 몇 가지 중요한 결과가 제시된다.Sewall Wright는 많은 것을 근친교배계수로 ^[27]^[37]해석했다.

감수분열 결정(b²)은 θ(1+g)이고 θ(1+f_(t-1))와 같다. 이는 g_(t-1) ^[68]= f임을 의미한다.비순서 랜덤 수정의_(t-1) 경우 f) = 0으로, 위의 선택 섹션에서 사용된 것과 같이 b = µ를 제공합니다².그러나 그 배경을 알고 있기 때문에 필요에 따라 다른 수정 패턴을 사용할 수 있다.또 다른 결정에는 근친교배도 포함된다. 즉, 수정 결정 a는² 1 / [ 2 (1_t + f )]이다.또 다른 상관관계는 근친교배 지표인 r_A = 2 f_t / ( 1 + f_(t-1) )이다.[공조계수의 대체 이름인 친족계수와 혼동하지 마십시오.「관계」의 개요를 참조해 주세요.이_A r은 분산 및 선택에 대한 하위 섹션에서 다시 발생합니다.

근친 교배와의 이러한 연관성은 당장 드러나지 않는 성적 번식에 대한 흥미로운 측면을 드러낸다.오른쪽 그래프는 근친교배계수에 대한 감수분열 및 승아미(비교배) 계수를 표시합니다.거기서 근친교배가 증가함에 따라 감수분열이 더 중요해지고(계수는 증가), 반면 이승혼은 덜 중요해진다는 것이 밝혀졌다.재생산의 전반적인 역할은 [이전 두 계수의 곱—r²] ^[69]그대로 유지됩니다.이러한 b의 증가는² 근친교배를 동반할 때 일련의 선택 과정에서 표현형 분산의 선택 잘림이 덜 상쇄된다는 것을 의미하기 때문에 선택과 특히 관련이 있다.

유전적 표류 및 선택

이전 섹션에서는 분산을 선택의 "보조"로 취급했으며, 이 두 가지가 잘 연동된다는 것이 명백해졌다.양적 유전학에서 선택은 보통 이러한 "생물학적" 방식으로 검사되지만, 평균의 변화(δG에 의해 모니터링됨)는 이 표면 아래의 대립 유전자와 유전자형 빈도의 변화를 반영한다."유전자 표류" 섹션은 대립 유전자 및 유전자형 빈도 및 관련 수단의 변화에도 영향을 미친다는 것을 상기시키며, 이는 여기에서 고려되는 분산의 동반 측면("동일한 동전의 반대쪽")이라는 것을 상기시킨다.그러나, 이러한 두 가지 주파수 변화의 힘은 거의 일치하지 않으며, 종종 서로 상반되게 작용할 수 있습니다.한 가지(선택)는 표현형에 작용하는 선택 압력에 의해 "방향성"으로 구동되며, 다른 한 가지(유전자 표류)는 수정 시 "찬스"(배우자 샘플의 2항 확률)로 구동됩니다.두 대립 유전자의 빈도가 같은 경향이 있는 경우, 이들의 "동일성"은 유전적 표류에서 해당 주파수 샘플을 얻을 확률이다. 그러나 "충돌" 가능성은 모든 대체 주파수 샘플의 확률의 합이다.극단적인 경우 단일 sungamy 샘플링은 선택이 이루어진 것을 되돌릴 수 있으며, 그 가능성이 이용 가능하다.이 점을 염두에 두는 것이 중요합니다.그러나, 선택 대상의 것과 유사한 표본 빈도를 초래하는 유전적 표류는 선택 목표를 향한 진행을 늦추는 대신 그렇게 급격한 결과로 이어지지 않는다.

「」를 참조해 주세요.

각주 및 참고 자료

^ Anderberg, Michael R. (1973). Cluster analysis for applications. New York: Academic Press.
^ Mendel, Gregor (1866). "Versuche über Pflanzen Hybriden". Verhandlungen Naturforschender Verein in Brünn. iv.
^ ^a ^b ^c Mendel, Gregor (1891). Translated by Bateson, William. "Experiments in plant hybridisation". J. Roy. Hort. Soc. (London). XXV: 54–78.
^ Bateson의 추가 코멘트를 포함한 Mendel G; Bateson W. (1891) 논문은 Sinnott E에 전재되어 있다.던 L.C.; 돕잔스키 T.(1958)"유전학의 원리"; 뉴욕, 맥그로힐: 419-443.각주 3(422페이지)은 Bateson이 원번역자임을 밝히고 해당 번역에 대한 참고 자료를 제공합니다.
^ QTL은 DNA 게놈에서 정량적 표현형 특성에 영향을 미치거나 연관된 영역입니다.
^ Watson, James D.; Gilman, Michael; Witkowski, Jan; Zoller, Mark (1998). Recombinant DNA (Second (7th printing) ed.). New York: W.H. Freeman (Scientific American Books). ISBN 978-0-7167-1994-6.
^ Jain, H. K.; Kharkwal, M. C., eds. (2004). Plant Breeding - Mendelian to molecular approaches. Boston Dordecht London: Kluwer Academic Publishers. ISBN 978-1-4020-1981-4.
^ ^a ^b ^c ^d Fisher, R. A. (1918). "The Correlation between Relatives on the Supposition of Mendelian Inheritance". Transactions of the Royal Society of Edinburgh. 52 (2): 399–433. doi:10.1017/s0080456800012163. Archived from the original on 8 October 2020. Retrieved 7 September 2020.
^ ^a ^b ^c ^d ^e ^f ^g Steel, R. G. D.; Torrie, J. H. (1980). Principles and procedures of statistics (2 ed.). New York: McGraw-Hill. ISBN 0-07-060926-8.
^ 다른 기호가 사용되는 경우도 있지만, 일반적으로 사용되는 기호입니다.
^ 대립 유전자 효과는 모든 배경 유전자형과 환경의 무한대에 걸쳐 관찰되었을 때, 한 궤적에서 대조되는 두 호모 접합체 표현형의 중간점으로부터 호모 접합체의 평균 표현형 편차이다.실제로 모수를 대체하는 것은 큰 비편향 표본의 추정치입니다.
^ 우세 효과는 모든 배경 유전자형과 환경의 무한대에 걸쳐 관찰되었을 때, 한 궤적에 있는 두 개의 호모 접합자의 중간 지점에서 헤테로 접합자의 평균 표현형 편차이다.실제로 모수를 대체하는 것은 큰 비편향 표본의 추정치입니다.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^aa ^ab ^ac ^ad ^ae ^af ^ag ^ah Crow, J. F.; Kimura, M. (1970). An introduction to population genetics theory. New York: Harper & Row.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^aa ^ab ^ac ^ad ^ae ^af ^ag ^ah ^ai ^aj ^ak ^al
Falconer, D. S.; Mackay, Trudy F. C. (1996). Introduction to quantitative genetics (Fourth ed.). Harlow: Longman. ISBN 978-0582-24302-6.
- William G Hill; Trudy F C Mackay (August 2004). "D. S. Falconer and Introduction to Quantitative Genetics". Genetics. 167 (4): 1529–1536. doi:10.1093/genetics/167.4.1529. PMC 1471025. PMID 15342495.
^ Mendel은 F1 > P1에 대한 이 특정 경향에 대해, 즉 줄기 길이에서의 하이브리드 활력의 증거에 대해 언급했다.그러나 차이가 크지 않을 수 있다. (범위와 표준 편차 사이의 관계가 알려져 있으므로 [Steel and Torrie(1980): 576], 이 현재 차이에 대한 대략적인 유의성 검정을 수행할 수 있다.)
^ Richards, A. J. (1986). Plant breeding systems. Boston: George Allen & Unwin. ISBN 0-04-581020-6.
^ Jane Goodall Institute. "Social structure of chimpanzees". Chimp Central. Archived from the original on 3 July 2008. Retrieved 20 August 2014.
^ Gordon, Ian L. (2000). "Quantitative genetics of allogamous F2: an origin of randomly fertiliized populations". Heredity. 85: 43–52. doi:10.1046/j.1365-2540.2000.00716.x. PMID 10971690.
^ 그러나 F1 개체(자기수정 F2)에 의해 유도되는 F2는 무작위로 수정된 모집단 구조의 기원이 아니다.Gordon(2001) 참조.
^ Castle, W. E. (1903). "The law of heredity of Galton and Mendel and some laws governing race improvement by selection". Proceedings of the American Academy of Arts and Sciences. 39 (8): 233–242. doi:10.2307/20021870. hdl:2027/hvd.32044106445109. JSTOR 20021870.
^ Hardy, G. H. (1908). "Mendelian proportions in a mixed population". Science. 28 (706): 49–50. Bibcode:1908Sci....28...49H. doi:10.1126/science.28.706.49. PMC 2582692. PMID 17779291.
^ Weinberg, W. (1908). "Über den Nachweis der Verebung beim Menschen". Jahresh. Verein F. Vaterl. Naturk, Württem. 64: 368–382.
^ 보통 과학 윤리학에서, 발견은 그것을 제안한 가장 이른 사람의 이름을 따서 명명된다.그러나 캐슬은 간과된 것으로 보인다.그리고 나중에 다시 발견되었을 때, "Hardy Weinberg"라는 제목은 너무 어디에나 있어서 업데이트하기에는 너무 늦은 것 같았다.'하디 와인버그 성'의 균형은 좋은 타협이 아닐까?
^ ^a ^b Gordon, Ian L. (1999). "Quantitative genetics of intraspecies hybrids". Heredity. 83 (6): 757–764. doi:10.1046/j.1365-2540.1999.00634.x. PMID 10651921.
^ Gordon, Ian L. (2001). "Quantitative genetics of autogamous F2". Hereditas. 134 (3): 255–262. doi:10.1111/j.1601-5223.2001.00255.x. PMID 11833289.
^ Wright, S. (1917). "The average correlation within subgroups of a population". J. Wash. Acad. Sci. 7: 532–535.
^ ^a ^b ^c ^d ^e ^f ^g Wright, S. (1921). "Systems of mating. I. The biometric relations between parent and offspring". Genetics. 6 (2): 111–123. doi:10.1093/genetics/6.2.111. PMC 1200501. PMID 17245958.
^ Sinnott, Edmund W.; Dunn, L. C.; Dobzhansky, Theodosius (1958). Principles of genetics. New York: McGraw-Hill.
^ ^a ^b ^c ^d ^e Fisher, R. A. (1999). The genetical theory of natural selection (variorum ed.). Oxford: Oxford University Press. ISBN 0-19-850440-3.
^ ^a ^b Cochran, William G. (1977). Sampling techniques (Third ed.). New York: John Wiley & Sons.
^ 이것은 유전자형 분산 섹션에서 그 뒤에 개략적으로 설명된다.
^ 둘 다 일반적으로 사용됩니다.
^ 앞의 인용문을 참조해 주세요.
^ Allard, R. W. (1960). Principles of plant breeding. New York: John Wiley & Sons.
^ ^a ^b 이것은 "company" 및/또는 "companary"로 읽힙니다.p와 q는 서로 보완적이기 때문에, σσ and and와 σ= = σ입니다.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Gordon, I.L. (2003). "Refinements to the partitioning of the inbred genotypic variance". Heredity. 91 (1): 85–89. doi:10.1038/sj.hdy.6800284. PMID 12815457.
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Wright, Sewall (1951). "The genetical structure of populations". Annals of Eugenics. 15 (4): 323–354. doi:10.1111/j.1469-1809.1949.tb02451.x. PMID 24540312.
^ 자가/알로 - 접합성의 문제는 상동 대립 유전자(A 및 A 또는 a 및 a)에만 발생할 수 있으며, 동일한 대립 유전자 기원을 가질 수 없는 비상동 대립 유전자(A 및 a)에는 발생할 수 없습니다.
^ 이 양에는 "β" 대신 "α"를 사용하는 것이 일반적이다(예: 이미 인용된 참고 자료).여기서 후자는 "a"와의 혼동을 최소화하기 위해 사용되며, 이는 동일한 방정식 내에서 자주 발생한다.
^ ^a ^b ^c ^d Mather, Kenneth; Jinks, John L. (1971). Biometrical genetics. Heredity. Vol. 26 (2 ed.). London: Chapman & Hall. pp. 349–364. doi:10.1038/hdy.1971.47. ISBN 0-412-10220-X. PMID 5285746. S2CID 46065232.
^ Mather의 용어로 글자 앞부분은 컴포넌트 라벨의 일부입니다.
^ 이러한 방정식의 각 행에서 성분은 동일한 순서로 표시됩니다.따라서 성분별 수직 비교는 다양한 형태로 각 성분의 정의를 제공합니다.이에 따라 Mather 구성요소는 Fisherian 기호로 변환되어 비교가 용이해졌다.번역문도 정식으로 작성되었습니다.Gordon 2003을 참조해 주세요.
^ ^a ^b 공분산은 두 데이터 집합 사이의 공변량입니다.분산과 마찬가지로 SS가 아닌 교차 산물의 합계(SCP)를 기반으로 합니다.따라서 분산이 공분산의 특수한 형태에 불과하다는 것이 분명합니다.
^ Hayman, B. I. (1960). "The theory and analysis of the diallel cross. III". Genetics. 45 (2): 155–172. doi:10.1093/genetics/45.2.155. PMC 1210041. PMID 17247915.
^ p = q일 때 또는 d = 0일 때 β [= a+(q-p)d]가 a에 "치환"되는 것이 관찰되었다.이러한²_a 상황에서는 숫자만²_A = 。그들은 여전히 하나이고 동일한 정체성이 되지 않았다.이것은 유전자 모델의 "우위"로 간주되는 "치환 편차"에 대해 앞에서 언급한 것과 유사한 비순서일 것이다.
^ 이전 절에서 이미 뒷받침되는 인용문이 제시되었다.
^ 피셔는 이러한 잔차들이 지배의 효과를 통해 발생한다는 것을 주목했지만, 그는 그것들을 "지배적 차이"로 정의하는 것을 자제했다.(앞의 인용문을 참조해 주세요).여기서 설명한 내용을 다시 참조해 주세요.
^ 용어의 출처를 고려하면서:Fisher는 또한 이 변동성의 척도에 대해 "분산"이라는 단어를 제안했습니다.Fisher(1999), p.311 및 Fisher(1918)를 참조한다.
^ ^a ^b ^c ^d Snedecor, George W.; Cochran, William G. (1967). Statistical methods (Sixth ed.). Ames: Iowa State University Press. ISBN 0-8138-1560-6.
^ ^a ^b ^c Kendall, M. G.; Stuart, A. (1958). The advanced theory of statistics. Volume 1 (2nd ed.). London: Charles Griffin.
^ 실험적인 "오차" 분산에 첨자가 없는 것이 일반적입니다.
^ 생체측정학에서, 그것은 부품이 전체의 분수로 표현되는 분산 비율이다. 즉, 결정 계수이다.이러한 계수는 회귀 분석에서 특히 사용됩니다.회귀 분석의 표준화된 버전은 경로 분석입니다.여기서 표준화는 데이터가 먼저 모든 속성에 대한 척도를 통합하기 위해 자체 실험 표준 오차로 분할되었음을 의미합니다.이러한 유전적 용도는 결정 계수의 또 다른 주요 출현이다.
^ Gordon, I. L.; Byth, D. E.; Balaam, L. N. (1972). "Variance of heritability ratios estimated from phenotypic variance components". Biometrics. 28 (2): 401–415. doi:10.2307/2556156. JSTOR 2556156. PMID 5037862.
^ Dohm, M. R. (2002). "Repeatability estimates do not always set an upper limit to heritibility". Functional Ecology. 16 (2): 273–280. doi:10.1046/j.1365-2435.2002.00621.x.
^ ^a ^b ^c ^d Li, Ching Chun (1977). Path analysis - a Primer (Second printing with Corrections ed.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-X.
^ 그들 제품의 근원
^ Moroney, M.J. (1956). Facts from figures (third ed.). Harmondsworth: Penguin Books.
^ ^a ^b Draper, Norman R.; Smith, Harry (1981). Applied regression analysis (Second ed.). New York: John Wiley & Sons. ISBN 0-471-02995-5.
^ ^a ^b ^c ^d Balaam, L. N. (1972). Fundamentals of biometry. London: George Allen & Unwin. ISBN 0-04-519008-9.
^ 과거에는 두 가지 형태의 부모-오프프링 공분산을 h 추정² 작업에 모두 적용했지만, 위의 하위 절에서 설명한 바와 같이 이들 중 한 가지(cov(MPO))만 실제로 적절하다.그러나 cov(PO)는 다음 주요 텍스트에서 보듯이 H를² 추정하는 데 유용합니다.
^ cov(HS)의 우위 성분을 무시하는 텍스트는 r "근사"( r h)를_HS² 잘못 암시한다.
^ Pritchard, Jonathan K.; Pickrell, Joseph K.; Coop, Graham (23 February 2010). "The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation". Current Biology. 20 (4): R208–215. doi:10.1016/j.cub.2009.11.055. ISSN 1879-0445. PMC 2994553. PMID 20178769.
^ Turchin, Michael C.; Chiang, Charleston W. K.; Palmer, Cameron D.; Sankararaman, Sriram; Reich, David; Genetic Investigation of ANthropometric Traits (GIANT) Consortium; Hirschhorn, Joel N. (September 2012). "Evidence of widespread selection on standing variation in Europe at height-associated SNPs". Nature Genetics. 44 (9): 1015–1019. doi:10.1038/ng.2368. ISSN 1546-1718. PMC 3480734. PMID 22902787.
^ Berg, Jeremy J.; Coop, Graham (August 2014). "A population genetic signal of polygenic adaptation". PLOS Genetics. 10 (8): e1004412. doi:10.1371/journal.pgen.1004412. ISSN 1553-7404. PMC 4125079. PMID 25102153.
^ Field, Yair; Boyle, Evan A.; Telis, Natalie; Gao, Ziyue; Gaulton, Kyle J.; Golan, David; Yengo, Loic; Rocheleau, Ghislain; Froguel, Philippe (11 November 2016). "Detection of human adaptation during the past 2000 years". Science. 354 (6313): 760–764. Bibcode:2016Sci...354..760F. doi:10.1126/science.aag0776. ISSN 0036-8075. PMC 5182071. PMID 27738015.
^ 이론적으로 꼬리는 무한하지만 실제로는 준끝이 있다.
^ ^a ^b Becker, Walter A. (1967). Manual of procedures in quantitative genetics (Second ed.). Pullman: Washington State University.
^ 이² b는 괄호 안에 "A"가 아닌 "세대 수준"으로 다시 작성된 페디그리 분석의 부모 수(f_AA)의 계수입니다.
^ b가 a보다 한² 세대 뒤바뀐다는 사실에서² 발생하는 작은 "흔들림"이 있습니다. 즉, 그들의 근친교배 방정식을 살펴보세요.
^ 제품의 제곱근으로 추정됩니다.

추가 정보

Falconer DS & Macay TFC (1996년).정량유전학개론 제4판롱맨, 에식스, 영국
Lynch M & Walsh B(1998).유전학 및 정량적 특성 분석.시나우어, 선덜랜드, 매사추세츠
Roff DA(1997).진화적 정량 유전학.채프먼 & 홀, 뉴욕
세이코라, 토니동물과학 3221 동물 사육테크 미니애폴리스:미네소타 대학교, 2011.인쇄.

외부 링크

사육자의 방정식
Michael Lynch와 Bruce Walsh의 양적 유전학 자원(Genetics and Analysis of Quantitive Fatures and Evolution and Selection of Quantitive Fatures) 교과서 두 권을 포함합니다.
자료: Nick Barton et al..'에볼루션'이라는 교과서에서요
G-Matrix 온라인

[Anderberg_1973-1] Anderberg, Michael R. (1973). Cluster analysis for applications. New York: Academic Press.

[Mendel-2] Mendel, Gregor (1866). "Versuche über Pflanzen Hybriden". Verhandlungen Naturforschender Verein in Brünn. iv.

[Mendel_Bateson-3] Mendel, Gregor (1891). Translated by Bateson, William. "Experiments in plant hybridisation". J. Roy. Hort. Soc. (London). XXV: 54–78.

[4] Bateson의 추가 코멘트를 포함한 Mendel G; Bateson W. (1891) 논문은 Sinnott E에 전재되어 있다.던 L.C.; 돕잔스키 T.(1958)"유전학의 원리"; 뉴욕, 맥그로힐: 419-443.각주 3(422페이지)은 Bateson이 원번역자임을 밝히고 해당 번역에 대한 참고 자료를 제공합니다.

[5] QTL은 DNA 게놈에서 정량적 표현형 특성에 영향을 미치거나 연관된 영역입니다.

[W&G&W&Z_1998-6] Watson, James D.; Gilman, Michael; Witkowski, Jan; Zoller, Mark (1998). Recombinant DNA (Second (7th printing) ed.). New York: W.H. Freeman (Scientific American Books). ISBN 978-0-7167-1994-6.

[J&K_2004-7] Jain, H. K.; Kharkwal, M. C., eds. (2004). Plant Breeding - Mendelian to molecular approaches. Boston Dordecht London: Kluwer Academic Publishers. ISBN 978-1-4020-1981-4.

[Fisher_1918-8] Fisher, R. A. (1918). "The Correlation between Relatives on the Supposition of Mendelian Inheritance". Transactions of the Royal Society of Edinburgh. 52 (2): 399–433. doi:10.1017/s0080456800012163. Archived from the original on 8 October 2020. Retrieved 7 September 2020.

[S_&_T-9] ^ ^a ^b ^c ^d ^e ^f ^g Steel, R. G. D.; Torrie, J. H. (1980). Principles and procedures of statistics (2 ed.). New York: McGraw-Hill. ISBN 0-07-060926-8.

[10] 다른 기호가 사용되는 경우도 있지만, 일반적으로 사용되는 기호입니다.

[11] 대립 유전자 효과는 모든 배경 유전자형과 환경의 무한대에 걸쳐 관찰되었을 때, 한 궤적에서 대조되는 두 호모 접합체 표현형의 중간점으로부터 호모 접합체의 평균 표현형 편차이다.실제로 모수를 대체하는 것은 큰 비편향 표본의 추정치입니다.

[12] 우세 효과는 모든 배경 유전자형과 환경의 무한대에 걸쳐 관찰되었을 때, 한 궤적에 있는 두 개의 호모 접합자의 중간 지점에서 헤테로 접합자의 평균 표현형 편차이다.실제로 모수를 대체하는 것은 큰 비편향 표본의 추정치입니다.

[Crow_&_Kimura-13] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^aa ^ab ^ac ^ad ^ae ^af ^ag ^ah Crow, J. F.; Kimura, M. (1970). An introduction to population genetics theory. New York: Harper & Row.

[Falconer_1996-14] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j ^k ^l ^m ⁿ ^o ^p ^q ^r ^s ^t ^u ^v ^w ^x ^y ^z ^aa ^ab ^ac ^ad ^ae ^af ^ag ^ah ^ai ^aj ^ak ^al Falconer, D. S.; Mackay, Trudy F. C. (1996). Introduction to quantitative genetics (Fourth ed.). Harlow: Longman. ISBN 978-0582-24302-6.
William G Hill; Trudy F C Mackay (August 2004). "D. S. Falconer and Introduction to Quantitative Genetics". Genetics. 167 (4): 1529–1536. doi:10.1093/genetics/167.4.1529. PMC 1471025. PMID 15342495.

[15] William G Hill; Trudy F C Mackay (August 2004). "D. S. Falconer and Introduction to Quantitative Genetics". Genetics. 167 (4): 1529–1536. doi:10.1093/genetics/167.4.1529. PMC 1471025. PMID 15342495.

[15] Mendel은 F1 > P1에 대한 이 특정 경향에 대해, 즉 줄기 길이에서의 하이브리드 활력의 증거에 대해 언급했다.그러나 차이가 크지 않을 수 있다. (범위와 표준 편차 사이의 관계가 알려져 있으므로 [Steel and Torrie(1980): 576], 이 현재 차이에 대한 대략적인 유의성 검정을 수행할 수 있다.)

[Richards_1986-16] Richards, A. J. (1986). Plant breeding systems. Boston: George Allen & Unwin. ISBN 0-04-581020-6.

[Chimpanzees_2014-17] Jane Goodall Institute. "Social structure of chimpanzees". Chimp Central. Archived from the original on 3 July 2008. Retrieved 20 August 2014.

[Gordon_2000-18] Gordon, Ian L. (2000). "Quantitative genetics of allogamous F2: an origin of randomly fertiliized populations". Heredity. 85: 43–52. doi:10.1046/j.1365-2540.2000.00716.x. PMID 10971690.

[19] 그러나 F1 개체(자기수정 F2)에 의해 유도되는 F2는 무작위로 수정된 모집단 구조의 기원이 아니다.Gordon(2001) 참조.

[Castle_1903-20] Castle, W. E. (1903). "The law of heredity of Galton and Mendel and some laws governing race improvement by selection". Proceedings of the American Academy of Arts and Sciences. 39 (8): 233–242. doi:10.2307/20021870. hdl:2027/hvd.32044106445109. JSTOR 20021870.

[Hardy_1908-21] Hardy, G. H. (1908). "Mendelian proportions in a mixed population". Science. 28 (706): 49–50. Bibcode:1908Sci....28...49H. doi:10.1126/science.28.706.49. PMC 2582692. PMID 17779291.

[Weinberg_1908-22] Weinberg, W. (1908). "Über den Nachweis der Verebung beim Menschen". Jahresh. Verein F. Vaterl. Naturk, Württem. 64: 368–382.

[23] 보통 과학 윤리학에서, 발견은 그것을 제안한 가장 이른 사람의 이름을 따서 명명된다.그러나 캐슬은 간과된 것으로 보인다.그리고 나중에 다시 발견되었을 때, "Hardy Weinberg"라는 제목은 너무 어디에나 있어서 업데이트하기에는 너무 늦은 것 같았다.'하디 와인버그 성'의 균형은 좋은 타협이 아닐까?

[Gordon_1999-24] Gordon, Ian L. (1999). "Quantitative genetics of intraspecies hybrids". Heredity. 83 (6): 757–764. doi:10.1046/j.1365-2540.1999.00634.x. PMID 10651921.

[Gordon_2001-25] Gordon, Ian L. (2001). "Quantitative genetics of autogamous F2". Hereditas. 134 (3): 255–262. doi:10.1111/j.1601-5223.2001.00255.x. PMID 11833289.

[Wright_1917-26] Wright, S. (1917). "The average correlation within subgroups of a population". J. Wash. Acad. Sci. 7: 532–535.

[Wright_1921_a-27] ^ ^a ^b ^c ^d ^e ^f ^g Wright, S. (1921). "Systems of mating. I. The biometric relations between parent and offspring". Genetics. 6 (2): 111–123. doi:10.1093/genetics/6.2.111. PMC 1200501. PMID 17245958.

[Sinnott_Dunn_&_Dobzhansky-28] Sinnott, Edmund W.; Dunn, L. C.; Dobzhansky, Theodosius (1958). Principles of genetics. New York: McGraw-Hill.

[Fisher_1999-29] Fisher, R. A. (1999). The genetical theory of natural selection (variorum ed.). Oxford: Oxford University Press. ISBN 0-19-850440-3.

[Cochran_1977-30] Cochran, William G. (1977). Sampling techniques (Third ed.). New York: John Wiley & Sons.

[31] 이것은 유전자형 분산 섹션에서 그 뒤에 개략적으로 설명된다.

[32] 둘 다 일반적으로 사용됩니다.

[33] 앞의 인용문을 참조해 주세요.

[Allard_1960-34] Allard, R. W. (1960). Principles of plant breeding. New York: John Wiley & Sons.

[varpq-35] 이것은 "company" 및/또는 "companary"로 읽힙니다.p와 q는 서로 보완적이기 때문에, σσ and and와 σ= = σ입니다.

[Gordon_2003-36] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ Gordon, I.L. (2003). "Refinements to the partitioning of the inbred genotypic variance". Heredity. 91 (1): 85–89. doi:10.1038/sj.hdy.6800284. PMID 12815457.

[Wright_1951-37] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j Wright, Sewall (1951). "The genetical structure of populations". Annals of Eugenics. 15 (4): 323–354. doi:10.1111/j.1469-1809.1949.tb02451.x. PMID 24540312.

[38] 자가/알로 - 접합성의 문제는 상동 대립 유전자(A 및 A 또는 a 및 a)에만 발생할 수 있으며, 동일한 대립 유전자 기원을 가질 수 없는 비상동 대립 유전자(A 및 a)에는 발생할 수 없습니다.

[39] 이 양에는 "β" 대신 "α"를 사용하는 것이 일반적이다(예: 이미 인용된 참고 자료).여기서 후자는 "a"와의 혼동을 최소화하기 위해 사용되며, 이는 동일한 방정식 내에서 자주 발생한다.

[M&J_1971-40] Mather, Kenneth; Jinks, John L. (1971). Biometrical genetics. Heredity. Vol. 26 (2 ed.). London: Chapman & Hall. pp. 349–364. doi:10.1038/hdy.1971.47. ISBN 0-412-10220-X. PMID 5285746. S2CID 46065232.

[41] Mather의 용어로 글자 앞부분은 컴포넌트 라벨의 일부입니다.

[42] 이러한 방정식의 각 행에서 성분은 동일한 순서로 표시됩니다.따라서 성분별 수직 비교는 다양한 형태로 각 성분의 정의를 제공합니다.이에 따라 Mather 구성요소는 Fisherian 기호로 변환되어 비교가 용이해졌다.번역문도 정식으로 작성되었습니다.Gordon 2003을 참조해 주세요.

[cov-43] 공분산은 두 데이터 집합 사이의 공변량입니다.분산과 마찬가지로 SS가 아닌 교차 산물의 합계(SCP)를 기반으로 합니다.따라서 분산이 공분산의 특수한 형태에 불과하다는 것이 분명합니다.

[Hayman_1960-44] Hayman, B. I. (1960). "The theory and analysis of the diallel cross. III". Genetics. 45 (2): 155–172. doi:10.1093/genetics/45.2.155. PMC 1210041. PMID 17247915.

[45] = q일 때 또는 d = 0일 때 β [= a+(q-p)d]가 a에 "치환"되는 것이 관찰되었다.이러한²_a 상황에서는 숫자만²_A = 。그들은 여전히 하나이고 동일한 정체성이 되지 않았다.이것은 유전자 모델의 "우위"로 간주되는 "치환 편차"에 대해 앞에서 언급한 것과 유사한 비순서일 것이다.

[46] 이전 절에서 이미 뒷받침되는 인용문이 제시되었다.

[47] 피셔는 이러한 잔차들이 지배의 효과를 통해 발생한다는 것을 주목했지만, 그는 그것들을 "지배적 차이"로 정의하는 것을 자제했다.(앞의 인용문을 참조해 주세요).여기서 설명한 내용을 다시 참조해 주세요.

[48] 용어의 출처를 고려하면서:Fisher는 또한 이 변동성의 척도에 대해 "분산"이라는 단어를 제안했습니다.Fisher(1999), p.311 및 Fisher(1918)를 참조한다.

[Snedecor_&_Cochran-49] Snedecor, George W.; Cochran, William G. (1967). Statistical methods (Sixth ed.). Ames: Iowa State University Press. ISBN 0-8138-1560-6.

[Kendall_&_Stuart-50] Kendall, M. G.; Stuart, A. (1958). The advanced theory of statistics. Volume 1 (2nd ed.). London: Charles Griffin.

[51] 실험적인 "오차" 분산에 첨자가 없는 것이 일반적입니다.

[52] 생체측정학에서, 그것은 부품이 전체의 분수로 표현되는 분산 비율이다. 즉, 결정 계수이다.이러한 계수는 회귀 분석에서 특히 사용됩니다.회귀 분석의 표준화된 버전은 경로 분석입니다.여기서 표준화는 데이터가 먼저 모든 속성에 대한 척도를 통합하기 위해 자체 실험 표준 오차로 분할되었음을 의미합니다.이러한 유전적 용도는 결정 계수의 또 다른 주요 출현이다.

[Gordon_Byth_Balaam_1972-53] Gordon, I. L.; Byth, D. E.; Balaam, L. N. (1972). "Variance of heritability ratios estimated from phenotypic variance components". Biometrics. 28 (2): 401–415. doi:10.2307/2556156. JSTOR 2556156. PMID 5037862.

[Dohm_2002-54] Dohm, M. R. (2002). "Repeatability estimates do not always set an upper limit to heritibility". Functional Ecology. 16 (2): 273–280. doi:10.1046/j.1365-2435.2002.00621.x.

[Li_1977-55] Li, Ching Chun (1977). Path analysis - a Primer (Second printing with Corrections ed.). Pacific Grove: Boxwood Press. ISBN 0-910286-40-X.

[56] 그들 제품의 근원

[Moroney_1956-57] Moroney, M.J. (1956). Facts from figures (third ed.). Harmondsworth: Penguin Books.

[Draper_&_Smith-58] Draper, Norman R.; Smith, Harry (1981). Applied regression analysis (Second ed.). New York: John Wiley & Sons. ISBN 0-471-02995-5.

[Balaam_1972-59] Balaam, L. N. (1972). Fundamentals of biometry. London: George Allen & Unwin. ISBN 0-04-519008-9.

[60] 과거에는 두 가지 형태의 부모-오프프링 공분산을 h 추정² 작업에 모두 적용했지만, 위의 하위 절에서 설명한 바와 같이 이들 중 한 가지(cov(MPO))만 실제로 적절하다.그러나 cov(PO)는 다음 주요 텍스트에서 보듯이 H를² 추정하는 데 유용합니다.

[61] v(HS)의 우위 성분을 무시하는 텍스트는 r "근사"( r h)를_HS² 잘못 암시한다.

[62] Pritchard, Jonathan K.; Pickrell, Joseph K.; Coop, Graham (23 February 2010). "The genetics of human adaptation: hard sweeps, soft sweeps, and polygenic adaptation". Current Biology. 20 (4): R208–215. doi:10.1016/j.cub.2009.11.055. ISSN 1879-0445. PMC 2994553. PMID 20178769.

[63] Turchin, Michael C.; Chiang, Charleston W. K.; Palmer, Cameron D.; Sankararaman, Sriram; Reich, David; Genetic Investigation of ANthropometric Traits (GIANT) Consortium; Hirschhorn, Joel N. (September 2012). "Evidence of widespread selection on standing variation in Europe at height-associated SNPs". Nature Genetics. 44 (9): 1015–1019. doi:10.1038/ng.2368. ISSN 1546-1718. PMC 3480734. PMID 22902787.

[64] Berg, Jeremy J.; Coop, Graham (August 2014). "A population genetic signal of polygenic adaptation". PLOS Genetics. 10 (8): e1004412. doi:10.1371/journal.pgen.1004412. ISSN 1553-7404. PMC 4125079. PMID 25102153.

[65] Field, Yair; Boyle, Evan A.; Telis, Natalie; Gao, Ziyue; Gaulton, Kyle J.; Golan, David; Yengo, Loic; Rocheleau, Ghislain; Froguel, Philippe (11 November 2016). "Detection of human adaptation during the past 2000 years". Science. 354 (6313): 760–764. Bibcode:2016Sci...354..760F. doi:10.1126/science.aag0776. ISSN 0036-8075. PMC 5182071. PMID 27738015.

[66] 이론적으로 꼬리는 무한하지만 실제로는 준끝이 있다.

[Becker_1967-67] Becker, Walter A. (1967). Manual of procedures in quantitative genetics (Second ed.). Pullman: Washington State University.

[68] 이² b는 괄호 안에 "A"가 아닌 "세대 수준"으로 다시 작성된 페디그리 분석의 부모 수(f_AA)의 계수입니다.

[69] 가 a보다 한² 세대 뒤바뀐다는 사실에서² 발생하는 작은 "흔들림"이 있습니다. 즉, 그들의 근친교배 방정식을 살펴보세요.

[70] 제품의 제곱근으로 추정됩니다.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

v t 유전학:양적 유전학
양적 유전학의 개념	유전성 우위 정량적 특성 궤적 후보 유전자 유효 모집단 크기
관련 토픽	집단유전학 유전체학 진화생물학 유전

v t 유전학
서론 개요 역사 색인 용어집
주요 컴포넌트	염색체 DNA RNA 게놈 유전 뉴클레오티드 돌연변이 유전적 변이 알레레 아미노산
필드	고전적인 보존. 세포유전학 생태학 면역유전학 미생물 분자의 인구. 양적
의 고고학	아프리카 아메리카 대륙 브리튼 제도 유럽 이탈리아 중동 남아시아
관련 토픽	행동유전학 후생유전학 유전학자 게놈 편집 유전체학 유전자 코드 유전공학 유전적 다양성 유전자 모니터링 유전계보 유전 허젠쿠이 사건 의학 유전학 분자 진화 식물유전학 모집단 유전체학 역유전학
리스트	유전자 코드 목록 유전학 연구 기관 목록
카테고리 공통 위키프로젝트

Search

양적 유전학

유전자 효과

대립 유전자 및 유전자형 빈도

무작위 수정

Mendel의 리서치 크로스– 대조

자가 수정 – 대안

모평균

랜덤 수정 후 평균

장기 자가 수태 후의 평균

평균 – 일반화된 수정

유전적 표류

샘플 색소뎀 – 유전적 표류

자손 계통 – 분산

동등한 분산 후 범믹틱– 근친교배

광범위한 이항 표본 추출 – 판믹시아는 복원되었습니까?

지속적인 유전자 이동 – 분산 및 근친교배 증가

§ 경유2p,q 분산

f를 통한 분산

무작위 수정 내에서 자가 생성

호모 접합성과 헤테로 접합성

확장된 원칙

기타 수정 패턴

'섬' 무작위 수정

대립 유전자 교환 – 대립 유전자 치환

유전자 효과 재정의

유전자형 대체 – 기대와 편차

유전자형 분산

유전자 모델 어프로치– Mather Jinks Hayman

대립 유전자 치환 접근법– Fisher

분산 및 유전자형 분산

§의2G(1) 파생

총 분산 유전자 분산 – β2A(f)f

전체 및 분할 분산 준지배적 분산

환경차이

유전성과 반복성

관계

혈통 분석

교차 곱셈 규칙

풀시브크로스(FS)

하프 시브 크로스(HS)

자가 수정(SF)

사촌 교배

백크로스(BC)

조상 유전자의 공헌

조상 유전자에 의한 관계

GRC – genepool 관계 계수

친척간의 유사성

부모-오프프링 공분산

한부모자녀(PO)

중간부모자녀(MPO)

응용 프로그램(부모 대상)

형제자매의 공유

같은 공통 부모(HS)의 하프시브(Half-sibs)

풀시브(FS)

응용 프로그램(자매)

선택.

기본 원칙

대체 δG

집단유전학에서의 다유전자적응모델

배경

표준화된 선택 – 정규 분포

감수분열 결정 – 생식 경로 분석

유전적 표류 및 선택

관련 속성

상관 관계의 근본 원인

「 」를 참조해 주세요.

각주 및 참고 자료

추가 정보

외부 링크

§ 경유²_p,q 분산

§의²_G(1) 파생

총 분산 유전자 분산 – β²_A(f)_f

「」를 참조해 주세요.