커 미터법

일반상대성이론
${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }=t_{\mu \nu }}$
서론 역사 수학 공식화 테스트
기본 개념 등가원칙 특수상대성이론 월드 라인 유사 리만 다양체
현상 케플러 문제 중력 렌즈 중력파 프레임 드래그 측지 효과 이벤트 호라이즌 특이점 블랙홀 시공간 시공간도 민코프스키 시공간 아인슈타인-로젠 다리
방정식 형식주의 방정식 선형 중력 아인슈타인 장 방정식 프리드만 측지학 매티슨-파페트루-딕슨 해밀턴-야코비-아인슈타인 형식주의 ADM BSSN 포스트뉴턴어 고급 이론 칼루자-클레인 이론 양자 중력
솔루션 슈바르츠실트(내부) 리스너-노르드스트롬 괴델 커 커-뉴먼 카스너 레마슈트르톨만 타우부 너트 밀른 로버트슨-워커 pp파 반스톡툼 더스트 바일루이스파파페트로우
과학자 아인슈타인 로렌츠 힐베르트 푸앵카레 슈바르츠실트 드 시터 리스너 노드스트롬 와일 에딩턴 프리드먼 밀른 즈위키 레마슈트르 괴델 휠러 로버트슨 바딘 워커 커 찬드라세카르 엘러스 펜로즈 호킹 레이쇼후리 테일러 헐스 반 스톡텀 타우브 뉴먼 야우 손 다른이들
물리 포털 카테고리
v t

커 메트릭 또는 커 지오메트리는 반구형 사건 지평선을 가진 축대칭 회전 블랙홀 주변의 빈 공간의 형상을 설명한다.커 메트릭은 일반 상대성 이론의 아인슈타인 장 방정식의 정확한 해이다; 이 방정식은 매우 비선형적이어서, 정확한 해법을 찾기가 매우 어렵다.

개요

커 메트릭은 1915년 칼 슈바르츠실트가 발견한 슈바르츠실트 메트릭의 회전체에 대한 일반화로서, 전하 없이, 구대칭으로 회전하지 않는 물체 주위의 시공간 기하학을 기술했습니다.하전된 구형 비회전 물체에 해당하는 해인 Reissner-Nordström 측정법이 곧 발견되었다(1916–1918).하지만, 충전되지 않은 회전하는 블랙홀에 대한 정확한 해법인 커 측정법은 로이 ^{[1][2]: 69–81} 커에 의해 발견된 1963년까지 미해결로 남아있었다.대전된 회전 블랙홀에 대한 자연적인 확장인 커-뉴먼 측정법은 1965년에 발견되었다.이 네 가지 관련 솔루션은 다음 표로 요약할 수 있습니다. 여기서 Q는 물체의 전하를 나타내고 J는 물체의 스핀 각 운동량을 나타냅니다.

	비회전(J = 0)	회전(J 0 0)
충전되지 않음(Q = 0)	슈바르츠실트	커
과금(Q 0 0)	리스너-노르드스트롬	커-뉴먼

Ker 측정법에 따르면 회전하는 물체는 프레임 드래깅(렌즈라고도 함)을 보여야 한다.세차운동) 일반상대성이론의 독특한 예측이다.이 프레임 드래그 효과의 첫 번째 측정은 2011년 중력 탐사선 B 실험을 통해 수행되었습니다.대략적으로 말하면, 이 효과는 회전하는 질량에 가까운 물체들이 그것의 회전에 참여하기 위해 말려들 것이라고 예측하는데, 이는 느낄 수 있는 어떠한 힘이나 토크 때문이 아니라 회전하는 물체와 연관된 시공간 자체의 소용돌이 곡률 때문이다.회전하는 블랙홀의 경우, 충분히 가까운 거리에서, 모든 물체들 - 심지어 빛-은 블랙홀과 함께 회전해야 합니다; 이것이 유지되는 영역을 에르고스피어라고 합니다.

멀리 있는 광원의 빛은 이벤트 수평선을 여러 번(충분히 가까운 경우) 이동할 수 있으며, 동일한 물체의 여러 이미지를 생성합니다.멀리 있는 시청자에게는 영상 사이의 명백한 수직 거리가 e(약 500)의^2π 배수로 감소합니다.그러나 빠르게 회전하는 블랙홀은 다중도 ^[3][4]이미지 사이의 거리가 더 짧습니다.

회전하는 블랙홀은 지표가 명백한 특이점을 갖는 것처럼 보이는 표면을 가지고 있습니다; 이러한 표면의 크기와 모양은 블랙홀의 질량과 각운동량에 따라 달라집니다.외부 표면은 에르고스피어를 둘러싸고 있으며 평평한 구와 비슷한 모양을 하고 있다.내부 표면은 사건의 지평선을 나타내며, 이 지평선의 내부로 들어가는 물체는 다시는 그 지평선 밖의 세계와 통신할 수 없습니다.그러나 두 표면 모두 다른 좌표계에서^{[citation needed]} 겉으로 보이는 특이점을 제거할 수 있기 때문에 진정한 특이점이 아닙니다.이 두 표면 사이의 물체는 위에서 설명한 바와 같이 회전하는 블랙홀과 함께 회전해야 합니다. 이 기능은 원칙적으로 회전하는 블랙홀에서 에너지를 추출하는 데 사용할 수 있으며, 그 불변 질량 에너지인² Mc까지 사용할 수 있습니다.

2016년 발표된 중력파를 최초로 검출한 LIGO 실험에서도 커 블랙홀 ^[5]쌍이 처음으로 직접 관측됐다.

미터법

커 메트릭은 일반적으로 보이어-린드퀴스트 형식과 커-실드 형식 중 하나로 표현된다.이는 뉴먼-펜로즈 형식주의(^[7]스핀-계수 형식주의라고도 함), 에른스트 ^[8]방정식 또는 엘립소이드 좌표 ^[9]변환에 의한 뉴먼-재니스 알고리즘을^[6] 사용하여 슈바르츠실트 측정법에서 쉽게 도출할 수 있다.

보이어-린드퀴스트 좌표

Ker 미터법은 $각운동량{\displaystyle }$ J$(또는$ 적절한 시간을^[11][12] 위한 동등한 라인 요소)로 $회전$하는 질량$$M(\$displaystyle$M$)$^[10] 부근의$$ 시공간 기하학적 구조를 나타냅니다.

${\displaystyle {signed}ds^{2}&=-c^{2}d\left(1-{\frac {r_{s}r}{\Sigma}}}{\right}c^{2}dt^{2}+{\frac {Sigma}{\Delta}}dr^2\Sigma}dr}dr}dr^{\S}dr}dr}{{{{{\}}\}}}}}\\\\\}dr}dr}d}d}dr}$

(1)

${\displaystyle \mathrm{여기}}$서 $좌표{\displaystyle }$ r${\displaystyle ,}$,,$${\({$displaystyle$r,\$theta,\phi})$는 데카르트^[13][14] 좌표와 동일한 표준 타원형 좌표입니다.

${\displaystyle x=syslogrt {r^{2}+a^{2}}}\sin \theta \cos \phi }$

(2)

${\displaystyle y=syslogrt {r^{2}+a^{2}}}\sin \theta \sin \phi }$

(3)

${\displaystyle z=r\cos \theta,}$

(4)

${\displaystyle {여기}_{}}$서 r$\$는 슈바르츠실트 반지름입니다.

${\displaystyle r_{s}=svsfrac {2}GM}{c^{2}}},}$

(5)

간결성을 위해 길이 $스케일{\displaystyle }$ a${\displaystyle ,}$(\$displaystyle$ a$,\Sigma)$ 및$$$\delta {\displaystyle \mathrm{}}$(\$displaystyle \Delta)$이 다음과 같이 도입되었습니다.

${\displaystyle a=syslogfrac {J}{Mc}},$

(6)

${\displaystyle \Sigma =r^{2}+a^{2}\cos^{2}\theta,}$

(7)

$\displaystyle \Delta = r^{2}-r_{s}r+a^{2}.}$

(8)

위의 메트릭에서 주목해야 할 주요 특징은 교차곱 $용어{\displaystyle }$ d ${\displaystyle t}$ ${\displaystyle d}$ ${\displaystyle .}$ $.\displaystyle dt,d\phi$ 입니다$.$ 이는$$ 블랙홀의 각운동량이 0이 되면 사라지는 회전면에서 시간과 움직임 사이에 결합이 있음을 의미합니다.

$M{\displaystyle }${\$displaystyle$M}($$또는 이에 $상당$하는 ${\displaystyle r_{}}$ s${\display r_$$s$})이 0이 되는 비상대론적 한계에서 Ker 메트릭은 타원체 좌표에 대한 직교 메트릭이 된다.

${\displaystyle g\mathop {\to 0}-c^{2}dt^{2}+{\frac {Sigma}{r^{2}+a^{2}}}dr^{2}+\Sigma d\theta^{2}+\left(r^{2}+a^{2})}\right)\sin ^{2}\theta d\phi ^{2}$

(9)

커-실드 좌표

커 메트릭은 다음과 ^[15][16][17]같이 특정한 데카르트 좌표 집합을 사용하여 "Kerr-Schild" 형식으로 표현할 수 있다.이 해법은 1965년 커와 실드에 의해 제안되었다.

$\displaystyle g_{\mu \nu }=\eta _{\mu \nu }+fk_{\mu }k_{\nu }\!}$

(10)

${\displaystyle f=flac {2}GMr^{3}}:{r^{4}+a^{2}z^{2}}}}$

(11)

$\displaystyle \mathbf {k} =(k_{x},k_{y},k_{z})=\left\frac {frac+ay}{r^{2}+a^{2}}}}, {\frac {ry-ax} {r^{2}+a^{2}}}}}, {\frac {z}{r}}\right}}$

(12)

${\displaystyle k_{0}=1.\!}$

(13)

k는 단위 3-벡터이며, g와 ^[18]θ에 대해 4-벡터를 늘벡터로 만듭니다.여기서 M은 방적물의 일정질량, θ는 민코프스키 텐서, a는 방적물의 일정회전 파라미터이다.$벡터{\displaystyle \stackrel{}{}}$ a $→$ {{$displaystyle {vec${a$$}}}은(는) 양의 z 축을 따라 향하는 것으로 파악됩니다.수량 r은 반지름이 아니라 암묵적으로 다음과 같이 정의됩니다.

${\displaystyle\frac{x^{2}+y^{2}}}{r^{2}+a^{2}}}+{\frac {z^{2}}{r^{2}}=1}$

(14)

수량 r이 통상적인 반지름 R이 되는 것에 주의해 주세요.

${\displaystyle r\to R=sqrt {x^{2}+y^{2}+z^{2}}}}}$

회전 파라미터 a가 0에 가까워질 때이 용액 형태에서는 빛의 속도가 통일성이 되도록 단위를 선택한다(c = 1).선원에서 먼 거리(R µ a)에서 이러한 방정식은 슈바르츠실트 메트릭의 에딩턴-핀켈슈타인 형태로 감소한다.

Kerr-Schild 형태의 Kerr-Schild에서, 측정 텐서의 행렬식은 모든 곳에서 음수 1과 동일하며,^[19] 심지어 선원 근처에서도 마찬가지이다.

솔리톤 좌표

커 메트릭(Ker-NUT 메트릭과 함께)은 축대칭이기 때문에 벨린스키-자하로프 변환을 적용할 수 있는 형태로 주조할 수 있다.이것은 커 블랙홀이 중력 솔리톤의 ^[20]형태를 가지고 있다는 것을 암시합니다.

회전 에너지 질량

블랙홀의 완전한 회전 에너지 E ${\displaystyle {\mathrm{r}}_{}}$ ${\displaystyle {\mathrm{o}}_{}}$ t ${\displaystyle {=}_{}}$ ${\displaystyle {c\mathrm{}}^{}}$2 (${\displaystyle M}$ - ${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{i}}_{}}$r$$) { $style$ E _ { \$rm {rot$} =$c^{2}\left (M-M_{\rm {rot}}\right)}$를 예를 들어 Penrose ^[21][22]공정에서 추출하면 나머지 질량은 축소할 수 없는 질량 이하로 줄어들 수 없다.따라서 블랙홀이 스핀$=M$과 함께 회전하는 경우, M$({$$displaystyle$ $myl$과 M$({$$displaystyle$ M$})$의 합계는 M({displaystyle$$M$})$이 동일한 슈바르츠실트 블랙홀에 비해 2$({$ 정도 높아집니다.$\rm {param$그 이유는 정적인 물체를 회전시키기 위해서는 시스템에 에너지가 가해져야 하기 때문입니다.질량-에너지 등가 때문에 이 에너지에는 시스템의 총 질량-에너지인 $(\displaystyle$ M$)$이 더해지는 질량-에너지 등가도 있다.

물체의 총 질량 $당량{\displaystyle }$ M$(회전$ 에너지 포함)$$과 환원 불가능한 $질량{\displaystyle {}_{}}$ $({$은 다음과 같이 관련된다^[23][24].

${\displaystyle 2M_{\rm {irr}^2}=M^{2}+{\sqrt {M^{2}-J^{2}c^{2}}/G^{2}}\long-rightarrow M^{2}=frac {4M_{\rm}{4}}}{4}}M_{\rm {irr}}^{2}-a^{2}c^{4}/G^{2}}}.}$

파동 연산자

커 메트릭에 대한 직접 확인도 번거로운 계산을 수반하므로, Boyer-Lindquist 좌표의 메트릭 텐서의 역변수 $성분{\displaystyle {}^{}}$ ${\displaystyle {\mathrm{gi}}^{}}$ k$(\$ g$^{ik})$는 4단계 ^[21]연산자의 제곱식에 대해 아래에 나와 있다.

$${\displaystyle g^{\mu \nu}{\frac x^{\frac}{\frac x^{\nu}}=-{\frac {1}{c^{2}\Delta }}}\left(r^{2}+a^2}+{frac } {\frac } {\frac }}}+{\frac {1}{\Delta \sin ^2}\theta }}}\left(1-{\frac {r_{s}r}{\Sigma}}}\left({\frac {\partial}}}{\frac {\fi}}}+{\frac Delta}}}}}}}}}}}}}}}}}}}}}}}}sigma }}}}}}}}}}}}}}}}}}}}}}}}\left$$

(15)

프레임 드래그

Ker 메트릭(1)을 다음과 같은 형태로 다시 작성할 수 있습니다.

${\displaystyle c^{2}d\display^{2}=\left(g_{tt}-{\frac {g_{t\phi}^2}{g_{\r}\r}dr^{2}+g_{\theta \ta }\ta^2}}{g}}{g}{g}{g}\ta}{g}{g}{dr}\ta}{g}{dr}{dr}{g}{g}\ta}{dr}{dr}{g}{g}}}$

(16)

이 메트릭은 각속도 δ로 회전하는 공회전 기준 프레임과 동일하며, 여기서 δ는 킬링 호라이즌이라고 불립니다.

$\displaystyle \Omega =-{\frac {g_{t\phi }}}{g_{\phi \phi }}=black {r_{s}rac}{\frac}시그마 \left(r^{2}+a^{2]}\right)+r_{s}ra^{2}\sin^{2}\theta}}.}$

(17)

따라서 관성 기준 프레임은 회전하는 중심 질량에 의해 결합되어 후자의 회전에 참여하게 됩니다. 이를 프레임 드래그라고 하며,^[25] 실험적으로 테스트되었습니다.질적으로 프레임 드래깅은 전자기 유도의 중력 유사체로 볼 수 있다.적도 상공의 궤도를 돌고 별에 대해 회전하고 있는 "아이스 스케이트 선수"가 팔을 뻗습니다.블랙홀 쪽으로 뻗은 팔은 회전 방향으로 회전합니다.블랙홀에서 뻗은 팔은 회전 방지 토크를 받게 됩니다.따라서 그녀는 블랙홀과 역회전하는 의미에서 회전 속도가 빨라질 것이다.이것은 일상 생활에서 일어나는 일과는 정반대입니다.만약 그녀가 팔을 뻗었을 때 이미 일정한 속도로 회전하고 있다면 관성 효과와 프레임 끌기 효과가 균형을 이루며 그녀의 스핀은 변하지 않을 것이다.등가성의 원리 때문에 중력 효과는 국소적으로 관성 효과와 구별할 수 없기 때문에, 그녀가 팔을 뻗었을 때 아무 일도 일어나지 않는 이 회전 속도는 비회전에 대한 국소 기준이 된다.이 프레임은 고정된 별에 대해 회전하고 있으며 블랙홀에 대해서는 역회전하고 있습니다.유용한 비유는 블랙홀이 태양 기어, 아이스 스케이터가 유성 기어, 외부 우주가 링 기어인 유성 기어 시스템입니다.이는 마하 원리로도 해석할 수 있다.

중요한 표면

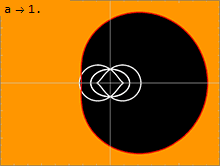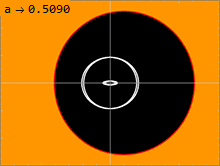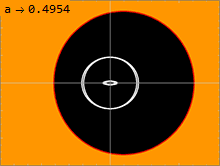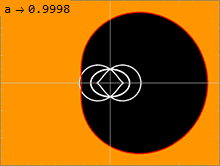
커 미터법(1)에는 몇 가지 중요한 지표면이 있습니다.내부 표면은 슈바르츠실트 메트릭에서 관측된 것과 유사한 사건 지평선에 해당하며, 이는 메트릭의 순수 방사 성분 g가_rr 무한대로 가는 곳에서 발생한다.2차 방정식 풀기1µg_rr = 0이면 다음과 같은 해답이 나옵니다.

${\displaystyle r_{\rm {H}}^{\pm}=blac {r_{s}\pm {blashrt {r_{s}^{2}-4a^{2}}}}{2}}$

이는 자연 단위(G = M = c = 1)로 다음과 같이 단순화된다.

${\displaystyle r_{\rm {H}}^{\pm}=1\pm {1-a^{2}}}$

슈바르츠실트 측정법에서 사건 지평선은 측정법 변화의 순수 시간 성분_tt g가 양수에서 음수로 다른 거리에서 발생하는 Ker 측정법은 다른 거리에서 발생한다.다시 2차_tt 방정식 g = 0을 풀면 다음과 같은 해답이 나옵니다.

${\displaystyle r_{\rm {E}}^{\pm}=pm {r_{s}\cos frac {r_{s}^2}-4a^{2}\cos ^{2}\theta }}} {2}$

또는 자연 단위:

${\displaystyle r_{\rm {E}}^{\pm}=1\pm({1-a^{2}\cos^{2}\theta }})$

제곱근의 cosθ² 항으로 인해, 이 외부 표면은 회전 축의 극에서 내부 표면에 닿는 평평한 구와 유사합니다. 여기서 결속도 θ는 0 또는 θ입니다. 이 두 표면 사이의 공간을 에르고스피어라고 합니다.이 볼륨 내에서 순수 시간 성분 g는_tt 음수이다. 즉, 순수 공간 측정 성분처럼 작용한다.결과적으로, 이 에르고스피어 내의 입자들이 시간적인 특성을 유지하려면 내부 질량과 함께 회전해야 합니다.움직이는 입자는 그 세계선과 시공간을 통과하는 경로를 따라 양의 적절한 시간을 경험합니다.단, 입자가 내부질량 M의 주위를 적어도 δ의 각속도로 공회전하지 않는 한 에르고스피어 내에서는_tt 불가능하다.따라서 에르고스피어 내에서는 어떤 입자도 중심 질량의 회전과 반대 방향으로 움직일 수 없습니다.

슈바르츠실트 메트릭의 사건 지평선과 마찬가지로, r에서의 명백한_H 특이점은 좌표의 선택 때문이다(즉, 좌표 특이점).실제로 적절한 좌표 선택에 의해 시공간이 매끄럽게 지속될 수 있다.반대로, r에서의_E 에르고스피어의 외부 경계는 $0$이 ${\displaystyle \mathrm{아닌}}$ d t ${\displaystyle d}$ ${\$ \ $displaystyle dtd$\ $phi$} 항으로$$ 인해 Ker 좌표에서도 특이하지 않다.

에르고스피어와 펜로즈 과정

일반적으로 블랙홀은 이벤트 지평선이라고 불리는 표면에 둘러싸여 있으며 비회전 블랙홀의 슈바르츠실트 반지름에 위치하고 있습니다. 여기서 탈출 속도는 빛의 속도와 같습니다.이 표면 내에서는 관측자/입자가 일정한 반지름을 유지할 수 없습니다.그것은 강제로 안쪽으로 떨어지게 되고, 그래서 이것은 정적 한계라고 불리기도 합니다.

회전하는 블랙홀은 사건의 지평선에서 같은 정적 한계를 가지고 있지만, 사건 지평선 바깥에는 다음과 같은 "ergosurface"라는 이름의 추가 표면이 있습니다.

${{displaystyle (r-M)^{2}=M^{2}-J^{2}\cos^{2}\theta }$

이는 직관적으로 "주변 공간의 회전 속도"가 빛의 속도와 함께 끌리는 구로 특징지을 수 있는 보이어-린드퀴스트 좌표.이 구체 내에서는 드래그 속도가 빛의 속도보다 크며 관찰자/입자가 강제로 공회전합니다.

이벤트 지평선 바깥이지만 회전 속도가 빛의 속도인 표면 안쪽에 있는 영역을 에르고스피어라고 부릅니다.에르고스피어 내에 떨어지는 입자는 더 빨리 회전하도록 강요되어 에너지를 얻는다.그들은 아직 사건의 지평선 밖에 있기 때문에 블랙홀을 탈출할 수도 있다.그 순 과정은 회전하는 블랙홀이 그 자체의 총 에너지를 희생하면서 에너지 입자를 방출하는 것이다.회전하는 블랙홀에서 스핀 에너지를 추출할 수 있는 가능성은 1969년 수학자 로저 펜로즈에 의해 처음 제안되었고, 따라서 펜로즈 과정이라고 불립니다.천체물리학에서 회전하는 블랙홀은 많은 양의 에너지의 잠재적 원천이며 감마선 폭발과 같은 에너지 현상을 설명하는 데 사용됩니다.

커 형상의 특징

Ker 기하학에는 많은 주목할 만한 특징이 있습니다. 최대 분석 확장에는 에르고스피어, 정지 한계 표면, 이벤트 호라이즌, 코시 호라이즌, 닫힌 타임라이크 곡선 및 링 모양의 곡률 특이점과 관련된 일련의 점근적 평탄한 외부 영역이 포함됩니다.측지방정식은 정확히 닫힌 형태로 풀 수 있다.Ker 형상은 두 개의 Killing 벡터 필드(시간 변환 및 축대칭에 해당) 외에 주목할 만한 Killing 텐서를 허용합니다.주요 늘 합치(ining과 outgoing) 쌍이 있습니다.Weyl 텐서는 대수적으로 특별하며, 사실 그것은 Petrov 타입 D를 가지고 있다.글로벌 구조가 알려져 있습니다.위상적으로 Ker 시공간 호모토피 타입은 단순히 각 정수점에 원이 부착된 선으로 특징지을 수 있다.

내부 Ker 형상은 내부 영역의 섭동과 관련하여 불안정합니다.이러한 불안정성은 Ker 측정이 축대칭이기는 하지만 중력 붕괴를 통해 생성된 블랙홀은 그렇지 ^[13]않을 수 있다는 것을 의미합니다.이러한 불안정성은 또한 위에서 설명한 커 기하학의 많은 특징들이 이러한 블랙홀 ^[27][28]안에 존재하지 않을 수도 있다는 것을 암시합니다.

빛이 블랙홀 주위를 도는 표면은 광자구라고 불린다.커 해는 안쪽과 바깥쪽 사이에 무한히 많은 광자구를 가지고 있다.비회전에서, 슈바르츠실트 용액은 a = 0일 때 내부 및 외부 광자구가 퇴화하여 단일 반지름에 하나의 광자구만 존재한다.블랙홀의 스핀이 클수록 내측과 외측 광자구는 서로 더 멀리 움직인다.블랙홀의 스핀과 반대 방향으로 이동하는 광빔은 외부 광자구에서 구멍 주위를 원을 그리며 돌 것입니다.블랙홀의 스핀과 같은 방향으로 이동하는 빛의 빔은 내부 광자구를 중심으로 원을 그리며 공전할 것입니다.블랙홀의 회전축에 수직인 각운동량을 가진 궤도측지학은 이 두 극단 사이의 광자구 위를 공전할 것이다.시공간이 회전하고 있기 때문에 이러한 궤도는 세차운동을 나타내며, $이$는 ${\$ $변수$에서 1주기를 완료한 후 ${\$ $변수{\displaystyle }$(\$displaystyle$$\theta \,)$에 변화가 있기 때문입니다.

궤적 방정식

커 시공간에서 테스트 입자에 대한 운동 방정식은 네 가지 운동 ^[29]상수에 의해 제어됩니다.첫 번째는 테스트 입자의 불변 $질량{\displaystyle }$μ$(\$style\$mu)$로, 다음 관계에 의해 정의된다.

${\displaystyle {여기}^{}}$서 pα$(\$ p$^{\alpha$})는$$ 입자의 4차원입니다.또한 커 시공간에서의 시간 이동 및 회전 대칭인 $에너지{\displaystyle }$E(\$displaystyle$ E$)$와 블랙홀 ${\displaystyle L_{}}$z(\$displaystyle L_{z$^[21][30]의 스핀에 평행한 궤도 각운동량의 성분인 두 가지 운동 상수가 있다.

그리고.

해밀턴-야코비 이론을 사용하여 브랜든 카터는$$네 번째 운동 상수 Q(현재는 카터 상수$)$가$$^[29]존재한다는 것을 보여주었다.그것은 입자의 총 각운동량과 관련이 있으며 다음과 같이 주어진다.

자유도에 대한 4개의 (독립적인) 운동 상수가 있기 때문에 Ker 시공간에서 테스트 입자에 대한 운동 방정식은 적분할 수 있다.

이러한 운동 상수를 사용하여 (G = M = c = ^[29]1의 자연 단위를 사용하여) 테스트 입자에 대한 궤적 방정식을 작성할 수 있다.

와 함께

• ${\displaystyle \Theta (\theta )=Q-\cos ^{2}\left(a^{2}\left(\mu ^{2}-E^{2}\right)+{\frac {L_{z}{2}{\sin ^{2}\theta }}}}\right}$
• ${\displaystyle P(r)=E\left(r^{2}+a^{2}}\right)-aL_{z}$
• $({displaystyle R(r)=P(r)^2}-\Delta \left(\mu ^{2}r^{2}+(L_{z}-aE)^{2}+Q\right)})$

Where, λ {\displaystyle \lambda } is an affine parameter such that d x α d λ = p α {\displaystyle {\frac {dx^{\alpha }}{d\lambda }}=p^{\alpha }} . In particular, when μ > 0 {\displaystyle \mu >0} the affine parameter λ {\displaystyle \lambda } , is related to the proper time τ {\displaystyle\tau } ~${\displaystyle }$=$μ$ \displaystyle \$displayda = \displays$ / $\$} $。$

프레임 드래그 효과로 인해 제로 앵글 모멘텀 옵서버(ZAMO)는 부기 $좌표시간{\displaystyle }$ t${displaystyle$\Omega$\}$^[31]에 대해 정의된 각속도$\delta {\displaystyle \mathrm{}}$(\$displaystyle$\Omega$$})에 따라 조정됩니다.시험입자의 $국부속도{\displaystyle }$v(\$displaystyle$ v$)$는$\delta {\displaystyle \mathrm{}}$(\$displaystyle\Omega$와 코로팅하는 프로브에 대해 측정된다. $(\displaystyle$ r$)$에 있는 ZAMO와 질량에서 멀리 떨어져 있는 정지 상태의 관찰자 사이의 중력시간팽창은 다음과 같다.

데카르트 커-실드 좌표에서, 광자에^[32] 대한 방정식은 다음과 같다.

$여기$서 C$(\displaystyle$ C$)$는 Carter 상수와 $비슷하고{\displaystyle }$ W$(\displaystyle$ W$)$는 유용한 양입니다.

a ${\displaystyle =}$ ${\displaystyle 0}${$style$ a$=0$을(를) $설정$하면 Schwarzschild 측지학이 복원됩니다.

대칭

커 메트릭의 등각선 그룹은 특이점의 2차원 궤적을 스스로 취하는 10차원 푸앵카레 그룹의 부분군이다.시간 변환(1차원)과 회전 축 주위의 회전(1차원)을 유지합니다.따라서 2차원이 있습니다.Poincaré 그룹과 같이, 그것은 4개의 연결된 구성 요소를 가지고 있습니다. 즉, 항등성의 구성 요소, 시간과 경도를 반전시키는 구성 요소, 적도면을 통해 반사하는 구성 요소, 그리고 둘 다 하는 구성 요소입니다.

물리학에서 대칭은 일반적으로 노에터의 정리에 따라 보존된 운동 상수와 연관되어 있다.위와 같이 측지방정식은 4개의 보존량을 가지고 있습니다.하나는 측지방정식의 정의에서 비롯되고, 2개는 커 형상의 시간변환과 회전대칭에서 발생합니다.네 번째 보존량은 표준적인 의미의 대칭에서 발생하지 않으며 일반적으로 숨겨진 대칭이라고 합니다.

과도한 Ker 솔루션

이벤트 호라이즌의 위치는 $\delta {\displaystyle \mathrm{}}$ ${\displaystyle =}$0의 더 큰 ${\displaystyle \mathrm{루트}}$(\$displaystyle \Delta$=$0$에 의해 결정됩니다./ $<\display r_{s}/2 <a}$ (즉, < \ $displaystyle$ GM$^{2}$ < $Jc$} )는 존재하지 않으며, 이 방정식은 실제의 해답은 존재하지 않습니다.우주의 다른 부분으로부터 그것을 숨길 수 있는 사건의 지평선이 없기 때문에, 블랙홀은 블랙홀이 아니라 벌거벗은 ^[33]특이점이 될 것입니다.

웜홀로서의 커 블랙홀

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 소스되지 않은 소재는 문제가 발생하여 삭제될 수 있습니다. (2011년 2월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다)

Ker 해는 δ = 0의 루트에서 특이하게 보이지만 실제로는 좌표 특이점이며, 적절한 새로운 좌표 선택으로 이러한 루트에 대응하는$$ r$\displaystyle$r의 $값$을 통해 Ker 해를 부드럽게 확장할 수 있다.이러한 뿌리가 클수록 이벤트 지평선의 위치가 결정되고, 작을수록 코시 지평선의 위치가 결정됩니다.(미래 지향, 시간과 같은) 곡선은 외부에서 시작하여 사건의 지평선을 통과할 수 있습니다.$이벤트{\displaystyle }$ 호라이즌을 통과하면$$r\$displaystyle$r 좌표가$$ 시간 좌표처럼 작동하므로 곡선이 코시 ^[34]호라이즌을 통과할 때까지 감소해야 합니다.

코시 지평선 너머에는 몇 가지 놀라운 특징이 있다.$\displaystyle$r 좌표는 다시$$ 공간 좌표처럼 동작하며 자유롭게 변화할 수 있습니다.내부 영역에는 반사 대칭이 있기 때문에 (미래 지향적인 시간과 유사한) 곡선이 대칭 경로를 따라 지속되며, 대칭 경로는 두 번째 코시 지평선을 지나 두 번째 사건 지평선을 지나 커 솔루션의 원래 외부 영역과 등각인 새로운 외부 영역으로 나갈 수 있다.그런 다음 곡선은 새 영역에서 무한대로 탈출하거나 새 외부 영역의 미래 사건 지평선에 진입하여 프로세스를 반복할 수 있습니다.이 두 번째 외관은 때때로 다른 우주처럼 여겨집니다.한편 커 해에서는 특이점은 고리이며 곡선은 이 고리의 중심을 통과할 수 있다.영역을 벗어나면 닫힌 시간 곡선이 허용됩니다.일반 상대성 이론에서 관측자와 입자의 궤적은 시간과 같은 곡선으로 설명되기 때문에, 이 지역의 관측자는 ^[27][28]과거로 돌아갈 수 있다.이 내부 해법은 물리적 해법이 아닐 가능성이 높으며 순수하게 수학적 ^[35]예술품으로 간주됩니다.

커 솔루션의 외부 영역은 안정적이고 모든 회전하는 블랙홀이 결국 커 메트릭에 근접할 것으로 예상되지만,^[36][13] 솔루션 내부 영역은 연필처럼 점으로 균형을 이룬 것처럼 불안정한 것으로 보입니다.이것은 우주 검열과 관련이 있다.

다른 정확한 솔루션과의 관계

커 기하학은 아인슈타인 장 방정식에 대한 고정 축 대칭 진공 해법의 특별한 예입니다.아인슈타인 장 방정식에 대한 모든 고정 축 대칭 진공 해군은 에른스트 진공이다.

커 솔루션은 블랙홀을 모델링하는 다양한 비진공 솔루션과도 관련이 있습니다.예를 들어 Ker-Newman 전기진공은 전하가 부여된 (회전하는) 블랙홀을 모델링하고 Ker-Vaidya null 먼지는 유입되는 전자기 복사를 가진 (회전하는) 구멍을 모델링한다.

특수 케이스 a ${\displaystyle =}$ ${\displaystyle 0}${$style$ a$=0}$의 Ker 측정값은 슈바르츠실트 좌표에서 정적 및 구형 대칭인 비회전 블랙홀을 모델링하는 슈바르츠실트 측정값을 산출합니다.(이 경우, 매 순간 매 순간 질량이 사라집니다.)

Kerr 기하학의 내부 또는 그 일부는 충돌 평면파 모델의 예인 Chandrasekhar-Ferari CPW 진공에 대해 국소적으로 등각적입니다.이 CPW 솔루션의 전역 구조는 Ker 기하학과는 상당히 다르고, 원칙적으로 실험자는 두 개의 적절한 중력 평면파의 충돌을 배열하여 Ker 내부(외부)의 기하학을 연구할 수 있기 때문에 이것은 특히 흥미롭다.

다극 모멘트

각각의 점근적으로 평탄한 에른스트 진공은 상대론적 다극 모멘트의 무한 시퀀스를 제공함으로써 특징지을 수 있으며, 그 중 처음 두 가지는 필드 소스의 질량과 각 운동량으로 해석될 수 있다.Hansen, Thorne, Geroch에 의한 상대론적 다극 모멘트의 대체 공식들이 있는데, 그것들은 서로 일치하는 것으로 판명되었다.커 기하학의 상대론적 다극자 모멘트는 한센에 의해 계산되었다; 그들은 판명되었다.

${\displaystyle M_{n}=M[ia]^{n}}$

따라서 슈바르츠실트 진공의 특수한 경우(a = 0)는 일반 상대성 ^[a]이론의 "쌍극점 소스"를 제공한다.

와일 다극 모멘트는 표준 유클리드 스칼라 다극 모멘트를 사용하여 모든 고정 축대칭 진공 용액의 에른스트 계열에 대해 바일-파페트로우 차트를 나타내는 특정 미터법 함수(정식적으로 뉴턴 중력 전위에 해당)를 처리하는 것에서 발생한다.위의 한센인에 의해 계산된 순간과는 구별됩니다.어떤 의미에서, 와일 모멘트는 고립된 소스의 "질량 분포"를 (간접적으로) 특징짓고, 짝수 순서 상대론적 모멘트에만 의존하는 것으로 드러났습니다.적도면을 가로질러 대칭인 해법의 경우 홀수차 Weyl 모멘트는 사라진다.커 진공 솔루션의 경우, 처음 몇 개의 와일 모멘트는 다음과 같이 주어진다.

$({displaystyle a_{0}=M,\qquad a_{1}=0,\qquad a_{2}=M\left({\frac {M^{2}}}:-a^{2}\right)})$

특히, 우리는 슈바르츠실트 진공이 0이 아닌 2차 와일 모멘트를 가지고 있다는 것을 알 수 있는데, 이는 "와일 모노폴"이 샤지-커존 진공용액이지 특정 유한 길이의 균일한 밀도 얇은 막대의 뉴턴 전위로부터 발생하는 슈바르츠실트 진공용액이 아니라는 사실에 해당한다.

약자장 일반상대성이론에서는 고립된 선원을 다른 유형의 다극자를 사용하여 처리하는 것이 편리하며, 이 다극자 모멘트를 질량 다극자 모멘트와 운동량 다극자 모멘트로 일반화하여 선원의 질량 분포와 운동량 모멘트를 각각 특징짓는다.이들은 적절한 대칭 및 반대칭 부분이 완전 비선형 이론에 대한 상대론적 모멘트의 실제 및 상상의 부분과 다소 복잡한 방식으로 관련될 수 있는 다중 지수화 양이다.

페레즈와 모레스키는 에른스트 진공의 표준 NP 사방근(Weyl-Papapetrou 차트의 반경 좌표)을 r의 힘으로 확장함으로써 "단일극 용액"의 대체 개념을 제공하였다.이 공식에 따르면:

• 각운동량이 0인 절연질량 모노폴 선원은 슈바르츠실트 진공족(파라미터 1개)
• 방사상 각운동량을 갖는 고립된 질량 모노폴 선원은 타우브-이다.NUT 진공 제품군(두 개의 매개 변수, 점근 평탄하지 않음),
• 축방향 각운동량을 갖는 고립된 질량 모노폴 선원은 Ker 진공 제품군이다(2개의 매개변수).

이런 의미에서 Ker 진공은 일반 상대성 이론에서 가장 단순한 정지축 점근대칭 진공 해법이다.

미해결 문제

커 형상은 회전하는 블랙홀의 모형으로 자주 사용되지만, 해법이 (특정 제한에 따라) 일부 콤팩트 영역 바깥에서만 유효하게 유지된다면, 원칙적으로 중성자와 같은 회전하는 거대한 물체 주변의 중력장을 모델링하기 위한 외부 해법으로 사용될 수 있어야 한다. 별, 혹은 지구.이는 회전하지 않는 케이스에 매우 적합합니다. 여기서 슈바르츠실트 진공 외관은 슈바르츠실트 유체 내부와 일치할 수 있으며, 보다 일반적인 정적 구면 대칭 완전 유체 솔루션과도 일치합니다.그러나 커 외부 또는 점근적으로 평평한 진공 외부 솔루션과 일치할 수 있는 회전 완전 유체 내부를 찾는 문제는 매우 어려운 것으로 입증되었습니다.특히, 한때 커의 외관과 일치할 수 있는 후보로 여겨졌던 왈퀴스트 유체는 이제 그러한 일치를 인정하지 않는 것으로 알려져 있다.현재, 천천히 회전하는 유체 볼을 모델링하는 대략적인 솔루션만 알려져 있는 것으로 보인다(이러한 것들은 질량과 각운동량이 0이 아닌 더 높은 다극 모멘트가 사라지는 타원형 볼의 상대론적 유사체이다).그러나 회전하는 얇은 디스크를 모델링하는 정확한 먼지 용액인 Neugebauer-Meinel 디스크의 외부는 제한된 경우 G ${\displaystyle {M2\mathrm{}}^{}}$ $=$ ${\displaystyle c}$ J ${\displaystyle$ GM$^{2$}= $cJ}$ Ker$$ $기하학$에 접근한다.Ker 시공간 일부를 식별하여 얻은 물리적 씬 디스크 솔루션도 ^[37]알려져 있습니다.

「 」를 참조해 주세요.

• 슈바르츠실트 측정법
• 커-뉴먼 미터법
• 레이스너-노르드스트롬 미터법
• 하틀-토른 미터법
• 스핀 플립
• 커-실드 시공간
• 회전 블랙홀

각주

레퍼런스

추가 정보

• Wiltshire, David L.; Visser, Matt; Scott, Susan M., eds. (2009). The Kerr Spacetime: Rotating Black Holes in General Relativity. Cambridge: Cambridge University Press. ISBN 978-0-521-88512-6.
• Stephani, Hans; Kramer, Dietrich; MacCallum, Malcolm; Hoenselaers, Cornelius; Herlt, Eduard (2003). Exact Solutions of Einstein's Field Equations. Cambridge: Cambridge University Press. ISBN 978-0-521-46136-8.
• Meinel, Reinhard; Ansorg, Marcus; Kleinwachter, Andreas; Neugebauer, Gernot; Petroff, David (2008). Relativistic Figures of Equilibrium. Cambridge: Cambridge University Press. ISBN 978-0-521-86383-4.
• O'Neill, Barrett (1995). The Geometry of Kerr Black Holes. Wellesley, Massachusetts: A. K. Peters. ISBN 978-1-56881-019-5.
• D'Inverno, Ray (1992). Introducing Einstein's Relativity. Oxford: Clarendon Press. ISBN 978-0-19-859686-8. 고급 학부 수준의 읽기 쉬운 소개는 19장을 참조하십시오.
• Chandrasekhar, S. (1992). The Mathematical Theory of Black Holes. Oxford: Clarendon Press. ISBN 978-0-19-850370-5. 고급 대학원 수준의 매우 철저한 연구는 6-10장을 참조하십시오.
• Griffiths, J. B. (1991). Colliding Plane Waves in General Relativity. Oxford: Oxford University Press. ISBN 978-0-19-853209-5. Chandrasekhar/Ferari CPW 모델은 13장을 참조하십시오.
• Adler, Ronald; Bazin, Maurice; Schiffer, Menahem (1975). Introduction to General Relativity (Second ed.). New York: McGraw-Hill. ISBN 978-0-07-000423-8. 7장을 참조해 주세요.
• Penrose, R. (1968). ed C. de Witt and J. Wheeler (ed.). Battelle Rencontres. W. A. Benjamin, New York. p. 222.
• Perez, Alejandro; Moreschi, Osvaldo M. (2000). "Characterizing exact solutions from asymptotic physical concepts". arXiv:gr-qc/0012100v1. 위에서 설명한 바와 같이 3가지 표준 진공 솔루션 패밀리의 특성 분석.
• Sotiriou, 토마스 P.;Apostolatos, Theocharis A(2004년)."그 Multipole 모멘트 축대칭 Electrovacuum에 Corrections과 댓글 Spacetimes".클래스입니다. 양자 Grav.21(24):5727–5733. arXiv:gr-qc/0407064.Bibcode:2004CQGra..21.5727S. doi:10.1088/0264-9381/21/24/003.S2CID 16858122.그 에른스트 공백(플러스는 전자파와 중력의 상대론적 다중극 순간들을 위해 전하를 일반화)의 상대론적 다중극 순간들을 발령한다.
• Carter, B. (1971). "Axisymmetric Black Hole Has Only Two Degrees of Freedom". Physical Review Letters. 26 (6): 331–333. Bibcode:1971PhRvL..26..331C. doi:10.1103/PhysRevLett.26.331.
• Wald, R. M. (1984). General Relativity. Chicago: The University of Chicago Press. pp. 312–324. ISBN 978-0-226-87032-8.
• Kerr, R. P.; Schild, A. (2009). "Republication of: A new class of vacuum solutions of the Einstein field equations". General Relativity and Gravitation. 41 (10): 2485–2499. Bibcode:2009GReGr..41.2485K. doi:10.1007/s10714-009-0857-z. S2CID 361088.
• Krasiński, 안제이, Verdaguer, 엔릭, 커, 로이 패트릭(2009년).는 논설에 관한 노트:R.P. 커와 A가실트, 아인슈타인은 필드의 진공 솔루션의 새로운 수업 equations".일반 상대성과 중력. 41(10):2469–2484. Bibcode:2009년.GReGr..41.2469K. doi:10.1007/s10714-009-0856-0."...이 노트 누가[그 커 해결의 어원이]. 정보를 확인하고 싶은 독자 위한 지침을 의미한다.."