Null 벡터

$q{\displaystyle (x,}$ ${\displaystyle y,}$ ${\displaystyle z}$)${\displaystyle }$= ${\displaystyle {x\mathrm{}}^{}}$ ${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$- ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$. ${\displaystyle q(x,y,z)=x^{2}+y^{2}-z^{2}.$$}$

수학에서, 관련 2차 형태 q를 가진 벡터 공간 X가 주어진 경우(X, q), null 벡터 또는 등방성 벡터는 q(x) = 0인 X의 비제로 원소 x이다.

실제 이선형식의 이론에서는 확실한 2차형과 등방성 2차형이 구별된다. 그것들은 후자에 대해서만 0이 아닌 null 벡터가 존재한다는 점에서 구별된다.

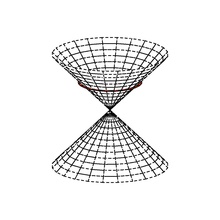
null 벡터가 있는 2차 공간(X, q)을 의사-유클리드 공간이라고 한다.

사이비-유클리드 벡터 공간은 직교 서브공간 A와 B, X = A + B로 분해될 수 있으며, 여기서 q는 A에서는 양의 결정체, B에서는 음의 결정체다. X의 null 콘 또는 등방성 콘은 균형 잡힌 구의 결합으로 구성된다.

$${\displaystyle \bigcup _{r\geq 0}\{x=a+b:q(a)=-q(b)=r,a\in A,b\in B\}.}$$

예

민코스키 공간의 빛과 같은 벡터는 null 벡터다.

4개의 선형 독립 바이쿼터니온 l = 1 + hi, n = 1 + hj, m = 1 + hk, m^∗ = 1 – hk는 null 벡터이며 { l, n, m, m }은^∗ 스페이스타임을 나타내는 데 사용되는 아공간을 위한 기초가 될 수 있다. Null 벡터는 스페이스타임 다지관에 대한 Newman-Penrose 형식주의 접근법에서도 사용된다.^[1]

구성 대수학은 그것이 null 벡터를 가지고 있을 때 분열된다. 그렇지 않으면 그것은 분할 대수다.

Lie 대수학의 Verma 모듈에는 null 벡터가 있다.

참조

• Dubrovin, B. A.; Fomenko, A. T.; Novikov, S. P. (1984). Modern Geometry: Methods and Applications. Translated by Burns, Robert G. Springer. p. 50. ISBN 0-387-90872-2.
• Shaw, Ronald (1982). Linear Algebra and Group Representations. Vol. 1. Academic Press. p. 151. ISBN 0-12-639201-3.
• Neville, E. H. (Eric Harold) (1922). Prolegomena to Analytical Geometry in Anisotropic Euclidean Space of Three Dimensions. Cambridge University Press. p. 204.