초직각
Hyperrectangle| 초직각 오르토톱 | |
|---|---|
 직사각형 입방체는 3개의 직교체이다. | |
| 유형 | 프리즘 |
| 면 | 2n |
| 꼭지점 | 2개n |
| 슐레플리 기호 | {} × {} ...× {}[1] |
| 콕서터-딘킨 도표 | |
| 대칭군 | [2n−1] 주문n 2 |
| 듀얼 | 직사각형 n-퓨질 |
| 특성. | 볼록, 조노면체, 등교 |
기하학에서 직교각[2](초직각 또는 상자라고도 함)은 직사각형을 더 높은 차원으로 일반화한 것입니다.이것은 공식적으로 직교 구간의 데카르트 곱으로 정의된다.초직각은 평행동위원소의 특별한 경우이다.
종류들
3차원 직교기는 또한 오른쪽 직사각형 프리즘, 직사각형 입방체 또는 직사각형 입방체라고 불린다.
모든 모서리의 길이가 동일한 n차원 직교계의 특수한 경우는 [2]n-입방체입니다.
유추적으로, "하이퍼렉트 앵글" 또는 "박스"라는 용어는 데이터베이스 이론의 키 범위나 [3]정수 범위와 같은 다른 종류의 직교 구간의 데카르트 곱을 나타낼 수 있다.
듀얼 폴리토프
| n점 | |
|---|---|
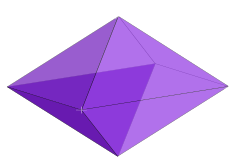 예: 3-퓨질 | |
| 면 | 2n |
| 꼭지점 | 2개n |
| 슐레플리 기호 | {} + {} + ...+ {} |
| 콕서터-딘킨 도표 | |
| 대칭군 | [2n−1] 주문n 2 |
| 듀얼 | n정통경 |
| 특성. | 볼록, 등방성 |
n-정통형의 이중 폴리토프는 직사각형 n-정통형, 마름모꼴 n-퓨실 또는 n-로젠지라고 다양하게 불려왔다.직교 직사각형 면의 중앙에 위치한 2n개의 점에 의해 구성됩니다.
n-fusil의 Schléfli 기호는 n개의 직교 선분의 합으로 나타낼 수 있다: { } + { } + ...+ { }.
1-퓨실은 선분입니다.2-퓨실은 마름모꼴이다.모든 축 쌍에서 평면 교차 선택은 마름모꼴입니다.
| n | 이미지 예시 |
|---|---|
| 1 | { } |
| 2 | 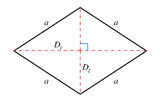 { } + { } |
| 3 | 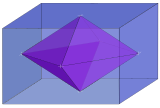 마름모꼴 3정통 내측 3정통 { } + { } + { } |
「 」를 참조해 주세요.
메모들
레퍼런스
- Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123. ISBN 0-486-61480-8.



