7차원 공간

수학에서, n개의 실수의 수열은 n차원 공간에서의 위치로 이해될 수 있다.n = 7일 때, 이러한 모든 위치의 집합을 7차원 공간이라고 한다.종종 그러한 공간은 거리에 대한 어떤 개념도 없이 벡터 공간으로 연구된다.7차원 유클리드 공간은 점곱으로 ^{[disputed – discuss]}정의되는 유클리드 메트릭을 갖춘 7차원 공간이다.

보다 일반적으로, 이 용어는 7차원 복소 벡터 공간, 예를 들어 14개의 실제 차원이 있는 7차원 벡터 공간을 가리킬 수 있습니다.또한 7차원 다지관이나 다양한 기하학적 구조를 나타낼 수도 있습니다.

7차원 공간에는 많은 특별한 성질이 있는데, 그 중 많은 성질이 8진수와 관련되어 있다.특히 구별되는 특성은 교차곱이 3차원 또는 7차원으로만 정의될 수 있다는 것입니다.이는 2차원, 4차원, 8차원 이외의 4차원, 8차원 등 대수적 구조의 존재를 금지하는 후르비츠의 정리와 관련이 있다.최초로 발견된 이국적인 구체는 7차원이었다.

기하학.

7 폴리토프

7차원의 폴리토프는 7-폴리토프라고 불립니다.가장 많이 연구된 것은 일반 폴리톱으로, 7차원에는 7단순, 7입방체, 7정통 세 가지 차원이 있다.더 넓은 계열은 콕서터 그룹에 의해 정의된 각 영역인 반사의 기본 대칭 영역으로 구성된 균일한 7-폴리토프이다.각 균일한 폴리토프는 고리 모양의 콕서터-딘킨 다이어그램에 의해 정의된다.7-데미큐브는 D 패밀리의₇ 고유 폴리토프이며, E₂₁ 패밀리의₇ 3, 2₃₁₃₂, 1 폴리토프입니다.

규칙적이고 균일한 7차원 폴리토플
(대칭의 각 콕서터 평면에서 직교 투영으로 표시됨)

A6.	B7.		D7.	E7.
71200x {3,3,3,3,3,3}	7큐브 {4,3,3,3,3,3}	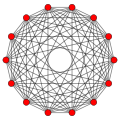7 직각 {3,3,3,3,3,4}	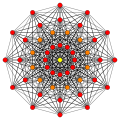7 데미큐브 = h{4,3,3,3,3} = {3,34,1}	3개21 {3,3,32,1}	2개31 {3,3,33,1}	1개32 {3,33,2}

6구

7차원 유클리드 공간의 6-구 또는 초구는 원점과 같은 점에서 6차원 표면 거리이다.기호⁶ S를 가지며 반지름 r의 6-sphere에 대한 공식 정의는 다음과 같습니다.

$\displaystyle S^{6}=\left\{x\in \mathbb {R}^{7}:\x\=r\right\}.}$

이 6-sphere로 둘러싸인 공간의 부피는

${\displaystyle V_{7}, = flac {16\pi ^{3}} {105}}, r^{7}$

이는 4.72477⁷ × r 또는 6-sphere를 포함하는 7-큐브의 0.0369입니다.

적용들

크로스 프로덕트

두 벡터의 벡터값, 쌍선형, 반교합 및 직교곱인 교차곱은 7차원으로 정의된다.보다 일반적인 3차원 교차 제품과 함께 사소한 제품을 제외한 유일한 교차 제품입니다.

이국적인 구체

1956년, 존 밀너는 7차원으로 이국적인 구를 만들었고 7-구에는 적어도 7개의 구별 가능한 구조물이 있다는 것을 보여주었다.1963년에 그는 그러한 구조물의 정확한 수가 28이라는 것을 보여주었다.

「 」를 참조해 주세요.

• 유클리드 기하학
• 지오메트리 토픽 리스트
• 일반 폴리토프 목록

레퍼런스

• H.S.M. 콕서터:일반 폴리토프.도버, 1973년
• J.W. 밀너:7-sphere와 동질적인 다지관에.수학연보 64, 1956

외부 링크

• "Euclidean geometry", Encyclopedia of Mathematics, EMS Press, 2001 [1994]