함수(수학)

이 기사는 검증을 위해 추가 인용이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. 미가공 재료는 도전하여 제거할 수 있습니다. 출처 찾기: "함수" 수학 – 뉴스 · 신문 · 책 · 학자 · JSTOR (2022년 7월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보기)

기능.
x ↦ f (x)
함수 개념의 연혁
도메인 및 코도메인의 예
${\displaystyle X}$ → ${\displaystyle \mathbb{B}}$ ${\$ $\},$ ${\displaystyle \mathbb {B} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {B} ^{n}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{Z}}$ ${\$ ${\displaystyle \mathbb {Z} }$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{R}}$ ${\$ ${\displaystyle \mathbb {R} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {R} ^{n}$ → ${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle \mathbb{C}}$ ${\$ $\},$ ${\displaystyle \mathbb {C} }$ → ${\displaystyle X}$ ${\displaystyle$ X$\},$ ${\displaystyle \mathbb {C} ^{n}$ → ${\displaystyle X}$
클래스/속성
일정한 신원 선형 다항식 합리적인 대수적 분석적 매끄러운 계속되는 측정가능 주사제 서젝티브 바이젝티브
시공
제한 구성. λ 인버스
일반화
이항 관계 부분적 다치 암시적 공간
v t

수학에서 집합 X에서 집합 Y로의 함수는 X의 각 원소에 정확히 Y의 원소 하나를 할당합니다.^[1] 집합 X를 함수의^[2] 정의역, 집합 Y를 함수의 정의역이라고 합니다.^[3]

함수는 원래 다양한 양이 다른 양에 따라 어떻게 달라지는지에 대한 이상화였습니다. 예를 들어, 행성의 위치는 시간의 함수입니다. 역사적으로 이 개념은 17세기 말에 무한소 미적분학으로 정교화되었으며, 19세기까지 고려된 함수는 미분 가능했습니다(즉, 높은 수준의 규칙성을 가지고 있었습니다). 함수의 개념은 19세기 말 집합론의 관점에서 공식화되었으며, 이는 개념의 적용 영역을 크게 확대시켰습니다.

함수는 f, g 및 h와 같은 문자로 표시되는 경우가 가장 많으며, 함수 f의 정의역의 원소 x에 있는 함수 f의 값은 f(x)로 표시되며, 특정 입력 값에서 함수 평가의 결과인 수치는 x를 이 값으로 대체하여 표시되며, 예를 들어 x = 4에 있는 f의 값은 f(4)로 표시됩니다. 함수가 이름이 지정되지 않고 식 E로 표시되는 경우 x = 4에서 함수의 값은 E로 표시될 수 있습니다. 예를 들어, x를$$(${\displaystyle x}$+ ${\displaystyle 1{}^{}}$ ${\displaystyle 2^{}}$ ${\displaystyle (x$+ $1)^{2}}$에 매핑하는 함수의 4에서 값은 ${\displaystyle {(x}_{}}$+ ${\displaystyle {1{}^{}}_{}}$ ${\displaystyle {2^{}}_{}}$ ${\displaystyle x_{}}$ = ${\displaystyle 4_{}}$ ${\displaystyle \left.(x$+ $1)^{2$)}로 표시될 수 있습니다.$}\right\vert$ _${x=4},$ 25입니다.

도메인과 코드 도메인이 주어지면 함수는 함수를 설명하는 일반적인 수단인 함수의 그래프라고 하는 모든 쌍(x, f(x))의 집합으로 고유하게 표현됩니다.^{[note 1][4]} 정의역과 공변역이 실수들의 집합일 때, 각각의 쌍은 평면상의 한 점의 직각좌표로 생각될 수 있습니다.

함수는 과학, 공학 및 대부분의 수학 분야에서 널리 사용됩니다. 함수는 대부분의 수학 분야에서 "중심적인 조사 대상"이라고 말해 왔습니다.^[5]

정의.

집합 X에서 집합 Y로의 함수 f는 Y의 원소를 X의 각 원소에 할당한 것입니다. 집합 X를 함수의 정의역, 집합 Y를 함수의 정의역이라고 합니다.

함수 f에 의해 Y의 원소 y가 X의 x에 할당되면 f는 x를 y에 매핑한다고 말하고, 이것은 일반적으로 $y$ = f${\displaystyle }$( ${\displaystyle x}$)라고 씁니다${\displaystyle .}$ ${\displaystyle$ y=$f(x).$$}$이 표기법에서$$ x는 함수의 인수 또는 변수입니다. X의 특정 요소 x는 변수의 값이고, Y의 해당 요소는 x에 있는 함수의 값 또는 함수 아래에 있는 x의 이미지입니다.

함수 f, 그 도메인 X 및 그 코드 도메인 Y는 종종 $f{\displaystyle :}$ ${\displaystyle X}$ → ${\displaystyle Y}$. ${\displaystyle f:X\to Y.}$라는 표기법으로 지정됩니다. 이 경우, ${\displaystyle y}$ =${\displaystyle }$f ($$x ) $대신$ $x$↦ y ${\displaystyle$ x$\mapstyle$ y}라고 쓸 수 있습니다. {\$displaystyle$y=f(x)).$}$이를$$ 통해 함수의 이름을 지정하지 않고 함수를 정의할 수 있습니다. 예를 들어 제곱 함수는 함수 ${\displaystyle x^{}}$ ↦ x $2$입니다. ${\displaystyle$ x$\mapssto$x^{2}}.

함수를 정의할 때 도메인과 코드 도메인이 항상 명시적으로 주어지지는 않습니다. 특히, 특정 함수의 도메인이 더 큰 집합에 포함되어 있다는 것을 일부(아마도 어려운) 계산 없이만 알 수 있는 것이 일반적입니다. 예를 들어 $f{\displaystyle }$: ${\displaystyle R}$ → R ${\displaystyle$ ${\displaystyle f}$ $:\mathbb {R} \to \mathbb {R} }$ 가 실수 함수인 경우 $함수$ ${\displaystyle x}$ ↦ 1${\displaystyle }$/ f$$( x ) ${\displaystyle$ x$\mapsto$1/f(x))} 의 정의역을 결정하려면 f 의 0을 알아야 합니다. 이것은 수학적 분석에서 "X에서 Y까지의 함수"가 X의 적절한 부분 집합을 갖는 함수를 정의역으로 지칭할 수 있는 이유 중 하나입니다.^{[note 2]} 예를 들어, "실수에서 실수로의 함수"는 정의역이 실수들의 적절한 부분 집합인 실수 변수의 실수 값 함수, 일반적으로 비어 있지 않은 열린 구간을 포함하는 부분 집합을 가리킬 수 있습니다. 그런 함수를 부분 함수라고 합니다.

함수의 범위 또는 이미지는 도메인에 있는 모든 요소의 이미지 집합입니다.^[6][7][8][9]

집합 S 상의 함수 f는 공동 도메인을 지정하지 않고 도메인 S로부터의 함수를 의미합니다. 그러나 일부 저자들은 함수가 f:S → S라고 말하는 축약어로 사용합니다.

형식적 정의

함수에 대한 위의 정의는 본질적으로 미적분학의 창시자인 라이프니츠, 뉴턴, 오일러의 정의입니다. 그러나 "과제"에 대한 수학적 정의가 없기 때문에 공식화할 수 없습니다. 집합론의 관점에서 함수에 대한 최초의 공식적인 정의가 제공될 수 있었던 것은 19세기 말입니다. 이 집합론적 정의는 함수가 도메인의 요소와 코드 도메인의 일부(아마도 모든) 요소 간의 관계를 설정한다는 사실에 기초합니다. Mathematically, a binary relation between two sets X and Y is a subset of the set of all ordered pairs ${\displaystyle (x,y)}$ such that ${\displaystyle x\in X}$ and ${\displaystyle y\in Y.}$ The set of all these pairs is called the Cartesian product of X and Y and denoted ${\displaystyle X\times Y.}$${\displaystyle$ X$\times Y.}$ 따라서$$, 상기 정의는 다음과 같이 공식화될 수 있습니다.

정의역 X와 공변역 Y를 갖는 함수는 다음 두 조건을 만족하는 X와 Y 사이의 이항 관계 R입니다.

• $X$ ${\displaystyle X}$의 모든 $x$ ${\displaystyle x}$에 대해 $Y$ ${\displaystyle Y}$에는$$(${\displaystyle x,}$ y${\displaystyle )}$ $R.{\displaystyle (x,$ y)\in R.}을(를) ∈ y
• ${\displaystyle (}$ $x$ ${\displaystyle y}$) $∈$ R ${\displaystyle (x,$ y)\in$$R}$및$(x${\displaystyle ,}$${\displaystyle }$$)$∈ $R {\displaystyle ($x, $z$)\in R}은$y$= z임을 $의미$합니다. {\$displaysty$${\displaystyle l}$$e$y=z.}

보다 형식적으로는 관계의 개념을 명시적으로 언급하지 않고 더 많은 표기법(세트 제작자 표기법 포함)을 사용합니다.

함수는 다음 세 조건을 만족하는$$ $도메인{\displaystyle }$ X${\displaystyle ,}$ ${\displaystyle X,}$ 코도메인 $Y$ ${\displaystyle$ $,}$ 및$$ $그래프{\displaystyle }$ R ${\displaystyle R}$의 세 집합으로 구성됩니다.

• ${\displaystyle R\subset \{(x,y)\mid x\in X,y\in Y\}$
• ${\displaystyle \in X,\in X,\in Y,\left (x,y\right)\in R\qquad}$
• ${\displaystyle (x,y)\in R\land (x,z)\in R\implies y=z\qquad }$

부분함수

부분 함수는 "총" 조건이 제거된 일반 함수와 유사하게 정의됩니다. 즉, X에서 Y까지의 부분 함수는 X와 Y 사이의 이진 관계 R이므로, $모든$ ${\displaystyle x}$ ∈ $X$에 대해 ${\displaystyle$x\in X,}에 대해 ${\displaystyle (}$x$)$ ∈ $R$x, y)\in R.}

함수 표기법을 사용하면 ${\displaystyle x}$ ∈ $X$가 주어졌을 때 ${\displaystyle$x\in X,}${\displaystyle }$f$$(x) ${\displaystyle$f(x))가 Y에 있거나 정의되지 않음을 의미합니다.

$f{\displaystyle (x)}$ ${\displaystyle$ f$(x))}$가 정의되고 Y에 속하도록 X의 요소 집합을 함수의 정의 영역이라고 합니다. 따라서 X에서 Y까지의 부분 함수는 함수의 정의역이라고 하는 X의 부분 집합을 정의역으로 갖는 일반 함수입니다. 정의 정의역이 X이면 부분 함수는 총 함수라고 말하는 경우가 많습니다.

수학의 여러 영역에서 "함수"라는 용어는 일반 함수가 아닌 부분 함수를 나타냅니다. 일반적으로 도메인을 결정하는 것을 어렵게 하거나 심지어 불가능하게 하는 방식으로 함수를 지정할 수 있는 경우가 이에 해당합니다.

미적분학에서 실수 변수 또는 실수 함수의 실수 값 함수는 실수의 집합$$ $R{\displaystyle \mathbb{}}$ ${\$에서 그 자체로의 부분 함수입니다. ${\displaystyle \mathrm{실수}}$ 함수 $f{\displaystyle }$: ${\displaystyle x}$ ↦ f$$( x) ${\displaystyle f$ : x$\mapssto$ f (x))}의 곱셈${\displaystyle }$역 ${\displaystyle x}$ ↦ 1 / f (x$)$ {\$displaystyle$x\mapsto 1/f(x)}도 실수 함수입니다. (부분) 함수의 곱셈 역의 정의 영역의 결정은 함수가 정의되지만 곱셈 역이 정의되지 않는 값인 함수의 0을 계산하는 데에 해당합니다.

마찬가지로, 복소수 변수의 함수는 일반적으로 복소수의 집합$$ $C{\displaystyle \mathbb{}}$ ${\$에 정의 영역이 포함된 부분 함수입니다. 복소 함수의 정의역을 결정하는 어려움은 리만 제타 ${\displaystyle \mathrm{함수}}$의 곱셈 역으로 설명됩니다. $함수$ z ↦ 1${\displaystyle }$/ ζ (z) {\$displaystyle z\mapsto$ 1/\zeta (z))의 정의역 결정은 다음 중 하나의 증명 또는 반증과 어느 정도 동등합니다. 수학의 주요 미해결 문제인 리만 가설.

계산가능성 이론에서 일반적인 재귀 함수(recursive function)는 알고리즘에 의해 값이 계산될 수 있는 정수에서 정수까지의 부분 함수입니다(대략적으로 말하면). 이러한 함수의 정의 영역은 알고리즘이 영원히 실행되지 않는 입력 집합입니다. 계산 가능성 이론의 기본 정리는 임의의 일반 재귀 함수를 입력으로 하고 0이 정의 영역에 속하는지 여부를 테스트하는 알고리즘이 존재할 수 없다는 것입니다(정지 문제 참조).

다변량 함수

다변량 함수, 다변량 함수 또는 여러 변수의 함수는 여러 인수에 의존하는 함수입니다. 이러한 기능은 흔히 접할 수 있습니다. 예를 들어, 도로에서 자동차의 위치는 이동한 시간과 평균 속도의 함수입니다.

형식적으로 n개 변수의 함수는 정의역이 n개의 쌍집합인 함수입니다.^{[note 3]} 예를 들어, 정수의 곱셈은 두 변수의 함수 또는 이변량 함수이며, 정의역은 정수의 모든 순서 쌍(2-쌍)의 집합이고, 코도메인은 정수의 집합입니다. 모든 이진 작업에 대해서도 마찬가지입니다. 일반적으로 n-튜플은 $({\displaystyle 1,}$ 2${\displaystyle ,\dots ,}$ ${\displaystyle n)}$과 같이 괄호 사이에 포함되어 표시됩니다${\displaystyle .}$ ${\displaystyle(1, 2,\ldots,n).$$}$함수 표기법을 사용할$$ 때 일반적으로 튜플을 둘러싼 괄호를 생략하고 $f{\displaystyle ({}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$${\displaystyle \dots ,}$ ${\displaystyle x_{}}$ ${\displaystyle n_{})}$ 대신$$ f${\displaystyle (}$x 1,${\displaystyle }$…,${\displaystyle {}_{}}$ n${\displaystyle {}_{}}$ ${\displaystyle f(x_{1},\ldots,x_{n})}$를 씁니다${\displaystyle .}$ ${\displaystyle$ f$(x_{1},\ldots,x_{n})}$

Given n sets ${\displaystyle X_{1},\ldots ,X_{n},}$ the set of all n-tuples ${\displaystyle (x_{1},\ldots ,x_{n})}$ such that ${\displaystyle x_{1}\in X_{1},\ldots ,x_{n}\in X_{n}}$ is called the Cartesian product of ${\displaystyle X_1,\dots ,}$${\displaystyle {Xn}_{}}$ ${\displaystyle X_{1},\ldots, X_{n},$ 및 $표시$된 X ${\displaystyle 1_{}{}_{}}$${\displaystyle {\times }_{}}$ ${\displaystyle {}_{}}$× $Xn$. {\$displaystyle X_${1$}\times \cdots$ \$times$X_{n}.$}$

따라서 다변량 함수는 데카르트 곱 또는 데카르트 곱의 적절한 부분 집합을 정의역으로 갖는 함수입니다.

${\displaystyle f:U\to Y,}$

도메인 U가 형태를 갖는 경우

${\displaystyle U\subseteq X_{1}\times \cdots \times X_{n}}$

$모든{\displaystyle {}_{}}$ ${\displaystyle {Xi}_{}}$ ${\$가 실수들의 $집합{\displaystyle \mathbb{}}$ R ${\$또는 복소수들의 집합 $C{\displaystyle \mathbb{}}$ ${\$와 같으면$$, 각각 여러 실수들의 함수 또는 여러 복소수들의 함수를 말합니다.

표기법

기능을 표시하는 표준 방법은 다양합니다. 가장 일반적으로 사용되는 표기법은 기능적 표기법으로, 아래에서 설명하는 첫 번째 표기법입니다.

함수 표기법

함수 표기법은 함수에 이름을 부여해야 하며, 지정되지 않은 함수의 경우 종종 문자 f가 됩니다. 그런 다음 함수를 인수에 적용하는 경우 함수의 이름 뒤에 인수(또는 다변량 함수의 경우 인수)가 다음과 같이 괄호 사이에 포함되어 표시됩니다.

${\displaystyle f(x),\quad \sin(3),\quad {\text{or}}\quad f(x^{2}+1).}$

괄호 사이의 인수는 함수의 도메인의 임의의 요소, 도메인의 특정 요소(위 예에서 3) 또는 도메인의 요소로 평가할 수 있는 식(${\displaystyle {}^{}}$ 예에서$$ x ${\displaystyle 2{}^{}}$+ 1 ${\displaystyle x^{2}+1})$을 나타내는 변수일 수 있습니다. 괄호 사이에 지정되지 않은 변수를 사용하면 "let $f{\displaystyle }$( ${\displaystyle x)}$ = ${\displaystyle {sin}^{}}$ ⁡ (${\displaystyle \mathrm{x}}$2$$+ 1 ) ${\displaystyle$f(x) =\$sin($x^{2} + 1 )"과 같은 함수를 명시적으로 정의하는 데 유용합니다.

함수를 나타내는 기호가 여러 문자로 구성되어 있고 모호성이 발생하지 않을 경우 함수 표기의 괄호가 생략될 수 있습니다. 예를 들어 sin(x) 대신 sin(x)를 쓰는 것이 일반적입니다.

함수 표기법은 1734년 레온하르트 오일러에 의해 처음 사용되었습니다.^[10] 널리 사용되는 일부 함수는 여러 문자로 구성된 기호(일반적으로 두 개 또는 세 개, 일반적으로 이름의 약어)로 표시됩니다. 이 경우 한 글자 기호의 이탤릭체 글꼴과 달리 사인 함수의 "sin"과 같은 로마자 유형이 대신 사용됩니다.

함수 표기법은 "$f{\displaystyle }$( ${\displaystyle x)}$ ${\displaystyle f(x)}$가 함수라고 하자"와 같이 함수를 언급하고 동시에 인수를 명명하는 데 구어적으로 자주 사용됩니다. 이것은 표기법을 남용하는 것으로 더 간단한 공식화에 유용합니다.

화살표 표기법

화살표 표기법은 함수에 이름을 부여할 필요 없이 함수의 규칙을 인라인으로 정의합니다. 예를 들어, ${\displaystyle \mathrm{x}}$ ↦ x + 1${\displaystyle$ x$\mapsto$ x+1}은 실수를 입력으로 받아 그 숫자에 1을 더한 값을 출력하는 함수입니다. $다시{\displaystyle \mathbb{}}$ R ${\$ 의 도메인과 코도메인이 암시됩니다$$.

도메인 및 코드 도메인은 다음과 같이 명시적으로 지정할 수도 있습니다.

${\displaystyle {\begin{align}\operatorname {sqr} \colon \mathbb {Z} & \to \mathbb {Z} \\x&\mapsto x^{2}.\end{align}}$

이것은 입력의 제곱을 반환하는 정수에서 정수로의 함수 sqr을 정의합니다.

화살표 표기법의 일반적인 응용으로 $f{\displaystyle :}$ X${\displaystyle X}$ ${\displaystyle X}$ → ${\displaystyle Y;}$(${\displaystyle x,}$ t${\displaystyle )}$ ↦ f${\displaystyle }$($,$ t) ${\displaystyle f:X\times$ X$\to$ Y$;\;(x$,t$)\mapsto$f (x,t)}를 두 변수의 함수라고 가정합니다. 그리고 새로운 함수명을 도입하지 않고 두 번째 인수를 t 값으로 고정하여 제작한 부분 적용 $함수$ ${\displaystyle X}$ → Y ${\displaystyle X\to Y}$를 참조하고자 합니다. 해당 맵은 화살표 표기법을 사용하여 ${\displaystyle {}_{}}$ ↦ f($,$ t 0) ${\displaystyle$ x$\mapsto f($x, t_{0})}로 표시할 수 있습니다. ${\displaystyle {}_{}}$ ↦ f ($,$ t 0) ${\displaystyle$ x$\mapsto$f $($x, t_{0})} (읽기: "x to f of x comm nough")는 이 새로운 함수를 단지 하나의 인수로 나타내는 반면, f (x, t)라는 표현은 점 (x, t)에서의 함수 f의 값을 나타냅니다.

색인표기

기능 표기 대신 인덱스 표기를 사용할 수도 있습니다. 즉, f (x)를 쓰는 대신 $f{\displaystyle {}_{}}$ ${\displaystyle x_{}}$를 씁니다${\displaystyle {}_{}}$ ${\displaystyle f_{x}}.$

이것은 일반적으로 자연수의 집합인 정의역을 갖는 함수의 경우입니다. 이러한 함수를 시퀀스라고 하며, 이 경우 ${\displaystyle {fn}_{}}$ ${\$ 요소를 시퀀스의 n번째 요소라고 합니다$$.

인덱스 표기법은 매개변수라고 하는 일부 변수를 "참 변수"와 구별하는 데 사용할 수도 있습니다. 실제로 모수는 문제를 연구하는 동안 고정된 것으로 간주되는 특정 변수입니다. For example, the map ${\displaystyle x\mapsto f(x,t)}$ (see above) would be denoted ${\displaystyle f_{t}}$ using index notation, if we define the collection of maps ${\displaystyle f_{t}}$ by the formula ${\displaystyle f_{t}(x)=f(x,t)}$ for all ${\displaystyle x,}$$t$ X ${\displaystyle$x,t$\backslash$in X}입니다.

점 표기법

${\displaystyle x}$ ↦${\displaystyle }$f$(x$), ${\displaystyle$ x$\mapssto$ f(x))} 기호 x는 어떤 값도 나타내지 않습니다. 이는 단순히 자리 표시자이므로, x가 화살표 왼쪽의 임의의 값으로 대체되면 화살표 오른쪽의 동일한 값으로 대체되어야 합니다. 따라서 x는 임의의 기호, 종종 상호작용 "⋅"로 대체될 수 있습니다. 함수 f(⋅)를 x에서의 함수 f(x) 값과 구별하는 데 유용할 수 있습니다.

예를 들어${\displaystyle ,}$ ${\displaystyle a^{}}$$($⋅$)$ 2 {\$displaystyle a(\cdot$)^{2}}는${\displaystyle {함수}^{}}$ x ↦ x $2${\$displaystyle$x$\backslash$mapsto${ax}_{^\{}^{}$2${\}\}}_{}^{}$를 나타내고$,$ ∫$$a$($⋅$)$f ($u) du {\textstyle$\int _{a}^{\,(\cdot )}f(u)\,$du}$은(는) 변수 ${}_{}^{}$이 있는 적분으로 정의된 함수 $x{}_{}^{}$$↦ ∫$$x$f ($)$ $du$ {\$textstyle x\mapsto \int _{a}^{x}f$(u$)\backslash ,$du}를 의미할 수 있습니다.

전문 표기법

수학 하위 분야의 함수에 대한 다른 전문 표기법이 있습니다. 예를 들어, 선형 대수 및 함수 분석에서는 선형 형태와 그에 작용하는 벡터를 이중 쌍을 사용하여 표시하여 기본 이중성을 보여줍니다. 이것은 양자역학에서 브라켓 표기법을 사용하는 것과 유사합니다. 논리학과 계산 이론에서 람다 미적분학의 함수 표기법은 함수 추상화와 응용의 기본 개념을 명시적으로 표현하는 데 사용됩니다. 범주 이론과 상동성 대수학에서 함수 네트워크는 위에서 설명한 함수에 대한 화살표 표기법을 확장하고 일반화하는 교환 다이어그램을 사용하여 함수와 그 구성이 서로 어떻게 통근하는지에 대해 설명합니다.

둘 이상의 변수의 함수

어떤 경우 함수의 인수는 일부 집합 또는 집합에서 가져온 요소의 순서 쌍일 수 있습니다. 예를 들어, 함수 f는 임의의 실수 쌍$({\displaystyle x,}$ y${\displaystyle }$) ${\displaystyle (x,$ y$))$을 그들의 제곱의 합인 $x$ ${\displaystyle 2^{}}$+ ${\displaystyle y^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle x^{2}+y^{2}}$에 매핑하는 것으로 정의될 수 있습니다$.$ 이러한 함수는 일반적으로 $f$ ${\displaystyle (x,}$ ${\displaystyle y)}$ = ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$+ ${\displaystyle y^{}}$ 2 ${\displaystyle$ f$(x,$$y)=x^{2}+y^{2}}$이며, "두 변수의 함수"라고 합니다. 마찬가지로 $f{\displaystyle (w,}$ ${\displaystyle x,}$ ${\displaystyle y)}$ ${\displaystyle$ f$(w, x,$ y$)\},$ $f{\displaystyle (w,}$ x${\displaystyle ,}$ ${\displaystyle y,}$ z${\displaystyle )}$ ${\displaystyle f(w, x,$ y,$z)}$와 같은 표기법으로 3개 이상의 변수 함수를 가질 수 있습니다$.$

기타조건

용어	"기능"과의 구별
지도/맵핑	없습니다. 용어는 동의어입니다.[11]
	지도는 어떤 집합도 코도메인으로 가질 수 있지만, 어떤 맥락에서는 일반적으로 오래된 책에서 함수의 코도메인은 특히 실수 또는 복소수의 집합입니다.[12]
	또는 맵은 특수 구조(예: 정의에 구조화된 코드 도메인을 명시적으로 지정함)와 연결됩니다. 예를 들어, 선형 지도입니다.[13]
동형	구조물의 동작을 보존하는 동일한 유형의 두 구조물 사이의 함수(예:[14] 그룹 동형화).
모피즘	범주의 객체가 집합이 아닌 경우에도 동형사상을 임의의 범주로 일반화하는 것입니다(예를 들어, 그룹은 하나의 객체만 있는 범주를 정의하며, 이는 그룹의 요소를 형태론으로 가지고 있습니다; 이 예와 다른 유사한 예에 대한 범주(수학) § 예제를 참조하십시오).

함수는 지도 또는 매핑이라고도 할 수 있지만 일부 저자는 "지도"와 "함수"라는 용어를 구별합니다. 예를 들어, "지도"라는 용어는 종종 일종의 특수 구조(예: 다양체 지도)를 가진 "함수"를 위해 예약됩니다. 간결성(예: G에서 H로의 그룹 동형화 대신 G에서 H로의 선형 맵 또는 맵)을 위해 동형화 대신 특정 맵을 사용할 수 있습니다. 일부 저자는^[13] 코드 도메인의 구조가 함수의 정의에 명시적으로 속하는 경우를 위해 단어 매핑을 예약합니다.

Serge Lang과 같은 일부 저자는 코드 도메인이 실수 또는 복소수의 부분 집합인 지도를 참조하는 데만 "함수"를 사용하고 ^[12]더 일반적인 함수에 매핑이라는 용어를 사용합니다.

동역학 시스템 이론에서 지도는 이산 동역학 시스템을 만드는 데 사용되는 진화 함수를 나타냅니다. 푸앵카레 지도 참조.

지도의 어떤 정의를 사용하든 도메인, 코드 도메인, 주입식, 연속형과 같은 관련 용어는 함수에 대한 것과 동일한 의미를 갖습니다.

함수 지정

Given a function ${\displaystyle f}$, by definition, to each element ${\displaystyle x}$ of the domain of the function ${\displaystyle f}$, there is a unique element associated to it, the value ${\displaystyle f(x)}$ of ${\displaystyle f}$ at ${\displaystyle x}$. $x{\displaystyle }$ ${\displaystyle x}$과 $f{\displaystyle (x)}$ ${\displaystyle f(x)}$의 관계를 명시적 또는 암시적으로$$지정하거나 설명하는 방법은 여러 가지가 있습니다. 때때로 정리나 공리는 더 정확하게 설명하지 않고 어떤 성질을 가진 함수의 존재를 주장합니다. 종종 사양 또는 설명을 함수 $f{\displaystyle }$ ${\displaystyle$ f$}$의 정의라고 합니다$.$

함수 값을 나열함으로써

유한 집합에서 함수는 도메인의 요소와 연관된 코드 도메인의 요소를 나열하여 정의할 수 있습니다. 예를 들어 $A$ =${\displaystyle }${${\displaystyle 1,}$ ${\displaystyle 2,}$ ${\displaystyle 3\}}$ ${\displaystyle$A =\{$1,$ 2,$3\}}$인$$경우 함수 $f{\displaystyle :}$ ${\displaystyle A}$ → R ${\displaystyle$ f$:$$A\to \mathbb {R} }$ by $f{\displaystyle }$(${\displaystyle 1)}$ $=$ ${\displaystyle 2,}$ ${\displaystyle f}$(${\displaystyle 2)}$ $=$ ${\displaystyle 3,}$ f${\displaystyle }$(${\displaystyle 3)}$ $=$ ${\displaystyle 4.}$ ${\displaystyle$ f$(1$)$=$$2,f(2$)$=$$3,f(3$)$=$$4.}$

수식으로

함수는 종종 산술 연산과 이전에 정의된 함수의 조합을 설명하는 표현식으로 정의됩니다. 이러한 공식을 사용하면 도메인의 모든 요소의 값에서 함수의 값을 계산할 수 있습니다. 예를 들어, 위의 예에서 $f$ ${\displaystyle f}$는 공식 $f$ ${\displaystyle (n)}$ = ${\displaystyle \mathrm{n}}$+ 1 ${\displaystyle f(n$)=$n+1$ ${\displaystyle \mathrm{n}}$ ∈${\displaystyle }${${\displaystyle 1,}$ 2$,$ 3} ${\displaystyle$n\$in \{$1$,$ 2, 3\}로 정의할 수 있습니다.

함수를 이러한 방식으로 정의하면 함수의 도메인을 결정하는 것이 어려운 경우가 있습니다. 함수를 정의하는 공식에 분할이 포함된 경우 분모가 0인 변수의 값은 도메인에서 제외되어야 합니다. 따라서 복잡한 함수의 경우 도메인의 결정은 보조 함수의 0의 계산을 거칩니다. 마찬가지로 $R{\displaystyle \mathbb{}}$ ${\$에서 $R{\displaystyle \mathbb{},}$ ${\displaystyle \mathbb {R}$까지 함수의 정의에 제곱근이 발생하면 정의역이$$ 제곱근의 인수가 음수가 아닌 변수 값 집합에 포함됩니다.

$예$를 들어 ${\displaystyle f}$( ${\displaystyle x)}$ = 1${\displaystyle \sqrt{}}$+ ${\displaystyle \sqrt{x^{}}}$ 2 ${\displaystyle$ f$(x$) = {\$sqrt {1+x^{2$}$}}}}$함수 $f{\displaystyle :}$ ${\displaystyle R}$ $→$ R ${\displaystyle$ f$:\mathbb {R} \to \mathbb {R}$ 를 정의합니다${\displaystyle .}$ ${\displaystyle \mathbb {R},}$은(는) $1{\displaystyle }$+ x ${\displaystyle 2^{}}$ ${\displaystyle 1+x^{2}}$는(는) 실수일 경우 항상 양수이기 때문입니다. $반면$에 f ${\displaystyle (x)}$ = 1${\displaystyle \sqrt{}}$- ${\displaystyle x}$ ${\displaystyle \sqrt{2^{}}}$ ${\displaystyle$ f$(x$) = {\$sqrt {1-x^{2}}}}}$는 정의역이 [-1, 1] 구간으로 축소된 실수에서 실수까지의 함수를 정의합니다. (옛날 텍스트에서는 이러한 정의역을 함수의 정의역이라고 불렀습니다.)

함수는 함수를 정의하는 수식의 특성에 따라 분류할 수 있습니다.

• 2차 함수는 $f$ ${\displaystyle (x)}$ = ${\displaystyle {}^{}}$ ${\displaystyle x}$ ${\displaystyle 2^{}}$+ b ${\displaystyle x}$+ ${\displaystyle c,}$ ${\displaystyle f(x$) = $ax^{2}$ + $bx+c,}$로 표기할 수 있는 함수이며, 여기서 a, b, c는 상수입니다.
• 더 일반적으로 다항 함수는 음수가 아닌 정수 거듭제곱에 대한 덧셈, 뺄셈, 곱셈 및 지수화만을 포함하는 공식으로 정의할 수 있는 함수입니다. 예를 들어, $f{\displaystyle }$( x${\displaystyle )}$ = ${\displaystyle {}^{}}$ ${\displaystyle 3^{}}$- ${\displaystyle 3}$ x${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle f(x$) = $x^{3}-3x-1}$ $및$ f${\displaystyle }$(${\displaystyle x)}$ =${\displaystyle }$(${\displaystyle \mathrm{x}}$- 1${\displaystyle )}$ (${\displaystyle x^{}}$ 3${\displaystyle {}^{}}$+ ${\displaystyle 1)}$+ 2 ${\displaystyle x^{}}$ ${\displaystyle 2{}^{}}$- 1 ${\displaystyle f(x$)= ($x-1)(x^{3}$ + $1)$ + $2x^{2}-1}$은 $x$ ${\displaystyle x}$의 다항 함수입니다$.$
• $유리$ 함수는 f${\displaystyle (x)}$ = ${\displaystyle x\frac{}{}}$- ${\displaystyle \frac{}{}}$ ${\displaystyle \frac{\mathrm{x}}{}}$+ 1${\displaystyle \frac{}{}}$ ${\displaystyle f(x$)={\$frac {x-1}{x+1}},$ $f{\displaystyle (x)}$ = ${\displaystyle 1}$ ${\displaystyle \frac{x}{}}$+ 1${\displaystyle \frac{}{}}$+ ${\displaystyle 1}$ + ${\displaystyle \frac{3}{}}$ ${\displaystyle \frac{x}{}}$- ${\displaystyle 2}$ x${\displaystyle \frac{}{}}$- 1 ${\displaystyle \frac{\mathrm{등}}{}}$의 분할도 허용됩니다${\displaystyle \frac{}{}}$ ${\displaystyle$ f$(x$)={\$frac {1}{x+1}}+{\frac {3}{x}}-{\frac {2}{x-1}}}$
• 대수 함수는 동일하며, n번째 근과 다항식의 근도 허용됩니다.
• 기본 함수는^{[note 4]} 로그 및 지수 함수가 허용되는 동일합니다.

역함수와 암시함수

도메인 X와 코드 도메인 Y가 있는 함수 ${\displaystyle f}$: ${\displaystyle X}$ → Y${\displaystyle ,}$ ${\displaystyle$ f : $X\to Y,}$는 이항이며, Y의 모든 y에 대해 y = f(x)가 되도록 X에 원소 x가 하나만 있습니다. 이 경우 f 의 역함수는 ${\displaystyle \mathrm{함수}}$ f${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$: Y → ${\displaystyle X}$ ${\displaystyle$ f$^{-1$:$y$ $=$ f(x)가 되도록 y $∈$ Y ${\displaystyle$y\in Y}를${\displaystyle \mathrm{요소}}$ $x$$∈$ X${\displaystyle$ x\in X}에 $매핑하는$ Y$\to X}$입니다. 예를 들어, 자연로그는 양수에서 실수로 가는 쌍사 함수입니다. 따라서 그것은 실수를 양수에 매핑하는 지수 함수라고 하는 역수를 가지고 있습니다.

함수 ${\displaystyle f}$: X → Y ${\displaystyle$ f : $X\to Y}$가 비투사적인 경우, ${\displaystyle \mathrm{부분집합}}$ E$$⊆ X ${\displaystyle E\$$subseteq$ X${\displaystyle \}}$ F ⊆ $Y${\$displaystyle$F\subseteq Y}를 선택하여 F에서 E로의 제한이 비투사적이므로 그 역을 가질 수 있습니다. 역삼각 함수는 이러한 방식으로 정의됩니다. 예를 들어, 코사인 함수는 제한에 의해 [0, π] 구간에서 [-1, 1] 구간으로 바이젝션을 유도하고, 아르코신이라고 하는 그 역함수는 [-1, 1]을 [0, π]에 매핑합니다. 다른 역삼각 함수도 유사하게 정의됩니다.

보다 일반적으로, 두 집합 X와 Y 사이의 이진 관계 R이 주어졌을 때, 모든 ${\displaystyle x}$ ∈ $E$에 대하여, ${\displaystyle$x\in E,}가 x Ry가 되는$y$ ∈ $Y {\displaystyle$ y\in Y}가 존재하도록, E를 X의 부분 집합이라고 하자. 만약 모든 x ∈ E에${\displaystyle }$대하여 $그러한{\displaystyle y}$를 선택할 수 있는 기준이 있다면,${\displaystyle$ x$\in E,}$ 이것은 함수 $f$를 정의합니다${\displaystyle :}$$$${\displaystyle E}$ ${\displaystyle \to }$ Y${\displaystyle ,}$ ${\displaystyle$ f$:$관계 R에 의해 암묵적으로 정의되기 때문에 암시적 함수라고 불리는$$ $E\to$ Y$,}.$

예를 들어, 단위 원 x ${\displaystyle 2^{}}$+ y ${\displaystyle 2^{}}$ = ${\displaystyle 1}$ ${\display$ x$^{2}$ + y$^{2$} = $1}$의 방정식은 실수에 대한 관계를 정의합니다. -1 < x < 1인 경우 y의 가능한 값은 양과 음의 두 가지입니다. x = ± 1인 경우 이 두 값은 모두 0이 됩니다. 그렇지 않으면 가능한 y 값이 없습니다. 이는 방정식이 도메인 [-1, 1]과 각각의 코도메인 [0, + ∞) 및 (- ∞, 0)을 갖는 두 개의 암시적 함수를 정의한다는 것을 의미합니다.

이 예제에서 방정식은 $y$ =${\displaystyle }$± 1${\displaystyle \sqrt{}}$- ${\displaystyle \sqrt{{}^{}}}$ ${\displaystyle \sqrt{2^{}}}$ ${\displaystyle$y =\$pm {\sqrt {1-x^{2}}}$를 제공하여 y로 풀 수 있지만, 더 복잡한 예제에서는 불가능합니다. 예를 들어 $관계$ y ${\displaystyle 5^{}}$+ y${\displaystyle }$+ ${\displaystyle x}$ = ${\displaystyle 0}$ ${\displaystyle$ y$^{5}+y+x$=$0}$은(는) $R$ ${\displaystyle \mathbb {R}$을(를) 도메인 및 범위로 갖는 x의 암시적 함수로 정의합니다. Bring radical은 4개의 산술 연산과 n번째 근으로 표현할 수 없습니다.

암시적 함수 정리는 점 근처에서 암시적 함수의 존재와 고유성에 대한 온화한 미분 가능성 조건을 제공합니다.

미분적분학을 이용한

많은 함수는 다른 함수의 선함수로 정의할 수 있습니다. 이것은 x = 1에 대해 0인 1/x의 반미분인 자연로그의 경우입니다. 또 다른 일반적인 예는 오류 함수입니다.

보다 일반적으로 대부분의 특수 함수를 포함한 많은 함수를 미분 방정식의 해로 정의할 수 있습니다. 가장 간단한 예는 아마도 지수 함수일 것인데, 지수 함수는 도함수와 동일하고 x = 0에 대해 값 1을 취하는 고유 함수로 정의될 수 있습니다.

멱급수를 사용하여 수렴하는 도메인의 함수를 정의할 수 있습니다. 예를 들어, $지수$ 함수는 $x$ = ∑ $\frac{n^{}}{}$ =$0$ ∞ x n ! {\textstyle e^{$x}$ =\$sum$_{n=$0}^{\infty }{$x$^\{$n} \over n!}로 정의됩니다. 그러나 급수의 계수가 매우 임의적이기 때문에 수렴하는 급수의 합인 함수는 일반적으로 다르게 정의됩니다. 그리고 계수의 순서는 또 다른 정의에 기초한 어떤 계산의 결과입니다. 그런 다음 멱급수를 사용하여 함수의 도메인을 확장할 수 있습니다. 일반적으로 실제 변수에 대한 함수가 일부 구간에서 테일러 급수의 합인 경우, 이 거듭제곱 급수를 사용하면 도메인을 복소수의 부분 집합, 즉 급수의 수렴 디스크로 즉시 확장할 수 있습니다. 그런 다음 분석 연속을 사용하면 복잡한 평면을 거의 전체 포함할 수 있는 도메인을 더 확장할 수 있습니다. 이 과정은 복소수의 로그, 지수 및 삼각함수를 정의하는 데 일반적으로 사용되는 방법입니다.

재발별

정의역이 음이 아닌 정수인 함수(시퀀스)는 반복 관계로 정의되기도 합니다.

음수가 아닌 정수의 요인 함수(${\displaystyle n}$ ↦ n! ${\displaystyle$ n$\mapston$는 반복 관계로 정의할 수 있으므로 기본 예제입니다.

${\displaystyle n!=n(n-1)!\quad {\text{for}}\quad n>0,}$

그리고 초기 상태.

${\displaystyle 0!=1.}$

함수의 표현

그래프는 일반적으로 함수의 직관적인 그림을 제공하는 데 사용됩니다. 그래프가 함수를 이해하는 데 어떻게 도움이 되는지에 대한 예로, 함수가 증가하는지 또는 감소하는지 그래프를 통해 쉽게 알 수 있습니다. 일부 함수는 막대 차트로 나타낼 수도 있습니다.

그래프 및 그림

함수 $f{\displaystyle :}$ ${\displaystyle X}$ → ${\displaystyle Y}$가 주어졌을 때${\displaystyle ,}$ ${\displaystyle$ f$:X\to$ Y$,}$의 그래프는 형식적으로 집합입니다.

${\displaystyle G=\{(x,f(x))\mid x\in X\}$

X와 Y가 실수들의 부분집합인 경우(또는 그러한 부분집합들, 예를 들어 간격들로 식별될 수 있는), $요소$(${\displaystyle x,}$ y${\displaystyle )}$∈ G {\$displaystyle (x,$ y)\in G}는 2차원 좌표계에서 좌표 x, y를 갖는 점, 예를 들어 직교 평면으로 식별될 수 있습니다. 이 부분은 함수를 나타내는 그림을 만들 수 있습니다. 그림의 사용은 매우 보편적이어서 함수의 그래프라고도 불립니다. 함수의 그래픽 표현은 다른 좌표계에서도 가능합니다. 예를 들어, 제곱 함수의 그래프

${\displaystyle x\mapsto x^{2}}$

${\displaystyle x}$ ∈ $R$에 대한 좌표 $({\displaystyle x,}$ x ${\displaystyle 2^{}}$ ${\displaystyle (x, x^{2})}$이(가) 있는 모든 점으로 구성되며, ${\displaystyle$x\$in \mathbb${R},}은(는) 잘 알려진 포물선을 직교 좌표로 묘사할 때 산출합니다. 동일한 2차 함수 ${\displaystyle x^{}}$ ↦ x 2, ${\displaystyle$ x$\mapsto$x^{2}}, 숫자 쌍으로 구성된 동일한 형식 그래프를 대신 ${\displaystyle \mathrm{극좌표}(}$r, θ${\displaystyle )}$ = (x, x 2),${\displaystyle$ (r$,\theta)$ = (x, x^{2})로 표시하면 얻은 그림은 페르마의 나선형입니다.

표

함수는 값의 표로 나타낼 수 있습니다. 함수의 정의역이 유한한 경우 함수는 이러한 방식으로 완전히 지정될 수 있습니다. 예를 들어, f${\displaystyle (x,}$ y${\displaystyle )}$ = ${\displaystyle \mathrm{xy}}$ ${\displaystyle f$$:$ {$1,$ ${\displaystyle 5{}^{}}$ ${\displaystyle 2}$ → R ${\dots, 5\}^{2}\to \mathbb {R} }$로 정의된 곱셈 $함수$ f${\displaystyle :}$ ${\displaystyle \{}$1, …, 5} 2 = \displaystyle f$(x,$ y) = $xy}$는 익숙한 곱셈표로 나타낼 수 있습니다.

y x	1	2	3	4	5
1	1	2	3	4	5
2	2	4	6	8	10
3	3	6	9	12	15
4	4	8	12	16	20
5	5	10	15	20	25

반면에 함수의 도메인이 연속적인 경우 테이블은 도메인의 특정 값에서 함수의 값을 제공할 수 있습니다. 중간값이 필요한 경우 보간을 사용하여 함수의 값을 추정할 수 있습니다. 예를 들어 사인 함수에 대한 표의 일부는 다음과 같이 주어질 수 있으며 값은 소수점 6자리로 반올림됩니다.

x	sinx
1.289	0.960557
1.290	0.960835
1.291	0.961112
1.292	0.961387
1.293	0.961662

휴대용 계산기와 개인용 컴퓨터가 등장하기 전에는 로그 및 삼각 함수와 같은 함수에 대해 이러한 표를 작성하고 게시하는 경우가 많았습니다.

막대 차트

막대 차트는 정의역이 유한 집합, 자연수 또는 정수인 함수를 나타낼 수 있습니다. 이 경우 도메인의 요소 x는 x축의 간격으로 표시되며, 함수의 해당 값 f(x)는 x에 해당하는 간격을 기본으로 하고 높이가 f(x)인 직사각형으로 표시됩니다(이 경우 막대는 x축 아래로 연장됩니다).

일반속성

이 섹션에서는 도메인 및 코드 도메인의 특정 속성과 무관한 함수의 일반 속성에 대해 설명합니다.

표준기능

자주 발생하는 표준 함수는 다음과 같습니다.

• 모든 집합 X에 대해 빈 집합에서 X까지 빈 함수 또는 빈 맵이라고 하는 고유 함수가 있습니다. 빈 함수의 그래프는 빈 집합입니다.^{[note 5]} 빈 함수의 존재는 이론의 일관성과 많은 진술의 빈 집합에 관한 예외를 피하기 위해 필요합니다. 함수를 순서 삼중항(또는 동등한 함수)으로 정의하는 일반적인 집합 theore 정의에서는 각 집합에 대해 정확히 하나의 빈 함수가 있으므로 빈$$함수 ∅ $X {\displaystyle$ \$varnothing$ $\$to X}는 X$$≠ Y {\$displaystyle \varnothing$ \to Y}와$$동일하지 않습니다$.$ X ∅ Y {\displaystyle \varnothing \to Y}인 ${\displaystyle \mathrm{경우}}$에만 해당합니다.$eq$ Y$\},$ 그들의 그래프는 둘 다 빈 집합입니다.
• 모든 집합 X 및 모든 싱글톤 집합 {s}에 대해 X의 모든 요소를 s로 매핑하는 X에서 {s}까지의 고유 함수가 있습니다. X가 빈 집합이 아닌 한 이는 (아래 참조) 사영입니다.
• 함수 ${\displaystyle f:}$ X → ${\displaystyle Y,}$ ${\displaystyle f:X\to$ Y$,}$가 주어지면 이미지 $f{\displaystyle (X)}$ =${\displaystyle }${${\displaystyle f(x)}$ ∣ $x$∈ X} {\$displaystyle f(X)$=$\{f($x)\mid x\in X\}는 x를 f(x)에 매핑하는 X에서 f(X)까지의 함수입니다.
• 집합 X의 모든 부분 집합 A에 대해 A의 X로의 포함 맵은 A의 모든 요소를 자신에게 매핑하는 주입 함수(아래 참조)입니다.
• 종종 id로_X 표시되는 집합 X의 항등 함수는 X를 그 자체에 포함시키는 것입니다.

함수구성

${\displaystyle 두}$ 함수 $f{\displaystyle :}$ ${\displaystyle X}$ → Y ${\displaystyle$ f$:X\to Y}$ 및 ${\displaystyle g:}$ Y → ${\displaystyle Z}$ ${\displaystyle$ g$:$G의 도메인이 f의 공변역이고, 그 구성이 다음으로 정의된 $함수$ ${\displaystyle g}$ $∘$ f: $X$$→$ Z ${\displaystyle g\circ$ f:$X\rightarrow$ Z}이 되도록 $Y\to$ Z$}$

${\displaystyle (g\circ f)(x)=g(f(x))}$

$즉$, ${\displaystyle g}$ ∘ f ${\displaystyle g$\circ f}의 값은 먼저 x에 f를 적용하여 y = f(x))를 구한 후, 결과 y에 g를 적용하여 g(y) = g(f(x))를 구함으로써 얻어집니다. 표기법에서 먼저 적용되는 함수는 항상 오른쪽에 쓰여집니다.

합성 ${\displaystyle g}$ ∘ f${\displaystyle$g\circ f}는 첫 번째 함수의 코도메인이 두 번째 함수의 도메인인 경우에만 정의되는 함수에 대한 연산입니다. $두$ ${\displaystyle g}$ ∘ f ${\displaystyle g$\circ $f{\displaystyle \}}$ $f$ ∘ g${\displaystyle$ f\circ g}가 이러한 조건을 만족하는 경우에도, 구성이 반드시 상호 교환적인 것은 아니며, $,$ 함수 g ∘ f$$${\displaystyle \{\backslash \mathrm{displaystyle}}$g\$circ$ f}$및 f$ ∘ g {\displaystyle f\circ g}는 동일할 필요는 없습니다. 그러나 동일한 인수에 대해 다른 값을 제공할 수 있습니다. 예를 들어, f(x) = x 및 g(x) = x + 1, $그리고$ g${\displaystyle (f(x))}$= ${\displaystyle x^{}}$ 2${\displaystyle {}^{}}$+ ${\displaystyle 1}$ ${\displaystyle g(f(x))$$=x^{2}+$1}$및$ f ($g{\displaystyle (x))}$$=$${\displaystyle }$(${\displaystyle x^{}}$ ${\displaystyle +1}$)${\displaystyle {}^{}2}$ ${\displaystyle$ f($g(x$))$=$(x+$1)^{2}}$는 $x$ $=$$$에 대해서만 동의합니다$.$ ${\displaystyle$ x$=$0}.$}$

함수 구성은$$(${\displaystyle h}$ ∘ $g)$ ∘ $f {\displaystyle (h\$circ $g{\displaystyle )\backslash \mathrm{circ}}$f}$h$∘ ($g$∘ f$)${\displaystyle h\circ (g\circ f)} 중 하나가 정의되면 다른 하나도${\displaystyle \mathrm{정의}}$되며${\displaystyle ,}$ ${\displaystyle \mathrm{이들}}$은 ${\displaystyle \mathrm{동등}}$하다는 것,${\displaystyle 즉}$ $h$∘$$g) ∘$$f$$=$$h$$∘ (g ∘ f$)$입니다. {\displaystyle (h\circ g)\circ f=h\circ (g\circ f).$}$$따라서$ ${\displaystyle h}$ $∘$ $g$$∘$ f. ${\displaystyle$h\circ g\circ f.}라고 쓰는 것이 일반적입니다.

ID 함수 ${\displaystyle {ID}_{}}$ X ${\$ _${X} 및$ ${\displaystyle {ID}_{}}$ Y ${\$는 각각 X에서 Y까지의 함수에 대한 오른쪽 ID 및 왼쪽 ID입니다. 즉, f가 도메인 X를 갖는 함수이고 코드 도메인 Y인 경우 ${\displaystyle f_{}}$ ∘ ${\displaystyle {id}_{}}$ X = ${\displaystyle \mathrm{id}}$ ${\displaystyle Y}$ ∘ $f$=$f$를 갖는다.${\displaystyle$ f\$circ \operatorname$ {id} _${X}$=$\operatorname$ {$id$} _{Y$}\circ$ f=f.}

• 
  복합 함수 g(f(x))는 두 "기계"의 조합으로 시각화할 수 있습니다.
• 
  함수 구성의 간단한 예
• 
  또 다른 구성. 이 예에서는 (g ∘ f )(c) = # 입니다.

이미지 및 프리이미지

$f{\displaystyle }$: ${\displaystyle X}$ → Y${\displaystyle }$. ${\displaystyle$ f$:X\to Y.}$ 도메인 X의 요소 x 아래의 이미지는 f(x)입니다. 만약 A가 X의 임의의 부분집합이라면, f(A)로 표시되는 f 밑의 A의 영상은 A의 원소들의 모든 영상들로 구성된 공변역 Y의 부분집합,^[6] 즉,

${\displaystyle f(A)=\{f(x)\mid x\in A\}$

f 의 이미지는 전체 도메인의 이미지, 즉 f(X)입니다.^[16] 범위라는 용어는 코도메인을 지칭할 수도 있지만 범위 off라고도 합니다.^{[6][7][8][9][9][16][17]}

반면에, 코도메인 Y의 원소 y의 역상 또는 역상은 이미지가 동등하게 밑에 있는 도메인 X의 모든 원소의 집합입니다.^[6] $기호$에서 y의 전치상은 ${\displaystyle {\mathrm{f}}^{}}$- 1${\displaystyle {}^{}}$(${\displaystyle y)}$ ${\displaystyle f^{-1}(y)}$로 표시되며$$ 다음 식으로 표시됩니다.

${\displaystyle f^{-1}(y)=\{x\in X\mid f(x)=y\}.}$

마찬가지로, 코도메인 Y의 부분집합 B의 전상은 B의 요소들의 전상들의 집합, 즉 이미지들이 B에 속하는 X의 모든 요소들로 구성된 도메인 X의 부분집합입니다.^[6] $f{\displaystyle {}^{}}$- ${\displaystyle 1^{}}$(${\displaystyle B)}$ ${\displaystyle f^{-1}(B)}$로 표시되며$$ 다음 식으로 표시됩니다.

${\displaystyle f^{-1}(B)=\{x\in X\mid f(x)\in B\}.}$

예를 들어 정사각형 함수 아래에$$ 있는${\displaystyle }${${\displaystyle 4,}$ 9${\displaystyle \}}$ ${\displaystyle \{4, 9\}$의 프리이미지는 ${\displaystyle \{-3,-2,}$ ${\displaystyle 2,}$ ${\displaystyle 3\}}$ ${\displaystyle \{-3, -2, 2,$ 3$\}$ 집합입니다$.$

함수의 정의에 따라 도메인의 원소 x의 이미지는 항상 코드 도메인의 단일 원소입니다. 그러나, 코도메인의 원소 y의 프리이미지 ${\displaystyle {\mathrm{f}}^{}}$- 1 ${\displaystyle {}^{}y)}$ ${\displaystyle f^{-1}(y)}$은 비어 있거나 임의의 수의 원소를 포함할 수 있습니다. 예를 들어 f가 모든 정수를 0으로 매핑하는 정수에서 자신으로의 함수라면 ${\displaystyle f{}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle {}^{}0)}$ = $Z$ ${\displaystyle f^{-1}(0$) =\$mathbb {Z} }$입니다$.$

$f{\displaystyle :}$ ${\displaystyle X}$ → Y ${\displaystyle f:X\to$ Y$}$가 함수이고, A와 B가 X의 부분 집합이고, C와 D가 Y의 부분 집합이라면, 하나는 다음과 같은 속성을 갖습니다.

• ${\display style A\subseteq B\long right arrow f(A)\subseteq f(B)}$
• ${\displaystyle C\subseteq D\Longrightarrow f^{-1}(C)\subseteq f^{-1}(D)}$
• ${\displaystyle A\subseteq f^{-1}(f(A))}$
• ${\displaystyle C\supseteq f(f^{-1}(C))}$
• ${\displaystyle f(f^{-1}(f(A)))=f(A)}$
• ${\displaystyle f^{-1}(f(f^{-1}(C)))=f^{-1}(C)}$

코도메인의 원소 y의 f에 의한 전상은 어떤 맥락에서는 f 밑의 y의 섬유라고 불리기도 합니다.

함수 f가 역수를 가지는 경우(아래 참조), 이 역수는 $f{\displaystyle {}^{}}$- ${\displaystyle 1^{}}$로 표시됩니다${\displaystyle {}^{}}$ ${\displaystyle$ $f$$^{-1$$}(C$)} 이$$ 때 $f{\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle {}^{}C)}$ ${\displaystyle$ f$^{-1$}(C$)}$는 $f{\displaystyle {}^{}}$- 1 ${\$로 표시되거나$$ f 의 f로 표시될 수 있습니다$$. 이 세트는 동일하기 때문에 문제가 되지 않습니다. 요소로 일부 부분 집합을 포함하는 집합(${\displaystyle 예}$:${\displaystyle }${ ${\displaystyle x,}${ x${\displaystyle \}\})}$의 경우 $f{\displaystyle }$ ${\displaystyle (A)}$ ${\$$displaystyle f(A$$)}$ 및 $f$ - $(C)}$ 표기법이 모호할$$ 수 있습니다${\displaystyle .}$ ${\displaystyle \{x,\{x\}\}$$}$이 경우$$ 예를 들어, 부분집합의 이미지 및 프리이미지에$$ $대괄호{\displaystyle }$ f${\displaystyle [A],}$ ${\displaystyle {\mathrm{f}}^{}}$- 1${\displaystyle {}^{}}$[${\displaystyle C]}$ ${\displaystyle f[A], f^{-1}[C]}$를 사용하고 요소의 이미지 및 프리이미지에 일반 괄호를 사용하여 약간의 주의가 필요할 수 있습니다.

주입식, 주입식, 주입식, 주입식 기능

$f{\displaystyle }$: ${\displaystyle X}$ → Y ${\displaystyle f:X\to Y}$를 함수라고 하자.

함수 f는 X의 서로 다른 두 원소 a와 b마다 f(a) ≠ f(b)이면 주입식(또는 일대일, 또는 주입식)입니다. 마찬가지로${\displaystyle ,}$ $f$는 ${\displaystyle \mathrm{모든}}$∈ Y에 $대해 {\displaystyle$ y\in $Y$,}${\displaystyle {}^{}\mathrm{프리이미지}}$f - 1 (y) ${\displaystyle$ f^{-1}(y)}이(가) 많아야 하나의 원소를 포함하는 경우에만 주입식입니다. 빈 함수는 항상 주입식입니다. X가 빈 집합이 아닌 경우 함수 $g{\displaystyle :}$ ${\displaystyle Y}$ → X ${\displaystyle$ g$:$즉, f가 왼쪽 역을 갖는 경우, g는 ${\displaystyle f_{}}$ $=$$$id X, ${\displaystyle$g\circ $f$$=$$\operatorname {id}$ _{X}}를 $∘$ $Y\to$ X$}.$ Proof: If f is injective, for defining g, one chooses an element ${\displaystyle x_{0}}$ in X (which exists as X is supposed to be nonempty),^{[note 6]} and one defines g by ${\displaystyle g(y)=x}$ if ${\displaystyle y=f(x)}$ and ${\displaystyle g(y)=x_{0}}$ if ${\displaystyle y\notin f(X).}$${\displaystyle y\n$$ot \in f(X).$$}$ Conversely, if ${\displaystyle g\circ f=\operatorname {id} _{X},}$ and ${\displaystyle y=f(x),}$ then ${\displaystyle x=g(y),}$ and thus ${\displaystyle f^{-1}(y)=\{x\}.$$}$

함수 f는 그 범위 $f{\displaystyle (X)}$ ${\displaystyle f(X)}$가 코드 도메인 $Y{\displaystyle }$ ${\displaystyle Y}$와 같으면$$$,$ 즉 코드 도메인의$$ 각 요소 $y{\displaystyle }$ ${\displaystyle y}$에 대해 사영적(또는 사영적)입니다. there exists some element ${\displaystyle x}$ of the domain such that ${\displaystyle f(x)=y}$ (in other words, the preimage ${\displaystyle f^{-1}(y)}$ of every ${\displaystyle y\in Y}$ is nonempty).^[16][19] 만약 현대 수학에서 일반적으로 선택 공리를 가정한다면, 함수 ${\displaystyle g}$가 존재하는 경우에만 f는 사영적입니다${\displaystyle :}$ ${\displaystyle Y}$ → X ${\displaystyle$ g$:$${\displaystyle F}$ $∘$ ${\displaystyle g_{}}$ $=$$id$ Y, ${\displaystyle$ f\circ g$$$=$$\operatorname {id}$_{Y}, 즉 f가 오른쪽 역을 가지면 Y$\to$ X$}$가 됩니다. 선택 공리가 필요한데, f가 sursive인 경우 $g{\displaystyle (y)}$ = x${\displaystyle ,}$ ${\displaystyle g(y$)= $x,}$로 정의하기 때문입니다. 여기서 $x$ ${\displaystyle$ $x$$}$는 $f{\displaystyle {}^{}}$- 1${\displaystyle {}^{}y)}$의 임의로 선택된 요소입니다${\displaystyle .}$ ${\displaystyle$ f$^{-1}(y).$$}$

함수 f가 주입식인 경우와 주입식인 경우 모두 주입식(또는 주입식 또는 일대일 대응)입니다.^[16][20] ${\displaystyle 즉}$, $모든$ ∈ $Y$에 대해 ${\displaystyle$y\in Y,}$개$의 ${\displaystyle {\mathrm{프리이미지}}^{}f}$-1$(y$) {\$displaystyle f^{-$1}(y))이 정확히 하나의 요소를 포함하는 경우 f는 바이젝티브입니다. ${\displaystyle \mathrm{함수}}$ f는 역함수, 즉 함수 $g{\displaystyle :}$ Y → ${\displaystyle X}$ ${\displaystyle$ g$:$${\displaystyle G}$$∘$ ${\displaystyle f_{}}$ $=$ $id$ X {\$display g$\circ f $=$$\$$operatorname$${id}$ _{$X{\displaystyle \}}$이고 f $∘$ $g$$=$ $id$ Y . {\$display$g$$$=$$\operatorname$ {id} _{Y}}(예외의 경우에는 선택 공리가 필요하지 않습니다. 증명은 간단합니다.)

모든 $함수$ f${\displaystyle :}$ ${\displaystyle X}$ → ${\displaystyle Y}$ ${\displaystyle$ $f$$:X\to Y}$는 사영에 이어 사영의 $합성$ ${\displaystyle i}$ ∘ ${\displaystyle$i\circs}로 인수분해될 수 있으며, 여기서 s는 f(X)에 대한 X의 표준 사영이고, i는 Y에 대한 f(X)의 표준 사영입니다. 이것이 f의 표준 인수분해입니다.

"일대일"과 "온토"는 오래된 영어 문헌에서 더 일반적인 용어입니다; "인젝티브", "서젝티브", "비젝티브"는 원래 부르바키 그룹에 의해 20세기 2/4분기에 프랑스 단어로 만들어졌고 영어로 수입되었습니다.^{[citation needed]} 주의할 점은 '일대일 함수'는 주사적인 함수이고, '일대일 대응'은 객관적인 함수를 말합니다. 또한 "f maps X to Y"라는 문장은 "f maps X to B"라는 문장과 다릅니다. 전자는 f가 피험적이라는 것을 암시하는 반면 후자는 f의 본질에 대해 어떤 주장도 하지 않는다는 점입니다. 복잡한 추론에서는 한 글자 차이를 쉽게 놓칠 수 있습니다. 이 오래된 용어의 혼란스러운 특성으로 인해 이 용어들은 부르바키어 용어에 비해 인기가 떨어졌으며, 이는 더 대칭적이라는 장점도 있습니다.

제한 및 연장

${\displaystyle f}$: ${\displaystyle X}$ → Y ${\displaystyle f$: $X\to$ Y$}$ 가 함수이고 S 가 X 의 부분 집합인 경우, $f$ ${\displaystyle {}_{}}$ ${\displaystyle$f$_{S}$ 로 표시되는 $f$ ${\displaystyle$ f$}$ ~ S$$의 제한은 다음과 같이 정의되는 S ~ Y 의 함수입니다.

${\displaystyle f _{S}(x)=f(x)}$

S의 모든 x에 대하여 f ${\displaystyle {}_{}}$ ${\$가 주입식이 되도록$$$$ $함수{\displaystyle }$ f ${\displaystyle f}$의 도메인의 부분 집합 S가 있는 경우, 제한을 사용하여 부분 역함수를 정의할 수 있습니다. 그러면 이미지 f ${\displaystyle {}_{}}$(${\displaystyle S)}$ = ${\displaystyle f(S)}$ ${\displaystyle$f$_$${S}($S)}에 $대한$ f ${\displaystyle {}_{}}$ ${\$displaystyle f _${S}(S$)=$f(S)}$의 표준 투영은 바이젝션이므로 $f{\displaystyle (S)}$ ${\displaystyle f(S)}$에서 S로 역함수를 갖습니다. 한 가지 응용 분야는 역삼각함수의 정의입니다. 예를 들어, 코사인 함수는 [0, π] 구간으로 제한될 때 주입식입니다. 이 제한의 이미지는 구간 [-1, 1]이므로 제한은 [-1, 1]에서 [0, π]까지의 역함수를 가지며, 이를 아르코신이라고 하며 아르코신이라고 합니다.

기능 제한은 "접착" 기능을 함께 사용할 수도 있습니다. $\underset{}{}$ =$$⋃ $i$ ∈ I $Ui$ {\$textstyle$X$$=$\bigcup$_{i\in I}U_{i}}를 부분집합의 합으로 분해하고${\displaystyle {}_{}}$ ${\displaystyle {함수}_{}}$ ${\displaystyle fi}$:$Ui$ → Y${\displaystyle$ f_{i}라고 가정하자.$U_{i}\to Y}$ is defined on each ${\displaystyle U_{i}}$ such that for each pair ${\displaystyle i,j}$ of indices, the restrictions of ${\displaystyle f_{i}}$ and ${\displaystyle f_{j}}$ to ${\displaystyle U_{i}\cap U_{j}}$ are equal. ${\displaystyle \mathrm{그러면}}$ 고유 함수 $f{\displaystyle :}$ X → ${\displaystyle Y}$ ${\displaystyle f:X\to Y}$가 정의됩니다. 이 함수는 ${\displaystyle {{UI}_{}}_{}}$ =$f$가 모든 i에 $대해$ ${{U_{i$}}=$f_{i}}$를 표시하도록 합니다. 이것이 다양체의 함수를 정의하는 방법입니다.

함수 f의 확장은 f가 g의 제한이 되도록 함수 g입니다. 이 개념의 전형적인 사용은 해석적 연속의 과정으로 정의역이 복소평면의 작은 부분인 함수를 거의 전체 복소평면인 함수로 확장할 수 있습니다.

실선의 호모그래피를 연구할 때 발생하는 함수 확장의 또 다른 고전적인 예는 다음과 같습니다. 호모그래피는 ad - bc ≠ 0이 되도록 $함수$ h${\displaystyle (x)}$ = ${\displaystyle \frac{x}{}}$+ ${\displaystyle \frac{}{}}$ ${\displaystyle \frac{x}{}}$+ ${\displaystyle \frac{d}{}}$ ${\displaystyle h(x$) = {\$frac {ax+b}$ {$cx+d}}$입니다. 도메인은${\displaystyle \mathrm{-d}}$/ ${\displaystyle c,}$ ${\displaystyle -d/c,}$과(와) 다른 모든 실수의 집합이고 이미지는${\displaystyle }$/${\displaystyle c}$와(와) 다른 모든 실수의 집합입니다${\displaystyle .}$ ${\displaystyle a/c.}$ ∞를 포함하여 실선을 투영적으로 확장한 실선으로 확장하면, ${\displaystyle h(}$∞${\displaystyle )}$ = /c${\displaystyle h$(\infty) = a/$c{\displaystyle \}}$및$h$d / c) =$$∞ ${\displaystyle$h (-d/c) =\infty }를 설정하여 확장 실선에서 자신으로의 바이젝션으로 h를 확장할 수 있습니다.

미적분학에서

새로운 무한소 미적분학은 17세기에 시작된 함수의 개념을 기본으로 삼았습니다. 당시에는 실수 변수의 실수 값 함수만을 고려하였으며, 모든 함수가 매끄러운 것으로 가정하였습니다. 그러나 그 정의는 곧 여러 변수의 함수와 복소 변수의 함수로 확장되었습니다. 19세기 후반에는 함수에 대한 수학적으로 엄밀한 정의가 도입되어 임의의 도메인과 코도메인을 갖는 함수가 정의되었습니다.

함수는 이제 수학의 모든 영역에서 사용됩니다. 미적분학 입문에서 단어 함수가 자격 없이 사용될 때는 단일 실수 변수의 실수 값 함수를 의미합니다. 함수에 대한 보다 일반적인 정의는 일반적으로 STEM 전공을 가진 2학년 또는 3학년 대학생들에게 소개되며, 고학년 때에는 실제 분석 및 복잡한 분석과 같은 과정에서 더 크고 엄격한 환경에서 미적분학에 소개됩니다.

실수함수

실수 함수는 실수 변수의 실수 값 함수, 즉 공역이 실수의 필드이고 영역이 구간을 포함하는 실수 집합인 함수입니다. 이 절에서는 이러한 함수를 단순히 함수라고 부릅니다.

수학과 그 응용 분야에서 가장 일반적으로 고려되는 함수는 일정한 규칙성을 갖는데, 그것은 연속적이고, 미분 가능하며, 심지어 분석적입니다. 이 규칙성은 이러한 함수를 그래프로 시각화할 수 있도록 보장합니다. 이 절에서 모든 함수는 어떤 구간에서 미분 가능합니다.

함수는 점 단위 연산을 누립니다. 즉, f와 g가 함수인 경우 그 합, 차분 및 곱은 다음과 같이 정의됩니다.

${\displaystyle {\begin{aligned}(f+g)(x)&=f(x)+g(x)\\(f-g)(x)&=f(x)-g(x)\\(f\cdot g)(x)&=f(x)\cdot g(x)\\\end{aligned}}.}$

결과 함수의 도메인은 f와 g의 도메인의 교차점입니다. 두 함수의 몫은 다음과 같이 정의됩니다.

${\displaystyle {\frac {f}{g}}(x)={\frac {f(x)}{g(x)}},}$

그러나 결과 함수의 정의역은 f와 g의 정의역의 교차점에서 g의 0을 제거함으로써 얻어집니다.

다항식 함수는 다항식으로 정의되며, 그 정의역은 실수의 전체 집합입니다. 여기에는 상수 함수, 선형 함수 및 이차 함수가 포함됩니다. 유리함수는 두 다항함수의 몫이고, 그 정의역은 0으로 나누는 것을 피하기 위해 유한한 수의 함수가 제거된 실수입니다. 가장 간단한 유리 함수는 $함수$ ${\displaystyle \frac{x}{}}$ ↦ 1 x, ${\displaystyle$ x$\maps to {\frac {$1}{x}}이며, 그래프는 쌍곡선이고 도메인은 0을 제외한 전체 실선입니다.

실수 미분 가능 함수의 도함수는 실수 함수입니다. 연속 실수 함수의 반미분은 원래 함수를 도함수로 갖는 실수 함수입니다. 예를 들어, 함수 $\frac{x}{}$ ↦ 1 x${\textstyle$ x$\maps to {\frac {$1}{x}}는 양수에서 연속적이고 심지어 미분 가능합니다. 따라서 x = 1에 대해 0 값을 취하는 하나의 반미분은 자연로그라 불리는 미분 가능한 함수입니다.

$f{\displaystyle \frac{}{}}$ ${\displaystyle \frac{(x)}{}}$- f ${\displaystyle \frac{(y)}{}}$ ${\displaystyle \frac{x}{}}$- ${\displaystyle \frac{}{}}$ ${\$의 부호가 구간의 x 및 y 선택에 의존하지$$ 않으면 실수 함수 f는 구간에서 단조롭습니다. 함수가 구간에서 미분 가능한 경우, 도함수의 부호가 구간에서 일정하면 단조롭습니다. 실수 함수 f가 구간 I에서 단조로운 경우 역함수를 갖는데, 이는 정의역 f(I)와 이미지 I을 갖는 실수 함수입니다. 이것은 역삼각 함수가 삼각 함수의 관점에서 정의되는 방법이며, 여기서 삼각 함수는 단조롭습니다. 또 다른 예: 자연로그는 양의 실수에서 단조롭고, 그 이미지는 전체 실수선입니다. 따라서 실수와 양의 실수 사이의 이항인 역함수를 갖습니다. 이 역은 지수 함수입니다.

다른 많은 실제 함수는 암시적 함수 정리(역함수는 특정 인스턴스) 또는 미분 방정식의 해로 정의됩니다. 예를 들어 사인 함수와 코사인 함수는 선형 미분 방정식의 해입니다.

${\displaystyle y'+y=0}$

그런 식으로

${\displaystyle \sin 0=0,\quad \cos 0=1,\quad {\frac {\partial \sin x}{\partial x}(0)=1,\quad {\frac {\partial \cos x}{\partial x}(0)=0.}$

벡터값함수

함수의 공변역의 원소가 벡터일 때, 함수는 벡터값 함수라고 합니다. 이러한 기능은 물리적 속성 모델링과 같은 응용 프로그램에서 특히 유용합니다. 예를 들어, 유체의 속도 벡터의 각 점과 관련된 함수는 벡터 값 함수입니다.

일부 벡터 값 함수는 ${\displaystyle {}^{}}$ ${\$의 하위 집합 또는$$ 다양체와$$같은 ${\displaystyle {}^{}}$ ${\$의 기하학적 또는 위상적 속성을 공유하는 다른 공간에 정의됩니다. 이러한 벡터 값 함수에는 벡터 필드라는 이름이 지정됩니다.

함수공간

수학적 분석, 특히 함수 분석에서 함수 공간은 특정 속성을 공유하고 위상 벡터 공간을 형성하는 스칼라 값 또는 벡터 값 함수의 집합입니다. 예를 들어, 콤팩트 서포트가 있는 실제 평활 함수(즉, 일부 콤팩트 세트 외부에서는 0임)는 분포 이론의 기초가 되는 함수 공간을 형성합니다.

함수 공간은 함수의 특성을 연구하기 위해 대수적 및 위상적 특성을 사용할 수 있도록 함으로써 고급 수학 분석에서 기본적인 역할을 합니다. 예를 들어, 상미분 방정식 또는 편미분 방정식의 해의 모든 존재 정리와 유일성은 함수 공간 연구의 결과입니다.

다치함수

실수 변수 또는 복소 변수의 함수를 지정하는 여러 방법은 점 또는 점 근처에서 함수의 로컬 정의에서 시작하여 연속성에 의해 함수를 훨씬 더 큰 도메인으로 확장합니다. 종종 시작점 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle x_{0}$의 경우 함수에 대해 몇 가지 가능한 시작 값이 있습니다$$.

예를 들어, 제곱근을 제곱 함수의 역함수로 정의할 때, 임의의 양수 x ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle x_{0}$에 대해 제곱근 값에는 두 가지 선택 사항이 있으며$$, 그 중 하나는 양수이고 $x{\displaystyle \sqrt{{}_{}}}$ ${\displaystyle \sqrt{0_{}}}$으로 표시된${\displaystyle {x_{0}}$입니다.$}$그리고$$ 부정적이고 표시된 다른 하나는 $-{\displaystyle }$ ${\displaystyle \sqrt{{x\mathrm{}}_{}}}$ ${\displaystyle 0\sqrt{{}_{}}}$ ${\displaystyle -{\sqrt {x_{0}}}$입니다.$}$이러한$$ 선택은 두 개의 연속 함수를 정의합니다. 둘 다 음이 아닌 실수를 도메인으로 하고, 음이 아닌 실수 또는 양이 아닌 실수를 이미지로 합니다. 이 함수들의 그래프를 보면, 이들이 함께 하나의 매끄러운 곡선을 이루고 있음을 알 수 있습니다. 따라서 이 두 제곱근 함수는 양의 x에 대해 두 개의 값을 가지며, 0에 대해 하나의 값을 가지며, 음의 x에 대해 값이 없는 단일 함수로 간주하는 것이 유용합니다.

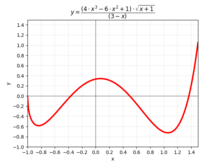
앞의 예제에서 한 가지 선택인 양의 제곱근이 다른 선택보다 더 자연스럽습니다. 일반적으로 그렇지 않습니다. 예를 들어, x ${\displaystyle 3^{}}$- ${\displaystyle 3}$ ${\displaystyle x}$- y = ${\displaystyle 0}$ ${\displaystyle$ x$^{3}-3x-y$=$0}$의 루트 x에 y를 매핑하는 암시적 함수를 생각해 보겠습니다(오른쪽 그림 참조). y = 0인 경우 x에 대해 $0{\displaystyle ,}$ 3${\displaystyle \text{또는}-3}$ ${\displaystyle$0, ${\sqrt {3}},$ {\$text{ 또는 }}-{\sqrt {3}}$를 선택할 수 있습니다. 암묵적 함수 정리에 의해 각 선택은 함수를 정의합니다. 첫 번째 경우 (maxim) 도메인은 구간 [-2, 2]이고 이미지는 [-1, 1]입니다. 두 번째 경우 도메인은 [-2, ∞)이고 이미지는 [1,]입니다. ∞); 마지막의 경우 도메인은 (-∞, 2]이고 이미지는 (-∞, -1)입니다. 세 개의 그래프가 함께 매끄러운 곡선을 형성하고, 하나의 선택을 선호할 이유가 없기 때문에, 이 세 함수는 종종 -2 < y < 2에 대해 3개의 값을 가지며, y ≤ -2 및 y ≥ -2에 대해 하나의 값만을 갖는 y의 단일 다중 값 함수로 간주됩니다.

다중 값 함수 개념의 유용성은 복잡한 함수, 일반적으로 분석 함수를 고려할 때 더 명확합니다. 해석적 연속에 의해 복소함수가 확장될 수 있는 영역은 일반적으로 거의 전체 복소평면으로 구성됩니다. 그러나 두 개의 다른 경로를 통해 도메인을 확장할 때 하나는 종종 다른 값을 얻습니다. 예를 들어, 양의 허수 부분을 갖는 복소수의 경로를 따라 제곱근 함수의 정의역을 확장할 때, -1의 제곱근에 대해 i를 얻는 반면, 음의 허수 부분을 갖는 복소수를 통해 확장할 때, -i를 얻습니다. 문제를 해결하는 방법은 일반적으로 두 가지가 있습니다. 어떤 곡선을 따라 연속적이지 않은 함수를 분기 절단이라고 정의할 수 있습니다. 이러한 함수를 함수의 주값이라고 합니다. 다른 방법은 다중 값 함수를 가지고 있다고 간주하는 것입니다. 다중 값 함수는 고립된 특이점을 제외하고는 모든 곳에서 분석되지만 특이점을 중심으로 닫힌 루프를 따라가면 그 값이 "점프"할 수 있습니다. 이 점프를 모노드로미라고 합니다.

수학의 기초에서

함수의 정의역과 공변역은 집합이어야 하기 때문에 이 글에 주어진 함수의 정의에는 집합의 개념이 필요합니다. 정의역이 명시적으로 정의되지 않더라도 정의역과 공변역이 잘 정의된 집합인 함수만을 고려하는 것이 일반적으로 어렵지 않기 때문에 이것은 일반적인 수학에서 문제가 되지 않습니다. 그러나 보다 일반적인 기능을 고려하는 것이 유용할 때가 있습니다.

예를 들어, 단일 톤 집합은 $함수$ ${\displaystyle x}$ ↦ {x$}$로 간주될 수 있습니다. ${\displaystyle$ x$\mapsto$\{x\}.$}$도메인은$$ 모든 집합을 포함하므로 집합이 아닙니다. 일반적인 수학에서는 도메인을 지정하여 이러한 종류의 문제를 피하는데, 이는 싱글톤 함수가 많다는 것을 의미합니다. 그러나 수학의 기초를 확립할 때는 도메인, 코드 도메인 또는 둘 다 지정되지 않은 함수를 사용해야 할 수 있으며, 일부 저자, 종종 논리학자는 이러한 약한 지정된 함수에 대해 정확한 정의를 제공합니다.^[21]

이러한 일반화된 함수는 수학의 기초를 공식화하는 개발에 중요할 수 있습니다. 예를 들어 폰 노이만-버네이스-괴델 집합론(Gödel set theory)은 모든 집합의 집합이 클래스인 집합론의 확장입니다. 이 이론은 치환 공리를 포함하며, X가 집합이고 F가 함수라면 F[X]는 집합입니다.

집합론이 아닌 유형론을 사용하는 수학의 기초에 대한 대안적인 공식화에서 함수는 다른 종류의 대상으로부터 정의되기보다는 원시적인 개념으로 간주됩니다. 이들은 함수 유형의 거주자이며 람다 미적분학의 식을 사용하여 구성할 수 있습니다.^[22]

컴퓨터과학에서

컴퓨터 프로그래밍에서 함수는 일반적으로 추상적인 함수 개념을 구현하는 컴퓨터 프로그램의 한 부분입니다. 즉, 각 입력에 대한 출력을 생성하는 프로그램 단위입니다. 그러나 많은 프로그래밍 언어에서 모든 서브루틴은 출력이 없을 때에도 함수라고 불리며, 함수는 단순히 컴퓨터 메모리의 일부 데이터를 수정하는 것으로 구성됩니다.

함수형 프로그래밍은 수학적 함수처럼 행동하는 서브루틴만을 사용하여 프로그램을 구축하는 것으로 구성된 프로그래밍 패러다임입니다. 예를들면, if_then_else 는 세 개의 함수를 인수로 사용하고 첫 번째 함수(true 또는 false)의 결과에 따라 두 번째 함수 또는 세 번째 함수 중 하나의 결과를 반환하는 함수입니다. 함수형 프로그래밍의 중요한 장점은 잘 정립된 이론인 람다 미적분학을 기반으로 하기 때문에 프로그램 증명을 더 쉽게 할 수 있다는 것입니다(아래 참조).

컴퓨터 언어 용어를 제외하고, "함수"는 컴퓨터 과학에서 일반적인 수학적 의미를 가지고 있습니다. 이 분야에서 주요 관심사는 함수의 계산 가능성입니다. 이 개념과 관련된 알고리즘 개념에 정확한 의미를 부여하기 위해 여러 계산 모델이 도입되었으며, 기존 모델은 일반 재귀 함수인 람다 미적분학과 튜링 머신입니다. 계산 가능성 이론의 기본 정리는 이 세 가지 계산 모델이 동일한 계산 가능 함수 집합을 정의하고, 지금까지 제안된 모든 계산 모델이 동일한 계산 가능 함수 집합 또는 더 작은 계산 함수 집합을 정의한다는 것입니다. 처치-튜링 논제는 계산 가능한 함수에 대한 철학적으로 허용되는 모든 정의가 동일한 함수를 정의한다는 주장입니다.

일반 재귀 함수는 다음과 같이 정의할 수 있는 정수에서 정수까지의 부분 함수입니다.

• 일정한 함수,
• 후계자, 그리고
• 프로젝션 함수

오퍼레이터를 통하여

• 작곡,
• 원시 재귀, 그리고
• 최소화

정수에서 정수까지의 함수에 대해서만 정의되지만 다음 속성의 결과로 계산 가능한 함수를 모델링할 수 있습니다.

• 계산은 유한한 수의 부호열(숫자, 공식의 digits, ...)을 조작하는 것입니다.
• 모든 기호 시퀀스는 비트 시퀀스로 코딩될 수 있습니다.
• 비트 수열은 정수의 이진법 표현으로 해석할 수 있습니다.

람다 미적분학은 집합 이론을 사용하지 않고 계산 가능한 함수를 정의하는 이론으로, 함수 프로그래밍의 이론적 배경입니다. 변수, 함수 정의(𝜆 용어) 또는 함수를 용어에 적용하는 용어로 구성됩니다. 용어는 이론의 공리인 일부 규칙(α 등가, β 감소 및 η 변환)을 통해 조작되며 계산 규칙으로 해석될 수 있습니다.

원래 형태에서 람다 미적분학은 함수의 정의역과 공변역의 개념을 포함하지 않습니다. 대략적으로 말하자면, 그것들은 타이핑된 람다 미적분학에서 타입이라는 이름으로 이론에 도입되었습니다. 대부분의 유형화된 람다 미적분은 유형화되지 않은 람다 미적분보다 더 적은 함수를 정의할 수 있습니다.

참고 항목

서브페이지

일반화

관련항목

메모들

참고문헌

원천

추가읽기

외부 링크

• Wolfram Functions – 많은 수학 함수의 공식과 시각화를 제공하는 웹사이트
• NIST 디지털 수학 기능 라이브러리