평균 제곱근
Root mean square이 글은 검증을 위해 추가 인용문이 필요합니다.: square – · · · · (2010년 3월 ( 템플릿메시지 및 시기 ) |
수학 및 그 응용 프로그램에서 숫자 i RMS 또는 rms로 줄여서 x {RMS 또는 x{RMS의 평균 제곱근은 다음과 같이 정의됩니다집합의 [1]제곱의 산술 평균).RMS는 2차 평균( {[2][3]이라고도 하며 일반화된 평균의 특정 경우입니다.연속적으로 변화하는 함수{RMS의 RMS는 사이클 중 순간값의 제곱의 적분으로 정의할 수 있습니다.
교류에서 RMS는 저항 부하에서 동일한 [1]전력 소실을 발생시키는 정전류 값과 동일합니다.추정 이론에서 추정기의 평균 제곱근 편차는 데이터에 대한 추정기의 적합성의 불완전성에 대한 척도입니다.
정의.
일련의 값(또는 연속 시간 파형)의 RMS 값은 값의 제곱에 대한 산술 평균의 제곱근 또는 연속 파형을 정의하는 함수의 제곱근입니다.물리학에서 RMS 전류 값은 "저항에서 동일한 전력을 소산하는 직류 전류 값"으로도 정의할 수 있습니다.
n개의값 { x, , n1},의 경우 RMS는 다음과 같습니다.
t 에 걸쳐 정의된 연속 함수(또는 파형) f(t)의 대응식은 다음과 같습니다.
모든 시간에 걸친 함수의 RMS는
주기 함수의 모든 시간에 걸친 RMS는 함수의 한 주기의 RMS와 동일합니다.연속 함수 또는 신호의 RMS 값은 등간격 관측치로 구성된 표본의 RMS를 취함으로써 근사치를 구할 수 있습니다.또한 Cartwright에서 [4]보듯이 미적분 없이 다양한 파형의 RMS 값을 결정할 수도 있습니다.
랜덤 공정의 RMS 통계량의 경우 평균 대신 기대값이 사용됩니다.
공통 파형
파형이 순수 사인파인 경우 진폭(피크 대 피크, 피크)과 RMS 사이의 관계는 연속 주기파에서와 마찬가지로 고정되고 알려져 있습니다.그러나 주기적 또는 연속적이지 않을 수 있는 임의 파형에는 해당되지 않습니다.0 평균 사인파의 경우 RMS와 피크 대 피크 진폭 사이의 관계는 다음과 같습니다.
- 피크 대 피크
다른 파형의 경우 사인파와 관계가 다릅니다.예를 들어, 삼각형 또는 톱니 모양의 파형의 경우
- 피크 대 피크
| 파형 | 변수 및 연산자 | RMS |
|---|---|---|
| 직류 | ||
| 사인파 | ||
| 사각파 | ||
| 직류 시프트 사각파 | ||
| 수정된 사인파 | ||
| 삼각파 | ||
| 톱니파 | ||
| 맥파 | ||
| 위상간 전압 | ||
| 여기서: | ||
파형 조합 중
알려진 단순 파형을 합산하여 만든 파형은 구성 요소 파형이 직교하는 경우(즉, 한 단순 파형과 다른 단순 파형의 곱의 평균이 파형 시간 [5]자체를 제외한 모든 쌍에 대해 0인 경우) 성분 RMS 값의 제곱합에 해당하는 RMS 값을 가집니다.
또는 파형이 완전히 양의 상관 관계이거나 서로 "위상"인 경우 RMS 값이 직접 합산됩니다.
사용하다
전기공학 분야
전압
파형 조합의 RMS의 특별한 경우는 다음과 같습니다.[6]
V은 신호의 직류(또는 평균) 과 AC를 나타냅니다.은 신호의 교류 성분입니다.
평균 전력
전기 엔지니어는 종종 전기 저항 R에 의해 소산되는 전력 P를 알아야 합니다.저항을 통해 일정한 전류 I가 있을 때 쉽게 계산할 수 있습니다.R옴의 부하에 대해 전력은 다음과 같이 정의됩니다.
그러나 전류가 시간 가변 함수 I(t)인 경우, 이 공식은 전류(및 순간 전력)가 시간에 따라 변화한다는 사실을 반영하도록 확장되어야 합니다.기능이 주기적인 경우(예: 가정용 AC 전원)에도 시간에 따라 분산되는 평균 전력에 대해 논의하는 것이 여전히 의미가 있습니다. 이 평균 전력 소산을 사용하여 계산됩니다.
따라서 함수 I(t)의 RMS 값 I는RMS 전류 I(t)의 시간 평균 전력 손실과 동일한 전력 손실을 생성하는 정전류입니다.
평균 전력은 RMS 값이RMS V인 시변전압 V(t)의 경우와 동일한 방법을 사용하여 확인할 수도 있습니다.
이 방정식은 정현파 또는 톱니 파형과 같은 모든 주기 파형에 사용할 수 있으므로 지정된 로드에 전달되는 평균 전력을 계산할 수 있습니다.
이 두 방정식의 제곱근을 구해서 곱하면 검정력은 다음과 같습니다.
두 유도 모두 비례하는 전압 및 전류에 따라 달라집니다(즉, 부하 R은 순전히 저항성임).무효 부하(즉, 에너지를 소산할 수 있을 뿐만 아니라 저장할 수 있는 부하)는 AC 전원의 주제에서 설명합니다.
I(t)가 사인파 전류일 때 교류하는 일반적인 경우, 주 전원에 대해 대략적으로 참인 것처럼 RMS 값은 위의 연속 케이스 방정식으로부터 쉽게 계산할 수 있습니다.I를 피크 전류로 정의하면 다음과p 같습니다.
여기서 t는 시간이고 θ는 각 주파수(θ = 2µ/T, 여기서 T는 파동의 주기)입니다.
나는 양의 상수이기 때문에p:
삼각 항등식을 사용하여 트리거 함수의 제곱을 제거합니다.
그러나 간격이 전체 사이클의 정수이므로(RMS 정의에 따라), 사인 항이 취소되고 다음과 같이 남습니다.
유사한 분석을 통해 정현파 전압에 대한 유사한 방정식이 도출됩니다.
여기서P I는 피크 전류를 나타내고P V는 피크 전압을 나타냅니다.
전력 계산의 실행에는 유용하기 때문에 전원 콘센트에 기재된 전압(예를 들어 미국에서는 120V, 유럽에서는 230V)은 거의 항상 피크값이 아닌 RMS 값으로 인용됩니다.피크 값은 위의 공식에서 얻은RMS RMS 값으로 계산할 수 있습니다. 이는 소스가 순수한 사인파라고 가정할 때 V = V × δ2를 의미합니다P.따라서 미국에서 주 전압의 피크 값은 약 120 × µ2, 즉 약 170V입니다.피크 대 피크 전압은 약 340볼트입니다.비슷한 계산으로 유럽의 피크 주 전압은 약 325V이고 피크 대 피크 주 전압은 약 650V입니다.
전류와 같은 RMS 양은 보통 한 사이클에 걸쳐 계산됩니다.다만, 송신 전력 손실을 계산할 때는, 장기에 걸친 RMS 전류가 필요합니다.같은 원리가 적용되어 (예를 들어) 24시간마다 12시간 동안 사용되는 10A의 전류는 평균 5A의 전류를 나타내지만 장기적으로는 7.07A의 RMS 전류를 나타냅니다.
RMS 전력이라는 용어는 오디오 업계에서 평균 전력 또는 평균 전력의 동의어로 잘못 사용되는 경우가 있습니다(이것은 저항 부하에서 RMS 전압 또는 RMS 전류의 제곱에 비례합니다).오디오 파워 측정과 그 단점에 대한 자세한 내용은 오디오 파워를 참조하십시오.
스피드
기체 분자의 물리학에서 평균 제곱 속도는 평균 제곱 속도의 제곱근으로 정의됩니다.이상 기체의 RMS 속도는 다음 방정식을 사용하여 계산됩니다.
여기서 R은 기체 상수 8.314J/(mol·K), T는 가스의 온도(켈빈 단위), M은 가스의 몰 질량(몰 당 킬로그램 단위)을 나타낸다.물리학에서 속도는 속도의 스칼라 크기로 정의된다.정지 상태의 기체의 경우, 분자의 평균 속도가 0일지라도 분자의 평균 속도는 약 수천 km/h가 될 수 있습니다.
에러
예를 들어 이론적인 예측에서 얻은 세트와 물리 변수의 실제 측정에서 얻은 두 데이터 세트를 비교할 때, 두 데이터 세트의 쌍별 차이의 RMS는 평균 오차가 0에서 얼마나 떨어져 있는지를 측정하는 역할을 할 수 있습니다.쌍별 차이의 절대값 평균은 차이의 변동성을 측정하는 데 유용한 척도가 될 수 있습니다.그러나 차이의 RMS는 일반적으로 선호되는 측정값으로, 아마도 수학적인 규칙과 다른 공식과의 호환성 때문일 것이다.
주파수 영역 내
RMS는 Parseval의 정리를 사용하여 주파수 영역에서 계산할 수 있습니다.샘플링 x [ ( ) { x [n] =의 경우, 서T { T는 샘플링 주기입니다.
서X [ { [ ] { X]=\{FFT} \{은 샘플 크기, 즉 샘플 및 FFT 계수의 관측치 수입니다.
이 경우 시간 도메인에서 계산된 RMS는 주파수 도메인에서와 동일합니다.
기타 통계와의 관계
x {\이(가) 산술 평균이고 _{이(가) 모집단 또는 파형의 표준 편차인 :[8]
이를 통해 RMS 값이 항상 평균보다 크거나 같음을 알 수 있습니다. RMS에는 "오류"/제곱 편차도 포함됩니다.
물리학자들은 입력 신호의 평균이 0이라고 가정할 때 표준 편차의 동의어로 루트 평균 제곱이라는 용어를 종종 사용합니다. 즉, 주어진 기준선 또는 [9][10]적합치로부터의 신호 평균 제곱 편차의 제곱근을 가리킵니다.이는 전기 엔지니어가 신호의 "AC 전용" RMS를 계산할 때 유용합니다.표준 편차는 약 0이 아닌 평균에 대한 신호 변동의 RMS입니다. DC 성분이 제거됩니다(즉, 평균 신호가 0이면 RMS(신호) = stdev(표준)).
「 」를 참조해 주세요.
레퍼런스
- ^ a b "Root-mean-square value". A Dictionary of Physics (6 ed.). Oxford University Press. 2009. ISBN 9780199233991.
- ^ Thompson, Sylvanus P. (1965). Calculus Made Easy. Macmillan International Higher Education. p. 185. ISBN 9781349004874. Retrieved 5 July 2020.
- ^ Jones, Alan R. (2018). Probability, Statistics and Other Frightening Stuff. Routledge. p. 48. ISBN 9781351661386. Retrieved 5 July 2020.
- ^ Cartwright, Kenneth V (Fall 2007). "Determining the Effective or RMS Voltage of Various Waveforms without Calculus" (PDF). Technology Interface. 8 (1): 20 pages.
- ^ Nastase, Adrian S. "How to Derive the RMS Value of Pulse and Square Waveforms". MasteringElectronicsDesign.com. Retrieved 21 January 2015.
- ^ "Make Better AC RMS Measurements with your Digital Multimeter" (PDF). Keysight. Keysight. Retrieved 15 January 2019.
- ^ AC = a 및 BC = b. OC = a 및 b의 AM이고 반지름 r = QO = OG인 경우.
피타고라스의 정리를 사용하여 QC² = QO² + OC² qc QC = q QO² + OC² = QM.
피타고라스의 정리를 사용하여 OC² = OG² + GC² gc GC = √OC² - OG² = GM.
비슷한 삼각형을 사용해서HC/GC = GC/OC h HC = GC²/OC = HM. - ^ Chris C. Bissell; David A. Chapman (1992). Digital signal transmission (2nd ed.). Cambridge University Press. p. 64. ISBN 978-0-521-42557-5.
- ^ Weisstein, Eric W. "Root-Mean-Square". MathWorld.
- ^ "ROOT, TH1:GetRMS". Archived from the original on 2017-06-30. Retrieved 2013-07-18.







 걸쳐 정의된 연속 함수(또는 파형) f(t)의 대응식은 다음과 같습니다.
걸쳐 정의된 연속 함수(또는 파형) f(t)의 대응식은 다음과 같습니다.![{\displaystyle f_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{[f(t)]}^{2}\,{\rm {d}}t}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e25b4df390e845aacaaa0c7dfd0ba6f1fc5cdde)
![{\displaystyle f_{\text{RMS}}=\lim _{T\rightarrow \infty }{\sqrt {{1 \over {2T}}{\int _{-T}^{T}{[f(t)]}^{2}\,{\rm {d}}t}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8870ffec7ed1b4dfeb7f145630d2cecbe7b23b3e)




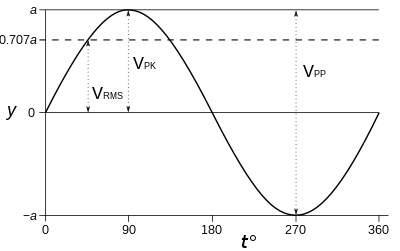




















 신호의
신호의  신호의
신호의 
![{\displaystyle {\begin{aligned}P_{av}&=\left(I(t)^{2}R\right)_{av}&&{\text{where }}\left(\cdots \right)_{av}{\text{ denotes the temporal mean of a function}}\\[3pt]&=\left(I(t)^{2}\right)_{av}R&&{\text{(as }}R{\text{ does not vary over time, it can be factored out)}}\\[3pt]&=I_{\text{RMS}}^{2}R&&{\text{by definition of root-mean-square}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2207a68433c8a7edc9a1744e866846470ebfd57e)


![{\displaystyle I_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}\int _{T_{1}}^{T_{2}}\left[I_{\text{p}}\sin(\omega t)\right]^{2}dt}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df0578a1a0e325cba1139ef81b4867340cf0bf0c)

![{\displaystyle {\begin{aligned}I_{\text{RMS}}&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{1-\cos(2\omega t) \over 2}\,dt}}}\\[3pt]&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}-{\sin(2\omega t) \over 4\omega }\right]_{T_{1}}^{T_{2}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6b151fc6495fb26320b04637150ff032c8d8797)
![{\displaystyle I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}\right]_{T_{1}}^{T_{2}}}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{{T_{2}-T_{1}} \over 2}}}={I_{\text{p}} \over {\sqrt {2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45eaa1a04872567a59a8400a8f100a1debe34ec7)


![{\displaystyle x[n]=x(t=nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de908f2452423bed903703e7bcdb147552d5859c)
 샘플링 주기입니다.
샘플링 주기입니다.![{\displaystyle \sum _{n=1}^{N}{x^{2}[n]}={\frac {1}{N}}\sum _{m=1}^{N}\left|X[m]\right|^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e5137ad83fb9b24095511bad31240b815a2d352)
![{\displaystyle X[m]=\operatorname {FFT} \{x[n]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbb904ef9c3708132d7dbe71992af50b2ec21f04) 샘플 크기, 즉 샘플 및 FFT 계수의 관측치 수입니다.
샘플 크기, 즉 샘플 및 FFT 계수의 관측치 수입니다. ![{\displaystyle {\text{RMS}}\{x[n]\}={\sqrt {{\frac {1}{N}}\sum _{n}{x^{2}[n]}}}={\sqrt {{\frac {1}{N^{2}}}\sum _{m}{{\bigl |}X[m]{\bigr |}}^{2}}}={\sqrt {\sum _{m}{\left|{\frac {X[m]}{N}}\right|^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaa1cc81ec8221d7db02af033f2d5424c477a416)

 (
( (
(


