전염병의 수학적 모델링

수학적 모델은 전염병(식물 포함)의 가능한 결과를 보여주고 공중 보건 및 식물 건강 개입을 알리는 데 도움이 되도록 감염병이 어떻게 진행되는지를 예측할 수 있습니다.모델은 수학과 함께 기본적인 가정이나 수집된 통계를 사용하여 다양한 전염병에 대한 매개 변수를 찾고 대량 백신 프로그램과 같은 다양한 개입의 효과를 계산합니다.모델링은 피해야 할 개입과 시도를 결정하거나 미래 성장 패턴 등을 예측하는 데 도움이 될 수 있습니다.

역사

전염병 모델링은 질병이 확산되는 메커니즘을 연구하고, 발병의 미래 경로를 예측하고,^[1] 전염병을 통제하기 위한 전략을 평가하는 데 사용된 도구입니다.

사망의 원인을 체계적으로 정량화하려고 노력한 최초의 과학자는 1662년에 작성된 그의 책 자연적, 정치적 관찰에서 존 그룬트였습니다.그가 연구한 법안들은 매주 발표되는 숫자와 사망 원인의 목록들이었습니다.그룬트의 사망 원인 분석은 데일리와 가니에 따르면 "현재 현대 역학자들 사이에서 잘 확립된 이론"인 "경쟁 위험 이론"의 시작으로 간주됩니다.

질병의 확산에 대한 수학적 모델링에 대한 최초의 설명은 1760년 다니엘 베르누이에 의해 수행되었습니다.의사로서 훈련을 받은 베르누이는 ^[2]천연두 예방 접종 관행을 방어하기 위한 수학적 모델을 만들었습니다.이 모델의 계산은 천연두에 대한 보편적인 접종이 기대 수명을 26세 7개월에서 29세 ^[3]9개월로 증가시킬 것이라는 것을 보여주었습니다.Daniel Bernoulli의 ^[4]연구는 세균 이론의 현대적 이해에 선행했습니다.

20세기 초, 윌리엄 해머와[5] 로널드^[6] 로스는 전염병 행동을 설명하기 위해 집단 행동의 법칙을 적용했습니다.

1920년대에는 구획 모델이 등장했습니다.커맥-맥켄드릭 전염병 모델(1927)과 리드-프로스트 전염병 모델(1928)은 모두 모집단에서 취약한 개체, 감염된 개체 및 면역 개체 간의 관계를 설명합니다.Kermack-McKendrick 전염병 모델은 많은 기록된 ^[7]전염병에서 관찰된 것과 매우 유사한 발병의 행동을 예측하는 데 성공했습니다.

최근에는 에이전트 기반 모델(ABM)이 더 단순한 구획 ^[8]모델과 교환하여 사용되고 있습니다.예를 들어, 역학적 ABM은 SARS-CoV-2의 ^[9]확산에 대한 공중 보건(비의약품) 개입을 알리기 위해 사용되었습니다.역학적 ABM은 복잡성과 높은 계산 능력이 요구됨에도 불구하고 가정을 ^[10][11]단순화하고 비현실적이라는 비판을 받아 왔습니다.그래도 ABM이 정확하게 ^[12]보정된 경우 완화 및 억제 조치에 관한 결정을 알리는 데 유용할 수 있습니다.

가정

모형은 모형의 기초가 되는 가정만큼만 좋습니다.모형이 관측 결과와 일치하지 않는 예측을 하고 수학이 올바른 경우에는 모형을 ^[13]유용하게 만들기 위해 초기 가정이 변경되어야 합니다.

• 직사각형 및 고정 연령 분포, 즉, 모집단의 모든 사람이 L세까지 살다가 사망하고, 각 연령(L세까지)마다 모집단의 수가 동일합니다.이것은 유아 사망률이 낮고 인구의 많은 부분이 기대 수명까지 사는 선진국들에게 종종 잘 정당화됩니다.
• 모집단의 동질적 혼합, 즉 정밀 조사 대상 모집단의 개체가 분류되고 무작위로 접촉하며 대부분 더 작은 하위 그룹에서 혼합되지 않습니다.사회 구조가 광범위하기 때문에 이러한 가정은 거의 정당화되지 않습니다.예를 들어, 런던의 대부분의 사람들은 다른 런던 사람들과만 접촉합니다.게다가, 런던 내에는 터키 공동체나 십대(두 가지 예를 들어보자면)와 같은 더 작은 하위 그룹이 있는데, 이들은 그룹 밖의 사람들보다 서로 더 많이 어울립니다.그러나 동질적 혼합은 수학을 다루기 쉽게 만드는 표준 가정입니다.

전염병 모델의 유형

확률론적

확률론적이란 무작위 변수가 있거나 있는 것을 의미합니다.확률적 모델은 시간이 지남에 따라 하나 이상의 입력에서 무작위 변동을 허용하여 잠재적 결과의 확률 분포를 추정하는 도구입니다.확률적 모델은 노출 위험, 질병 및 기타 질병 역학의 확률 변화에 따라 달라집니다.소규모 또는 대규모 인구에서 통계적 에이전트 수준의 질병 전파는 확률적 ^[14]방법에 의해 결정될 수 있습니다.^[15][16]

결정론적

결핵의 경우와 같이 많은 인구를 다룰 때 결정론적 또는 구획적 수학 모델이 종종 사용됩니다.결정론적 모델에서 모집단의 개인은 각각 ^[17]전염병의 특정 단계를 나타내는 서로 다른 하위 그룹 또는 구획에 할당됩니다.

한 클래스에서 다른 클래스로의 전이 속도는 수학적으로 미분 방정식을 사용하여 공식화됩니다.이러한 모델을 구축하는 동안, 구획의 인구 크기는 시간에 따라 차별화될 수 있고 전염병 프로세스는 결정론적이라고 가정해야 합니다.즉,^[7] 구획의 모집단 변화는 모형을 개발하는 데 사용된 이력만을 사용하여 계산할 수 있습니다.

하위 지수 성장

유행병의 증가에 대한 일반적인 설명은 한 사람이 2명을 감염시키고, 그 2명이 4명을 감염시키고, 그 외에도 매 세대마다 감염자의 수가 두 배로 증가한다는 것입니다.이것은 태그 게임과 유사합니다. 한 사람이 태그 2를, 태그를 단 적이 없는 2명이 태그 4를 하는 것입니다.이 게임이 진행됨에 따라 태그가 지정된 실행이 이전에 태그가 지정된 실행을 지나 태그가 지정된 적이 없는 사람을 추적함에 따라 점점 더 열광하게 됩니다.따라서 이 전염병 모델은 모든 인구가 감염되었기 때문에 0으로 추락할 때까지 기하급수적으로 증가하는 곡선으로 이어집니다. 즉,^[18] 집단 면역이 없고 현실에서 볼 수 있는 정점 및 점진적인 감소가 없습니다.

복제번호

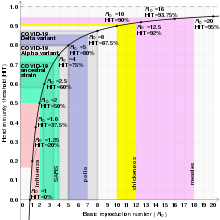
기본 생식 수(R로 표시₀)는 질병이 얼마나 전이 가능한지를 나타내는 척도입니다.한 명의 감염자가 감염 과정에서 감염되는 평균 사람 수입니다.이 양은 감염이 잠재적으로 증가할 것인지, 소멸될 것인지 또는 지속적으로 유지될 것인지를 결정합니다. 만약₀ R이 1보다 크면, 각 사람은 평균적으로 한 명 이상의 다른 사람을 감염시켜 질병이 확산될 것입니다. R이₀ 1보다 작으면, 각 사람은 평균적으로 한 명 미만을 감염시켜 질병이 소멸될 것입니다₀. 그리고 R = 1,그러면 각 사람들은 평균적으로 정확히 한 명의 다른 사람들을 감염시킬 것이고, 그래서 그 질병은 풍토병이 될 것입니다: 그것은 인구 전체에 걸쳐 움직이지만 증가하거나 ^[19]감소하지는 않을 것입니다.

고유 정상 상태

전염병은 외부의 투입 없이 인구에서 지속될 수 있을 때 풍토병이라고 합니다.이것은 평균적으로 각 감염자가 정확하게 한 명의 다른 사람을 감염시키고 있다는 것을 의미합니다(더 이상 감염자의 수는 기하급수적으로 증가할 것이고 전염병이 발생할 것이며 질병은 더 이상 소멸될 것입니다).수학적으로 말하면, 다음과 같습니다.

${\displaystyle \R_{0}S\ =1}$

모든 사람이 감수성이 있다고 가정할 때 질병의 기본 생식 수(R₀)는 실제 감수성이 있는 인구 비율(S)에 곱해야 합니다(감수성이 없는 사람은 질병에 걸릴 수 없기 때문에 우리의 계산에 포함되지 않기 때문입니다).이 관계는 질병이 풍토적으로 안정된 상태에 있기 위해서는 기본 생식 수가 높을수록 취약 인구의 비율이 낮아야 하며 그 반대도 마찬가지라는 것을 의미합니다.이 표현식에는 민감도 비율에 대한 제한이 있습니다. 예를 들어 R이 0.5이면 S가₀ 2여야 하지만 이 비율이 모집단 ^{[citation needed]}크기를 초과합니다.

직사각형 고정 연령 분포를 가정하고 감염 연령도 각 출생 연도에 대해 동일한 분포를 갖도록 합니다.예를 들어, A보다 어린 사람들이 영향을 받기 쉽고 A보다 나이가 많은 사람들이 면역이 될 때(또는 전염성이 있을 때) 평균 감염 연령을 A라고 가정합니다.그런 다음 영향을 받기 쉬운 모집단의 비율이 다음과 같이 주어진다는 것을 쉽게 증명할 수 있습니다.

${\displaystyle S=novfrac {A}{L}}을(를) 표시합니다.}$

우리는 L이 이 모델에서 모든 개인이 죽는 것으로 가정되는 나이라는 것을 반복합니다.그러나 고유의 정상 상태에 대한 수학적 정의는 다음과 같이 재정렬될 수 있습니다.

${\displaystyle S=novfrac {1}{R_{0}}.}$

따라서 전이 특성으로 인해:

$표시({style{frac {1}{R_{0}}={A}{L}}\오른쪽 화살표 R_{0}={L}{A}}).}$

쉽게 사용할 수 있는 데이터를 사용하여 모수₀ R을 추정하는 간단한 방법을 제공합니다.

지수 연령 분포를 가진 모집단의 경우

${\displaystyle R_{0}=1+{\frac {L}{A}}.}$

이를 통해 두 유형의 모집단 분포 모두에서 A와 L이 지정된 질병의 기본 생식 수를 확인할 수 있습니다.

역학의 구획 모델

구획 모델은 마르코프 ^[20]체인으로 공식화됩니다.전염병학의 전형적인 구획 모델은 전염병을 모델링하기 위한 간단한 모델로 사용될 수 있는 SIR 모델입니다.다른 여러 유형의 구획 모델도 사용됩니다.

SIR 모델

1927년, W.O. 커맥과 A.G. 맥켄드릭은 3개의 구획만을 가진 고정 모집단을 고려한 모델을 만들었습니다. 민감한 $(t$ $감염$된 I$(t$ R$($${\displaystyle ),}$$회복$된 R($t$이 모델에 사용되는 구획은 세 가지 ^[21]클래스로 구성됩니다.

• ${\displaystyle }$S$)$ {\$displaystyle$ S$(t)}$는 시간 t에서 아직 질병에 감염되지 않은 개인 또는 모집단의 질병에 취약한 개인을 나타내는 데 ${\displaystyle \mathrm{사용}}$됩니다.
• ${\displaystyle I}$($)$ {\$displaystyle I($t)}는$$ 해당 질병에 감염되어 취약 범주에 속하는 사람들에게 질병을 전파할 수 있는 모집단의 개인을 의미합니다.
• ${\displaystyle R}$($)$ {\$displaystyle R($t)}은$$ 면역 또는 사망으로 인해 감염되었다가 질병에서 제거된 모집단의 개인을 위해 사용되는 구획입니다.이 범주에 속한 사람은 다시 감염되거나 다른 사람에게 감염을 전송할 수 없습니다.

기타 구획 모델

SIR 모델에는 출생과 사망을 포함한 많은 수정 사항이 있으며, 회복 시 면역이 없는 경우(SIS 모델), 면역이 짧은 기간 동안만 지속되는 경우(SIRS, SEIS 및 SEIR),유아가 면역력(MSIR)을 가지고 태어날 수 있는 경우.

전염병 역학

수학적 모델은 호스트-병원체 상호 작용에서 생성되는 증가하는 데이터 볼륨을 통합해야 합니다.인간을 포함한 동식물의 감염성 질병의 인구 역학, 구조 및 진화에 대한 많은 이론적 연구가 이 ^[22]문제와 관련이 있습니다.

연구 주제는 다음과 같습니다.

• 항원 이동
• 역학적 네트워크
• 저항의 진화와 확산
• 면역항체학
• 호스트 내 역학
• 유행병
• 병원체 집단 유전학
• 숙주 내 병원체의 지속성
• 계통역학
• 감염 저장소의 역할 및 식별
• 숙주 유전인자의 역할
• 공간 역학
• 통계적, 수학적 도구와 혁신
• 스트레인(생물학) 구조 및 상호작용
• 감염의 전염, 확산 및 통제
• 독극

집단 백신 접종의 수학

만약 면역이 있는 인구의 비율이 질병에 대한 집단 면역 수준을 초과하면, 질병은 더 이상 인구에서 지속될 수 없고 전염은 ^[23]사라집니다.따라서, 백신 접종이나 질병에 대한 이전 노출로부터의 회복으로 충분한 사람들이 면역이 된다면 질병은 인구에서 제거될 수 있습니다.예를 들어 천연두 근절, 1977년 야생 폴리오 바이러스 3종 중 2종(2015년 2종, 1999년 마지막 보고 사례 이후, 2019년 3종,^[24] 2012년 마지막 보고 사례 이후)의 토종 감염 근절 인증.

무리 면역 수준은 q로 표시됩니다. 안정적인 상태를 위해 다음을 기억하십시오.

${\displaystyle R_{0}\cdot S=1.}$

결국.

${\displaystyle R_{0}={N}}={{mu N\operatorname {E}(T_{L})}{\mu N\operatorname {E}[\min(T_{L},T_{S})}}={\operatorname {E}}},{T_{T}}}}{\frac{operatorname{T_{T_{T}}}}}},$

대략적으로 다음과 같습니다.

$표시({style}{frac{operatorname{E}(T_{L})}{\operatorname{E}(T_{S})}=1+{\frac{\mu}}={frac{n}{v}).}$

S는 (1 - q)이 될 것입니다. q는 면역이 있는 모집단의 비율이고 q + S는 1과 같아야 합니다(이 단순화된 모델에서는 모든 사람이 민감하거나 면역이 됩니다).그러면:

$표시({style}) &R_{0}\cdot(1-q)=1,\\[6pt]&1-q=cdfrac{1}{R_{0}},\[6pt]&q=1-{\frac{1}{R_{0}}}}.\end{aligned}}}$

이것은 임계값 레벨입니다.집단 예방 접종 프로그램으로 인해 면역 개체의 비율이 이 수준을 초과하는 경우에만 전염성 사망이 발생합니다.

우리는 방금 임계 면역 임계값(표시된_c q)을 계산했습니다.인구에서 감염이 소멸되기 위해서는 출생 시(또는 출생 시)에 예방 접종을 받아야 하는 인구의 최소 비율입니다.

${\displaystyle q_{c}=1-{\frac {1}{R_{0}}}.}$

감염되지 않은 모집단 p의 최종 크기 분율은 다음과 같이 정의될 수 있기 때문입니다.

${\displaystyle \lim _{t\to \infty}S(t)=e^{-\int _{0}^{\infty}\dt(t)\colon(t)\,dt}=1-p.}$

이런 이유로,

${\displaystyle p=1-e^{-\int _{0}^{\infty}\colon I(t)\,dt}=1-e^{-R_{0}p}.}$

$({$을 해결하면 다음을 얻을 수 있습니다.

${\displaystyle R_{0}=displayfrac {-\discovery(1-p)}{p}}.}$

집단면역을 초과할 수 없는 경우

사용된 백신의 효과가 충분하지 않거나 필요한 적용 범위에 도달할 수 없는 경우 프로그램이 q를 초과하지_c 못할 수 있습니다.그러한 프로그램은 백신 접종을 받은 사람들을 질병으로부터 보호할 것이지만, 전염의 역학을 바꿀 수도 있습니다.

모집단 q의 비율(여기서 q_c < q)이 태어날 때 R > 1의₀ 감염에 대해 면역이 된다고 가정합니다.예방접종 프로그램은 R을 R로_q 변경합니다₀. 여기서

${\displaystyle R_{q}=R_{0}(1-q)}$

이러한 변화는 단순히 감염될 수 있는 감염 가능성이 인구에서 더 적기 때문에 발생합니다.R은_q 단순히₀ R에서 일반적으로 감염될 수 있는 것들을 뺀 것이지만 그들이 면역이 있기 때문에 지금은 그럴 수 없습니다.

이 낮은 기본 생식 수의 결과로, 백신을 맞지 않은 사람들에게서 A 감염의 평균 연령도 A 값으로_q 바뀔 것입니다.

R, A 및 L을 연결한₀ 관계를 상기합니다.기대 수명이 변경되지 않았다고 가정하면 다음과 같습니다.

${\displaystyle R_{q}=displayfrac {L}{A_{q}},}$

${\displaystyle A_{q}=tftfrac {L}{R_{q}}=tftfrac {L}{R_{0}(1-q)}.}$

하지만₀ R = L/A 그래서:

${\displaystyle A_{q}={(L/A)(1-q)}}={L(1-q)}={A}{1-q}}.}$

따라서 백신 프로그램은 평균 감염 연령을 높일 수 있으며, 백신을 접종하지 않은 개인은 백신 접종 그룹의 존재로 인해 감염력이 감소하게 됩니다.노인 인구에서 더 큰 임상적 심각성으로 이어지는 질병의 경우, 백신을 접종하지 않은 인구의 비율은 백신이 없는 경우보다 수명이 더 길어질 수 있습니다.

집단접종이 집단면역을 초과할 때

백신 프로그램이 한 모집단에서 면역 개체의 비율이 상당한 시간 동안 임계 임계값을 초과하게 하면 해당 모집단에서 감염병의 전염이 중단됩니다.만약 제거가 모든 곳에서 동시에 일어난다면, 이것은 근절로 이어질 수 있습니다.

제거

각각의 감염된 개체가 서로 미만으로 감염될 경우 발생하는 감염성 질병의 풍토병 전염 중단은 면역 개체의 비율을 중요한 면역 임계값 이상으로 유지하기 위해 백신 적용 범위를 유지함으로써 달성됩니다.

근절

감염원이 소멸되도록 동시에 모든 곳에서 제거(예: 천연두 및 진딧물).

신뢰성.

모형에는 단일 예측 대신 여러 결과를 동시에 검토할 수 있는 장점이 있습니다.모델은 사스, SARS-CoV-2,^[25] 돼지 독감, 메르스 및 ^[26]에볼라와 같은 과거 유행병에서 광범위한 수준의 신뢰성을 보여주었습니다.

참고 항목

레퍼런스

진일보한 내용

외부 링크

소프트웨어

• 모델-빌더:ODE 모델을 구축, 시뮬레이션 및 분석하는 대화형(GUI 기반) 소프트웨어.
• GLEaMviz Simulator: 전 세계에 퍼져있는 신흥 전염병의 시뮬레이션을 가능하게 합니다.
• STEM: Eclipse Foundation을 통해 제공되는 역학 모델링을 위한 오픈 소스 프레임워크.
• R 패키지 보안 감시:유행현상의 시간적, 시공간적 모델링 및 모니터링