케플러의 행성 운동 법칙

시리즈의 일부
아스트로다이나믹스
궤도역학
궤도 원소 압시스 근일점 논법 편심 성향 평균이상현상 궤도 마디 반장축 참 변칙
2체 궤도의 종류: 괴이한 짓 원궤도 타원 궤도 전이궤도 (Hohmann transfer orbit) 쌍타원궤도) 포물선 궤도 쌍곡 궤도 반지름 궤도 붕괴궤도
방정식 동역학적 마찰 탈출 속도 케플러 방정식 케플러의 행성 운동 법칙 공전주기 궤도속도 표면중력 비궤도 에너지 Vis-viva 방정식
천체역학
중력의 영향 중심 언덕구 섭동 세력권
N체 궤도 라그랑지안 점 (헤일로 궤도) 리사쥬 궤도 랴푸노프 궤도
엔지니어링 및 효율성
프리플라이트 엔지니어링 질량비 페이로드 분율 추진제 질량 분율 치올코브스키 로켓 방정식
효율성측도 중력 어시스트 오버트 효과
v t

천문학에서 요하네스 케플러가 1609년에서 1619년 사이에 발표한 케플러의 행성 운동 법칙은 태양 주위의 행성들의 궤도를 설명합니다. 이 법칙들은 니콜라우스 코페르니쿠스의 태양 중심 이론을 수정하여 원형 궤도와 에피사이클을 타원 궤도로 대체하고 행성 속도가 어떻게 변하는지를 설명했습니다. 세 가지 법률은 다음과 같습니다.^[1][2]

1. 행성의 궤도는 두 초점 중 하나에 태양이 있는 타원입니다.
2. 행성과 태양을 연결하는 선분은 동일한 시간 간격 동안 동일한 영역을 쓸어냅니다.
3. 행성의 궤도 주기의 제곱은 궤도의 반장축 길이의 세제곱에 비례합니다.

행성들의 타원 궤도는 화성 궤도의 계산으로 표시되었습니다. 이를 통해 케플러는 태양에서 멀리 떨어진 천체를 포함한 태양계의 다른 천체들도 타원 궤도를 가지고 있다고 추론했습니다. 두 번째 법칙은 행성이 태양에 더 가까울 때 더 빨리 이동한다는 것을 확립하는 데 도움이 됩니다. 세 번째 법칙은 행성이 태양에서 멀어질수록 궤도 속도가 느려지고, 그 반대의 경우도 마찬가지라고 표현합니다.

아이작 뉴턴은 1687년 케플러와 같은 관계가 자신의 운동 법칙과 만유인력 법칙의 결과로 태양계에 적용된다는 것을 보여주었습니다.

더 정확한 역사적 접근은 Astronomia nova와 Epitome Astronomiae Copernicanae에서 발견됩니다.

코페르니쿠스와의 비교

요하네스 케플러의 법칙은 코페르니쿠스의 모델을 향상시켰습니다. 코페르니쿠스에 따르면:^[3][4]

1. 행성 궤도는 에피사이클이 있는 원입니다.
2. 태양은 대략 궤도의 중심에 있습니다.
3. 주 궤도에 있는 행성의 속도는 일정합니다.

행성들이 태양 주위를 돈다는 말은 옳았지만, 코페르니쿠스는 그들의 궤도를 정의하는 것은 틀렸습니다. 케플러는 단순한 기하학을 넘어 우주에서의 움직임에 대한 물리적 설명을 소개하면서 행성의 궤도를 다음과 같이 정확하게 정의했습니다.^{[1][2][5]: 53–54}

1. 행성 궤도는 에피사이클이 있는 원이 아니라 타원입니다.
2. 태양은 중심이 아니라 타원 궤도의 초점에 있습니다.
3. 궤도상에 있는 행성의 선속도 각속도도 일정하지 않지만 (역사적으로 각운동량의 개념과 밀접하게 연결된) 영역속도는 일정합니다.

지구 궤도의 이심률은 3월 분점에서 9월 분점까지의 시간을 약 186일 정도로, 9월 분점에서 3월 분점까지의 시간과 약 179일 정도로 동일하게 만듭니다. 지름은 궤도를 같은 부분으로 자를 것이지만, 지구 적도와 평행한 태양을 통과하는 평면은 186 대 179의 비율로 면적을 두고 궤도를 두 부분으로 자를 것이므로, 지구 궤도의 이심률은 대략

${\displaystyle e\approx {\frac {\pi}{4}}{\frac {186-179}{186+179}}\approx 0.015,}$

올바른 값(0.016710218)에 가깝습니다. 이 계산의 정확성을 위해서는 선택한 두 날짜가 타원 궤도의 단축을 따라 있어야 하며, 각 절반의 중간 지점이 장축을 따라 있어야 합니다. 여기서 선택한 두 날짜가 분점이므로 지구가 태양에 가장 가까운 날짜인 근일점이 동지에 해당할 때 이는 정확할 것입니다. 현재 근일점은 1월 4일로 12월 21일이나 22일의 동지에 상당히 가깝습니다.

명명법

현재 케플러의 작업 공식이 정착된 형태를 갖추는 데 거의 2세기가 걸렸습니다. 1738년에 출판된 볼테르의 뉴턴 철학(뉴턴 철학의 요소)은 "법칙"이라는 용어를 사용한 최초의 출판물입니다.^[6][7] 케플러에 관한 글에서 천문학자들의 전기 백과사전(620쪽)은 이러한 발견에 대한 과학적 법칙들의 용어들이 적어도 조셉 드 랄랑드 시대부터 최신이라고 말합니다.^[8] 세 번째 법칙을 추가하여 세 가지 법칙을 구성한 것은 케플러(1814)의 천문학적 발견에 대한 설명에서 로버트 스몰의 설명이었습니다.^[9] 스몰은 또한 역사에 반하여 이것들은 귀납적 추론에 기초한 경험적 법칙이라고 주장했습니다.^[7][10]

게다가, "케플러의 제2법칙"의 현재 사용법은 잘못된 이름입니다. 케플러는 정성적인 의미에서 "거리 법칙"과 "면적 법칙"이라는 두 가지 버전을 가지고 있었습니다. "면적 법칙"은 세 개의 집합에서 제2법칙이 된 것입니다. 그러나 케플러 자신은 그런 방식으로 특권을 부여하지 않았습니다.^[11]

역사

케플러는 1609년에 타이코 브라헤의 천체 관측을 분석하여 행성 운동에 관한 그의 첫 번째 두 법칙을 발표했습니다.^{[12][13][14][15][5]: 53} 케플러의 세 번째 법칙은 1619년에 발표되었습니다.^[16][14] 케플러는 원형 궤도를 요구하는 태양계의 코페르니쿠스 모델을 믿었지만, 브라헤의 매우 정밀한 관측과 화성의 궤도에 대한 원형 적합성을 조화시킬 수 없었습니다. 공교롭게도 화성은 수성을 제외한 모든 행성 중 이심률이 가장 높습니다.^[17] 그의 첫 번째 법칙은 이 발견을 반영했습니다.

1621년, 케플러는 그의 세 번째 법칙이 목성의 가장 밝은 네 개의 위성에 적용된다고 언급했습니다.^{[Nb 1]} 고드프로이 웬델린도 1643년에 이 관측을 했습니다.^{[Nb 2]} 두 번째 법칙은 1664년에 출판된 책에서 니콜라오스 메르카토르가 주장했지만, 1670년에는 그의 철학적 거래가 찬성했습니다.^[18][19] 세기가 진행됨에 따라 그것은 더 널리 받아들여지게 되었습니다.^[20] 독일에서의 반응은 뉴턴의 원리가 출판되고 기본적으로 코페르니쿠스로 받아들여졌던 1688년과 케플러에 대한 고트프리트 라이프니츠의 연구가 출판된 1690년 사이에 눈에 띄게 변화했습니다.^[21]

뉴턴은 두 번째 법칙이 중력의 역제곱 법칙에 특별하지 않다는 것을 이해한 것으로 인정받았는데, 이는 그 법칙의 방사상 특성의 결과이며, 반면 다른 법칙들은 인력의 역제곱 형태에 의존합니다. 칼 ^[22]룬지와 빌헬름 렌츠는 나중에 행성 운동의 위상 공간에서 대칭 원리를 발견했는데, 이는 뉴턴 중력의 경우 제1법칙과 제3법칙을 설명하며, 각운동량의 보존은 제2법칙의 회전 대칭을 통해 이루어지는 것입니다.

수식

법칙의 적용을 받는 행성의 운동학에 대한 수학적 모델은 광범위한 추가 계산을 가능하게 합니다.

제1법칙

모든 행성의 궤도는 태양이 두 초점 중 하나에 있는 타원입니다.

수학적으로 타원은 다음 공식으로 나타낼 수 있습니다.

${\displaystyle r={\frac {p}{1+\varepsilon \,\cos \theta}}}$

여기서 p ${\displaystyle$ p$}$는 반-라투스 직장, ε은 타원의 이심률, r은 태양에서 행성까지의 거리, θ은 태양에서 볼 때 행성의 가장 가까운 접근에서 행성의 현재 위치까지의 각도입니다. 따라서 (r, θ)는 극좌표입니다.

타원 0 < ε < 1의 경우, 제한된 경우 ε = 0의 경우, 궤도는 태양이 중심에 있는 원입니다(즉, 편심이 0인 경우).

θ = 0°, 근일점에서 거리가 최소입니다.

${\displaystyle r_{\min}={\frac {p}{1+\varepsilon}}}$

θ = 90° 및 θ = 270°에서 거리는 p $displaystyle$ p}와 $같습니다.$

θ = 180°, 원뿔에서 거리는 최대입니다(정의에 따라 원뿔은 항상 – 근일점 + 180°).

${\displaystyle r_{\max}={\frac {p}{1-\varepsilon}}}$

반 장축 a는 r과_min r 사이의_max 산술 평균입니다.

${\displaystyle {\begin{aligned}a&={\frac {r_{\max}+r_{\min}}{2}}\[3pt]a&={\frac {p}{1-\varepsilon ^{2}}\end{aligned}}}$

반단축 b는 r과_min r 사이의_max 기하평균입니다.

${\displaystyle {\begin{aligned}b&={\sqrt {r_{\max }r_{\min}}}\\[3pt]b&={\frac {p}{\sqrt {1-\varepsilon ^{2}}\end{aligned}}$

반라투스 직장 p는 r과_min r 사이의_max 조화 평균입니다.

${\displaystyle {\begin{aligned}p&=\left ({\frac {r_{\max }^{-1}+r_{\min }^{-1}}\r}\right)^{-1}\pa&=r_{\max }r_{\min }=b^{2}\,\end{aligned}}}$

편심 ε는 r과 r 사이의 변동 계수입니다.

${\displaystyle \varepsilon ={\frac {r_{\max }-r_{\min }}{r_{\max }+r_{\min }}}.}$

타원의 면적은

${\displaystyle A=\piab\,}$

원의 특수한 경우는 ε = 0이므로 r = p = r = a = b 및 A = πr이 됩니다.

제2법칙

행성과 태양을 잇는 선은 동일한 시간 간격 동안 동일한 면적을 쓸어냅니다.^[23]

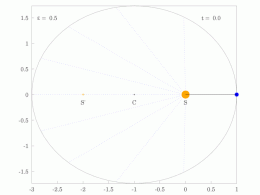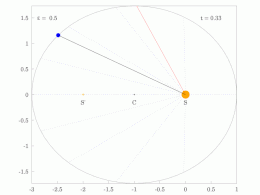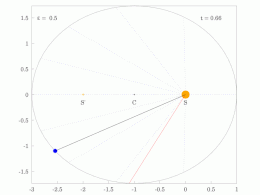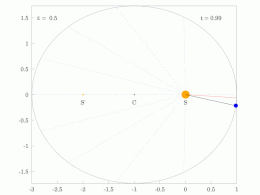
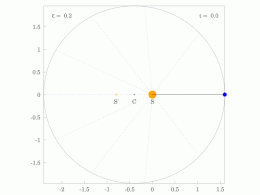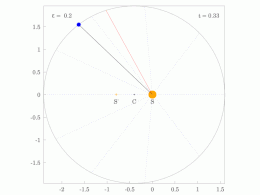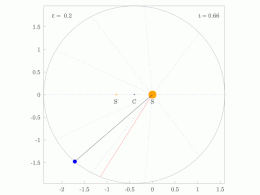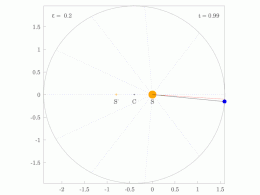
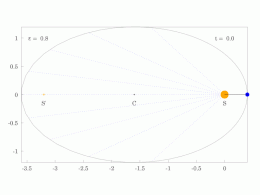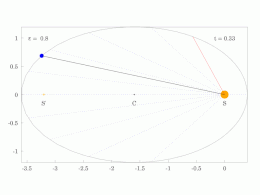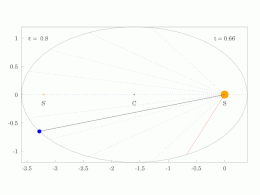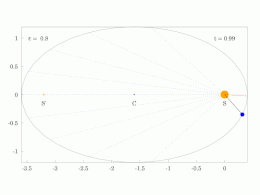
타원 궤도에 있는 행성의 궤도 반지름과 각속도는 다양할 것입니다. 이것은 애니메이션에서 보여집니다: 행성은 태양에 가까울 때 더 빠르게 이동하고, 태양에서 멀어질 때 더 느리게 이동합니다. 케플러의 제2법칙에 따르면 청색 영역은 일정한 면적을 가지고 있습니다.

작은 ${\displaystyle \mathrm{시간}}$ dt ${\displaystyle dt}$에서 행성은 $기준선$ ${\displayr}$과 높이 ${\displaystyle rd}$θ ${\displayr$\,d$\$theta} 및 $\mathrm{면적}$ d $A$ =$\mathrm{12}$ ⋅ r ⋅ rd θ${\textstyle dA$ = {\$frac$ {1}{2}}\cdotr\cd\theta}를 갖는 작은 삼각형을 쓸어 버립니다. 따라서 일정한 면적 속도는

타원 궤도로 둘러싸인 영역은$$π a b ${\displaystyle$piab}입니다. 따라서$주기$ T ${\displaystyle$ T}는 다음을 만족합니다.

${\displaystyle T\cdot {\frac {r^{2}}{2}}{\frac {d\theta }{dt}}=\pi ab}$

그리고 태양 주위의 행성의 평균적인 움직임.

${\displaystyle n={\frac {2\pi}{T}}$

만족스러운

${\displaystyle r^{2}\,d\theta =abn\,dt.}$

그래서.

다양한 이심률을 가진 행성들의 궤도.

로우	높은
태양 주위를 원형 궤도로 도는 행성 (e=0.0)	e=0.5인 궤도로 태양 주위를 도는 행성
e=0.2인 궤도로 태양 주위를 도는 행성	e=0.8인 궤도로 태양 주위를 도는 행성
적색 광선은 일정한 각속도로 회전하며 행성과 동일한 궤도 시간 주기인 $T$ = ${\$displaystyle T = 1}로 회전합니다. S: 1차 초점에서의 태양, C: 타원의 중심, S': 2차 초점. 각 경우에 표시된 모든 섹터의 면적은 동일합니다.

제3법칙

물체의 궤도 주기의 제곱과 궤도의 반장축의 세제곱의 비율은 같은 기본 궤도를 도는 모든 물체에 대해 동일합니다.

이것은 태양으로부터 행성들의 거리와 그들의 궤도 주기 사이의 관계를 포착합니다.

케플러는 1619년에^[16] 그가 "구들의 음악"으로 본 것을 정확한 법칙에 따라 결정하고 그것을 음악적인 기보법으로 표현하기 위한 고된 시도로 이 세 번째 법칙을 발표했습니다.^[24] 그래서 이것은 조화 법칙으로 알려졌습니다.^[25]

뉴턴의 중력 법칙(1687년 출판)을 사용하면 구심력을 중력과 같게 설정하여 원궤도의 경우 다음과 같은 관계를 알 수 있습니다.

${\displaystyle mr\omega ^{2}=G{\frac {mM}{r^{2}}}}$

그런 다음 각속도 ω을 궤도$주기$ T ${\displaystyle${T}로 표현한 다음 재배열하면 케플러의 제3법칙이 나타납니다.

${\displaystyle mr\left({\frac {2\pi }{T}}\right)^{2}=G{\frac {mM}{r^{2}}}\rightarrow T^{2}=\left({\frac {4\pi ^{2}}{GM}}\right)r^{3}\rightarrow T^{2}\propto r^{3}}$

더 자세한 유도는 원이 아닌 일반적인 타원 궤도로 수행할 수 있으며, 질량이 큰 궤도 대신 질량 중심을 공전할 수 있습니다. 따라서 원형 반지름 $r{\displaystyle }$ ${\displaystyle$ r$\}$을 반장축인$${\$displaystyle$ a$\}$로 대체하고 한 질량의 타원 상대 운동을 다른 질량에 $대해{\displaystyle }$ {\$displaystyle$ $}$을 M${\displaystyle }$+ ${\displaystyle m}$ ${\displaystyle$ $M$$+m}$으로 대체합니다$.$ 그러나 행성의 질량이 태양보다 훨씬 작기 때문에 이 보정은 종종 무시됩니다. 전체 대응 공식은 다음과 같습니다.

${\displaystyle {\frac {a^{3}}{T^{2}}}={\frac {G(M+m)}{4\pi ^{2}}}\approx {\frac {GM}{4\pi ^{2}}}\approx 7.496\times 10^{-6}{\frac {{\text{AU}}^{3}}{{\text{days}}^{2}}{\text{ is constant}}}$

where ${\displaystyle M}$ is the mass of the Sun, ${\displaystyle m}$ is the mass of the planet, ${\displaystyle G}$ is the gravitational constant, ${\displaystyle T}$ is the orbital period and ${\displaystyle a}$ is the elliptical semi-major axis, and ${\displaystyle {\text{$$AU}}}$은 지구에서 태양까지의 평균 거리인 천문 단위입니다.

테이블

다음 표는 케플러가 자신의 법칙을 경험적으로 도출하기 위해 사용한 데이터를 보여줍니다.

케플러(1618)가 사용한 데이터

행성	평균거리 태양까지(AU)	기간 (일)	${\$$T^{2$10AU-63/일2)
수성.	0.389	87.77	7.64
금성	0.724	224.70	7.52
지구	1	365.25	7.50
화성	1.524	686.95	7.50
목성	5.20	4332.62	7.49
토성	9.510	10759.2	7.43

이 패턴을 발견한 케플러는 다음과 같이 썼습니다.^[26]

처음엔 꿈을 꾸고 있다고 믿었는데... 그러나 어떤 두 행성의 주기 시간 사이에 존재하는 비율이 평균 거리의 3/2제곱의 비율이라는 것은 절대적으로 확실하고 정확합니다.

— translated from Harmonies of the World by Kepler (1619)

비교를 위해 다음은 현대적인 추정치입니다.

현대 데이터(Wolfram Alpha Knowledge Base 2018)

행성	반장축(AU)	기간(일)	${\$$T^{2$10AU-63/일2)
수성.	0.38710	87.9693	7.496
금성	0.72333	224.7008	7.496
지구	1	365.2564	7.496
화성	1.52366	686.9796	7.495
목성	5.20336	4332.8201	7.504
토성	9.53707	10775.599	7.498
천왕성	19.1913	30687.153	7.506
해왕성	30.0690	60190.03	7.504

행성가속도

아이작 뉴턴은 그의 철학 æ 자연 원리 수학에서 케플러의 제1법칙과 제2법칙에 따라 움직이는 행성의 가속도를 계산했습니다.

1. 가속도의 방향은 태양 쪽입니다.
2. 가속도의 크기는 태양으로부터의 거리의 제곱에 반비례합니다.

이것은 태양이 행성 가속의 물리적인 원인일 수도 있다는 것을 암시합니다. 그러나 뉴턴은 자신의 프린시피아에서 힘을 물리적인 것이 아니라 수학적인 관점에서 생각하고, 따라서 도구주의적인 관점을 취한다고 말합니다.^[27] 게다가, 그는 중력에 원인을 부여하지 않습니다.^[28]

뉴턴은 행성에 작용하는 힘을 질량과 가속도의 곱으로 정의했습니다. 그래서.

1. 모든 행성은 태양을 향해 끌립니다.
2. 행성에 작용하는 힘은 행성의 질량에 정비례하고 태양으로부터의 거리의 제곱에 반비례합니다.

태양은 비 대칭적인 역할을 하는데, 이는 정당하지 않습니다. 그래서 그는 뉴턴의 만유인력 법칙에서 다음과 같이 가정했습니다.

1. 태양계의 모든 물체는 서로를 끌어당깁니다.
2. 두 물체 사이의 힘은 질량의 곱에 정비례하고 두 물체 사이의 거리의 제곱에 반비례합니다.

행성들은 태양에 비해 질량이 작기 때문에 궤도들은 대략 케플러의 법칙과 일치합니다. 뉴턴의 모델은 케플러의 모델을 개선하여 실제 관측치에 더 정확하게 적합합니다. (양체 문제 참조)

아래는 케플러의 제1법칙과 제2법칙에 따라 움직이는 행성의 가속도를 구체적으로 계산한 것입니다.

가속도 벡터

태양중심 관점에서 행성 $r$ = ${\displaystyle r}$ $^$ ${\displaystyle \mathbf {r}$ = r{\hat {\mathbf {r}}}에 대한 벡터를 고려합니다. 여기서 r {\displaystyle r}은 행성까지의 거리이고 r^ {\hat {\mathbf {r}}은 행성을 가리키는 단위 벡터입니다.

여기서 θ ^ ${\displaystyle${\$boldsymbol$ {\theta$}}}$는 방향이 r^ {\displaystyle {\hat {\mathbf {r}}}의 90도 반시계 방향인 단위 벡터이고, θ {\displaystyle \theta}는 극각이고, 여기서 변수 위의 점은 시간에 대한 미분을 의미합니다.

위치 벡터를 두 번 미분하여 속도 벡터와 가속도 벡터를 구합니다.

그렇게

반경 가속도가 있는 곳에서 그리고 가로 방향 가속도는

역제곱 법칙

케플러의 제2법칙은

일정합니다.

θ$${\displaystyle $a_{\$theta}}의 횡단 가속도는 0입니다.

그래서 케플러의 제2법칙을 따르는 행성의 가속도는 태양을 향합니다.

반경 방향 가속도는$${\$displaystyle a_{\text{$r}}입니다.

케플러의 제1법칙에 따르면 궤도는 다음과 같은 식으로 설명됩니다.

시간에 대한 차별화

아니면

한번 더 차별화하기

반경 가속도$${\$displaystyle a_{\text${r}}이$($가) 만족합니다.

타원의 방정식을 대입하면

${\displaystyle {b2}^{}}$ = ${\displaystyle \mathrm{pa}}${\displaystyle b^{2}= pa} 관계는 간단한 최종 결과를 제공합니다.

이것은 케플러의 제1법칙과 제2법칙을 따르는 행성의 $가속도$ $벡터$ r ¨ {\$displaystyle \mathbf {\$ddot ${$r}}가 역제곱 법칙을 만족한다는 것을 의미합니다.

어디에 는 상수이고 r${\displaystyle \stackrel{}{}}$ ${\$은 태양에서 행성을 향하는 단위 벡터이고 $r{\displaystyle }$ ${\$은 행성과 태양 사이의 거리입니다.

평균 운동 $n$ = ${\displaystyle 2}$π T {\displaystyle n = ${\$frac {2\pi}{T}}이며, 여기서 T {\displaystyle T}는 주기이므로 케플러의 제3법칙에 따르면 α {\displaystyle \alpha}는 모든 행성에 대해 동일한 값을 갖습니다. 그래서 행성 가속도에 대한 역제곱 법칙은 태양계 전체에 적용됩니다.

역제곱 법칙은 미분 방정식입니다. 이 미분방정식의 해는 그림과 같이 케플러 운동을 포함하지만, 궤도가 쌍곡선 또는 포물선이거나 직선인 운동도 포함합니다. (케플러 궤도 참조)

뉴턴의 중력 법칙

뉴턴의 제2법칙에 의해 행성에 작용하는 중력은 다음과 같습니다.

$여기$서 m ${\displaystyle {\text{행성}}_{}}$ ${\$은 행성의 질량이고 $\alpha {\displaystyle }$ ${\displaystyle \alpha}$은 태양계의 모든 행성에 대해 동일한 값을$$ 갖습니다. 뉴턴의 제3법칙에 의하면 태양은 같은 크기의 힘에 의해 행성으로 끌립니다. 힘은 행성의 질량에 비례하기 때문에 대칭적인 고려하에 그것은 또한 태양, m 태양의 질량에 비례해야 합니다$.$ $m{\displaystyle {}_{}}$ ${\displaystyle {\text{태양}}_{}}$ {\$displaystyle m_{\text}$$태양$ 그래서.

$여기$서 G ${\displaystyle$ G$}$는 중력 상수입니다.

뉴턴의 법칙에 따르면 태양계 차체 번호 i의 가속도는 다음과 같습니다.

$여기$서 ${\displaystyle {mj}_{}}$ ${\$는 물체 j의 질량이고, ${\displaystyle {\mathrm{rj}}_{}}$ ${\$는 물체 i와 물체 j 사이의 거리이며, ${\displaystyle r_{\stackrel{}{}}}$i {\$displaystyle$ {\$hat${\$mathbf$ {$r}}_{$ij$}}$는 물체 i에서 물체 j로 향하는 단위 벡터이며$$, 벡터 합은 태양계의 모든 물체에 걸쳐 있습니다. i 그 자체 말고도.

태양계에 지구와 태양의 두 물체만 있는 특별한 경우, 가속도는

그것은 케플러 운동의 가속도입니다. 그래서 이 지구는 케플러의 법칙에 따라 태양 주위를 돕니다.

만약 태양계의 두 물체가 달과 지구라면 달의 가속도는

그래서 이 근사식에서 달은 케플러의 법칙에 따라 지구 주위를 돌게 됩니다.

3체의 경우 가속도는

이 가속도들은 케플러 궤도들의 가속도들이 아니며, 삼체 문제는 복잡합니다. 그러나 케플러 근사는 섭동 계산의 기초가 됩니다. (달 이론 참조)

시간의 함수로서의 위치

케플러는 시간의 함수로서 행성의 위치를 계산하기 위해 그의 두 가지 첫 번째 법칙을 사용했습니다. 그의 방법은 케플러 방정식이라고 불리는 초월 방정식의 해를 포함합니다.

근일점 이후 시간 t에 대한 행성의 태양중심 극좌표(r, θ)를 계산하는 절차는 다음 다섯 단계입니다.

1. 평균 움직임 n = (2 π rad)/P를 계산합니다. 여기서 P는 주기입니다.
2. 평균 변칙 M = nt를 계산합니다. 여기서 t는 근일점 이후의 시간입니다.
3. 케플러 방정식을 풀어서 편심 이상 E를 계산합니다.
   $${\displaystyle M=E-\varepsilon \sin E,}$$

   
   여기서$$ε ${\displaystyle$ \varepsilon}은(는) 이심률입니다.
4. 방정식을 풀어서 실제 이상 θ를 계산합니다.
   $${\displaystyle (1-\varepsilon )\tan ^{2}{\frac {\theta }{2}}=(1+\varepsilon )\tan ^{2}{\frac {E}{2}}}$$

   
5. 태양 중심 거리 r을 계산합니다.
   $${\displaystyle r=a(1-\varepsilon \cos E),}$$

   
   $여기$서 ${\displaystyle$ a$}$는 반장축입니다.

이제 위치 극좌표(r, θ)를 데카르트 $벡터$ p =${\displaystyle }$r ⟨ 코스$$⁡ θ, sin${\displaystyle }$⁡ θ ⟩ {\displaystyle \mathbf {p} = r\left\lang \cos {\theta},\sin {\theta}\right\rangle }로 쓸 수 있으며 데카르트 속도 벡터는 v = μar ⟨ - sin ⁡ E,${\displaystyle \sqrt{1}}$-$ε$ 2 c${\displaystyle \sqrt{\mathrm{o}}}$s$⁡$E ⟩ {\displaystyle \$mathbf {$ {\$frac${\$sqrt {\mu a}}$ {$r}\le$ang -\sin {$E},$ {\$sqrt {1-\varepsilon$2}}\$cos${E}\$right\rangle },$ 여기서 μ {\displaystyle \mu}는 표준 중력 매개변수입니다.

원형 궤도의 중요한 특수한 경우인 ε =0은 θ =E=M을 제공합니다. 균일한 원형 운동은 정상적인 것으로 간주되었기 때문에 이 운동에서 벗어난 것은 비정상적인 것으로 간주되었습니다.

이 절차의 증명은 아래와 같습니다.

평균 변칙, M

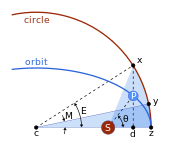
케플러 문제는 타원 궤도를 가정한 것으로, 네 가지 점을 가정한 것입니다.

• s 태양(타원의 한 초점에서);
• 근일점을 보다
• 타원의 중심을 보다
• 세상을 떠나다

그리고.

• ${\displaystyle a}$ = $,$ {\displaystyl${\displaystyle e}$ a = cz,} 중심과 근일점 사이의 거리, 반장축,
• ${\displaystyle \frac{\epsilon }{}}$ =${\displaystyle }$c$$a, ${\$displaystyle \varepsi${\displaystyle l}$on ={ cs \over a}} 이심률,
• ${\displaystyle b}$ = ${\displaystyle a}$ - ε 2, {\displaystyl${\displaystyle e}$ b =a{\sqrt {1-\varepsilon ^{2}}, 반소축,
• ${\displaystyle r}$ = $,$ {\displa${\displaystyle y}$ r = sp,} 태양과 행성 사이의 거리.
• ${\displaystyle \theta }$ ${\displaystyle \mathrm{=}}$ $∠$ zsp, {\displaystyle \th${\displaystyle e}$ta =\angle zsp,} 태양에서 볼 때 행성으로 가는 방향, 즉 진정한 변칙입니다.

문제는 근일점 t 이후부터 행성의 극좌표(r, θ)를 계산하는 것입니다.

단계별로 해결됩니다. 케플러는 장축이 있는 원을 지름으로 간주했고,

• ${\displaystyle x,}$ ${\displaystyle$ x$,}$ 보조 원에 대한 행성의 투영$$
• ${\displaystyle y,}$ ${\displaystyle y,}$ 섹터 영역 zcy와 zsx가 같은 원 위의 점$$,
• ${\displaystyle M}$ = ${\displaystyle \angle }$zcy, {\displaystyl${\displaystyle e}$ M =\angle zcy,} 평균 이상입니다.

섹터 영역은 ${\displaystyle \mathrm{zsp}}$ = $ba$⋅ zs x. {\displaystyle zsp = {\frac {b}{a}}\cdot zsx.}와 관련이 있습니다.

원형 섹터 영역 ${\displaystyle \mathrm{zcy}}$ = ${\displaystyle a}$ $2M.$ {\displaystyle zcy = {\frac {a^{2$}$M}{2}}.

그 지역은 근일점 이후로 휩쓸려갔고,

근일점 이후 시간에 비례하는 케플러의 제2법칙에 의한 것입니다. 따라서 평균 변칙 M은 근일점 t 이후 시간에 비례합니다. 여기서 n은 평균 운동입니다.

편심 이상, E

평균 이상 M이 계산되면 실제 이상 θ을 계산하는 것이 목표입니다. 그러나 θ = f(M) 함수는 기본이 아닙니다. 케플러의 해결책은

중심에서 볼 수 있는 x, 중간 변수로서 편심 변칙, 그리고 먼저 아래 케플러 방정식을 풀어서 M의 함수로서 E를 계산한 다음 편심 변칙 E로부터 실제 변칙 θ을 계산합니다. 자세한 내용은 다음과 같습니다.

a²/2로 나누면 케플러 방정식이 나옵니다.

이 식은 M을 E의 함수로 제공합니다. 주어진 M에 대하여 E를 결정하는 것은 역의 문제입니다. 반복적인 수치 알고리즘이 일반적으로 사용됩니다.

편심 이상 E를 계산한 다음, 다음 단계는 실제 이상 θ을 계산하는 것입니다.

그러나 참고: 타원의 중심을 기준으로 하는 직각좌표는 (cos E, bin E)

태양을 기준으로 (좌표 (c,0) = (ae,0)), r = (cos E – ae, bin E)

실제 변칙은 arctan(rx)이고, r의 크기는 √r · r입니다.

진정한 변칙, ,

그림에서 다음과 같이 기록합니다.

하도록

${\displaystyle$ a$}$로 나누고$$ 케플러의 제1법칙에서 삽입

갖기 위해

결과는 편심 이상 E와 실제 이상 θ 사이의 사용 가능한 관계입니다.

삼각형 항등식에 대입하면 계산적으로 더 편리한 형태가 나타납니다.

얻다

1 + ε을 곱하면 결과가 나옵니다.

이것은 궤도에서 시간과 위치 사이의 연결의 세 번째 단계입니다.

거리, r

네 번째 단계는 케플러의 제1법칙에 의해 실제 변칙 θ으로부터 태양 중심 거리 r을 계산하는 것입니다.

θ와 E 사이의 위 관계를 이용하여 거리 r에 대한 최종 방정식은 다음과 같습니다.

참고 항목

해설주

인용

일반 서지학

• 케플러의 생애는 523-627쪽에 요약되어 있고, 그의 대작인 Harmonice Mundi (세계의 조화)의 5권은 "거인들의 어깨에" 635-732쪽에 다시 인쇄되어 있습니다. 물리학과 천문학의 위대한 작품(코페르니쿠스, 케플러, 갈릴레오, 뉴턴, 아인슈타인의 작품). Stephen Hawking, Ed. 2002 ISBN 0-7624-1348-4
• 케플러의 행성 운동 제3법칙의 유도는 공학 역학 수업의 표준 주제입니다. 예를 들어 의 161~164페이지를 참조하십시오.
• Murray and Dermott, Solar System Dynamics, Cambridge University Press 1999, ISBN 0-521-57597-4
• V. I. 아놀드, 고전역학의 수학적 방법, 2장. Springer 1989, ISBN 0-387-96890-3

외부 링크

• B.Surendranath Reddy; 케플러의 법칙 애니메이션: Wayback Machine에서 애플릿 아카이브 2013-10-06
• 물리학 스택 익스체인지의 "케플러 법칙의 파생" (뉴턴의 법칙에서).
• Crowell, Benjamin, Light and Matter, 미적분학을 사용하지 않고 제1법칙의 증명을 제공하는 온라인 책 (섹션 15.7 참조)
• David McNamara와 Gianfranco Vidali, Kepler의 제2법칙 – Java Interactive Tutorial, https://web.archive.org/web/20060910225253/http ://www.phy.syr.edu/courses/java/mc_html/kepler.html, 케플러의 제2법칙에 대한 이해를 돕는 대화형 Java 애플릿.
• 오디오 – 케인/게이 (2010) 천문학, 요하네스 케플러와 그의 행성 운동 법칙 캐스팅
• 테네시 대학의 학과. 물리학과 천문학: 요하네스 케플러의 천문학 161쪽: 행성운동의 법칙[1]
• 케플러와 동등한 수준: 상호작용 모델 [2] 웨이백 머신에서 아카이브된 2008-12-26
• 케플러의 제3법칙: 상호작용 모델 [3] 웨이백 머신에서 아카이브된 2008-12-26
• 태양계 시뮬레이터(대화형 애플릿)
• 케플러와 그의 법칙, 데이비드 P의 교육용 웹페이지. 스턴
• 유튜브 태양중심모형과 케플러의 행성운동 법칙 - 케플러의 행성운동 3법칙과 발견의 역사적 맥락을 설명하고 시각화한 영상