뉴턴 폴리곤

이 글에는 여러 가지 문제가 있다. 이 문제를 개선하거나 대화 페이지에서 토의하십시오. (이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "뉴턴 폴리곤" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2008년 3월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) 이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다. 기술 세부 정보를 제거하지 않고 비전문가가 이해할 수 있도록 개선하십시오.(2021년 10월) (이 템플릿 메시지 제거 방법 및 시기 학습) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

수학에서 뉴턴 폴리곤은 국소 분야에 대한 다항식의 행동을 이해하는 도구다.^{[disputed (for: it applies to polynomials with polynomial coefficients) – discuss]}

원래의 경우, 국지적인 관심 분야는 불확정 X의 공식 Laurent 시리즈 분야,^{[disputed (for: in the original case, Laurent series were not invented nor used implicitly) – discuss]} 즉 공식 파워 시리즈 링의 분수 분야였다.

K[X],

K가 실제 숫자 또는 복잡한 숫자 필드인 K에 대해. 이것은 푸이섹스 확장에 관해서는 여전히 상당한 효용이다. 뉴턴 폴리곤은 선행 용어를 이해하는 데 효과적인 장치다.

AX^r

등식에 대한 파워 시리즈 확장 솔루션

P(F(X)) = 0

여기서 P는 K[X]에 계수가 있는 다항식, 즉 암묵적으로 정의된 대수함수인 다항식이다. 여기서의 지수 r은 선택한 분기에 따라 특정 합리적인 숫자로, 솔루션 자체는 파워 시리즈로,

K[Y]

분기에 해당하는 분모 d에 대해 Y = X로^1/d 표시한다. 뉴턴 폴리곤은 d 계산에 효과적이고 알고리즘적인 접근법을 제공한다.

p-adic 숫자의 도입 이후, 뉴턴 폴리곤은 지역 분야의 래미화 문제, 그리고 따라서 대수적 숫자 이론에서도 마찬가지로 유용하다는 것을 보여주었다. 뉴턴 폴리곤은 타원곡선 연구에도 유용했다.

정의

priori는 밭 위에 다항식을 주어, 뿌리가 있다고 가정할 때 뿌리의 행동을 알 수 없을 것이다. 뉴턴 폴리곤은 뿌리의 행동에 대한 연구를 위한 하나의 기법을 제공한다.

$K{\displaystyle }$ ${\displaystyle K}$을(를) 이산 평가 $V{\displaystyle {}_{}}$ ${\displaystyle K_{}}$ ${\$를 포함하는 로컬 필드로 설정하고$$$$

${\displaystyle f(x)=a_{n}x^{n}+\cdots +a_{1}x+a_{0}\\in K[x]}$

${\displaystyle 0_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle \mathrm{n}}$ ${\displaystyle {}_{}}$ 0 ${\displaystyle a_{0}a_{n}\neq$ 0$}$을(를) 사용하여$$. 그 후 $f{\displaystyle }$ ${\displaystyle f}$의 뉴턴 폴리곤은 점 집합의 하단 볼록 선체로 정의된다$$.

${\displaystyle P_{i}=\left(i,v_{K})(a_{i}\right),}$

${\displaystyle i_{}}$= ${\displaystyle 0}$ ${\displaystyle a_{i}=0}$을(를) 사용하여 점을 무시한 채 기하학적으로 재작성하여 이 모든 점 P를_i xy-plane에 표시하십시오$.$ 점 지수가 왼쪽에서 오른쪽으로 상승한다고 가정합시다(P는₀ 가장 왼쪽, P는_n 가장 오른쪽). 그런 다음 P에서₀ 시작하여 Y축과 평행하게 직선으로 아래쪽으로 광선을 그리고 이 광선이 P 지점에_k1 닿을 때까지(필수 P는₁ 아님) 시계 반대 방향으로 회전시킨다. 여기서 광선을 깨뜨려라. 이제_k1 P에서 두 번째 광선을 Y축과 평행하게 아래로 그리고 이 광선이 P_k2 지점에 닿을 때까지 시계 반대 방향으로 회전시킨다. 공정이 P_n 지점에 도달할 때까지 계속한다; 결과 폴리곤(P₀, P_k1, P_k2, ..., P, P_kmn)은 뉴턴 폴리곤이다.

이 과정을 보다 직관적으로 볼 수 있는 또 다른 방법은 다음과 같다: 모든₀ 점 P, ..., P를_n 둘러싼 고무 밴드를 생각해 보십시오. 밴드가 일부 점들에 의해 아래쪽에 고착되도록 밴드를 위로 뻗으십시오(점들은 못처럼 작용하며 부분적으로 xy 평면에 박혀 있다). 뉴턴 폴리곤의 정점은 바로 그러한 점들이다.

이에 대한 깔끔한 도표는 JWS Cassels, LMS 학생 텍스트 3, CUP 1986의 "로컬 필드"의 Ch6 §3를 참조한다. 1986년 페이퍼백 판의 p99에 있다.

역사

뉴턴 폴리곤은 1676년부터 헨리 올덴버그에게 전달된 서신에서 처음으로 폴리곤과 그 용도의 일부를 설명한 아이작 뉴턴의 이름을 따서 명명되었다.^[1]

적용들

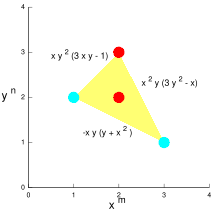
A Newton Polygon is sometimes a special case of a Newton polytope, and can be used to construct asymptotic solutions of two-variable polynomial equations like ${\displaystyle 3x^{2}y^{3}-xy^{2}+2x^{2}y^{2}-x^{3}y=0}$

뉴턴 폴리곤의 또 다른 적용은 다음과 같은 결과에서 온다.

내버려두다

${\displaystyle \mu _{1},\mu _{2},\ldots,\mu _{r}}$

$f{\displaystyle }$( ${\displaystyle x}$) ${\displaystyle f(x)}($위에서 정의한 바와 같이)의 뉴턴 폴리곤 선 세그먼트의 기울기가 되고, 다음과 같이 한다.

${\displaystyle \prodda _{1},\prodda _{r},\dots,\proda _{r}}$

X 축에 투영된 선 세그먼트의 해당 길이(즉, $포인트{\displaystyle {}_{}}$ ${\displaystyle P_{}}$ i$${\$displaystyle P_{i}$와 ${\displaystyle P_{}}$ j$${\$displaystyle P_{j}$ 사이에 연장되는 선 세그먼트가 있는 경우, $길이$는 ${\displaystyle j}$- i ${\displaystyle j-i}).$ 그 다음 각 $정수{\displaystyle \mathrm{}}$ 1 ${\displaystyle \le }$ ${\displaystyle \kappa }$ $≤$ r {\$displaystyle$ \\$leq \cappa \$$leq{\displaystyle r}$$\},$ f$$( x ) {\$displaystyle$ \lambda$_{\cappa }}}}$에 대해 정확히 roots ${\displaystyle {\lambda }_{}}$ ${\$ -$\mu_${\\$mu_{\\\\\\\capa }$을 갖는다$$$.$

대칭함수설명

평가의 맥락에서, 우리는 다항식의 뿌리에 대한 기본적인 대칭함수의 평가의 형태로 특정한 정보를 제공받으며, 대수학적 폐쇄에서 실제 뿌리의 가치평가에 대한 정보를 요구한다. 이것은 라면 이론과 특이성 이론의 양면을 모두 가지고 있다. 가능한 유효한 추론은 뉴턴의 정체성에 의한 힘의 합계의 가치에 관한 것이다.

참고 항목

• F-결정
• 아이젠슈타인의 기준
• 뉴턴-오쿤코프 본체
• 뉴턴 폴리토프

참조

• Goss, David (1996), Basic structures of function field arithmetic, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-61480-4, ISBN 978-3-540-61087-8, MR 1423131
• 구베아, 페르난도: p-adic 숫자: 소개. 스프링거 버랙 1993 페이지 199

외부 링크

위키미디어 커먼즈에는 뉴턴 폴리곤과 관련된 미디어가 있다.

• 뉴턴 폴리곤을 그리는 애플릿