궤도
Orbit천체역학에서 궤도는 별 주위의 행성이나 행성 주위의 자연 위성의 궤적이나 행성, 달[1], 소행성 또는 라그랑주점 같은 우주의 물체나 위치를 둘러싼 인공위성의 곡선 궤적이다.일반적으로 궤도는 반복되지 않는 궤적을 의미하기도 하지만 정기적으로 반복되는 궤적을 가리킨다.가까운 근사치로, 행성과 위성은 타원 궤도를 따라다니며,[2] 질량의 중심은 케플러의 행성 운동 법칙에 의해 설명되는 타원의 중심점에서 궤도를 돈다.
대부분의 상황에서 궤도 운동은 뉴턴 역학에 의해 충분히 근사치가 되는데, 이것은 중력을 역제곱 법칙에 따르는 힘이라고 설명한다.[3]그러나 지구지오디션을 따르는 궤도를 가진 알버트 아인슈타인의 일반 상대성 이론은 궤도 운동 역학을 보다 정확하게 계산하고 이해하게 해준다.
역사
| 다음에 대한 시리즈 일부 |
| 우주 비행 |
|---|
| 역사 |
| 적용들 |
| 우주선 |
| 우주 발사 |
| 우주 비행 유형 |
| 우주국 |
| 우주군 |
| 스페이스 명령어 |
| 개인 우주 비행 |
| |
역사적으로 행성의 명백한 움직임은 유럽과 아랍 철학자들이 천체의 사상을 이용하여 묘사하였다.이 모델은 별과 행성이 부착된 완벽한 움직이는 구나 고리의 존재를 실증했다.그것은 천하가 구들의 움직임과는 별개로 고정되어 있고 중력에 대한 이해도 없이 발달되어 있다고 가정했다.행성의 움직임을 보다 정확하게 측정한 후에는 배변과 에피사이클과 같은 이론적 메커니즘이 추가되었다.모델은 하늘에서 행성의 위치를 합리적으로 정확하게 예측할 수 있었지만, 측정이 더 정확해짐에 따라 점점 더 많은 에피사이클이 필요하게 되었고, 따라서 모델은 점점 더 다루기 어려워졌다.원래 지구중심적이었던 코페르니쿠스는 모델을 단순화하기 위해 태양을 중심에 놓도록 수정했다.이 모델은 16세기 동안 혜성이 구를 가로지르는 것이 관찰되면서 더 많은 도전을 받았다.[4][5]
궤도에 대한 현대적인 이해를 위한 기초는 그의 세 가지 행성 운동 법칙에 요약된 결과를 요하네스 케플러에 의해 처음으로 공식화되었다.먼저 그는 우리 태양계에 있는 행성들의 궤도는 이전에 믿었던 것처럼 원형(혹은 에피사이클릭)이 아닌 타원형이며, 태양이 궤도의 중심에 있지 않고 오히려 하나의 초점에 있다는 것을 발견했다.[6]둘째로, 그는 각 행성의 궤도 속도가 이전에 생각했던 것처럼 일정하지 않고, 오히려 그 속도는 태양으로부터 행성의 거리에 달려 있다는 것을 발견했다.셋째, 케플러는 태양 주위를 돌고 있는 모든 행성의 궤도 특성 사이에 보편적인 관계를 발견했다.행성의 경우, 태양으로부터의 거리의 정육면체는 그들의 궤도 주기의 정사각형에 비례한다.예를 들어 목성과 금성은 각각 태양으로부터 약 5.2년과 0.723AU 떨어져 있으며, 궤도 주기는 각각 약 11.86년과 0.615년이다.그 비례성은 목성의 비율인 53.2/11.86이2 금성의 비율인 0.7233/02.615와 사실상 같다는 사실로 볼 수 있다.이 규칙들을 충족시키는 이상적인 궤도를 케플러 궤도로 알려져 있다.

아이작 뉴턴은 케플러의 법칙이 그의 중력 이론에서 파생될 수 있고, 일반적으로 중력의 대상이 되는 몸의 궤도는 원뿔 부분(이는 중력의 힘이 순간적으로 전파된다고 가정한다)이라는 것을 증명했다.뉴턴은 한 쌍의 신체에 대해 궤도의 크기가 질량에 반비례하며, 그 신체가 질량의 공통 중심을 공전한다는 것을 보여주었다.한 몸체가 다른 몸보다 훨씬 더 큰 경우(행성을 공전하는 인공위성의 경우처럼) 더 큰 몸체의 중심과 일치하여 질량의 중심을 차지하는 것이 편리한 근사치다.
뉴턴 역학의 발전은 다른 신체에 의한 섭동이나 구면체보다는 스피로이드의 영향과 같이 케플러 궤도에 숨겨진 단순한 가정으로부터의 변화를 탐구하는 데 이용되었다.라그랑주(1736–1813)는 힘보다 에너지를 더 강조하는 뉴턴 역학에 대한 새로운 접근법을 개발하여, 세 가지 신체 문제를 진전시켜 라그랑주 포인트를 발견하였다.고전역학에 대한 극적인 정당화에서 1846년 우르바인 르 베리에가 천왕성의 궤도에서 설명할 수 없는 동요를 바탕으로 해왕성의 위치를 예측할 수 있었다.
알버트 아인슈타인(1879~1955)은 1916년 논문 '일반상대성이론 기초'에서 중력은 시공간의 곡률에 기인한다고 설명하면서 변화가 순간적으로 전파된다는 뉴턴의 가정을 없앴다.이는 천문학자들이 뉴턴 역학이 궤도를 이해하는 데 있어 가장 높은 정확도를 제공하지 못했다는 것을 인식하게 했다.상대성 이론에서 궤도는 보통 뉴턴의 예측에 의해 매우 잘 근사하게 추정되는 지질 궤적을 따르지만(매우 강한 중력장과 매우 빠른 속도가 있는 곳은 제외) 차이는 측정할 수 있다.본질적으로 그 이론들을 구별할 수 있는 모든 실험 증거는 실험 측정 정확도 내에서 상대성 이론과 일치한다.일반 상대성 이론의 원래 증명은 르 베리에가 처음 주목한 수성의 위계(perielion)의 경과에 있어서 설명할 수 없는 남은 양을 설명할 수 있었다는 것이다.그러나 뉴턴의 솔루션은 사용하기가 상당히 쉽고 충분히 정확하기 때문에 여전히 대부분의 단기적인 목적에 사용된다.
행성 궤도
이 섹션은 검증을 위해 추가 인용구가 필요하다.(2020년 9월)(이를 과 시기 |
행성계 내에서 행성, 왜성, 소행성 및 다른 작은 행성, 혜성, 우주 파편들이 시스템의 중심부를 타원 궤도로 돈다.쌍성 중심 주위를 도는 포물선이나 쌍성 궤도에 있는 혜성은 중력적으로 항성과 결합되지 않기 때문에 항성의 행성계의 일부로 간주되지 않는다.자연 위성이든 인공 위성이든 중력적으로 행성들 중 하나에 묶여 있는 물체는 그 행성 근처나 그 안에 있는 바리센터 주위를 공전한다.
상호 중력 섭동 때문에 행성 궤도의 편심도는 시간이 지남에 따라 변한다.태양계에서 가장 작은 행성인 수성은 가장 편심 궤도를 가지고 있다.현재 시대에는 화성이 다음으로 큰 편심률을 가진 반면, 가장 작은 궤도 편심률은 금성과 해왕성에서 볼 수 있다.
두 물체가 서로 궤도를 돌면서, 두 물체가 서로 가장 가까운 지점이고, 아포아피스는 가장 먼 지점이다.(특정 신체에 더 구체적인 용어를 사용한다.예를 들어, 페리거와 아포기는 지구 주위의 궤도에서 가장 낮고 가장 높은 부분인 반면, 페리히온과 아펠리온은 태양 주위의 궤도에서 가장 가깝고 가장 먼 지점이다.)
항성을 공전하는 행성의 경우 항성과 항성의 모든 위성의 질량은 바이센터라고 불리는 한 지점에 있는 것으로 계산된다.별의 모든 위성의 경로는 그 중심부 주위에 타원형 궤도가 있다.이 시스템의 각 위성은 타원의 한 초점에 바이리센터와 함께 자체 타원 궤도를 가질 것이다.궤도를 따라 어느 지점에서든, 어떤 위성은 바이리 중심과 관련하여 운동 에너지와 전위 에너지의 특정 값을 가질 것이며, 그 에너지는 궤도를 따라 가는 모든 지점에서 일정한 값이다.결과적으로, 행성이 periapsis에 접근함에 따라, 행성은 잠재적 에너지가 감소함에 따라 속도가 증가할 것이고, 행성이 apapapsis에 접근함에 따라, 행성은 잠재적인 에너지가 증가함에 따라 속도가 감소할 것이다.
궤도 이해
궤도를 이해하는 몇 가지 일반적인 방법이 있다.
- 중력과 같은 힘은 물체가 직선으로 날아가려고 할 때 물체를 곡선으로 끌어당긴다.
- 물체가 거대한 몸쪽으로 쏠리면서 그 몸쪽으로 떨어진다.그러나 충분한 접선속도를 가지면 몸속으로 떨어지지 않고 그 몸체에 의해 야기된 곡선을 무한정 따라갈 것이다.이어 이 물체는 신체의 궤도를 돌고 있다고 한다.
행성 주위의 궤도를 보여주는 삽화로서, 뉴턴의 대포알 모델은 유용한 것으로 증명될 수 있다(아래 이미지 참조).이것은 높은 산꼭대기에 있는 대포가 임의의 선택된 주둥이로 수평으로 포탄을 발사할 수 있는 '생각 실험'공기 마찰이 대포알에 미치는 영향은 무시된다(혹은 산이 높아서 대포가 지구 대기권 위에 있는 것도 마찬가지일 것이다).[7]

포탄이 낮은 초속도로 공을 발사하면 공의 궤적이 아래로 휘어지며 그라운드를 타격(A)한다.사격 속도가 빨라질수록 대포는 대포에서 더 멀리(B) 땅에 닿게 되는데, 그 이유는 공이 여전히 땅 쪽으로 떨어지는 동안 점점 더 그쪽으로 지면이 휘어지기 때문이다(위 1점 참조).이러한 모든 움직임은 사실 기술적 의미에서 "궤도"이지만, 중력 중심 주위의 타원형 경로의 일부를 묘사하고 있다. 하지만 궤도는 지구를 타격함으로써 중단된다.
충분한 스피드로 포탄을 쏘면 공이 떨어지는 만큼 땅은 공에서 떨어져 커브를 그리기 때문에 공은 절대 땅을 치지 않는다.그것은 지금 비침해적이거나 순환적인 궤도라고 불릴 수 있는 곳에 있다.행성의 무게중심과 질량 위의 어떤 특정한 높이 조합에 대해서는 (C)와 같이 원형 궤도를 생성하는 하나의 특정한 발사 속도(공 질량의 영향을 받지 않는 것으로 추정되며, 지구 질량에 비해 매우 작은 것으로 가정한다)가 있다.
이 이상으로 발사 속도가 증가함에 따라 (D)에 표시된 것과 같이 비간격 타원 궤도가 생성된다.만약 초기 발사가 그림과 같이 지구 표면 위에 있다면, 느린 발화 속도로도 비침투성 타원 궤도가 있을 것이다; 이것들은 원궤도 바로 반대쪽인 원궤도 아래에서 지구와 가장 가까운 궤도의 반쪽 지점에서 지구와 가장 가까이 올 것이다.
행성의 질량과 바리 중심으로부터의 물체의 거리에 따라 탈출 속도라고 불리는 특정한 수평 발사 속도에서 포물선 경로를 갖는 열린 궤도(E)가 달성된다.훨씬 더 빠른 속도에서 물체는 다양한 쌍곡선 궤적을 따를 것이다.실용적인 의미에서 이 두 종류의 궤적은 모두 물체가 행성의 중력을 "파쇄"하고 있다는 것을 의미하며, "우주로 나가는 것"은 결코 돌아오지 않는다는 것을 의미한다.
따라서 질량이 있는 두 이동 물체의 속도 관계는 다음과 같은 하위 유형을 가진 네 가지 실제 등급에서 고려될 수 있다.
- 궤도 없음
- 아보르바이탈 궤적
- 중단된 타원 경로의 범위
- 궤도 궤도 궤도(또는 단순 궤도)
- 발화 지점 반대편에 가장 가까운 점이 있는 타원 경로의 범위
- 원형 경로
- 발화 지점에서 가장 가까운 점이 있는 타원 경로 범위
- 개방(또는 탈출) 궤도
- 포물선 경로
- 쌍곡선 경로
처음에는 궤도 로켓을 수직으로 발사해 로켓을 대기권( 마찰력을 유발하는 것) 위로 끌어올린 뒤 천천히 투구해 대기와 평행하게 로켓 엔진 발사를 마쳐 궤도 속도를 달성한다는 점에 주목할 필요가 있다.
일단 궤도에 진입하면, 그들의 속도는 그들을 대기권 위의 궤도에 있게 한다.예를 들어 타원형 궤도가 밀도 높은 공기로 미끄러지면 물체는 속도를 잃고 다시 진입한다(즉, 낙하).때때로 우주선은 일반적으로 에어로브레이킹 기법이라고 불리는 행동에서 의도적으로 대기를 가로채게 된다.
뉴턴의 운동 법칙
뉴턴의 중력 법칙과 두 신체 문제에 대한 운동 법칙
대부분의 상황에서 상대론적 효과는 무시될 수 있으며, 뉴턴의 법칙은 운동에 대한 충분한 정확한 설명을 제공한다.신체의 가속도는 그것에 작용하는 힘의 합계와 같으며, 그 질량으로 나누어지며, 신체에 작용하는 중력은 끌어당기는 두 신체의 질량의 산물에 비례하고 그들 사이의 거리의 제곱과 반비례하여 감소한다.이 뉴턴 근사치에 대해, 2점 질량이나 구형 몸체의 시스템에 대해서, 그들의 상호 인력에 의해서만 영향을 받는 그들의 궤적은 정확히 계산될 수 있다.행성을 공전하는 위성이나 작은 달의 경우나 태양을 공전하는 지구의 경우처럼 무거운 육체가 작은 것보다 훨씬 더 거대하다면, 무거운 육체를 중심으로 한 좌표계의 관점에서 움직임을 묘사하기에 충분하고 편리하며, 우리는 가벼운 육체가 더 무거운 육체를 중심으로 한 궤도에 있다고 말한다.. 두 신체의 질량이 비교 가능한 경우, 정확한 뉴턴 해법은 여전히 충분하며 좌표계를 시스템 질량의 중심에 배치함으로써 가질 수 있다.
중력 전위 에너지 정의
에너지는 중력장과 연관되어 있다.다른 사람으로부터 멀리 떨어져 있는 정지된 몸은 그것을 향해 잡아당기면 외부 작업을 할 수 있고, 따라서 중력 전위 에너지를 가지고 있다.중력의 당김에 대항하여 두 몸을 분리하는 작업이 필요하므로, 이들의 중력 전위 에너지는 분리될수록 증가하며, 서로 가까워질수록 감소한다.점 질량의 경우, 중력에너지는 영분리에 가까워질수록 영(0)으로 감소한다.무한히 떨어져 있을 때 잠재적 에너지를 0 값을 갖는 것으로 할당하는 것이 편리하고 관습적이며, 따라서 더 작은 유한 거리에 대해서는 (0에서 감소하기 때문에) 음의 값을 갖는다.
궤도 에너지 및 궤도 형태
오직 두 개의 중력체만이 상호작용할 때, 그들의 궤도는 원뿔 단면을 따른다.궤도는 개방될 수 있다(물체는 결코 돌아오지 않는다) 또는 폐쇄될 수 있다(회귀할 수 있다).그것은 시스템의 총 에너지(키네틱 + 전위 에너지)에 따라 달라진다.열린 궤도의 경우, 궤도의 어떤 위치에서든 속도는 적어도 그 위치에 대한 탈출 속도인데, 폐쇄된 궤도의 경우 속도는 항상 탈출 속도보다 낮다.운동 에너지는 무한 분리 시 잠재적 에너지를 0으로 받아들이는 공통 관례를 채택한다면 결코 음이 아니기 때문에, 경계 궤도는 음의 총 에너지를 가지며, 포물선 궤도는 총 에너지를 0으로 하고, 쌍곡선 궤도는 양의 총 에너지를 가진다.
열린 궤도는 궤도에 있는 그 지점에서 탈출속도의 정확한 속도를 가지면 포물선 모양을 갖게 되며, 탈출속도보다 속도가 클 때 하이퍼볼라 모양을 갖게 된다.탈출속도 이상의 육체가 서로 접근하면 가장 가까운 곳에 접근한 시점에 짧게 서로 휘어지게 되고, 그 다음 영원히 분리된다.
닫힌 궤도는 모두 타원형이다.원형 궤도는 타원의 초점이 일치하는 특별한 경우다.공전하는 신체가 지구와 가장 가까운 지점을 페리지(Periigee)라고 하며, 궤도가 지구 이외의 신체에 관한 것일 때 페리옵시스(적어도 덜 적절하게, "페리포쿠스" 또는 "페리센트론")라고 부른다.위성이 지구에서 가장 멀리 떨어져 있는 지점을 아포기, 아포캡시스 또는 때로는 아피포쿠스 또는 아포콘트론이라고 부른다.복도에서 아포아피스로 이어지는 선은 압사이드의 선이다.이것은 타원의 주요 축이며, 가장 긴 부분을 통과하는 선이다.
케플러의 법칙
닫힌 궤도를 따라가는 시체들은 그 시기라고 불리는 특정한 시간을 가지고 그들의 길을 반복한다.이 운동은 뉴턴의 법칙에서 수학적으로 도출할 수 있는 케플러의 경험적 법칙에 의해 설명된다.이것들은 다음과 같이 공식화될 수 있다.
- 태양 주위의 행성의 궤도는 타원이고, 태양은 타원의 초점 중 하나에 있다.[이 초점은 사실 태양 행성계의 쌍중점이다. 단순성을 위해 이 설명은 태양의 질량이 저 행성의 질량보다 무한히 크다고 가정한다.]행성의 궤도는 궤도면이라고 불리는 평면에 놓여 있다.유인체에 가장 가까운 궤도의 지점은 근막이다.유인체에서 가장 멀리 떨어진 지점을 아포캡시스라고 한다.특정 신체에 대한 궤도에 대한 구체적인 용어들도 있다; 태양을 공전하는 사물은 상피와 상피, 지구를 공전하는 사물은 상피와 상피, 그리고 달을 공전하는 사물은 각각 상피와 아폴로네(또는 상피와 아포셀렌과 아포셀렌을 가지고 있다.태양뿐만 아니라 어떤 항성 주위의 궤도는 페리아스트론과 아파스트론을 가지고 있다.
- 행성이 궤도를 돌 때 태양에서 행성으로 가는 선은 그 시간 동안 행성의 궤도의 어느 부분을 추적하든 상관없이 일정 시간 동안 궤도 비행기의 일정한 영역을 쓸어버린다.이것은 행성이 그것의 부속물 근처보다 그것의 주변 근처로 더 빨리 이동한다는 것을 의미한다. 왜냐하면 더 작은 거리에서는 같은 지역을 커버하기 위해 더 큰 호를 추적해야 하기 때문이다.이 법은 보통 "평등한 시간대의 평등한 지역"으로 명시된다.
- 주어진 궤도의 경우, 반주축의 입방체 대 그 기간의 제곱의 비율은 일정하다.
뉴턴의 중력 법칙의 한계
뉴턴 중력장이 있는 점 질량이나 구형 몸체의 경계 궤도는 닫힌 타원(closed tallips)이며, 이 타원은 정확히 같은 경로를 무한정 반복하지만 비구형 또는 비뉴턴 효과(예: 지구의 경미한 말살이나 상대론적 효과에 의해 발생하여 중력장의 동작을 변화시킨다.ior 거리)는 궤도의 형상이 뉴턴의 2-body 움직임의 닫힌 타원 특성에서 벗어나게 할 것이다.두 신체 용액은 1687년 뉴턴에 의해 프린키아의 출판되었다.1912년 카를 프리티오프 순드만은 3체 문제를 해결하는 수렴 무한 시리즈를 개발했지만, 너무 느리게 수렴하여 많은 활용을 하지 못한다.라그랑지안 점과 같은 특수한 경우를 제외하고는 네 개 이상의 몸을 가진 시스템에 대한 운동 방정식을 해결할 수 있는 방법은 알려져 있지 않다.
다체 문제에 대한 접근 방식
정확한 밀폐형 폼솔루션보다는 몸체가 많은 궤도를 임의의 높은 정확도로 근사하게 추정할 수 있다.이러한 근사치에는 두 가지 형태가 있다.
- 한 형태는 순수한 타원 운동을 기본으로 삼고 섭동 용어를 추가하여 여러 신체의 중력 영향을 고려한다.이것은 천문체의 위치를 계산하는데 편리하다.달, 행성, 그리고 다른 신체의 움직임 방정식은 매우 정확하게 알려져 있으며, 천체 항해를 위한 표를 생성하는 데 사용된다.그래도 포스트 뉴턴 방식으로 대처해야 하는 세속적인 현상들이 있다.
- 미분 방정식 형식은 과학적 또는 임무 계획 목적으로 사용된다.뉴턴의 법칙에 따르면, 신체에 작용하는 모든 힘의 합은 신체의 질량이 가속도를 곱한 것과 같을 것이다(F = ma).따라서 가속은 위치의 관점에서 표현될 수 있다.섭동 용어는 이 형태로 설명하기가 훨씬 쉽다.위치 및 속도의 초기 값에서 후속 위치와 속도를 예측하는 것은 초기 값 문제를 해결하는 것과 일치한다.수치적 방법은 물체의 위치와 속도를 향후 짧은 시간 동안 계산한 다음 계산 ad 메스탐을 반복한다.그러나 컴퓨터의 수학의 제한된 정확도로 인한 작은 산술적 오류는 누적되어 이 접근법의 정확성을 제한한다.
개체 수가 많은 차등 시뮬레이션은 질량 중심 간의 계층적 쌍방향 방식으로 계산을 수행한다.이 방법을 사용하여 은하, 항성 클러스터 및 다른 큰 물체 집합체가 시뮬레이션되었다.[citation needed]
뉴턴의 궤도 운동 분석
다음과 같은 파생은 그러한 타원 궤도에 적용된다.우리는 중심체를 향한 중력 가속도가 그들 사이의 거리의 제곱, 즉 정사각형의 역행과 관련이 있다는 뉴턴 인력의 법칙에서 출발한다.
여기서 F는2 m에2 대한 중력 끌어당김 질량 m에1 의해 발생하는 질량 m에2 작용하는 힘이고, G는 보편적인 중력 상수, r은 두 질량 중심 사이의 거리다.
뉴턴의 제2법칙에서 m에2 작용하는 힘의 합계는 그 신체의 가속도와 관련이 있다.
여기서 A는2 m에2 작용하는 m의1 중력 끌어당김 F의2 힘에 의해 m의2 가속이다.
Eq. 1과 2의 조합:
가속을 위한 해결 방법 A2:
여기서 은(는) 표준 중력 파라미터로, 이 경우 1 설명 중인 시스템이 m인2 것으로 이해되므로 첨자를 삭제할 수 있다.
우리는 중심체가 정지해 있다고 볼 수 있을 만큼 충분히 거대하다고 가정하고 우리는 일반 상대성 이론의 더 미묘한 영향을 무시한다.
When a pendulum or an object attached to a spring swings in an ellipse, the inward acceleration/force is proportional to the distance Due to the way vectors add, the component of the force in the or in the 방향도 거리의 각 구성 요소에 비례하며, x = A = - 따라서 전체 분석은 이러한 차원에서 별도로 할 수 있다.이로 인해 고조파 포물선 방정식 = A ( ) 과 = ( ) 이 타원의 결과가 된다.로 관계 A =/ A 감소하는 관계로 치수는 분리할 수 없다[citation needed]
현재 시간 에서 궤도를 선회하는 물체의 위치는 표준 유클리드 기초와 힘의 중심과 일치하는 기원과 극좌표에서 벡터 미적분을 사용하여 평면에 위치한다. 을(를) 물체와 중심 사이의 거리로 하고 을(를) 물체가 회전한 각도로 한다.Let and be the standard Euclidean bases and let and be the radial and transverse polar basis with the first being the unit vector pointing from the central body to the current location of the orbiting object and t그는 두 번째로 직교 단위 벡터로서, 시계 반대 방향으로 선회할 경우 궤도를 선회하는 물체는 시계 반대 방향으로 선회한다.그러면 궤도를 도는 물체에 대한 벡터는
˙{\과(와) 을(를) 사용하여 이 거리와 각도가 시간에 따라 어떻게 변하는지 표준 파생 모델을 표시한다.벡터의 파생 모델을 사용하여 시간 의 위치를 시간 t + 에서 Δ t t에서 빼고 t{\ t로 나누면 시간이 지남에 따라 어떻게 변하는지 알아본다결과도 벡터다.우리의 기본 벡터 r 이(가) 개체 궤도로 이동하기 때문에 이를 차별화하는 것으로 시작한다.From time to , the vector keeps its beginning at the origin and rotates from angle to which moves its head a 수직방향 ta
우리는 이제 궤도를 선회하는 물체의 속도와 가속도를 찾을 수 있다.
과() 의 계수는 방사상 및 횡방향으로 가속도를 부여한다.말했듯이 뉴턴은 중력에 의한 이것을 먼저 주는데 -/ 2 }}이고 두 번째는 0이다.
-
(1)
-
(2)
등식 (2)는 부품별 통합을 이용하여 재배열할 수 있다.
궤도를 도는 물체가 충돌하지 않는 한 0이 아니기 때문에 r으로 곱할 수 있다.그런 다음 파생상품을 0으로 설정하면 함수가 상수라는 것을 알 수 있다.
-
(3)
이것은 실제로 케플러의 제2법칙에 대한 이론적 증거다(행성과 태양이 같은 시간 간격 동안 동일한 영역을 휩쓸어 가는 선).통합의 상수인 h는 단위 질량당 각도 운동량이다.
방정식(1)에서 궤도에 대한 방정식을 얻으려면 시간을 없애야 한다.[8](비넷 방정식을 참조하십시오.)극좌표에서 이것은 중심으로부터 궤도를 선회하는 의 거리 r{\을 각도 의 함수로 표현한다 그러나 보조 변수 = / 을(를) 소개하고 u}을θ의 함수로 표현하는 것이 더 쉽다.시간에 관한 각도에 관한 의 파생상품으로 다시 쓸 수 있다.
- = r 2 = 2 {\r^{재작업 (3))
이러한 기능을 (1)에 연결하면
-
(4)
따라서 중력, 즉 보다 일반적으로는 역제곱력 법칙에 대해 방정식의 오른손은 상수가 되고 방정식은 조화 방정식(의존변수의 원점 이동까지)으로 보인다.해결책은 다음과 같다.
여기서 A와 θ은0 임의의 상수다.물체의 궤도에 대한 이 결과 방정식은 초점 중 하나에 상대적인 극성 형태의 타원의 방정식이다.은 / e을(를) 편심성으로 하고, / - 2) h (를 반주요축으로 하여 보다 표준적인 형태로 한다.마지막으로 타원의 긴 축이 양의 x 좌표를 따라 오도록 을(를) 허용한다.
2-바디 시스템이 토크의 영향을 받을 때 각운동량 h는 상수가 아니다.다음 계산 후:
우리는 2-바디 시스템의 스터름-리우빌 방정식을 얻을 것이다.[9]
-
(5)
상대성 궤도 운동
위와 같은 궤도 역학의 고전적(뉴턴어) 분석은 프레임 끌기, 중력 시간 팽창과 같은 일반 상대성 이론의 더 미묘한 효과는 무시할 수 있다고 가정한다.상대론적 영향은 매우 거대한 물체 가까이에 있을 때(태양에 대한 수성의 궤도의 진행과 같이), 또는 (GPS 위성에 대한 궤도 요소와 시간 신호 기준의 계산과 같이) 극도의 정밀도가 필요할 때 무시해도 될 정도로 사라진다.[10]
궤도면
지금까지의 분석은 2차원이었다. 즉, 우주에 고정된 평면에서 흔들리지 않는 궤도는 2차원이며, 따라서 3차원까지 확장하려면 단순히 2차원 평면을 관련 행성체의 극에 비례하여 필요한 각도로 회전해야 한다는 것이 밝혀졌다.
이것을 3차원으로 하기 위한 회전은 고유하게 결정하는데 3개의 숫자를 필요로 한다; 전통적으로 이것들은 3개의 각도로 표현된다.
궤도 주기
궤도 주기는 단순히 궤도를 선회하는 신체가 하나의 궤도를 완성하는 데 걸리는 시간이다.
궤도 지정
신체에 대한 케플러안 궤도를 지정하려면 6개의 매개변수가 필요하다.예를 들어 신체의 초기 위치를 지정하는 3개의 숫자와 그 속도를 지정하는 3개의 값은 시간에 따라 앞으로(또는 뒤로) 계산할 수 있는 고유한 궤도를 정의하게 된다.그러나 전통적으로 사용되는 매개변수는 약간 다르다.
전통적으로 사용되는 궤도 원소의 집합은 요하네스 케플러와 그의 법칙의 이름을 따서 케플러 원소의 집합이라고 불린다.케플러 원소는 6개:
원칙적으로 궤도 원소가 신체에 대해 알려지면 그 위치는 시간에 따라 무한정 앞뒤로 계산할 수 있다.그러나 실제로 궤도는 가정된 점원(다음 절 참조)에서 단순한 중력 이외의 다른 힘에 의해 영향을 받거나 혼란에 빠지며, 따라서 궤도 원소는 시간에 따라 변한다.
궤도 섭동
궤도 섭동은 주력을 받는 몸의 전체적인 힘이나 평균적인 충동보다 훨씬 작고 궤도를 선회하는 두 신체에 외부적인 힘이나 충동이 가속을 일으켜 시간이 지남에 따라 궤도의 매개변수를 변화시키는 것을 말한다.
방사형, 프로그램 및 횡방향 섭동
궤도에 있는 신체에 주어지는 작은 방사상 충동은 편심도를 변화시키지만 궤도 주기(첫 번째 순서)는 변화시키지 않는다.프로그램 또는 역행 충동(즉 궤도 운동을 따라 가해지는 충동)은 편심률과 궤도 주기를 모두 변화시킨다.특히 페리옵시스에서의 프로그램 임펄스는 아파옵시스(apapapsis)에서 고도를 높이고, 반대로 그 반대로 역행하는 임펄스는 그 반대로 작용한다.횡방향 임펄스(궤도면 바깥쪽)는 주기나 편심도를 바꾸지 않고 궤도면의 회전을 일으킨다.모든 경우에 닫힌 궤도는 여전히 섭동 지점을 교차할 것이다.
궤도 붕괴
만약 궤도가 대기권이 유의미한 행성체일 경우, 그 궤도는 드래그 때문에 붕괴될 수 있다.특히 각각의 주기에 물체는 에너지를 잃으면서 대기 중의 드래그를 경험한다.매번, 궤도는 덜 편심하게 된다. 왜냐하면 물체는 정확히 그 에너지가 최대일 때 운동 에너지를 잃기 때문이다.이것은 가장 낮은 지점에서 진자를 느리게 하는 효과와 비슷하다; 진자의 흔들림 중 가장 높은 지점은 낮아진다.연속적으로 속도가 느려질 때마다 궤도의 경로가 대기에 의해 더 많이 영향을 받고 그 효과는 더욱 뚜렷해진다.결국 그 효과는 너무 커져서 최대 운동 에너지가 대기 드래그 효과의 한계 이상의 궤도를 되돌릴 수 없을 정도로 충분치 않다.이렇게 되면 신체는 빠르게 아래로 소용돌이치며 중심체와 교차하게 된다.
대기의 경계는 매우 다양하다.태양 최대치 동안, 지구의 대기는 태양 최소치보다 최대 100킬로미터 더 높은 거리를 끌어 올린다.
긴 전도성 테더를 가진 일부 위성도 지구 자기장으로부터의 전자기력 항력 때문에 궤도 붕괴를 경험할 수 있다.전선이 자기장을 자르면 전자가 한쪽 끝에서 다른 쪽 끝으로 이동하는 발전기의 역할을 한다.궤도 에너지는 전선에서 열로 변환된다.
궤도는 그 경로의 어느 지점에서 신체의 운동 에너지를 변화시키는 로켓 엔진의 사용을 통해 인위적으로 영향을 받을 수 있다.이것은 화학적 또는 전기적 에너지를 운동에너지로 전환하는 것이다.이런 방식으로 궤도 형태나 방향의 변화를 촉진할 수 있다.
인공적으로 궤도에 영향을 미치는 또 다른 방법은 태양 돛이나 자기 돛을 사용하는 것이다.이러한 추진 형태는 태양 이외의 추진체나 에너지 투입을 필요로 하지 않기 때문에 무한정 사용할 수 있다.제안된 용도에 대해서는 statite를 참조하십시오.
궤도 붕괴는 그들이 궤도를 돌고 있는 신체의 동기 궤도 이하의 물체에 대한 조력력 때문에 발생할 수 있다.궤도를 선회하는 물체의 중력은 일차적으로 조석 불룩을 일으키며, 동기 궤도 아래에서는 궤도를 선회하는 물체가 몸 표면보다 빠르게 움직이고 있으며, 그 불룩은 그 뒤로 짧은 각도로 뒤처져 있다.돌출부의 중력은 1차 위성 축에서 약간 벗어나 있어 위성의 움직임과 함께 구성 요소가 있다.멀리 돌출된 물체보다 가까운 돌출부가 물체의 속도를 더 느리게 하고, 그 결과 궤도가 감소한다.반대로 돌출부에 있는 위성의 중력은 1차에 토크를 가하고 회전 속도를 높인다.인공 위성은 궤도를 도는 행성들에 눈에 띄는 조석 효과를 주기에는 너무 작지만, 태양계의 몇몇 달들은 이 메커니즘에 의해 궤도 붕괴를 겪고 있다.화성의 가장 안쪽 달인 포보스가 대표적인 예로서 화성의 표면에 충격을 주거나 5000만년 이내에 고리로 분해될 것으로 예상된다.
궤도는 중력파의 배출을 통해 붕괴할 수 있다.이 메커니즘은 대부분의 항성 물체에는 극히 약하며, 블랙홀이나 서로 근접하게 궤도를 선회하는 중성자 별과 같이 극한 질량과 극한 가속도의 조합이 있는 경우에만 의미가 있다.
오블리시티
궤도를 선회하는 신체의 표준 분석은 모든 신체가 균일한 구체 또는 보다 일반적으로 균일한 밀도의 동심 껍질로 구성된다고 가정한다.그러한 몸체는 중력적으로 점원과 동등하다는 것을 알 수 있다.
그러나 실제 세계에서는 많은 신체들이 회전하며, 이것은 중력장을 말살하고 왜곡하며, 중력장에 4극 모멘트를 주는데, 이것은 신체의 반지름에 비견되는 거리에서 유의한 것이다.일반적인 경우, 예를 들어 행성과 같은 회전하는 신체의 중력 전위는 구면 대칭으로부터 행성의 이탈을 설명하는 다중점 단위로 확장된다.위성 역학의 관점에서 볼 때, 특히 관련이 있는 것은 그들이 궤도 기간보다 더 긴 시간에 걸쳐 누적되는 세속적인 궤도 섭동을 유도하기 때문에 소위 고른 지역 조화 계수 또는 조날이다.[11][12][13]그것들은 우주에서 신체의 대칭 축의 방향에 따라 결정되며, 일반적으로 전체 궤도에 영향을 미친다. 단, 반조르 축은 예외로 한다.
다중 중력체
다른 육체를 끌어당기는 효과는 상당할 수 있다.예를 들어 달의 궤도는 지구뿐 아니라 태양의 중력의 작용을 허락하지 않고는 정확하게 묘사될 수 없다.한 가지 대략적인 결과는, 만약 그들이 더 무거운 몸의 힐 영역 내에서 선회한다면, 이러한 동요에도 불구하고, 보통 육체는 더 무거운 행성이나 달 주위를 상당히 안정적인 궤도를 가지고 있을 것이라는 것이다.
두 개 이상의 중력체가 있을 때 이를 n-body 문제라 한다.대부분의 n-body 문제는 일부 특수 사례가 공식화되었지만 닫힌 형태 해결책이 없다.
빛 방사선과 별빛 바람
특히 몸집이 작은 신체의 경우, 빛과 별빛 바람은 신체의 움직임의 태도와 방향에 상당한 동요를 일으킬 수 있으며, 시간이 지남에 따라 상당한 동요를 일으킬 수 있다.행성체들 중에서, 소행성의 움직임은 특히 소행성이 태양에 대해 회전할 때 많은 기간에 걸쳐 영향을 받는다.
이상한 궤도
수학자들은 질량, 위치 또는 속도의 작은 섭동에 관해 대부분의 그러한 궤도는 안정적이지 않지만 주기적으로 반복되는 비엘리틱 궤도에 여러 개의 몸을 갖는 것이 원칙적으로 가능하다는 것을 발견했다.그러나, 3개의 움직이는 시체가 점유한 평면 그림 8 궤도를 포함하여, 몇몇 특별한 안정적 사례가 확인되었다.[14]추가 연구들은 4개의 대략적인 원형 연동 궤도로 움직이는 12개의 질량을 포함하는 질량들이 큐옥타헤드론 가장자리와 위상적으로 동등한 궤도를 포함하는 것을 포함하여 비 평면 궤도 또한 가능하다는 것을 발견했다.[15]
우주에서 자연적으로 일어나는 그러한 궤도를 발견하는 것은, 우연한 기회에 일어나는 필수 조건의 실현 가능성이 희박하기 때문에, 극히 가능성이 희박하다고 생각된다.[15]
아스트로다이나믹스
궤도역학 또는 우주역학(Astrodynamics)은 탄도학 및 천체역학을 로켓과 다른 우주선의 움직임에 관한 실제적인 문제에 적용하는 것이다.이러한 물체의 운동은 보통 뉴턴의 운동 법칙과 뉴턴의 만유인력의 법칙에서 계산된다.그것은 우주 임무 설계와 통제 안에 있는 핵심 훈련이다.천체역학은 우주선과 항성계, 행성, 달, 혜성 등 자연천체 등 중력의 영향을 받는 시스템의 궤도역학을 보다 광범위하게 다룬다.궤도역학은 궤도기동, 궤도비행기 변화, 행성간 이동 등 우주선 궤도에 초점을 맞추고 있으며, 임무기획자가 추진기동 결과를 예측하는 데 사용한다.일반 상대성 이론은 궤도를 계산하는 뉴턴의 법칙보다 더 정확한 이론이며, 때로는 더 큰 정확성이나 고중력 상황(태양에 가까운 궤도와 같은)에서 필요한 경우도 있다.
지구 궤도
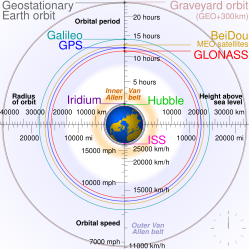
- 지구 저궤도(LEO): 최대 2,000km(0–1,240마일)의 고도를 가진 지구 궤도.[16]
- 중간 지구 궤도(MEO): 고도 2000km(1,240마일)에서 35,786km(22,236mi)에서 지구동기 궤도 바로 아래까지 이르는 지구중심 궤도.중간 원형 궤도라고도 한다.이들은 "가장 흔하게 궤도 주기가 12시간인 2만200km(1만2600mi), 즉 2만650km(1만2830mi)로 나타났다"[17]고 설명했다.
- 지오동기궤도(GSO)와 정지궤도(GEO)는 모두 지구의 사이드리얼 회전 기간과 일치하는 지구 주위의 궤도다.모든 지오동기 및 정지궤도는 4만2,164km(26,199mi)의 반주축이다.[18]모든 정지궤도 역시 지리적이고, 모든 정지궤도들이 정지궤도인 것은 아니다.정지궤도는 정확히 적도 상공에 머무르는 반면, 지리적인 궤도는 더 많은 지구 표면을 덮기 위해 남북으로 흔들릴 수 있다.둘 다 (태양이 아닌 별에 상대적인) 사이드리얼 하루당 지구의 전체 궤도를 1회 완성한다.
- 높은 지구 궤도:지동 궤도 고도 35,786 km (22,240 마일)[17] 위의 지동 궤도 궤도.
중력 스케일링
중력 상수 G는 다음과 같이 계산되었다.
- (6.6742 ± 0.001) × 10−11 (kg/m3)−1s−2.
따라서 상수는 치수 밀도−1 시간을−2 갖는다.이는 다음과 같은 속성에 해당한다.
거리 스케일링(신체의 크기 포함, 밀도를 동일하게 유지함)은 스케일링 없이 비슷한 궤도를 형성한다. 예를 들어 거리가 절반으로 줄어들면 질량이 8로, 중력이 16으로, 중력이 2로 나눈다.따라서 속도는 반감되고 궤도 주기와 중력과 관련된 다른 이동 시간은 동일하게 유지된다.예를 들어, 탑에서 물체를 떨어뜨렸을 때, 지상으로 떨어지는 데 걸리는 시간은 지구의 축척 모델에 있는 탑의 축척 모형과 동일하게 유지된다.
질량을 동일하게 유지하면서 거리를 스케일링하면(점 질량의 경우 또는 밀도를 조정하여) 유사한 궤도를 얻을 수 있다. 거리를 4로 곱하면 중력 및 가속도가 16으로 나누어지고, 속도는 반감되며 궤도 주기는 8로 곱해진다.
모든 밀도에 4를 곱하면 궤도는 같다; 중력력은 16을 곱하고 가속도는 4를 곱하면 속도가 2배, 궤도 주기는 반감된다.
모든 밀도에 4를 곱하고, 모든 크기가 반감되고, 궤도가 유사하며, 질량을 2로 나누면 중력이 같으며, 중력 가속도가 2배로 증가한다.따라서 속도는 같고 궤도 주기는 반감된다.
이 모든 스케일링의 경우. 밀도를 4로 곱하면 시간이 반으로 줄고, 속도를 2배로 늘리면 힘이 16으로 곱해진다.
이러한 특성은 공식에 설명되어 있다(궤도 기간의 공식에서 파생됨).
반주축 a가 있는 타원 궤도에 대해, 반지름 r과 평균 밀도 ρ의 구형 몸체 주위의 작은 몸체의 Twoal 궤도. 여기서 T는 궤도 주기다.케플러의 제3법칙도 참조한다.
특허
특정 유용한 목적에 특정한 궤도나 궤도 기동을 적용하는 것은 특허의 대상이 되어 왔다.[19]
조수 잠금
어떤 육체는 다른 육체로 간결하게 잠겨 있는데, 이는 천체의 한쪽이 영구히 숙주물체와 마주하고 있다는 것을 의미한다.지구-달과 명왕성-채론 체계가 그렇다.
참고 항목
메모들
참조
- ^ "orbit (astronomy) – Britannica Online Encyclopedia". Archived from the original on 5 May 2015. Retrieved 28 July 2008.
- ^ "The Space Place :: What's a Barycenter". Archived from the original on 29 January 2013. Retrieved 26 November 2012.
- ^ 쿤, 코페르니쿠스 혁명, 238쪽, 246–252쪽
- ^ 브리태니커 백과사전, 1968년, 제2권, 페이지 645
- ^ M Caspar, Kepler(1959, Abelard-Schuman), pp.131–140; A Koyré, The 천문학 혁명: 코페르니쿠스, 케플러, 보렐리(1973, 메투엔), 페이지 277–279
- ^ Jones, Andrew. "Kepler's Laws of Planetary Motion". about.com. Archived from the original on 18 November 2016. Retrieved 1 June 2008.
- ^ 이 '캐논볼' 사고 실험의 원본은 뉴턴의 "세계의 시스템 치료" 2016년 12월 30일 웨이백 머신(서면 1685년, 영어 1728년 번역, 뉴턴의 '프린키피아' – 예비 버전 참조)에서 6~8페이지를 참조하라.
- ^ Fitzpatrick, Richard (2 February 2006). "Planetary orbits". Classical Mechanics – an introductory course. The University of Texas at Austin. Archived from the original on 3 March 2001.
- ^ Luo, Siwei (22 June 2020). "The Sturm-Liouville problem of two-body system". Journal of Physics Communications. 4 (6): 061001. Bibcode:2020JPhCo...4f1001L. doi:10.1088/2399-6528/ab9c30.
- ^ 포게, 리처드 W.; "실제 세계 상대성: GPS 내비게이션 시스템" 웨이백 머신에 2015년 11월 14일 보관.2008년 1월 25일 회수.
- ^ Iorio, L. (2011). "Perturbed stellar motions around the rotating black hole in Sgr A* for a generic orientation of its spin axis". Physical Review D. 84 (12): 124001. arXiv:1107.2916. Bibcode:2011PhRvD..84l4001I. doi:10.1103/PhysRevD.84.124001. S2CID 118305813.
- ^ Renzetti, G. (2013). "Satellite Orbital Precessions Caused by the Octupolar Mass Moment of a Non-Spherical Body Arbitrarily Oriented in Space". Journal of Astrophysics and Astronomy. 34 (4): 341–348. Bibcode:2013JApA...34..341R. doi:10.1007/s12036-013-9186-4. S2CID 120030309.
- ^ Renzetti, G. (2014). "Satellite orbital precessions caused by the first odd zonal J3 multipole of a non-spherical body arbitrarily oriented in space". Astrophysics and Space Science. 352 (2): 493–496. Bibcode:2014Ap&SS.352..493R. doi:10.1007/s10509-014-1915-x. S2CID 119537102.
- ^ Chenciner, Alain; Montgomery, Richard (31 October 2000). "A remarkable periodic solution of the three-body problem in the case of equal masses". arXiv:math/0011268.
- ^ a b Peterson, Ivars (23 September 2013). "Strange Orbits". Science News. Archived from the original on 22 November 2015. Retrieved 21 July 2017.
- ^ "NASA Safety Standard 1740.14, Guidelines and Assessment Procedures for Limiting Orbital Debris" (PDF). Office of Safety and Mission Assurance. 1 August 1995. Archived from the original (PDF) on 15 February 2013., 37-38페이지(6-1,6-2); 그림 6-1.
- ^ a b "Orbit: Definition". Ancillary Description Writer's Guide, 2013. National Aeronautics and Space Administration (NASA) Global Change Master Directory. Archived from the original on 11 May 2013. Retrieved 29 April 2013.
- ^ Vallado, David A. (2007). Fundamentals of Astrodynamics and Applications. Hawthorne, CA: Microcosm Press. p. 31.
- ^ Ferreira, Becky (19 February 2015). "How Satellite Companies Patent Their Orbits". Motherboard. Vice News. Archived from the original on 18 January 2017. Retrieved 20 September 2018.
추가 읽기
- Abell; Morrison & Wolff (1987). Exploration of the Universe (fifth ed.). Saunders College Publishing. ISBN 9780030051432.
- Linton, Christopher (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press. ISBN 978-1-139-45379-0.
- Frank Swetz; John Fauvel; Bengt Johansson; Victor Katz; Otto Bekken (1995). Learn from the Masters. MAA. ISBN 978-0-88385-703-8.
- 안드레아 밀라니와 조반니 F.그론치.궤도 결정 이론(Cambridge University Press; 378페이지; 2010)자연과 인공 천체의 궤도를 결정하기 위한 새로운 알고리즘을 논의한다.
외부 링크
| 무료 사전인 Wiktionary에서 궤도를 찾아 보십시오. |
| 위키미디어 커먼즈에는 오르빗과 관련된 미디어가 있다. |
- CalcTool: 행성 계산기의 궤도 주기.다양한 유닛 선택 가능.JavaScript 필요.
- 궤도 운동에 대한 자바 시뮬레이션.Java 필요.
- 기후 강제성 데이터의 NOAA 페이지에는 지난 5천만 년 동안 그리고 향후 2천만 년 동안 지구 궤도 변동에 대한 (계산된) 데이터가 포함되어 있다.
- 온라인 궤도 플로터.JavaScript 필요.
- 궤도역학 (로켓과 우주기술)
- 바라디, 길, 런네가(2003)의 궤도 시뮬레이션은 지구 궤도 편심도에 대해 약간 다른 시리즈를 제공하며 궤도 기울기에 대해서도 시리즈를 제공한다.다른 행성의 궤도는 에 의해 계산되었지만 지구와 수성의 편심 데이터만 온라인에서 이용할 수 있다.
- 직접 조작을 사용하여 궤도를 이해하십시오.JavaScript 및 Macromedia 필요
- Merrifield, Michael. "Orbits (including the first manned orbit)". Sixty Symbols. Brady Haran for the University of Nottingham.











 (는)
(는) 













 (와)
(와)








![{\displaystyle {\begin{aligned}{\hat {\mathbf {O} }}&=r{\hat {\mathbf {r} }}\\{\dot {\mathbf {O} }}&={\frac {\delta r}{\delta t}}{\hat {\mathbf {r} }}+r{\frac {\delta {\hat {\mathbf {r} }}}{\delta t}}={\dot {r}}{\hat {\mathbf {r} }}+r\left[{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]\\{\ddot {\mathbf {O} }}&=\left[{\ddot {r}}{\hat {\mathbf {r} }}+{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}\right]+\left[{\dot {r}}{\dot {\theta }}{\hat {\boldsymbol {\theta }}}+r{\ddot {\theta }}{\hat {\boldsymbol {\theta }}}-r{\dot {\theta }}^{2}{\hat {\mathbf {r} }}\right]\\&=\left[{\ddot {r}}-r{\dot {\theta }}^{2}\right]{\hat {\mathbf {r} }}+\left[r{\ddot {\theta }}+2{\dot {r}}{\dot {\theta }}\right]{\hat {\boldsymbol {\theta }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92049db70580d670e5dd37a305c3ebd3073f2b2)