충격 깊이
Impact depth물리학자인 아이작 뉴턴 경은 높은 속도로 이동하는 발사체의 충격 깊이에 대한 대략적인 근사치를 얻기 위해 이 아이디어를 처음 개발했다.
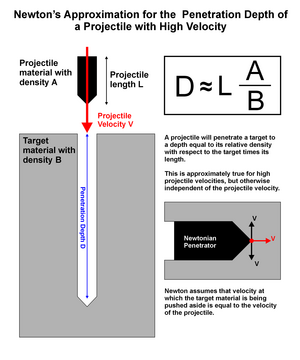
충격 깊이에 대한 뉴턴의 근사치
높은 속도에서 발사체에 대한 뉴턴의 충격 깊이에 대한 근사치는 오직 운동량 고려사항에 기초한다. 임팩터의 운동에너지가 어디로 가는지, 발사체가 정지된 후 모멘텀에 어떤 일이 일어나는지에 대해서는 아무런 언급도 없다.
기본 아이디어는 간단하다. 임팩터는 일정한 추진력을 가진다. 임팩터를 멈추려면 이 추진력을 다른 질량으로 전달해야 한다. 임팩터의 속도가 너무 높아 목표물질 내의 응집력을 소홀히 할 수 있기 때문에 임팩터 바로 앞에 있는 물질(질량)에만 탄력이 전달될 수 있어 임팩터의 속도로 추진력은 임팩터 바로 앞에 있는 소재(질량)에만 전달될 수 있다. 임팩터가 이 속도로 자신의 질량과 동일한 질량을 밀었을 경우, 그 전체 운동량이 앞의 질량으로 전달되어 임팩터가 정지된다. 원통형 임팩터의 경우 정지할 때까지 대상 물질에 대한 상대 밀도의 곱에 해당하는 깊이까지 침투한다.
이 접근방식은 무딘 임팩터(공기역학적 형태 없음)와 섬유(응집력 없음)가 없는 표적 물질만 수용하며 최소한 임팩터의 속도에서는 수용하지 않는다. 임팩터의 속도가 목표물 내 음속보다 훨씬 높은 경우 대개 그렇다. 그렇게 높은 속도에서 대부분의 물질은 액체처럼 작용하기 시작한다. 그런 다음 충격(확산되지 않음) 중에는 발사체가 콤팩트한 형태를 유지하는 것이 중요하다.
적용들
- 발사체: 전체 금속 발사체는 우라늄(19.1g/cm3)이나 납(11.3g/cm3)과 같이 밀도가 매우 높은 물질로 제작해야 한다. 뉴턴의 근사치에 따르면, 우라늄으로 만들어진 완전한 금속 발사체는 자신의 철갑옷 길이의 약 2.5배를 관통하게 된다.
- 모양 전하, 바주카: 형상의 전하(안티탱크)가 강판을 관통하기 위해서는 폭발이 긴 중금속제트를 생성하는 것이 필수적이다(안티탱크 사용을 위한 형상의 전하에서는 원뿔 모양의 금속 라이닝에서 폭발이 고속 금속제트를 생성한다). 이 제트기는 뉴턴 근사치의 임팩터로 볼 수 있다.
- 운석: 기압에서 결론날 수 있듯이, 대기의 물질은 약 10m의 물과 같다. 얼음은 물과 거의 같은 밀도를 가지고 있기 때문에, 15 km/s 정도의 속도로 이동하는 우주에서 온 얼음 입방체는 10 m의 길이를 가져야 빠른 속도로 지구 표면에 도달할 수 있다. 더 작은 얼음 덩어리가 단자 속도로 느려질 것이다. 그러나, 큰 얼음 덩어리 또한 매우 낮은 각도로 들어오기 때문에 많은 대기를 뚫어야 하는 한 느려질 수 있다. 길이 1.3m의 철 운석은 대기를 관통할 것이다; 작은 운석은 공기에 의해 느려지고 땅으로 가는 단자 속도로 떨어질 것이다.
- 임팩터, 벙커 버스터: 핵탄두 대신 고체 임팩터를 사용해 지하 깊숙한 벙커에 침투할 수 있다. 뉴턴의 근사치에 따르면 고속, 길이 1m의 우라늄 발사체(밀도 19g/cm3)는 6m의 암석(밀도 3g/cm3)을 뚫고 나아간 뒤 정지한다.
참고 항목
추가 읽기
- Young, C.W. (1967). The Development of Empirical Equations for Predicting Depth of an Earth Penetrating Projectile (Report). SC-DR-67-60. Albuquerque NM: Sandia National Laboratories.
- Young, C.W. (1997). Penetration Equations (PDF) (Report). SAND94-2726. Albuquerque NM: Sandia National Laboratories.
This is a standalone report documenting the latest updated version of the Young/Sandia penetration equations and related analytical techniques to predict penetration into natural earth materials and concrete. See Appendix A & B for intro to penetration equations.
- Alekseevskii, V. P. (1966). "Penetration of a Rod into a Target at High Velocity". Combustion, Explosion, and Shock Waves (Fizika Goreniya i Vzryva). 2 (2): 99–106. doi:10.1007/BF00749237. ISSN 0010-5082. S2CID 97258659.
- Tate, A. (1 November 1967). "A Theory for the Deceleration of Long Rods After Impact" (PDF). Journal of the Mechanics and Physics of Solids. 15 (6): 387–399. Bibcode:1967JMPSo..15..387T. doi:10.1016/0022-5096(67)90010-5. Archived from the original (PDF) on March 26, 2012. Retrieved 23 June 2011.
- Bernard, Robert S. (1978). Depth and Motion Prediction for Earth Penetrators (PDF) (Report). ADA056701. Vicksburg, MS: Army Engineer Waterways Experiment Station Vicksburg.
- Walters, William P.; Segletes, Steven B. (1991). "An Exact Solution of the Long Rod Penetration Equations". International Journal of Impact Engineering. 11 (2): 225–231. doi:10.1016/0734-743X(91)90008-4.
- Segletes, Steven B.; Walters, William P. (2002). Efficient Solution of the Long-Rod Penetration Equations of Alekseevskii-Tate (PDF) (Report). ARL-TR-2855. Aberdeen, MD: Army Research Lab Aberdeen Proving Ground MD.
- Segletes, Steven B.; Walters, William P. (2003). "Extensions to the Exact Solution of the Long-Rod Penetration/Erosion Equations" (PDF). International Journal of Impact Engineering. 28 (4): 363–376. doi:10.1016/S0734-743X(02)00071-4. Retrieved 23 June 2011.