쌍곡선 궤적

다음에 대한 시리즈 일부
아스트로다이나믹스
궤도역학
궤도 원소 압시스 근막염의 논거 편심성 기울기 평균 이상 현상 궤도 노드 반주축 참 변칙
기준 2차체 궤도 유형 괴벽. 원궤도 타원 궤도 전송 궤도 (호만 전이 궤도 바이엘립트 전이 궤도) 포물선 궤도 쌍곡 궤도 방사 궤도 붕괴 궤도
방정식 동적 마찰 탈출속도 케플러 방정식 케플러의 행성 운동 법칙 궤도 주기 궤도 속도 표면 중력 특정 궤도 에너지 점-비바 방정식
천체역학
중력 영향 바리센터 힐 구 섭동 영향권
N-바디 궤도 라그랑쥬 포인트 (할로 궤도) 리사주 궤도 랴푸노프 궤도
엔지니어링 및 효율성
비행 전 엔지니어링 질량비 페이로드 분율 추진제 질량분수 티올코프스키 로켓 방정식
효율성 측정 그라비티 어시스트 오베르 효과
v t

우주역학이나 천체역학에서 쌍곡선 궤적은 중심 물체의 중력에서 벗어날 수 있을 만큼 충분한 속도를 가진 중심체 주위의 물체의 궤적을 말한다.그 이름은 뉴턴 이론에 따르면 그러한 궤도가 하이퍼볼라 모양을 하고 있다는 사실에서 유래되었다.보다 기술적인 측면에서 이는 궤도 편심률이 1보다 크다는 조건으로 표현할 수 있다.

단순화된 가정 하에서, 이 궤적을 따라 이동하는 신체는 중심 신체에 상대적인 최종 초과 속도에 안착하면서 무한을 향해 돌진할 것이다.포물선 궤도와 유사하게, 모든 쌍곡선 궤도는 탈출 궤적이기도 하다.쌍곡선 궤도의 특정 에너지는 양이다.

중력 슬링샷에 사용되는 행성 플라이비스는 쌍곡선 궤적을 사용하여 행성의 영향권 내에서 설명할 수 있다.

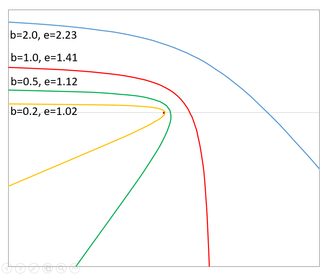
쌍곡선 궤적을 설명하는 매개변수

타원궤도와 마찬가지로, 주어진 시스템에 대한 쌍곡선 궤적은 준주축과 편심률에 의해 정의될 수 있다(거부 방향).그러나 쌍곡선 궤도를 돌면 다른 매개변수가 신체의 움직임을 이해하는 데 더 유용할 수 있다.다음 표에는 표준 가정 하에서 다른 가정에 따라 쌍곡선 궤적을 따르는 신체의 경로를 설명하는 주요 매개변수와 이들을 연결하는 공식이 열거되어 있다.

이러한 방정식은 부정확할 수 있다.추가 참고자료가 필요하다.

쌍곡 궤도 방정식

요소	기호	공식	$∞{\$$또는{\displaystyle }$ ${\displaystyle a}$ ) $$$및{\displaystyle }$ b ${\displaystyle b}$ 사용
표준 중력 파라미터	$\displaystyle \mu \,}$	${\displaystyle {\frac {v^{2}}{(2/r-1/a)}}}$	${\displaystyle bv_{\nothy}^{2}\nothes \theta_{\nothy}}}$
편심률(>1)	$(\displaystyle e}$	${\displaystyle {\frac {\ell}{r_{p}:1}}$	${\displaystyle {\sqrt {1+b^{2}/a^{2}}:$
반주축(<0)	$A\,\!}$	${\displaystyle 1/(2/r-v^{2}/\mu )}$	${\displaystyle -\mu /v_{\nothy}^{2}}$
쌍곡선 초과 속도	${\displaystyle v_{\fty}}$	${\displaystyle {\sqrt {-\mu /a}}$
(외부) 점근각	$_{\displaystyle 2\theta_{\infully }}$	${\displaystyle 2\cos ^{-1}(-1/e)}$	${\displaystyle \pi +2\tan ^{-1}(b/a)}$[2]
점근과 결합 축 사이의 각도 쌍곡선 접근 경로의	$2\displaystyle 2\nu }$	${\displaystyle 2\theta _{\nothy}-\pi }$	${\displaystyle 2\sin ^{-1}{\bigg (}{\frac {1}{{p}v_{\inflt }^{2}/\mu )}}{\bigg )}}}}}}}}}}}}}$
충격 매개변수(반미관 축)	$(\displaystyle b)$	${\displaystyle -a{\sqrt {e^{2}-1}$	${\displaystyle }$
반유성직장	$\displaystyle \ell }$	${\displaystyle a(e^{2}-1)}$	${\displaystyle -b^{2}/a=h^{2}/\mu }$
페리압시스 거리	${\displaystyle r_{p}}$	${\displaystyle -a(e-1)}$	${\displaystyle {\sqrt {a^{2}+b^{2}}}}+a}$
특정 궤도 에너지	$\displaystyle \varepsilon }$	$-\mu /2a}$	${\displaystyle v_{\put }^{2}/2}$
특정 각운동량	$(\displaystyle h}$	${\displaystyle {\sqrt {\mu \ell}}}$	${\displaystyle bv_{\fty}}$
시간 당 쓸어올린 영역	${\displaystyle {\frac {\Delta A}{\Delta t}}$	${\displaystyle {\frac {h}{2}}:}$

반주축, 에너지 및 쌍곡선 초과 속도

반주축$displaystyle a\,\!}$)은 쌍곡선 궤적으로 바로 보이지는 않지만 두 점증상이 교차하는 지점까지의 거리인 만큼 구성할 수 있다.일반적으로 관례상 다양한 방정식을 타원 궤도와 일치시키는 것은 음이다.

반주축은 ${\displaystyle }$ 궤도 에너지( energy ${\$ $\backslash ,\})$ 또는 특성$$ 에너지 $C{\displaystyle {}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$에 직접 연결되며, 거리가 무한대로 기울면서 신체가 도달하는 속도, 쌍곡 초과 속도(${\displaystyle {}_{}}$ ${\displaystyle {\infty \mathrm{}}_{}}$ $displaystyle v_{\port },\},\}!}).$

${\displaystyle v_{}^{}}$ ${\displaystyle {\infty \mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$= ${\displaystyle 2}$ ${\displaystyle ϵ}$= ${\displaystyle {C\mathrm{}}_{}}$ ${\displaystyle {}_{}}$= -${\displaystyle \mu }$/ ${\displaystyle a}$ ${\displaystyle v_{\infit }^{2}=2\epsilon=2\c_{3}=-\mu$/a$$${\displaystyle \}}$ $또는{\displaystyle }$a = -${\displaystyle \mu {}_{}^{}}$ / v${\displaystyle {\mathrm{}}_{\mathrm{}}^{}}$2 {\$displaystystysty$a=-{$v_{{\mu_{\nmu_${\}}}}}}}}}}}}}}}}}}}2$}}:}}}}}}}}}}}}}}}}}}}}}}$

여기서: $\mu {\displaystyle }$= ${\displaystyle \mathrm{Gm}}$ $displaystyle \mu,\!}$은(는) 표준 중력 매개변수, ${\displaystyle {C\mathrm{}}_{}}$ 3 ${\$은(는) 특성 에너지로서$$, 행성간 임무 계획 시 일반적으로 사용된다.

총 에너지는 쌍곡선 궤적(타원 궤도에 대해 음성이므로)의 경우 양성이라는 점에 유의하십시오.

접근과 출발 사이의 편심 및 각도

쌍곡선 궤적을 사용하는 경우 궤도 편심률(${\displaystyle }$ ${\$ e$\,}$)은 1보다 크다.이심률은 점근상 사이의 각도와 직접적인 관련이 있다.기이함이 1을 조금 넘는 하이퍼볼라는 날카로운 "v"모양이다.$e{\displaystyle }$= ${\displaystyle 2\sqrt{\mathrm{}}}$ ${\$ e$={\sqrt{2}}$에서 점근은 직각이다.e> $[\displaystyle e>2}$을(를) 사용하면 점근 거리는 120° 이상 떨어져 있고, 근막거리는 반주축보다 크다.편심성이 더욱 증가함에 따라 운동은 직선에 접근한다.

중심체로부터의 점근 방향과 점근각 사이의 각도는 거리가 무한대로 기울어짐에 따른 참된 이상 현상이다($$${\displaystyle {}_{}}$ ${\displaystyle {\infty \mathrm{}}_{}}$ \${\displaystyle {}_{}}$\ \ \$theta$ _${\flotty$_ $_$$,}).$ $따라서{\displaystyle \mathrm{}}$ 2${\displaystyle {\mathrm{}}_{}}$\ \ $displaystyle 2\tea _{\$ftimptottottote 사이$)$이다.그러면

${\displaystyle \theta {}_{}}$= ${\displaystyle {\cos }^{}}$ -${\displaystyle 1^{}}$ ${\displaystyle {}^{}}$(${\displaystyle }$- ${\displaystyle 1}$/ $e$${\displaystyle }$) ${\$ 또는$$ $e{\displaystyle }$=${\displaystyle }$- ${\displaystyle 1}$/ ${\displaystyle \cos }$ ${\displaystyle {}_{\mathrm{}}}$ ${\displaystyle \backslash {}_{}}$ {\$displaysty$ style $e=-1/\cos \ta{\}},},}$

충격 매개변수 및 가장 가까운 접근 거리

충격 매개변수는 흔들리지 않는 경로에서 계속된다면 가장 가까운 거리에서 중심체를 놓칠 수 있는 거리를 의미한다.신체가 중력을 경험하고 쌍곡선 궤적을 따르는 경우 그것은 쌍곡선의 반 미니어처 축과 같다.

우주선이나 혜성이 행성에 접근하는 상황에서는 충격 매개변수와 초과 속도를 정확하게 알 수 있을 것이다.만약 중심체가 알려지면, 접근하는 주체가 얼마나 근접한 지 등 궤적을 이제 찾을 수 있다.만약 이것이 행성의 반지름보다 작다면 충격이 예상되어야 한다.가장 가까운 접근 거리 또는 주변 거리는 다음과 같다.

${\displaystyle r_{p}=-a(e-1)=\mu /v{_{\inflt }{{\inflt }{1+(bv{_{}}}}^{2}}/\mu ){2}}-1)}$

따라서 12.5km/s의 속도로 지구에 접근하는 혜성(유효한 반경 ~6400km)이 지구와의 충돌을 피하기 위해서라면(외부 태양계로부터 오는 신체의 대략적인 최소 접근 속도) 충격 매개변수는 적어도 8600km, 즉 지구 반경보다 34% 더 많아야 할 것이다.5.5 km/s의 속도로 외부 태양계로부터 목성(반경 70000 km)에 접근하는 신체는 충돌을 피하기 위해 충격 매개변수가 최소 77만 km 또는 목성 반지름의 11배여야 한다.

중심체의 질량을 알 수 없는 경우, 표준 중력 매개변수, 즉 그 질량은 충격 매개변수 및 접근 속도와 함께 작은 신체의 편향에 의해 결정될 수 있다.전형적으로 이 모든 변수들은 정확하게 결정될 수 있기 때문에, 우주선 비행은 신체의 질량을 충분히 추정할 수 있을 것이다.

${\displaystyle \mu }$= ${\displaystyle b{\mathrm{}}_{}^{}}$ ${\displaystyle \mathrm{2탄}\Delta \mathrm{}}$/ 2 ${\displaystyle \mu =bv_{\inflt }^{2}\tan \ / /$2} 여기서$$ Δ${\displaystyle }$= ${\displaystyle {}_{}}$ -${\displaystyle {}_{}}$- -$$ {\$displaysty$\ \ = $2\theta _{\inftra-\pi }}$은 작은 몸체가 직선으로 꺾어지는 각도다$$.

운동 방정식

포지션

쌍곡선 궤적에서 참 이상 징후 $\theta {\displaystyle }$ ${\displaystyle \theta}$은 궤도 방정식에 의해 궤도를 선회하는 물체 사이의 거리(${\displaystyle }$ ${\$ r$\backslash ,\})$에 연결된다$$.

${\displaystyle r={\frac {\ell }{1+e\cdot \cdot \coses \theta}}}$

참 변칙 θ과 편심 변칙 E(대체로 쌍곡 변칙 H) 사이의 관계는 다음과 같다.^[3]

${\displaystyle \cosh {E}={{\cos {\theta }+e} \over {1+e\cdot \cos {\theta }}}}$ or ${\displaystyle \tan {\frac {\theta }{2}}={\sqrt {\frac {e+1}{e-1}}}\cdot \tanh {\frac {E}{2}}}$ or ${\displaystyle \tanh \frac{E}{2}=\sqrt{\frac{e-1}{}}}$${\$

편심 이상 징후 E는 케플러 방정식에 의한 평균 이상 징후 M과 관련이 있다.

$M=e=sinh E-E}$

평균 이상 징후는 시간에 비례한다.

${\displaystyle M}$= ${\displaystyle \mu }$ -${\displaystyle \sqrt{\frac{{3\mathrm{}}^{}}{}}}$.${\displaystyle }$( t -$τ$)${\displaystyle }$, ${\displaystyle M={\sqrt {\frac {}{-a^{3}}}}.}$ 여기서$$ μ는 중력 파라미터이고 a는 궤도의 반주축이다.

비행 경로 각도

비행 경로 각도( ()는 속도 방향과 방사 방향과 직각을 이루는 각도로서, 근거리에서는 0이며 무한대에서는 90도를 지향하는 경향이 있다.

${\displaystyle \tan(\phi )={\frac {e\cdot \sin \sin \theta }{1+e\cdot \coses }}}$

속도

표준 가정 하에서 쌍곡선 궤적을 따라 이동하는 신체의 궤도 속도(${\displaystyle }$ ${\$는 vis-viva 방정식을 통해 다음과 같이 계산할 수 있다.

${\displaystyle v={\sqrt {\mu \left2 \over{r}-{1 \over {a}\오른쪽)}}}$

여기서:

• $[\$은(는) 표준 중력 파라미터,
• $[\$은(는) 중심체로부터 선회하는 차체의 방사상 거리,
• ${\displaystyle a}$ $displaystyle$ a$\,\!]$는 (음) 반주축이다.

표준 가정 하에서 궤도의 어느 위치에서든 궤도 속도(${\displaystyle }$ ${\$ v$\,}),$ $$국소 탈출 속도(${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ s ${\c{v_{esc$ 쌍곡 초과 속도(${\displaystyle {}_{}}$ ${\displaystyle {\infty \mathrm{}}_{}}$ $displaystyle v_{\fty},\})$에 대한 관계는 다음과 같다.$$

${\displaystyle v^{2}={v_{esc}^{2}+{v_{\nothy }^{2}}$

이는 탈출 속도까지 가속할 필요가 있는 위의 비교적 작은 추가 델타-V는 무한대에서 상대적으로 큰 속도를 초래한다는 것을 의미한다는 점에 유의한다.예를 들어 탈출 속도가 11.2km/s인 곳에서 0.4km/s를 더하면 3.02km/s의 쌍곡 초과 속도가 발생한다.

${\displaystyle {\sqrt {11.6^{2}-11.2^{2}}}=3.02}$

이것은 오베르스 효과의 한 예다.반대는 또한 사실이다. 속도가 탈출 속도 이하로 떨어지기 위해서, 몸을 포획하기 위해서 쌍곡선 초과 속도(예를 들어 근위기에 의한 항력)에 비해 신체는 많이 느려질 필요가 없다.

방사 쌍곡선 궤적

방사형 쌍곡선 궤적은 두 물체의 상대 속도가 항상 탈출 속도를 초과하는 직선상의 비주기적 궤적을 말한다.두 가지 경우가 있는데, 시체가 서로에게서 멀어지거나 서로 쪽으로 움직인다는 것이다.이것은 반 미니어처 축 = 0, 편심 = 1을 갖는 쌍곡 궤도다.이심률은 1이지만 포물선 궤도는 아니다.

상대론적 이체 문제

일반상대성이성의 2체 문제의 맥락에서, 다른 하나의 중력에서 벗어날 수 있을 만큼 충분한 에너지를 가진 물체의 궤도는 더 이상 하이퍼볼라처럼 형성되지 않는다.그럼에도 불구하고, 이러한 유형의 궤도를 설명하기 위해 "하이퍼볼릭 궤적"이라는 용어가 여전히 사용된다.

참고 항목

• 궤도
• 궤도 방정식
• 케플러 궤도
• 궤도 목록
• 유성 플라이비
• 쌍곡성 소행성
• 쌍곡 혜성

참조

외부 링크

• 궤도
• 오르빗
• 쌍곡선