궤도 원소

궤도 원소는 특정 궤도를 고유하게 식별하는 데 필요한 매개변수다.천체역학에서 이 원소들은 케플러 궤도를 사용하는 두 개의 몸체 시스템에서 고려된다.같은 궤도를 수학적으로 기술하는 방법에는 여러 가지가 있지만, 각각 6개의 매개변수 집합으로 구성된 특정한 체계들은 천문학이나 궤도 역학에서 흔히 사용된다.

실제 궤도와 그 원소들은 다른 물체에 의한 중력 동요와 일반 상대성 효과로 인해 시간이 지남에 따라 변한다.케플러 궤도는 특정 시간에 궤도에 대한 이상화된 수학적 근사값이다.

케플러 원소

이 다이어그램에서 궤도면(노란색)은 기준면(회색)과 교차한다.지구 궤도를 도는 인공위성의 경우 기준면은 보통 지구의 적도면이고, 태양 궤도에 있는 인공위성의 경우 황도면이다.이 교차점은 질량의 중심을 오름차순과 내림차순 노드와 연결하기 때문에 노드의 선이라고 불린다.기준면은 버날 포인트(♈︎)와 함께 기준 프레임을 설정한다.

전통적인 궤도 원소는 요하네스 케플러와 그의 행성 운동 법칙에 이은 6개의 케플러 원소다.

관성 프레임에서 볼 때, 궤도를 선회하는 두 개의 몸체는 뚜렷한 궤도를 추적한다.이 궤적들은 각각 질량의 공통의 중심에 초점을 두고 있다.신체 중 하나에 중심을 둔 비침투 프레임에서 볼 때, 반대 신체의 궤적만 뚜렷이 나타난다; 케플러 원소들은 이러한 비침투 궤적을 설명한다.궤도는 어떤 몸을 기준으로 사용하느냐에 따라 두 세트의 케플러 원소를 가지고 있다.기준체(보통 가장 거대하다)는 1차체, 다른 1차체는 2차체라고 한다.1차 질량은 반드시 2차 질량보다 많은 것은 아니며, 신체가 같은 질량일 때에도 궤도 원소는 1차 질량의 선택에 따라 달라진다.

타원의 모양과 크기를 정의하는 두 가지 요소:

편심률( $e$ )—타원 모양, 원(도표에는 표시되지 않음)에 비해 얼마나 긴지를 기술한다.
Semimajor 축 ( $a$ ) — periapsis와 apapappsis 거리의 합을 2로 나눈다.고전적인 2체 궤도의 경우 세미조르 축은 질량 중심에서 육체의 거리가 아니라 육체의 중심 사이의 거리를 의미한다.

두 원소는 타원이 내장된 궤도면의 방향을 정의한다.

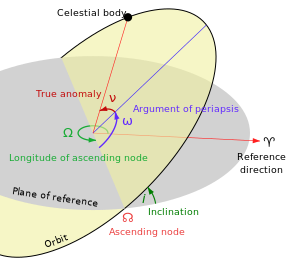
기울기( $i$ ) — 기준면에 대한 타원의 수직 기울기, 상승 노드(궤도가 기준면을 통해 위쪽으로 통과하는 곳, 다이어그램의 녹색 $각도$ i)에서 측정.기울기 각도는 궤도면과 기준면 사이의 교차선에 수직으로 측정된다.타원의 어떤 세 점이라도 타원 궤도면을 정의할 것이다.평면과 타원은 둘 다 3차원 공간에서 정의된 2차원 물체다.
상승 노드의 경도( $Ω$ ) — 기준 프레임의 버날 포인트에 대해 타원의 상승 노드(궤도가 기준면을 통해 위쪽으로 통과하는 위치, $☊$ 으로 상징됨)의 방향을 수평으로 맞춘다.이 값은 기준면에서 측정되며, 다이어그램에서 녹색 각도 $Ω$ 으로 표시된다.

나머지 두 요소는 다음과 같다.

periapsis( $Ω$ )의 인수는 궤도 평면에서의 타원의 방향을 상승 노드에서 periapsis까지 측정한 각도(위성 물체가 궤도를 도는 1차 물체에 도달하는 가장 가까운 지점, 다이어그램에서 파란 각도 $Ω$ )로 정의한다.
epoch( $t 0$ )의 참 변칙( $true$ , $θ$ 또는 $f$ )은 특정 시간("epoch")에 타원을 따라 선회하는 신체의 위치를 정의한다.

평균 이상 징후 $M$ 은 수학적으로 편리한 가상의 "각도"로 시간에 따라 선형적으로 변화하지만 실제 기하학적 각도와 일치하지 않는다.그것은 타원 평면의 실제 기하학적 각도를 나타내는 참 변칙 $ν$ 으로 변환될 수 있는데, 이 변칙 ν은 페리압시스(중앙체에 가장 근접한 접근)와 궤도를 선회하는 물체의 위치 사이에 있다.따라서 다이어그램에서 실제 이상 징후는 적색 각도 $ν$ 으로 표시되며, 평균 이상 징후는 표시되지 않는다.

경사의 각도, 오름차순의 경도, 그리고 근막의 인수는 기준 좌표계에 상대적인 궤도의 방향을 정의하는 오일러 각이라고도 설명할 수 있다.

비엘리틱 궤적도 존재하지만 닫히지 않으며 따라서 궤적이 아니라는 점에 유의하십시오.편심도가 1보다 크면 궤적이 하이퍼볼라다.편심도가 1과 같고 각운동량이 0이면 궤적이 방사형이다.편심도가 1이고 각운동량이 있다면 궤적은 포물선이다.

필수 매개 변수

관성 기준 프레임과 임의의 에폭(특정 시점)을 감안할 때, 임의의 및 방해받지 않는 궤도를 명확하게 정의하기 위해 정확히 6개의 매개변수가 필요하다.

그 문제에는 6도의 자유도가 포함되어 있기 때문이다.이것들은 위치를 정의하는 3개의 공간적 차원(카테시안 좌표계에서의 $x$ , $y$ , $z$ )에 해당하며, 각 차원에서의 속도도 여기에 해당한다.이것들은 궤도 상태 벡터라고 설명할 수 있지만, 이것은 궤도를 나타내기에는 종종 불편한 방법이기 때문에 케플러안 원소들이 대신 일반적으로 사용되는 것이다.

때때로 이 시대는 기준 프레임의 일부라기보다는 "7" 궤도 매개변수로 간주된다.

만일 원소 중 하나가 0인 순간에 그 시대가 있다고 정의된다면 불특정 원소의 수는 5개로 줄어든다.(궤도를 정의하기 위해서는 여전히 여섯 번째 매개변수가 필요하며, 단지 실제 시계 시간과 관련하여 그 시대의 정의에 따라 숫자적으로 0으로 설정되거나 "이동"될 뿐이다.)

대체 매개 변수

케플러안 원소는 수동 변환이나 컴퓨터 소프트웨어로 궤도 상태 벡터(위치에 대한 3차원 벡터, 속도에 대한 또 다른 벡터)에서 얻을 수 있다.^[1]

다른 궤도 매개변수는 주기, 아포캡시스, 주립자와 같은 케플러안 요소에서 계산할 수 있다.(지구 궤도를 돌 때, 마지막 두 용어는 어포지와 퍼리지로 알려져 있다.)케플러 원소 집합에서 반주축 대신 기간을 지정하는 것이 일반적이며, 각각은 중심체에 표준 중력 파라미터인 $GM$ 이 주어진다면 다른 축에서 계산할 수 있기 때문이다.

epoch에서의 평균 이상 대신 평균 이상 $징후$ M, 평균 경도, 참 이상 징후 $ν 0$ 또는 (경도) 편심 이상 징후가 사용될 수 있다.

예를 들어, "emoch에서의 mean 변칙" 대신 "mean 변칙"을 사용하는 것은 시간 $t$ 를 일곱 번째 궤도 원소로 지정해야 함을 의미한다.때때로 평균 이상 징후는 (이 시대의 적절한 정의를 선택하여) epoch에서 0이라고 가정하고, 5개의 다른 궤도 원소만 명시하도록 한다.

다양한 천체에는 서로 다른 원소 집합이 사용된다.편심, $e$ , 그리고 반주축, $a$ 또는 periapsis의 거리, $q$ 중 하나를 사용하여 궤도의 모양과 크기를 명시한다.상승 노드의 경도 $Ω$ , 기울기, $i$ 및 periapsis, $Ω$ 또는 periapsis의 경도 ,은 $평면$ 에서 궤도의 방향을 명시한다.epoch에서의 경도 $L 0$ , epoch에서의 평균 이상, M $또는 0$ perihelion passion의 시간 $T$ 를₀ 사용해 궤도에서 알려진 점을 지정한다.선택사항은 춘분 또는 노드를 1차 참조로 사용할지 여부에 따라 결정된다.반주축은 평균 운동과 중력 질량을 알면 알려져 있다.^[2]^[3]

$또한 0$ 시간에 $관한 0$ 다항식 함수로 M이나 L 중 하나를 중간 단계로 하지 않고 평균 이상( $M$ )이나 평균 경도( $L$ )를 직접 표현하는 경우도 꽤 흔하다.이 표현 방법은 계수의 하나로 평균 운동( $n$ )을 다항식으로 통합한다.외형은 $L$ 이나 $M$ 이 좀 더 복잡한 방식으로 표현될 것이지만, 우리는 궤도 원소 하나를 덜 필요로 하는 것처럼 보일 것이다.

또한 평균 운동은 궤도 주기 $P$ 의 인용 뒤에 가려질 수 있다.^{[clarification needed]}

궤도 원소 세트
오브젝트	사용된 요소
주요 행성	$e, a, i, Ω, ϖ, L 0$
혜성	$e, q, i, Ω, Ω 0, T$
소행성	$e, a, i, Ω, Ω 0, M$
두 줄 원소	$e 0, i, Ω, Ω, n, M$

오일러 각도 변환

각도 $Ω$ , $i$ , $Ω$ 은 좌표계의 방향을 특징짓는 오일러 각도(이 글에서 사용된 표기법에서 $α$ , $β$ , $γ$ 에 대응함)이다.

$관성$ 좌표 틀 $î$ , $ŷ$ , $Kẑ$ 에서 x $̂,$ $ŷ$ $,$ $ẑ$

여기서:

$î$ , $ĵ$ 은 중심체의 적도면에 있다. $î$ 은 춘분 방향이다. $ĵ$ 은 $î$ 에 수직이며 $î$ 과 함께 기준면을 정의한다. $K̂$ 는 기준면에 수직이다.태양계에 있는 신체의 궤도 요소들(행성, 혜성, 소행성, ...)은 보통 그 평면으로 황색체를 사용한다.
$x̂,$ $ŷ$ 은 궤도면에 있고 x $̂$ 은 periacenter(periapsis) 방향으로 있다. $ẑ$ 은 궤도면에 수직이다. $ŷ$ 은 $x̂$ 과 $ẑ$ 에 상호 수직이다.

$그런$ 다음, ,, ,, $K$ $coordinate$ 좌표 프레임에서 오일러 각 $Ω$ , $i$ , $Ω$ 을 $갖는$ x $,,$ ,, $frame$ 프레임으로의 변환은 다음과 같다.

{\displaystyle{\begin{정렬}x_{1}&, =\cos\cdot\cos\omega-\sin \Omega\cdot \cosi\cdot \sin \omega\와 같이 \Omega, \\x_{2}&,=\sin \Omega\cdot\cos\omega +\cos\cdot \cosi\cdot \sin \omega\와 같이 \Omega, \\x_{3}&, =\sini\cdot \sin \omega, \\\,\\y_{1}&, =-\cos\cdot\sin\omega-\sin \Omega\cdot \cosi\cdot \cos \omega\와 같이 \Omega, \\y_{2}&.;=-\sin \Omega \cdot\sin \omega +\cos \Omega \cdot \cos i\cdot \cos \omega \ ;\\y_{3}&=\sin i\cdot \cos \omega \ ;\\\,\\z_{1}&=\sin i\cdot \sin \Omega \ ;\\z_{2}&=-\sin i\cdot \cos \Omega \ ;\\z_{3}&=\cos i\ ;\\\,\end{aligned}}}

\left[{\put{array}{ccc}x_{1}&x_{2}&x_{3}}\\y_{1}&, y_{2}&, y_{3}\\z_{1}&, z_{2}&, z_{3}\end{배열}}\right]=\left[{\begin{배열}{ccc}\cos\omega&\sin \omega&0\\-\sin \omega&\cos \omega&0\\0&, 0&, 1\end{배열}}\right]\,\left[{\begin{배열}{ccc}1&, 0&, 0\\0&,\cos i&, \sin i\\0&, -\sin i&,\cos i\end{배열}}\right]\,\left-LSB-{\begin{배열}{ccc}\cos cm이다.오메가&\sin \Omega&0\\-\sin \Omega&\cos \Omega&0\\0&, 0&, 1\end{array}\오른쪽]\,;

어디에

{\begin{aigned}\mathbf {\x} &=x_{1}\mathbf {\hat {I} +x_{2}\mathbf {\j} +x_{3}}\mathbf {\hat {K}} ~;\\\mathbf {\hat {y}} &=y_{1}\mathbf {\hat {I}} +y_{2}\mathbf {\hat {J}} +y_{3}\mathbf {\hat {K}} ~;\\\mathbf {\hat {z}} &=z_{1}\mathbf {\hat {I}} +z_{2}\mathbf {\hat {J}} +z_{3}\mathbf {\hat {K}} ~.\\\,\end{aligned}}

x-y-z 시스템에서 3개(2개) 좌표가 주어진 I-J-K 시스템의 3개 좌표를 계산하는 역 변환은 역행렬로 표현된다.행렬 대수 규칙에 따르면 3회전 행렬의 곱셈의 역행렬은 3 행렬의 순서를 뒤집고 3 오일러 각의 기호를 전환하여 구한다.

$x̂,$ $ŷ$ , $ẑ$ 에서 오일러 각도 $Ω$ , i, $Ω$ 으로 변환:

{\begin{igned}\Oomega &=\operatorname {arg} \left(-z_{2},z_{1}\right)\\i&=\filename {arg} \left(z_{3},{\sqrt {{z_{1}:{1}^{2}+{z_{2}}:}\오른쪽)\\\omega &=\messagedname {arg} \left(y_{3}},x_{3}\right)\\\,\end{aigned}}}}

여기서 $arg(x, y)$ 는 표준 함수로 계산할 수 있는 극지방 인수를 나타낸다.많은 프로그래밍 언어로 제공되는 atan2(y,x)

궤도예측

완벽하게 구형 중심체와 제로 섭동의 이상적인 조건에서 평균 이상을 제외한 모든 궤도 원소는 상수다.평균 이상 징후는 시간에 따라 선형적으로 변화하고 평균 움직임에 따라 ^[2]확장되며

n={\sqrt {\frac {}{a^{3}}}}}.

따라서 임의의 순간 $t$ 에서₀ 궤도 파라미터가 [ $e 0,$ $a 0$ , $i 00,$ Ω, $Ω 0,$ $M 0]$ 인 경우, $시간$ t = $t 0$ + $Δt$ 의 $원소$ 는₀ $[e 0$ , a $, i 00, Ω 0, Ω 0,$ M + $Δt]$ 에 의해 주어진다.

섭동 및 원소 분산

동요하지 않는, 두 개의 몸체, 뉴턴의 궤도는 항상 원뿔형 단면이기 때문에 케플러의 원소는 타원체, 파라볼라 또는 하이퍼볼라를 정의한다.실제 궤도는 동요를 가지고 있으므로, 주어진 케플러안 원소 집합은 오직 시대에서의 궤도를 정확하게 묘사한다.궤도 원소의 진화는 일차 이외의 신체의 중력, 일차, 대기 드래그, 상대론적 효과, 방사선 압력, 전자기력 등에 의해 일어난다.

케플러안 원소들은 시대와 가까운 시기에 유용한 예측을 하는 데 종종 사용될 수 있다.또는 실제 궤적을 오스카("키스" 또는 터치)하는 케플러안 궤도의 시퀀스로 모델링할 수 있다.그것들은 또한 라그랑주, 가우스, 델라우나이, 푸앵카레 또는 힐에 의해 개발된 다른 형태로 나타나는 소위 행성 방정식, 미분 방정식으로 설명될 수 있다.

두 줄 원소

케플러안 요소 매개변수는 다양한 형식의 텍스트로 인코딩할 수 있다.그 중 가장 흔한 것은 NASA/NORAD "투라인 요소"(TLE) 형식인데,^[4] 원래는 80개의 칼럼 펀치 카드와 함께 사용하도록 설계되었지만, 여전히 가장 일반적인 형식이기 때문에 사용 중이며, 현대적인 모든 데이터 저장장치에서도 쉽게 처리할 수 있다.

응용 프로그램 및 물체 궤도에 따라 30일 이상 경과한 TLEs에서 도출된 데이터는 신뢰할 수 없게 될 수 있다.궤도 위치는 SGP / SGP4 / SDP4 / SGP8 / SDP8 알고리즘을 통해 TLEs에서 계산할 수 있다.^[5]

두 줄 요소의 예:^[6]

1 27651U 03004A 07083.496287 .00000119 00000-119 00000-0 30706-4 0 2692 2 27651 039.9951 132.2059 0025931 073.4582 286.9047 14.81909376225249

델라우나이 변수

Delaunay 궤도 원소는 Charles-Eugenne Delaunay에 의해 달의 움직임에 대한 연구 중에 소개되었다.^[7]일반적으로 델라우나이 변수라고 불리는 그것들은 작용각 좌표인 표준 변수들의 집합이다.각도는 케플러안 각도의 일부에 대한 단순한 합이다.

$\ell =M+\omega +\Omega ~:$ = $\ell =M+\omega +\Omega ~:$ + $\ell =M+\omega +\Omega ~:$ + $\ell =M+\omega +\Omega ~:$ : $\ell =M+\omega +\Oomega ~:$ 평균 $\ell =M+\omega +\Omega ~:$ 경도
$g=\omega +\Omega ~:$ = $g=\omega +\Omega ~:$ + $g=\omega +\Omega ~:$ : $g=\omega +\Oomega ~:$ periapsis 경도 $g=\omega +\Omega ~:$
$h=\Omega ~:$ = $h=\Omega ~:$ : $h=\Oomega ~:$ 오름차순 노드의 경도 $h=\Omega ~:$

각각의 결합 모멘트, $L$ , $G$ , $H$ 와 함께.^[8]순간 $L$ , G, $H$ 는 작용 변수로서 케플러아 $요소$ a, $e$ , $i$ 의 보다 정교한 조합이다.

예를 들어 계층적 3중 시스템에서 코자이-리도프 진동을 조사하는 동안 델라우나이 변수는 천체 역학에서 섭동 계산을 단순화하는 데 사용된다.^[8]Delaunay 변수의 이점은 $e$ 및/ $또는$ i가 매우 작을 때 잘 정의되고 비노래적( $h$ , 용인할 수 있는 h 제외)으로 유지된다는 것이다.시험 입자의 궤도가 매우 원형인 경우( $e\approx 0$ $e\approx 0$ $e\approx 0$ {\ $displaystyle e\$ 약 $0}),$ 또는 매우 "평탄한" $i\approx 0$ ( $i\approx 0$ $≈$ 0 {\ $displaystyle i\$ 약 0}). $i\approx 0$

참고 항목

참조

^ 예를 들어, 와 함께."VEC2TLE". amsat.org.
^ ^a ^b Green, Robin M. (1985). Spherical Astronomy. Cambridge University Press. ISBN 978-0-521-23988-2.
^ Danby, J.M.A. (1962). Fundamentals of Celestial Mechanics. Willmann-Bell. ISBN 978-0-943396-20-0.
^ Kelso, T.S. "FAQs: Two-line element set format". celestrak.com. CelesTrak. Archived from the original on 26 March 2016. Retrieved 15 June 2016.
^ Seidelmann, K.P., ed. (1992). Explanatory Supplement to the Astronomical Almanac (1st ed.). Mill Valley, CA: University Science Books.
^ "SORCE". Heavens-Above.com. orbit data. Archived from the original on 27 September 2007.
^ Aubin, David (2014). "Delaunay, Charles-Eugène". Biographical Encyclopedia of Astronomers. New York, NY: Springer New York. pp. 548–549. doi:10.1007/978-1-4419-9917-7_347. ISBN 978-1-4419-9916-0.
^ ^a ^b Shevchenko, Ivan (2017). The Lidov–Kozai effect: applications in exoplanet research and dynamical astronomy. Cham: Springer. ISBN 978-3-319-43522-0.

외부 링크

Gurfil, Pini (2005). "Euler parameters as nonsingular orbital elements in Near-Equatorial Orbits". J. Guid. Contrl. Dynamics. 28 (5): 1079–1084. Bibcode:2005JGCD...28.1079G. doi:10.2514/1.14760.

"Tutorial". AMSAT. Keplerian elements. Archived from the original on 14 October 2002.

"Orbits Tutorial". marine.rutgers.edu.

"Orbital elements visualizer". orbitalmechanics.info.

Report No. 3 (PDF). celestrak (Report). Spacetrack. North American Aerospace Defense Command (NORAD). – 궤도 원소의 심각한 처리

"FAQ". Celestrak. Two-Line Elements. Archived from the original on 26 March 2016.

"The JPL HORIZONS online ephemeris". – 또한 많은 수의 태양계 객체를 위한 궤도 요소 제공

"Mean orbital parameters". ssd.jpl.nasa.gov. Planetary satellites. JPL / NASA.

"Introduction to exporting". ssd.jpl.nasa.gov. JPL planetary and lunar ephemerides. JPL / NASA.

"State vectors: VEC2TLE". MindSpring (software). Archived from the original on 3 March 2016. – VEC2에 대한 액세스TLE 소프트웨어

"Function 'iauPlan94'" (C software source). IAU SOFA C Library. – 주요 행성의 궤도 요소

[1] 예를 들어, 와 함께."VEC2TLE". amsat.org.

[Green-2] Green, Robin M. (1985). Spherical Astronomy. Cambridge University Press. ISBN 978-0-521-23988-2.

[Danby-3] Danby, J.M.A. (1962). Fundamentals of Celestial Mechanics. Willmann-Bell. ISBN 978-0-943396-20-0.

[Kelso_FAQ-4] Kelso, T.S. "FAQs: Two-line element set format". celestrak.com. CelesTrak. Archived from the original on 26 March 2016. Retrieved 15 June 2016.

[5] Seidelmann, K.P., ed. (1992). Explanatory Supplement to the Astronomical Almanac (1st ed.). Mill Valley, CA: University Science Books.

[6] "SORCE". Heavens-Above.com. orbit data. Archived from the original on 27 September 2007.

[Aubin-2014-7] Aubin, David (2014). "Delaunay, Charles-Eugène". Biographical Encyclopedia of Astronomers. New York, NY: Springer New York. pp. 548–549. doi:10.1007/978-1-4419-9917-7_347. ISBN 978-1-4419-9916-0.

[Shevchenko-2017-8] Shevchenko, Ivan (2017). The Lidov–Kozai effect: applications in exoplanet research and dynamical astronomy. Cham: Springer. ISBN 978-3-319-43522-0.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search