교정
Cofibration수학에서, 특히 호모토피 이론에서, 위상 공간들 사이의 연속적인 매핑.
- X
모든 위상 S S에 대해 호모토피 확장 속성을 갖는 경우의 보정입니다. 즉, i i는 각 위상 S S와 모든 연속 f : f, S g \ g g \f 임의의 에 :A × → { hf}에서 f f까지의 A I S 맵: X { g모든 디스플레이 A에 대해 h'(i), t(a) = h(a) → h(a) = h(a) ( h(a, t)가 표시되도록 g{{displaystyle h': X\times I\to S}와 동형 h(X×I)는 표시 간격을 나타낸다
이 정의는 공식적으로 모든 공간에 대한 호모토피 리프팅 특성을 만족시키는 데 필요한 진동의 정의와 이중적입니다. 이것은 위상에서 더 넓은 에크만-힐튼 이중성의 한 예입니다.
교배는 호모토피 이론의 기본 개념입니다.퀼렌은 더 일반적인 범주에서 호모토피 이론을 수행하기 위한 공식 프레임워크로서 모델 범주의 개념을 제안했습니다. 모델 범주는 특정 리프팅 및 인수 분해 공리를 만족시키는 섬유화, 공생 및 약한 동등성이라고 불리는 세 가지 구별된 형태 분류로 부여됩니다.
정의.
호모토피 이론
다음에서 I [ { I = [이(가) 단위 간격을 나타낸다고 .
임의의[1]pg 51 f → {\ f: A ▁sX {\fAS는 X 스타일 X에 대한 확장이 있음을 의미하며, 는 f : X ({ f\S), ∘ ({ fi=의 호모토피를 확장할 수 있음을 합니다. I S - H :X × ({ H IS 여기서
우리는 이 조건을 다음의 교환 다이어그램에서 인코딩할 수 있습니다.
서 S는 콤팩트 오픈 토폴로지가 장착된 S S의 경로 공간입니다.
예
위상학적 구조
위상학자들은 오랫동안 "좋은 부분 공간 임베딩"의 개념을 연구해 왔으며, 이 중 많은 것은 지도가 조정이거나 반대이거나 호몰로지와 관련하여 유사한 형식적 특성을 가지고 있음을 암시합니다.1937년, 보르수크는 X가 이항 정규 공간이라면(X{displaystyle X}는 정규이고, X×I의 곱은 정규) X의 모든 닫힌 부분 공간은 절대 이웃 수축에 대해 호모토피 확장 특성을 갖는다는 것을 증명했다.마찬가지로, 만약 A({displaystyle A})가 X({displaystyle X})의 닫힌 부분 공간이고 부분 공간 포함 A×I ∪ X×1 ⊂ X×I({displaystyle A\times I\cup X\times {1}\subset X\times I)가 절대 이웃 후퇴라면, X({displaystyle X}에 A}를 포함하는 것은 조정이다.[2][2][3]해처의 입문 교과서 대수 위상은 교정과 관련된 단일 호몰로지에서 동일한 길고 정확한 시퀀스를 갖는 좋은 쌍의 기술적 개념을 사용하지만 동등하지 않습니다.교정의 개념은 호모토피 이론적 정의가 공식 분석 및 일반화에 더 적합하기 때문에 이것들과 구별됩니다.
만약 : : {\Y}가 위상 공간 사이의 연속 맵이라면 f {\f의 실린더라고 불리는 관련 위상 가 있습니다.아래의 교환 다이어그램에서 그림과 같이 i iMf}와 r \ rY와 투영맵 Y가 . i i는 교정이고 r는 호모토피 등가입니다.이 결과는 "모든 맵은 호모토피 범주에서 교정과 동일하다"고 요약할 수 있습니다.
Arne Strøm은 모든 맵 {\ f Y 요소가 교정의 구성이며 또한 [4]교정인 호모토피 등가물이라는 이 결과의 강화를 증명했습니다.
포함 x {{ {X가 조정일 경우 구분 기준점가 있는 X X가 잘 조정된다고 합니다.
솔리드 디스크 경계 구의 포함 S D은 모든 {n에 대한 교정입니다.
흔히 사용되는 사실은 세포 포함이 교정이라는 것입니다. (예를 ,( A {\ A이 CW 쌍이면→ X{\ X는 교정입니다.)이것은 이전의 사실과 푸시아웃 하에서조정이 안정적이라는 사실을 따른 것입니다. 푸시아웃은 스타일의 골격에 대한 접착 맵이기 때문입니다.
연쇄 복합체
A}}를 충분한 투영을 가진 아벨 범주로 .
만약 우리가 C + (A) {\displaystyle C_{+}({\mathcal {A}})를 q << 0 {{\displaystyle q<<0}의 0인 체인 복합체의 범주로 둔다면, 약한 등가물은 준동형이고, 섬유는 에피모픽이며, 조화는 맵인 모델 범주 구조가 있다
이들은 정도적으로 모닉이고 코커널 코커(i) {{코커{\은 A{{displaystyle {A에 있는 투영 객체의 복합체입니다.
단순 집합
단순[5]pg 1.3 집합의 SSet}})에는 진동이 정확하게 Kan 진동이고, 공진동은 모두 주입 맵이며, 약한 등가물은 기하학적 실현 함수를 적용한 후 호모토피 등가물이 되는 단순 맵인 모델 범주 구조가 있습니다.
특성.
- 하우스도르프 공간의 경우, 모든 교정은 닫힌 포함(닫힌 이미지가 있는 주입)이며, 결과는 약한 하우스도르프 공간으로 일반화됩니다.
- 보정의 푸시아웃은 보정입니다.즉, g {\g \ A B가 (콤팩트하게 생성된 공간 사이의) 임의의 (연속적인) 이고 i {\ i A가 조정이라면 유도 맵 → {는 조정입니다.
- 매핑 실린더는 i: A → X \ displaystyle i\ to X 및 임베딩(단위 간격의 한쪽 끝에서) i 0 : A → A × I \ displaystyle i_{0}\ display A\ to A \ times I. 즉, 매핑 실린더는 I = X ( A × I )에 의해 \ displaystyle= Mi x \ timesters I로 정의될 수 있다푸시아웃의 i는 모든 공간 X에 대해 매핑 실린더를 생성할 수 있는 정확한 조정입니다.
- X× (\ XI) (×{ )\displaystyle I0으로 후퇴하는 경우에만 보정(A, X)이 있으며, 이는 그림의 모든 타당한 공간에 지도를 유도하기 때문입니다.
- 변형-수축 쌍과 인접 변형-수축 쌍에 대해서도 유사한 동등성이 명시될 수 있습니다.
교배가 있는 구조물
협심증 치환술
모델 M에서 i∗ i X가 교정이 아닌 경우 매핑 Mi가 공생 대체를 형성합니다.사실, 우리가 단지 위상 공간의 범주에서만 작업을 한다면, 한 지점에서 한 공간까지의 지도에 대한 공선 치환은 공선 치환을 형성합니다.
코파이버
A {\ A X의 경우, 우리는 코파이버를 유도 계수 X / {\X/로 정의합니다. 일반적으로f : → {\ f Y의 경우, 코파이버는[1]pg 59 계수 공간으로 정의됩니다.
이는 f f의 매핑 원뿔이다. 호모토피적으로, 코파이버는 f { f Y의 호모토피적 코커널 역할을 한다. 사실, 점이 있는 위상 공간의 경우, 의 호모토피적 코커널
실제로 X → f \ X Y C_의 순서는 삼각형 범주에서 구분 삼각형처럼 작용하는 코파이버 시퀀스와 함께 제공됩니다.
참고 항목
레퍼런스
- ^ a b May, J. Peter. (1999). A concise course in algebraic topology. Chicago: University of Chicago Press. ISBN 0-226-51182-0. OCLC 41266205.
- ^ Edwin Spanier, 대수 위상학, 1966, 57페이지
- ^ Garth Warner, 위상과 호모토피 이론의 주제, 섹션 6.
- ^ Arne Strøm, 호모토피 범주는 호모토피 범주입니다.
- ^ a b Quillen, Daniel G. (1967). Homotopical algebra. Berlin: Springer-Verlag. ISBN 978-3-540-03914-3. OCLC 294862881.
- 피터 메이, "대수 위상학의 간결한 과정": 제6장은 조화를 정의하고 논의하며, 그것들은 전체적으로 사용됩니다.
- Brown, Ronald. "7. Cofibrations". Topology and Groupoids. ISBN 978-1-4196-2722-4. 7장에는 다른 곳에서는 찾을 수 없는 많은 결과가 있습니다.


 각 위상
각 위상 



 f
f
![[0,1]](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
![{\displaystyle I=[0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87ec65159c44769434523e46928bc1b82681f842) (가) 단위 간격을 나타낸다고
(가) 단위 간격을 나타낸다고 







 콤팩트 오픈 토폴로지가 장착된 S
콤팩트 오픈 토폴로지가 장착된 S




 호모토피 등가입니다.이 결과는 "모든 맵은 호모토피 범주에서 교정과 동일하다"고 요약할 수 있습니다.
호모토피 등가입니다.이 결과는 "모든 맵은 호모토피 범주에서 교정과 동일하다"고 요약할 수 있습니다.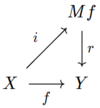


 모든
모든

 교정입니다.)이것은 이전의 사실과 푸시아웃 하에서
교정입니다.)이것은 이전의 사실과 푸시아웃 하에서


 A
A
 (콤팩트하게 생성된 공간 사이의) 임의의 (연속적인)
(콤팩트하게 생성된 공간 사이의) 임의의 (연속적인)  조정입니다.
조정입니다.
 i
i 교정이 아닌 경우 매핑
교정이 아닌 경우 매핑  공생 대체를 형성합니다.사실, 우리가 단지 위상 공간의 범주에서만 작업을 한다면, 한 지점에서 한 공간까지의 지도에 대한 공선 치환은 공선 치환을 형성합니다.
공생 대체를 형성합니다.사실, 우리가 단지 위상 공간의 범주에서만 작업을 한다면, 한 지점에서 한 공간까지의 지도에 대한 공선 치환은 공선 치환을 형성합니다.


 순서는 삼각형
순서는 삼각형 

