보조 펑커스
Adjoint functors수학에서, 특히 범주 이론에서, 결합은 두 개의 functor가 가질 수 있는 관계다.이 관계에 서 있는 두 개의 functor는 보조 functor라고 알려져 있는데, 하나는 왼쪽, 다른 하나는 오른쪽 functor이다.조정형 펑커의 쌍은 수학에서 어디서나 볼 수 있으며 종종 대수 집합에 자유 집단을 건설하거나 또는 위상학적 공간을 압축하여 다음 위치에 건설하는 것과 같은 특정 문제에 대한 "최적 해결책"의 구성(즉, 특정한 보편적 특성을 갖는 물체의 구성)에서 발생한다.정치학
정의상 범주 과(와) 사이의 결합은 한 쌍의 펑거(공변량이라고 가정함)이다.
- : → F {오른쪽 {C G :C → G {
그리고, 객체에 대해, C{\{\의 X{\ 및 {D}의 Y {\displaystyle Y 각 형태론 집합 간의 편향
such that this family of bijections is natural in and . Naturality here means that there are natural isomorphisms between the pair of functors and for a fixed in , and also the pair of functors and {\{D):D {\displaystyle 의 고정 Y 에 대한 \mathrm }{D}에 대한 {\mathcal
Functor 은는) 좌측 조정자 또는 에 대한 좌측 조정자 또는 조정자 또는 에 대한 오른쪽 조정자라고 한다
과(와) 사이의 결합은 C 사이의 동등성의 "약한 형태"와 다소 유사하며, 모든 동등성은 결합이다.많은 상황에서 관련 범주 및 펑터의 적절한 자연적 수정으로 결합을 동등성으로 "업그레이드"할 수 있다.null
용어와 표기법
부성어와 부성어 모두 사용되며, 하나의 용어는 라틴어에서 직접 가져온 것이고, 다른 용어는 불어를 통해 라틴어에서 가져온 것이다.일하는 수학자를 위한 고전 텍스트 범주에서 맥 레인은 둘 사이를 구별한다.가족이 있다.
of hom-set bijections, we call an adjunction or an adjunction between and . If is an arrow in , is the righ 의 부가물(페이지 81).Functor 은(는) 에 왼쪽 이고,G 은참고: 는 그 자체로 과 상당히 다른 오른쪽 맞춤을 가질 수 있다).null
일반적으로 " 은(는) 왼쪽 맞춤이고" "{\}은(는) 오른쪽 맞춤"은 이와 동등하다.null
만약 F가 G에 맞춰져 있다면, 우리는 또한 글을 쓴다.
이 용어는 hilbert T with 의 공간 아이디어에서 유래되었으며, 이는 공식적으로 hom-setset 간의 위와 유사하다.힐버트 공간의 지도에 대한 비유는 어떤 맥락에서 정밀하게 만들어질 수 있다.[1]null
소개 및 동기 부여
슬로건은 "어느 곳에서나 성직자가 일어난다"이다.
— Saunders Mac Lane, Categories for the Working Mathematician
이 글의 긴 예시 목록은 일반적인 수학 구조는 종종 functors에 보조를 맞춘다는 것을 보여준다.결과적으로, 좌/우 부호화 펑커에 대한 일반적인 이론은 유용하고 그렇지 않은 많은 결과의 세부사항을 암호화한다.그러한 일반적인 이론에는 조정된 공구의 다양한 정의의 등가성, 주어진 좌/우 조정된 공칭 공칭 공칭이 각각 대장/한계를 보존한다는 사실(수학의 모든 영역에서 발견되기도 함), 그리고 조건을 제시하지 않는 일반 조정 공칭 공칭 이론이 포함된다.음, 주어진 functor가 왼쪽/오른쪽 보조자임.null
최적화 문제에 대한 솔루션
어떤 의미에서, 조정관은 공식화된 방법을 통해 어떤 문제에 가장 효율적인 해결책을 주는 방법이다.예를 들어 링 이론에서 기본적인 문제는 rng(승수적 정체성을 갖지 않을 수도 있는 링과 같은 것)를 링으로 만드는 방법이다.가장 효율적인 방법은 원소 '1'을 rng에 결합하고, 고리 공리를 만족시키는 데 필요한 모든 요소(예: 링의 각 r에 r+1)를 결합하는 것이며, 공리에 의해 강요되지 않는 새로 형성된 고리에는 어떤 관계도 부과하지 않는 것이다.더욱이 이 구조는 어떤 rng에도 본질적으로 같은 방식으로 작용한다는 점에서 공식적이다.null
이것은 다소 모호하지만 시사적이기는 하지만 범주 이론의 언어로 정밀하게 만들어질 수 있다: 건설은 보편적인 속성을 만족시킬 경우 가장 효율적이며, 펑터를 정의한다면 공식적이다.보편적 특성은 초기 특성과 터미널 특성의 두 가지 유형으로 나타난다.이것들은 이중 관념이기 때문에, 그 중 한 가지에 대해서만 논하면 된다.null
초기 속성을 사용하는 아이디어는 어떤 보조 범주 E의 관점에서 문제를 설정하여 당면한 문제가 E의 초기 대상을 찾는 것과 일치하도록 하는 것이다.이는 최적화(공정에서 가장 효율적인 솔루션을 찾는다는 의미)가 어떤 엄밀한 것을 의미하고, 우월감의 달성처럼 인식 가능하다는 장점이 있다.범주 E는 항상 조정자를 건설하는 펑터의 요소 범주이기 때문에 이 구성에서 공식적이다.null
다시 예시해 봅시다: 주어진 rng R을 가지고, 범주가 rng 동형체 R → S인 범주 E를 만드세요.R → S와1 R → S사이의2 E의 형태는 형태(R → S1, R → S2 → S12)의 역삼각형이며, 여기서1 S → S는2 링맵(정체성을 보존한다)이다.(rng에 단일 링을 포함시키는 것에 대한 R의 쉼표 범주의 정의라는 점에 유의하십시오.)R → S와1 R → S2 사이에 형태론의 존재는 S가1 적어도 우리의 문제에 대한 S만큼2 효율적인 해결책임을 암시한다.S는2 S보다1 공리에 의해 부과되지 않는 더 많은 결합 요소 및/또는 더 많은 관계를 가질 수 있다.따라서 객체 R → R*이 E에서 초기라는 주장, 즉 그것으로부터 E의 다른 요소에 이르는 형태론이 존재한다는 주장은 링 R*이 우리 문제에 대한 가장 효율적인 해결책이라는 것을 의미한다.null
rng를 링으로 바꾸는 이 방법이 가장 효율적이고 공식적이라는 두 가지 사실은 부교감 functor를 정의한다고 말해 동시에 표현할 수 있다.좀 더 명시적으로: F는 rng에 정체성을 붙이는 위의 과정을 의미하므로 F(R)=R*. G는 "링 S가 정체성을 가지고 있는지 잊어버리고 단순히 rng로 간주하므로 본질적으로 G(S)=S"라는 과정을 의미한다.그리고 F는 G의 왼쪽 부관이다.
그러나 우리가 실제로 R*를 구성하지 않았다는 것에 주목하라; 그러한 좌뇌 부교장 R → R*가 실제로 존재한다는 것은 중요하고 전혀 사소한 대수학적 사실이 아니다.null
최적화 문제의 대칭성
functor F부터 시작하여, 다음 (vague) 질문을 제기하는 것도 가능하다: 어떤 F가 가장 효율적인 해결책인가?null
F가 G가 제기하는 문제에 대한 가장 효율적인 해결책이라는 개념은, 어떤 엄밀한 의미에서 G가 F가 해결하는 가장 어려운 문제를 제기한다는 개념과 같다.null
이것은 짝을 지어 짝을 이룬다는 사실 뒤에 있는 직감을 준다: F가 G에 왼쪽을 맞추고 G를 F에 오른쪽을 맞춘다.null
형식 정의
보조 functor에는 다음과 같은 다양한 동등한 정의가 있다.
- 보편적 형태론을 통한 정의는 진술하기 쉬우며, 조정자를 구성하거나 두 개의 조정자가 일치한다는 것을 증명할 때 최소한의 검증이 필요하다.그것들은 또한 최적화와 관련된 우리의 직관과 가장 유사하다.
- 동음이의 집합을 통한 정의는 대칭을 가장 뚜렷하게 하며, 조정이라는 단어를 사용하는 이유다.
- 상담-단위 첨부를 통한 정의는 직접 조작할 수 있는 공식을 제공하기 때문에 조정된 것으로 알려진 functors에 대한 입증에 편리하다.
이 정의의 등가성은 꽤 유용하다.수학의 모든 영역에서 부조화작용은 어디에서나 일어난다.이러한 정의 중 어느 하나에서든 구조는 다른 정의의 구조를 발생시키기 때문에, 그 정의들 사이의 전환은 모든 주제 영역에서 별도로 반복되어야 할 많은 지루한 세부사항을 암묵적으로 사용한다.null
관습
조정 이론은 그 기초에 좌우의 용어를 가지고 있으며, 고려 중인 C와 D의 두 범주 중 하나에 살고 있는 요소들이 많다.따라서 "lefthand" 범주 C 또는 "8번째 범주 D" 범주에서 살고 있는지에 따라 알파벳 순서로 글자를 선택하고 또한 가능하면 이 순서로 적을 수 있다.null
예를 들어 이 글자에서 X, F, F, f, ε은 C 범주에 살고 있는 것을 일관되게 나타낼 것이며, Y, G, g, η은 D 범주에 살고 있는 것을 일관되게 나타낼 것이며, 가능할 때마다 그러한 것들을 왼쪽에서 오른쪽으로 순서대로 언급할 것이다(functor F : D → C는 그 산출물을 "살아있는"로 생각할 수 있다).(C)이다.null
보편적 형태론을 통한 정의
정의에 따르면 functor : → C is a left adjoint functor if for each object in there exists a universal morphism from to . Spelled out, this means that for each object in there exists an object in and a morphism such that for every object in and every morphism there exists a unique morphism 가 인Y =f {\}\ F)=f.
후자의 방정식은 다음과 같은 정류 도표로 표현된다.
이런 상황에서 을(를) 펑터 : C → [\ in a unique way such that for all morphisms in ; is then called a left adjoint to .
이와 유사하게, 우리는 우경화 펑커를 정의할 수 있다.Functor : → D is a right adjoint functor if for each object in , there exists a universal morphism from to . Spelled out, this means that for each object in , there exists an object ) 의 과(와) 형태론 :Y→ (( Y) 의 모든 객체 및 형태주의 g : Y → G ( X ) 에는 한f : F( )→ f:(이(가) G (f ) Y= }=가 있다
이 은는) 고유하게 :D → C {\로 변환될 수 있다.( ) Y= η Y = g {\g))\ _'}\ for : → → Y {\ 의 형태론 Y G을(를) F 에 대한 오른쪽 부호라고 한다
용어에서 알 수 있듯이, 이가) G에 오른쪽을 연결하는 에만 F}에 왼쪽을 맞춘다는 것은 사실이다
보편적 형태론을 통한 이러한 정의는 종종 주어진 펑터가 그들의 요구조건에서 최소적이기 때문에 왼쪽 또는 오른쪽 정렬이라는 것을 확립하는 데 유용하다.보편적 형태론을 찾는 것이 최적화 문제를 해결하는 것과 같다는 점에서도 직관적으로 의미가 있다.null
홈셋 연결을 통한 정의
두 범주 C와 D 사이의 홈셋 연결은 두 개의 functor F : D → C 및 G : C → D와 자연 이형성으로 구성된다.
- : m ( F-,-)→ D(-, -) .
이것은 한 패밀리의 반대여부를 명시한다.
모든 물체에 대해 X는 C로, Y는 D로 표시한다.null
이 상황에서 F는 G에 왼쪽, G는 F에 오른쪽을 맞춘다.
이 정의는 보편적 형태론 정의보다 다소 충족하기 어렵고 상담 단위 정의보다 즉각적인 함의가 적다는 점에서 논리적 타협이다.그것은 명백한 대칭성 때문에 유용하며, 다른 정의들 사이의 디딤돌로서 유용하다.null
φ을 자연 이형성으로 해석하기 위해서는 homC(F–, –)과 homD(–, G–)을 functor로 인식해야 한다.사실 둘 다 Dop × C에서 Set(세트의 범주)까지의 분기점이다.자세한 내용은 홈 펑커스에 대한 기사를 참조하십시오.명시적으로 φ의 자연성은 모든 형태변수 f : X → C의 X와 D의 모든 형태변수 g : Y′ → Y에 대해 다음과 같은 도표가 통용되는 것을 의미한다.
이 다이어그램의 수직 화살표는 구성에 의해 유도된 화살표가 된다.형식적으로 Hom(Fg, f) : HomC(FY, X) → HomC(FY′, X′)은 HomC(FY, X)의 각 h에 대해 h → f o o o Fg에 의해 주어진다.홈(g, gf)도 비슷하다.null
카운슬링 단위접합을 통한 정의
두 범주 C와 D 사이의 상담 단위 연결은 두 개의 functor F : D → C 및 G : C → D와 두 개의 자연 변환으로 구성된다.
각각 카운티와 부속의 단위(범용 대수에서 추출한 것)라고 불리는데, 그러한 구성들은 다음과 같다.
F와 G에서 각각 1과F 1의G 아이덴티티 변환이다.null
이러한 상황에서 우리는 F가 G에 왼쪽, G가 오른쪽, F 에 인접한다고 말하고 G{\(\ )을 써서 이 관계를 나타낼 수 있다 또는 간단히 F
방정식 형식에서 (1998, η)에 대한 위의 조건은 상담 단위 방정식이다.
즉, 각 X는 C, Y는 D,
{ 에서 식별 functor를 , 1F Y }는 functor F에서 자체로의 ID 자연 변환을 나타냄에 유의하십시오.는 물체 FY의 정체성 형태주의를 나타낸다.null
이 방정식들은 대수학적 조작에 보조적인 펑커스에 대한 증거를 줄이는 데 유용하다.그들은 때때로 삼각형 정체성 또는 때로는 지그재그 방정식이라고 불리는데, 이는 해당 문자열 도표의 외관상 때문이다.이들을 기억하는 방법은 우선 비논리적 1= η η η 1을(를) 적은 다음 구성을 정의한 간단한 방법 중 하나로 F 또는 G 중 하나를 채우는 것이다.null
참고: 여기서 상담에서 "co"라는 접두사를 사용하는 것은 콜리밋이 초기 특성을 만족하는 반면 상담 형태는 말단 특성을 만족시키므로 제한 및 콜리밋의 용어와 일치하지 않는다.여기서 단위라는 용어는 정체성 1을 모노이드에 삽입하는 것처럼 보이는 모나드 이론에서 차용한 것이다.null
역사
보조의사상은 1958년 다니엘 칸에 의해 소개되었다.[2]범주 이론의 많은 개념들과 마찬가지로, 그것은 계산에 전념할 당시였던 동역학 대수학의 필요에 의해 제안되었다.그 주제에 대해 깔끔하고 체계적인 발표를 하는 것에 직면한 사람들은 다음과 같은 관계를 알아차렸을 것이다.
- hom(F(X), Y) = hom(X, G(Y))
아벨 그룹 범주에서 F는 펑터(functor) - {\ A즉, A와 함께 텐서 제품을 복용함), G는 펑터 홈(A,–) (이것은 현재 텐서홈 접합이라고 알려져 있다)이었다.등호 부호의 사용은 표기의 남용이다. 이 두 집단은 실제로 동일하지는 않지만 자연스런 방법으로 그들을 식별할 수 있다.첫째, 이것들은 X × A에서 Y까지의 이선형 매핑에 대한 두 가지 대안적 설명이라는 것을 근거로 자연스럽다고 볼 수 있다.그러나 그것은 텐서 제품의 경우에 특별한 것이다.범주 이론에서, 자연 이형주의 개념에 편향의 '자연성'이 포함되었다.null
유비쿼터스
만약 누군가가 이러한 보조적인 쌍의 펑커를 찾기 시작한다면, 그것들은 추상 대수학에서 그리고 다른 곳에서도 매우 흔한 것으로 판명된다.아래의 예제 섹션은 이에 대한 증거를 제공한다. 더 나아가, 어떤 사람들에게는 더 친숙할 수 있는 보편적 구조는 수많은 보조적 쌍의 펑커를 발생시킨다.null
Sunders Mac Lane의 생각에 따라, 수학에서 충분히 광범위하게 일어나는 부교감 같은 어떤 아이디어도 그 자체를 위해 연구되어야 한다.[citation needed]null
개념은 문제를 해결하는 데 사용하는 것뿐만 아니라 이론을 구축하는 데 사용하는 것에 따라 판단할 수 있다.이 두 가지 동기 사이의 긴장은 특히 카테고리 이론이 처음 개발된 1950년대에 대단했다.범주 이론을 사용하여 다른 작업에서 나침반 베어링을 가져간 알렉산더 그로텐디크(Alexander Grotendiek)를 기능 분석, 호몰로지 대수 및 마지막으로 대수 기하학에서 입력하십시오.null
그가 조정자 개념을 고립적으로 추진했다고 말하는 것은 아마도 잘못되었을 것이다: 그러나 부속의 역할에 대한 인식은 그로텐디크의 접근법에 내재되어 있었다.예를 들어, 그의 주요 업적 중 하나는 세레 이중성을 상대적 형태로, 즉 느슨하게, 연속적인 대수적 변종 계열로 공식화한 것이다.그 모든 증거는 어떤 방첩자에게 권리의 존재를 돌렸다.이것은 부정할 수 없이 추상적이고, 비건설적이지만[discuss], 또한 그 나름대로 강력한 것이다.null
예
자유 그룹
자유 집단의 건설은 공통적이고 명쾌한 예다.null
Let F : Set → Grp는 Y의 요소에 의해 생성된 자유 그룹을 각 세트 Y에 할당하는 functor가 되고, G : Grp → Set는 각 그룹 X에 그 기본 세트를 할당하는 망각적인 functor가 된다.그런 다음 F는 G:에 맞춰져 있다.
초기 형태론.각 세트 Y에 대해, 세트 GFY는 Y가 생성하는 자유 그룹 FY의 기본 세트일 뿐이다.η :→ 는 "발전기 포함"에 의해 제공된 설정 맵이다.일부 그룹 W의 Y에서 기본 설정 GW까지의 모든 세트 맵은 η : Y→ 를 통해 고려되기 때문에 Y에서 G까지의 초기 형태론이다.FY에서 W까지 독특한 집단 동형식을 통해 이것은 정확히 Y에 있는 자유 집단의 보편적 재산이다.
말단 형태론.각 그룹 X에 대해 그룹 FGX는 X의 요소인 GX에 의해 자유롭게 생성되는 자유 그룹이다.ε : → 은(는) FGX의 생성자를 그들이 대응하는 X의 원소로 보내는 집단 동형상이며, 자유집단의 보편적 속성에 의해 존재한다.그 다음에 각각 (G X, ) 은 F에서 X까지의 말단 형태론인데, FZ에서 X로 이어지는 모든 집단 동형성은 ε : → 를 통해 고려되기 때문이다Z에서 GX까지 고유한 세트 맵을 통해 이것은 (F,G)가 부선 쌍이라는 것을 의미한다.null
홈셋 부속품.자유 그룹 FY에서 그룹 X로 그룹 동형성은 설정된 Y에서 설정된 GX까지의 지도에 정확히 대응한다. FY에서 X까지의 각 동형성은 자유 그룹의 보편적 속성의 또 다른 재작성인 발전기에 대한 그것의 작용에 의해 완전히 결정된다.이 서신이 자연 변형인지 직접 검증할 수 있는데, 이는 쌍(F,G)에 대한 홈셋 부속물임을 의미한다.null
상담 단위 부속또한 ε과 η이 자연스럽다는 것을 직접 확인할 수 있다.그런 다음, 그들이 상담 단위 부속서를 형성한다는 직접적인 검증( :,): G ):은(는) 다음과 같다.
첫 번째 상담 단위 방정식 F = Fη 은(는) 각 세트 Y에 대해 합성을 말한다.
정체성이 있어야 한다.중간 그룹 FGFY는 자유 그룹 FY의 말에 의해 자유롭게 생성되는 자유 그룹이다. (이 단어들을 괄호 안에 넣어 독립 생성기임을 나타내도록 생각하라.)화살표 F Y){\ F_{는 FY에서 FGFY로 각 발전기 y를 FGFY의 생성기로 해당 길이 1(y)에 보내는 그룹 동형성이다.화살표 ε 는 FGFI에서 FY까지 각 발전기를 해당하는 단어로 보내는 동일성 집단이다(그래서 이 지도는 "낙하 괄호"이다).이 지도들의 구성은 확실히 회계연도의 정체성이다.null
두 번째 상담 단위 방정식 G= G η G 에 따르면 각 그룹 X에 대한 구성은 다음과 같다.
정체성이 있어야 한다.중간 집합 GFGX는 FGX의 기본 집합일 뿐이다.화살표 η 는 설정된 GX에서 설정된 GFGX로 "발생기 포함" 세트 맵이다.화살표 G ( ) G는 GFGX에서 GX까지의 세트 맵으로, FGX의 각 생성기를 X의 요소에 보내는 그룹 동형성의 기초가 된다("드롭핑 괄호").이 지도들의 구성은 실로 GX 상의 정체성이다.null
자유로운 구성과 망각적인 펑크
자유 객체는 모두 그 기초적인 집합에 대수적 객체에 할당하는 망각적인 펑터(functor)에 대한 좌편향의 예다.이러한 대수적 자유형 펑커스는 일반적으로 위의 자유군 상황에 대한 상세한 설명과 동일한 설명을 가지고 있다.null
대각선 펑커 및 한계
제품, 섬유제품, 이퀄라이저, 커널 등은 모두 한계의 범주형 개념의 예다.임의의 한계 펑터는 해당 대각선 펑터(범주에 문제의 한계 유형이 있는 경우)와 바로 일치하며, 부속서의 상담은 한계 객체(즉, 한계 위의 대각선 펑터 범주에서)에서 정의 지도를 제공한다.다음은 몇 가지 구체적인 예들이다.null
- 제품 렛 렛 렛 let : Grp2 → Grp 제품군 X1×X2 각2 쌍(X1, X)에 할당하는 functor, Δ : Grp → Grp2 제품군 Grp의2 모든 그룹 X에 쌍(X, X)을 할당하는 대각선 functor가 되도록 한다.제품군의 보편적 속성은 Δ가 Δ에 우위임을 나타낸다.이 부속문제의 협의는 X1×X에서21 X와2 X까지의 투영 맵의 정의 쌍이며, 단위는 X×X에 그룹 X를 대각선으로 포함하는 것이다(mapping x to (x,x)).
- 세트의 데카르트 제품, 반지의 제품, 위상학적 공간의 제품 등은 동일한 패턴을 따른다. 또한 단지 두 가지 이상의 요소로 직설적으로 확장될 수 있다.더 일반적으로, 어떤 유형의 한계도 대각선 펑터에 바로 인접한다.
- 낟알.아벨 그룹 동형성의 범주 D를 고려한다.f1 : A1 → B, f122 : A → B가2 D의 두 대상이라면 f에서1 f까지의2 형태론은 gfB1 = fg와2A 같은 형태론의 쌍(gAB, g)이다.G : D → Ab는 각 동형성에 그것의 커널을 할당하는 functor가 되고 F : Ab → D는 동형성 A → 0에 그룹 A를 매핑하는 functor가 된다.그러면 G는 커널의 보편적 속성을 나타내는 F에 바로 붙는다.이 부속의 협의는 동형성의 알맹이를 동형성의 영역에 규정하는 것으로, 단위는 동형성 A → 0의 알맹이로 그룹 A를 식별하는 형태론이다.
- 또한 이 예제의 적절한 변화는 벡터 공간과 모듈에 대한 커널 펑터가 오른쪽 정렬이라는 것을 보여준다.유사하게, 아벨 그룹, 벡터 공간, 모듈 등을 위한 코커넬 펑터가 좌현으로 되어 있다는 것을 보여줄 수 있다.
콜리밋 및 대각선 펑커
코프로덕트, 섬유화된 코프로덕트, 등가제, 코커넬 등은 모두 콜리밋의 범주형 개념의 예다.모든 콜리미트 펑터는 해당 대각선 펑터(범주에 해당 콜리미트의 유형이 있는 경우)에 맞춰져 있으며, 부속물의 단위는 콜리미트 객체에 정의 지도를 제공한다.다음은 몇 가지 구체적인 예들이다.null
- 코프로덕트.F : Ab2 → Ab가 아벨리아 그룹의 모든 쌍(X1, X2)에 직접 합계를 할당하고, G : Ab → Ab가2 모든 아벨리아 그룹 Y에 쌍(Y, Y)을 할당하는 펑터라면 F는 다시 G에 비례하게 되며, 이는 직접 합계의 보편적 속성의 결과물이다.이 부선 쌍의 단위는 X와1 X에서2 직접 합계로 포함하는 포함 맵의 정의 쌍이며, 카운티는 (X,X)의 직접 합에서 X까지(직접 합계의 요소(a,b)를 X의 요소 a+b로 전송)하는 부가 맵이다.
추가 예
대수학
- 정체성과 rng를 연결한다.이 예는 위의 동기 섹션에서 논의되었다.rng R이 주어진 경우, RxZ를 취하고 (r,0)(0,1) = (0,1)(r,0) = (r,0), (r,0) = (r,0), (r,0), (r,0), (0,1) = (0,1) = (0,1)로 Z-편향 제품을 정의함으로써 승법적 아이덴티티티 요소를 추가할 수 있다.이것은 밑에 있는 rng로 반지를 가져가는 좌뇌를 구성한다.
- 세미그룹에 정체성을 연결한다.마찬가지로, Sem그룹 S에 주어진 경우, 우리는 Identity 요소를 추가하여 Identity 요소를 얻을 수 있으며, Disconnection Union S 1}를 취하고, S에 대한 연산을 확장하고 1이 Identity 요소인 이항연산을 정의함으로써 Monoid를 얻을 수 있다.이 구조는 기초적인 세미그룹에 모노이드(monoid)를 가져가는 펑터(functor)에 왼쪽 맞춤을 부여한다.
- 링 익스텐션.R과 S가 고리라고 가정하고, → : R → S는 고리 동형이다.그러면 S는 (왼쪽) R-모듈로 볼 수 있고, S가 있는 텐서 제품은 functor F : R-Mod → S-Mod를 산출한다.그런 다음 F는 건망증이 심한 Functor G : S-Mod → R-Mod에 보조를 맞춘다.
- 텐서 제품.R이 링이고 M이 R모듈이면 M이 있는 텐서 제품은 F : R모드 → Ab를 산출한다.Functor G : Ab → R-Mod는 모든 아벨 그룹 A에 대해 G(A) = homZ(M,A)으로 정의되며 F에 대한 오른쪽 부호다.
- 모노이드와 집단에서 반지까지.일체형 모노이드 링 구조는 모노이드에서 링까지 펑터를 제공한다.이 플럭터는 주어진 링에 기초하는 승수 단모형을 연결하는 플럭터(functor)에 보조를 맞춘다.마찬가지로, 일체형 그룹 링 구조는 그룹부터 링까지 펑터를 생산하고, 주어진 링에 유닛 그룹을 할당하는 펑터에게 왼쪽 맞춤을 한다.또한 K 필드에서 시작하여 고리 범주 대신 K-알게브라의 범주를 고려해 K 위로 모노이드와 그룹 링을 얻을 수 있다.
- 분수장.주입형 형태론이 있는 통합 도메인의 Domm 범주를 고려하십시오.필드의 건망증이 심한 Functor Field → Dom은m 왼쪽 부호를 가지고 있으며, 모든 필수 영역에 분수 필드를 할당한다.
- 다항식 고리.렛* 링은 단결성이 있는 뾰족한 정류 고리의 범주가 되게 한다(A,a) 여기서 A는 고리, a A는 모피즘이 구별되는 요소들을 보존한다).건망증이 심한 펑터 G:링* → 링은 좌측 조정점을 가지고 있다 – 모든 링 R에 쌍(R[x],x)을 할당한다. 여기서 R[x]은 R에서 계수를 갖는 다항식 링이다.
- 아벨리아화.아벨 그룹 범주에서 그룹 범주까지 포함 펑터 G : Ab → Grp를 고려한다.그것은 모든 그룹 G에 지수 그룹 Gab=G/[G,G,G]를 할당하는 아벨리아화라고 불리는 왼쪽 부호를 가지고 있다.
- 그로텐디크 그룹.K-이론에서 출발점은 위상학적 공간에 있는 벡터 번들의 범주가 직접 합계에 따른 정류적 모노이드 구조를 갖는 것을 관찰하는 것이다.각 묶음(또는 등가 등급)에 대해 공식적으로 첨가된 역(inverse)을 추가함으로써 이 모노이드인 그로텐디크 그룹으로부터 아벨리아 그룹을 만들 수도 있다.또는 각 그룹에 대해 기본 모노이드(거부)를 사용하는 펑터에는 왼쪽 정렬이 있음을 관찰할 수 있다.이것은 위의 제3부 논의에 따른, 일거수일투족 공사다.즉, 음수의 구성을 모방할 수 있지만, 존재의 정리에는 다른 선택사항이 있다.미세한 대수 구조의 경우, 존재 자체가 보편적 대수학, 즉 모델 이론으로 언급될 수 있다. 자연스레 범주 이론에 적응한 증명도 있다.
- 그룹의 대표이론에서 프로베니우스 상호주의: 유도된 대표성을 보라.이 예는 일반론을 반세기 가량 예시하였다.
위상
- 왼쪽과 오른쪽이 나란히 있는 펑터.G는 위상학적 공간의 functor가 되어 모든 위상학적 공간과 연관되도록 한다(위상, 즉 위상은 잊어버린다).G에는 F가 왼쪽 정렬되어 있으며, Y에 이산 공간을 만들고, H는 Y에 사소한 위상을 만든다.
- 서스펜션 및 루프 공간.위상학적 공간 X와 Y를 주어, X의 서스펜션 SX에서 Y까지의 맵의 호모토피 등급의 공간[SX, Y]은 X의 루프 공간 ΩY에 이르는 맵의 공간[X, ΩY]에 자연적으로 이형성이 있다.따라서 서스펜션 펑터는 호모토피 이론의 중요한 사실인 호모토피 범주의 루프 공간 펑터에 인접해 있다.
- 스톤-체흐 콤팩트화.KHAus는 콤팩트한 하우스도르프 공간의 범주로, G : KHAus → Top은 위상적 공간의 범주에 대한 포함 펑터가 되도록 한다.그 다음 G는 왼쪽 F : Top → KHAus, 스톤-체크 콤팩트화를 가지고 있다.이 보조선 쌍의 단위는 모든 위상학적 공간 X에서 스톤-체크 압축까지 연속적인 지도를 산출한다.
- 피복의 직사 및 역사 이미지.위상학적 공간 사이의 모든 연속 지도 f → Y는 X의 피복 범주(세트 또는 아벨리아 그룹, 또는 링...)에서 피복자 f를 직접 ∗ 이미지 피복자인 Y의 피복 범주로 유도한다.그것은 또한 Y의 아벨리아 그룹의 피복 범주에서 역 이미지 피복자인 X의 아벨리아 그룹의 피복 범주로 functor −1 f를 유도한다.f는 −1 f와 ∗ 나란히 있다.여기서 더 미묘한 점은 일관성 있는 자루를 위한 왼쪽 맞춤은 자루를 위한 것과 다르다는 것이다.
- 술이 깨다.스톤 이중성에 관한 기사는 위상학적 공간의 범주와 술이 깨는 것으로 알려진 맑은 공간의 범주의 연관성을 기술하고 있다.특히 이 글에는 무의미한 토폴로지에서 착취된, 냉정한 공간과 공간적 지역이라는 유명한 이중성을 위한 길을 준비하는 또 다른 부속물에 대한 자세한 설명도 담겨 있다.
포셋
부분 순서의 모든 집합은 범주로 볼 수 있다(포셋의 요소가 범주의 객체가 되고 x y y인 경우에만 x에서 y까지의 단일 형태론을 가진다).부분적으로 순서가 정해진 두 세트 사이의 보조형 펑커스를 갈루아 연결(또는 반대편 갈루아 연결인 경우)이라고 한다.몇 가지 예를 들자면, 갈루아 이론의 경우는 물론 선도적인 이론이다.모든 갈루아 연결은 폐쇄 연산자를 발생시키고 해당 폐쇄 요소 사이의 역순 보존 편차를 발생시킨다.null
갈루아 집단의 경우와 마찬가지로, 진정한 관심은 종종 이중성에 대한 대응관계(즉, 반격론적 질서 이형성)를 정비하는 데 있다.카플란스키에 의한 이러한 선에 따른 갈루아 이론의 처리가 이곳의 일반적인 구조를 인정하는 데 영향을 미쳤다.null
부분 순서 사례에서는 부속 정의가 상당히 눈에 띄게 무너지지만 다음과 같은 몇 가지 주제를 제공할 수 있다.
- 결합은 이중성이나 이형성이 아닐 수 있지만, 그 상태로 업그레이드하기 위한 후보일 수 있다.
- 폐쇄 운영자는 해당 모노드(cf. Kuratowski 폐쇄 공리)로 부속물의 존재를 표시할 수 있다.
- 윌리엄 로비어의[3] 매우 일반적인 논평은 구문과 의미론들이 일치한다는 것이다: C를 모든 논리 이론들의 집합으로 삼는다(축소화), 그리고 D 모든 수학 구조들의 집합의 힘 집합으로 삼는다.C에서 이론 T의 경우 G(T)를 공리 T를 만족하는 모든 구조물의 집합으로 하고, 수학 구조 S의 집합에 대해서는 F(S)를 S의 최소 공리화 되도록 한다.F(S)가 논리적으로 T를 암시하는 경우에만 S가 G(T)의 부분집합이라고 말할 수 있다: "제반적 펑터" G가 "합성 펑터" F와 정확히 일치한다.
- 분열은 (일반적으로) 곱셈을 뒤집으려는 시도지만, 이것이 가능하지 않은 상황에서 우리는 종종 조정자를 구성하려고 시도한다: 이상적인 몫은 링 이상에 의해 곱셈에 비례하고, 명제논리에 있어서의 함축은 논리적 결합에 비례한다.
범주론
- 동등성.F : D → C가 범주의 등가라면, 역등가 G : C → D가 있고, 두 개의 functor F와 G는 부선 쌍을 이룬다.단위와 상담은 이 경우 자연 이형이다.
- 일련의 부속품들.범주에 그것의 연결된 구성요소 집합을 할당하는 functor π은0 해당 집합의 이산형 범주에 할당하는 functor D에 왼쪽 맞춤이다.또한 D는 각 범주에 객체 집합을 할당하는 객체 펑터 U에 왼쪽 적응하고, 마지막으로 U는 A에 왼쪽 적응하며, A는 해당 집합에 있는 각 비구체 범주에[4] 할당된다.
- 지수 객체.데카르트 폐쇄 범주에서 –×A가 제공한 엔드ofunctor C → C는 우측 조정자를 가진다.A이 쌍을 흔히 꾸물꾸물하고 꾸물거리지 않는 것으로 일컬어지는데, 많은 특별한 경우, 그들은 또한 연속적이며 동형성을 형성한다.
범주형 논리학
- 수량화. 가 일부 속성을 표현하는 단항 술어인 경우 충분히 강한 집합 이론이 속성을 충족하는 의 Y={ y Y ( }(y 집합의 존재를 증명할 수 있다.A proper subset and the associated injection of into is characterized by a predicate expressing a strictly more restrictive property.
- 술어 로직에서 정량자의 역할은 명제를 형성하는 데 있고 또한 더 많은 변수로 공식을 닫음으로써 정교한 술어를 표현하는 데 있다.를 들어, 및 Y 의 두 개의 열린 변수를 포함하는 라는 술어를 생각해 보십시오 계량자를 사용하여 을(를)를 닫으면 집합을 구성할 수 있다
- f {\ Y}의 요소중 {\ y에 된 속성이 인 요소 중 S {\ _ 교차점처럼 정리 작업을 설정하십시오. 두 세트 중 \cap }은(는) 술어의 {\과(와) 직접 일치한다.범주형 논리학에서 topos 이론의 하위 분야인 정량자는 풀백 펑터(pullback functor)에 대한 조정으로 식별된다.그러한 실현은 세트이론을 이용한 명제논리의 논의와 유사하게 볼 수 있지만 일반적인 정의는 보다 풍부한 범위의 로직을 만든다.
- 풀백이 있는 범주에서 개체 을(를) 고려하십시오. 형태론 : X→ Y은(는) functor를 유도한다.
- 하위 객체의 사전 순서인 범주에.It maps subobjects of (technically: monomorphism classes of ) to the pullback . If this functor has a left- or right adjoint, they are called and 각각 [5]They both map from back to . Very roughly, given a domain to quantify a relation expressed via over, the functor/quantifier closes in 를) 반환하고 그에 따라 된Y {\ 부분 집합을 반환하십시오
- 예: 에서 세트와 함수의 범주에서 표준 하위 개체는 부분 집합(또는 표준 주입)이다.풀백 = X f of an injection of a subset into along is characterized as the largest set which knows all about and the injection of into . It therefore turns out to be (in bijec역 이미지 -[ T f X.
- 의 경우 다음을 통해 정의되는 왼쪽 조정점을 파악해 봅시다
- 여기서 말하는 것은 단지
- - [ f
- Consider . We see . Conversely, If for an we also have , then clearly . So implies . We conclude that left adjoint to the inverse image functor is given by the direct image.논리 해석에 더 부합하는 이 결과의 특성화가 여기에 있다. 에 S{\의 이미지는 의 전체 집합으로, - [{ } S f S가 비어 있지 않다.는 f[ 의 보완에 있는 을(를) 정확히 무시하기 때문에 작동된다
- 이것을 우리의 동기 ∈ . ( , y) S (x ) S ( x ) }
- 여기서 계산을 수행하지 않고 역 영상 펑터에 대한 오른쪽 맞춤이 주어진다.
- 의 부분 집합 는{\ f에 대한역 이미지가 포함된 속성과 y \{s의 전체 집합으로 특징지어진다 pr에 유의하십시오. 이가) {\displaystyle 으)로 대체되는 것을 제외하고 세트를 결정하는 것은 위와 같다.
- 파워셋을 참조하십시오.
완전 결합
따라서 모든 부속물과 관련된 수많은 환자와 자연적 변환이 존재하며, 나머지는 작은 부분만으로도 충분하다.null
범주 C와 D 사이의 연결은 다음과 같이 구성된다.
- 좌편향 F : D → C라고 하는 좌편향
- 오른쪽 부정을 나타내는 Functor G : C → D
- 자연 이형성 Ⅱ : homC(F–,–) → homD(–,G–)
- 자연변형 ε : FG → 1C council이라 부른다.
- 자연변환 ηD : 1 → 단위라고 하는 GF
X가 C의 어떤 물체를 나타내고 Y가 D의 어떤 물체를 나타내는 등가 공식은 다음과 같다.
- For every C-morphism f : FY → X, there is a unique D-morphism ΦY, X(f) = g : Y → GX such that the diagrams below commute, and for every D-morphism g : Y → GX, there is a unique C-morphism Φ−1Y, X(g) = f : FY → X in C such that the diagrams below commute:
이 주장을 통해 다음과 같은 사실을 회복할 수 있다.
- 변환 ε, η, φ은 방정식에 의해 관련된다.
- 변환 ε, η은 상담 단위 방정식을 만족시킨다.
특히 위의 방정식을 통해 ,, and, η, η을 세 가지 중 어느 하나에 관해서도 정의할 수 있다.그러나 일반적으로 부선 functor F와 G만으로는 부선을 결정하기에 충분하지 않다.이러한 상황의 동등성은 아래에 제시되어 있다.null
보편적 형태는 홈셋 결합을 유도한다.
오른쪽 조정자 G : C → D; 초기 형태론의 관점에서, 다음과 같은 단계를 수행하여 유도된 홈셋 결합을 구성할 수 있다.null
- functor F : D → C와 자연변환 η을 구성한다.
- D의 각 객체 Y에 대해 초기 형태론(F(Y), ηY)을 Y에서 G로 선택하여 ηY : Y → G(F(Y))로 한다.우리는 물체에 대한 F의 지도와 형태론 η을 가지고 있다.
- 각 f : Y0 → Y에1 대해 (F(Y0), ηY0)는 초기 형태론으로서, η로Y0 ηY1 o f를 인수하여 F(F) : F(Y0) → F(Y1)를 얻는다.이것은 형태론에 대한 F의 지도다.
- 그 요소화의 통근 도표는 자연변화의 통근 도표를 함축하고 있으므로 soD : 1 → G o F는 자연변혁이다.
- 그러한 요소화와 G가 functor라는 고유성은 형태론에 대한 F의 지도가 구성과 정체성을 보존한다는 것을 의미한다.
- 자연 이형성 φ : homC(F-,-) → homD(-,G-)을 생성한다.
- C에서 각 객체 X에 대해 (F(Y), ),)는Y 초기 형태론으로서 D에서 각 객체 Y는 초기 형태론이며, 여기서 φY, XY, X(f : F(Y) → X) = G(f) oY η이다.
- η is a natural transformation, G is a functor, then for any objects X0, X1 in C, any objects Y0, Y1 in D, any x : X0 → X1, any y : Y1 → Y0, we have ΦY1, X1(x o f o F(y)) = G(x) o G(f) o G(F(y)) o ηY1 = G(x) o G(f) o ηY0 o y = G(x) o ΦY0, X0(f) o y, and then Φ is natural in both arguments.
유사한 논거는 단자 형태에서 좌측 부선 functor로 홈셋 결합을 구성할 수 있게 한다.(많은 조정자 쌍의 오른쪽 조정자는 사소한 것으로 정의된 포함 또는 건망증이 있는 펑터이기 때문에 오른쪽 조정자로 시작하는 구성은 약간 더 흔하다.)null
상담 단위접합을 유도하다.
functor F : D → C, G : C → D, 상담 단위 연결 (ε, η) : F 를 주어 다음과 같은 단계에서 자연 변형 φ : homC(F-,-) → homD(-, G-)을 찾아 hom-set 접합부를 구성할 수 있다.
- 각 f : FY → X 및 각 g : Y → GX에 대해 정의한다.
- η과 ε의 변형은 because과 ε이 자연적이기 때문에 자연스럽다.
- 순서에 따라 F는 functor이고, ε은 자연적이며, 카운슬 단위 방정식FY 1 = εFY o F(ηY)를 사용하여, 우리는 얻는다.
- 따라서 ψφ은 정체성 변환이다.
- Dallally, 그 G는 functor이고, 그 η은 자연적이며, 상담 단위 방정식 1GX = G(εX) o η을GX 사용하여 얻는다.
- 따라서 φψ은 정체성 변환이다.따라서 φ은 역 φ−1 = ψ을 갖는 자연 이형성이다.
홈셋 연결은 위의 모든 것을 유도한다.
F : D → C, G : C → D, 그리고 Home set adjection φ : homC(F-,-) → hom(-, G-)을D 주어 상담 단위 접합부를 구성할 수 있다.
- ,
다음 단계에서 초기 형태 및 단자 형태 패밀리를 정의한다.
- Let for each X in C, where is the identity morphism.
- Let for each Y in D, where 은(는) 정체성 형태론이다.
- φ의 생물성과 자연성은 각각(GX, εX)은 C에서 F에서 X까지의 말단 형태론이며, 각(FY, ηY)은 D에서 Y에서 G까지의 초기 형태론임을 암시한다.
- φ의 자연성은 ε과 η의 자연성을 내포하고 있으며, 두 공식은 ε과 η의 자연성을 내포하고 있다.
- 각 f에 대해: FY → X 및 g: Y → GX(EX를 완전히 결정함).
- 두 번째 공식에서 X와 η에Y FY를 대체하는 = forY, FY(1)은FY 첫 번째 상담 단위 방정식을 제공한다.
- F
- 그리고 첫 번째 공식에서 GX를 Y로 대체하고 f = φX−1GX, X(1)을GX f로 대체하면 두 번째 상담-단위 방정식이 주어진다.
- = G ( X) G
특성.
존재
모든 functor G : C → D가 좌뇌를 인정하는 것은 아니다.만약 C가 완전한 범주라면, 왼쪽 맞춤이 있는 functors는 Peter J의 조정형 functor 정리로 특징지어질 수 있다. Freyd: G는 연속적이고 특정 소형의 조건이 충족되는 경우에만 왼쪽 부호를 가진다: D의 모든 대상 Y에 대해 형태론 계열이 존재한다.
- fi : Y → G(Xi)
모든 형태론이 적절한 클래스가 아닌 세트 I에서 나온 지수의 경우
- h : Y → G(X)
라고 쓸 수 있다.
- h = G(t) o fi
I의 일부와 형태론 때문에
- t : Xi → X in C.
유사한 진술은 그 교묘한 속임수들의 특징을 나타낸다.null
중요한 특별한 경우는 현지에서 제시할 수 있는 범주의 경우다.: C→ D 은(는) 지역적으로 표시할 수 있는 범주 사이의 functor로,
- F가 작은 콜리미트를 보존하는 경우에만 F가 오른쪽에 정렬됨
- F가 작은 한계를 보존하고 접근 가능한 functor인 경우에만 F에 왼쪽 부선이 있다.
유니크함
functor F : D → C가 G와 G′ 두 개의 오른쪽 부교환을 가지고 있다면 G와 G′은 자연적으로 이형성이 있다.좌경도 마찬가지다.null
반대로 F가 G에 인접하고 G가 자연적으로 G에 이형성인 경우 F도 G에 인접한다.보다 일반적으로, 〈F, G, ,, 〉〉이 부속물이라면(의사 단위(의사 단위)와, and
- σ : F → F′
- τ : G → G′
자연 이형성인 경우, 〈F′, G′, η′, η′〉은 부속물로서, 다음과 같다.
여기서 은 자연적 변환의 수직적 구성을 나타내며, {\은 수평 구성을 나타낸다.null
구성
부속품은 자연스런 방식으로 작곡될 수 있다.구체적으로 〈F, G, ε, η〉이 C와 D의 부속물이고 〈F′, G′, ε′, η′〉이 D와 E의 부속물이라면 펑터다.
에 연좌되다
보다 정확하게는 FF'와 G'G 사이에 각각 구성에서 주어지는 단위와 상담이 연결되어 있다.
이 새로운 결합을 주어진 결합 두 개의 구성이라고 한다.null
범주 C와 그 자체 사이에 신분적 결합을 정의하는 자연적인 방법도 있기 때문에, 모든 개체가 작은 범주이고 형태론이 결합인 범주를 형성할 수 있다.null
한계보존
조정의 가장 중요한 특성은 연속성이다. 왼쪽 조정(따라서 오른쪽 조정)을 가진 모든 조정자는 연속적이다(즉, 범주의 이론적 의미에서의 한계로 통근). 오른쪽 조정(따라서 왼쪽 조정)을 가진 모든 조정자는 연속적이다(즉, 콜리밋과 통근).null
수학에서 흔히 볼 수 있는 구조는 한계나 집단이기 때문에, 이것은 풍부한 정보를 제공한다.예를 들면 다음과 같다.
- 물체의 생산물에 우측 보조 기구 적용은 이미지의 산출물을 산출한다.
- 물체의 공동 유도체에 좌측 보조 펑터를 적용하면 이미지의 공동 유도물이 생성된다.
- 두 개의 아벨리아 범주 사이의 모든 우측 부선장은 정확히 왼쪽이다.
- 두 아벨의 범주들 사이의 모든 좌뇌 부호장은 정확하다.
부가성
C와 D가 사전 가법 범주이고 F : D → C가 오른쪽 부호 G : C → D를 갖는 첨가제 펑터라면 G는 또한 첨가제 펑터와 홈셋 편향이다.
사실, 아벨 집단들의 이소모르프다.Dallally, G가 왼쪽 부호 F와 함께 첨가제인 경우 F도 첨가제인 것이다.null
더욱이 C와 D가 모두 가법 범주(즉, 모든 유한한 바이프로덕트를 가진 사전 가법 범주)인 경우, 이들 사이의 어떤 조정형 펑커 쌍도 자동으로 가법적이다.null
관계들
유니버설 구조
앞에서 설명한 바와 같이 범주 C와 D의 결합은 C의 각 대상과 D의 각 대상에게 각각 하나씩 보편적 형태론 계열을 낳는다.반대로 D의 모든 물체로부터 functor G : C → D에 대한 보편적 형태주의가 존재한다면 G는 왼쪽 부선을 가진다.null
그러나 보편적 구조는 조정자보다 일반적이다: 보편적 구조는 최적화 문제와 같다; 이 문제가 D의 모든 대상(균등하게, C의 모든 대상)에 대한 해결책을 가지고 있는 경우에만 조정자 쌍을 만든다.null
범주의 동등성
functor F : D → C가 범주의 등가성의 1/2인 경우, 그것은 범주, 즉 단위와 카운슬이 이형인 부속품에서 좌의정이다.null
모든 부속물 〈F, G, ε, η〉은 특정 하위 카테고리의 등가성을 확장한다.C를1X 이형성인 C의 대상 X로 구성된 C의 전체 하위 범주로 정의하고, D를1Y D의 대상 Y로 구성된 전체 하위 범주로 정의한다.그런 다음 F와 G를1 D와1 C로 제한하고 이러한 하위 범주의 역등가성을 산출할 수 있다.null
어떤 의미에서, 조정은 "일반화"된다.그러나 F의 오른쪽 역행(즉, FG가 자연적으로 이형성인 F1과D 같은 functor G)은 F의 오른쪽(또는 왼쪽)이 될 필요는 없다.조정자는 양면 인버들을 일반화한다.null
모나드
모든 부속물 〈F, G, ε, μ〉는 D 카테고리에서 관련 모나드 〈T, μ〉를 낳는다.방범기
T = GF로 주어진다.모나드의 단위
부속과 곱셈 변환의 단위 is에 불과하다.
μ = GεF로 주어진다.다월, 삼중 〈FG, ε, F,G〉는 C에서 코모나드를 정의하고 있다.null
모든 모나드는 위와 같은 방식으로, 사실상 많은 결합에서 비롯된다.에일렌베르크-모어알헤브라의 범주와 클라이슬리 범주로 불리는 두 개의 구조는 주어진 모나드를 발생시키는 부속물을 건설하는 문제에 대한 두 가지 극단적 해결책이다.null
메모들
- ^ Baez, John C. (1996). "Higher-Dimensional Algebra II: 2-Hilbert Spaces". arXiv:q-alg/9609018.
- ^ Kan, Daniel M. (1958). "Adjoint Functors" (PDF). Transactions of the American Mathematical Society. 87 (2): 294–329. doi:10.2307/1993102.
- ^ 법률상, F. 윌리엄, "재단에서의 성직" 1969년 사투리카오늘날에는 표기법이 다르다; 이러한 강의 노트에서 피터 스미스가 더 쉽게 소개한 것도 이 개념을 인용한 기사에 기인한다.
- ^ "Indiscrete category". nLab.
- ^ 맥 레인, 선더스, 무어디크, 이케(1992) 쉐이브 인 기하학과 논리학, 스프링거-베를라크.ISBN 0-387-97710-4 58페이지 참조
참조
- Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990). Abstract and Concrete Categories. The joy of cats (PDF). John Wiley & Sons. ISBN 0-471-60922-6. Zbl 0695.18001.
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.
외부 링크
- YouTube의 결합 재생 목록 – The Catsters의 Eugenia Cheng의 결합에 대한 7개의 짧은 강의
- WildCats는 Mathematica의 카테고리 이론 패키지다.물체의 조작 및 시각화, 형태론, 범주, 펑터, 자연 변형, 범용 특성.
 (와)
(와) 







 대한 \mathrm
대한 \mathrm 


















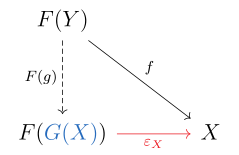




















 물체 FY의 정체성 형태주의를 나타낸다.null
물체 FY의 정체성 형태주의를 나타낸다.null

 "발전기 포함"에 의해 제공된 설정 맵이다.일부 그룹 W의 Y에서 기본 설정 GW까지의 모든 세트 맵은 η
"발전기 포함"에 의해 제공된 설정 맵이다.일부 그룹 W의 Y에서 기본 설정 GW까지의 모든 세트 맵은 η  (는) FGX의 생성자를 그들이 대응하는 X의 원소로 보내는 집단 동형상이며, 자유집단의 보편적 속성에 의해 존재한다.그 다음에 각각 (G X
(는) FGX의 생성자를 그들이 대응하는 X의 원소로 보내는 집단 동형상이며, 자유집단의 보편적 속성에 의해 존재한다.그 다음에 각각 (G X


 FY에서 FGFY로 각 발전기 y를 FGFY의 생성기로 해당 길이 1(y)에 보내는 그룹 동형성이다.화살표 ε
FY에서 FGFY로 각 발전기 y를 FGFY의 생성기로 해당 길이 1(y)에 보내는 그룹 동형성이다.화살표 ε 






 Y
Y



















![f^{{-1}}[T]\subseteq X](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a55cb02881c04c713a24cbe82ece550243ab558)


![\exists _{f}S\subseteq T\leftrightarrow S\subseteq f^{-1}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c821337e6e35974fb9c9d1977c1a3b5da169aab)
![f[S]\subseteq T](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b5dbaa58a61b4955053e8d30ee59bfe257e6c4c)
![S\subseteq f^{{-1}}[f[S]]\subseteq f^{{-1}}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c2845f7f5ca6c49df476c5de6e8c4c4385f1539)

![x\in f^{{-1}}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/43e43732bf6ed7b2b03201f6bbb1eea85f573f74)

![S\subseteq f^{-1}[T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/bad773de89f2d30a93a8442ac7c86eb44e8980bd)


![f^{-1}[\{y\}]\cap S](https://wikimedia.org/api/rest_v1/media/math/render/svg/872d2d997b54463e913e7ea72920cfe094e89342)

![f[S]](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc136e58f23572a4001b784eea645e59b735ce49)
![\exists _{f}S=\{y\in Y\mid \exists (x\in f^{-1}[\{y\}]).\,x\in S\;\}=f[S].](https://wikimedia.org/api/rest_v1/media/math/render/svg/24265e6a1e4e9b58e13a76ba7662185d2527e460)
![\forall _{f}S=\{y\in Y\mid \forall (x\in f^{-1}[\{y\}]).\,x\in S\;\}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92d205846301c35cf45cd5cf9e17c4fd5937bd3)
 부분 집합
부분 집합  대한
대한



 주어 다음과 같은 단계에서 자연 변형 φ : homC(F-,-) → homD(-, G-)을 찾아 hom-set 접합부를 구성할 수 있다.
주어 다음과 같은 단계에서 자연 변형 φ : homC(F-,-) → homD(-, G-)을 찾아 hom-set 접합부를 구성할 수 있다.





 (는) 정체성 형태론이다.
(는) 정체성 형태론이다.


 (는) 지역적으로 표시할 수 있는 범주 사이의 functor로,
(는) 지역적으로 표시할 수 있는 범주 사이의 functor로,

 수평 구성을 나타낸다.null
수평 구성을 나타낸다.null









