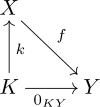커널(카테고리 이론)
Kernel (category theory)범주 이론과 수학의 다른 분기에 대한 그것의 응용에서, 커널은 그룹 동형성의 알맹이, 모듈 동형성의 알맹이 그리고 대수에서 나온 특정한 다른 알맹이의 일반화다.직관적으로 형태론 f : X → Y의 낟알은 (따라서) f로 구성하면 0이 되는 "가장 일반적인" 형태론 k : K → X이다.null
커널 쌍과 차이 커널(이진 이퀄라이저라고도 함)은 때때로 "커널"이라는 이름으로 통하기도 하지만, 관련성이 있는 반면, 이러한 커널은 전혀 동일하지 않으며 이 문서에서 논의되지 않는다는 점에 유의하십시오.null
정의
C를 범주로 삼자.일반적인 범주-이론적 의미에서의 커널을 정의하기 위해서는 C는 영점 형태론을 가질 필요가 있다.그 경우, f : X → Y가 C에서 임의의 형태론이라면, f의 낟알은 f의 등가선이고, 영점 형태론은 X에서 Y까지이다.기호:
- ker(f) = eq(f, 0XY)
좀 더 명시적으로 말하면 다음과 같은 보편적 특성을 사용할 수 있다.f의 낟알은 다음과 같은 형태론 k : K → X와 함께 개체 K이다.
- f ∘k는 K에서 Y까지의 영점 형태론이다.
- f ∘k′이 0 형태론인 형태론 k′ → X를 보면, k givenu = k′과 같은 독특한 형태론 u : K → → K가 있다.
많은 구체적인 맥락에서, 어떤 사람은 형태론 k가 아니라 사물 K를 "커널"로 지칭할 것이라는 점에 유의한다.그러한 상황에서 K는 X의 부분집합일 것이고, 그것은 k를 포함 지도로 재구성하기에 충분할 것이다; 대조적으로, 우리는 어떻게 X의 하위 개체로 해석되는지를 설명하기 위해 형태론 k가 필요하다.어떤 경우든 k는 (정형적인 의미에서는) 항상 단형주의라는 것을 보여줄 수 있다.어떤 사람은 단순히 K나 K만으로 생각하기 보다는 커널을 쌍(K, k)으로 생각하는 것을 선호할 수 있다.null
모든 형태론이 커널을 가질 필요는 없지만, 커널을 가질 필요가 있다면, 그 커널은 모두 강한 의미에서의 이형성인데, 만약 k : K → X와 : : L → X가 f : X → Y의 커널이라면, ℓφφ = k와 같은 독특한 이형성 φ : K → L이 존재한다.
예
커널은 고정 링(고정 필드 위의 벡터 공간 포함) 위에 있는 그룹의 범주나 (좌측) 모듈의 범주 등 추상 대수로부터 많은 범주에서 친숙하다.명시적으로 말하면, f : X → Y가 이러한 범주들 중 하나에서 동형상이고 K가 통상적인 대수적 의미에서는 그것의 커널이라면, K는 X의 아형상이고 K에서 X까지의 동형상 포함은 범주적 의미에서의 커널이다.null
모노이드 범주에서 범주-이성 커널은 그룹과 마찬가지로 존재하지만, 이러한 커널은 대수적 목적을 위해 충분한 정보를 가지고 있지 않다는 점에 유의한다.따라서 단성 이론으로 연구된 커널의 개념은 약간 다르다(아래 #대수성 커널과의 관계 참조).null
단이탈 링의 범주에서 범주-이론적 의미에는 커널이 없다. 실제로 이 범주는 0 형태론조차 가지고 있지 않다.그럼에도 불구하고 비유니탈 링의 범주에 속하는 커널에 해당하는 링 이론에서 연구된 커널의 개념은 여전히 존재한다.null
뾰족한 위상학적 공간의 범주에서 f : X → Y가 연속적인 점 지도라면, 구분점인 K의 전상은 X의 아공간이다.X에 K를 포함하는 지도는 f의 범주형 커널이다.null
기타 범주형 개념과의 관계
커널의 그것과 이중 개념은 코커넬의 그것이다.즉, 형태론의 알맹이는 반대 범주에 있는 그것의 코커넬이며, 그 반대도 마찬가지다.null
위에서 언급했듯이, 커널은 이진 이퀄라이저 또는 차이 커널의 한 유형이다.반대로, 사전 추가 범주에서는 모든 이진 이퀄라이저를 커널로 구성할 수 있다.구체적으로 말하면, 형태변수 f와 g의 등가체는 차이 g - f의 커널이다.기호:
- eq(f, g) = ker(g - f)
형태론을 뺄 수 없는 비선형 범주에서도 이항 이등분자를 '차이 커널'이라고 부르는 것은 이런 사실 때문이다.null
모든 알맹이는 다른 이퀄라이저와 마찬가지로 단성형이다.반대로 단형주의는 어떤 형태론의 알맹이라면 정상이라고 부른다.모든 단성형이 정상이면 범주를 정상이라고 한다.null
특히 아벨의 범주는 항상 정상이다.이런 상황에서, 어떤 형태론의 코커넬의 알맹이(항상 아벨의 범주에 존재한다)가 그 형태론의 이미지로 판명된다; 기호로는:
- im f = ker coker f(아벨리아 범주)
m이 단성형일 때는 그 자체의 이미지여야 한다. 따라서 모든 단성형은 알맹이일 뿐 아니라, 우리는 어떤 형태주의가 그것의 코커넬의 알맹이인지 알고 있다.기호:
- m = ker(코커 m) (아벨의 범주에 있는 단형체의 경우)
대수적 커널과의 관계
유니버설 대수학은 같은 종류의 두 대수 구조들 사이의 동형성에 대한 커널의 개념을 정의한다.이 커널의 개념은 주어진 동형성이 주입되는 것과 얼마나 멀리 떨어져 있는지를 측정한다.위에서 언급한 그룹과 모듈의 상황을 일반화하기 때문에 이 대수적 개념과 커널의 범주적 개념 사이에는 약간의 중복이 있다.그러나 일반적으로 커널의 범용-알지브라틱 개념은 커널 쌍의 범주-이론적 개념에 더 가깝다.특히 커널 쌍은 단성 이론으로 커널을 해석하거나 범주의 이론으로 링 이론을 해석하는 데 사용할 수 있다.null
원천
- Awodey, Steve (2010) [2006]. Category Theory (PDF). Oxford Logic Guides. Vol. 49 (2nd ed.). Oxford University Press. ISBN 978-0-19-923718-0.
- 커널(nLab)