모나드(범주론)

범주 이론에서, 수학의 한 분야인 모나드(또한 3중, 3중, 3중, 표준 구성 및 기본 구성)^[1]는 특정 일관성 조건을 충족하기 위해 필요한 두 개의 자연 변환과 함께 엔도프럭터(범주를 자신에게 매핑하는 펑터)이다.모나드는 보조형 펑커 쌍 이론에 사용되며, 부분적으로 순서가 정해진 세트의 폐쇄 연산자를 임의의 범주에 일반화한다.

도입 및 정의

모나드는 일종의 엔도프랙터다.예를 들어, $F{\displaystyle }$ ${\displaystyle F}$과 G ${\$$displaystyle$ G$}$이(가$)$ $G{\displaystyle }$${\$$displaystyle G$}에 연결된$$ 연결 펑커의 한 쌍이라면$,$ $구성{\displaystyle }$ ${\displaystyle G}$f F$${\$displaystyle$G\$circule F}$은(모나드)이다$$.$F{\displaystyle }$ ${\displaystyle F}$ 및$$ $G{\displaystyle }$ ${\displaystyle G}$이(가) 역 펑터인 경우 해당 모나드가 ID 펑터인 것이다.일반적으로 결합은 동등하지 않다. 서로 다른 성질의 범주와 관련된다.모나드 이론은 '보존'이라는 결합이 무엇인지 파악하려는 노력의 일환으로 중요하다.$F{\displaystyle }$ ${\displaystyle \circ }$ ${\displaystyle G}$ ${\displaystyle F\circle G}$을(를) 고려함으로써 마찬가지로 배울 수 있는 것에 대한 이론의 나머지 절반은 코모나드의 이중 이론으로 논의된다$.$

형식 정의

이 $문서$에서 C ${\displaystyle C}$은 범주를 나타낸다$$.A monad on ${\displaystyle C}$ consists of an endofunctor ${\displaystyle T\colon C\to C}$ together with two natural transformations: ${\displaystyle \eta \colon 1_{C}\to T}$ (where ${\displaystyle 1_{C}}$ denotes the identity functor on ${\displaystyle C}$) and ${\displaystyle \mu :T^2\to }$${\displaystyle T}$ ${\displaystyle \mu \colon$T^{$2}\$$to{\displaystyle {}^{}}$ ${\displaystyle {T\mathrm{}}^{}}$}($$$$여기서$$T 2 {\$displaystyle$ T$^{2}}$는 펑터 T ${\displaystyle \mathrm{ctor}}$ $T{\displaystyle }$ ${\displaystyle \{\backslash }$$displaystyle C}$에서 C ${\displaysty C}$까지입니다$).$이러한 조건은 다음과 같은 조건(일종의 일관성 조건이라고도 함)을 충족하기 위해 필요하다.

• ${\displaystyle \mu \circ T\mu =\mu \circ \mu T}$ (as natural transformations ${\displaystyle T^{3}\to T}$); here ${\displaystyle T\mu }$ and ${\displaystyle \mu T}$ are formed by "horizontal composition"
• ${\displaystyle \mu \circ T\eta =\mu \circ \eta T=1_{T}}$ (as natural transformations ${\displaystyle T\to T}$; here ${\displaystyle 1_{T}}$ denotes the identity transformation from ${\displaystyle T}$ to ${\displaystyle T}$).

우리는 다음과 같은 대응 도표를 사용하여 이러한 조건을 다시 작성할 수 있다.

$T{\displaystyle }$ ${\displaystyle \mu }$ ${\displaystyle T\mu }$ 및$$ ${\displaystyle \mathrm{\mu T}}$ ${\displaystyle \mu T}$에 대한 설명은 자연 변환 관련 기사를 참조하거나$,$ 이러한 개념을 사용하지 않는 정류 다이어그램 아래를 참조하십시오.

첫 번째 공리는 $\mu {\displaystyle }$ ${\displaystyle \mu }$을(를) 모노이드의 이항 연산으로 생각하면 모노이드의 연관성과 유사하며, 두 번째 공리는 (우리가 $\eta {\displaystyle }$ ${\displaystyle \eta }$에 의해 주어진 것과 같이) ID 요소의 존재와 유사하다.$$$실제로{\displaystyle }$ $C{\displaystyle }$ ${\displaystyle C}$의 모노이드 대신 ${\displaystyle {\mathbf{En}}_{}}$ ${\displaystyle {}_{}}$ C ${\$ 범주에 있는 모노이드로 정의할 수 있으며$$, 이$$ 개체들은 C ${\displaystyle C}$의 끝단자국이며 이들$$ 사이의 자연스러운 변형인 형태는 구성으로 유도된다.종말의

전원 세트 모나드

The power set monad is a monad ${\displaystyle {\mathcal {P}}}$ on the category ${\displaystyle \mathbf {Set} }$: For a set ${\displaystyle A}$ let ${\displaystyle T(A)}$ be the power set of ${\displaystyle A}$ and for a function ${\displaystyle f\colon A\to B}$ let ${\displaystyle T(f)}$${\displaystyle T(f)}$ be the function between the power sets induced by taking direct images under ${\displaystyle f}$. For every set ${\displaystyle A}$, we have a map ${\displaystyle \eta _{A}\colon A\to T(A)}$, which assigns to every ${\displaystyle a\in A}$ the singleton ${$$\displaystyle \{a$함수

$\displaystyle \mu _{A}\colon T(A)\to(A)}$

조합에 집합하다.이 자료들은 모나드를 묘사하고 있다.

언급

모나드의 공리는 공식적으로 모노이드 공리와 비슷하다.사실, 모노이드들은 모노이드의 특별한 경우로, 즉 그것들은 정확히 엔도폰서 ${\displaystyle \mathrm{End}}$ ${\displaystyle }$ $){\displaystyle \operatorname {End} (C$ 중에서 모노이드들이며, 엔도폰서들의 구성에 의해 주어진 곱셈을 갖추고 있다.

모나드의 구성은 일반적으로 모나드가 아니다.예를 들어 이중 전원 세트 펑터 $P{\displaystyle \mathcal{}}$ ${\displaystyle \circ }$ ${\displaystyle P\mathcal{}}$ ${\$은(는) 모나드 구조를 인정하지 않는다$$.^[2]

코모나드

범주형 이중 정의는 코모나드(또는 cotriple)의 공식 정의로, $범주{\displaystyle }$C {\$displaystyle C}$에 대한 코모나드가 $반대{\displaystyle {}^{}}$ ${\displaystyle {범주\mathrm{}}^{}}$ C ${\displaystyle {\mathrm{o}}^{}}$p {\$displaystyle$C^{\$mathrm$${$op$}}}}}$에 대한 모나드라는$$ 용어로 빠르게 말할 수 있다$.$ $따라서{\displaystyle }$ C$${$styp$의 $펑터{\displaystyle }$ U${\displaysty$}방금 주어진 정의의 모든 곳에 있는 화살을 뒤집는 것에서 오는 상담과 복제를 위한 일련의 공리들을 가지고 그 자체로$$ $le$ C$}.$

모나드는 모노이드와 코모노이드와 마찬가지로 모노이드에 해당한다.모든 세트는 독특한 방식으로 코모노이드여서 모노이드보다 추상대수학에서는 코모노이드에 익숙하지 않지만, 통상적인 텐서 제품을 가진 벡터공간의 범주에 있는 코모노이드들은 중요하고, 콜지브라라는 이름으로 널리 연구되고 있다.

터미네이션 역사

모나드의 개념은 1958년 로저 고데이션에 의해 "표준구축"이라는 이름으로 발명되었다.1960년대와 1970년대에 많은 사람들이 "트리플"이라는 이름을 사용했다.현재 표준 용어인 "모나드"는 Sunders Mac Lane 때문이다.^{[citation needed]}

예

결합에서 발생하는 모나드

모든 부속품

$(\displaystyle F:C\우측 왼쪽 열 D:G}$

C에 모나드를 낳는다.이 매우 광범위한 시공은 다음과 같다: Endofunctor는 복합재다.

$T=G\circle F.}$

이 단면도(endofunctor)는 단면도(monad)로 금방 나타나는데, 단위지도는 부속의 ${\displaystyle {단위지도}_{}}$ ${\displaystyle \mathrm{ID}}$ ${\displaystyle C{}_{}}$→ G $∘$ F ${\daystyle$ \$operatorname {id} _{C}\to$ G\$circ F}$에서 유래하며, 다음과 같은 부속의 상담지도를 사용하여 곱셈도를 구성한다.

${\displaystyle T^{2}=G\circ F\circle F\circle F\circle F\xrightrow {G\circle {\text{counit}\circle F=T}}$

사실, 어떤 모나드도 Eilenberg-Moore 범주 C ${\displaystyle T^{}}$ ${\$$T{\displaystyle }$ ${\displaystyle T}$ -algebras$$ 범주)를 사용하여 펑커의 명시적인 결합으로 발견할 수 있다.^[3]

이중화

고정 필드 k에 대한 이중 이중 이중화 단일화는 부속서에서 발생한다.

${\displaystyle(-)^{*}:\mathbf {Vect} _{k}\우측좌파 \mathbf {Vect} _{k}^{op}:(-)^{*}}}}}$

where both functors are given by sending a vector space V to its dual vector space ${\displaystyle V^{*}:=\operatorname {Hom} (V,k)}$. The associated monad sends a vector space V to its double dual ${\displaystyle V^{**}}$. This monad is discussed, in much greater generality, by Kock (1970).

부분적으로 정렬된 세트의 폐쇄 연산자

${\displaystyle \mathrm{부분}}$ 순서 집합$({\displaystyle P}$, ${\displaystyle \le }$) ${\displaystyle (P,\$$leq$ $)}($$x$ {\$displaystyle$ x$}$에서 y ${\$$displaystyle y}$까지 단일 형태론 포함)$$$$에서 발생하는 범주의 경우 형식주의는 훨씬 단순화되며, 조정 쌍은 갈루아 연결이고 모노드는 폐쇄 연산자다.

자유잊음부착

예를 들어 $G{\displaystyle }$ ${\displaystyle G}$을(를) 그룹의 Grp 범주에서 집합 범주로의 망각적인 functor로 하고$$, F${\displaystyle }${\$displaystyle F$}을$$(를) 집합 범주에서 그룹 범주로의 자유 그룹 functor로 한다.Then ${\displaystyle F}$ is left adjoint of ${\displaystyle G}$. In this case, the associated monad ${\displaystyle T=G\circ F}$ takes a set ${\displaystyle X}$ and returns the underlying set of the free group ${\displaystyle \mathrm {Free} (X)}$.이 모나드의 단위 지도는 지도에 의해 주어진다.

$[\displaystyle X\to T(X)}$

$X{\displaystyle }$ {\$displaystyle X}$을(를$)$ 세트 $F{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{r}}$ ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{e}}$( ${\displaystyle X)}$ ${\displaystyle \mathrm {Free}(X)$에 길이$$ 1의 문자열로 포함.게다가 이 모나드의 곱셈은 지도다.

$[\displaystyle T(T(X)]\to T(X)}$

'현악의 현악기'의 자연 결합이나 '현악기'로 만든 것이다.이것은 두 가지 자연 변형이다.자유집단에 관한 앞의 예시는 보편대수학에서 다양한 알헤브라의 의미로 어떤 형태의 대수학으로도 일반화할 수 있다.그러므로, 그러한 모든 종류의 대수학은 집합의 범주에 모나드를 낳는다.중요한 것은 대수형은 모나드(에일렌베르크-모어 알헤브라의 범주로서)에서 회복될 수 있기 때문에 모나드도 보편적 알헤브라의 품종을 일반화하는 것으로 볼 수 있다.

부속물에서 발생하는 또 다른 모나드는 $T{\displaystyle }$ ${\displaystyle T}$이(가) 벡터 $공간{\displaystyle }$ V ${\$$displaystyle$ $V$$}$을(를) 텐서 대수 T$V)$에 매핑하고$$선형 지도를 텐서 제품에 매핑하는 벡터 공간 범주의 Endoforctor일$$ 때 발생한다.그 다음 $우리$는 V ${\displaystyle V}$을 텐서 대수학으로$$ 내장하는 것에 해당하는 자연적 변환을 하고, 단순히 모든 텐서 제품을 확장하여 얻은$$ $T{\displaystyle }$${\displaystyle (}$${\displaystyle T)}$ (${\displaystyle T)}$ ${\$$displaystytle T($V)}에서 T$)}$까지의 지도에 해당하는 자연적 변환을 갖는다$.$

코드크래프트 모나드

가벼운 조건에서는 좌뇌 부정을 인정하지 않는 의사들도 소위 '대형성 모나드'라는 모나드를 낳는다.예를 들어, 포함

${\displaystyle \mathbf {FinSet} \subset \mathbf {Set} }$

좌의정을 인정하지 않다그것의 대칭모나드는 X의 초저광필터 세트로 임의의 X 세트를 보내는 모나드다.이와 유사한 예는 라이스터(2013년)에서 논의한다.

알헤브라스(모나드용

Given a monad ${\displaystyle (T,\eta ,\mu )}$ on a category ${\displaystyle C}$, it is natural to consider ${\displaystyle T}$-algebras, i.e., objects of ${\displaystyle C}$ acted upon by ${\displaystyle T}$ in a way which is compatible with the unit and multiplication of the monad.$좀{\displaystyle }$ 더 형식적으로 T ${\displaystyle$ $T}$ -algebra$$ (${\displaystyle x}$,${\displaystyle h}$ )$${\$displaystyle (x,h)}$은 C ${\displaystyle$$C$}의$$ $개체{\displaystyle }$ x ${\displaystyle x}$이며, ${\displaystyle \mathrm{화살표}}$h : T${\displaystyle x}$ → ${\displaystyle x}$ ${\displaystystyleon Tx\to x$$}$은 대수도의 구조 맵이라고 한다$$.

그리고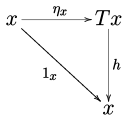

통근하다

$T{\displaystyle }$ ${\displaystyle T}$ -algebras의$$ $형태론{\displaystyle }$ f${\displaystyle }$:${\displaystyle }$( ${\displaystyle x}$, h${\displaystyle }$)${\displaystyle }$→ ( $($, ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$) {\$displaystyle$ f$\$$colon$$(x,h)\$$to$$$($x$$', h')}$는 도표와 같은$$ $C{\displaystyle }$ ${\displaysty C}$의 ${\displaystyle \mathrm{화살표}}$ f${\displaystyle }$: ${\displaystyle {}^{}}$→ x$$이다.

통근하다${\displaystyle T}$ ${\displaystyle T$} -algebras는$$ Eilenberg-Moore 범주라고 하는 범주를 형성하며, $C{\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\$로 표시된다$.$

예

알헤브라가 자유 그룹 모나드 위에 있다.

예를 들어 위에서 설명한 자유 그룹 모나드의 $경우{\displaystyle }$, $T{\displaystyle }$ ${\displaystyle$T} -algebra는$$ X$${\$displaystyle$ X$}$에서 $X{\displaystyle }$ ${\displaystyle$ X$}$에 의해$$ 생성된 자유 그룹으로부터 지도와 함께 $X$ {\displaystyle X$}$의 연관성과 단일성 조건에 따라 설정된$$ X ${\displaysty$ X}이다.그러한 구조는 $X{\displaystyle }$ ${\displaystyle X}$이(가) 그룹 그 자체라고 말하는 것과 같다.

알헤브라가 분포 모나드 위에 있음

또 다른 예는 집합 범주의 분포$$ 모나드 $D{\displaystyle \mathcal{}}$ ${\$ {$D}$이다.집합 $X{\displaystyle }$ ${\displaystyle X}$을(를$$) $f{\displaystyle }$: X${\displaystyle }$→${\displaystyle }$[ ${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle f:X\to [0,1]$로 전송하여 정의하며, 그러한 합이 $1{\displaystyle \mathrm{}}$ ${\displaystyle 1}$과(와) 같도록 한다$.$ 세트빌더 표기법에서는 이 집합이다.

정의를 검사하면, 분포 모나드 위의 알헤브라는 볼록 세트 즉, $r{\displaystyle }$ ${\displaystyle \in }$[ ${\displaystyle 0,}$ ${\displaystyle 1}$ {\$displaystyle r\in [0,$${\displaystyle 1}$$]$에 대해$$ $연산{\displaystyle }$ x${\displaystyle {}_{}}$+ ${\displaystyle {}_{}}$ y ${\displaystyle$ x$+_{r}y}$가 장착된 세트에 해당하며$$, 볼록 선형 결합 ${\displaystyle r}$ x${\displaystyle }$+ (${\displaystyle 1}$-${\displaystyle }$) ${\displaystyle y}$)의 거동을 유사하게 된다.$$유클리드 공간에 있는$$ ${\displaystyle rx+(1-r)y}$^[4]

대칭 단면 위의 알제브라

모나드의 또 다른 유용한 예는 R ${\displaystyle R}$ -상호환 $R{\displaystyle }$ ${\displaystyle$ R$}$의 $범주$에 있는 대칭 대수 펑터다$.$

$R{\displaystyle }$ {\$displaystyle R}$ -module$$ $M{\displaystyle }${\$displaystyle$ M$}$을(를) 대칭 텐서 전원의 직접 합으로 전송$$where ${\displaystyle {\text{Sym}}^{0}(M)=R}$. For example, ${\displaystyle {\text{Sym}}^{\bullet }(R^{\oplus n})\cong R[x_{1},\ldots ,x_{n}]}$ where the ${\displaystyle R}$-algebra on the right is considered as a module.그러면 이 모나드 위에 있는 대수학(geargebras)은 $역행{\displaystyle }$ R ${\displaystyle R}$ -algebras이다$$.또한 교번 텐서 ${\displaystyle {\text{Alt}}^{}}$∙ (${\displaystyle }$-${\displaystyle }$) ${\displaystyle {\text{$$Alt}^{\bullet }(-)}$ 및$$ 총 텐서 $펑커{\displaystyle {}^{}}$ T ${\displaystyle {\bullet }^{}}$(${\displaystyle }$-${\displaystyle }$) ${\displaystyle$ T$^{\bullet }(-)}}$ 대칭 R {\$displaystyle R}$ -algebras$$, $무료$ R ${\displaystyle R}$ -algebras$$.여기서 첫 번째 링은 $n{\displaystyle }$ ${\displaystyle n}$ -generator에서$$$$ $R{\displaystyle }$ ${\displaystyle R}$에 대한 자유 대칭 대수이고 두 $번째{\displaystyle }$ 링은 $n{\displaystyle }$ ${\displaystyn}$-gener에$$$$ 있는 R ${\displaystyle$ $R$$}$에 대한 자유 대칭 대수다.

E-infinity 링 스펙트럼 내 정류 알헤브라스

A의 M이 한{\displaystyle{{M\mathcal}}_{A}}은 범주에는 교환 S{\displaystyle \mathbb{S}}-algebras[5]pg 113에 대한 가환 가환 S{\displaystyle \mathbb{S}의{A\displaystyle}-algebras을 준다 유사한 건설}한{A\displaystyle}-algebra 있다. {\displ$aystyle A}$ -modules$$ $다음$에 functor P${\displaystyle }$: M ${\displaystyle A_{}}$→ M ${\displaystyle A_{}}$ ${\$이(가) 제공한 모나드다$$.

어디에 ${\displaystyle j}$ $[\displaystyle j}$ -filense$$.그 다음 이 모나드 위에 있는 알헤브라의$$ $범주$에서 정류 $A{\displaystyle }$ ${\displaystyle {\$$mathcal{C}_{A}$와 연관된 범주 ${\displaystyle C_{}}$가 있다.

모나드 및 부속품

위에서 언급했듯이, 어떤 부속물도 모나드를 낳는다.반대로, 모든 모나드는 어떤 부속물, 즉 자유-잊혀지지 않는 부속물에서 생긴다.

$[\displaystyle T(-):C\우측좌표 C^{T}:{\text{forget}}$

왼쪽 부호는 물체 X를 T-알지브라 T(X)에 보낸다.However, there are usually several distinct adjunctions giving rise to a monad: let ${\displaystyle \mathbf {Adj} (C,T)}$ be the category whose objects are the adjunctions ${\displaystyle (F,G,e,\varepsilon )}$ such that ${\displaystyle (GF,e,G\varepsilon F)=($$T,\eta ,\mu )}$ and whose arrows are the morphisms of adjunctions that are the identity on ${\displaystyle C}$. Then the above free–forgetful adjunction involving the Eilenberg–Moore category ${\displaystyle C^{T}}$ is a terminal object in ${\displaystyle \mathbf {Adj} (C,T)}$. An initial object is theKleisli 범주, 즉 C의 일부 객체 x에 대해$$ $T{\displaystyle }$ (${\displaystyle }$x${\displaystyle }$) ${\displaystyle T(x)}$ 형식의 T-algebras로만 구성된$$ $C{\displaystyle {}^{}}$ ${\displaystyle T^{}}$ ${\$의 전체 하위 범주.

단음절

부속물$({\displaystyle F}$: ${\displaystyle C}$→ D${\displaystyle }$, ${\displaystyle G}$: ${\displaystyle D}$→ ${\displaystyle C}$ ,${\displaystyle \eta }$ )${\displaystyle (F:$$C\to D, G:D\to$ C$,\eta,\varepsilon$ )}$$관련 모나드 T와 함께$$ functor G를 다음과 같이 고려할 수 있다.

${\displaystyle D{\stackrel {\tild{G}}{{\\}C^{{}}T}{\\stackrel {\text{forget}{\\\c,}$

즉, G(Y)는 D의 모든 Y에 대한 T-알지브라 구조를 자연적으로 부여할 수 있다.최초의 함수 기호 G일{\displaystyle{\tilde{G}}}범주의 D와 광의로 그 Eilenberg–Moore 범주 CT{\displaystyle C^{T}}.[6], 함수 기호 G사이에 등가를 산출한다 그 첨가는 단항의 첨가:D→ C{G\colon D\to C\displaystyle}만약 왼쪽 adj다 단항 된다고 한다라고 불린다.어이nt $F{\displaystyle }$ ${\displaystyle F}$이(가) 단일 결합을 형성하고$$ 있다.예를 들어, 관련 모나드 위에 있는 알헤브라는 그룹이기 때문에 그룹과 세트 사이의 자유-잊혀지지 않는 결합은 단음절이다.일반적으로 부속물이 단음절이라는 것을 알면 C와 T-action의 물체에서 D의 물체를 재구성할 수 있다.

벡의 단일성 정리

벡의 단일성 정리는 결합이 단일성이 되기 위한 필요하고도 충분한 조건을 제공한다.이 정리의 단순화된 버전은 G가 보수적이라면(또는 G가 이소모르프리즘을 반영하면, 즉 D의 형태론은 C의 이소모르프리즘인 경우에만 이소모르프리즘이라고), C가 가지고 있고 G가 동등분자를 보존하고 있다고 기술하고 있다.

예를 들어 콤팩트한 하우스도르프 공간의 범주에서 셋트하는 건망증이 심한 펑터는 모나디드다.그러나 모든 위상학적 공간에서 세트까지 망각적인 펑터는 동형성이 되지 못하는 연속적인(비 컴팩트 공간 또는 비 하우스도르프 공간 사이)의 생체 지도가 존재하기 때문에 보수적이지 않다.그러므로, 이 건망증이 있는 펑터는 단조로운 것이 아니다.^[7]벡의 정리의 이중 버전은 코모나치적 결합을 특징짓는 것으로, 토포스 이론이나 강하와 관련된 대수 기하학의 주제 등 다른 분야와 관련이 있다.첫 번째 혼합물의 예로는 혼합물이 있다.

${\displaystyle -\otimes _{A}B:\mathbf {Mod} _{A}\오른쪽 왼쪽 줄 \mathbf {Mod} _{B:\operatorname {forget} }}}$

${\displaystyle \mathrm{교환}}$ 고리 사이의$$ 고리 동형성 $A{\displaystyle }$→ B ${\displaystyle A\to B}$에 대해.이 부속물은 B가 A-모듈로서 충실하게 평탄할 경우에만 벡의 정리에 의해 코모나치적이다.따라서 강하 기준점(즉, 부속물에 의해 주어진 코모나드의 작용)을 갖춘 B-모듈을 A-모듈로 하강시킬 수 있다.성실하게 평강하행의 결과 이론은 대수 기하학에서 광범위하게 적용되고 있다.

사용하다

모나드는 순차 연산 유형(때로는 부작용)을 표현하기 위해 기능 프로그래밍에 사용된다.기능 프로그래밍의 모노드와 수학 지향 Wikibook 모듈 b를 참조하십시오.하스켈/카테고리 이론.

범주형 논리학에서는 모나드-코모나드 이론과 폐쇄 연산자, 내부 알헤브라를 통한 모달 논리학, 그리고 S4 모델과 직관적 논리학과의 관계 사이에 유추된 것이 있다.

일반화

2-카테고리 $C{\displaystyle }$ ${\displaystyle C}$에서 모노드를 정의할 수 있다$.$ $위$에서 설명한 모노드는 C${\displaystyle }$= C ${\displaystyle a\mathbf{}}$ ${\displaystyle \mathbf{t}}$ ${\$ C$=\mathbf {Cat}}$에 대한 모노드 입니다$.$

참고 항목

• 모나드간 분배법
• 로베레 이론
• 모나드(기능 프로그래밍)
• 폴리아드
• 스트롱 모나드

참조

추가 읽기

• Barr, Michael; Wells, Charles (1999), Category Theory for Computing Science (PDF)
• Godement, Roger (1958), Topologie Algébrique et Théorie des Faisceaux., Actualités Sci. Ind., Publ. Math. Univ. Strasbourg, vol. 1252, Paris: Hermann, pp. viii+283 pp
• Kock, Anders (1970), "On Double Dualization Monads", Mathematica Scandinavica, 27: 151, doi:10.7146/math.scand.a-10995
• Leinster, Tom (2013), "Codensity and the ultrafilter monad", Theory and Applications of Categories, 28: 332–370, arXiv:1209.3606, Bibcode:2012arXiv1209.3606L
• MacLane, Saunders (1978), Categories for the Working Mathematician, Graduate Texts in Mathematics, vol. 5, doi:10.1007/978-1-4757-4721-8, ISBN 978-1-4419-3123-8
• Pedicchio, Maria Cristina; Tholen, Walter, eds. (2004). Categorical Foundations. Special Topics in Order, Topology, Algebra, and Sheaf Theory. Encyclopedia of Mathematics and Its Applications. Vol. 97. Cambridge: Cambridge University Press. ISBN 0-521-83414-7. Zbl 1034.18001.
• Riehl, Emily (2017), Category Theory in Context, ISBN 9780486820804
• Turi, Daniele (1996–2001), Category Theory Lecture Notes (PDF)

외부 링크

• 모나드, 5개의 짧은 강의(부록 1개 포함)
• 존 배즈의 이번 주 수학 물리학에서 발견(89주)은 2개 범주의 모나드를 다룬다.