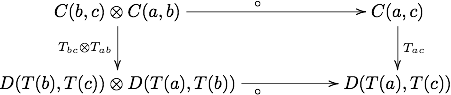농축분류

수학의 한 분야인 범주 이론에서, 풍요로운 범주는 일반적인 단일 범주의 물체로 홈 세트를 대체함으로써 범주의 사상을 일반화한다.많은 실제 적용에서 홈 세트는 예를 들어 형태론의 벡터 공간 또는 형태론의 위상학적 공간과 같이 존중되어야 할 추가적인 구조를 가지고 있다는 관찰에 의해 동기 부여된다.농축 범주에서, 모든 개체 쌍과 연관된 형태론(홈 집합) 집합은 "home-objects"의 고정된 단일 범주에서 개체로 대체된다.일반 범주에서 형태론의 (연관적) 구성을 모방하기 위해, 홈 범주는 연관적 방식으로 호몰 객체를 구성하는 수단을 가져야 한다. 즉, 어떤 맥락에서는 조작이 콤뮤타(commuta)가 필요할 수도 있지만 최소한 단일 범주의 구조를 제공하는 개체에 대해 2진 연산이 있어야 한다.또한 우측 부선(즉, 범주를 각각 대칭 단원형 또는 심지어 대칭으로 닫힌 단원형)을 가질 수 있다.^{[citation needed]}

따라서 농축 범주 이론은 다음과 같은 다양한 구조를 동일한 프레임워크 내에서 포괄한다.

홈셋이 세트 이상의 추가 구조를 갖는 일반적인 범주즉, 구성에 의해 존중되어야 하는 형태론의 운영 또는 특성(예를 들어, 2-카테고리에서의 형태론과 그것의 수평적 구성 사이에 2-셀의 존재 또는 아벨리아 범주에서의 형태론에 대한 추가 연산)이 있다.
범주형 실체들 자체에는 개별 형태주의에 대한 개념이 없지만 홈 오브젝트가 유사한 구성적 측면(예: 구성 규칙이 transitability를 보장하는 사전 순서 또는 홈 오브젝트가 숫자 거리이고 구성 규칙이 삼각형 불평등을 제공하는 Rawever의 메트릭 공간)을 가지고 있는 범주형 실체들.

hom-object 범주가 일반적인 데카르트 제품을 사용한 세트 범주가 되는 경우, 농축 범주의 정의, 농축 펑터 등...보통 범주 이론에서 원래 정의로 축소하다

단면체 범주 M의 홈 객체가 있는 농축 범주는 M에 대한 농축 범주 또는 M의 농축 범주 또는 단순히 M 범주라고 한다.Mac Lane이 단면체 범주를 참조할 때 문자 V를 선호하기 때문에, 농축된 범주를 일반적으로 V-category라고도 부르기도 한다.

정의

레트 $(M, \otimes,$ $I,$ $α,$ $λ$ , $ρ)$ 는 단면체 범주가 된다.그 다음, 농축 범주 C(대안적으로, 단면체 범주의 선택이 명시적이어야 하는 상황에서, M 범주 또는 M 범주보다 농축된 범주)는 다음과 같이 구성된다.

C 등급 오브젝트,
화살표 $f:a\rightarrow b$ 를 $f:I\rightarrow C(a,b)$ 하는 데 사용되는 모든 개체 a, b in C의 각 쌍에 대한 M의 $개체$ C( $a,$ $b)$ : $f:a\rightarrow b$ → $f:a\rightarrow b$ : b : b $f:a\rightarrow b$ 를 $f:a\rightarrow b$ 화살표 f $f:I\rightarrow C(a,b)$ : $f:I\rightarrow C(a,b)$ → $f:I\rightarrow C(a,b)$ $f:I\rightarrow C(a,b)$ $f:I\rightarrow C(a,b)$ ) ${\displaystyf:$ M에 $f:I\rightarrow C(a,b)$ $있는$ C $(a,b)$ 의 $오른쪽 화살표$
화살표 $id a : I$ → $C (a,$ $a)$ in C의 모든 물체에 대한 ID를 지정하는 M의 경우,
화살 °abc:C(b, c)⊗ C(a, b)→ C(, c)M에 있는 개체 Cg로, b, Cc, f의 작문:→ b{\displaystyle f:a\rightarrow b}과 g을 규정하는 데 사용되:b→ c{\displaystyle g:b\rightarrow c}Cf)∘ abc(g⊗ f){\displaystyle g\circ_{\textbf{C}∘의 각 3배로 작문.}f=아래에서 설명하는 3개의 통근 다이어그램과 함께 $g\circ _{\textbf {C}}f={^{\circ }}_{abc}(g\otimes f)$ ${^{\loss }_{poss}(g\otimes$ f $)}}$

첫 번째 도표는 구성의 연관성을 나타낸다.

$Math-enriched category associativity.svg$

즉, 연관성 요건은 현재 단면 범주 M의 연관자에 의해 인수된다.

For the case that M is the category of sets and $(\otimes, I, α, λ, ρ)$ is the monoidal structure $(\times, {•}, \dots)$ given by the cartesian product, the terminal single-point set, and the canonical isomorphisms they induce, then each $C (a, b)$ is a set whose elements may be thought of as "individual morphisms" of C, while °, now a function, defines how consecutive형태론이 형성되다이 경우 첫 번째 도표에서 $C (a,$ $d)$ 로 이어지는 각 경로는 세 가지 연속적인 $개별$ 형태론 a → b → $c$ → $d$ , 즉 $C (a,$ b $),$ $C (b,$ $c)$ 및 $C (c,$ $d$ )의 요소들을 구성하는 두 가지 방법 중 하나에 해당한다 $.$ 도표의 동시성은 두 구성 순서가 모두 일반 범주에서 요구하는 것과 정확히 동일한 결과를 제공한다는 진술에 불과하다.

여기서 새로운 것은 위의 그림들이 풍부한 범주 C에서 개별 형태에 대한 명시적인 참조 없이 연관성에 대한 요구사항을 표현하고 있다는 것이다. 다시 말해, 이러한 도표는 C에서가 아닌 단노이드 범주 M의 형태에 대한 것으로서, 홈 오브젝트가 있는 일반적인 경우에서 구성의 연관성에 대한 개념을 의미 있게 만든다. $C (a,$ $b)$ 는 추상적이며, C 자체는 개별적인 형태론에 대한 개념조차 가질 필요가 없다.

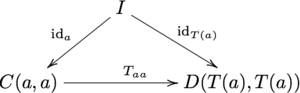
일반 범주가 반드시 신분 형태론을 가져야 한다는 개념은 두 번째와 세 번째 도표로 대체되며, 이 도표는 왼쪽과 오른쪽 단위의 관점에서 정체성을 표현한다.

$Math-enriched category identity1.svg$

그리고

$Math-enriched category identity2.svg$

M이 데카르트 제품을 사용한 세트의 범주인 경우, 형태론 $ID a :$ $I$ → $C (a,$ $a)$ 는 원포인트 집합 I에서 함수가 되고, 그 다음, 주어진 객체 a에 대해, 각 집합 $C (a,$ $a$ )의 특정 요소를 식별해야 하며 $,$ 이 때 우리가 "c in a에 대한 동일성 형태론"이라고 생각할 수 있다.후자 두 도표의 동시성은 이러한 구별되는 개별 "C의 식별 형태"를 포함하는 구성(함수 °에 의해 정의됨)이 일반 범주의 식별 규칙에 따라 정확히 작동한다는 진술이다.

여기서 언급되는 "식별성"에 대한 몇 가지 뚜렷한 개념이 있다는 점에 유의하십시오.

M의 단성 정체성 개체 $I$ 는 단성-이성-이성적 의미에서만 ⊗의 정체성이며, 그 후에도 표준적 이형성 $(異形性,$ $ρ)$ 까지만 존재한다.
정체성 $형태론 C (a, b)$ 1 : $C (a,$ $b)$ → $C (a,$ $b)$ M이 (적어도) 통상적인 범주라는 이유로 각각의 대상에 대해 가지는 C(a, b)
농축 범주 $ID a$ : $I$ → $C$ in C 각 물체 a에 대한 $C (a,$ a)이며, 이것은 다시 M의 형태론이며, C가 그 자체의 개별적 형태론을 가지고 있다고 간주되는 경우에도 반드시 특정한 것을 식별하는 것은 아니다.

농축 범주의 예

일반 범주는 위에 언급한 바와 같이 카르테시안 제품을 단면 연산으로 하는 세트 범주인 (Set, ×, {•})에 대해 농축된 범주다.
2-카테고리란 작은 범주의 범주인 Cat보다 풍부한 범주로, 데카르트 제품에 의해 단조로운 구조가 주어진다.이 경우, 형태론 a → b와 그것들과 관련된 수직 구성 규칙 사이의 2-셀은 일반 범주 C(a, b)와 그 자체의 구성 규칙의 형태론에 해당한다.
국소적으로 작은 범주는 (SmSet, ×) 위에 농축된 범주로, 데카르트 제품을 단면 연산으로 한 작은 범주의 범주로 한다. (국소적으로 작은 범주는 hom-objects가 작은 범주의 범주로 한다.)
국소적으로 유한한 범주는 유추에 의해 카르테시안 제품을 단면 연산으로 하는 유한 집합의 범주인 (FinSet, ×)에 걸쳐 농축된 범주다.
사전 정렬된 집합은 특정 단일 범주에 걸쳐 농축된 범주(2), 그 사이에 FALSE → TRUE로 쓸 수 있는 단일 비식별성 화살표로 구성되어 있으며, 이 범주는 단일 유형으로 결합되어 있으며, TRUE는 단일 유형으로 작성될 수 있다.그러면 home-objects 2(a, b)는 단순히 주어진 객체 쌍(a, b)에 대한 특정한 이항 관계를 부정하거나 단언한다. 더 친숙한 표기법을 사용하기 위해 우리는 이 관계를 ≤ $b$ 로 쓸 수 있다.2 이상 농축된 범주에 필요한 구성과 정체성의 존재는 각각 다음과 같은 공리로 즉시 해석된다.

a ≤ b와 b ≤ c ⇒ c (투명성)

TRUE ⇒ a ≤ (가변성)

그것은 다름아닌 앎이 선주문이라는 공리들이다.그리고 모든 다이어그램이 2번 통근에 있기 때문에, 이것은 2번 이상 농축된 범주에 대한 농축 범주 공리의 유일한 내용이다.

윌리엄 Lawvere의 일반화된 계량 공간 또한pseudoquasimetric 공간으로 알려진 이 범주는 비음의 확장된 실수를 R+∞, 후자는 평소의 순서(즉, 존재하는 사상 r→ siff r≥ s)의 역과monoidal 구조를 통해 추가(+)고 제로(0을 통해 평범한 범주 구조를 볼 것인지에 대해 농축.cm이다.home-objects $R +\infty (a,$ $b)$ 은 본질적으로 거리 d(a, b)이며, 구성과 정체성의 존재는 다음과 같이 해석된다.

d(b, c) + d(a, b) ≥ d(a, c) (불평등)

0 ≥ d(a, a)

형태변수가 0인 범주는 단일체 연산으로서 스매시 제품이 있는 점 집합의 범주인 (Set*, ∧)에 걸쳐 농축된 범주다. 홈 객체 Hom(A, B)의 특수 지점은 A에서 B까지의 영점 형태론에 해당한다.
아벨 그룹의 범주 Ab와 모듈들의 범주 R-Mod, 그리고 주어진 영역에 걸친 벡터 공간의 범주 Vect는 그들 자신에 대해 풍부하게 되며, 여기서 형태론은 대수학적 구조를 "지점"으로 계승한다.보다 일반적으로, 가독성 이전의 범주는 (Ab, ⊗)에 걸쳐서 (Ab, ⊗) 텐서 제품을 모노이드 연산(Abelian groups를 Z-module로 생각)으로 하여 농축된 범주들이다.

모노이드 펑커와의 관계

단면체 범주 M에서 단면체 범주 N까지 단면체 범주가 있는 경우, M을 통해 농축된 범주는 N을 통해 농축된 범주로 재해석할 수 있다. 모든 단면체 범주 M은 집합 범주에 단면체 펑터 M(I, –)을 포함하므로 모든 농축 범주는 기본 일반 범주를 가진다.많은 예에서(위의 예와 같이) 이 펑터는 충실하기 때문에 M보다 강화된 범주는 특정한 추가적인 구조나 특성을 가진 일반적인 범주로 설명할 수 있다.

농축환기

풍요로운 펑터는 풍요로운 범주에 대한 펑터의 개념을 적절히 일반화한 것이다.그런 다음 농축된 펑터는 농축된 구조를 존중하는 농축된 범주 간의 맵이 된다.

만약 C및 DM-categories(그것은, 범주monoidal 범주 위에 M강화) M-enriched T:이는 C의 각 개체 D의 개체와 개체의 각 쌍에 대해 a와 bCM탭에서 사상을 제공한다 할당합니다 C→ D지도가 있어:C(a, b)→ D(T(를), T(b)=C와 D(M의 개체)의 hom-objects 사이에, enriche을 충족시키는 함수 기호.dfunctor의 공리 버전, 신원 및 구성의 viz 보존.

왜냐하면 홈 오브젝트는 풍부한 범주에 설정될 필요가 없기 때문에 특정한 형태론을 말할 수 없다.더 이상 정체성 형태론의 개념도, 두 형태론의 특정한 구성도 없다.그 대신 단위에서 홈 오브젝트로의 형태는 정체성을 선택하는 것으로 간주되어야 하며, 단면체 제품으로부터의 형태는 구성으로 간주되어야 한다.일반적인 통사 공리는 이러한 형태론을 포함하는 해당 역학 도표로 대체된다.

상세하게 말하자면, 그 도표는

방정식에 해당하는 통근.

T_{aaa}\circule \operatorname {id} _{a}=\operatorname {id} _{T(a)}

여기서 나는 M의 단위 물체다.이것은 일반 펑커의 F(id_a) = id_F(a) 규칙과 유사하다.또한 다이어그램이

일반 펑커의 F(fg)=F(f)F(g) 규칙과 유사한 통근.

참고 항목

참조

Kelly,G.M. (2005) [1982]. Basic Concepts of Enriched Category Theory. Reprints in Theory and Applications of Categories. Vol. 10.
Mac Lane, Saunders (September 1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer. ISBN 0-387-98403-8.
Lawvere, F.W. (2002) [1973]. Metric Spaces, Generalized Logic, and Closed Categories. Reprints in Theory and Applications of Categories. Vol. 1.
nLab의 농축 범주

Search

농축분류

네임스페이스

더

목차

정의

농축 범주의 예

모노이드 펑커와의 관계

농축환기

참고 항목

참조