한계(범주 이론)

수학의 한 분야인 범주 이론에서 한계의 추상적 개념은 제품, 풀백, 역 한계와 같은 보편적 구성의 본질적 특성을 포착한다.콜리밋의 이중 개념은 해체조합, 직접합계, 합금, 푸시아웃, 직접한계 등의 건설을 일반화한다.

보편적 특성과 부조화 펑커의 강한 관련 개념처럼 한계와 콜리미트는 높은 추상화 수준으로 존재한다.그것들을 이해하기 위해서, 먼저 이러한 개념들이 일반화하기 위해 의도된 구체적인 예들을 연구하는 것이 도움이 된다.

정의

범주 $C$ $C$ 의 제한과 콜리미트는 $C$ $C$ 의 다이어그램에 의해 정의된다 $C$ $C$ 형식적으로 $C$ ${\displaystyle$ $C}$ 의 $J$ 형상 $J$ ${\displaystyle$ $J$ $}$ 에서 $C$ ${\displaysty$ C $}$ 까지의 $J$ functor가 된다 $C$ $C$

(\displaystyle F:C.}

범주 $J$ $J$ 은(는) 색인 범주로 생각되며 $J$ , 도표 $F$ $F$ 는 J ${\displaystyle J$ 에 패턴이 $C$ $있는$ C ${\\displaysty C}$ 에서 개체와 형태론의 집합을 인덱싱하는 것으로 생각된다 $F$ .

하나는 $범주$ J{\ $displaystyle$ J}이 $J$ (가) 작거나 심지어 유한한 범주인 경우에 가장 관심이 많다.도표는 $J$ $J$ 이(가) 있을 $J$ 때마다 작거나 유한하다고 한다.

한계

$F:J\to C$ : J $F:J\to C$ → C ${\displaystyle F:$ $J\to C}$ 은 $F:J\to C$ $범주$ C {\ $displaystyle$ $C$ $}$ 의 $J$ J ${\displaystyle J$ $}$ 도형입니다. $C$ $F$ 에서 F ${\displaystyle$ F $}$ 은(는 $F$ ) $\psi _{X}:N\to F(X)$ $\psi _{X}:N\to F(X)$ : $\psi _{X}:N\to F(X)$ → F $)$ 와 함께 $C$ ${\displaystysty$ C $}$ 의 $N$ $개체$ N ${\\\$ $displaystystyle$ N $}$ 이다. $N\to F(X)}$ of morphisms indexed by the objects $X$ of $J$ , such that for every morphism $f:X\to Y$ in $J$ , we have $F(f)\circ \psi _{X}=\psi _{Y}$ .

$F:J\to C$ $F:J\to C$ : $F:J\to C$ → C ${\displaystyle F:$ $J$ $F$ $\to C}$ 은 $F:J\to C$ (는) 원뿔 $(L,\phi )$ $(N,\psi )$ $(L,\phi )$ , $(L,\phi )$ ) ${\displaystyle(L,\pi$ ) $(L,\phi )$ ~ $F$ ${\$ $displaystyle$ F $}$ 에 대해 다른 원뿔(N $(N,\psi )$ , $(N,\psi )$ ) $(N,\psi )$ $displaystyle$ $(N,\psi$ ) ~ $}$ 에 $(N,\psi )$ $F$ 대해 고유한 모피즘 $u:N\to L$ : $u:N\to L$ → L ${\displaystystystyleasestylease$ sty $u:N\to L$ : $J$ $\phi _{X}\circ u=\psi _{X}$ $displaystyle J}$ 의 $X$ 모든 $X$ ${\$ $displaystyle X}$ 에 $\phi _{X}\circ u=\psi _{X}$ 대해 $\phi _{X}\circ u=\psi _{X}$ $\phi _{X}\circ u=\psi _{X}$ {\ $displaystyle \phi _{X}\circu u$ =\psi $_{X$ }가 $u:N\to L$ 되도록 N $\to L$ $J$

하나는 원추형 $(N,\psi )$ , $(N,\psi )$ ) $(N,\psi )$ {\ $displaystyle (N,\psi )}$ 인자가 $(N,\psi )$ 원추형 $(L,\phi )$ $L$ , $(L,\phi )$ ) ${\$ $displaystyle$ $(L,\phi )$ ( $L$ $,\phi$ $)}$ 을 $(L,\phi )$ 통해 인자가 나타난다고 한다 $u$ 형태론 $u$ $u$ 을(를) 매개 형태론이라고도 한다 $u$ .

한계는 보편적 속성으로 특징지어지기 때문에 보편적 원추라고도 한다(자세한 내용은 아래 참조).모든 보편적 속성과 마찬가지로, 위의 정의는 일반성의 균형 잡힌 상태를 설명한다.한계 객체 $L$ $L$ 은(는) 다른 원뿔이 통과할 수 있을 정도로 일반적이어야 하며 $L$ , $L$ 에 L $L$ 은(는) 충분히 구체적이어야 하며 $L$ , 따라서 모든 원뿔에 대해 그러한 인수화가 하나만 가능해야 한다.

한계치는 또한 F에 대한 원추 범주의 단자 객체로서 특징지어질 수 있다.

다이어그램에는 제한이 전혀 없을 수도 있다.그러나 다이어그램에 한계가 있다면, 이 한계는 본질적으로 고유하다: 그것은 고유한 이형성에까지 고유한 것이다.이 때문에 F의 한계에 대해 말하는 경우가 많다.

콜리미츠

한계와 원추의 이중 개념은 콜리밋과 코콘이다.위의 정의에서 모든 형태론을 뒤집어서 이것들의 정의를 얻는 것은 간단하지만, 우리는 여기서 명시적으로 다음과 같이 명시할 것이다.

다이어그램 $F:J\to C$ : $F:J\to C$ → $F:J\to C$ ${\displaystyle F:$ $J\to C}$ 은 $F:J\to C$ (는) $C$ $C$ 의 $N$ 개체 $N$ $N$ 과(와 $C$ ) 형태론 계열이다.

\psi _{X}F(X)\to N

for every object $X$ of $J$ , such that for every morphism $f:X\to Y$ in $J$ , we have $\psi _{Y}\circ F(f)=\psi _{X}$ .

다이어그램 $F:J\to C$ : $F:J\to C$ → C ${\displaystyle F:$ $J\to C}$ is a co-cone $(L,\phi )$ of $F$ such that for any other co-cone $(N,\psi )$ of $F$ there exists a unique morphism ${\displaystyle u:$ $J$ $u:L\to N$ {\\ $displaystyle J$ 의 $X$ 모든 $X$ ${\$ $displaystyle$ X $}$ 에 $u\circ \phi _{X}=\psi _{X}$ 대해 $L\to$ $}$ \pci $u:L\to N$ \psi _ ${X}.$

콜리밋은 유니버설 코콘이라고도 한다.그것들은 $F$ $F$ 의 공동 콘 카테고리에서 초기 개체로 특징지어질 수 있다 $F$

제한과 마찬가지로, 도표 $F$ $F$ 에 콜리미트가 있으면 $F$ 이 콜리미트는 고유한 이소모르퍼시즘에 따라 고유하다.

변형

한계와 콜리미트는 도표를 사용하지 않고 물체와 형태론의 집합에 대해 정의될 수 있다.정의는 동일하다(위의 정의에서는 $J$ ${\displaystyle$ J $}$ 의 형태론 구성을 사용할 필요가 전혀 없다는 점에 유의한다). $J$ 그러나 이러한 변동은 새로운 정보를 추가하지 않는다.어떤 물체들과 형태론들의 모음은 a (아마도 큰) 방향 $그래프$ G $G$ 을 정의한다 $G$ 만약 $J$ 가 J $J$ 을 $G$ $G$ 에 의해 생성된 자유 범주가 되게 $J$ 한다면 $G$ 범용도 $F:J\to C$ : $F:J\to C$ → $F:J\to C$ ${\displaystystyle F:$ 이미지에 $G$ $G$ 이(가) 포함되어 있는 $F:J\to C$ $J\to$ C $G$ 이 다이어그램의 한계(또는 콜리밋)는 원래 개체와 형태론의 집합의 한계(또는 콜리밋)와 동일하다.

약한 한계와 약한 콜리미트를 한계와 콜리미트와 같이 정의하는데, 매개 형태론의 고유성 특성이 떨어진다는 것을 제외한다.

예

한계

한계의 정의는 실제 환경에서 유용한 몇 가지 구조를 충분히 만족시킬 수 있을 정도로 일반적이다.다음에서는 도표 F : J → C의 한계(L, φ)를 검토한다.

터미널 개체.J가 빈 범주인 경우 J 형상의 도표는 빈 범주(세트 이론의 빈 기능과 유사함)가 하나만 있다.빈 도표의 원뿔은 본질적으로 C의 물체일 뿐이다.F의 한계는 다른 모든 물체에 의해 독특하게 고려되는 어떤 물체다.이것은 단지 말단 객체의 정의일 뿐이다.
제품.J가 별개의 범주인 경우, 도표 F는 J에 의해 색인화된 C의 개체군에 지나지 않는다.F의 한계 L은 이러한 물체의 산물이라고 불린다.원뿔 φ은 제품의 투영이라고 불리는 형태론 φ_X : L → F(X)의 계열로 구성된다.예를 들어 세트의 범주에서 제품은 데카르트 제품에 의해 제공되고 투영은 다양한 요인에 대한 자연 투영일 뿐이다.
- powers. 제품의 특별한 경우는 도표 F가 C의 물체 X에 대한 일정한 functor일 때 이다.이 도표의 한계는 X의^th J power라고 하며^J X를 나타낸다.
이퀄라이저.만약 J가 두 개의 물체와 두 개의 평행 형태론을 한 물체에서 다른 물체로 가지고 있는 범주라면, 형상 J의 도표는 C에서 한 쌍의 평행 형태론이다.그러한 도표의 한계 L은 그러한 형태론의 등가선이라고 불린다.
- 낟알.커널은 형태론 중 하나가 제로 형태론인 이퀄라이저의 특별한 경우다.
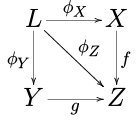
풀백.비식별성 형태만이 f : X → Z이고 g : Y → Z인 C에서 X, Y, Z 세 물체를 골라내는 도표가 되도록 하자.F의 한계 L을 풀백 또는 섬유제품이라고 한다.그것은 서로 다른 정사각형으로 잘 시각화될 수 있다.

역 한계.J를 방향 집합(화살표 i → j if, if and only if, if and only i ≥ j)으로 하고 F : J → C를^op 도표로 삼는다.F의 한계는 역 한계 또는 투영 한계라고 한다.
만약 J = 1이면, 하나의 물체와 형태론을 가진 범주, 형상 J의 도표는 본질적으로 C의 물체 X일 뿐이다.물체 X에 대한 원뿔은 코도메인 X에 의한 형태론일 뿐이다.형태론 f : Y → X는 f가 이형성일 경우에만 도표 X의 한계다.보다 일반적으로, J가 초기 객체 i를 가진 범주라면, 형상 J의 어떤 도표는 F(i)에 대한 이형성을 가진 한계를 가진다.그러한 이형성은 F에 대한 보편적인 원뿔을 독특하게 결정한다.
위상학적 한계.함수의 한계는 다음과 같은 범주형 한계와 관련된 필터 한계의 특별한 경우다.Given a topological space X, denote by F the set of filters on X, x ∈ X a point, V(x) ∈ F the neighborhood filter of x, A ∈ F a particular filter and $F_{x,A}=\{G\in F\mid V(x)\cup A\subset G\}$ the set of filters finer than A and that converge to x.필터 F는 A ⊆ B인 경우에만 화살표 A → B를 추가하여 작고 얇은 카테고리 구조를 부여한다.주입 $I_{x,A}:F_{x,A}\to F$ $I_{x,A}:F_{x,A}\to F$ , $I_{x,A}:F_{x,A}\to F$ : $I_{x,A}:F_{x,A}\to F$ x $I_{x,A}:F_{x,A}\to F$ , $I_{x,A}:F_{x,A}\to F$ → $I_{x,A}:F_{x,A}\to F$ ${\displaystyle I_{x,A}:$ $F_{x,A}\to F}$ 가 functor가 되고 $I_{x,A}:F_{x,A}\to F$ 다음과 같은 동등성이 유지된다.

x는

I_{x,A}

가 I

I_{x,A}

,

I_{x,A}

{\

displaystyle I_{x,A}

의 범주형 한계인 경우에만 A의 위상적 한계값이다.

콜리미츠

콜리밋의 예는 위의 예제의 이중 버전에 의해 제시된다.

초기 물체는 빈 다이어그램의 콜리밋이다.
코프로덕트는 개별 범주에 의해 색인화된 다이어그램의 콜리밋이다.
- 복사기는 이산형 범주의 상수 다이어그램의 콜리밋이다.
동등분자는 평행한 한 쌍의 형태론의 콜리미트다.
- 코커넬은 형태론과 평행 영 형태론의 동일제다.
푸시아웃은 공통 영역이 있는 한 쌍의 형태론의 콜리미트다.
직접 한계는 지시된 집합에 의해 색인화된 다이어그램의 콜리밋이다.

특성.

한계 존재

주어진 도표 F : J → C는 C에 한계(또는 콜리밋)가 있을 수도 있고 없을 수도 있다.사실, 만능 원뿔은 말할 것도 없고, 원뿔에서 F까지의 원뿔도 없을지도 모른다.

범주 C는 형상 J의 모든 다이어그램에 C의 한계가 있을 경우 형상 J의 한계가 있다고 한다.구체적으로 범주 C는 다음과 같다.

모든 작은 이산형 범주 J에 대해 형상 J의 한계가 있는 경우(대형 제품은 필요 없음),
모양 한계가 있는 경우 $\bullet \rightrightarrows \bullet$ $\bullet \rightrightarrows \bullet$ $\bullet \rightrightarrows \bullet$ ${\displaystyle \bullet \rightarrows \bullet$ }( $\bullet \rightrightarrows \bullet$ 즉, 모든 평행한 형태 쌍에 동점자가 있음)
$\bullet \rightarrow \bullet \leftarrow \bullet$ → $\bullet \rightarrow \bullet \leftarrow \bullet$ $\bullet \rightarrow \bullet \leftarrow \bullet$ ∙ ∙ $\bullet \rightarrow \bullet \leftarrow \bullet$ ${\displaystyle \rightarrow \reftarrow \reftarrow \reftarrow$ \ $}($ 즉, 공통 코도메인이 있는 모든 형태에는 풀백이 있다).

전체 범주는 모든 작은 한계(즉, 모든 작은 범주 J에 대한 형상 J의 모든 한계)를 가진 범주다.

또한 이중 정의를 내릴 수 있다.J형상의 모든 다이어그램에 C형상의 콜리미트가 있을 경우 범주는 J형상의 콜리미트를 가진다.cocomful 카테고리는 모든 작은 콜리미트를 가지고 있는 카테고리다.

한계에 대한 존재 정리는 범주 C에 이퀄라이저와 등급 Ob(J)와 Hom(J)에 의해 지수화된 모든 제품이 있다면, C에는 형상 J의 모든 한계가 있다고 명시한다.^[1]^{: §V.2 Thm.1}이 경우 도표 F : J → C의 한계는 두 형태론의^[1]^{: §V.2 Thm.2} 이퀄라이저로 구성할 수 있다.

s,t:\prod _{i\in \operatorname {Ob}(J)}F({f\in \operatorname {Hom}(J)}F(\operatorname {cod})(f)

에 의해 주어지는 (구성 요소 형태로)

{\begin{aligned}s&={\bigl (}F(f)\circ \pi _{\operatorname {dom} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}\\t&={\bigl (}\pi _{\operatorname {cod} (f)}{\bigr )}_{f\in \operatorname {Hom} (J)}.\end{aligned}}

코리미트에 대한 이중 존재 정리가 동등제 및 복사물의 관점에서 존재한다.이 두 가지 이론은 모두 형상 J의 모든 (코)한계 존재에 충분하고 필요한 조건을 제시한다.

보편적 재산

한계와 콜리밋은 보편적인 건축의 중요한 특별한 경우다.

C를 범주로 하고 J를 작은 지수 범주로 하자.펑터 범주 C는^J C에서 형상 J의 모든 도표의 범주로 생각할 수 있다.대각선 펑터

\Delta :{\mathcal{C}\to {\mathcal{C}^{\mathcal{J}}

C의 각 개체 N을 상수 펑터 Δ(N)에 매핑하는 펑터 : J → C ~ N.즉, Δ(N)(X) = 각 물체 X에 대한 N, Δ(N)(f) = id를_N 각각 J에 대한 형태론 f에 대한 Δ(N)이다.

도표 F: J → C (C에서^J 개체로 생각됨)를 볼 때, 자연적 변환 δ : Δ(N) → F (C^J 범주에서 단지 형태론일 뿐)는 N에서 F까지의 원뿔과 같은 것이다.이를 보려면 먼저 Δ(N)(X) = 모든 X에 대한 N은 ψ의 성분이 모두 도메인 N을 공유하는 형태론 isms_X : N → F(X)임을 암시한다.더욱이 이 ψ이 자연적 변환이라는 이유만으로 원뿔의 도표가 통근해야 한다는 요건은 참이다.(단순히 자연적 변환 ψ : F → Δ(N)는 F에서 N까지의 코콘과 동일하다.)

따라서 한계와 코리밋의 정의는 다음과 같은 형태로 재작성될 수 있다.

F의 한계는 Δ에서 F까지의 범용 형태론이다.
F의 콜리미트는 F에서 Δ까지의 보편적 형태론이다.

부속품

모든 보편적인 구조와 마찬가지로, 한계와 코리밋의 형성은 자연에서 우스꽝스러운 것이다.즉, 형상 J의 모든 다이어그램이 C(J small)에 한도가 있으면(J small의 경우) 한계 펑터가 존재한다.

\lim :{\mathcal{C}^{\mathcal{J}\to {\mathcal{C}}

각 다이어그램의 한계와 각 자연적 변환 : : F → G 고유 형태론 림 : : lim F → lim G 해당 보편적 원뿔을 이용한 출퇴근을 할당한다.이 functor는 대각선 functor Δ : C → C에^J 바로 인접해 있다.이 결합은 N에서 림 F까지의 모든 형태론과 N에서 F까지의 모든 원뿔의 집합 사이에 편차를 제공한다.

\operatorname {Hom}(N,\lim F)\cong \operatorname {Cone}(N,F)

변수 N과 F에서 자연스럽다.이 부속물의 상담은 단순히 림 F에서 F까지 보편적인 원뿔이다.지수 범주 J가 연결되어 있는 경우(그리고 비어 있지 않은 경우) 결합의 단위는 이형성이므로 임은 Δ의 왼쪽 역이 된다.J가 연결되어 있지 않으면 실패한다.예를 들어 J가 이산형 범주인 경우, 단위의 성분은 대각선 형태 Δ : N → N이다^J.

Dally, 형상 J의 모든 도표가 C에 콜리밋(J small)을 갖는 경우 콜리밋 펑터가 존재한다.

\operatorname {colim}:{\mathcal {C}^{\mathcal {J}\to {\mathcal {C}}

각 다이어그램에 콜리미트를 할당한다.이 functor는 대각선 functor Δ : C → C에^J 맞춰져 있으며, 하나는 자연 이형성을 가진다.

{\displaystyle \operatorname {Hom}(\operatorname {colim}F,N)\cong \operatorname {Cocone}(F,N).

이 부속물의 단위는 F에서 콜림F까지의 범용코콘이다.J가 연결되어 있으면(그리고 비어 있지 않으면) 상담은 이형성이기 때문에 콜림은 Δ의 왼쪽 역행이다.

한계와 콜리미트 펑커 모두 공변성 펑커라는 점에 유의하십시오.

functors의 표현으로

Hom functors를 사용하여 범주 C의 한계와 집합의 범주 Set의 한계를 연관시킬 수 있다.이는 부분적으로 공변량 Hom functor Hom(N, –) : C → Set는 C의 모든 한계를 보존한다는 사실에서 나타난다.이중성에 의해, 반대되는 홈 펑터는 제한까지 콜리미트를 가져가야 한다.

도표 F : J → C가 lim F로 표시된 C에 한계가 있다면, 정론적 이형성이 있다.

\operatorname {Hom}(N,\lim F)\cong \lim \operatorname {Hom}(N,F-)

N 변수에서 자연스럽다.여기서 functor Hom(N, F–)은 F와 함께 Hom functor Hom(N, –)의 구성이다.이 이형성은 한정된 원뿔을 존중하는 독특한 것이다.

위의 관계를 이용하여 C에서 F의 한계를 정의할 수 있다.첫 번째 단계는 펑터 홈(N, F–)의 한도를 N에서 F까지 모든 원뿔 집합으로 식별할 수 있음을 관찰하는 것이다.

\lim \operatorname {Hom}(N,F-)=\operatorname {Cone}(N,F).

The limiting cone is given by the family of maps π_X : Cone(N, F) → Hom(N, FX) where $π$ _X(ψ) = ψ_X. If one is given an object L of C together with a natural isomorphism Φ : Hom(–, L) → Cone(–, F), the object L will be a limit of F with the limiting cone given by Φ_L(id_L).화려한 말로 표현하면 F의 한계는 펑터콘(–, F) : C → Set의 표현이라고 할 수 있다.

도표 F : J → C가 C에 콜리밋이 있고 콜림 F로 표시된다면, 독특한 표준 이형성이 있다.

\operatorname {Hom}(\operatorname {colim}F,N)\cong \lim \operatorname {Hom}(F-,N)

변수 N에서 자연스럽고 콜리메이트 원뿔을 존중한다.설정된 Cocone(F, N)과 Hom(F–, N)의 한계를 식별하여, 이 관계를 사용해 도표 F의 콜리미트를 펑터 Cocone(F, –)의 표현으로 정의할 수 있다.

세트의 한계와 코리미트의 상호 교환

나는 유한 범주가 되고 J는 작은 여과 범주가 되게 하라.모든 분기점에 대해

(\displaystyle F:I\time J\to \mathbf {Set},}

자연 이형성이 있다.

\operatorname {colim} \limits _{J}\lim_{I}F(i,j)\오른쪽 화살표 \lim_{I}\operatorname {colim} \limits _{J}F(i,j) \limits.

즉, 한정된 한계로 설정된 통근에서 필터링된 콜리밋.그것은 또한 작은 콜리미트가 작은 한계로 통근하는 것을 보유한다.^[2]

펑터 및 한계

F : J → C의 도표, G : C → D가 functor라면 구성(도표가 functor일 뿐임을 상기)으로 GF : J → D 도표를 얻는다.그렇다면 당연한 질문은 다음과 같다.

"GF의 한계는 F의 한계와 어떤 관계가 있는가?"

한계 보존

Functor G : C → D는 원뿔(F)에서 원뿔(GF)으로 지도를 유도한다. 만약 ψ이 N에서 F까지 원뿔이라면 Gψ은 GN에서 GF까지 원뿔이다.functor G는 (GL, Gφ)이 (L, φ)의 한계일 때마다 GF의 한계일 경우 F의 한계를 보존한다고 한다.(F의 한도가 존재하지 않을 경우 G는 F의 한계를 공허하게 보존한다는 점에 유의한다.)

functor G는 모든 도표 F : J → C의 한계를 보존하면 형상 J의 모든 한계를 보존한다고 한다.예를 들어 G는 제품, 이퀄라이저, 풀백 등을 보존한다고 할 수 있다.연속형 플럭터는 모든 작은 한계를 보존하는 것이다.

콜리밋에 대해 유사한 정의를 내릴 수 있다.예를 들어, Functor G는 G(L, φ)가 GF의 콜리미트일 때마다 F의 콜리미트를 보존한다(L, φ).코콘틴 플럭터는 모든 작은 콜리미트를 보존하는 것이다.

C가 완전한 범주라면, 위의 한계 존재 정리에 의해 functor G : C → D는 (소형) 제품과 이퀄라이저를 보존하는 경우에만 연속된다.G는 (소형) 결합제와 동등제를 보존할 경우에만 한 달에 한 번씩 응결된다.

부선장치의 중요한 특성은 모든 우측 부선장은 연속적이고 모든 좌측 부선장은 연속적이라는 것이다.부연성 펑커스는 풍부하게 존재하기 때문에, 이것은 연속성 및 연속성 펑커의 수많은 예를 제공한다.

주어진 도표 F : J → C 및 functor G : C → D에 대해 F와 GF 모두 한계를 지정했다면 고유한 표준형 형태론이 있다.

\tau _{F:G\lim F\to \lim GF

해당 한계 원뿔을 존중한다.functor G는 만약 이 지도만이 이형성일 경우 F의 한계를 보존한다.범주 C와 D가 형상 J의 모든 한계를 가지고 있다면, 임은 functor이고 형태 ctor은_F 자연적 변환의 구성요소를 형성한다.

\displaystyle \tau :G\lim \to \lim G^{J}}

functor G는 만약 τ이 자연 이형성일 경우에만 형상 J의 모든 한계를 보존한다.이런 의미에서 functor G는 한계(규범적 자연 이형성까지)로 통근한다고 할 수 있다.

한계와 콜리밋의 보존은 공변성 펑커에만 적용되는 개념이다.반대편 펑커의 경우 해당 개념은 콜리미트를 제한하거나 콜리미트를 제한하는 펑터가 될 수 있다.

한계 해제

functor G : C → D는 도표 F : J → C에 대한 한계를 해제한다고 하는데, 만약 (L, φ)가 GF의 한계치(L, ′)가 있을 때마다 (L, ′) = (L, φ)와 같은 F의 한계치(L, exists)가 존재한다면 도표 F : J → C에 대한 한계를 해제한다고 한다.Functor G는 J 형상의 모든 다이어그램에 대한 제한을 해제할 경우 J 형상의 한계를 해제한다.따라서 리프팅 제품, 이퀄라이저, 풀백 등에 대해 이야기할 수 있다.마지막으로, G가 모든 한계를 들어 올린다면 한계를 들어 올린다고 말한다.콜리밋 리프팅에 대한 이중적 정의가 있다.

functor G는 (L′, φ′)가 F와 G(Lφ, = limit) = (L, φ)의 한계와 같은 고유한 프리이미지 콘(L (, ′′)이 있는 경우 도표 F에 대해 고유하게 한계를 들어 올린다.G가 한계를 들어 올리고 면책할 경우에만 독특하게 한계를 들어 올린다는 것을 보여줄 수 있다.

한계 해제는 분명히 한계 보존과 관련이 있다.도표 F에 대한 G 리프트 한도가 있고 GF에 한계가 있다면 F도 한계가 있고 G도 F의 한도를 보존한다.그 다음은 다음과 같다.

만약 G가 모든 형상 J의 한계를 들어 올리고 D가 형상 J의 모든 한계를 가지고 있다면, C는 형상 J의 모든 한계를 가지고 있고 G는 이러한 한계를 보존한다.
G가 모든 작은 한계를 들어 올리고 D가 완성되면 C도 완성되고 G도 연속된다.

콜리미트에 대한 이중 진술도 똑같이 유효하다.

한계 생성 및 반영

F : J → C를 도표로 한다.Functor G : C → D라고 한다.

(L, φ)이 GF의 한계일 때마다 (L, φ) = (L, φ) = (L, φ)와 같은 고유한 원추(L′, φ′)가 F의 한계일 경우 F의 한계를 만든다.
G 하의 이미지가 GF의 한계인 F에 대한 각 원뿔의 한계가 이미 F의 한계인 경우 F에 대한 한계를 반영한다.

한 달에 한 번 꼴리밋의 생성과 반사를 정의할 수 있다.

다음과 같은 문장이 등가라고 쉽게 볼 수 있다.

Functor G는 한계를 만든다.
Functor G는 한계를 고유하게 들어 올리고 한계를 반영한다.

한도를 고유하게 들어올리지만 한도를 만들거나 반영하지 않는 펑커스의 예가 있다.

예

대표 가능한 모든 functor C → Set resistance limits (colimits)특히 C의 어떤 물체 A에 대해서는 공변량 Hom functor Hom(A,–) : C → Set에 해당된다.
건망증이 심한 functor U : Grp → Set는 모든 작은 한계와 여과된 콜리미트를 생성(및 보존)하지만 U는 공동효율을 보존하지 않는다.이 상황은 대수학적으로 건망증이 심한 환자들의 전형이다.
프리 펑터 F : Set → Grp (모든 세트 S에 S보다 자유 그룹을 할당함)은 건망증이 심한 펑터 U에 보조를 두며, 따라서, cocontinuous이다.G와 H 두 프리그룹의 자유상품이 G와 H의 발전기 분리조합에 의해 생성되는 자유집단인 까닭이다.
포함 functor Ab → Grp는 한계를 만들지만 coproducts (두 개의 아벨리아 그룹의 coproduct가 직접 합이 됨)를 보존하지 않는다.
건망증이 심한 functor Top → 리프트 제한과 콜리미트를 독특하게 설정하지만 둘 다 만들지 않는다.
Met은_c 형태론에 대한 연속적인 함수를 가진 미터법 공간의 범주가 된다.건망증이 심한 functor Met_c → Set는 유한한 한도를 들어올리지만 그것들만을 독특하게 들어올리지는 않는다.

용어에 대한 참고 사항

오래된 용어는 한계를 "역행 한계" 또는 "투영 한계"라고 불렀고, 콜리밋을 "직접 한계" 또는 "귀납 한계"라고 불렀다.이것이 많은 혼란의 원인이 되어 왔다.

현대 용어를 기억하는 몇 가지 방법이 있다.우선, 다른 무엇보다 먼저

코커넬들,
코프로덕트,
동등분자,
코도메인

콜리미트의 유형인 반면,

커널,
상품들
이퀄라이저 및
도메인

제한의 유형이다.둘째, 접두사 "co"는 " $\operatorname {Hom}$ $\operatorname {Hom}$ "의 첫 번째 변수"를 의미한다. $\operatorname {Hom}$ "동호몰로지" 및 "진동"과 같은 용어는 모두 $\operatorname {Hom}$ {\ $displaystyle \operatorname {Hom}$ 분리기의 $\operatorname {Hom}$ 첫 번째 변수, 즉 역변수와의 연관성이 약간 더 강하다.

참고 항목

데카르트 폐쇄 범주 – 범주 이론의 범주 유형
이퀄라이저(수학) – 둘 이상의 함수가 동일한 값을 갖는 인수 집합
역한계 - 범주 이론에서의 구성
제품(범주 이론) – 범주 이론에서 일반화된 객체

참조

^ ^a ^b Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.
^ "limit". nLab.

추가 읽기

Adámek, Jiří; Horst Herrlich; George E. Strecker (1990). Abstract and Concrete Categories (PDF). John Wiley & Sons. ISBN 0-471-60922-6.
Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.
Borceux, Francis (1994). "Limits". Handbook of categorical algebra. Encyclopedia of mathematics and its applications 50-51, 53 [i.e. 52]. Vol. 1. Cambridge University Press. ISBN 0-521-44178-1.

외부 링크

유한 집합 범주에서 한계와 콜리밋의 예를 생성하는 대화형 웹 페이지.조슬린 페인이 썼어
nLab의 제한

[Mac_Lane-1] Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. Vol. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. Zbl 0906.18001.

[2] "limit". nLab.

[1]

[2]

Search

한계(범주 이론)

네임스페이스

더

목차

정의

한계

콜리미츠

변형

예

한계

콜리미츠

특성.

한계 존재

보편적 재산

부속품

functors의 표현으로

세트의 한계와 코리미트의 상호 교환

펑터 및 한계

한계 보존

한계 해제

한계 생성 및 반영

예

용어에 대한 참고 사항

참고 항목

참조

추가 읽기

외부 링크