모노이드 펑터
Monoidal functor범주 이론에서, 모노이드 함수는 모노이드 구조를 보존하는 모노이드 범주 사이의 함수이다.보다 구체적으로, 두 개의 모노이드 범주 사이의 모노이드 함수는 두 개의 일관성 맵과 함께 범주 사이의 함수로 구성됩니다. 각각 모노이드 곱셈과 단위를 보존하는 형태론입니다.수학자들은 모노이드 구조를 얼마나 엄격하게 보존하고 싶은지에 따라 추가적인 특성을 만족시키기 위해 이러한 일관성 맵을 필요로 합니다; 이러한 특성들은 모노이드 함수의 약간 다른 정의를 낳습니다.
- 느슨한 모노이드 함수의 일관성 맵은 추가 특성을 만족하지 않으며 반드시 반전할 수 있는 것은 아닙니다.
- 강한 모노이드 함수의 일관성 맵은 반전할 수 있습니다.
- 엄밀한 모노이드 함수의 일관성 맵은 아이덴티티 맵입니다.
여기서 우리는 이러한 다른 정의들을 구별하지만, 저자들은 이러한 단순한 모노이드 함수들 중 하나를 부를 수 있다.
정의.
, , ) { ( \ { C } , , _ { \ { C )}( ( ( ( 、 ( ) 、、 ( \ { } ) 、 \ , I { \ { } } be be be be beoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesoriesories{C})에서 Ddisplaystyle {까지의 느슨한 모노이드 함수는 자연 변환과 함께 F F로 구성됩니다.
C × F F로, 형태론
- FI_
C(\displaystyle{의 3개 A(\ BB) 및 C(\ C마다 다이어그램이 표시되도록 하는 일관성 맵 또는 구조 형태라고 합니다.
D(\ 에서 α,,(\로 표시된 다양한 자연 변환은 C D(\의 모노이드 구조의 일부입니다.
변종
- 모노이드 함수의 쌍대 함수는 코모노이드 함수이며, 코히렌스 맵이 반전되는 모노이드 함수입니다.코모노이드 함수는 또한 옵모노이드, 콜락스 모노이드 또는 오플락스 모노이드 함수로도 불릴 수 있다.
- 강한 모노이드 펑터는 코히렌스 맵 A { _가 반전 가능한 모노이드 펑터입니다.
- 엄밀한 모노이드 펑터는 일관성 맵이 동일성인 모노이드 펑터입니다.
- 편조모노이드 펑터는 편조모노이드 카테고리( 카테고리 사이에 있는 모노이드 펑터(< \로 다음 그림은 C(\의 모든 객체 A, B 쌍에 대응합니다.
- 대칭 모노이드 펑터는 도메인과 코도메인이 대칭 모노이드 범주인 편조 모노이드 펑터입니다.
예
- 기본 : (A , , Z ) ( t, ×, { ) \ U \ ( \ { , \ _ { \ , \ { } ) \ ( \ times ) 、 \ { \ } 경우 맵 : () × ( ) ( ) _ , }\U ()\U ( )\U ( B )} (A B )가 U ( B)에 송신됩니다
- R{\ R이(가)환인 S t - {\ R {\{-은(는 강한 단방향함수까지 확장됩니다( (e ,× ,{∗} ) ( - d , ,) ( \ { } , \ , \ { \ \ } )\ { \ { - } , \,) )
- R R S가 교환환의 동형인 제한함수 - d ,S , ) ( - d ,R )\({ \ { - } , \ ) } 。- d ,S ,) \ ({ \ { - } , \_ { } , \({ \ { - } , \ { S , S )는 강한 단수형이다.
- 대칭 모노이드 함수의 중요한 예는 최근에 개발된 위상 양자장 이론의 수학적 모델이다. - , n { } _rangle}}을 n-1,n차원 다지관의 코비즘의 범주로서, 이관합집합에 의해 주어진 텐서곱을 갖는 n차원 다지관 및 빈 다지관의 단위라고 하자.차원 n의 위상 양자장 이론은 모노이드 F :( r dn -, , , k) ( , , ) .\ F \ ( \ { } { \ - 1 , \ \ } ) 。
- 호몰로지 함수는 (h ( - d) , 、 [ 0( - d , , [ 0 ) ( ( \ - ) , \ [ } )와같이 입니다. { H _ { \} ( _ { )\otimes H_ { \ast }( H_}( []
대체 개념
, C) { ( \ { C} , \, { \ {} } ) } ( ( ( ( 、 ( ) ( \ { } ) 、 \ , I _ { \ { D )、 \ { Dhom hom hom hom hom hom hom hom hom hom hom hom hom hom hom hom hom hom hom (가독성을 위해 첨자를 삭제한다) 다른 공식도 있습니다.
- : : F(A b B) → FAAB f FB
functional programming에서 일반적으로 사용되는 commonly의AB 경우.and과AB is의AB 관계는 다음 교환도에 나타나 있습니다.
특성.
- ( , , ){ (, \ , \ ) } 이 { \ } 의 모노이드 객체인 ( , F , ){ , F , \ \ c \ ) 、
모노이드 함수 및 부가사
함수 : F {{이) n : D ) , {\style n}, {C}, {cal {cal} {cal}에 인접해 있다고 가정합니다.으로는( nG n)\displaystyle, n)\displaystyle, n)에 의해 되는 코모노이드 구조 m를 가집니다.
그리고.
- I_
F F의 유도구조가 강하면 교합의 단위와 카운티는 모노이드 자연변환이며, 교합은 모노이드 교합이라고 하며, 반대로 모노이드 교합의 왼쪽 교합은 항상 강한 모노이드 함수이다.
마찬가지로 코모노이드 펑터에 대한 오른쪽 인접은 모노이드이며, 코모노이드 펑터의 오른쪽 인접은 강한 모노이드 펑터이다.
「 」를 참조해 주세요.
레퍼런스
- Kelly, G. Max(1974), "의사 보조", 수학 강의 노트, 420, 257–280




 구성됩니다.
구성됩니다.

 , 형태론
, 형태론


 다이어그램이 표시되도록 하는 일관성 맵 또는 구조 형태라고 합니다.
다이어그램이 표시되도록 하는 일관성 맵 또는 구조 형태라고 합니다.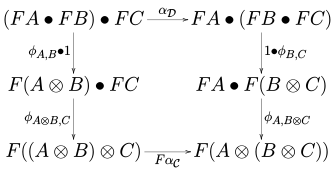

 표시된 다양한 자연 변환은 C
표시된 다양한 자연 변환은 C 반전 가능한 모노이드 펑터입니다.
반전 가능한 모노이드 펑터입니다.
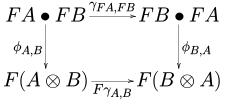
 U (
U ( (가)환인
(가)환인  (는
(는
 교환환의 동형인
교환환의 동형인 













