산술

산술(고대 그리스어 ἀριθ μ ός의 '숫자'와 τική[τέχνη]의 '예술, 공예')은 덧셈, 뺄셈, 곱셈, 나눗셈의 전통적인 연산을 연구하고 사용하는 수학의 기초적인 부분입니다.지수화, 근의 추출, 로그를 취하는 것도 포함한다고 볼 수 있습니다.산술적으로 조작되는 숫자의 종류에는 양을 세는 데 사용되는 자연수; 양의 자연수 1, 2, 3, ...의 음수를 포함하는 정수; 정수 사이에 들어갈 수 있는 분수 또는 유리수; 그리고 다른 모든 실수,함께 완전한 숫자 라인을 형성합니다.산술은 복소수와 같이 훨씬 더 넓은 맥락에서 적용될 수 있습니다.

산술의 관행은 적어도 수천 년에서 아마도 수만 년 전의 것입니다.이집트와 수메르를 비롯한 고대 문명은 산술을 이용해 실제적인 문제를 풀었고, 유클리드의 원소들은 초기에 수론, 즉 추상 속의 수를 탐구하는 결과를 기록하고 있습니다.산술의 논리적 기반에 관한 작업의 대부분은 19세기로 거슬러 올라가며, 전자 컴퓨터에 산술 연산을 구현하는 것은 20세기 동안 주요 관심사가 되었습니다.아직도 답을 알 수 없는 산술에 대한 의문이 남아 있습니다.

정의, 어원 및 관련 분야

산술은 수와 그 연산을 연구하는 수학의 기본 분야입니다.특히 덧셈, 뺄셈, 곱셈, 나눗셈의 산술 연산을 이용한 수치 계산을 다루고 있습니다.^[1][2][3][4]더 넓은 의미에서는 지수화, 뿌리 추출, 로그도 포함합니다.^[4][5][6][7]산술이라는 용어는 고대 그리스 단어인 όςμητική τέχνη(산술)와 "계산의 기술"을 의미하는 ἀριθμἀριθ(산술)에서 유래한 라틴어 산술에 뿌리를 두고 있습니다.

정확한 정의에 대해서는 이견이 있습니다.좁은 특성에 따르면 산술은 자연수만을 다룹니다.^[11][12]그러나 더 일반적인 견해는 정수, 유리수, 실수, 그리고 때로는 복소수에 대한 연산을 그 범위에 포함시키는 것입니다.^[1][2][3][4]일부 정의는 산술을 수치 계산 분야로 제한합니다.^[13]더 넓은 의미로 이해하면 수 개념이 어떻게 발전했는지, 수의 성질과 관계 분석, 산술 연산의 공리적 구조 검토 등의 연구도 포함됩니다.^[4][14][15]

산술은 수론과 밀접한 관련이 있으며 일부 저자는 이 용어를 동의어로 사용합니다.^[16][17]그러나 좀 더 구체적인 의미에서 정수론은 정수에 대한 연구에 국한되며, 정수의 성질과 가분성, 인수분해, 원시성 등의 관계에 초점을 맞추고 있습니다.^{[18][19][20][21]}전통적으로, 그것은 상위 산술로 알려져 있습니다.^[22][21]

산술은 수치 연산에 의존하는 수학의 많은 분야와 밀접하게 연결되어 있습니다.대수학은 변수를 사용하여 방정식을 풀기 위해 산술 원리에 의존합니다.이 원리들은 또한 변화율과 곡선 아래의 면적을 결정하려는 시도에서 미적분학에서 핵심적인 역할을 합니다.기하학은 산술 연산을 사용하여 도형의 특성을 측정하고 통계는 수치 데이터를 분석하는 데 이를 활용합니다.^{[23][24][25][26]}

숫자

숫자는 양을 세고 크기를 측정하는 데 사용되는 수학적 물체입니다.모든 산술 연산이 숫자에 대해 수행되기 때문에 산술의 기본 요소입니다.다양한 유형의 숫자와 이를 나타내는 다양한 숫자 체계가 있습니다.^[27][28][29]

종류들

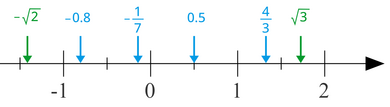
산술에서 사용되는 수의 주요 유형은 자연수, 정수, 유리수, 실수입니다.^[30][31][28]자연수는 1에서 시작하여 무한대로 가는 정수입니다.그들은 0과 음수를 제외합니다.이들은 계수라고도 하며 {1, 2, 3, 4, ...}로 표현할 수 있습니다.자연수의 기호는 $N{\displaystyle \mathbb{}}$ ${\$입니다$.$ 정수는 자연수와 동일하며 유일한 차이점은 0을 포함한다는 것입니다.그들은 {0, 1, 2, 3, 4, ...}로 표현될 수 있고 $기호$는 N ${\displaystyle {\mathrm{}}_{}}${\$displaystyle \mathbb {$N$}_{0}$입니다$.$^{[32][30][33][34]} 어떤 수학자들은 자연수 집합에 0을 포함시킴으로써 자연수와 정수의 구별을 그리지 않습니다.^[35][36]정수의 집합은 양수와 음수를 모두 포함합니다.$기호$는 Z$${\$displaystyle \mathbb {Z}}$이며 {..., -2, -1, 0, 1, 2, ...}^{[32][30][33][37]}로 표현할 수 있습니다.

숫자는 두 정수의 비율로 표현될 수 있다면 유리합니다.예를 들어 유리수 ${\displaystyle \frac{12}{}}$ ${\displaystyle$ {\tfrac ${1}{2}}$는 분자라고 불리는 정수 1을 분모라고 불리는 정수 2로 나누어 형성됩니다$$.다른 예로는 ${\displaystyle \frac{34}{}}$ ${\$ 및 ${\displaystyle \frac{\mathrm{2813<img\; alt="\{\backslash tfrac\; \{3\}\{4\}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline\; mw-invert"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/8ec6051ef87eb0dafdaeaacd61f340052fcbf2bf"\; style="vertical-align:\; -1.171ex;\; width:1.658ex;\; height:3.509ex;">}}{}}$ ${\$이 있습니다$.$유리수 집합은 분모가 1인 분수인 모든 정수를 포함합니다.유리수의 $기호$는 Q ${\$입니다$.$^{[32][30][33][38]} 0.3과 25.12 같은 소수점 분수는 분모가 10의 거듭제곱이므로 특수한 유형의 유리수입니다.예를 들어, 0.3은 ${\displaystyle \frac{310}{}}$ ${\$이고$,$ 25.12는 ${\displaystyle \frac{2512}{}}$ ${\displaystyle \frac{100}{}}$ ${\$입니다$.$^[39][40] 모든 유리수는 유한 또는 반복되는 소수에 해당합니다.^[41]

무리수는 두 정수의 비율로 표현할 수 없는 숫자입니다.예를 들어 $2$ ${\displaystyle {\sqrt {2}}$과 같은 많은 제곱근과$$π 및 e(Euler's number)와 같은 숫자가 있습니다.무리수의 소수 표현은 소수를 반복하지 않고 무한대입니다.^[42][43]유리수의 집합과 무리수의 집합은 실수의 집합을 구성합니다.실수들의 $기호$는 R$${\$displaystyle \mathbb {R}$입니다$.$^[32][33] 더 넓은 부류의 수들은 복소수들과 사분원들을 포함합니다.^[33][44]

숫자는 사용 방법에 따라 기수와 순서수로 구분할 수 있습니다.기수는 1, 2, 3과 같이 물체의 양을 표현하는 숫자입니다.그들은 "몇 개?"라는 질문에 답합니다.첫 번째, 두 번째, 세 번째와 같은 순서 숫자는 일련의 순서나 배치를 나타냅니다.그들은 "어떤 입장?"^[45][46]이라는 질문에 답합니다.

수계

숫자는 숫자를 나타내는 기호이고 숫자 체계는 표현 체계입니다.^[47][48][49]그들은 일반적으로 특정 숫자를 직접적으로 나타내는 제한된 양의 기본 숫자를 가지고 있습니다.이 시스템은 이 기본 숫자들이 어떤 숫자를 표현하기 위해 어떻게 결합될 수 있는지를 결정합니다.^[50][51]숫자 시스템은 위치 또는 비위치입니다.모든 초기 숫자 체계는 비위치적이었습니다.^[52][53][54]위치가 아닌 숫자 체계의 경우, 숫자의 값은 숫자의 위치에 따라 달라지지 않습니다.^[53][54]

가장 단순한 비위치 체계는 단수 체계입니다.숫자 1은 하나의 기호에 의존합니다.모든 높은 숫자는 이 기호를 반복하여 적습니다.예를 들어, 숫자 7은 기호를 17번 반복하여 나타낼 수 있습니다.이 시스템은 큰 숫자를 쓰는 것을 번거롭게 만들기 때문에 많은 비위치 시스템이 더 큰 숫자를 직접 나타내기 위해 추가 기호를 포함합니다.^[50][55][56]일진수 시스템의 변형은 움푹 들어간 부분과 집계 표시를 사용하여 집계 스틱에 사용됩니다.^[57][58]

이집트 상형문자는 더 복잡한 비위치수 체계를 가지고 있었습니다.10, 100, 1000 및 10,000과 같은 숫자에 대한 추가 기호가 있습니다.이 기호들은 합으로 결합하여 더 큰 숫자를 더 편리하게 표현할 수 있습니다.예를 들어, 10,405에 대한 숫자는 10,000에 대한 기호의 1배, 100에 대한 기호의 4배, 1에 대한 기호의 5배를 사용합니다.이와 유사하게 잘 알려진 틀이 로마 숫자 체계입니다.숫자 1, 5, 10, 50, 100, 500, 1000을 나타내는 기본 숫자로 기호 I, V, X, L, C, D, M을 가지고 있습니다.^[50][55][59]

복소식에서 기본수의 위치가 그 값을 결정한다면 수 체계는 위치적입니다.위치 숫자 시스템에는 서로 다른 위치의 곱셈기 역할을 하는 기수가 있습니다.각 후속 위치에 대해 래딕스가 더 높은 전력으로 상승합니다.힌두 아라비아숫자 체계라고도 불리는 일반적인 십진법에서, 반지름은 10입니다.즉, 첫 번째 자리에 ${\displaystyle {100\mathrm{}}^{}}$ ${\$을$$곱하고 다음 자리에 ${\displaystyle {101\mathrm{}}^{}}$ ${\$을 곱합니다$.$예를 들어, 10진수 ${\displaystyle {532}^{}}$는 5 ⋅${\displaystyle {}^{}}$ + 3$$⋅ 10 1 + 2 ⋅ 100 {\displaystyle 5\cdot 10^{2}+3\cdot 10^{1}+2\cdot 10^{0}}를 나타냅니다. 숫자 532는 숫자의 위치의 영향으로 같은 숫자라도 숫자 325와 253과 다릅니다.

컴퓨터 산술에서 광범위하게 사용되는 또 다른 위치수 체계는 반지름이 2인 이진법입니다.즉, 첫 번째 자리에 $20 {\$ 2$^{0}}$을$$곱하고 다음 자리에 ${\displaystyle {21\mathrm{}}^{}}$ ${\$ 2$^{1}}$을 곱합니다$.$예를 들어, 숫자 13은 ${\displaystyle 1}$ ⋅${\displaystyle }$2 ${\displaystyle {}^{}}$+$1$ ⋅ 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 {\displaystyle 1\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}을 나타내는 이진법에서 1101로 표기됩니다.컴퓨팅에서 이진법 표기법의 각 숫자는 하나의 비트에 해당합니다.^[64][65][66]가장 초기의 위치 체계는 고대 바빌로니아 사람들에 의해 개발되었으며 60의 반지름을 가졌습니다.^[67]

산술연산

산술 연산은 숫자를 결합, 변환 또는 조작하는 방법입니다.입력과 출력으로 모두 숫자가 있는 함수입니다.^[68][69][70]산술에서 가장 중요한 연산은 덧셈, 뺄셈, 곱셈, 나눗셈입니다.^[71][4][72]추가 연산에는 지수화, 뿌리 추출 및 로그가 포함됩니다.^{[4][6][5][7][72]}이러한 연산이 숫자가 아닌 변수에 대해 수행되는 경우 대수 연산이라고도 합니다.^[73][74]

산술 연산과 관련하여 두 가지 중요한 개념은 항등원 요소와 역원 요소입니다.작업의 ID 요소 또는 중립 요소는 다른 요소에 적용해도 변경되지 않습니다.예를 들어, 숫자와 0의 합은 모두 같은 숫자가 되기 때문에 덧셈의 항등식 요소는 0입니다.역요소는 다른 요소와 결합할 때 동일성 요소가 되는 요소입니다.예를 들어, 숫자 6의 덧셈 역수는 그들의 합이 0이므로 -6입니다.^[75][76][77]

역수뿐만 아니라 역수 연산도 있습니다.비공식적인 의미에서 하나의 연산은 첫 번째 연산을 취소하면 다른 연산의 역수입니다.예를 들어,${\displaystyle 13}$ +${\displaystyle 4}$ - ${\displaystyle 4}$ =${\displaystyle 13}${\displaystyle 13+4-4 = 13}과 같이 두 번째 숫자를 먼저 더하고 그 뒤에 빼면 숫자가 원래 값으로 되돌아가기 때문에 뺄셈은 덧셈의 역입니다. 더 형식적으로 정의하면,the operation "${\displaystyle \star }$" is an inverse of the operation "${\displaystyle \circ }$" if it fulfills the following condition: ${\displaystyle t\star s=r}$ if and only if ${\displaystyle r\circ s=t}$.^[78][79]

교환성과 결합성은 일부 산술 연산이 수행될 수 있는 순서를 지배하는 법률입니다.결과에 영향을 주지 않고 인수의 순서를 변경할 수 있는 경우 연산은 교환적입니다.예를 들어 ${\displaystyle 7}$+ ${\displaystyle 9}$ ${\displaystyle 7+9}$는 $9{\displaystyle \mathrm{}}$+ 7 ${\displaystyle$ 9+$7}과 같습니다$연관성은 일련의 작업을 수행할 수 있는 순서에 영향을 미치는 규칙입니다.일련의 두 작업에서 어떤 작업이 먼저 수행되는지가 중요하지 않으면 작업이 연관됩니다.예를 들어${\displaystyle }$(${\displaystyle 5}$× ${\displaystyle 4)}$× 2 ${\displaystyle (5\times$ 4$)\times$ 2$}$은(는) $5{\displaystyle \mathrm{}}$×${\displaystyle }$(${\displaystyle 4}$× ${\displaystyle 2)}$ ${\displaystyle 5\times (4\times 2)}$와 같기 때문에 곱셈의 경우입니다$.$^[77][76]

덧셈과 뺄셈

덧셈은 덧셈이라고 불리는 두 개의 숫자가 합이라고 불리는 하나의 숫자로 합쳐지는 산술 연산입니다.덧셈의 기호는$+{\displaystyle +}$입니다$.$ 예를 들어 $2{\displaystyle }$+ 2 = ${\displaystyle 4}$ ${\$$displaystyle$ 2+2=4$}$와 6.3 + 1.26 = 7.56 {\displaystyle 6.3 + 1.26 = 7.56}입니다. 합산이라는 용어는 여러 개의 덧셈이 연속적으로 수행되는 경우에 사용됩니다.카운팅은 숫자 1이 계속해서 더해지는 반복 덧셈의 한 유형입니다.^[81]

뺄셈은 덧셈의 역수입니다.그 속에서 서브트렌드라고 알려진 하나의 숫자는 미뉴엔드라고 알려진 다른 숫자로부터 빼앗깁니다.이 작업의 결과를 차이라고 합니다.The symbol of subtraction is ${\displaystyle -}$.^{[60][82][78][79]} Examples are ${\displaystyle 14-8=6}$ and ${\displaystyle 45-1.7=43.3}$. Subtraction is often treated as a special case of addition: instead of subtracting a positive number, it is also possible to add a negative number.예를 들어 ${\displaystyle 14}$- 8 = ${\displaystyle 14}$+$$( - 8 ) {\displaystyle 14-8 = 14 + (-8)}입니다.이는 계산을 수행하는 데 필요한 기본 산술 연산의 수를 줄여 수학적 계산을 단순화하는 데 도움이 됩니다.^[83][84][85]

가법 항등식 요소는 0이고 수의 가법 역수는 해당 숫자의 음수입니다.예를 들어, ${\displaystyle 13}$+ 0 = ${\$$displaystyle$ $13+0$ = 13} 및 13 + ( - 13 ) = 0 {\displaystyle 13+(-13) = 0}입니다. 덧셈은 교환적이면서도 연관적입니다.

곱셈과 나눗셈

곱셈은 곱셈과 곱셈이라고 불리는 두 개의 숫자가 곱이라는 하나의 숫자로 합쳐지는 산술 연산입니다.^[60][87]곱셈의 $기호$는$$× ${\displaystyle \times$ $\},$ ⋅ {\$displaystyle$\cdot } 및 *입니다. 예를 들어 2 × 3 = 6 {\displaystyle 2\times 3=6} 및 0.3 ⋅ 5 = 1.5 {\displaystyle 0.3\cdot 5=1.5}입니다. 곱셈기가 자연수이면 곱셈은 반복 덧셈과 같습니다.$2{\displaystyle }$× ${\displaystyle 3}$ = ${\displaystyle 2}$+ 2 + 2 {\displaystyle 2\times 3 = 2 + 2 + 2}과 같이 표시됩니다.

나눗셈은 곱셈의 역수입니다.그 안에서, 배당이라고 알려진 하나의 숫자는 나눗셈이라고 알려진 또 다른 숫자에 의해 몇 개의 같은 부분으로 나누어집니다.이 연산의 결과를 몫이라고 합니다.The symbols of division are ${\displaystyle \div }$ and ${\displaystyle /}$. Examples are ${\displaystyle 48\div 8=6}$ and ${\displaystyle 29.4/1.4=21}$.^[60][83][79] Division is often treated as a special case of multiplication: instead of dividing by a number,그것의 역수를 곱하는 것도 가능합니다.어떤 숫자의 역수는 그 숫자로 1을 나눈 값입니다.예를 들어 ${\displaystyle 48}$ ÷ 8 = ${\displaystyle 48\frac{}{}}$×$18$ {\displaystyle $48\$div 8 = 48\time {\tfrac {1}{8}}입니다.

곱셈 항등원은 1이고 어떤 수의 곱셈 역수는 그 수의 역수입니다.예를 들어, ${\displaystyle 13}$× 1 = ${\$$displaystyle$ $13\times$1=$13}$ 및 13 × 113 = 1 {\displaystyle 13\times {\tfrac {1}{13}}=1}입니다. 곱셈은 교환적이면서도 연관적입니다.

지수화 및 로그

지수화는 밑으로 알려진 숫자를 지수로 알려진 다른 숫자의 거듭제곱으로 올리는 산술 연산입니다.이 작업의 결과를 동력이라고 합니다.지수화는 기호 ^를 사용하여 표현하기도 하지만 더 일반적인 방법은 지수를 밑줄 바로 뒤에 위첨자로 쓰는 것입니다.Examples are ${\displaystyle 2^{4}=16}$ and ${\displaystyle 3}$^${\displaystyle 3=27}$. If the exponent is a natural number then exponentiation is the same as repeated multiplication, as in ${\displaystyle 2^{4}=2\times 2\times 2\times 2}$.^[89][90]

근은 분수 지수를 사용하는 특수한 유형의 지수입니다.예를 들어, 숫자의 제곱근은 숫자를 ${\displaystyle \frac{12}{}}$ ${\$의 거듭제곱으로 올리는 것과 같고$$, 숫자의 세제곱근은 숫자를 ${\displaystyle \frac{13}{}}$ ${\$의 거듭제곱으로 올리는 것과 같습니다$.$예는 $4$ = ${\displaystyle 4}$ 1 $2$= 2 {\$displaystyle$ ${\sqrt${4}}= 4^{\tfrac {1}{2}=2} 및 273 = 27 13 = 3 {\displaystyle {\sqrt[{3}}}= 27^{\tfrac {1}{3}}= 3}입니다.

로그는 지수화의 역수입니다.그 안에서, 밑과 로그의 인수는 인수를 생성하기 위해 밑을 올려야 하는 힘을 결정하는 데 사용됩니다.이 작업의 결과를 안티 로그(Anti-logarithm)라고 합니다.예를 들어, 밑 2에 대한 로그 값 16을 구하기 위해서는 밑 2에 어떤 지수를 사용해야 결과 값이 16이 되는지 알아내야 합니다.이 연산의 반로그는 16에서 2가 4로 증가하므로 4입니다.^[93][94]

지수화와 로그는 덧셈과 곱셈과 같은 일반적인 항등원과 역원을 가지고 있지 않습니다.${\displaystyle {\mathrm{지수}}^{}}$와 관련된 지수의 중립 요소는 ${\displaystyle {141}^{}}$ =${\displaystyle 14}${\displaystyle 14^{1}=14}와 같이 1입니다.그러나 지수화는 1이 베이스의 중립 요소가 아니므로 일반적인 항등식 요소를 갖지 않습니다.^[88][76]지수화와 로그는 교환적이지도 않고 연관적이지도 않습니다.^[95][96]

정수연산

정수 산술은 양수와 음수의 조작을 다루는 산술의 한 분야입니다.^[32][33][37]간단한 한 자리 수 연산은 덧셈표나 곱셈표처럼 가능한 모든 조합의 결과를 제시하는 표를 따르거나 암기하여 수행할 수 있습니다.다른 일반적인 방법은 언어로 세는 것과 손가락으로 세는 것입니다.^[97][98][99]

덧셈표

+	0	1	2	3	4	...
0	0	1	2	3	4	...
1	1	2	3	4	5	...
2	2	3	4	5	6	...
3	3	4	5	6	7	...
4	4	5	6	7	8	...
...	...	...	...	...	...	...

곱셈표

×	0	1	2	3	4	...
0	0	0	0	0	0	...
1	0	1	2	3	4	...
2	0	2	4	6	8	...
3	0	3	6	9	12	...
4	0	4	8	12	16	...
...	...	...	...	...	...	...

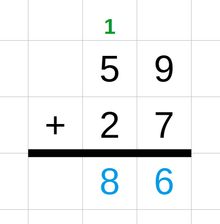
두 자리 이상의 숫자에 대한 연산의 경우 여러 개의 한 자리 수 연산을 연속으로 사용하여 결과를 계산하는 데 다양한 기법을 사용할 수 있습니다.예를 들어 운반과 함께 추가하는 방법에서 두 숫자는 서로 위에 쓰여집니다.맨 오른쪽 숫자부터 각 숫자 쌍이 함께 추가됩니다.합계의 맨 오른쪽 자리는 그 아래에 쓰여 있습니다.합이 두 자리 숫자이면 가장 왼쪽에 있는 "캐리"라고 불리는 숫자가 왼쪽에 있는 다음 숫자 쌍에 추가됩니다.이 과정은 모든 숫자가 추가될 때까지 반복됩니다.^[100][101]정수 덧셈에 사용되는 다른 방법은 숫자선법, 부분합법, 보상법입니다.^[102][103]이와 유사한 기술이 뺄셈에 사용됩니다. 또한 한 자리 뺄셈의 결과가 음수일 경우 왼쪽 열에 "차입" 또는 음수 캐리를 사용합니다.^[104]

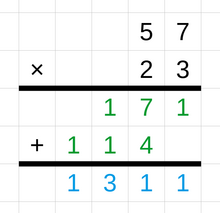
정수 곱셈의 기본 기법은 반복 덧셈을 사용합니다.예를 들어, 3 × 4의 곱은 3 + 3 + 3 + 3으로 계산될 수 있습니다.^[105] 더 큰 수를 갖는 곱셈에 대한 일반적인 기술은 긴 곱셈이라고 불립니다.이 방법은 곱셈기 위에 곱셈기를 쓰는 것으로 시작합니다.계산은 곱셈기의 가장 오른쪽 숫자로만 곱하고 가장 오른쪽 열에서 시작하여 아래 결과를 쓰는 것으로 시작합니다.곱셈기의 각 숫자에 대해서도 동일하게 수행되며 각 경우의 결과는 왼쪽으로 한 위치 이동됩니다.마지막 단계로 모든 개별 제품이 추가되어 두 개의 다자리 숫자의 전체 제품에 도달합니다.^[106][107]곱셈에 사용되는 다른 기술은 격자법과 격자법입니다.^[108]컴퓨터 과학은 카라츠바 알고리즘, 쇤하게-스트라센 알고리즘, 툼-쿡 알고리즘 등 매우 큰 정수를 효율적으로 곱할 수 있도록 계산 복잡도가 낮은 곱셈 알고리즘에 관심을 가지고 있습니다.^[109][110]나눗셈에 사용되는 일반적인 기술은 롱 나눗셈이라고 합니다.다른 방법으로는 짧은 분할과 청킹이 있습니다.^[111]

정수 산술은 나눗셈으로 닫히지 않습니다.이것은 한 정수를 다른 정수로 나눌 때 결과가 항상 정수가 아니라는 것을 의미합니다.예를 들어, 7을 2로 나눈 것은 정수가 아니라 3.5입니다.^[112]결과가 정수가 되도록 하는 한 가지 방법은 결과를 정수로 반올림하는 것입니다.그러나 이 방법은 원래 값이 변경됨에 따라 부정확하게 됩니다.^[113]또 다른 방법은 분할을 부분적으로만 수행하고 나머지는 유지하는 것입니다.예를 들어 7을 2로 나눈 값은 3이고 나머지는 1입니다.이러한 어려움은 분수의 정확한 표현을 허용하는 합리적 산술에 의해 방지됩니다.^[114]

지수를 계산하는 간단한 방법은 반복 곱하기입니다.예를 들어 3의⁴ 지수는 3 × 3 × 3 × 3으로 계산할 수 있습니다.^[115] 큰 지수에 사용되는 더 효율적인 기법은 제곱에 의한 지수입니다.계산을 여러 제곱 연산으로 나눕니다.예를 들어, 지수 3은⁶⁵ ((((3²)))²²²²² × 3과 같이 쓸 수 있습니다. 반복 제곱 연산의 이점을 이용하면 규칙적인 반복 곱셈에 필요한 64개 연산이 아니라 7개의 개별 연산만 필요합니다.^[116][117]로그를 계산하는 방법에는 테일러 급수와 연속 분수가 포함됩니다.^[118][119]정수 산술은 대수 및 음의 지수로 지수화할 때 닫혀 있지 않으며, 이는 이러한 연산의 결과가 항상 정수가 아님을 의미합니다.^[120][118]

수론

정수론은 정수들의 구조와 성질, 그리고 정수들 사이의 관계와 법칙을 연구합니다.^{[34][121][122]}현대 정수론의 주요 분과로는 초등수론, 분석수론, 대수적 수론, 기하학적 수론 등이 있습니다.^[123][124]초등수 이론은 기초적인 방법을 사용하여 조사할 수 있는 정수의 측면을 연구합니다.이와 관련하여 해석학과 미적분학에서 발견되는 방법의 사용은 제외됩니다.주제에는 분할성, 인수분해 및 기본성이 포함됩니다.^[125][126]이에 반해 해석적 수론은 해석학과 미적분학의 기법에 의존합니다.소수의 분포 방식과 모든 짝수는 두 소수의 합이라는 주장 등의 문제를 조사합니다.^[123][127]대수적 수론은 대수적 구조를 이용하여 수의 성질과 수 사이의 관계를 분석합니다.예를 들어, 정수의 고리와 같은 대수적 숫자장에서와 같이, 필드와 고리의 사용이 있습니다.기하학적 숫자 이론은 숫자를 연구하기 위해 기하학의 개념을 사용합니다.예를 들어, 정수 좌표를 가진 격자점이 평면에서 어떻게 행동하는지 조사합니다.^[128][129]수론의 또 다른 분야는 확률적 수론, 조합적 수론, 계산적 수론, 응용적 수론입니다.^[124][130]

수론에서 영향력 있는 정리로는 산술의 기본 정리, 유클리드의 정리, 페르마의 마지막 정리 등이 있습니다.^[34][131]산술의 기본 정리에 따르면 1보다 큰 모든 정수는 소수이거나 소수의 고유한 곱으로 표현될 수 있습니다.예를 들어 숫자 18은 소수가 아니며 2 ×${\displaystyle }3{\displaystyle \mathrm{}}$ ×${\displaystyle 3}$ ${\displaystyle 2\times$ 3$\times 3}$로 표현할 수 있으며 모두$$소수입니다.반대로 19라는 숫자는 다른 소인수분해가 없는 소수입니다.^[132][133]유클리드의 정리는 무한히 많은 소수들이 있다는 것을 말합니다.^[34][134]Fermat's last theorem is the statement that no positive integer values can be found for ${\displaystyle a}$, ${\displaystyle b}$, and ${\displaystyle c}$, to solve the equation ${\displaystyle a^{n}+b^{n}=c^{n}}$ if ${\displaystyle n}$ is greater than ${\displaystyle 2}$.^[34][135]

합리적산술

합리적 산술은 두 정수의 비율로 표현할 수 있는 수를 조작하는 것을 다루는 산술의 한 분야입니다.^{[136][32][33][38]}유리수에 대한 대부분의 산술 연산은 분자와 관련된 수의 분모에 대해 일련의 정수 산술 연산을 수행함으로써 계산될 수 있습니다.만약 두 유리수가 같은 분모를 가지고 있다면, 그들의 분자를 더하고 공통분모를 유지함으로써 더해질 수 있습니다.$예$를 들어,${\displaystyle 27}$ + ${\displaystyle \frac{37}{}}$ =$${\displaystyle {\tfrac {2}{7}}+{\tfrac {3}{7}}={\tfrac {5}{7}}와 같이 뺄셈에도 비슷한 절차가 사용됩니다.만약 두 숫자가 같은 분모를 가지고 있지 않다면, 그들은 공통 분모를 찾기 위해 변환되어야 합니다.이것은 첫 번째 숫자를 두 번째 숫자의 분모로 스케일링하고 두 번째 숫자를 첫 번째 숫자의 분모로 스케일링함으로써 달성될 수 있습니다.For example, ${\displaystyle {\tfrac {1}{3}}+{\tfrac {1}{2}}={\tfrac {1\cdot 2}{3\cdot 2}}+{\tfrac {1\cdot 3}{2\cdot 3}}={\tfrac {2}{6}}+{\tfrac {3}{6}}={\tfrac {5}{6}}}$.^[137][138]

${\displaystyle \frac{}{}}$ ⋅ 25 =${\displaystyle \frac{}{}}$2 ⋅ $23$ ⋅ 5 = 4 $15 {\displaystyle {\tfrac {2$}{3}}\cdot {\$tfrac {2$}{$5}}$=${\$tfrac {$2\cdot$ 2}{3\cdot 5}={\tfrac {4}{15}}와 같이 두 유리수는 각각 분자와 분모를 곱하여 곱합니다.유리수 하나를 다른 유리수로 나누는 것은 첫 번째 수에 두 번째 수의 역수를 곱하면 달성할 수 있습니다.이것은 두 번째 숫자의 분자와 분모가 위치를 바꾼다는 것을 의미합니다.예를 들어 ${\displaystyle \frac{35}{}}$ :${\displaystyle \frac{27}{}}$ = ${\displaystyle 35}$⋅ 72 = 21 $10 {\displaystyle {\tfrac${3}{5}}:${\tfrac {2}{7$}}$={\tfrac {3$}{5$}}\cdot${\$tfrac {$7}{2$}}={\tfrac$ {21$}{10$ 유리수는 정수 연산과 달리 약수가 0이 아닌 한 나눗셈으로 닫혀 있습니다.

정수 산술과 유리 산술은 모두 지수화 및 로그 하에서 닫히지 않습니다.^[140]분수 지수를 사용하여 지수를 계산하는 한 가지 방법은 두 가지로 나누어 계산하는 것입니다. 하나는 지수의 분자를 사용하여 지수를 계산한 다음 지수의 분모를 기준으로 결과의 n번째 루트를 그리는 것입니다.예를 들어 $52$ ${\displaystyle {\frac{23}{}}^{}}$ = ${\displaystyle \text{exception 25:}}$3 {\displaystyle 5^{\tfrac {2}{3}} = {\sqrt[{3}]{5^{2}}}입니다.첫 번째 연산은 반복 곱셈이나 제곱에 의한 지수화와 같은 방법을 사용하여 완료할 수 있습니다.두 번째 연산에 대한 근사 결과를 얻는 한 가지 방법은 뉴턴의 방법을 사용하는 것인데, 뉴턴의 방법은 일련의 단계를 사용하여 초기 추측이 원하는 정확도에 도달할 때까지 점진적으로 정교화하는 것입니다.^{[141][142][143]}Taylor series 또는 continued fraction 방법을 사용하여 로그를 계산할 수 있습니다.^[118][119]

소수 분수 표기법은 분모가 10의 거듭제곱인 유리수를 나타내는 특별한 방법입니다.For example, the rational numbers ${\displaystyle {\tfrac {1}{10}}}$, ${\displaystyle {\tfrac {371}{100}}}$, and ${\displaystyle {\tfrac {44}{10000}}}$ are written as 0.1, 3.71, and 0.0044 in the decimal fraction notation.^[40][144]운반이 있는 덧셈과 긴 곱셈과 같은 정수 계산 방법의 수정된 버전은 소수 분수가 있는 계산에 적용될 수 있습니다.^[145][146]모든 유리수가 소수 표기법에서 유한한 표현을 갖는 것은 아닙니다.예를 들어 유리수 ${\displaystyle \frac{13}{}}$ ${\$은(는) 0.333...에$$ 해당합니다.무한히 3개의 수를 가진이런 종류의 반복 십진법의 단축 표기법은 0.3입니다.^[147][144]모든 반복 십진법은 유리수를 표현합니다.^[41]

실산

실수 연산은 유리수와 무리수의 조작을 모두 다루는 산술의 한 분야입니다.무리수는 2의 근이나 π처럼 분수나 반복되는 소수를 통해 표현할 수 없는 수입니다.실제 산술은 유리수와 달리 양수를 기본으로 사용하는 한 지수화 하에서 닫혀 있습니다.로그 밑이 1이 아닌 양수인 경우에는 양수 실수의 로그도 마찬가지입니다.^{[150][151][152]}

무리수는 무한히 반복되지 않는 소수의 수열을 포함합니다.$이$ 때문에 2${\displaystyle }$+$$π {\displaystyle${\sqrt${2}+\$pi{\displaystyle \}}$e ⋅ 3${\displaystyle$ e$\backslash$cdot {\sqrt {3}}과 같이 산술 연산의 결과를 간단하고 정확하게 표현할 수 있는 방법이 없는 경우가 많습니다. 절대적인 정밀도가 필요하지 않은 경우,실수에 대한 산술 연산을 계산하는 문제는 일반적으로 잘림이나 반올림으로 해결됩니다.잘라내기의 경우, 왼쪽에 있는 특정 숫자의 유효숫자가 유지되고 마지막 유효숫자의 오른쪽에 있는 추가 숫자가 제거됩니다.예를 들어, 숫자 π는 3.14159로 시작하는 무한한 숫자를 가지고 있습니다. 만약 이 숫자를 4자리의 유효숫자로 자르면 결과는 3.141입니다.반올림은 다음 자리가 5 이상일 경우 마지막 의미 있는 자리를 1개씩 늘리는 것과 유사한 과정입니다.다음 숫자가 5보다 작으면 마지막 숫자는 그대로 유지됩니다.예를 들어, 숫자 π를 유효숫자 4로 반올림하면 다음 숫자가 5이므로 결과는 3.142입니다.이러한 방법은 컴퓨터가 실수에 대한 계산을 효율적으로 수행할 수 있도록 하는 데 필수적입니다.^[156]

매우 큰 실수와 매우 작은 실수는 종종 정규화된 과학적 표기법을 사용하여 표현됩니다.그 안에서 숫자는 소위 의미를 사용하고 10의 거듭제곱을 곱한 것으로 표현됩니다.sigidand는 소수점과 일련의 숫자 뒤에 오는 숫자입니다.예를 들어, 숫자 8276000의 정규화된 과학 표기법은 $8{\displaystyle .276}$× ${\displaystyle {106\mathrm{}}^{}}$ ${\$이고, 숫자 0.00735의 정규화된 과학 표기법은 $7{\displaystyle .35}$× ${\displaystyle {10}^{}}$- ${\displaystyle 3^{}}$ ${\$입니다$.$^[157][158]

컴퓨터가 실제 산술을 근사하기 위해 사용하는 일반적인 방법은 부동 소수점 산술이라고 합니다.그것은 과학적 표기법과 유사한 실수를 세 가지 숫자, 즉 기댓값, 기댓값, 지수를 통해 나타냅니다.^[159]기호와 기호의 정밀도는 기호를 나타내기 위해 할당된 비트 수에 의해 제한됩니다.산술 연산에서 사용 가능한 것보다 더 많은 비트를 필요로 하는 숫자가 나오면 컴퓨터는 결과를 가장 가까운 대표 숫자로 반올림합니다.이로 인해 반올림 오류가 발생합니다.^{[156][159][160]}이러한 행동의 결과는 부동 소수점 산술에 의해 특정 산술 법칙이 위반된다는 것입니다.예를 들어, 도입된 반올림 오차는 덧셈 순서에 따라 달라질 수 있으므로 부동 소수점 덧셈은 연관성이 없습니다.${\displaystyle 즉},{\displaystyle }$ (${\displaystyle a}$+ ${\displaystyle b}$)${\displaystyle }$+ c ${\displaystyle (a$+ b) + $c}$의 결과가${\displaystyle }$+${\displaystyle }$(${\displaystyle b}$+ c${\displaystyle }$) ${\displaystyle a$+ ($b$+ $c)}$의 결과와 다를$$ 수 있습니다$.$^[161][162]부동 소수점 연산에 사용되는 가장 일반적인 기술 표준은 IEEE 754라고 합니다.그 중에서도 숫자를 어떻게 나타내는지, 산술 연산과 반올림을 어떻게 하는지, 오류와 예외를 어떻게 처리하는지를 결정합니다.^{[163][164][165]}

십진법 연산

십진 표기법은 일반적으로 아라비아 숫자를 기수 10("십진") 위치 표기법의 숫자로 사용하는 문자 숫자 체계를 의미합니다. 그러나 그리스어, 키릴 문자, 로마자 등 10의 거듭제곱을 기반으로 하는 모든 숫자 체계는 다음과 같습니다.또는 중국 숫자는 개념적으로 "십진 표기법" 또는 "십진 표기법"으로 설명될 수 있습니다.

네 가지 기본 연산( 덧셈, 뺄셈, 곱셈, 나눗셈)에 대한 현대적인 방법은 인도의 브라마굽타에 의해 처음 고안되었습니다.이것은 중세 유럽에서 "Modus Indorum" 또는 "Method of the Indians"로 알려졌습니다.위치 표기법("place-value notation"이라고도 함)은 크기의 다른 순서(예: "한 자리", "십 자리", "백 자리")에 대해 동일한 기호를 사용하고, 반지름 점을 사용하여 분수(예: "십 자리", "백 자리")를 나타내는 동일한 기호를 사용하여 숫자를 표현하거나 인코딩하는 것을 말합니다.예를 들어, 507.36은 500(10²), 0 10(10¹), 7 단위(10⁰), 3/10(10⁻¹), 600/100(10⁻²)을 나타냅니다.

0의 개념은 다른 기본 숫자와 유사한 숫자로서 0의 개념이 자리지킴이로서의 사용의 개념과 0과 함께 곱하기와 덧셈의 정의와 마찬가지로 이 표기법에 필수적입니다.0을 자리지킴이로 사용하는 것은, 따라서 위치 표기법의 사용은, 기원후 458년의 로카비브하가라는 제목의 인도의 자인 텍스트에서 처음으로 증명되고 있으며, 이러한 개념들이 아랍 세계의 학문을 통해 전해진 것은 13세기 초의 일입니다.피보나치는^[166] 힌두 아라비아 수 체계를 사용하여 유럽에 유입되었습니다.

알고리즘은 이런 종류의 기록된 숫자를 사용하여 산술 연산을 수행하는 모든 규칙으로 구성됩니다.예를 들어 덧셈은 두 임의의 숫자의 합을 생성합니다.결과는 동일한 위치를 차지하는 각 숫자에서 오른쪽에서 왼쪽으로 진행되는 한 자리 숫자의 반복적인 덧셈에 의해 계산됩니다.열 개의 행과 열 개의 열로 구성된 덧셈 표에는 각 합계에 대해 가능한 모든 값이 표시됩니다.개별 합계가 9를 초과할 경우 결과는 두 자리 숫자로 표시됩니다.가장 오른쪽 자리는 현재 위치에 대한 값이고, 이후 왼쪽에 숫자를 추가한 결과는 항상 1(0이 아닌 경우)인 두 번째(가장 왼쪽) 자리의 값만큼 증가합니다.이 조정을 값 1의 운반이라고 합니다.

임의의 두 수를 곱하는 과정은 덧셈 과정과 비슷합니다.열 개의 행과 열 개의 열로 구성된 곱셈표에는 각 자릿수 쌍에 대한 결과가 나열됩니다.자릿수 쌍의 개별 곱이 9를 초과하면 캐리 조정을 통해 자릿수에서 왼쪽으로 이어지는 모든 곱의 결과가 1에서 8까지의 값인 두 번째(가장 왼쪽) 자릿수와 동일한 값으로 증가합니다(9 × 9 = 81).추가 단계를 통해 최종 결과를 정의할 수 있습니다.

뺄셈과 나눗셈에도 비슷한 기술이 존재합니다.

곱셈에 대한 올바른 프로세스의 생성은 인접한 숫자의 값 사이의 관계에 의존합니다.숫자의 한 자리 수 값은 위치에 따라 달라집니다.또한 왼쪽의 각 위치는 오른쪽의 위치보다 10배 큰 값을 나타냅니다.수학적 용어로 10의 반지름(기저)에 대한 지수는 1 증가(왼쪽)하거나 1 감소(오른쪽)합니다.따라서 임의의 숫자에 대한 값에 정수 n을 갖는 형태 10의ⁿ 값을 곱합니다.한 자리에 가능한 모든 위치에 해당하는 값 목록은 {..., 10², 10, 1, 10⁻¹, 10⁻², ...}로 기록됩니다.

이 목록에 있는 모든 값에 10을 곱하면 목록에서 다른 값이 생성됩니다.수학 용어에서 이 특성은 폐쇄로 정의되며 이전 목록은 곱셈에서 폐쇄로 설명됩니다.이전의 기법을 이용하여 곱셈의 결과를 올바르게 찾을 수 있는 근거가 됩니다.이 결과는 정수론을 사용한 한 예입니다.

복합단위산술

복합^[167] 단위 산술은 피트, 인치, 갤런, 파인트, 파운드, 실링, 펜스 등과 같은 혼합 라디칼 양에 산술 연산을 적용하는 것입니다.십진법에 기초한 화폐와 측정 단위 체계 이전에, 복합 단위 산술은 상업과 산업에서 널리 사용되었습니다.

기초연산

복합 단위 산술에 사용되는 기법은 수세기에 걸쳐 발전되었으며 여러 언어로 된 많은 교과서에 잘 기록되어 있습니다.^{[168][169][170][171]}복합 단위 산술은 십진법 산술에서 볼 수 있는 기본 산술 함수 외에도 다음과 같은 세 가지 함수를 더 사용합니다.

• 예를 들어, 야드, 피트 및 인치로 표시된 거리를 인치로 표시된 거리로 변환하는 등, 복합 수량이 단일 수량으로 감소하는 축소.^[172]
• 감소에 대한 역함수인 팽창은 단일 측정 단위로 표현되는 양을 24온즈에서 1lb 8온즈로 팽창시키는 것과 같은 화합물 단위로 변환하는 것입니다.
• 정규화(normalization)는 화합물 단위의 집합을 표준 형태로 변환하는 것입니다. 예를 들어, "1 ft 13 in"을 "2 ft 1 in"으로 다시 쓰는 것입니다.

다양한 측정 단위, 그 배수 및 하위 배수 간의 관계에 대한 지식은 복합 단위 산술의 필수적인 부분을 형성합니다.

복소단위산술의 원리

복합 단위 산술에는 두 가지 기본 접근 방식이 있습니다.

• 모든 복합 단위 변수를 단일 단위 변수로 축소하고 계산을 수행한 후 결과를 다시 복합 단위로 확장하는 축소-확장 방법.이 접근 방식은 자동화된 계산에 적합합니다.Microsoft Excel이 모든 시간 간격을 일 및 소수점 단위로 내부적으로 처리하는 시간 처리가 대표적인 예입니다.
• 각 유닛을 별도로 처리하고 솔루션이 발전함에 따라 문제를 지속적으로 정규화하는 진행형 정규화 방법.고전 텍스트에서 널리 설명되는 이 접근 방식은 수동 계산에 가장 적합합니다.덧셈에 적용된 진행 중인 정규화 방법의 예는 아래와 같습니다.

추가 작업은 오른쪽에서 왼쪽으로 수행되며, 이 경우 펜스가 먼저 처리된 다음 실링이 처리되고 파운드가 처리됩니다."답변 줄" 아래의 숫자는 중간 결과입니다.

펜스 기둥의 합계는 25입니다.1실링에 12페니가 있으므로 25를 12로 나누어 나머지가 1인 2를 줍니다.그런 다음 "1" 값이 답변 행에 기록되고 "2" 값이 실링 열로 전달됩니다.이 작업은 실링 열의 값을 사용하여 반복되며, 페니 열에서 이월된 값을 추가하는 단계가 추가됩니다.1파운드에 20실링이 있으므로 중간 합계는 20으로 나뉩니다.그런 다음 파운드 열이 처리되지만 파운드가 고려되는 가장 큰 단위이므로 파운드 열에서 값이 이월되지 않습니다.

단순함을 위해 선택한 예제에는 먼 것들이 없었습니다.

실무작업

19세기와 20세기 동안 특히 상업적 용도에서 복합 장치의 조작을 돕기 위해 다양한 보조 장치가 개발되었습니다.가장 일반적인 보조 도구는 파운드, 실링, 펜스 및 먼 것들을 수용하기 위해 영국과 같은 나라에서 개조된 기계적인 틸과 다양한 금액의 백분율 또는 배수와 같은 다양한 일상적인 계산의 결과를 목록화한 상인을 대상으로 하는 책인 레디 계산기였습니다.150페이지에 이르는 한 전형적인^[173] 책자는 "1개에서 1파운드까지 다양한 가격으로" 여러 개의 표를 작성했습니다.

복소 단위 산술의 번거로운 특성은 수년 동안 인식되어 왔습니다. 1586년, 플랑드르의 수학자 시몬 스테빈은 데 티엔데("^[174]열 번째")라는 작은 팜플렛을 출판하여 십진법 동전, 측도, 가중치의 보편적인 도입은 단지 시간의 문제라고 선언했습니다.현대에는 Microsoft Windows 7 운영 체제 계산기에 포함된 것과 같은 많은 변환 프로그램이 확장 형식을 사용하는 대신 축소된 십진 형식으로 컴파운드 단위를 표시합니다(예: "2 ft 6 in"이 아닌 "2.5 ft"가 표시됨).

교육에서 산술

수학에서 초등교육은 흔히 자연수, 정수, 분수, 소수의 산술(소수 자릿값 체계 사용)을 위한 알고리즘에 초점을 둡니다.이 연구는 때때로 알고리즘으로 알려져 있습니다.

이러한 알고리즘의 난이도와 동기 부여되지 않은 모습으로 인해 교육자들은 더 중심적이고 직관적인 수학적 아이디어의 초기 교육을 옹호하면서 이 교육 과정에 의문을 제기해 왔습니다.이러한 방향으로의 주목할 만한 움직임 중 하나는 1960년대와 1970년대의 뉴 수학으로 고등 수학의 지배적인 경향의 반향인 집합론에서 공리적인 발전의 정신으로 산술을 가르치려고 시도한 것입니다.^[175]

또한 이슬람 학자들은 자카트와 이르스와 관련된 판결의 적용을 가르치기 위해 산술을 사용했습니다.이것은 압드 알 파타 알 두미야티의 산술의 최고라는 제목의 책에서 행해졌습니다.^[176]이 책은 수학의 기초부터 시작하여 이후 장에서 적용을 진행합니다.

역사

산술의 가장 초기 형태는 때때로 수량을 추적하는 데 사용되는 계산 및 집계 표시로 거슬러 올라갑니다.일부 역사학자들은 레봄보 뼈(약 43,000년 전)와 이산고 뼈(약 22,000년에서 30,000년 전)가 가장 오래된 산수유물이라고 주장하지만, 이러한 해석은 논란의 여지가 있습니다.^{[177][178][179]}그러나 기본적인 숫자에 대한 감각은 이러한 발견보다 앞서 있을 수 있으며 언어가 발달하기 전에도 존재했을 수 있습니다.^[180][181]

그러나 고대 문명이 출현한 이후에야 산술에 대한 보다 복잡하고 체계적인 접근법이 기원전 3000년경부터 시작되었습니다.보관 품목을 추적하고 토지 소유를 관리하며 교환을 주선해야 할 필요성이 증가했기 때문에 이는 필요하게 되었습니다.^[182][183]모든 주요 고대 문명은 숫자의 표현을 용이하게 하기 위해 비위치 수 체계를 개발했습니다.그들은 또한 덧셈과 뺄셈과 같은 연산에 대한 기호를 포함하고 분수를 알고 있었습니다.이집트 상형문자와 수메르, 중국, 인도에서 사용되는 숫자 체계가 그 예입니다.^[184][185]최초의 위치수 체계는 기원전 1800년경부터 바빌로니아 사람들에 의해 개발되었습니다.이것은 큰 수를 표현하고 그 수에 대한 계산을 더 효율적으로 만들었기 때문에 이전의 수 체계에 비해 크게 개선되었습니다.^[186][187]아바커스는 복잡한 계산을 수행하기 위한 효율적인 수단으로 예로부터 손으로 조작하는 계산 도구로 사용되었습니다.^[188][189]

초기 문명은 주로 구체적인 실용적인 목적으로 수를 사용했고 수 자체에 대한 추상적인 개념은 없었습니다.^[190][191]이것은 고대 그리스 수학자들이 수가 특정 문제에 어떻게 적용되는지를 연구하기보다 추상적인 성질을 탐구하기 시작하면서 바뀌었습니다.^[192][191]또 다른 새로운 특징은 수학적 진리를 확립하고 이론을 검증하기 위해 증명을 사용했다는 것입니다.^[192][193]또 다른 기여는 짝수, 홀수, 소수와 같은 다양한 종류의 수를 구별하는 것이었습니다.^[194][195]여기에는 특정 기하학적 길이에 대한 숫자는 비합리적이므로 분수로 표현할 수 없다는 발견이 포함되었습니다.^[196][197]기원전 7세기와 6세기의 밀레토스의 탈레스와 피타고라스의 작품들은 흔히 그리스 수학의 시초로 여겨집니다.^[198][199]디오판토스는 수론에 대한 수많은 공헌과 대수 방정식에 대한 산술 연산의 적용에 대한 탐구로 인해 기원전 3세기 그리스 산술의 영향력 있는 인물이었습니다.^[200][201]

고대 인도인들은 계산에 사용될 숫자로서 0의 개념을 최초로 개발했습니다.그 운영의 정확한 규칙들은 기원전 628년경 Brahmagupta에 의해 기록되었습니다.^{[202][203][204]}일반적인 용어로서의 0의 개념은 훨씬 이전부터 존재했지만, 그것은 산술 연산의 대상이라기보다는 빈 자리지킴이로 이해되었습니다.^[205][206]브라마굽타는 또한 음수를 사용한 계산과 신용 및 부채와 같은 문제에 대한 적용에 대한 자세한 논의를 제공했습니다.^{[207][203][204]}음수의 개념 자체는 훨씬 더 오래된 것으로 기원전 1천 년에 중국 수학에서 처음으로 탐구되었습니다.^[208][209]

인도 수학자들은 오늘날 흔히 볼 수 있는 십진법을 개발했습니다.예를 들어, 6세기경 아리야바타에 의해 그 운영에 대한 상세한 처리가 제공되었습니다.^[210][204]인도 십진법은 알콰리즈미와 같은 아랍 수학자들에 의해 이슬람 황금기 동안 더욱 정교해지고 확장되었습니다.그의 업적은 십진법 체계를 이전에 비위치 로마 숫자 체계에 의존했던 서구 세계에 소개하는 데 영향을 미쳤습니다.^[211][204]그곳에서, 그것은 12세기와 13세기에 살았고 또한 피보나치 수열을 개발한 레오나르도 피보나치와 같은 수학자들에 의해 대중화되었습니다.^[212][213]중세와 르네상스 시대에는 상업을 위한 실용적인 계산을 다루기 위해 많은 인기 있는 교과서가 출판되었습니다.또한 이 시기에는 학대가 널리 퍼지게 되었습니다.^[214][215]16세기에 수학자 제롤라모 카르다노는 3차 방정식을 푸는 방법으로 복소수 개념을 생각해 냈습니다.^[216][217]

최초의 기계적 계산기는 17세기에 개발되었으며 블레즈 파스칼의 계산기와 고트프리트 빌헬름 라이프니츠의 계단식 계산기와 같은 복잡한 수학적 계산을 크게 용이하게 했습니다.^{[219][220][221]}17세기에는 존 네이피어에 의해 로그가 발견되기도 했습니다.^[222][223]

18세기와 19세기에 레온하르트 오일러와 칼 프리드리히 가우스와 같은 수학자들은 현대 정수론의 기초를 세웠습니다.^{[224][225][226]}이 시기의 또 다른 발전은 게오르크 칸토어의 집합론과 자연수 산술의 공리화로 사용된 데데킨트-페아노 공리와 같은 산술의 형식화와 기초에 관한 연구입니다.^[227][228]컴퓨터와 전자 계산기는 20세기에 처음 개발되었습니다.그들의 광범위한 사용은 복잡한 산술 계산도 계산할 수 있는 정확성과 속도 모두에 혁명을 일으켰습니다.^{[229][230][231]}

참고 항목

• 연산개요
• 임의의 정밀한 산술 - 컴퓨터를 이용한 산술의 가장 가까운 구현이지만 여전히 불완전합니다.
• 계산기 - 대부분의 계산기는 제한적이며 임의의 정밀도 연산에 적합하지 않습니다.

관련주제

참고문헌

인용

원천

더보기

외부 링크

• 산술에 관한 Math World 기사
• 신입생 참고 작품/산술(역사)
• 인도인들에 따르면, 막시무스 플라누데스의 위대한 계산 – 수렴에서 산술에 관한 초기 서양 작품
• Weyde, P. H. Vander (1879). "Arithmetic" . The American Cyclopædia.