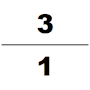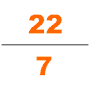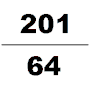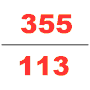중국어 수학

중국의 수학은 기원전 ^[1]11세기에 독립적으로 등장했다.중국은 독자적으로 상당히 큰 숫자와 음수, 하나 이상의 숫자 체계(베이스 2와 베이스 10), 대수, 기하학, 수 이론과 삼각법을 포함하는 실수 체계를 개발했다.

한대 이후, 디오판틴 근사법은 중요한 수치법이었기 때문에, 중국인들은 다항식 평가에서 상당한 진전을 이루었다.레귤러 폴시와 같은 알고리즘과 연속 분수와 같은 표현은 널리 사용되고 있으며 그 이후로 잘 문서화되어 왔다.그들은 의도적으로 양의 n번째 근과 ^[2][3]방정식의 근을 찾는다.이 시기의 주요 교재인 수학예술 9장과 숫자와 계산서는 일상생활에서 ^[4]다양한 수학 문제를 푸는 과정을 상세히 알려줬다.모든 절차는 두 텍스트 모두에서 계수판을 사용하여 계산되었으며, 역요소 및 유클리드 나눗셈을 포함하였다.텍스트는 선형 대수에 대한 ^[5]가우스 제거 및 호너의 방법과 유사한 절차를 제공한다.중국 대수의 업적은 원나라 때인 13세기에 천원사의 발달로 절정에 달했다.

내용뿐만 아니라 명백한 언어·지리적 장벽의 결과로서, 중국 수학과 고대 지중해의 수학은 수학 예술 9장이 최종 형태에 도달하기 전까지 다소 독립적으로 발전한 것으로 추정되며, 반면에 숫자와 계산에 관한 책과 화인은 거의 독립적으로 발전한 것으로 보인다.anzi는 고전 그리스 수학과 대략 동시대적이다.적어도 로마 시대부터 알려진 문화 교류를 통해 아시아 전역에서 어떤 의견 교환이 있을 것 같다.종종, 초기 사회의 수학의 요소들은 기하학이나 수 이론과 같은 현대 수학의 분과에서 나중에 발견되는 기초적인 결과에 대응합니다.예를 들어 피타고라스의 정리는 주공 시대에 증명되었다.파스칼의 삼각형에 대한 지식은 송나라의 중국 polymathShen Kuo와 같이 ^[6]파스칼보다 수 세기 전에 중국에 존재했던 것으로 또한 증명되었다.

중국의 과학기술사
디스커버리 목록 발명 목록 4대 발명품
과목별
농업 양잠 연금술 아키텍처 고전적인 정원 브리지 천문학 캘린더 지도 제작 세라믹스 코인지 지리 수학 측정 단위 전통의학 허브학 야금학 군사의 네이비 인쇄 비단 산업 운송 내비게이션
시대별
신석기 시대와 초기 청동기 시대 한 탕 노래 위안 인민 공화국 농업 공간
v t

초기 중국어 수학

Oracle bone script에 대한 간단한 수학은 상 왕조(기원전 1600–1050년)로 거슬러 올라간다.현존하는 가장 오래된 수학 작품 중 하나는 주나라 (기원전 1050년-256년) 동안 쓰여진 문학에 큰 영향을 준 이칭이다.수학에 있어서, 그 책은 육각형의 정교한 사용을 포함했다.라이프니츠는 이칭(이징)이 이진수 요소를 포함하고 있다고 지적했다.

상나라 시대부터, 중국인들은 이미 십진법을 완전히 발전시켰다.옛날부터, 중국인들은 기본적인 산수, 대수, 방정식, 그리고 음수를 ^{[citation needed]}막대기로 이해했다.비록 중국인들은 천문학적 사용을 위해 산수와 고급 대수학에 더 집중했지만, 음수, 대수 기하학(중국 기하학만) 그리고 십진법의 사용을 개발한 최초의 사람들이기도 했다.

수학은 리이(李–) 또는 육예( the of) 중 하나였으며, 학생들은 주나라 (기원전 1122년-256년)에 숙달해야 했다.이 모든 것을 완벽하게 익히는 것은 완벽한 신사, 즉 중국어로 "르네상스 맨"이 되기 위해 요구되었습니다.육예는 유교 철학에 뿌리를 두고 있다

중국에서 기하학에 관한 현존하는 가장 오래된 저작은 모지 추종자들에 의해 편찬된 기원전 330년 경의 철학적인 모히스트 규범에서 나온 것이다.모징은 물리학과 관련된 많은 분야의 다양한 측면을 설명했고 수학에 대한 약간의 정보도 제공했다.그것은 기하학적 점의 '원자적' 정의를 제공하여 선이 여러 부분으로 분리되고, 남은 부분이 없는 부분(즉, 더 작은 부분으로 분할할 수 없음)이 ^[7]점임을 명시했다.유클리드의 첫 번째와 세 번째 정의와 플라톤의 '줄의 시작'처럼, 모징은 "점은 출산 시 머리표현처럼 (줄의) 끝에 서거나 그것의 시작 부분에 서 있을 수 있다. (그 눈에 보이지 않는 것과 같이) 그것과 ^[8]비슷한 것은 없다."고 말했다.데모크리투스의 원자론자들과 비슷하게, 모징은 "아무것도"^[8]를 반으로 줄일 수 없기 때문에 1점은 가장 작은 단위이며 반으로 자를 수 없다고 말했다.길이와 ^[9]평행의 비교를 위한 정의와 더불어 공간과 유계 공간의 원리를 ^[10]제공하면서 길이가 같은 두 선은 항상 같은 ^[8]장소에서 끝난다고 명시했다.또 두께가 없는 평면은 ^[11]서로 접촉할 수 없어 쌓을 수 없다는 점도 설명했다.이 책은 ^[12]부피의 정의와 함께 둘레, 지름, 반지름에 대한 단어 인식을 제공했다.

수학 발전의 역사에는 몇 가지 증거가 부족하다.특정 수학 고전에 대한 논쟁은 여전히 있다.예를 들어, 저우비 쑤안징은 기원전 1200-1000년 전으로 거슬러 올라가지만, 많은 학자들은 그것이 기원전 300년에서 250년 사이에 쓰여졌다고 믿었다.저우비 쑤안징은 구구정리(피타고라스 정리의 특별한 경우)에 대한 심층적인 증거를 포함하고 있지만, 천문학적인 계산에 더 초점을 맞추고 있다.하지만, 기원전 305년 경의 청화 대나무 조각의 고고학적 발견은 최초의 알려진 십진 곱셈표와 ^[13]같은 이전 진 수학의 몇 가지 측면을 드러냈습니다.

주판은 기원전 2세기에 작은 대나무 막대기를 체커판에 ^[14]연속된 정사각형에 놓는 '봉 계산'과 함께 처음 언급되었다.

진수학

기원전 213~210년경에 책을 불태우고 학자들을 매장했기 때문에 진 왕조 수학에 대해서는 많이 알려져 있지 않습니다.이 시기에 대한 지식은 토목 프로젝트와 역사적 증거에서 확인할 수 있다.진 왕조는 표준 무게 체계를 만들었다.진나라의 토목사업은 인간공학의 중요한 위업이었다.진시황은 많은 사람들에게 궁궐 무덤을 위해 다른 절과 신사와 함께 크고 생명력 있는 조각상을 세우라고 명령했고, 무덤의 모양은 기하학적인 건축 기술로 설계되었다.인류 역사상 가장 위대한 위업 중 하나인 만리장성이 많은 수학적 기술을 필요로 했다는 것은 확실하다.모든 진나라 건물과 웅장한 프로젝트는 부피, 면적, 비율에 대한 고급 계산식을 사용했습니다.

여류학원이 홍콩의 골동품시장에서 구입한 진죽 현금은 수학 논문의 가장 오래된 경구 표본을 포함하고 있다.

한수학

한나라에서는 숫자가 자리수 십진법으로 발전해 주안이라 불리는 숫자 막대와 함께 숫자판에 사용되었으며 숫자판에는 0을 ^[3]나타내는 공백이 있는 9개의 기호로만 구성되어 있다.음수와 분수 또한 그 ^[4]시대의 위대한 수학 텍스트의 해법에 통합되었다.당시의 수학 교과서인 손수주와 주장수안은 덧셈, 뺄셈, 곱셈, ^[4]나눗셈과 같은 기본적인 산술 문제를 풀었다.게다가 그들은 제곱근과 입방근 추출을 위한 과정을 주었고, 이는 결국 3차까지 2차 ^[5]방정식을 푸는 데 적용되었다.두 텍스트 모두 선형 대수학, 즉 복수의 ^[15]미지수를 갖는 방정식의 체계를 푸는 데 상당한 진전을 이뤘다.파이의 값은 두 ^[16]텍스트 모두에서 3과 같은 것으로 간주됩니다.하지만 수학자 류신(Liu Xin, d. 23)과 장형(78–139)은 이전 ^[4]세기의 중국인들이 사용했던 것보다 더 정확한 파이 근사치를 제시했습니다.수학은 토지분할이나 ^[17]분납과 관련된 문제 등 당시의 현실적인 문제를 해결하기 위해 개발되었다.중국인들은 면적이나 ^[18]부피를 구하는 방정식을 증명하는 현대적 의미의 기하학이나 대수학에 기초한 이론적 증명에 초점을 맞추지 않았다.계산의 책과 수학 예술에 관한 아홉 장은 일상생활에서 ^[18]사용될 수 있는 많은 실제적인 예를 제공한다.

쑨수

선서( the書)는 190개의 대나무 ^[19]조각에 쓰여진 약 7000자의 수학에 관한 고대 중국 문헌이다.1984년 고고학자들이 후베이(湖北)성 장자산(張家山)에 무덤을 열면서 다른 글들과 함께 발견됐다.이 무덤은 서한 ^[4]초기인 기원전 186년에 폐쇄된 것으로 알려져 있다.9장과의 관계는 아직 학자들에 의해 논의되고 있지만, 그 내용들 중 일부는 분명히 그것과 유사하다.그러나 손술의 본문은 구장보다 훨씬 체계적이지 않고, 여러 ^[19]출처에서 인용된 몇 개의 독립적인 짧은 부분으로 구성되어 있는 것으로 보인다.

계산서에는 수학예술에 ^[19]관한 아홉 개의 장에서 확장될 수 있는 문제에 대한 많은 특전이 포함되어 있습니다.Suann sh the shu의 기초 수학의 예로서, 제곱근은 "초과부족을 제수로 결합한다.결손분자에 과잉분모를 곱한 것과 과잉분자에 결손분모를 곱한 것을 취한다.게다가 「계산서」는, 같은 ^[15]오위치법을 사용해 2개의 방정식과 2개의 미지의 시스템을 해결합니다.^[19]

수학 예술에 관한 9장

수학술 9장은 중국의 수학책으로, 가장 오래된 고고학 연대는 서기 179년(전통 기원전 1000년)이지만,^[20] 아마도 기원전 300-200년쯤 되었을 것이다.저자는 알려지지 않았지만 동양에 큰 공헌을 했다.문제는 질문과 ^[17]절차 바로 뒤에 이어지는 질문과 함께 설정됩니다.본문에는 정식 수학적 증명은 없고 단계별 ^[21]절차일 뿐이다.류혜의 해설은 ^[3]본문 안에 주어진 문제들에 대한 기하학적, 대수적 증거를 제공했다.

수예 9장은 중국의 모든 수학 서적 중 가장 영향력 있는 것 중 하나로 246개의 ^[20]문제로 구성되어 있다.그것은 나중에 10개의 컴퓨터 교칙에 통합되었고, 이것은 이후 ^[17]수세기 동안 수리 교육의 핵심이 되었다.이 책은 측량, 농업, 파트너십, 공학, 과세, 계산, 방정식의 해법, 직각 삼각형의 특성에 ^[17]관한 246개의 문제를 포함하고 있다.9장은 호너의 ^[5]방법과 유사한 방식으로 2차 방정식을 푸는 데 중요한 것을 추가했다.그것은 또한 "팡청" 또는 현재 선형 ^[15]대수학으로 알려진 것에 진보적인 기여를 했다.7장은 계산서와 ^[15]유사하게 잘못된 위치 방법을 사용하여 두 개의 미지수를 갖는 선형 방정식의 체계를 푼다.8장에서는 양의 숫자와 음의 숫자를 사용하여 결정 및 불확정 동시 선형 방정식을 풀며, 하나의 문제는 5개의 ^[15]미지수로 4개의 방정식을 푸는 것을 다룬다.9장은 현대의 가우스 제거 및 ^[15]역치환과 유사한 방법을 사용하여 방정식 시스템을 해결합니다.

현대 연주의 기초가 된 구장본은 학자 대진의 노력의 결과다.영락대백과사전에서 직접 문제를 옮겨 적은 그는 원문에 대한 수정 작업을 진행하였고,^[22] 수정의 이면에 대한 자신의 논리를 설명하는 자신의 주석도 포함시켰다.그의 완성된 작품은 1774년에 처음 출판되었지만, 1776년에 여러 가지 오류를 바로잡기 위해 새로운 개정판이 출판되었을 뿐만 아니라, Lui Hui와 Li Chunfeng의 해설을 포함한 남송의 아홉 장의 판본을 포함할 것이다.다이젠의 작품의 최종판은 1777년에 리플 파빌리온이라는 제목으로 나왔고, 이 최종판은 널리 배포되어 현대판 구장의 ^[23]표준이 될 것이다.그러나 이 판본은 편집본이 여전히 많은 오류를 포함하고 있고 원본 수정이 모두 대진 자신이 ^[22]한 것은 아니라고 주장하면서 궈수천으로부터 정밀 조사를 받고 있다.

파이 계산

수학 예술에 관한 9장의 문제들은 원과 구와 관련된 문제들, 예를 들어 구형 ^[20]표면적과 같은 문제들을 계산할 때 파이가 3과 같다는 것을 받아들인다.파이를 3으로 계산하기 위한 명시적인 공식은 본문 내에 없지만, 그것은 ^[16]같은 시기에 제작된 수학 예술에 관한 아홉 장과 인공의 기록의 문제 전반에 걸쳐 사용된다.역사학자들은 ^[20]원둘레와 지름 사이의 3:1 관계를 사용하여 원주율을 계산했다고 믿는다.파이를 3.154로 ^[4]추정하는 류신과 같은 일부 한족 수학자들은 이 숫자를 개선하려고 시도했다.나중에 Liu Hui는 파이를 3.141024(낮은 추정치)로 계산하여 계산을 개선하려고 했습니다.류는 6각형 안에 있는 폴리곤을 ^[24]원에 비해 낮은 한계로 사용하여 이 숫자를 계산했다.주종지는 24,576개의 변을 가진 다각형을 사용하여 나중에 파이의 계산은 3.1415926 < < 3.1415927이라는 것을 알아냈다.이 계산은 16세기 ^[25]동안 유럽에서 발견될 것이다.

그가 이 ^[4]견적을 어떻게 계산했는지에 대한 명시적인 방법이나 기록은 없다.

분할 및 루트 추출

덧셈, 뺄셈, 곱셈, 나눗셈과 같은 기본적인 산술 과정이 한나라 ^[4]이전부터 존재했다.수학예술에 관한 9장은 이러한 기본적인 연산을 당연하게 여기며 단순히 독자들에게 그것들을 ^[15]수행하도록 지시한다.한 수학자는 제곱근과 세제곱근을 나눗셈과 비슷하게 계산하고, 나눗셈과 뿌리뽑기 문제는 수학술 ^[26]9장 4장에서 모두 발생한다.숫자의 제곱근과 세제곱근의 계산은 나눗셈과 같은 연속적인 근사치를 통해 이루어지며,^[5] 종종 프로세스 전체에서 배당(si)과 제수(fa)와 같은 유사한 용어를 사용합니다.이 연속 근사 프로세스는 호너의 [5]방법과 유사한 방법을 사용하여 x${\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle a}$ ${\displaystyle =}$ {\$displaystyle$ x$^{2}+a=b$와 같은 2차 및 3차 4차 방정식을 푸는 것으로 확장되었다.이 방법은 한나라 때 N차 4차 방정식을 풀기 위해 확장되지 않았지만, 결국 이 ^[5]방정식을 풀기 위해 사용되었다.

선형 대수

계산서는 두 ^[15]개의 미지의 방정식을 푸는 최초의 알려진 텍스트이다.계산서에는 잘못된 위치법으로 방정식을 푸는 것과 관련된 총 세 가지 문제가 있는데, 이것은 다시 실용적인 ^[15]용어로 표현된다.수학술 9장의 7장은 또한 두 개의 미지수를 갖는 두 개의 방정식의 체계를 잘못된 위치법으로 ^[15]푸는 것을 다룬다.미지의 두 가지 중 더 큰 부분을 해결하기 위해, false position method는 독자에게 ^[15]mu라는 큰 항 또는 zi(초과 및 결손에 대해 주어진 값)를 교차 곱하도록 지시한다.미지의 두 가지 중 작은 것을 해결하려면 단순히 작은 항을 ^[15]합산하면 됩니다.

수학예술에 관한 9장 중 8장은 무한 ^[15]미지의 무한 방정식을 푸는 것을 다룬다.이 과정은 ^[15]장 전체에서 "팡청 절차"라고 합니다.많은 역사학자들은 팡청이라는 용어의 의미에 대한 상반된 증거 때문에 번역되지 않은 채로 두기로 결정했다.오늘날 많은 역사가들이 그 단어를 선형대수로 번역한다.이 장에서는 많은 미지의 ^[15]방정식 시스템을 풀기 위해 가우스 제거 및 역치환 프로세스를 사용합니다.문제는 계수판에서 이루어졌고 음수뿐만 아니라 ^[15]분수 사용도 포함되었습니다.카운팅 보드는 사실상 하나의 방정식의 첫 번째 변수이고 마지막 ^[15]변수가 되는 행렬이었다.

류후이(劉')의 수학술 9장 해설

류후이(劉')의 수학예술 9장에 대한 해설은 원문의 가장 오래된 ^[20]판본이다.후이는 대부분 한나라 직후에 수학자로 여겨진다.그의 논평에서, Hui는 대수적 ^[18]또는 기하학적 관점에서 몇 가지 문제들을 검증하고 증명했다.예를 들어, 수학 예술에 관한 9개의 장에 걸쳐, 원이나 ^[16]구에 관한 문제에서 파이의 값은 3과 같은 것으로 여겨진다.Liu Hui는 그의 논평에서 ^[16]탈진법을 사용하여 파이의 더 정확한 추정치를 찾아냅니다.이 방법은 결국 고차 다각형 면적이 원의 ^[16]면적과 동일하도록 원 안에 연속 다항식을 만드는 것을 포함한다.이 방법에서 류후이는 파이 값이 약 3.14라고 ^[4]단언했다.류후이(劉 also)는 또한 그리스 방식과 유사한 정사각형과 입방체 근추출의 기하학적 증거를 제시했는데, 이는 어떤 선이나 단면에서 정사각형이나 입방체를 자르고 나머지 ^[26]직사각형의 대칭을 통해 제곱근을 결정하는 것을 포함한다.

분열기 수학

3세기에 류후이(劉 wrote)는 9장에 대한 해설을 썼고, 피타고라스의 정리(이미 9장으로 알려져 있음)를 이용한 해다오 선징(海田 su京)과 측량 3중, 4중 삼각측량을 다룬 해다오 선징(ida多an)을 저술했다. 그의 수학측량 업적은 서양에서 달성한 것보다 천 ^[27]년 이상 높았다.그는 algorithm 알고리즘으로 =3.1416을 계산한 최초의 중국 수학자였다.그는 실린더의 부피에 대한 정확한 공식을 찾기 위해 카발리에리 원리의 사용을 발견했고, 기원후 3세기 동안 극소 미적분의 요소들을 발전시켰다.

4세기에, 또 다른 영향력 있는 수학자 Zu Chongzhi가 Da Ming Li를 소개했습니다.이 달력은 특정 기간 동안 발생할 많은 우주론적 주기를 예측하기 위해 특별히 계산되었습니다.그의 삶에 대해 알려진 것은 거의 없다.오늘날, 유일한 출처는 수서이며, 우리는 이제 주종지가 수학자 세대 중 한 명이었다는 것을 안다.그는 12288곤에 적용된 류후이(劉')의 파이알고리즘을 사용하여 이후 900년 동안 사용 가능한 가장 정확한 소수점 7자리(3.1415926~3.1415927 사이)의 파이 값을 구했다.그는 또한 천문학 및 수학적 작업에서 분수를 사용하여 무리수를 근사하는 것에 He Chengtian의 보간법을 적용하였고, 그는 파이에 근사한 분수로 $355 113$을 ${\displaystyle \frac{\mathrm{얻었습니다}}{}}$; 요시오 미카미는 그리스인, 힌두교도, 아랍인 모두 이 분수에 대해 알지 못했습니다$.$1585년 네덜란드 수학자 아드리안 안토니스줌이 이를 재발견할 때까지 파이로의 위상은 "따라서 중국인들은 ^[28]유럽보다 앞선 천년 동안 모든 분수 값 중 가장 특이한 것을 가지고 있었다."

주종지는 그의 아들 주겅과 함께 카발리에리의 원리를 적용하여 구체의 부피를 계산하기 위한 정확한 해답을 찾아냈다.구체의 부피에 대한 공식을 포함하는 것 외에도, 그의 책은 또한 입방정식의 공식과 정확한 파이 값을 포함했다.송나라 때 그의 작품인 '주서'는 수학요목에서 버려져 없어졌다.많은 사람들은 Zhui Shu가 선형, 행렬 대수, θ의 값을 계산하는 알고리즘, 구체의 부피에 대한 공식 등을 포함하고 있다고 믿었다.이 텍스트는 또한 우리의 현대 수학과 유사하게 지식을 포함하는 그의 천문학적인 보간법과도 연관되어야 한다.

서기 200년에서 400년 사이의 Sunzi 수학 고전이라고 불리는 수학 설명서는 막대 세기를 사용한 곱셈과 나눗셈 알고리즘에 대한 가장 자세한 단계별 설명을 포함하고 있다.흥미롭게도, Sunzi는 장소-가치 체계와 장소-가치 체계 그리고 서양의 관련 갤리 부서의 발전에 영향을 미쳤을지도 모른다.유럽의 자료들은 13세기에 알-크와리즈미의 9세기 초 라틴어 번역으로부터 장소 가치 기술을 배웠다.Khwarizmi의 프레젠테이션은 문체적인 문제(예를 들어 후행 0을 나타내기 위해 빈 공간을 사용)에 관해서도 Sunzi의 나눗셈 알고리즘과 거의 동일하다; 유사성은 결과가 독립적인 발견이 아닐 수 있음을 시사한다.알-크와리즈미의 작품에 대한 이슬람 평론가들은 그것이 주로 힌두교의 지식을 요약한 것이라고 믿었다; 알-크와리즈미의 출처를 인용하지 않은 것은 그 출처가 차례로 ^[29]중국으로부터 절차를 배웠는지 아닌지를 결정하는 것을 어렵게 한다.

5세기에 "장취지안 쑤안징"이라는 매뉴얼은 선형 방정식과 이차 방정식을 논의했다.이때쯤 중국인들은 음수라는 개념을 갖게 되었다.

당 수학

당나라 때 수학 공부는 대학교에서 상당히 표준적이었다.십계통(十 ten通)은 중국 당나라 초기 수학자 이춘봉(李春李, 602~670)이 수학 시험을 위한 공식 수학 교재로 편찬한 10개의 수학 작품을 모은 것이다.수나라와 당나라가 '계산학원'^[30]을 운영했다.

왕샤오통(王小通)은 당나라 초기의 위대한 수학자로, 일반 입방정식이 최초로 등장하는^[31] 수치해법을 쓴 《고대 수학의 연속》을 저술하였다

티베트인들은 630년 ^[32][33]사망한 남리 스롱방탄 치세 때 중국에서 수학(산수)에 대한 첫 지식을 얻었다.

인도 수학자 아랴바타의 사인표는 서기 718년 당나라 ^[34]때 편찬된 중국 수학책으로 번역됐다.비록 중국인들이 입체 기하학, 이항 정리, 그리고 복잡한 대수 공식과 같은 수학의 다른 분야에서 뛰어났지만, 초기 형태의 삼각법은 현대 인도와 이슬람 ^[35]수학에서처럼 널리 인식되지 않았다.

수학자이자 승려인 이싱은 접선표를 계산한 공로를 인정받았다.대신에 초기 중국인들은 청차라고 알려진 경험적 대체물을 사용했고 사인, 탄젠트, 그리고 분초를 사용할 때 평면 삼각법의 실용적인 사용은 ^[34]알려져 있었다.이싱은 그의 천재성으로 유명했고 바둑에서 가능한 포지션의 수를 계산한 것으로 알려져 있다.

송원 수학

북송 수학자 자헌은 제곱근과 입방근을 추출하는 가법 곱셈법을 개발하여 호너 ^[36]법칙을 구현하였다.

송나라와 원나라, 특히 12세기와 13세기에 네 명의 뛰어난 수학자들이 생겨났다.양후이, 진주샤오, 리즈(리예), 주석제.양후이, 진주샤오, 주시제는 모두 600년 전에 호너-루피니법을 사용하여 특정한 종류의 연립 방정식, 근, 2차, 입방정식, 4차 방정식을 풀었다.양후이는 또한 파스칼의 삼각형을 이항 증명과 함께 발견하고 증명한 최초의 사람이기도 하다.한편, Li Zhi는 Tiann Yuan Shù에 기초한 대수기하학의 형태를 조사했다.그의 책; Ceyuan haising은 피타고라스 정리를 사용하는 전통적인 방법 대신 대수학으로 이 기하학 문제를 변화시킴으로써 원을 삼각형으로 새기는 아이디어를 혁신했습니다.이 시대의 궈수징은 정확한 천문 계산을 위해 구면 삼각법도 연구했습니다.수학 역사의 이 시점에서, 많은 현대 서양 수학은 이미 중국 수학자들에 의해 발견되었다.13세기 중국 수학의 르네상스 시대까지 상황은 한동안 조용해졌다.이것은 중국의 수학자들이 18세기까지 유럽이 알지 못했던 방법으로 방정식을 푸는 것을 보았다.이 시대의 정점은 주석제의 두 권의 책인 선서기맹과 사위안위전으로 나타났다.보도에 따르면 그는 가우스의 중심 응축과 동등한 방법을 제공했다고 한다.

진주샤오 (1202년경–1261년)는 ^[37]중국 수학에 0 기호를 도입한 최초의 인물이다.이 혁신 이전에는 ^[38]막대 계수 시스템에 0 대신 공백 공간이 사용되었습니다.진주샤오의 가장 중요한 공헌 중 하나는 고차수 방정식을 푸는 방법이었다.미카미 요시오는 진의 4차 방정식에 대한 해법을 언급하며 "누가 호너의 빛나는 과정이 유럽보다 적어도 6세기 일찍 중국에서 사용되었다는 사실을 부인할 수 있겠는가?"라고 말했다.^[39]진은 또한 10차 ^[40]방정식을 풀었다.

Pascal's triangle was first illustrated in China by Yang Hui in his book Xiangjie Jiuzhang Suanfa (詳解九章算法), although it was described earlier around 1100 by Jia Xian.^[41]1299년 주시제(13세기)가 쓴 계산학 입문에는 중국 대수학에서 새로운 내용은 없었지만 일본 ^[42]수학의 발전에 큰 영향을 미쳤다.

대수학

세위안하이징

Ceyuan haising(중국어: 圓 ha pin pin; 병음:Céyuan Hijijung)은 692개의 공식과 삼각형의 내접원과 관련된 170개의 문제를 모은 것으로, Li Zhi (또는 Li Ye) (1192–1272 AD)에 의해 쓰여졌다.그는 복잡한 기하학 문제를 순수 대수학 문제로 변환하기 위해 천원서를 사용했다.그리고 나서 그는 팬 fa, 즉 호너의 방법을 사용하여 6개의 차수의 방정식을 풀었지만,^[43] 방정식을 푸는 방법을 설명하지는 않았다."1206년 쿠블라이 칸으로부터 벼슬을 제안받았지만 정중하게 거절할 구실을 찾은 베이징의 수학자 리치(또는 리예, 1192–1279)입니다.그의 체위안하이칭(원 측정의 바다거울)에는 다항식 6급으로 이어지는 문제 중 일부를 다루는 170개의 문제가 포함되어 있습니다.그는 그의 방정식 해법을 설명하지는 않았지만, 그것은 추시제나 호너가 사용한 것과 크게 다르지 않았던 것으로 보인다.호너법을 사용한 다른 사람들은 진주소(金九小, 1202년–1261년)와 양회( hui會, 1261년–1275년)이다.

네 명의 미지의 옥거울

시위안위젠(西an ad)은 서기 1303년 주시제에 의해 쓰여졌으며 중국 대수학의 발전의 정점을 나타낸다.하늘, 땅, 사람, 물질이라고 불리는 네 가지 원소는 그의 대수 방정식에서 알려지지 않은 네 가지 양을 나타냈다.이것은 연립 방정식과 14개의 차수 방정식을 다룹니다.저자는 이 방정식을 ^[44]풀기 위해 오늘날 호너의 방법이라고 불리는 부채꼴의 방법을 사용한다.

거울에는 증거 없이 주어진 많은 덧셈 급수 방정식이 있다.다음과 같은 합계 시리즈가 있습니다.^[45]

$\displaystyle 1^{2}+2^{2}+3^{2}+\cdots +n^{2}={n(n+1)(2n+1)\over 3!}}$

${\displaystyle 1+8+30+80+\cdots + {n^{2}(n+1)(n+2)\over 3!}={n(n+1)(4n+1)\over 5!}}$

9개 섹션의 수학 논문

수서창은 부유한 총독이자 장관인 진추소(陳u小, 1202년경~1261년경)가 쓴 것으로 동시 합치 풀이법의 발명과 함께 중국의 부정 ^[43]분석의 절정을 이룬다.

마법의 사각형과 마법의 서클

가장 먼저 알려진 3보다 큰 순서의 마법 정사각형은 ^[46]10개 이상의 순서의 마법 정사각형으로 작업한 양희(1261년–1275년)에 기인한다.그는 또한 마법의 서클과 함께 일했다.

삼각법

중국의 삼각법의 태동 상태는 송 왕조(960–1279) 동안 서서히 변화하고 발전하기 시작했고, 송 왕조(960–1279)는 중국의 수학자들이 달력 과학과 천문 ^[34]계산에서 구면 삼각법의 필요성을 강조하기 시작했다.박식한 중국의 과학자, 수학자 그리고 관리인 Shen Kuo (1031–1095)는 화음과 ^[34]호의 수학 문제를 풀기 위해 삼각함수를 사용했습니다.Victor J. Katz는 Shen의 공식에서 s = c + 2v²/d의 원호 근사치를 만들었다고 썼다. 여기서 d는 직경, v는 베르사인, c는 ^[47]호를 따르는 현 c의 길이이다.Sal Restivo는 원의 호 길이에 대한 Shen의 연구가 수학자이자 천문학자 Guo Shoujing (1231–1316)^[48]에 의해 13세기에 개발된 구면 삼각법의 기초를 제공했다고 쓰고 있다.역사학자 L. Gauchet과 Joseph Needham이 말했듯이, Guo Shoujing은 달력 체계와 중국 ^[34][49]천문학을 개선하기 위해 구면 삼각법을 계산에서 사용했습니다.17세기 후반의 궈의 수학적 증거에 대한 중국 삽화와 함께 니덤은 다음과 같이 말한다.

궈는 사각형 구형의 피라미드를 사용했는데, 이 피라미드는 하나의 적도 호와 하나의 황도 호로 구성되어 있고, 두 개의 자오선 호가 있고, 그 중 하나는 하지점을 통과하고...이러한 방법을 통해 그는 황도의 정도에 대응하는 적도의 도, 지차(황도 호에 대한 현의 값) 및 차루(호 사이의 현의 ^[50]1도 차이)를 얻을 수 있었다.

심과 궈의 삼각법 연구의 업적에도 불구하고, 중국 관리이자 천문학자 쉬광치 (1562–1633)와 이탈리아 예수회 마테오 리치 (1552–1610)^[51]에 의한 유클리드 원소의 이중 출판과 함께 1607년까지 중국 삼각법에서의 또 다른 실질적인 연구가 다시 출판되지 않을 것이다.

명 수학

원나라가 멸망한 후 중국은 몽골이 좋아하는 지식을 의심하게 되었다.법원은 식물학과 약리학으로 수학과 물리학을 외면했다.과거사에는 수학이 거의 포함되어 있지 않았고, 그것이 무엇을 포함했는지는 최근의 발전을 무시했다.Martzloff는 다음과 같이 쓰고 있습니다.

16세기 말, 중국인들이 알고 있는 자기중심 수학은 거의 아무것도 아니었고, 17세기와 18세기에는 유럽 과학계의 혁명적인 진보와 비교할 수 있는 것이 없었다.게다가 이 시기에는 중국인들이 그것에 대해 단편적인 지식밖에 가지고 있지 않았기 때문에 아무도 더 먼 과거에 무슨 일이 일어났는지 보고할 수 없었다.중국 자체에서는 18세기 ^[52]마지막 4분의 1 이전까지는 자기연수가 대규모로 재발견되지 않았다는 것을 잊어서는 안 된다.

이에 따라 고잉샹이나 탕순즈 같은 저명한 수학자들은 톈위안수([53]天元水) 방식을 몰랐던 것으로 보인다.구두로 설명하는 대화자가 없으면 텍스트는 순식간에 이해할 수 없게 되었고, 더 나쁜 것은 대부분의 문제를 보다 기본적인 방법으로 해결할 수 있었다는 점이다.보통 학자들에게는 톈위안은 숫자학처럼 보였다.오징은 역대 왕조의 모든 수학 작품을 '수예 9장 계산 주석'으로 정리할 때 천원서와 증배법을 ^{[54][failed verification]}생략했다.

대신, 수학적 진보는 계산 도구에 집중되었다.15세기에 주판은 선안팬의 형태가 되었다.사용 및 휴대가 간편하고 빠르고 정확하여 로드 미적분을 제치고 선호하는 계산 형태가 되었습니다.주판을 통한 산술 계산인 Zhusuan은 많은 새로운 작품에 영감을 주었다.청다웨이가 1592년에 펴낸 17권짜리 작품인 쑤안파통종은 300년 ^[55]넘게 사용되고 있다.정왕 주자이는 81자리의 주판을 이용해 2~25자리의 제곱근과 입방근을 계산해 등온계를 발전시켰다.

막대 세기에서 주판으로의 전환은 계산 시간을 줄일 수 있었지만, 중국 수학의 정체와 쇠퇴로 이어졌을 수도 있다.계수판에 있는 막대 숫자의 패턴이 풍부한 레이아웃은 분수의 교차 곱셈 원리, 선형 방정식을 푸는 방법 등 많은 중국의 수학 발명품에 영감을 주었습니다.마찬가지로, 일본의 수학자들은 행렬의 개념에 대한 정의에서 계수봉의 숫자 배치에 영향을 받았다.주판알고리즘은 비슷한 개념적 진보로 이어지지 않았다.(물론 이 구별은 현대적이다.20세기까지 중국 수학은 컴퓨터 과학뿐이었다.)^[56]

16세기 후반, 마테오 리치는 궁정에서 지위를 확립하기 위해 서양의 과학 작품을 출판하기로 결정했다.서광기의 도움으로, 그는 고전 불교 ^[57]경전을 가르치던 것과 같은 기술을 사용하여 유클리드 원소를 번역할 수 있었다.다른 선교사들은 중국 ^[58]전통에서 무시되었던 특수 함수(트리거메트리, 로그)에 대한 서양의 작품들을 번역하면서 그의 사례를 따랐다.하지만, 현대의 학자들은 해결된 문제가 아니라 증거에 중점을 두고 있는 것을 당혹스럽게 여겼고, 대부분은 고전적인 텍스트만으로 ^[59]작업을 계속했다.

청나라

예수회로부터 서양의 수학을 배우고 외부의 지식과 사상에 개방된 강희제 시절, 중국 수학은 짧은 기간 동안 공식적인 지지를 ^[60]받았다.강희의 지시로, 메이거청과 다른 세 명의 뛰어난 수학자들은 서양의 수학 ^[61]지식을 체계적으로 소개한 53권짜리 《수학적 연구의 정수》(1723쇄)를 편찬하였다.동시에 메이고청은 메이시 콩슈 지양도 전개했다.메이시 콩슈 지양은 그 당시 거의 모든 중국 수학 학파의 백과사전 요약본이었지만, 고청의 할아버지 ^[62][63]메이 원딩(1633-1721년)의 문화 간 작품도 포함되어 있었다.이 사업은 서양 수학에 종사하는 중국 수학자들이 ^[64]인용문을 찾는 데 어려움을 덜기 위해 노력했다.

그러나 백과사전이 발간되자마자 영정제가 즉위하였다.영정은 중국 정책에 급격한 반서방적 태도를 취했고, 대부분의 선교사를 궁정에서 추방했다.서양의 교과서와 이해할 수 있는 중국어 교과서를 모두 접하지 못하면서, 중국 수학은 정체되었다.

1773년 건륭제는 시쿠관수(四 qu ()를 편찬하기로 결정했다.대진(1724-1777)은 영락대백과와 한나라와 ^[65]당나라의 다른 수학 작품 몇 가지를 선정하여 교정했다.서원위전, 서원해경 등 송원시대 수학작품이 발견돼 인쇄되면서 새로운 연구 ^[66]물결이 일었다.가장 많은 주석이 달린 작품은 리황의 주장수시카오투슈오(the江水西o)와 뤄시린(^[67]oo林)의 스위안위안시카오(石元-)가 기고했다.

서양의 영향

1840년, 제1차 아편 전쟁은 중국이 문을 열고 바깥세계를 바라보게 했고, 이것은 또한 이전 세기에 비할 수 없는 속도로 서양의 수학 연구들이 유입되게 했다.1852년, 중국의 수학자 Li Shanlan과 영국의 선교사 Alexander Wylie는 이후 9권의 원소와 13권의 ^[68][69]대수학을 함께 번역했다.조셉 에드킨스의 도움으로 천문학과 미적분에 대한 더 많은 연구가 곧 뒤따랐다.중국 학자들은 처음에 신작에 접근해야 할지 망설였다: 서양 지식에 대한 연구가 외국 침략자들에 대한 복종 형태였는가?그러나 20세기 말까지 중국은 서양의 작품들을 통합해야만 주권을 회복할 수 있다는 것이 분명해졌다.(번역된) 서양 선교 학교에서 가르치는 중국 학자서양 문서들, 토착 전통과 빠르게 연락이 끊겼습니다.Martzloff가 언급했듯이, "1911년부터 서양 수학만이 중국에서 ^[70]연습되었다."

근대 중국의 서양 수학

1912년 근대 중국 공화국이 수립된 이후 중국 수학이 크게 부활했다.그 이후로 현대 중국 수학자들은 다양한 수학 분야에서 수많은 업적을 남겼다.

유명한 현대 중국계 수학자는 다음과 같습니다.

• Shiing-Shen Chern은 기하학의 리더이자 20세기의 가장 위대한 수학자 중 한 명으로 널리 간주되었고 그의 엄청난 수학적 ^[71][72]공헌으로 울프상을 받았다.
• Ky Fan은 수학의 다양한 분야에 많은 기본적인 공헌을 했습니다.그의 고정점 이론 연구는 비선형 함수 해석에 영향을 미칠 뿐만 아니라 수리 경제학 및 게임 이론, 잠재 이론, 변분 미적분, 미분 방정식에 광범위하게 적용되었습니다.
• 야우싱둥은 물리학과 수학에 모두 영향을 미쳐 기하학과 이론물리학의 경계에서 활약해 왔으며, 그 공로로 필즈상을 수상했습니다.
• 16세 때 석사학위를 받은 중국 신동 테렌스 타오는 10세 때 처음 출전한 국제수학올림피아드 역사상 최연소 참가자로 동메달, 은메달, 금메달을 땄다.그는 올림픽 역사상 3개의 메달 중 각각 최연소 우승자로 남아 있다.그는 계속해서 필즈상을 받았다.
• 소수 사이의 간격에 대한 최초의 유한한 경계를 확립한 숫자 이론가 이탕 장.
• 충분히 큰 모든 짝수는 2개의 소수, 혹은 소수와 반소수의 합으로 쓰여질 수 있다는 것을 증명한 숫자 이론가인 Chen Jingrun은 현재 Chen의 ^[73]정리라고 불린다.그의 연구는 골드바흐의 추측 연구에 획기적인 사건으로 알려져 있다.

중화인민공화국의 수학

1949년, 중화인민공화국 건국 초기, 정부는 비록 나라가 자금 부족의 곤경에 처했지만 과학의 원인에 많은 관심을 기울였습니다.중국과학원은 1949년 11월에 설립되었다.수학연구소는 1952년 7월에 정식으로 설립되었다.그 후, 중국수학회와 그 창간지들은 복원되고 다른 특별한 저널들을 추가했다.1949년 이후 18년 동안 발표된 논문 수는 1949년 이전 전체 기사 수의 3배 이상을 차지했다.이들 중 상당수는 중국의 과거 공백을 메웠을 뿐 아니라 세계의 선진 ^[74]수준에 도달했다.

문화대혁명의 혼란 속에서 과학은 쇠퇴했다.수학 분야에서는 천징런, 화뤄궁, 장광후 등 수학자들이 연구를 계속하기 위해 고군분투하고 있다.참사 이후 궈모루의 문학 '과학의 봄'이 출간되면서 중국 과학과 수학이 부활했다.1977년 베이징에서 새로운 수학 발전 계획이 수립되고, 수학 학회의 작업이 재개되고, 저널이 재발행되고, 학술지가 발행되고, 수학 교육이 강화되고, 기초 이론 연구가 ^[74]강화되었다.

멱함수 체계 방향에서 중국 수학자의 중요한 수학적 업적은 1988년 샤즈훙이 어떻게 페인리브 추측을 증명했는가이다.N개 천체의 초기 상태가 있을 때, 한 천체는 제한된 시간 내에 무한대 또는 속도로 달렸습니다.무한대에 도달했습니다. 즉, 충돌하지 않는 특이점이 있습니다.Painleve 추측은 1895년에 제안된 권력 시스템 분야에서 중요한 추측이다.4체 문제에 대한 매우 중요한 최근 발전은 2013년 ^[75]경에 Xue Jinxin과 Dolgopyat이 4체 시스템의 단순화된 버전에서 비충돌 특이점을 증명했다는 것이다.

게다가 2007년, Shen Weixiao와 Kozlovski, Van-Strien은 리얼 파투 추측을 증명했다: 리얼 쌍곡 다항식은 고정된 차수의 실제 다항식 공간에서 밀도가 높다.이 추측은 1920년대에 파투로 거슬러 올라갈 수 있고, 나중에 스메일이 1960년대에 그것을 제시했습니다.실제 파투 추측의 증거는 지난 10년간 ^[75]등각역학에서 가장 중요한 발전 중 하나이다.

IMO에서의 퍼포먼스

중국은 국제수학올림피아드 참가국과 비교했을 때 팀 성적이 가장 높고 IMO 전체 멤버 금상을 가장 ^[76]많이 수상했다.

수학 교재

주나라

저우비 쑤안징(周 suan) 기원전 1000년

• 천문학 이론 및 계산 기술
• 피타고라스 정리의 증명(상고정리)
• 분수 계산
• 천문학적 목적을 위한 피타고라스 정리

기원전 1000년 수학예술 9장?– 50 CE

• ch.1, 계산 알고리즘, 평면도형 영역, GCF, LCD
• 2장, 비율
• ch.3, 비율
• ch.4, 제곱근, 입방근, 알 수 없는 항목 찾기
• ch.5, 파이의 부피와 사용 3
• ch.6, 비율
• ch,7, 결정 방정식
• 8장, 가우스 제거 및 행렬
• 9장, 피타고라스 정리 (구구정리)

한나라

숫자와 계산에 관한 책 202 BC-186 BC

• 다양한 3차원 형상의 부피 계산
• 직사각형의 알 수 없는 변, 주어진 면적 및 한 변의 계산
• 근을 찾아 근사 제곱근을 추출하기 위한 거짓 위치 방법 사용
• 다른 유닛간의 변환

교육에서의 수학

중국에서 수학을 배우는 데 사용되는 책에 대한 첫 번째 언급은 2세기(호한주: 24, 862; 35,1207)로 거슬러 올라간다.우리는 마수(Ma Xu)와 정선(127-200)이 둘 다 수학 절차 9장을 공부했다고 한다.C.Cullen은 수학은 의학과 비슷한 방식으로 구두로 가르쳤다고 주장한다.장자산의 선서(à書)의 문체적 특징을 보면, 이 문자는 여러 출처에서 취합된 후 ^[77]성문화 과정을 거쳤음을 알 수 있다.

「 」를 참조해 주세요.

• 중국 천문학
• 수학의 역사
  • 인도 수학
  • 이슬람 수학
  • 일본 수학
• 중국의 발견 목록
• 중국의 수학자 목록
• 중국 문화에서의 숫자

레퍼런스

인용문

원천

• Boyer, C. B. (1989). A History of Mathematics. rev. by Uta C. Merzbach (2nd ed.). New York: Wiley. ISBN 978-0-471-09763-1. (1991년판).ISBN 0-471-54397-7)
• Dauben, Joseph W. (2007). "Chinese Mathematics". In Victor J. Katz (ed.). The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. ISBN 978-0-691-11485-9.
• 착륙선, 브라이언"중국 초기 하천 제방의 국가 관리: 중부 양쯔 지역의 환경 역사에 대한 새로운 자료"동파오 100.4-5 (2014): 325~62.
• Martzloff, Jean-Claude (1987). A history of chinese mathematics (PDF). Translated by Wilson, Stephen S. Berlin: Springer. p. 4. doi:10.1007/978-3-540-33783-6. ISBN 9783540337836. OCLC 262687287. Retrieved 1 December 2018.
• Needham, Joseph (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books, Ltd.

퍼블릭 도메인

• 이 기사는 1911년에 출판된 휴 치솔름의 브리태니커 백과사전: 예술, 과학, 문학 및 일반 정보 사전, 제26권의 텍스트를 포함하고 있으며, 현재는 미국의 공공 영역이다.
• 이 기사는 1907년 출판된 William Woodville Rockhill, Ernst Leumann, Bunyu Nanjio에 의해 번역된 Bkah-hgyur와 Bstan-hgyur의 티베트 작품에서 파생된 붓다의 생애와 그의 주문 초기 역사를 포함하고 있다. 미국

외부 링크

• 초기 수학 교재(중국어) - 중국어 교재 프로젝트
• 중국어 수학의 개요
• 한대를 통한 중국 수학
• 주석제의 수학 입문