산 해리 상수
Acid dissociation constant| 산과 염기 |
|---|
 |
| 산 타입 |
| 베이스 타입 |
산해리상수a K(산도상수 또는 산이온화상수라고도 함)는 용액 중 산의 강도를 정량적으로 측정하는 값이다.그것은 화학반응의 평형상수이다.
해리 상수는 다음과 같이 정의됩니다[note 2].
여기서 대괄호 안의 양은 평형 [note 3][2]상태에 있는 종의 농도를 나타낸다.
이론적 배경
산에 대한 산 해리 상수는 해리 반응의 기본 열역학의 직접적인 결과이며, pKa 값은 반응에 대한 표준 깁스 자유 에너지 변화에 정비례합니다.pK의a 값은 온도에 따라 변화하며, 르 샤텔리에의 원리에 따라 질적으로 이해할 수 있다. 즉, 반응이 흡열성일 때a K는 증가하고 pK는a 온도가 상승함에 따라 감소한다. 발열성 반응의 경우 그 반대이다.
pK의a 값은 또한 많은 방법으로 산의 분자 구조에 의존한다.예를 들어 Pauling은 폴리프로틴산 연속 pK에a 대한 규칙(아래 폴리프로틴산 참조)과 =O 및 -OH 그룹의 수에 따라 산소산의 pK를a 추정하는 규칙(아래 pKa 값에 영향을 미치는 요인 참조) 두 가지를 제안했다.산 해리 상수의 크기에 영향을 미치는 다른 구조적 요인으로는 유도 효과, 중합체 효과 및 수소 결합이 있습니다.해밋형 방정식은 pK의a [3][4]추정에 자주 적용되어 왔다.
용액 내 산과 염기의 정량적 거동은 pKa 값이 알려진 경우에만 이해할 수 있다.특히 모든 산과 염기의 분석농도와 pK값을a 알고 있을 때 용액의 pH를 예측할 수 있으며, 반대로 pH를 알고 있을 때 용액의 산과 염기의 평형농도를 계산할 수 있다.이러한 계산은 화학, 생물학, 의학 및 지질학의 다양한 분야에 적용됩니다.예를 들어 약산 또는 염기로 약산 또는 염기가 많이 사용되며, 이 pKa 값에 대한 지식은 옥탄올-수분할계수와 함께 혈류에 들어가는 정도를 추정하는데 사용할 수 있다.산해리 상수는 물의 산도가 기본적인 역할을 하는 수중 화학과 화학 해양학에서도 필수적이다.살아있는 유기체에서 산염기 항상성과 효소 역학은 세포와 체내에 존재하는 많은 산과 염기의 pKa 값에 의존한다.화학에서 pKa 값에 대한 지식은 완충용액의 제조에 필요하며, 또한 복합체를 형성하기 위한 산이나 염기와 금속 이온 간의 상호작용을 정량적으로 이해하기 위한 전제 조건이다.실험적으로 pKa 값은 전위차(pH) 적정으로 결정할 수 있지만 pKa 값이 약 2개 미만 또는 약 11개 이상인 경우에는 pH 측정이 현실적으로 어렵기 때문에 분광광도 측정 또는 NMR 측정이 필요할 수 있다.
정의들
아레니우스의 원래 분자 정의에 따르면, 산은 수용액에서 분해되어 수소 이온+ H(양성자)[5]를 방출하는 물질이다.
- HA a− A + H+
이 해리 반응에 대한 평형 상수는 해리 상수로 알려져 있다.해방된 양성자는 물 분자와 결합해 하이드로늄(또는 옥소늄) 이온3+ HO(나체 양성자는 용액에 존재하지 않음)를 생성한다.그래서 아레니우스는 나중에 해리가 산염기 반응으로 기록되어야 한다고 제안했다.
- HA + HO2 a− A + HO3+
Brönsted와 Lowry는 이를 양성자 교환 [6][7][8]반응으로 더욱 일반화했다.
- 산 + 염기 ⇌ 켤레 염기 + 켤레산.
산은 양성자를 잃고 켤레 염기를 남긴다; 양성자는 염기로 전달되어 켤레산을 생성한다.산성 HA 수용액의 경우 염기는 물, 켤레 염기는− A, 켤레산은 하이드로늄 이온이다.브뢴스테드-로우리 정의는 디메틸 술폭시드와 같은 다른 용매에 적용됩니다. 용매 S는 염기로 작용하여 양성자를 수용하고 켤레산+ SH를 형성합니다.
- HA + S a− A + SH+
용액화학에서는 용매에 관계없이 용매화된 수소이온의 약자로 H를 사용하는+ 것이 일반적이다.수용액+ 중 H는 [9][10]양성자가 아닌 용해된 하이드로늄 이온을 나타낸다.
산 또는 염기를 "공역"으로 지정하는 것은 상황에 따라 다릅니다.염기 B의 결합산+ BH는 다음과 같이 분해된다.
- BH+ + OH− † B + HO2
이것은 균형과 반대되는 것이다.
- HO2(산) + B(염기) oh−+ OH(공역염기) + BH(공역산).
잘 알려진 염기인 수산화 이온− OH는 여기서 산성수의 켤레 염기 역할을 합니다.따라서 산과 염기는 각각 양성자의 공여체와 수용체로 간주됩니다.
산 해리의 보다 넓은 정의는 물 분자의 분열에 의해 양성자가 생성되는 가수분해를 포함한다.예를 들어 붕산(B(OH))3은 양성자 [11]공여자인 것처럼 HO를 생성하지만3+, 이는 가수분해 [12]평형 때문이라는 것이 라만 분광법에 의해 확인되었다.
- B(OH)3 + 22 HO b B(OH)4− + HO3+.
마찬가지로 금속 이온 가수분해는 [Al(HO2)]63+와 같은 이온을 [13]약산으로 작용시킨다.
- [알(HO2)]63+ + 호2 [ [알3+(HO2)(5OH)]2+ + 호
루이스의 원래 정의에 따르면, 산은 전자쌍을 받아들여 좌표 공유 [14]결합을 형성하는 물질이다.
평형 상수
산 해리 상수는 평형 상수의 특별한 예이다.희석 용액에서 모노프로톤산인 HA의 해리는 다음과 같이 표시될 수 있다.
- HA a− A + H+
열역학적 평형 상수 {\ K}}는 다음과 같이 정의할[15] 수 있습니다.
여기서 {X}는 화학종 의 평형상태에서의 활성을 나타낸다. K 활성은 차원적이지 않으므로 차원적이지 않다.해리 생성물의 활성은 분자에 배치되고, 반응물의 활성은 분모에 배치된다.이 식에 대한 파생은 활성 계수를 참조하십시오.
활성은 집중력 및 활성계수(γ)의 산물이므로 정의는 다음과 같이 작성될 수 있다.
활성의 복잡함을 피하기 위해 가능한 한 이온 강도가 높은 매체, 즉가 항상 [15]일정하다고 가정할 수 있는 조건에서 해리 상수를 구한다.예를 들어, 배지는 0.1 몰(M) 질산나트륨 용액이나 과염소산칼륨 3 M 용액일 수 있다.이런 가정 하에
누적 및 단계적 상수
β(\로 되는 누적 평형 상수는 K K로 표시되는 단계적 상수의 곱과 관련된다. 2염기산의 경우 단계적 상수와 전체 상수의 관계는 다음과 같다.
금속-리간드 복합체 형성의 맥락에서, 금속 복합체 형성을 위한 평형 상수는 일반적으로 연관 상수로 정의됩니다.이 경우, 배위자 양성자화를 위한 평형 상수도 연관 상수로 정의된다.연관상수 번호는 해리상수 번호의 역수입니다.이 에서는 log 1 a {\ _}=\
연관 및 해리 상수
산의 성질을 논할 때 평형 상수를 K로 나타내는a 산 해리 상수로 지정하는 것이 일반적이며, 기호는 pK이다a.
한편, 연관 상수는 기저값으로 사용됩니다.
그러나 실험 데이터로부터 평형 상수 값을 도출하는 데 사용되는 범용 컴퓨터 프로그램은 산과 염기 모두에 대한 연관 상수를 사용합니다.금속-배위자 복합체에 대한 안정성 상수는 항상 연결 상수로 지정되기 때문에, 배위자 양성자화는 연결 [15]반응으로도 지정되어야 합니다.정의는 산 해리 상수의 값이 대응하는 연관 상수 값의 역수임을 보여준다.
- Kdissoc = 1 / Kassoc
- logdissoc K = -logassoc K
- pKdissoc = 로그assoc K
메모들
- 특정 산 또는 염기 pKa + pKb = pK에w 대하여 물의 자가 이온화 상수.
- 초분자 복합체 형성을 위한 연관 상수는 K로 표시될a 수 있다. 이 경우, "a"는 "산"이 아니라 "관련"을 의미한다.
- 다단백산의 경우 단계적 연관 상수의 번호는 해리 상수의 번호 지정과 반대입니다.예를 들어 인산(아래 #폴리프로틴산 상세)의 경우
온도 의존성
모든 평형 상수는 van't Hoff[17] 방정식에 따라 온도에 따라 달라진다.
R은 기체 상수이고 T는 절대 온도입니다.따라서 발열반응의 경우 표준 엔탈피 변화량인 H \ \ H는 음이 되며 K는 온도에 따라 감소한다.흡열반응은 δ {\ H}}이 양성이며 K는 온도에 따라 증가한다.
키르히호프의 열화학 법칙에 따르면 반응의 표준 엔탈피 변화는 그 자체로 온도의 함수입니다.
치수
식에서
K는a 집중력 차원으로 보입니다., δ G - K \ G=- K이므로 K(\K는 물리치수를 가질 수 없다.이 명백한 역설은 다양한 방법으로 해결될 수 있다.
- 활동계수의 몫이 1이라고 가정하면 K(\K)는 열역학 K K와 같은 수치이다.
- 각 농도값을 비율 c/c로0 표현한다. 여기서0 c는 [hypotical] 표준상태의 농도이며,[18] 정의상 수치는 1이다.
- 몰 분율 척도로 농도를 표현한다.몰 분율은 차원이 없기 때문에, 정의상, 농도의 몫은 순수수가 될 것이다.
절차 (1)과 (2)는 평형 상수에 대해 동일한 수치를 제공한다.또한 농도 i는 몰 }) 및 에 단순히 비례하기 때문에
생화학에서는 계산에 사용된 농도 값의 척도, 밀리몰(M) 또는 마이크로몰(μM)을 나타내기 위해 예를 들어 "Ka = 30 mM"과 같은 치수의 값을 인용하는 것이 일반적이다.
강한 산과 염기
산은 분해되지 않은 종의 농도가 너무 낮아 [6]측정할 수 없을 때 "강"으로 분류된다.pKa 값이 0보다 작은 수산은 거의 완전히 탈양성되며 [19]강산으로 간주됩니다.이러한 모든 산은 양자를 물로 옮기고 용매 양이온 종(수용액에서 HO)을3+ 형성하여 기본적으로 동일한 산도를 가지며, 용매 [20][21]레벨링이라고 알려진 현상을 가집니다.이들은 해리 생성물과 평형 상태인 미분리산의 양이 검출 한계 미만이기 때문에 수용액에서 완전히 해리된다고 한다.마찬가지로 약 14보다 큰 pK에a 대응하는 관련 상수 pK가b 약 0보다 작은 수성 염기는 OH로− 레벨화되어 강한 [21]염기로 간주된다.
pK 값이 ca. -1.7인 질산은 pH가 [22]1 이상인 수용액에서 강산 역할을 한다.낮은 pH 값에서는 약한 산처럼 작용합니다.
강산에 대한 pKa 값은 이론적인 [23]방법으로 추정되었습니다.예를 들어, 수성 HCl의 pKa 값은 -9.3으로 추정되었습니다.
단프로톤산
K를 정의하는a 식을 재배치하고 pH = -log10[H+]를 대입하면 다음과 같이 된다[24].
이것은 헨더슨-하셀발흐 방정식이며, 여기서 다음과 같은 결론을 도출할 수 있다.
- half-neutralization에서 그 비율.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.border-top:1px 고체}.mw-parser-output .sr-onlyᆪ[A−]/는 경우HA] = 1. log(1) = 0이므로 반중화 시 pH는 수치적으로 pK와a 같습니다.반대로 pH = pK일a 때 HA의 농도는 A의− 농도와 같다.
- 완충영역은 대략적인a pK ± 2 범위에 걸쳐 있다. 완충영역은 pKa ± 1 범위를 벗어나 약하다. pH pa pK - 2에서는 물질이 완전히 양성자화되고 pH pa pK + 2에서는 완전히 해리된다(탈양성자).
- pH를 알고 있는 경우에는 비율을 계산할 수 있습니다.이 비율은 산의 분석 농도와는 무관합니다.
물에서 측정 가능한 pKa 값은 강한 산의 경우 약 -2에서 매우 약한 산(또는 강한 염기)의 경우 약 12까지입니다.
원하는 pH의 완충용액은 약산과 그 켤레 염기의 혼합물로 제조할 수 있다.실제로 이 혼합물은 산을 물에 녹여 필요한 양의 강산 또는 염기를 첨가함으로써 생성될 수 있다.산의 pK와a 분석 농도를 알면 ICE 표를 이용하여 모노프로톤산 용액의 해리 정도와 pH를 쉽게 계산할 수 있다.
폴리프로틴산
폴리프로틴산은 1개 이상의 양성자를 잃을 수 있는 화합물이다.단계적 해리 상수는 각각 단일 양성자의 손실에 대해 정의됩니다.첫 번째 양성자의 해리에 대한 상수는 Ka1, 연속 양성자의 해리에a2 대한 상수는 K 등으로 표시될 수 있다.인산, HPO는34 세 개의 양성자를 잃을 수 있기 때문에 폴리프로틴산의 한 예이다.
평형 pK의 정의와[25] 가치 HPO
3
4 † HPO
2−
4 + H+HPO
2−
4 † HPO2−
4 + H+HPO2−
4 † PO3−
4 + H+
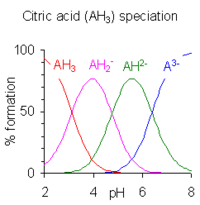
연속되는 pK값의 차이가 약 4개 이상일 때,[26] 이 예에서와 같이 각 종 자체가 산으로 간주할 수 있으며, 실제로 HPO의
2−
4 염은 pH를 약 5.5로 조절하여 용액에서 결정화 될 수 있으며, HPO의2−
4 염은 약 10으로 조절하여 결정화 될 수 있다.종 분포도는 두 이온의 농도가 pH 5.5와 10에서 최대치임을 나타낸다.
연속되는 pK 값의 차이가 약 4 미만이면 평형 상태에 있는 종의 pH 범위 사이에 중복이 있다.차이가 작을수록 겹치는 부분이 많아집니다.구연산의 경우는 오른쪽에 표시되며, 구연산의 용액은 pH 2.5~7.5의 전체 범위에 걸쳐 완충된다.
폴링의 첫 번째 규칙에 따르면 특정 산의 연속 pK 값이 증가한다(pKa2 > pKa1).[27]동일한 원자 상에 둘 이상의 이온화 수소를 가진 산소의 경우 위의 인산 예시와 같이 pKa 값이 제거된 [28][29]양성자마다 약 5 단위씩 증가하는 경우가 많다.
두 번째 양성자가 음전하를 띤 종에서 제거되는 것은 위의 표에서 볼 수 있다.양성자는 양전하를 띠기 때문에 이를 제거하기 위해서는 추가적인 작업이 필요하다.pK가a2 pK보다a1 큰 이유는 추가 전하 분리가 있기 때문입니다.pK가a3 pK보다a2 큽니다.폴링 규칙에 대한 예외가 발견되면 구조에도 큰 변화가 발생하고 있음을 나타냅니다.VO(aq)의2+ 경우 바나듐은 8면체, 6좌표이며 바나듐은 4면체, 4좌표이다.이것은 네 개의 "입자"가 첫 번째 해리와 함께 방출되지만, 두 개의 "입자"만이 다른 해리와 함께 방출된다는 것을 의미하며, 결과적으로 첫 번째 반응에 대한 표준 깁스 자유 에너지 변화에 다른 것보다 훨씬 더 큰 엔트로피 기여가 발생한다.
평형 pKa [VO2(HO2)]4+ § HVO34 + H+ + 2HO2 HVO34 † HVO
2−
4 + H+HVO
2−
4 † HVO2−
4 + H+HVO2−
43−
4 † VO + H+
등전점
용액의 물질에 대해 등전점(pI)은 양전하 종 농도의 총합이 음전하 종 농도의 가중합과 동일한 pH로 정의된다.각 종류별로 1종이 있는 경우에는 pK 값에서 직접 등전점을 구할 수 있다.AH로 정의되는 글리신의 예를 들어보자.고려해야 할 두 가지 해리 평형이 있다.
- AH+
2+ + H; [AH][H+] = K1[AH+
2] - AH− ⇌ A + H+; [A−][H+] = K2[AH]
제2방정식의 [AH]식을 제1방정식으로 대체한다.
- [A−] [H+]2 = KK12[아+
2]
등전점에서는 양전하 종(AH2+)의 농도는 음전하 종(A−)의 농도와 같다.
- [H+]2 = KK12
따라서, cologatrix를 취하면, pH는 다음과 같이 주어진다.
아미노산에 대한 pI 값은 단백질 생성 아미노산에 기재되어 있다.두 개 이상의 하전종이 서로 평형을 이루면 완전한 종분화 계산이 필요할 수 있다.
베이스와 베이직리티
염기에 대한 평형 상수b K는 일반적으로 결합산인 HB를+ 형성하기 위한 염기 B의 양성자화를 위한 결합 상수로 정의된다.
- B + HO2 h+ HB + OH−
이전에 사용한 것과 유사한 추론 사용
K는b 켤레산a K와 관련이 있다.물에서 수산화 이온의 농도 [OH−]는 K = [H][의w+ 수소 이온 농도와 관련이 있다.오−]
[OH−]의 식을 K의b 식에 대입하면 다음과 같이 됩니다.
Ka, Kb, K를w 동일한 온도 및 이온 강도 조건에서 구하면 pKb = pKw - pK가a 된다.25 °C의 수용액에서 pK는w 13.[30]9965이므로
대부분의 실용적인 목적을 위해 충분한 정확성을 가지고.실제로 pK를b [31]pK와a 별도로 정의할 필요는 없지만 pKb 값만 오래된 문헌에서 찾을 수 있는 경우가 많기 때문에 여기서는 pK 값을 정의합니다.
가수분해 금속 이온의 경우, K는b 단계적 해리 상수로 정의될 수도 있다.
이것은 복합체의 형성에 대한 연관 상수의 역수이다.
결합산의 해리 상수로 나타나는 염기성
pKb = pKw - pKa 관계는 수용액에서만 유지되기 때문에(다른 양성용매에도 유사한 관계가 적용되지만), 일반적으로 비수용액을 다루는 유기화학 등의 화학 하위분야에서는 일반적으로 pK를b 염기성 측정값으로 사용하지 않는다.대신 염기성을 정량화할 필요가 있을 때 pK로aH 나타나는 켤레산의 pK를a 인용한다.염기 B와 평형 상태에 있는 그 켤레산+ BH의 경우, 이것은 다음과 같이 정의된다.
pKaH 값이 클수록 베이스가 강해집니다.예를 들어 pKaH(CHN55) = 5.25 및 pKaH(CH32)3N = 10.75 값은 (CH32)3N(트리에틸아민)이 CHN(피리딘)보다55 더 강한 염기임을 나타낸다.
양성 물질
양성 물질은 pH에 따라 산이나 염기로 작용할 수 있는 물질이다.물(아래)은 양성입니다.양성 분자의 또 다른 예는 평형에서 탄산 분자23 HCO의 켤레 염기인 중탄산 이온−
3 HCO이다.
- HCO23 + HO2 h−
3 HCO + HO3+
또한 평형에서의 탄산 이온2−
3 CO의 결합산(반대)
- HCO−
3 + OH− © CO2−
3 + HO2.or
아미노산은 또한 양성자이며 중성분자는 염기성 아미노기가 산성 카르복실기로부터 양성자를 끌어당겨 결합시켜 zwitterion을 형성하는 내부 산염기 평형을 받는다는 합병증을 수반한다.
- NHCHRCOH22 © NHCHRCO+
3−
2
pH가 약 5 미만일 때 카르복실기 및 아미노기 모두 양성자화된다.pH가 증가하면 다음과 같이 산이 분해된다.
- NHCHRCOH+
3
2 nh+
3−
2 NHCHRCO + H+
높은 pH에서는 두 번째 해리가 발생할 수 있습니다.
- NHCHRCO+
3−
2 © NHCHRCO
2−
2 + H+
따라서 아미노산 분자는 양성자화되거나 탈양성자화 될 수 있기 때문에 양성자이다.
물의 자가 이온화
물 분자는 양성자를 얻거나 잃을 수 있다.그것은 양친매라고 알려져 있다.이온화 평형을 기록할 수 있습니다.
- HO2 oh− OH + H+
여기서 수용액에서+ H는 용해된 양성자를 나타낸다.종종 이것은 하이드로늄 이온3+ HO라고 쓰여지지만, 사실 두 개 이상의 물 분자에 의한 용해가 있고 HO, HO73+, HO와 같은52+94+ 종들도 [32]존재하기 때문에 이 공식은 정확하지 않다.
평형 상수는 다음과 같이 주어진다.
용질 농도가 매우 높지 않은 용액에서는 용질에 관계없이 [HO2] 농도는 일정하다고 가정할 수 있다. 그러면 이 식은 다음과 같이 대체될 수 있다.
따라서 물의 자기 이온화w 상수 K는 산 해리 상수의 특별한 경우일 뿐입니다.pK와a 유사한 로그 형식을 정의할 수도 있다.
| T(°C) | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| pKw | 14.943 | 14.734 | 14.535 | 14.346 | 14.167 | 13.997 | 13.830 | 13.680 | 13.535 | 13.396 | 13.262 |
이러한 데이터는 다음과 같은 포물선에 적합할 수 있습니다.
- pKw = 14.94 - 0.04209T + 0.0001718T2.
이 방정식에서 pKw = 24.87°C에서 14입니다.이 온도에서 수소 이온과 수산화 이온의 농도는 모두 10M이다−7.
비수용액 중 산도
용매는 다음과 같은 [34]상황에서 용해된 산성 분자의 이온화를 촉진할 가능성이 더 높습니다.
유기화합물의 pKa 값은 종종 비프로톤 용제 디메틸 술폭시드(DMSO)[34] 및 아세토니트릴(ACN)[35]을 사용하여 구한다.
| 용제 | 기부자[34] 번호 | 유전율[34] |
|---|---|---|
| 아세토니트릴 | 14 | 37 |
| 디메틸설폭시드 | 30 | 47 |
| 물. | 18 | 78 |
DMSO는 물보다 유전율이 낮고 극성이 낮아 무극성 소수성 물질을 더 쉽게 녹이기 때문에 물의 대안으로 널리 사용됩니다.측정 가능한 pKa 범위는 약 1 ~30 입니다.아세토니트릴은 DMSO보다 염기성이 낮기 때문에 일반적으로 산은 약하고 염기는 이 용매에서 강합니다.아세토니트릴(ACN)[36][37][38]과 디메틸설폭시드(DMO)[39]의 25°C에서의 pKa 값은 다음과 같다.물 값은 비교를 위해 포함되어 있습니다.
| HA a− A + H+ | ACN | DMSO | 물. |
|---|---|---|---|
| p-톨루엔술폰산 | 8.5 | 0.9 | 강한. |
| 2,4-디니트로페놀 | 16.66 | 5.1 | 3.9 |
| 안식향산 | 21.51 | 11.1 | 4.2 |
| 아세트산 | 23.51 | 12.6 | 4.756 |
| 페놀 | 29.14 | 18.0 | 9.99 |
| BH+ b B + H+ | ACN | DMSO | 물. |
| 피롤리딘 | 19.56 | 10.8 | 11.4 |
| 트리에틸아민 | 18.82 | 9.0 | 10.72 |
| 프로톤 스펀지 | 18.62 | 7.5 | 12.1 |
| 피리딘 | 12.53 | 3.4 | 5.2 |
| 아닐린 | 10.62 | 3.6 | 4.6 |
산의 이온화는 물보다 산성 용매에서 더 적다.예를 들어 염화수소는 아세트산에 녹았을 때 약한 산이다.이것은 아세트산이 물보다 훨씬 약한 염기이기 때문입니다.
- HCl + CHCOH32 cl− Cl + CHC
3(OH)+
2 - 산+염기γ공역염기+공역산
이 반응을 아세트산이 더 산성인 순수한 황산에[40] 녹았을 때 일어나는 반응과 비교한다.
HSO24 + CHCOH32 h−
4 HSO + CHC
3(OH)+
2
가능성이 희박한 쌍둥이자리 디올 종 CHC
3(OH)+
2는 이러한 환경에서 안정적입니다.수용액의 경우 pH 척도가 가장 편리한 산도 [41]함수이다.비수성 배지에 대한 다른 산도 함수는 제안되었으며, 가장 주목할 만한 것은 초산성 배지에 대한 해밋 산도 함수0 H와 초염기성 [42]배지에 대한 수정 버전 H이다−.
비프로톤성 용매는 잘 알려진 아세트산 이합체 등의 올리고머를 수소 결합에 의해 형성할 수 있다.산은 또한 그 켤레 염기에 수소 결합을 형성할 수 있다.호모결합으로 알려진 이 과정은 결합 염기를 안정화시킴으로써 산의 산성도를 높이고 유효 pKa 값을 낮추는 효과가 있다.호모결합은 아세토니트릴 용액에서 톨루엔술폰산의 양성자 기증력을 약 [43]800배 향상시킨다.
수용액에서는 물이 산보다 결합 염기에 더 강한 수소 결합을 형성하기 때문에 호모 결합이 일어나지 않는다.
혼합 용제
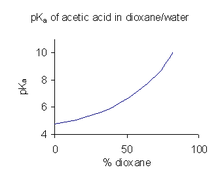
화합물이 물에 용해성이 제한적인 경우(예: 제약업계에서) 물/다이옥산 또는 물/메탄올과 같은 용매 혼합물의 pKa 값을 결정하는 것이 일반적이며, 이 경우 화합물이 더 [45]잘 용해됩니다.오른쪽에 표시된 예에서는 혼합물의 유전율이 감소함에 따라 다이옥산 비율이 증가함에 따라 pKa 값이 가파르게 상승합니다.
혼합용매에서 얻은 pK 값은a 수용액에 직접 사용할 수 없다.그 이유는 용제가 표준 상태에 있을 때 용제의 활성이 하나로 정의되기 때문입니다.예를 들어 혼합비가 9:1인 물: 다이옥산 혼합물의 표준 상태는 용질을 첨가하지 않은 용매 혼합물이다.수용액에 사용할 pKa 값을 구하려면 다양한 공동용매 혼합물에서 얻은 값에서 0 공동용매 농도로 추정해야 한다.
이러한 사실은 일반적으로 pK를a 정의할 때 사용되는 식에서 용제가 누락되어 가려지지만, 주어진 혼합용매에서 얻을 수 있는 pKa 값을 서로 비교할 수 있어 상대적인 산 강도를 얻을 수 있다.DMSO와 같은 특정 비수성 용매에서 얻어진 pKa 값도 마찬가지다.
서로 다른 두 용제의 표준 상태를 비교할 수 있는 알려진 방법이 없기 때문에 산 해리 상수에 대한 일반적인 용제 독립 척도가 개발되지 않았습니다.
pKa 값에 영향을 미치는 요인
폴링의 두 번째 규칙은 공식m XO(nOH)의 산들에 대한 첫 번째 pKa 값은 주로 옥소기 m의 수에 의존하며, 히드록시기 n과 중심 원자 X의 수에 거의 독립적이라는 것이다.pK의a 대략적인 값은 m = 0의 경우 8, m = 1의 경우 2, m = 2의 경우 -3, m [27]= 3의 경우 < -10이다.또는 pKa = 8 - 5m(벨의 [28][46]법칙으로 알려져 있음), pKa = 7 - 5m [29][47]또는 pKa = 9 - 7m [28]등 다양한 수치식이 제안되었다.m에 대한 의존성은 중심 원자의 산화 상태 X: 산화 상태가 높을수록 산소가 강해진다.예를 들어 HClO의 pK는a 7.2, HClO는2 2.0, HClO는3 -1, HClO는4 강산(pKa 0 0)[7]이다.옥소기를 첨가할 때 산도가 증가하는 것은 추가적인 산소 [46]원자에 대한 음전하의 탈국재화에 의한 켤레 염기의 안정화 때문이다.이 규칙은 분자 구조를 할당하는 데 도움이 될 수 있다. 예를 들어, 인산(HPO33)은 2에a 가까운 pK를 가지며, 이는 나중에 NMR 분광법에 의해 확인된 것처럼 구조가 HPO(OH)2이며,[47] 8에 가까운 pK를a 가질 것으로 예상되는 P(OH)3가 아니다.
유기산의 유도 효과와 중합체 효과는 pKa 값에 영향을 미칩니다.아세트산 중의 수소 원자를 보다 전기음성 염소 원자로 치환하는 효과로 간단한 예를 제공한다.치환기의 전자 인출 효과는 이온화를 쉽게 하므로 0, 1, 2, 또는 3 염소 원자가 [48]존재할 경우 연속 pKa 값이 4.7, 2.8, 1.4, 0.7로 감소한다.Hammett 방정식은 [49]치환기의 효과에 대한 일반식을 제공합니다.
- log(Ka) = log(K0
a) + ρ 。
K는a 치환화합물의 해리상수0
a, K는 치환기가 수소일 때의 해리상수, θ는 치환화합물의 특성, θ는 치환기마다 특정값을 가진다.θ에 대한 로그(Ka)의 그래프는 가로채기 로그0
a(K)와 기울기 θ를 갖는 직선이다.이는 log(Ka)가 표준 자유 에너지 변화에 비례하므로 선형 자유 에너지 관계의 예입니다.Hammett은[50] 원래 직교 및 파라 위치에 서로 다른 성분으로 구성된 벤조산 데이터와의 관계를 공식화했다. 일부 수치 값은 Hammett 방정식에 있다.이와 다른 연구를 통해 치환기를 전자 인출력 또는 전자 방출력에 따라 정렬하고 유도 효과와 중합체 효과를 [51][52]구별할 수 있었다.
알코올은 일반적으로 물에서 산으로 작용하지 않지만, OH기와 인접한 이중 결합의 존재는 케토-에놀 호변이성 메커니즘에 의해 pK를a 상당히 감소시킬 수 있습니다.아스코르브산이 이 효과의 한 예이다.디케톤 2,4-펜탄디온(아세틸아세톤)도 케토-에놀 평형 때문에 약한 산이다.OH 치환기를 가진 페놀 등의 방향족 화합물에서는 방향족 고리 전체와의 결합에 의해 탈양성자의 안정성이 크게 향상된다.
구조적 효과도 중요할 수 있습니다.푸마르산과 말레인산의 차이는 전형적인 예이다.푸마르산은 트랜스 이성질체인 (E)-1,4-부트-2-엔디오산이며 말레인산은 대응하는 시스 이성질체, 즉 (Z)-1,4-부트-2-엔디오산이다(cis-trans 이성질체 참조).푸마르산은 약 3.0과 4.5의 pKa 값을 가진다.반면 말레인산은 약 1.5와 6.5의 pKa 값을 가진다.이렇게 큰 차이가 나는 이유는 시스 이성질체(말레인산)에서 하나의 양성자가 제거되면 근처에 남아있는 카르복실기와 강한 분자 내 수소 결합이 형성되기 때문이다.이것은 말레산염+ H의 형성을 선호하고, 그 종에서 두 번째 양성자를 제거하는 것을 반대한다.트랜스 이성질체는 2개의 카르복실기가 항상 멀리 떨어져 있기 때문에 수소 결합이 [53]관찰되지 않는다.
프로톤 스폰지, 1,8-비스(디메틸아미노) 나프탈렌은 pKa 값이 12.1이다.그것은 알려진 가장 강한 아민 염기 중 하나이다.높은 염기성은 양성자화와 강력한 내부 수소 [54][55]결합에 의한 변형 완화로 기인한다.
용매 및 용매화의 효과도 이 절에서 언급해야 합니다.이러한 영향은 위에서 언급한 유전 매체의 영향보다 더 미묘하다는 것이 밝혀졌습니다.예를 들어 methylamines의 염기도, Me3N >의,(메틸 substituents의 전자 효과에 의해)과 기체상에서 관찰된 순서 Me2NH >, MeNH2<>를 사용하여 NH3, 물로 Me2NH하기 위해서 바뀝니다;MeNH2>Me3N<>를 사용하여 NH3.중성 수소 원자의 분자들이 물을 분자로 한 수용체, N–HOH, 상호 작용과 가끔씩만 그냥 노래를 통해 주로 hydrogen-bonded 있다.기증자 결합이2 하나 더 있는데, NH-OH입니다.따라서 메틸기 수에 관계없이 메틸아민은 수화작용에 의해 거의 같은 정도로 안정화된다.이와는 대조적으로 해당 메틸암모늄 양이온은 항상 공여체 NH-OH2 결합에 사용 가능한 모든 양성자를 이용한다.따라서 메틸암모늄 이온의 상대적인 안정화는 메틸기 수가 메틸아민의 [4]물 염기성 순서를 설명함에 따라 감소한다.
열역학
평형 상수는 반응에 대한 표준 Gibbs 에너지 변화와 관련되므로, 산 해리 상수에 대해
R은 기체 상수이고 T는 절대 온도입니다.pKa = -log(Ka) 및 2.120 µ ln(10)이라는 점에 유의하십시오.25°C에서 δG⊖(kJ·mol−1) 5 5.708 pKa(1kJ·mol−1 = 몰당 1000줄).자유 에너지는 엔탈피 항과 엔트로피 [11]항으로 구성됩니다.
표준 엔탈피 변화는 열량 측정 또는 van't Hoff 방정식을 사용하여 결정할 수 있지만 열량 측정 방법이 바람직하다.표준 엔탈피 변화와 산 해리 상수가 모두 결정되면 위의 식에서 표준 엔트로피 변화를 쉽게 계산할 수 있다.다음 표에서는 pK와a δH의⊖ 실험값에서 엔트로피 항을 계산한다.데이터는 결정적으로 선택되었으며 물에서 [11]25°C와 제로 이온 강도를 나타낸다.
| 컴파운드 | 평형 | pKa | δG⊖(kJ−1·[a]mol) | δH⊖(kJ−1·mol) | - TΩS⊖ (kJ·mol−1)[b] |
|---|---|---|---|---|---|
| HA = 아세트산 | HA h+ H + A− | 4.756 | 27.147 | −0.41 | 27.56 |
| HA2+ = 글리신H+ | HA2+ † HA + H+ | 2.351 | 13.420 | 4.00 | 9.419 |
| HA h+ H + A− | 9.78 | 55.825 | 44.20 | 11.6 | |
| HA2 = 말레인산 | HA2 † HA− + H+ | 1.92 | 10.76 | 1.10 | 9.85 |
| HA− h+ H + A2− | 6.27 | 35.79 | −3.60 | 39.4 | |
| HA3 = 구연산 | HA3 † HA2− + H+ | 3.128 | 17.855 | 4.07 | 13.78 |
| HA2− † HA2− + H+ | 4.76 | 27.176 | 2.23 | 24.9 | |
| HA2− a3− A + H+ | 6.40 | 36.509 | −3.38 | 39.9 | |
| HA3 = 붕산 | HA3 † HA2− + H+ | 9.237 | 52.725 | 13.80 | 38.92 |
| HA3 = 인산 | HA3 † HA2− + H+ | 2.148 | 12.261 | −8.00 | 20.26 |
| HA2− † HA2− + H+ | 7.20 | 41.087 | 3.60 | 37.5 | |
| HA2− a3− A + H+ | 12.35 | 80.49 | 16.00 | 54.49 | |
| HA− = 황산수소 | HA− a2− A + H+ | 1.99 | 11.36 | −22.40 | 33.74 |
| HA2 = 옥살산 | HA2 † HA− + H+ | 1.27 | 7.27 | −3.90 | 11.15 |
| HA− a2− A + H+ | 4.266 | 24.351 | −7.00 | 31.35 |
| 컴파운드 | 평형 | pKa | δH⊖(kJ−1·mol) | - TΩS⊖ (kJ·mol−1) |
|---|---|---|---|---|
| B = 암모니아 | HB+ † B + H+ | 9.245 | 51.95 | 0.8205 |
| B = 메틸아민 | HB+ † B + H+ | 10.645 | 55.34 | 5.422 |
| B = 트리에틸아민 | HB+ † B + H+ | 10.72 | 43.13 | 18.06 |
주목할 첫 번째 포인트는 pK가a 양수일 때 해리 반응에 대한 표준 자유 에너지 변화도 양수라는 것이다.둘째, 발열반응과 흡열반응이 있는데, δH가⊖ 음의⊖ 경우 δG가⊖ 양성으로 판정되는 우성인자가 된다.마지막으로, 이러한 반응에서 엔트로피의 기여는 항상 바람직하지 않다(δS⊖ < 0).수용액 속의 이온은 주변 물 분자의 방향을 잡는 경향이 있으며, 이는 용액을 명령하고 엔트로피를 감소시킨다.엔트로피에 대한 이온의 기여는 부분 몰 엔트로피이며, 특히 작거나 높은 하전 [56]이온의 경우 종종 음이 됩니다.중성산의 이온화는 엔트로피가 감소하도록 두 개의 이온을 형성한다(δS⊖ < 0).같은 산의 두 번째 이온화에서는 현재 3개의 이온이 존재하며 음이온은 전하를 띠기 때문에 엔트로피가 다시 감소한다.
반응의 표준 자유 에너지 변화는 표준 상태의 반응 물질에서 표준 상태의 생성물로의 변화입니다.반응물과 생성물의 화학적 잠재력이 평형에서 동일하기 때문에 평형에서의 자유 에너지 변화는 0이다.
실험적 결정
pKa 값의 실험적 측정은 일반적으로 높은 이온 강도와 일정한 [57]온도에서 적정을 통해 수행됩니다.일반적인 절차는 다음과 같습니다.배지 중의 화합물 용액을 강산으로 산화하여 완전히 양성자화한다.그런 다음 모든 양성자가 제거될 때까지 용액은 강한 염기로 적정된다.적정 pH는 유리전극과 pH계를 이용해 각각 측정한다.평형 상수는 최소 [58]제곱법을 사용하여 계산된 pH 값을 관측값에 적합시켜 구합니다.
첨가된 강염기의 총 부피는 이온 강도를 거의 일정하게 유지하기 위해 티트란 용액의 초기 부피보다 작아야 한다.이렇게 하면 적정 중에 pK가a 불변하게 유지됩니다.
산출된 옥살산에 대한 적정곡선을 오른쪽에 나타낸다.옥살산은 1.27과 4.27의 pKa 값을 가진다.따라서 버퍼 영역의 중심은 약 pH 1.3과 pH 4.3입니다.완충 영역은 완충 영역을 따라 산과 켤레 염기의 농도가 변화함에 따라 pKa 값을 얻는 데 필요한 정보를 전달합니다.
2개의 버퍼 영역 사이에는 약 pH 3의 엔드 포인트, 즉 등가점이 있습니다.이 엔드 포인트는 날카롭지 않고 버퍼 영역이 소량 겹치는 전형적인 디프로테산입니다.이a2 예에서는 pK - pK가a1 약 3입니다.(pK 값의 차이가 약 2 이하일 경우 엔드 포인트는 눈에 띄지 않습니다.)두 번째 엔드 포인트는 약 pH 6.3에서 시작하여 날카롭습니다.이것은 모든 양성자가 제거되었음을 나타냅니다.이 경우 용액은 완충되지 않고 소량의 강한 염기를 첨가하여 pH가 가파르게 상승한다.단, pH가 무한히 상승하는 것은 아닙니다.새로운 완충 영역은 약 pH 11(pKw - 3)에서 시작되며, 여기서 물의 자가 이온화가 중요하다.
Nernst 방정식은 낮은 pH 값에서 분해되기 때문에 유리 전극이 있는 수용액에서 2개 미만의 pH 값을 측정하는 것은 매우 어렵다.약 2개 미만 또는 약 11개[59][60] 이상의 pK 값을 결정하려면 pH 측정 대신 NMR 측정 또는 NMR[61][62] 측정을 사용할 수 있습니다.
유리 전극을 사용할 수 없는 경우에는 비수용액과 마찬가지로 분광광도 측정법을 자주 사용한다.[37]여기에는 흡광도 또는 형광 측정이 포함될 수 있습니다.두 경우 모두 측정된 양은 각 광활성 종의 기여 합계에 비례한다고 가정한다. 흡광도 측정의 경우 Beer-Lambert 법칙이 적용된다고 가정한다.
등온적정열량측정(ITC)을 사용하여 pK값과 산해리를 [63]위한 대응하는 표준엔탈피를 결정할 수 있다.계산을 수행하기 위한 소프트웨어는 간단한 시스템을 위해 계측기 제조업체에서 제공합니다.
H NMR 측정에는 정상수를 사용하는 수용액을 사용할 수 없지만 중수인 DO를2 사용해야 한다.13단, C NMR 데이터는 일반 물, H NMR 스펙트럼은 비수성 매체에 사용할 수 있다.NMR로 측정한 양은 NMR 시간 척도에서 양성자 교환이 빠르기 때문에 시간 평균 화학적 이동이다.P와 같은 다른 화학적 변화를 측정할 수 있습니다.
미소 상수
일부 분자의 경우, 해리(또는 연관성)는 2가 이상의 부위에서 발생할 수 있으며, 관찰된 거시적 평형 상수 또는 거시 상수는 다른 종을 포함하는 미세 상수의 조합이다.하나의 반응물이 두 개의 생성물을 동시에 형성할 때 매크로콘스탄트는 K X + Y (\ K 개의 미소콘스탄트의 합이 된다. 예를 들어 중성 zwitterion HS-CH2)로서 용액에 존재하는 아미노산 시스테인의 탈양성자가 탈양성된 경우이다.두 미세상수물은 황 또는 질소에서 탈양성자를 나타내며, 여기서 거시상수 합계는 산 해리 상수a K = Ka(-SH) + Ka(-NH3+)[64]이다.
마찬가지로, 스펠민과 같은 염기는 양성자화가 일어날 수 있는 둘 이상의 부위가 있다.예를 들어 모노프로토네이션은 말단 –NH2 그룹 또는 내부 –NH 그룹에서 발생할 수 있다.하나b 또는 다른 부위에서 양성자화된 정자의 해리에 대한 K 값은 미세상수의 예이다.pH, 흡광도, 형광 또는 NMR 측정으로 직접 측정할 수 없으며, 측정된 Kb 값은 미세 반응에 대한 K 값의 합계이다.
그럼에도 불구하고 양성자화 부위는 생물학적 기능에 매우 중요하기 때문에 미세상수 [65]결정을 위한 수학적 방법이 개발되었다.
두 개의 반응물이 동시에 하나의 생성물을 형성하면 매크로 1/ / X + / Y{ 1/K=/ K _ { X } + / K _ { { K _ { K}예를 들어 Y}}.[64], 스페르민에 전기와 같은 평형 2호변 켤레 산의 Ka가치 면에서, 이 경우 macroconstant 1/Ka=1/K을 버무린 터미널+1/K는, 내부{\displaystyle 1/K_{\text{}}=1{{\text{}},{{단말\text}}}+1{{\text{}},{\text{토장으로 여겨질 수 있다.nal}}K {\displaystyle {는 1/a {\1/{a에하므로 위의 식과
반응물이 연속적으로 두 가지 반응을 보일 때, 결합된 반응에 대한 매크로 상수는 두 단계의 마이크로 상수의 산물이다.예를 들어 상기 시스테인 zwiterion은 황과 질소에서 각각 1개씩 2개의 양성자를 잃을 수 있으며, 2개의 양성자를 잃기 위한 전체 거시상수는 2개의 해리상수 K = Ka(-SH) K(-NH3+)[64]의a 곱이다.이는 로그 상수로도 pK = pKa(-SH) + pKa(-NH3+)로 표기할 수 있다.
응용 프로그램 및 중요도
pKa 값에 대한 지식은 용액에서 산-염기 평형을 포함하는 시스템의 정량적 처리에 중요하다.예를 들어, 단백질의 pKa 값과 아미노산 곁사슬은 효소의 활성과 [66]단백질의 안정성에 매우 중요하다.단백질 pKa 값은 항상 직접 측정할 수는 없지만 이론적인 방법을 사용하여 계산할 수 있습니다.완충용액은 생화학적 [67]반응 연구를 위한 생리학적 pH 또는 그 근처에서 용액을 제공하기 위해 광범위하게 사용된다. 이러한 용액의 설계는 그 성분의 pKa 값에 대한 지식에 따라 달라진다.중요한 완충 용액으로는 pH 7.2 용액을 제공하는 MOPS와 [68][69]겔 전기영동에 사용되는 트리신이 있습니다.완충은 산염기 항상성을 [70]포함한 산염기 생리의 필수적인 부분이며, 산염기 [71][72][73]장애와 같은 장애를 이해하는 데 중요하다.주어진 분자의 등전점은 pK값의 함수이기 때문에 분자들마다 등전점이 다릅니다.이것은 2D 겔 폴리아크릴아미드 겔 전기영동에 의한 단백질 분리에 사용되는 아이소 일렉트릭 [74]포커싱이라고 불리는 기술을 허용합니다.
완충액은 분석 화학에서도 중요한 역할을 합니다.용액의 pH를 특정 값으로 고정할 필요가 있을 때 사용합니다.완충액의 pH는 수용액에 비해 강산 또는 강염기를 소량 첨가해도 비교적 둔감하다.단순[75] 완충용액의 완충용량은 pH = pK일a 때 가장 크다.산염기 추출에서는 적절한 완충제를 사용하여 수상의 pH를 조절함으로써 에테르 등의 유기상으로의 화합물 추출 효율을 최적화할 수 있다.최적 pH에서는 전기적으로 중성적인 종의 농도가 최대화된다.이러한 종은 물속보다 유전율이 낮은 유기용매에 더 잘 용해된다.이 기술은 약한 산과 [76]염기의 정화에 사용된다.
pH 지표는 약산 또는 약염기이며, 전이 pH 범위(약a pK ± 1)에서 색상이 변화한다.범용 지표의 설계에는 인접한 pKa 값이 약 2개씩 다른 지표의 혼합이 필요하며, 따라서 이들의 전이 pH 범위는 단지 겹친다.
약리학에서 화합물의 이온화는 그 물리적 거동과 용해성과 친유성과 같은 거시적 특성을 변화시킨다, log p).예를 들어, 어떤 화합물의 이온화는 물에서 용해도를 증가시키지만 친유성은 감소시킨다.이는 약제 개발에서 이온화 [77]그룹의 pK를a 조절하여 혈액 내 화합물의 농도를 증가시키는 데 이용된다.
pKa 값에 대한 지식은 루이스산 역할을 하는 금속 이온m+ M과 루이스 염기 역할을 하는 배위자 L의 상호작용에 의해 형성되는 배위 복합체를 이해하는 데 중요하다.그러나 리간드는 양성자화 반응도 할 수 있으므로 수용액에서 착체의 형성은 반응에 의해 상징적으로 나타날 수 있다.
- [M(HO2)]nm+ + 좌측 [ [M(HO2)n−1(m−1)+L] + HO3+
리간드가 양성자를 잃는 이 반응에 대한 평형 상수를 결정하기 위해서는 양성자화 리간드의 pK를a 알아야 한다.실제로 배위자는 다프로틱일 수 있습니다. 예를4− 들어 EDTA는 4개의 양성자를 수용할 수 있습니다. 이 경우 모든 pKa 값을 알아야 합니다.또한 금속 이온은 가수분해되기 때문에 약산으로서 작용하므로 가수분해 반응에 대한 pK 값도 [78]알아야 한다.
산이나 염기와 관련된 위험을 평가하려면 pKa [79]값에 대한 지식이 필요할 수 있습니다.예를 들어 시안화수소는 철함유효소 시토크롬c산화효소를 억제하기 때문에 매우 독성이 강한 기체이다.시안화수소는 pK가a 약 9인 수용액 중의 약산이다.예를 들어, pH 11 이상의 강알칼리성 용액에서는 시안화나트륨이 "완전 해리"되기 때문에 시안화수소 가스에 의한 위험이 크게 감소한다.반면에 산성 용액은 모든 시안화물이 산성 형태이기 때문에 매우 위험하다.시안화물의 구강 섭취는 시토크롬c 산화효소와의 반응 때문에 pH와 무관하게 치명적일 수 있다.
환경과학에서 산-염기 평형은 호수와 [81][82]강에서[80] 중요하다. 예를 들어, 후민산은 자연수의 중요한 구성요소이다.화학해양학에서는 [83]다른 예로서 다양한 염분에서의 해수 중 철(III)의 용해도를 정량화하기 위해 [84]수산화철의 용해성 생성물과 함께 철(III) 가수분해물 Fe(OH),2+ Fe(OH)+
2 및 Fe(OH)3의 형성에 관한 pK값을a 구했다.
일반적인 물질에 대한 값
화학물질의 pK를a 결정하는 데는 여러 가지 기법이 있으며, 이로 인해 서로 다른 선원 간에 약간의 불일치가 발생한다.잘 측정된 값은 일반적으로 서로 0.1 단위 이내입니다.여기에 제시된 데이터는 [7][85]물에서 25°C에서 채취했다.더 많은 값은 위의 열역학 섹션에서 확인할 수 있습니다.DMSO로 측정한 탄소산 pKa 표는 카르보니온 페이지에 나와 있습니다.
| 화학의 | 평형 | pKa |
|---|---|---|
| BH = 아데닌 | BH b− B + H+ | 4.17 |
| BH+ 2 bh BH + H+ | 9.65 | |
| HA3 = 비산 | HA3 † HA2− + H+ | 2.22 |
| HA2− † HA2− + H+ | 6.98 | |
| HA2− a3− A + H+ | 11.53 | |
| HA = 벤조산 | HA h+ H + A− | 4.204 |
| HA = 낙산 | HA h+ H + A− | 4.82 |
| HA2 = 크롬산 | HA2 † HA− + H+ | 0.98 |
| HA− a2− A + H+ | 6.5 | |
| B = 코드라인 | BH+ b B + H+ | 8.17 |
| HA = 크레졸 | HA h+ H + A− | 10.29 |
| HA = 포름산 | HA h+ H + A− | 3.751 |
| HA = 불산 | HA h+ H + A− | 3.17 |
| HA = 시안 수소산 | HA h+ H + A− | 9.21 |
| HA = 셀렌화수소 | HA h+ H + A− | 3.89 |
| HA = 과산화수소(90%) | HA h+ H + A− | 11.7 |
| HA = 젖산 | HA h+ H + A− | 3.86 |
| HA = 프로피온산 | HA h+ H + A− | 4.87 |
| HA = 페놀 | HA h+ H + A− | 9.99 |
| HA2 = L-(+)-아스코르브산 | HA2 † HA− + H+ | 4.17 |
| HA− a2− A + H+ | 11.57 |
「 」를 참조해 주세요.
- 산증
- 와인의 산: 주석산, 사과산, 구연산이 와인의 주요 산입니다.
- 알칼로시스
- 동맥혈 가스
- 화학적 평형
- 도전성(전기 분해)
- 그로투스 메커니즘: 양성자가 하이드로늄 이온과 물 분자 사이에서 어떻게 전달되는지, 양성자의 이온 이동성이 매우 높습니다(애니메이션).
- Hammett 산도 함수: 초산을 포함한 강한 산의 매우 농축된 용액에 사용되는 산도의 측정값.
- 이온수송번호
- 해양 산성화: 대기 중 이산화탄소의 용해는 바닷물의 pH에 영향을 미친다.반응은 총 무기 탄소와 석회암과 돌로마이트와 같은 고체 탄산염과의 용해성 평형에 따라 달라집니다.
- 희석법칙
- PCO2
- pH
- 우위도: 폴리옥시 음이온을 포함한 평형도와 관련이 있습니다a.이러한 도표를 작성하려면 pK 값이 필요합니다.
- 양성자 친화력: 기체상의 염기성 측정값.
- 복합체의 안정성 상수: 복합체의 형성은 종종 산의 해리의 산물인 리간드를 위한 양성자와 금속 이온 사이의 경쟁으로 보일 수 있습니다.
메모들
레퍼런스
- ^ Whitten, Kenneth W.; Gailey, Kenneth D.; Davis, Raymond E. (1992). General Chemistry (4th ed.). Saunders College Publishing. p. 660. ISBN 0-03-072373-6.
- ^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General Chemistry (8th ed.). Prentice Hall. pp. 667–8. ISBN 0-13-014329-4.
- ^ Perrin DD, Dempsey B, Serjeant EP (1981). "Chapter 3: Methods of pKa Prediction". pKa Prediction for Organic Acids and Bases. (secondary). London: Chapman & Hall. pp. 21–26. doi:10.1007/978-94-009-5883-8. ISBN 978-0-412-22190-3.
- ^ a b Fraczkiewicz R (2013). "In Silico Prediction of Ionization". In Reedijk J (ed.). Reference Module in Chemistry, Molecular Sciences and Chemical Engineering. (secondary). Reference Module in Chemistry, Molecular Sciences and Chemical Engineering [Online]. Vol. 5. Amsterdam, The Netherlands: Elsevier. doi:10.1016/B978-0-12-409547-2.02610-X. ISBN 9780124095472.
- ^ Miessler, Gary L.; Tarr, Donald A. (1991). Inorganic Chemistry (2nd ed.). Prentice Hall. ISBN 0-13-465659-8. 6장: 산-염기 및 기증자-수용체 화학
- ^ a b Bell, R.P. (1973). The Proton in Chemistry (2nd ed.). London: Chapman & Hall. ISBN 0-8014-0803-2. 많은 유기 브뢴스테드산에 대한 논의를 포함합니다.
- ^ a b c Shriver, D.F; Atkins, P.W. (1999). Inorganic Chemistry (3rd ed.). Oxford: Oxford University Press. ISBN 0-19-850331-8. 5장: 산과 염기
- ^ Housecroft, C. E.; Sharpe, A. G. (2008). Inorganic Chemistry (3rd ed.). Prentice Hall. ISBN 978-0-13-175553-6. 제6장 수용액 중의 산, 염기 및 이온
- ^ Headrick, J.M.; Diken, E.G.; Walters, R. S.; Hammer, N. I.; Christie, R.A.; Cui, J.; Myshakin, E.M.; Duncan, M.A.; Johnson, M.A.; Jordan, K.D. (2005). "Spectral Signatures of Hydrated Proton Vibrations in Water Clusters". Science. 308 (5729): 1765–69. Bibcode:2005Sci...308.1765H. doi:10.1126/science.1113094. PMID 15961665. S2CID 40852810.
- ^ Smiechowski, M.; Stangret, J. (2006). "Proton hydration in aqueous solution: Fourier transform infrared studies of HDO spectra". J. Chem. Phys. 125 (20): 204508–204522. Bibcode:2006JChPh.125t4508S. doi:10.1063/1.2374891. PMID 17144716.
- ^ a b c Goldberg, R.; Kishore, N.; Lennen, R. (2002). "Thermodynamic Quantities for the Ionization Reactions of Buffers" (PDF). J. Phys. Chem. Ref. Data. 31 (2): 231–370. Bibcode:2002JPCRD..31..231G. doi:10.1063/1.1416902. Archived from the original (PDF) on 2008-10-06.
- ^ Jolly, William L. (1984). Modern Inorganic Chemistry. McGraw-Hill. pp. 198. ISBN 978-0-07-032760-3.
- ^ Burgess, J. (1978). Metal Ions in Solution. Ellis Horwood. ISBN 0-85312-027-7. 섹션 9.1 "용해 양이온의 산도"는 많은 pKa 값을 열거한다.
- ^ Petrucci, R.H.; Harwood, R.S.; Herring, F.G. (2002). General Chemistry (8th ed.). Prentice Hall. ISBN 0-13-014329-4. 페이지 698
- ^ a b c Rossotti, F.J.C.; Rossotti, H. (1961). The Determination of Stability Constants. McGraw–Hill. 제2장: 활동과 집중력 지수
- ^ "Project: Ionic Strength Corrections for Stability Constants". International Union of Pure and Applied Chemistry. Retrieved 2019-03-28.
- ^ Atkins, P.W.; de Paula, J. (2006). Physical Chemistry. Oxford University Press. ISBN 0-19-870072-5. 제7.4절: 온도에 대한 평형 반응
- ^ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey (2002). General chemistry: principles and modern applications (8th ed.). Prentice Hall. p. 633. ISBN 0-13-014329-4.
Are you wondering... How using activities makes the equilibrium constant dimensionless?
- ^ Shriver, D.F; Atkins, P.W. (1999). Inorganic Chemistry (3rd ed.). Oxford University Press. ISBN 0-19-850331-8. 제5.1c조 강약산 및 염기
- ^ Porterfield, William W. (1984). Inorganic Chemistry. Addison-Wesley. p. 260. ISBN 0-201-05660-7.
- ^ a b Shriver, D.F; Atkins, P.W. (1999). Inorganic Chemistry (3rd ed.). Oxford University Press. ISBN 0-19-850331-8. 제5.2조 용제 레벨링
- ^ Levanov, A. V.; Isaikina, O. Ya.; Lunin, V. V. (2017). "Dissociation constant of nitric acid". Russian Journal of Physical Chemistry A. 91 (7): 1221–1228. Bibcode:2017RJPCA..91.1221L. doi:10.1134/S0036024417070196. S2CID 104093297.
- ^ Trummal, Aleksander; Lipping, Lauri; Kaljurand, Ivari; Koppel, Ilmar A.; Leito, Ivo (2016). "Acidity of Strong Acids in Water and Dimethyl Sulfoxide". The Journal of Physical Chemistry A. 120 (20): 3663–3669. Bibcode:2016JPCA..120.3663T. doi:10.1021/acs.jpca.6b02253. PMID 27115918.
- ^ Mehta, Akul (22 October 2012). "Henderson–Hasselbalch Equation: Derivation of pKa and pKb". PharmaXChange. Retrieved 16 November 2014.
- ^ 값은 25°C와 0명의 이온 강도– 파월, Kipton J., 브라운, 폴 L.; 번, 로버트 H.;Gajda, 바샤리;Hefter, 글렌, Sjöberg, Staffan, Wanner, 한스(2005년) 있다.환경적으로 중요한 중금속의 무기 ligands과 함께 화학 종분화.Part1:그 Hg2+, Cl−, OH−, CO2−3, SO2−4, PO3−4 수성 systems".순수 Appl.화학. 77(4):739–800. doi:10.1351/pac200577040739.
- ^ Brown, T.E.; Lemay, H.E.; Bursten, B.E.; Murphy, C.; Woodward, P. (2008). Chemistry: The Central Science (11th ed.). New York: Prentice-Hall. p. 689. ISBN 978-0-13-600617-6.
- ^ a b Greenwood, N.N.; Earnshaw, A. (1997). Chemistry of the Elements (2nd ed.). Oxford: Butterworth-Heinemann. p. 50. ISBN 0-7506-3365-4.
- ^ a b c Miessler, Gary L.; Tarr Donald A. (1999). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 164. ISBN 0-13-465659-8.
- ^ a b Huheey, James E. (1983). Inorganic Chemistry (3rd ed.). Harper & Row. p. 297. ISBN 0-06-042987-9.
- ^ Lide, D.R. (2004). CRC Handbook of Chemistry and Physics, Student Edition (84th ed.). CRC Press. ISBN 0-8493-0597-7. 섹션 D~152
- ^ Skoog, Douglas A.; West, Donald M.; Holler, F. James; Crouch, Stanley R. (2014). Fundamentals of Analytical Chemistry (9th ed.). Brooks/Cole. p. 212. ISBN 978-0-495-55828-6.
- ^ Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 163. ISBN 978-0-13-039913-7.
- ^ Harned, H.S.; Owen, B.B (1958). The Physical Chemistry of Electrolytic Solutions. New York: Reinhold Publishing Corp. pp. 634–649, 752–754.
- ^ a b c d Loudon, G. Marc (2005), Organic Chemistry (4th ed.), New York: Oxford University Press, pp. 317–318, ISBN 0-19-511999-1
- ^ March, J.; Smith, M. (2007). Advanced Organic Chemistry (6th ed.). New York: John Wiley & Sons. ISBN 978-0-471-72091-1. 제8장: 산과 염기
- ^ Kütt, A.; Movchun, V.; Rodima, T; Dansauer, T.; Rusanov, E.B.; Leito, I.; Kaljurand, I.; Koppel, J.; Pihl, V.; Koppel, I.; Ovsjannikov, G.; Toom, L.; Mishima, M.; Medebielle, M.; Lork, E.; Röschenthaler, G-V.; Koppel, I.A.; Kolomeitsev, A.A. (2008). "Pentakis(trifluoromethyl)phenyl, a Sterically Crowded and Electron-withdrawing Group: Synthesis and Acidity of Pentakis(trifluoromethyl)benzene, -toluene, -phenol, and -aniline". J. Org. Chem. 73 (7): 2607–2620. doi:10.1021/jo702513w. PMID 18324831.
- ^ a b Kütt, A.; Leito, I.; Kaljurand, I.; Sooväli, L.; Vlasov, V.M.; Yagupolskii, L.M.; Koppel, I.A. (2006). "A Comprehensive Self-Consistent Spectrophotometric Acidity Scale of Neutral Brønsted Acids in Acetonitrile". J. Org. Chem. 71 (7): 2829–2838. doi:10.1021/jo060031y. PMID 16555839.
- ^ Kaljurand, I.; Kütt, A.; Sooväli, L.; Rodima, T.; Mäemets, V.; Leito, I; Koppel, I.A. (2005). "Extension of the Self-Consistent Spectrophotometric Basicity Scale in Acetonitrile to a Full Span of 28 pKa Units: Unification of Different Basicity Scales". J. Org. Chem. 70 (3): 1019–1028. doi:10.1021/jo048252w. PMID 15675863.
- ^ "Bordwell pKa Table (Acidity in DMSO)". Archived from the original on 9 October 2008. Retrieved 2008-11-02.
- ^ Housecroft, C. E.; Sharpe, A. G. (2008). Inorganic Chemistry (3rd ed.). Prentice Hall. ISBN 978-0-13-175553-6. 8장: 비수성 매체
- ^ Rochester, C.H. (1970). Acidity Functions. Academic Press. ISBN 0-12-590850-4.
- ^ Olah, G.A; Prakash, S; Sommer, J (1985). Superacids. New York: Wiley Interscience. ISBN 0-471-88469-3.
- ^ Coetzee, J.F.; Padmanabhan, G.R. (1965). "Proton Acceptor Power and Homoconjugation of Mono- and Diamines". J. Am. Chem. Soc. 87 (22): 5005–5010. doi:10.1021/ja00950a006.
- ^ Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic chemistry. McGraw–Hill. p. 203. ISBN 0-07-050115-7.
- ^ Box, K.J.; Völgyi, G.; Ruiz, R.; Comer, J.E.; Takács-Novák, K.; Bosch, E.; Ràfols, C.; Rosés, M. (2007). "Physicochemical Properties of a New Multicomponent Cosolvent System for the pKa Determination of Poorly Soluble Pharmaceutical Compounds". Helv. Chim. Acta. 90 (8): 1538–1553. doi:10.1002/hlca.200790161.
- ^ a b Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic chemistry (2nd ed.). Harlow, U.K.: Pearson Prentice Hall. pp. 170–171. ISBN 0-13-039913-2.
- ^ a b 더글러스 B, 맥대니얼 D.H.와 Alexander J. J. 무기화학의 개념과 모델 (제2판).Wiley 1983) 페이지 526 ISBN 0-471-21984-3
- ^ Pauling, L. (1960). The nature of the chemical bond and the structure of molecules and crystals; an introduction to modern structural chemistry (3rd ed.). Ithaca (NY): Cornell University Press. p. 277. ISBN 0-8014-0333-2.
- ^ Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic Chemistry. McGraw–Hill. ISBN 0-07-050115-7. 제13-3절 치환효과의 정량적 상관관계 (B부) - 해밋 방정식
- ^ Hammett, L.P. (1937). "The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives". J. Am. Chem. Soc. 59 (1): 96–103. doi:10.1021/ja01280a022.
- ^ Hansch, C.; Leo, A.; Taft, R. W. (1991). "A Survey of Hammett Substituent Constants and Resonance and Field Parameters". Chem. Rev. 91 (2): 165–195. doi:10.1021/cr00002a004.
- ^ Shorter, J (1997). "Compilation and critical evaluation of structure-reactivity parameters and equations: Part 2. Extension of the Hammett σ scale through data for the ionization of substituted benzoic acids in aqueous solvents at 25 °C (Technical Report)". Pure and Applied Chemistry. 69 (12): 2497–2510. doi:10.1351/pac199769122497. S2CID 98814841.
- ^ Pine, S.H.; Hendrickson, J.B.; Cram, D.J.; Hammond, G.S. (1980). Organic chemistry. McGraw–Hill. ISBN 0-07-050115-7. 제6절 2절 산도와 염기성에 미치는 구조적 영향
- ^ Alder, R.W.; Bowman, P.S.; Steele, W.R.S.; Winterman, D.R. (1968). "The Remarkable Basicity of 1,8-bis(dimethylamino)naphthalene". Chem. Commun. (13): 723–724. doi:10.1039/C19680000723.
- ^ Alder, R.W. (1989). "Strain Effects on Amine Basicities". Chem. Rev. 89 (5): 1215–1223. doi:10.1021/cr00095a015.
- ^ Atkins, Peter William; De Paula, Julio (2006). Atkins' physical chemistry. New York: W H Freeman. p. 94. ISBN 978-0-7167-7433-4.
- ^ Martell, A.E.; Motekaitis, R.J. (1992). Determination and Use of Stability Constants. Wiley. ISBN 0-471-18817-4. 제4장: 금속 착체 평형의 전위차 pH 측정을 위한 실험 절차
- ^ Leggett, D.J. (1985). Computational Methods for the Determination of Formation Constants. Plenum. ISBN 0-306-41957-2.
- ^ Allen, R.I.; Box, K.J.; Comer, J.E.A.; Peake, C.; Tam, K.Y. (1998). "Multiwavelength Spectrophotometric Determination of Acid Dissociation Constants of Ionizable Drugs". J. Pharm. Biomed. Anal. 17 (4–5): 699–712. doi:10.1016/S0731-7085(98)00010-7. PMID 9682153.
- ^ Box, K.J.; Donkor, R.E.; Jupp, P.A.; Leader, I.P.; Trew, D.F.; Turner, C.H. (2008). "The Chemistry of Multi-Protic Drugs Part 1: A Potentiometric, Multi-Wavelength UV and NMR pH Titrimetric Study of the Micro-Speciation of SKI-606". J. Pharm. Biomed. Anal. 47 (2): 303–311. doi:10.1016/j.jpba.2008.01.015. PMID 18314291.
- ^ Popov, K.; Ronkkomaki, H.; Lajunen, L.H.J. (2006). "Guidelines for NMR easurements for Determination of High and Low pKa Values" (PDF). Pure Appl. Chem. 78 (3): 663–675. doi:10.1351/pac200678030663. S2CID 4823180.
- ^ Szakács, Z.; Hägele, G. (2004). "Accurate Determination of Low pK Values by 1H NMR Titration". Talanta. 62 (4): 819–825. doi:10.1016/j.talanta.2003.10.007. PMID 18969368.
- ^ Feig, Andrew L., ed. (2016). "Methods in Enzymology". Calorimetry. Elsevier. 567: 2–493. ISSN 0076-6879.
- ^ a b c Splittgerber, A. G.; Chinander, L.L. (1 February 1988). "The spectrum of a dissociation intermediate of cysteine: a biophysical chemistry experiment". Journal of Chemical Education. 65 (2): 167. Bibcode:1988JChEd..65..167S. doi:10.1021/ed065p167.
- ^ Frassineti, C.; Alderighi, L; Gans, P; Sabatini, A; Vacca, A; Ghelli, S. (2003). "Determination of Protonation Constants of Some Fluorinated Polyamines by Means of 13C NMR Data Processed by the New Computer Program HypNMR2000. Protonation Sequence in Polyamines". Anal. Bioanal. Chem. 376 (7): 1041–1052. doi:10.1007/s00216-003-2020-0. PMID 12845401. S2CID 14533024.
- ^ Onufriev, A.; Case, D.A; Ullmann G.M. (2001). "A Novel View of pH Titration in Biomolecules". Biochemistry. 40 (12): 3413–3419. doi:10.1021/bi002740q. PMID 11297406.
- ^ Good, N.E.; Winget, G.D.; Winter, W.; Connolly, T.N.; Izawa, S.; Singh, R.M.M. (1966). "Hydrogen Ion Buffers for Biological Research". Biochemistry. 5 (2): 467–477. doi:10.1021/bi00866a011. PMID 5942950.
- ^ Dunn, M.J. (1993). Gel Electrophoresis: Proteins. Bios Scientific Publishers. ISBN 1-872748-21-X.
- ^ Martin, R. (1996). Gel Electrophoresis: Nucleic Acids. Bios Scientific Publishers. ISBN 1-872748-28-7.
- ^ Brenner, B.M.; Stein, J.H., eds. (1979). Acid–Base and Potassium Homeostasis. Churchill Livingstone. ISBN 0-443-08017-8.
- ^ Scorpio, R. (2000). Fundamentals of Acids, Bases, Buffers & Their Application to Biochemical Systems. Kendall/Hunt Pub. Co. ISBN 0-7872-7374-0.
- ^ Beynon, R.J.; Easterby, J.S. (1996). Buffer Solutions: The Basics. Oxford: Oxford University Press. ISBN 0-19-963442-4.
- ^ Perrin, D.D.; Dempsey, B. (1974). Buffers for pH and Metal Ion Control. London: Chapman & Hall. ISBN 0-412-11700-2.
- ^ Garfin, D.; Ahuja, S., eds. (2005). Handbook of Isoelectric Focusing and Proteomics. Vol. 7. Elsevier. ISBN 0-12-088752-5.
- ^ Hulanicki, A. (1987). Reactions of Acids and Bases in Analytical Chemistry. Masson, M.R. (translation editor). Horwood. ISBN 0-85312-330-6.
- ^ Eyal, A.M (1997). "Acid Extraction by Acid–Base-Coupled Extractants". Ion Exchange and Solvent Extraction: A Series of Advances. 13: 31–94.
- ^ Avdeef, A. (2003). Absorption and Drug Development: Solubility, Permeability, and Charge State. New York: Wiley. ISBN 0-471-42365-3.
- ^ Beck, M.T.; Nagypál, I. (1990). Chemistry of Complex Equilibria. Horwood. ISBN 0-85312-143-5.
- ^ van Leeuwen, C.J.; Hermens, L. M. (1995). Risk Assessment of Chemicals: An Introduction. Springer. pp. 254–255. ISBN 0-7923-3740-9.
- ^ Skoog, D.A; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th ed.). Thomson Brooks/Cole. ISBN 0-03-035523-0. 제9장-6장 산성비와 호수의 완충용량
- ^ Stumm, W.; Morgan, J.J. (1996). Water Chemistry. New York: Wiley. ISBN 0-471-05196-9.
- ^ Snoeyink, V.L.; Jenkins, D. (1980). Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters. New York: Wiley. ISBN 0-471-51185-4.
- ^ Millero, F.J. (2006). Chemical Oceanography (3rd ed.). London: Taylor and Francis. ISBN 0-8493-2280-4.
- ^ Millero, F.J.; Liu, X. (2002). "The Solubility of Iron in Seawater". Marine Chemistry. 77 (1): 43–54. doi:10.1016/S0304-4203(01)00074-3.
- ^ Speight, J.G. (2005). Lange's Handbook of Chemistry (18th ed.). McGraw–Hill. ISBN 0-07-143220-5. 제8장
추가 정보
- Albert, A.; Serjeant, E.P. (1971). The Determination of Ionization Constants: A Laboratory Manual. Chapman & Hall. ISBN 0-412-10300-1. (이전 판은 로 발행)
- Atkins, P.W.; Jones, L. (2008). Chemical Principles: The Quest for Insight (4th ed.). W.H. Freeman. ISBN 978-1-4292-0965-6.
- Housecroft, C. E.; Sharpe, A. G. (2008). Inorganic Chemistry (3rd ed.). Prentice Hall. ISBN 978-0-13-175553-6. (비수성 용제)
- Hulanicki, A. (1987). Reactions of Acids and Bases in Analytical Chemistry. Horwood. ISBN 0-85312-330-6. (정보 에디터:메리 R.마손)
- Perrin, D.D.; Dempsey, B.; Serjeant, E.P. (1981). pKa Prediction for Organic Acids and Bases. Chapman & Hall. ISBN 0-412-22190-X.
- Reichardt, C. (2003). Solvents and Solvent Effects in Organic Chemistry (3rd ed.). Wiley-VCH. ISBN 3-527-30618-8. 제4장: 균질 화학 평형의 위치에 대한 용제의 영향.
- Skoog, D.A.; West, D.M.; Holler, J.F.; Crouch, S.R. (2004). Fundamentals of Analytical Chemistry (8th ed.). Thomson Brooks/Cole. ISBN 0-03-035523-0.
외부 링크
- 비수성 용제의 산성-염기성 데이터 DMSO, 아세토니트릴, THF, 헵탄, 1,2-디클로로에탄 및 기상에서의 pKa 값의 광범위한 참고 문헌
- Curtipot All-in-One 프리웨어(pH 및 산-염기 평형 계산 및 스프레드시트를 사용한 전위차적정곡선 시뮬레이션 및 분석용)
- SPARC 물리/화학 속성 계산기 SMIES 또는 CAS 레지스트리 번호를 사용하여 검색할 수 있는 수상, 비수상 및 기체상의 pK 값을 가진 데이터베이스를 포함합니다a.
- 다양한 산과 염기에 대한 수성-균형 상수 pKa 값.일부 용해성 제품 표 포함
- pKa 및 로그 p 해석 및 측정 무료 가이드 웨이백 머신에 보관 2016-08-10 약리학과의 관련성 설명
- 무료 온라인 예측 도구(Marvin) pKa, 로그 p, 로그 d 등From Chem으로액손
- Chemicalize.org:예측된 구조 기반 특성 목록
- pKa 관리도 [1] by David A. 에반스

![{\displaystyle K_{\text{a}}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cdd9efda0e3a32060020b5c9e5b2c78981b2a93)
![{\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}K_{\text{a}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7af05bf129db2f9bc618fe809660b6e4ff8dce9)
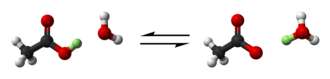



![{\displaystyle K^{\ominus }={{\frac {[{\ce {A^-}}][{\ce {H+}}]}{{\ce {[HA]}}}}\Gamma },\quad \Gamma ={\frac {\gamma _{{\ce {A^-}}}\ \gamma _{{\ce {H+}}}}{\gamma _{{\ce {HA}}}\ }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e9373db7091aeb4f51a26757a677b420f0a8418)
 활성 계수의 비율입니다.
활성 계수의 비율입니다. ![{\displaystyle K_{\text{a}}={\frac {K^{\ominus }}{\Gamma }}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a5a59c740de89347ec4c96d982292fc05c64b2f)
![{\displaystyle \mathrm {p} K_{{\ce {a}}}=-\log _{10}{\frac {[{\ce {A^-}}][{\ce {H^+}}]}{[{\ce {HA}}]}}=\log _{10}{\frac {{\ce {[HA]}}}{[{\ce {A^-}}][{\ce {H+}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bed5fbab82167a42994a6d735931d08b06f1e7a5)



![{\displaystyle \beta _{2}={\frac {{\ce {[H_2A]}}}{[{\ce {A^{2-}}}][{\ce {H+}}]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3306fbf9ccf8d12352eab96dfb5461897f2c3a15)

![{\displaystyle K_{\text{dissoc}}=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} :\mathrm {p} K_{\text{a}}=-\log K_{\text{dissoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5f9c1efd45de9edf690ebf6a72cc806eb2b0331)
![{\displaystyle K_{\text{assoc}}=\mathrm {\frac {[HA]}{[A^{-}][H^{+}]}} :\mathrm {p} K_{\text{b}}=-\log K_{\text{assoc}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77a0453338b1d420214ac7c127d3faa13374fce0)




![{\displaystyle K_{\mathrm {a} }=\mathrm {\frac {[A^{-}][H^{+}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df1424aa532585fc7ad6dd660a596705ee31a2b)





 상수이므로 (3)을 이용하여 구한 평형 상수 값은 (1)과 (2)로 구한 값에 단순히 비례한다.
상수이므로 (3)을 이용하여 구한 평형 상수 값은 (1)과 (2)로 구한 값에 단순히 비례한다. 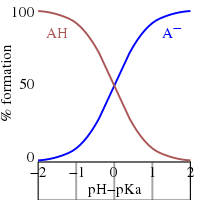
![{\displaystyle \mathrm {pH} =\mathrm {p} K_{\text{a}}+\log \mathrm {\frac {[A^{-}]}{[HA]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/25e874f2b8ea8e4127605788c356393cfd7fff37)

![{\displaystyle \mathrm {p} K_{{\ce {a1}}}=\log _{10}{\frac {[{\ce {H_3PO_4}}]}{[{\ce {H_2PO_4^{-}}}][{\ce {H^+}}]}}=2.14}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dff6e67381cb8a691b8873fbf884dad30b001352)
![{\displaystyle \mathrm {p} K_{{\ce {a2}}}=\log _{10}{\frac {[{\ce {H_2PO_4^{-}}}]}{[{\ce {HPO_4^{2-}}}][{\ce {H^+}}]}}=7.2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efe9f5a620a62c8de4a6567f58faf01e66829903)
![{\displaystyle \mathrm {p} K_{{\ce {a3}}}=\log _{10}{\frac {[{\ce {HPO_4^{2-}}}]}{[{\ce {PO_4^{3-}}}][{\ce {H^+}}]}}=12.37}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf6cf97c1d47ba55db3a383374b9d8cd4eda22ee)





![{\displaystyle {\begin{aligned}K_{\text{b}}&=\mathrm {\frac {[HB^{+}][OH^{-}]}{[B]}} \\\mathrm {p} K_{\text{b}}&=-\log _{10}\left(K_{\text{b}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dea1aac629a595476e18c042a8f4365a50f0efc)
![{\displaystyle \mathrm {[OH^{-}]} ={\frac {K_{\mathrm {w} }}{\mathrm {[H^{+}]} }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab7f583da9f8b50145990ffa4342919930edfa16)
![{\displaystyle K_{\text{b}}={\frac {[\mathrm {HB^{+}} ]K_{\text{w}}}{\mathrm {[B][H^{+}]} }}={\frac {K_{\text{w}}}{K_{\text{a}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/921c3abd37a1c5c00c31831509d3b090394c0d47)


![{\displaystyle K_{\mathrm {b} }={\frac {[\mathrm {M} _{p}(\mathrm {OH} )_{q-1}^{+}][\mathrm {OH} ^{-}]}{[\mathrm {M} _{p}(\mathrm {OH} )_{q}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb70331666676f62afda8017ff13fd1e941241a)
![{\displaystyle \mathrm {p} K_{\mathrm {aH} }(\mathrm {B} )=\mathrm {p} K_{\mathrm {a} }(\mathrm {BH} ^{+})=-\log _{10}{\Big (}{\frac {[\mathrm {B} ][\mathrm {H^{+}} ]}{[\mathrm {BH} ^{+}]}}{\Big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa04a34c3fecca06d502586ca2f7c523c391233a)
![{\displaystyle K_{\text{a}}=\mathrm {\frac {[H^{+}][OH^{-}]}{[H_{2}O]}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc540ad193c8f1661c1897698be93153fc5fb84)
![{\displaystyle K_{\text{w}}=[\mathrm {H} ^{+}][\mathrm {OH} ^{-}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0039f77db244ea2f6d03d3475dc7a232a8ccb16)











 1/
1/



