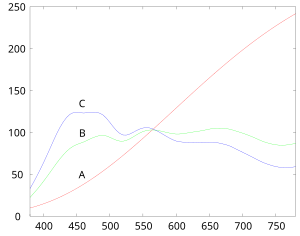
적정곡선

강한 염기, 수산화나트륨으로 적정한 2중산, 옥살산의 대표적인 적정 곡선이다. 두 개의 등가점이 모두 보인다.

적정치는 흔히 적정곡선이라는 그래프에 기록되는데, 적정곡선은 일반적으로 독립변수로 적정량의 부피와 종속변수로 용액의 pH를 포함하고 있다(두 용액의 구성에 따라 달라지기 때문이다).^[1]

그래프의 등가점은 모든 시작 용액(대개 산성)이 적분(대개 염기)에 의해 중화된 지점이다. 적정곡선의 두 번째 파생상품을 찾아 변곡점(그래프가 응집성을 바꾸는 곳)을 계산해 정밀하게 계산할 수 있지만, 대부분의 경우 곡선의 단순한 육안검사로 충분하다. 우측에 주어진 곡선에서는 NaOH 용액의 약 15 mL와 30 mL를 옥살산 용액에 적정한 후 두 개의 등가점을 모두 볼 수 있다. 산분해 상수(pK_a)를 계산하려면 반등분점에서 부피를 찾아야 하는데, 이 지점에서는 다음 화합물을 형성하기 위해 적정량의 반을 첨가한 것이다(여기서는 수소 옥살산 나트륨, 이후 이소듐 옥살산염). 각 동등성 지점의 중간인 7.5 mL와 22.5 mL에서 관측된 pH는 약 1.5와 4로 pK를_a 나타냈다.

약한 단극산에서는 곡선의 시작점(정량제가 첨가되기 전)과 등가점 사이의 중간 지점에 유의하다: 그 시점에서 두 종(산 및 결합 베이스)의 농도가 같다. 따라서 헨더슨-하셀발치 방정식은 다음과 같은 방법으로 해결할 수 있다.

${\displaystyle \mathrm {pH} =\mathrm {a}+\log \좌측({\frac {[{\mbox{base}}}]{\mbox{acid}}}}}}}}{\mbox{acid}}}}}}}\오른쪽)}$

${\displaystyle \mathrm {pH} =\mathrm {p}K_{\mathrm {a}+\log(1)\,}$

${\displaystyle \mathrm {pH} =\mathrm {p}K_{\mathrm {a}\,}$

따라서 곡선의 시작점과 등가점 사이의 중간에 있는 점의 pH를 찾아 단순화된 방정식을 풀면 약한 단극산의 pK를_a 쉽게 찾을 수 있다. 표본 곡선의 경우 K는_a 육안 검사에서 약 1.78×10이⁻⁵ 될 것이다(실제 K는_a2 1.7×10⁻⁵).

폴리프로틱산의 경우, 산 분해 상수를 계산하는 것은 약간 더 어려울 뿐이다: 첫 번째 산 분해 상수는 단구산에서 계산되는 것과 같은 방법으로 계산할 수 있다. 그러나 두 번째 산분해 상수는 첫 번째 등가점과 두 번째 등가점 사이의 중간 지점(인산 등 두 개 이상의 양성자를 방출하는 산의 경우 등)이다.

참조