효소동력학
Enzyme kinetics효소 키네틱스는 효소-카탈리시스 화학반응의 비율을 연구하는 학문이다.효소 운동학에서는 반응률을 측정하고 반응 조건의 변화 효과를 조사한다.이런 식으로 효소의 운동학을 연구하면 이 효소의 촉매 메커니즘, 신진대사에 있어서의 역할, 그 활성도 조절 방법, 약이나 수식어(억제기 또는 활성제)가 그 속도에 어떤 영향을 미칠 수 있는가를 밝혀낼 수 있다.
효소(E)는 일반적으로 다른 분자인 기질(S)의 반응을 촉진하는 단백질 분자다.이는 효소-하향 복합체 ES를 생성하기 위해 효소의 활성 부위와 결합되며, 변환 상태 ES*를 통해 효소-제품 복합체 EP와 거기서 제품 P로 변환된다.일련의 단계를 메커니즘이라고 한다.
- E + S ⇄ ES ⇄ ES* ⇄ EP ⇄ E + P
이 예는 하나의 기질과 하나의 제품에 대한 반응의 가장 단순한 경우를 가정한다.예를 들어, 인광글루코무타제와 같은 돌연변이는 한 위치에서 다른 위치로 인광 그룹의 전달을 촉진하며, 이소머라제는 삼인산 이소메타아제와 같이 한 부하의 단일 제품 반응을 촉진하는 효소의 보다 일반적인 용어다.그러나 그러한 효소는 그리 흔하지 않으며, 두 가지 제품 반응을 촉진하는 효소에 의해 수적으로 우세하다. 예를 들어, 여기에는 NAD에+ 의한 에탄올의 산화를 촉진하는 알코올 탈수소효소와 같은 NAD 의존성 탈수소효소가 포함된다.서너 기판이나 제품에 대한 반응은 덜 흔하지만, 그것들은 존재한다.예를 들어 글리세랄알데히드 3인산 탈수소효소는 기질 3개와 제품 2개가 있다.
효소가 디하이드로폴레이트 환원효소(오른쪽 표시)와 같은 여러 기판을 결합할 때 효소 키네틱스도 이들 기판이 결합하는 순서와 제품이 방출되는 순서를 보여줄 수 있다.단일 기질을 묶고 여러 제품을 방출하는 효소의 한 예는 단백질 기질을 두 개의 폴리펩타이드 제품으로 갈라놓는 프로테아제다.다른 것들은 뉴클레오티드와 DNA를 연결하는 DNA 중합효소와 같은 두 기판을 함께 결합한다.이러한 메커니즘은 종종 복잡한 일련의 단계들이지만, 일반적으로 전체 운동학을 결정하는 하나의 요율 결정 단계가 있다.이 속도 결정 단계는 효소로부터 제품을 방출하는 것과 관련된 것과 같은 효소 또는 기판의 화학적 반응 또는 순응적 변화일 수 있다.
효소의 구조에 대한 지식은 운동 데이터를 해석하는 데 도움이 된다.예를 들어, 구조는 기판과 제품이 카탈루션 중에 어떻게 결합되는지, 반응 중에 어떤 변화가 발생하는지, 그리고 심지어 메커니즘에서 특정한 아미노산 잔류물의 역할까지 제안할 수 있다.어떤 효소들은 메커니즘을 하는 동안 형태가 크게 변한다. 이러한 경우 효소 반응을 겪지 않는 결합 기질 아날로그와 결합되지 않은 효소 구조를 결정하는 것이 도움이 된다.
모든 생물학적 촉매들이 단백질 효소인 것은 아니다: 리보솜이나 리보솜과 같은 RNA 기반 촉매들은 RNA 스플라이싱과 번역과 같은 많은 세포 기능에 필수적이다.리보체와 효소의 주요 차이점은 RNA 촉매가 뉴클레오티드로 구성되는 반면 효소는 아미노산으로 구성된다는 점이다.리보임은 또한 반응 메커니즘과 운동학을 동일한 방법으로 분석 및 분류할 수 있지만 더 제한적인 일련의 반응을 수행한다.
통칙, 일반원칙
효소에 의해 촉매되는 반응은 정확히 같은 반응물질을 사용하며, 무가산 반응과 정확히 동일한 제품을 생산한다.다른 촉매와 마찬가지로 효소는 기판과 제품 사이의 평형 위치를 바꾸지 않는다.[1]그러나, 무가산 화학 반응과 달리, 효소-카탈라이스 반응은 포화동력학을 나타낸다.[2]주어진 효소 농도와 상대적으로 낮은 기질 농도의 경우, 반응 속도는 기질 농도와 함께 선형적으로 증가한다. 효소 분자는 대체로 자유롭게 반응을 촉진하며 기질 농도를 증가시키는 것은 효소와 기질 분자가 서로 마주치는 증가 속도를 의미한다.그러나 비교적 높은 기질 농도에서 반응률은 이론적 최대치에 접근한다. 효소 활성 부위는 거의 모두 기질에 의해 점유되어 포화 상태가 되며, 반응률은 효소의 내적 회전율에 의해 결정된다.[3]이 두 제한 사례 사이의 중간에 있는 기질 농도는M K가 나타낸다.따라서 K는M 반응속도가 최대 속도의 절반인 기질농도다.[3]
효소 운동학의 두 가지 중요한 성질은 효소가 기질로 얼마나 쉽게 포화될 수 있는가 하는 것과 그것이 달성할 수 있는 최대 비율이다.이러한 성질을 아는 것은 효소가 세포에서 무엇을 할 수 있는지를 시사하며, 효소가 이러한 조건들의 변화에 어떻게 반응할지를 보여줄 수 있다.
효소분석
효소 측정은 효소 반응 속도를 측정하는 실험실 절차다.효소는 촉매작용을 하는 반응에 의해 소비되지 않기 때문에, 효소 분석은 보통 반응 속도를 측정하기 위해 기판이나 제품의 농도 변화를 따른다.측정 방법에는 여러 가지가 있다.분광도 측정은 제품과 반응제 사이의 빛의 흡광도의 변화를 관찰한다. 방사선 측정은 시간 경과에 따른 제품의 양을 측정하기 위해 방사능을 통합하거나 방출하는 것을 포함한다.분광도 측정은 반응 속도를 연속적으로 측정할 수 있기 때문에 가장 편리하다.방사선량 검사에는 검체의 제거와 개수가 필요하지만(즉, 그것들은 불연속 검사임) 일반적으로 매우 민감하며 매우 낮은 수준의 효소 활성도를 측정할 수 있다.[4]유사한 접근법은 질량 분광법을 사용하여 기질이 제품으로 전환될 때 안정적 동위원소의 결합이나 배출을 감시하는 것이다.때때로 검사에 실패하며 실패한 검사를 부활시키기 위해서는 접근법이 필수적이다.
가장 민감한 효소 분석은 현미경을 통해 집중된 레이저를 사용하여 단일 효소 분자의 반응을 촉진시킬 때 변화를 관찰한다.이러한 측정은 효소의 반응 메커니즘 동안 공효소의 형광 변화 또는 촉매 중 발생하는 움직임을 보고하기 위해 단백질의 특정 부위에 첨가된 형광 염료 변화를 사용한다.[5]이러한 연구들은 수백만 개의 효소 분자의 평균 행동을 관찰하는 전통적인 효소 키네틱스와는 달리 단일 효소의 운동학과 역학에 대한 새로운 관점을 제공하고 있다.[6][7]
효소 검사에 대한 진행 곡선의 예는 위에 나와 있다.효소는 반응 시작 후 짧은 기간 동안 대략 선형인 초기 속도로 제품을 생산한다.반응이 진행되어 기질이 소모되면 속도는 계속 느려진다(기질이 아직 포화상태에 있지 않은 한).초기 (및 최대) 비율을 측정하기 위해, 효소 측정은 일반적으로 전체 완성을 위해 몇 퍼센트만 반응이 진행되는 동안 수행된다.초기 요율 주기의 길이는 검사 조건에 따라 달라지며 밀리초에서 시간까지 다양할 수 있다.그러나 액체를 빠르게 혼합하기 위한 장비는 1초 미만의 초기 속도에서 빠른 운동 측정을 허용한다.[8]이러한 매우 빠른 측정은 아래에서 설명하는 안정 전 상태의 운동학적 측정을 위해 필수적이다.
대부분의 효소 운동학 연구는 효소 반응의 초기, 대략 선형 부분에 집중한다.그러나 전체 반응 곡선을 측정하여 이 데이터를 비선형 비율 방정식에 적합시킬 수도 있다.이러한 효소 반응을 측정하는 방법을 진행-곡선 분석이라고 한다.[9]이 접근방식은 초기 속도가 너무 빨라서 정확하게 측정할 수 없을 때 급속한 운동학에 대한 대안으로 유용하다.
단침반동작
단일하중 메커니즘을 가진 효소에는 삼인산염화효소나 비스포스포글리세르산 무타아제와 같은 이소머라이즈, 아데닐산염 사이클라아제와 같은 분자 내 라이아제, RNA 리보아제인 망치헤드 리보아제 등이 있다.[10]그러나 단일 기질만 가지고 있는 일부 효소는 이 기질 범주에 속하지 않는다.카탈라아제는 효소가 과산화수소 기질의 첫 번째 분자와 반응하여 산화되어 두 번째 분자에 의해 감소되는 것을 예로 들 수 있다.단일 기질이 관련되기는 하지만, 변형효소 중간이 존재한다는 것은 카탈라아제의 메커니즘이 실제로 탁구 메커니즘이라는 것을 의미하며, 이는 아래 다부하 반응 섹션에서 논의되는 메커니즘의 일종이다.
미카엘리스-멘텐 운동학
효소-카탈리시스 반응은 포화성이기 때문에 촉매변환율은 증가하는 기질에 대해 선형 반응을 보이지 않는다.초기 반응속도를 기판농도 범위([S]로 표시)에서 측정하면, 오른쪽과 같이 [S]가 증가함에 따라 초기 반응속도( 가 증가한다.그러나 [S]가 높아질수록 효소는 기질에 포화 상태가 되고 초기율은 효소의 최대 속도인 V에max 도달한다.
오른쪽에는 단일하강반응의 Michaelis-Menten 운동모델이 표시된다.효소 E와 기질 S 사이에 초기 2분자 반응이 있어 효소-하향 복합 ES를 형성한다.효소 반응 속도는 기질 농도가 V라는max 특정 수준까지 증가함에 따라 증가하며, V에서는max 기질 농도의 증가는 기질(S)과 반응할 수 있는 효소(E)가 더 이상 없기 때문에 반응률의 증가를 유발하지 않는다.여기서 반응속도는 ES 콤플렉스에 의존하게 되고 반응은 0의 순서로 단분자 반응이 된다.단분자 반응 → k + P E + P에 대한 효소 메커니즘은 상당히 복잡할 수 있지만, 으로 이 반응을 명백한 단분자 비율 상수로cat 하나의 촉매 스텝으로 모델링할 수 있는 요율 결정 효소 단계가 있다.만약 반응 경로가 하나 또는 여러 중간자에 걸쳐 진행된다면, k는cat 몇 개의 기본 속도 상수의 함수가 되는 반면, 단일 초등 반응의 가장 단순한 경우(예: 중간자가 없음)는 기초 단분자 속도 상수 k와2 동일할 것이다.겉보기 비분자율 상수 k는cat 회전수라고도 하며, 초당 촉매되는 효소 반응의 최대 수를 나타낸다.
Michaelis-Menten 방정식은[11] (초기) 반응 속도 v가0 기판 결합 평형 위치 및 비율 상수2 k에 어떻게 의존하는지 설명한다.
- (마이클리스-멘텐 방정식)
상수로
이 Michaelis-Menten 방정식은 대부분의 단하 효소 운동학의 기초가 된다.[12]이 방정식의 기초가 되는 두 가지 중요한 가정(중간 또는 제품 억제만을 수반하는 메커니즘에 대한 일반적인 가정과는 별개로, 유사성이나 협력성은 없다).첫 번째 가정은 소위 준안정상태 가정(또는 유사안정상태 가설), 즉 기질결합 효소(그리고 또한 결합되지 않은 효소)의 농도가 제품과 기질보다 훨씬 느리게 변화하여 복합체의 시간에 따른 변화는 [ 로 설정될 수 있다는 것이다.두 번째 가정은 총효소농도가 시간이 지남에 따라 변하지 않기 때문에 = [E + [ = ! ce 여기에서 완전한 파생어를 찾을 수 있다.
Michaelis 상수 K는M 효소 반응 속도가 절반 V인max 농도로 실험적으로 정의되는데, 이는 [S] = K를M Michaelis-Menten 방정식에 대입하여 검증할 수 있으며 그래픽으로도 확인할 수 있다.속도 결정 효소 단계가 기질 분해에 비해 느린 경우( - Michaelis 상수 K는M 대략 ES 복합체의 분해 상수 K이다D.
If is small compared to then the term and also very little ES complex is formed, thus 가 근사치 따라서 제품 형성률은
따라서 제품 형성률은 효소 농도와 기질 농도에 따라 달라지는데, 이 방정식은 해당 의사초순수율 k 2/ K 에 대한 양분자 반응을 닮았다 이 상수는 촉매효율을 측정하는 것이다.가장 효율적인 효소 108– 1010M−1 s−1의 범위에 있는 k2/KM{\displaystyle k_{2}{M}}에 달한다.이러한 효소들은 그렇게 그들이 효과적으로 위해 공존과 효율성(확산 제한)에 유리한 이론적 한계에 다다라기질 분자 발생할 때마다 반응 catalyse, 되고라고 부른다 효율적이다.동역학적으로 완벽한 [13]효소하지만 대부분의 효소는 완벽과는 거리가 멀:k2의 평균 값/KM{\displaystyle k_{2}{\rm{M}}}이고, k2{\displaystyle k_{2}}는 약 105을 − 1M1{10^{5\displaystyle}{\rm{s}}^{)}{\rm{M}}^{)}−}과 10을 1{\displaystyle 10{\rm{s}}^{)}}, 각각 − 있다.[14]
시간 코스 운동 분석을 위한 Michaelis-Menten 방정식의 직접 사용
Michaelis-Menten 방정식에 의해 예측된 관측된 속도는 Michaelis-Menten 방정식을 화학적 운동학적 1차 방정식에 통합함으로써 기질의 타임 코스 소멸과 제품의 생산을 직접 모델링하는 데 사용할 수 있다.하지만 만약 한 문제를 오일러의 번호의 첫번째 주문 반응 속도론의 설명에서 사용과 관련된 인식 이것은. 계산을 단일은 각 기간 이후에 나머지 기질을 나타내는 상수로 다시 쓸 수 있게 체계적인 실수를 소개한다 i.e. e−k은 분할된 상수 달성할 수 있다.[15]
1983년 스튜어트 벨(그리고 독립적으로 산티아고 슈넬과 클라우디오 멘도자 1997년)은 Michaelis-Menten 메커니즘의 시간 코스 운동학적 분석을 위한 폐쇄형 폼 솔루션을 도출했다.[16][17]Schnell-Mendoza 방정식으로 알려진 이 해결책은 다음과 같은 형태를 가지고 있다.
여기서 W[ ]는 램버트-W 함수다.[18][19]그리고 F(t)가 있는 곳
이 방정식은 베르베란-산토스가 얻은 아래의 방정식에 포함되며,[20] 초기 기질 농도가 효소의 그것과 가까울 때도 유효하다.
여기서 W[ ]는 다시 램버트-W 함수다.
Michaelis-Menten 방정식의 선형 그림
위의 v 대 [S]의 플롯은 선형적이지 않다. 처음에는 낮은 [S]에서 선형이지만 높은 [S]에서 포화되도록 구부러진다.컴퓨터에 비선형 곡선을 맞추는 현대 이전에는 이러한 비선형성이 K와M V의max 정확한 추정을 어렵게 할 수 있었다.따라서, 몇몇 연구자들은 라인위버-버크 플롯, 이디-와 같은 미카엘리스-멘텐 방정식의 선형화를 개발했다.호프스티 도표와 하네스-울프 플롯.이러한 모든 선형 표현은 데이터를 시각화하는 데 유용할 수 있지만, 비선형 회귀 분석 방법에 의한 보다 정확한 결정을 가능하게 하는 컴퓨터 소프트웨어를 쉽게 이용할 수 있기 때문에 운동 매개변수를 결정하는 데 사용해서는 안 된다.[21]
Lineweaver-Burk 플롯 또는 이중 역수 플롯은 운동 데이터를 나타내는 일반적인 방법이다.이것은 Michaelis-Menten 방정식의 양쪽의 역수를 취함으로써 만들어진다.오른쪽에서 보듯이 이것은 Michaelis-Menten 방정식의 선형 형태로서, 1/V에max 해당하는 y 절편과 -1/K를M 나타내는 그래프의 x 절절을 가진 y = mx + c 방정식으로 직선을 만든다.
당연히 음의 1/[S]에서는 어떤 실험 값도 취할 수 없다. 하한값 1/[S] = 0(y-절편)은 무한 기질 농도에 해당하며, 여기서 우측과 같이 1/v=1/V이므로max x 절편은 양의 농도에서 취한 실험 데이터의 외삽이다.보다 일반적으로 Lineweaver-Burk 그림은 낮은 기질 농도에서 취한 측정의 중요성을 왜곡하므로 V와 K의maxM 부정확한 추정치를 산출할 수 있다.[22]보다 정확한 선형 플로팅 방법은 이디-이다.호프스티 플롯.이 경우 v/[S]에 대해 v가 구성된다.세 번째 공통 선형 표현인 Hanes-Woolf 플롯에서 [S]/v는 [S]에 대해 플롯된다.일반적으로 데이터 정규화는 실험 작업의 양을 줄이는 데 도움이 될 수 있고 출력의 신뢰성을 높일 수 있으며, 그래픽 분석과 수치 분석에 모두 적합하다.[23]
운동 상수의 실제적 유의성
효소 운동학에 대한 연구는 두 가지 기본적인 이유로 중요하다.첫째, 효소가 어떻게 작용하는지를 설명하는 데 도움이 되고, 둘째, 살아있는 유기체에서 효소가 어떻게 작용하는지를 예측하는 데 도움이 된다.위에서 정의한 운동 상수 K와M V는max 효소가 신진대사를 조절하기 위해 어떻게 함께 작용하는지를 이해하려는 시도에 매우 중요하다.
이러한 예측을 하는 것은 간단한 시스템에서도 사소한 것이 아니다.예를 들어 옥살로아세테이트는 미토콘드리온 내 말산탈수소효소에 의해 형성된다.옥살로아세테이트를 구연산 싱타아제, 인산염피루브산 카르복시킨아제 또는 아스파르트아미노트란스페라제로 섭취할 수 있으며, 구연산 사이클, 글루코네제네시스 또는 아스파르트산 생합성제로 섭취할 수 있다.옥살로아세테이트가 어느 경로로 들어가는지 예측할 수 있는 것은 옥살로아세테이트의 농도와 이들 효소의 농도 및 운동학적 지식을 필요로 한다.대사 경로의 행동을 예측하는 이 목표는 방대한 양의 운동 및 유전자 표현 데이터를 전체 유기체의 수학적 모델로 합성하는 데 있어 가장 복잡한 표현에 도달한다.또는, 대사 모델링 문제의 유용한 단순화 중 하나는 기초 효소 운동학을 무시하고 플럭스 밸런스 분석이라는 기술인 반응 네트워크의 스토이치측정법에 관한 정보에만 의존하는 것이다.[24][25]
중간값의 Michaelis-Menten 운동학
또한 덜 간단한 사례도 고려할 수 있다.
효소와 중간이 있는 콤플렉스가 존재하고 그 중간이 두 번째 단계에서 제품으로 전환되는 경우.이 경우 우리는 매우 유사한 방정식을[26] 가지고 있다.
하지만 상수는 다르다.
제한 사례 따라서 EI E+ P {> E + 의 마지막 단계가 이전 단계보다 훨씬 빠를 때 원래의 방정식을 다시 얻는다.수학적으로 K k c a t k k_{cat
다부하 반응
다중-하향 반응은 기판이 어떻게 결합하고 어떤 순서로 결합하는지를 설명하는 복잡한 비율 방정식을 따른다.기질 A의 농도가 일정하게 유지되고 기질 B가 변화한다면 이러한 반응의 분석은 훨씬 간단하다.이러한 조건 하에서 효소는 단하 효소와 똑같이 작용하며 [S]에 의한 v의 플롯은 기질 B에 대한 명백한 K와M V 상수를max 제공한다.이러한 측정 세트가 A의 서로 다른 고정 농도에서 수행되는 경우, 이러한 데이터를 사용하여 반응 메커니즘이 무엇인지 파악할 수 있다.기판 A와 B 두 개를 가져다가 P와 Q 두 개로 만드는 효소의 경우, 3차 복합체와 탁구라는 두 가지 메커니즘이 있다.
3차 복합 메커니즘
이러한 효소에서는 두 기질 모두 효소와 동시에 결합하여 EAB ternary 콤플렉스를 생성한다.바인딩 순서는 무작위(임의의 메커니즘)이거나 기판은 특정 시퀀스(순서된 메커니즘)에서 바인딩해야 한다.ternary-complex 메커니즘을 가진 효소의 v by [S] 곡선 세트(고정 A, 가변 B)를 Lineweaver-Burk 플롯에 표시하면 생성된 선 세트가 교차한다.
3차 복합 메커니즘을 가진 효소는 글루타티온 S-전달효소,[27] 디하이드로폴리스 환원효소[28], DNA 중합효소를 포함한다.[29]다음 링크는 디하이드로폴레이트 환원효소와[β] DNA 중합효소의[γ] 3차 복합 메커니즘의 짧은 애니메이션을 보여준다.
탁구 메커니즘
오른쪽에 보이는 것처럼 탁구 메커니즘을 가진 효소는 E와 화학적으로 변형된 형태의 E*라는 두 가지 상태로 존재할 수 있다. 이 변형 효소는 중간 효소로 알려져 있다.그러한 메커니즘에서 기질 A는 결합하고, 예를 들어 화학 그룹을 활성 부위로 전송함으로써 효소를 E*로 변화시킨 다음 방출된다.첫 번째 기질이 방출된 후에야 기질 B가 변형된 효소와 결합하여 반응하여 변형되지 않은 E 형태를 재생할 수 있다.탁구 메커니즘이 있는 효소의 v by [S] 곡선 세트(고정 A, 가변 B)를 라인위버-버크 플롯에 표시하면 일련의 평행선이 생성된다.이것을 이차 줄거리라고 한다.
탁구 메커니즘이 있는 효소에는 티오레독신 페록시다아제와 같은 산화효소,[30] 아킬네우라마네이트 시티딜전달효소와[31] 같은 전달효소, 트립신, 치모트리핀과 같은 세린 프로테아제가 포함된다.[32]세린 프로테아제는 소화 효소(트립신, 치모트립신, 엘라스타아제), 혈액 응고 폭포의 여러 효소 등을 포함한 매우 흔하고 다양한 효소군이다.이러한 세린 프로테아제들에서 E* 중량은 단백질 기질 내의 펩타이드 결합에 활성 사이트 세린 잔류물의 공격에 의해 형성된 아킬-엔자임 종이다.키모트립신의 메커니즘을 보여주는 짧은 애니메이션이 여기에 연결되어 있다.[δ]
가역성 촉매 및 홀데인 방정식
외부 요인은 양방향으로 반응을 촉진하는 효소의 능력을 제한할 수 있다(여기서 촉매의 성질 자체는 미세한 가역성의 원리에 따라 하나의 방향만 촉매할 수 없다는 것을 의미한다).우리는 양방향으로 반응을 촉진시키는 효소의 경우를 고려한다.
The steady-state, initial rate of the reaction is
은(는) 전방 방향으로 반응이 진행되면 양이고(→ P 그렇지 않으면 음이다.
Equilibrium requires that , which occurs when . This shows that thermodynamics fo4가지 속도 상수의 값 사이의 관계를 분석한다.
The values of the forward and backward maximal rates, obtained for , , and , , respectively, are and , respectively.이들의 비율은 평형 상수와 같지 않은데, 이는 열역학적으로 최대 속도의 비율을 구속하지 않는다는 것을 의미한다.이것은 효소가 반응의 한 특정한 방향에서 훨씬 더 좋은 "촉매"가 될 수 있다는 것을 설명한다.[33]
On can also derive the two Michaelis constants and .The Haldane equation is the relation .
따라서 열역학에서는 a / K {{max 값 사이의 비율을 구속하고, Vm 의 비율은 구속한다
비마이클리스-멘텐키네틱스
많은 다른 효소 체계는 비 Michaelis-Menten 행동을 따른다.[34]선별된 몇 가지 예로는 자가 촉매 효소, 협동 효소 및 알로스테릭 효소, 계면 및 세포내 효소, 공정 효소 등의 운동학을 들 수 있다.일부 효소는 활성 부지에 대한 기질의 공동 결합을 나타내는 S자형 v를 [S] 플롯으로 생성한다.이것은 하나의 기질 분자의 결합이 후속 기질 분자의 결합에 영향을 미친다는 것을 의미한다.이러한 행동은 여러 활성 부위가 상호작용하는 복합 효소에서 가장 흔하다.[35][36]여기서 협력의 메커니즘은 헤모글로빈과 유사하며, 하나의 활성 사이트에 기질이 결합되어 기질 분자에 대한 다른 활성 부위의 친화력을 변화시킨다.양의 협력성은 첫 번째 기질 분자의 결합이 기질에 대한 다른 활성 부위의 친화력을 증가시킬 때 발생한다.음의 협력성은 첫 번째 기질 결합이 다른 기질 분자에 대한 효소의 친화력을 감소시킬 때 발생한다.
알로스테릭 효소에는 부협동성을 보이는 포유류 티로실 tRNA-싱테타아제,[37] 양성협동성을 보이는 세균성 아스파라테이트 트랜스카르바모일라제[38], 인포프로토키나제 등이 있다.[39]
협력성은 놀라울 정도로 흔하며 기질 농도의 변화에 대한 효소의 반응을 조절하는데 도움을 줄 수 있다.[35]양의 협력성은 효소를 [S]에 훨씬 더 민감하게 만들고 그들의 활동은 좁은 범위의 기질 농도에 걸쳐 큰 변화를 보일 수 있다.반대로, 부정적인 협력성은 [S]의 작은 변화에 효소를 무감각하게 만든다.
힐 방정식은[40] 종종 비마이클리스-멘텐 운동학에서 협력성의 정도를 정량적으로 설명하는데 사용된다.파생 힐 계수 n은 한 활성 사이트에 대한 기질 결합이 다른 활성 사이트에 대한 기질 결합에 얼마나 영향을 미치는지 측정한다.힐 계수 <1>은 음의 협력성을 나타내고, 계수 >1은 양의 협력성을 나타낸다.
안정 전 상태 운동학
효소가 기질에 섞이고 난 후 첫 순간, 어떤 제품도 형성되지 않았고 어떤 매개체도 존재하지 않는다.다음 몇 밀리초의 반응에 대한 연구는 안정 전 상태의 운동학이라고 불린다.따라서 안정 전 상태 운동학은 정상 상태 농도에 도달할 때까지 효소-하중 중간자(ES 또는 E* 등)의 형성 및 소비와 관련이 있다.
이 접근법은 처음에 키모트립신(Chymotrypsin)에 의해 촉매된 가수분해 반응에 적용되었다.[41]종종 중간 물질의 검출은 효소가 어떤 메커니즘을 따르는지 조사하는 데 있어 중요한 증거물이다.예를 들어, 위에 나타낸 탁구 메커니즘에서 빠른 운동 측정은 제품 P의 방출을 따르고 수정된 효소 중간 E*[42]의 형성을 측정할 수 있다.키모트립신의 경우, 이 중간은 활성 부위의 핵포실 세린에 의한 기질에 대한 공격과 아킬-엔자임 중간체의 형성에 의해 형성된다.
오른쪽 그림에서 효소는 반응의 처음 몇 초 안에 E*를 빠르게 생성한다.그리고 나서 안정 상태에 도달하면 속도가 느려진다.이 반응의 빠른 폭발 위상은 효소의 단 한번의 회전율을 측정한다.결과적으로, 그래프의 y축에 대한 절편으로 보이는 이 버스트에서 방출되는 제품의 양 또한 검사에 존재하는 기능성 효소의 양을 제공한다.[43]
화학 메커니즘
효소 운동학을 측정하는 중요한 목표는 효소 반응의 화학적 메커니즘, 즉 기질을 제품으로 변형시키는 화학적 단계의 순서를 결정하는 것이다.위에서 논의한 운동적 접근방식은 어떤 비율의 매개체가 형성되고 상호변환되는지를 보여줄 것이지만, 이들 매개체가 정확히 무엇인지 확인할 수는 없다.
다양한 용액 조건이나 약간 변형된 효소나 기판에 대해 취한 운동학적 측정은 반응에서 속도 결정 단계나 매개체를 드러내기 때문에 종종 이 화학적 메커니즘을 밝혀낸다.예를 들어, 수소 원자에 대한 공밸런트 결합의 파기는 일반적인 요율 결정 단계다.수소 전이 가능성 중 어느 것이 속도 결정인가에 대해서는 안정적인 동위원소인 중수소로 각 수소를 대체하는 운동 효과를 측정함으로써 알 수 있다.임계수소가 교체되면 1차 운동동위원소 효과로 속도가 달라지는데, 이는 수소에 대한 결합보다 중수소에 대한 결합이 깨지기 어렵기 때문이다.[44]C/12C, O/16O와 같은 다른 동위원소 대체물과 유사한 효과를 측정하는 것도 가능하지만, 이러한 효과는 더욱 미묘하다.[45]
동위원소는 또한 최종 생산물에서 기질 분자의 다양한 부분의 운명을 밝히는 데 사용될 수 있다.예를 들어, 최종 생산물에서 산소 원자의 기질을 식별하는 것은 때때로 어렵다. 왜냐하면 그것은 물이나 기질의 일부에서 왔을 수 있기 때문이다.이것은 반응에 참여하는 다양한 분자에 산소의 안정적인 동위원소 O를 체계적으로 대체하고 제품의 동위원소를 확인함으로써 결정될 수 있다.[46]화학적 메커니즘은 또한 서로 다른 pH 조건 하에서 운동학 및 동위원소 효과를 검사하거나,[47] 금속 이온 또는 기타 결합 공작용제를 변경하거나,[48] 보존된 아미노산 잔류물의 현장 유도 돌연변이 유발에 의해 또는 기질 유사성이 존재하는 곳에서 효소의 행동을 연구함으로써 해명될 수 있다.[49]
효소억제 및 활성화
효소억제제는 효소 활동을 줄이거나 폐지하는 분자, 효소 활성제는 효소의 촉매율을 높이는 분자다.이러한 상호작용은 되돌릴 수 있거나(즉, 억제제를 제거하면 효소 활성이 회복된다) 되돌릴 수 없거나(즉, 억제제가 효소를 영구적으로 비활성화) 되돌릴 수 있다.
가역억제제
전통적으로 가역성 효소 억제제는M K와max V에 미치는 영향에 따라 경쟁성, 비경쟁성 또는 비경쟁성으로 분류되어 왔다.이러한 다른 효과는 각각 효소 E, 효소-하향 복합체 ES, 또는 둘 다에 대한 억제제 결합에서 비롯된다.이러한 등급의 분할은 파생되는 문제에서 발생하며, 하나의 바인딩 이벤트에 서로 다른 두 개의 바인딩 상수를 사용해야 하는 결과를 초래한다.억제제의 결합과 효소 활성도에 대한 그것의 영향은 두 가지 분명히 다른데, 이것은 전통적인 방정식이 인정하지 않는 또 다른 문제다.비경쟁적 억제에서 억제제의 결합은 효소의 100% 억제만을 초래하며, 그 사이에 있는 어떤 것의 가능성을 고려하지 않는다.[50]비경쟁적 억제에서 억제제는 그 알로스테릭 부위에서 효소와 결합하므로, 효소와 기질의 결합 친화력, 즉 K의M 역행성은 그대로 유지된다.반면에 V는max 억제되지 않은 효소에 비해 감소할 것이다.Lineweaver-Burk 플롯에서 비경쟁 억제제의 존재는 1/V로max 정의되는 y 절편의 변화에 의해 설명된다.-1/K로M 정의된 x절은 그대로 유지된다.경쟁 억제에서 억제제는 기질과 경쟁하면서 활성 부위의 효소와 결합한다.이에 따라 K는M 늘어나고 V는max 그대로 유지될 것이다.[51]억제 용어의 일반적인 형태는 또한 효소에 대한 억제제 결합과 다른 결합 용어와 그것의 관계를 흐리게 한다. 그것은 Michaelis-Menten 방정식 또는 리간드 수용체 결합과 관련된 선량 반응 곡선이다.관계를 입증하기 위해 다음과 같은 재배치를 할 수 있다.
하단에 0 추가([I]-[I])
[I]+K로i 나누기
이 표기법은 반응 속도가 기질과 상호작용하는 효소 모집단의 백분율에 따라 달라지는 Michaelis-Menten 방정식과 유사하게 억제제의 효과는 억제제와 상호작용하는 효소 모집단의 백분율의 결과라는 것을 보여준다.현재 형태에서 이 방정식의 유일한 문제는 억제제 결합으로 효소의 절대 억제를 가정하는 것인데, 실제로 기질 회전의 100% 억제에서 단지 0% 미만으로 넓은 범위의 효과가 있을 수 있다.이를 설명하기 위해 델타 Vmax 항을 포함함으로써 다른 수준의 억제를 허용하도록 방정식을 쉽게 수정할 수 있다.
또는
이 용어는 억제제가 모집단의 개별 효소와 상호작용할 때 존재하는 잔류 효소 활성을 정의할 수 있다.그러나 이 용어의 포함은 2차max V 용어가 최초 용어보다 더 높은 것으로 판명될 경우 활성화될 가능성을 허용하는 부가가치를 가진다.활성화 가능성과 함께 설명하기 위해 억제제 "I"를 여기서 "X"로 나타내는 수식어로 대체하는 표기법을 다시 작성할 수 있다.
이 용어는 Michaelis-Menten 방정식의 최대 속도와 관련된 운동 효과를 다루는 단순화된 방법을 도출하지만, K와M 관련된 영향을 설명하는 데 사용되는 용어로 잠재적인 문제를 강조한다.기질에 대한 효소의 친화력과 관련된 K는M 대부분의 경우 효소 억제제 상호작용에 의해 직접 발생할 수 있는 효소의 결합 부위의 잠재적 변화와 관련되어야 한다.V를max 수정하기 위해 위에서 제안한 것과 유사한 용어가 대부분의 상황에서 적절해야 한다.[52]
경쟁적이고 비경쟁적인 모델에 속하는 가역적 억제의 몇 가지 예가 다음 논문에서 논의되었다.[53][54][55]
되돌릴 수 없는 억제제
효소 억제제는 또한 일반적으로 활성 부위의 잔여물을 공동 수정함으로써 효소를 불가역적으로 비활성화할 수 있다.자살 기질이라고 할 수 있는 이러한 반응은 기하급수적인 붕괴 기능을 따르며 대개 포화상태에 이른다.포화도 이하에서는 억제제와 관련하여 첫 번째 순서 운동학을 따른다.되돌릴 수 없는 억제는 두 가지 뚜렷한 유형으로 분류될 수 있다.친화력 라벨 표시는 고반응성 기능 그룹이 관심 단백질에 촉매적으로 임계 잔류물을 수정하여 억제를 발생시키는 되돌릴 수 없는 억제 유형이다.반면에 메커니즘 기반 억제는 억제제를 결합한 후 효소 매개 변형을 통해 후자를 불가역적으로 수정하는 반응성 그룹으로 변형시키는 것을 포함한다.
억제력의 가역성과 불가역성에 대한 철학적 담론
위의 두 가지 제목에서 가역적 억제와 되돌릴 수 없는 억제를 논의한 경우, 가역성(또는 불가역성)의 개념은 분석의 시간 프레임, 즉 억제제의 연관성과 분리를 수반하는 가역적 측정에 전적으로 의존하는 순수 이론적 구조라는 점을 지적할 필요가 있을 것이다.검사 결과가 초 단위로 평가되고 그 반대의 경우 분자는 되돌릴 수 없는 것처럼 보일 수 있다.주어진 비임의 검사 시간 틀에서 가역성과 불가역성을 포괄하는 억제제 행동의 연속성이 있다.느린 온셋 행동을 보이는[53] 억제제들이 있고, 이러한 억제제들의 대부분은, 변함없이, 관심 있는 단백질 목표물에 긴밀하게 결합하는 것을 보여준다.[53][54]
촉매제

효소-하향 상호작용에 대해 선호하는 모델은 유도 적합 모델이다.[56]이 모델은 효소와 기질 사이의 초기 상호작용은 비교적 약하지만, 이러한 약한 상호작용은 결합을 강화하는 효소의 순응적 변화를 빠르게 유도한다고 제안한다.또한 이러한 순응적 변화는 활성 부위의 촉매 잔류물을 반응에서 변경될 기질 내의 화학적 결합에 가깝게 만든다.[57]순응적 변화는 원형 이분법 또는 이중 편광 간섭법을 사용하여 측정할 수 있다.결합이 이루어진 후, 하나 이상의 촉매변환 메커니즘은 반응에 대한 대체 화학적 경로를 제공함으로써 반응 전환 상태의 에너지를 낮춘다.촉매변환 메커니즘에는 결합 변형률, 근접성 및 방향성, 활성 사이트 양성자 또는 수용자에 의한 촉매변환, 공동 촉매변환 및 양자 튜닝이 포함된다.[42][58]
효소 운동학은 어떤 형태의 촉매제가 효소에 의해 사용되는지를 증명할 수 없다.그러나 일부 운동 데이터는 다른 기법으로 검사될 가능성을 제시할 수 있다.예를 들어, 폭발 위상 전 안정 상태 운동학을 가진 탁구 메커니즘은 이 효소의 메커니즘에서 공동 촉매 촉매제가 중요할 수 있다는 것을 암시할 수 있다.또는 K가M 아닌 V에max 대한 강한 pH 영향을 관찰하면 활성 부위의 잔류물이 특정 이온화 상태에 있어야 강직화가 발생할 수 있다.
역사
1902년 빅토르 앙리(Victor Henri)는 효소 운동학의 정량적 이론을 제안했지만,[59] 당시에는 수소 이온 농도의 실험적 중요성이 아직 인정되지 않았다.후에 피터 Lauritz 쇠 렌센과 1909[60]에 있는 독일 화학자 Leonor 마이클 리스 박사와 모드 레오노라 Menten(마이클 리스의 연구실에 있는 시간에 박사 후 연구원)과 이제는 일반적으로 Michaelis-Ment로 여기어 진다 그의 방정식을 확인 앙리의 실험을 다시 해 버퍼링의 개념을 도입했다 대수 pH-scale 명시되어 있었다.en키네틱스(Henri-Michaelis-Menten kinetics)도 있다.[61]그들의 연구는 G. E. Briggs와 J. B. S. Haldane에 의해 더욱 발전되었는데, 그는 오늘날에도 여전히 효소 활동을 모델링하는 출발점으로 널리 여겨지는 운동 방정식을 도출했다.[62]
앙리-마이클리스-멘텐 접근법의 주요 공헌은 두 단계로 나누어 효소 반응을 생각하는 것이었다.첫째, 기질은 역행적으로 효소에 결합하여 효소-하강 복합체를 형성한다.이것은 때때로 마이클리스 콤플렉스라고 불린다.그리고 효소는 반응의 화학적 단계를 촉진하여 제품을 방출한다.많은 효소의 운동학은 단순한 Michaelis-Menten 모델에 의해 적절하게 설명되지만, 모든 효소는 모델에서 설명되지 않는 내부 운동을 가지고 있으며 전체 반응 운동학에 상당한 기여를 할 수 있다.이것은 기본적인 Michaelis Menten 메커니즘의 수학적 확장인 [63][64][65]변동률과 연결된 여러 Michaelis-Menten 경로를 도입하여 모델링할 수 있다.[66]
소프트웨어
ENZO(Enzyme Kinetics)는 효소 촉매 반응의 운동 모델을 구축하기 위한 그래픽 인터페이스 툴이다.ENZO는 규정된 효소 반응 체계에서 자동으로 상응하는 미분 방정식을 생성한다.이러한 미분 방정식은 실험적으로 관측된 시간 코스 곡선을 위해 미분 방정식의 계수에 맞는 숫자 해결기와 회귀 알고리즘에 의해 처리된다.ENZO는 라이벌 반응 체계의 신속한 평가를 가능하게 하고 효소 운동학에서 일상적인 테스트에 사용될 수 있다.[67]
참고 항목
각주
참조
- ^ Wrighton MS, Ebbing DD (1993). General chemistry (4th ed.). Boston: Houghton Mifflin. ISBN 978-0-395-63696-1.
- ^ Srinivasan, Bharath (27 September 2020). "Words of advice: teaching enzyme kinetics". The FEBS Journal. 288 (7): 2068–2083. doi:10.1111/febs.15537. ISSN 1742-464X. PMID 32981225.
- ^ a b Fromm H.J., Hargrove M.S. (2012) 효소 키네틱스.인: 생화학 필수품.베를린 하이델베르크 스프링거
- ^ Danson M, Eisenthal R (2002). Enzyme assays: a practical approach. Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-963820-8.
- ^ Xie XS, Lu HP (June 1999). "Single-molecule enzymology". The Journal of Biological Chemistry. 274 (23): 15967–70. doi:10.1074/jbc.274.23.15967. PMID 10347141.
- ^ Lu HP (June 2004). "Single-molecule spectroscopy studies of conformational change dynamics in enzymatic reactions". Current Pharmaceutical Biotechnology. 5 (3): 261–9. doi:10.2174/1389201043376887. PMID 15180547.
- ^ Schnell JR, Dyson HJ, Wright PE (2004). "Structure, dynamics, and catalytic function of dihydrofolate reductase". Annual Review of Biophysics and Biomolecular Structure. 33: 119–40. doi:10.1146/annurev.biophys.33.110502.133613. PMID 15139807.
- ^ Gibson QH (1969). "[6] Rapid mixing: Stopped flow". Rapid mixing: Stopped flow. Methods in Enzymology. Vol. 16. pp. 187–228. doi:10.1016/S0076-6879(69)16009-7. ISBN 978-0-12-181873-9.
- ^ Duggleby RG (1995). "[3] Analysis of enzyme progress curves by nonlinear regression". Analysis of enzyme progress curves by non-linear regression. Methods in Enzymology. Vol. 249. pp. 61–90. doi:10.1016/0076-6879(95)49031-0. ISBN 978-0-12-182150-0. PMID 7791628.
- ^ Murray JB, Dunham CM, Scott WG (January 2002). "A pH-dependent conformational change, rather than the chemical step, appears to be rate-limiting in the hammerhead ribozyme cleavage reaction". Journal of Molecular Biology. 315 (2): 121–30. doi:10.1006/jmbi.2001.5145. PMID 11779233. S2CID 18102624.
- ^ Michaelis L.와 M.L. Kinetik 데르 Invertinwirkung 생화학.Z. 1913; 49:333–369 영어 번역 액세스 2007년 4월 6일
- ^ Srinivasan, Bharath (2021). "A Guide to the Michaelis-Menten equation: Steady state and beyond". The FEBS Journal. n/a (n/a). doi:10.1111/febs.16124. ISSN 1742-4658. PMID 34270860.
- ^ Stroppolo ME, Falconi M, Caccuri AM, Desideri A (September 2001). "Superefficient enzymes". Cellular and Molecular Life Sciences. 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526. S2CID 24874575.
- ^ Bar-Even A, Noor E, Savir Y, Liebermeister W, Davidi D, Tawfik DS, Milo R (May 2011). "The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters". Biochemistry. 50 (21): 4402–10. doi:10.1021/bi2002289. PMID 21506553.
- ^ Walsh R, Martin E, Darvesh S (January 2010). "A method to describe enzyme-catalyzed reactions by combining steady state and time course enzyme kinetic parameters". Biochimica et Biophysica Acta (BBA) - General Subjects. 1800 (1): 1–5. doi:10.1016/j.bbagen.2009.10.007. PMID 19840832.
- ^ Beal SL (December 1983). "Computation of the explicit solution to the Michaelis-Menten equation". Journal of Pharmacokinetics and Biopharmaceutics. 11 (6): 641–57. doi:10.1007/BF01059062. PMID 6689584. S2CID 32571415.
- ^ Schnell S, Mendoza C (1997). "Closed Form Solution for Time-dependent Enzyme Kinetics". Journal of Theoretical Biology. 187 (2): 207–212. Bibcode:1997JThBi.187..207S. doi:10.1006/jtbi.1997.0425.
- ^ Goudar CT, Sonnad JR, Duggleby RG (January 1999). "Parameter estimation using a direct solution of the integrated Michaelis-Menten equation" (PDF). Biochimica et Biophysica Acta (BBA) - Protein Structure and Molecular Enzymology. 1429 (2): 377–83. doi:10.1016/s0167-4838(98)00247-7. PMID 9989222. Archived from the original (PDF) on 9 November 2015.
- ^ Goudar CT, Harris SK, McInerney MJ, Suflita JM (December 2004). "Progress curve analysis for enzyme and microbial kinetic reactions using explicit solutions based on the Lambert W function". Journal of Microbiological Methods. 59 (3): 317–26. doi:10.1016/j.mimet.2004.06.013. PMID 15488275.
- ^ Berberan-Santos MN (2010). "A General Treatment of Henri Michaelis Menten Enzyme Kinetics: Exact Series Solution and Approximate Analytical Solutions" (PDF). MATCH Communications in Mathematical and in Computer Chemistry. 63: 283.
- ^ Jones ME (December 1992). "Analysis of algebraic weighted least-squares estimators for enzyme parameters". The Biochemical Journal. 288 (Pt 2): 533–8. doi:10.1042/bj2880533. PMC 1132043. PMID 1463456.
- ^ Tseng SJ, Hsu JP (August 1990). "A comparison of the parameter estimating procedures for the Michaelis-Menten model". Journal of Theoretical Biology. 145 (4): 457–64. Bibcode:1990JThBi.145..457T. doi:10.1016/S0022-5193(05)80481-3. PMID 2246896.
- ^ Bravo IG, Busto F, De Arriaga D, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (September 2001). "A normalized plot as a novel and time-saving tool in complex enzyme kinetic analysis". The Biochemical Journal. 358 (Pt 3): 573–83. doi:10.1042/bj3580573. PMC 1222113. PMID 11577687.
- ^ Almaas E, Kovács B, Vicsek T, Oltvai ZN, Barabási AL (February 2004). "Global organization of metabolic fluxes in the bacterium Escherichia coli". Nature. 427 (6977): 839–43. arXiv:q-bio/0403001. Bibcode:2004Natur.427..839A. doi:10.1038/nature02289. PMID 14985762. S2CID 715721.
- ^ Reed JL, Vo TD, Schilling CH, Palsson BO (2003). "An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR)". Genome Biology. 4 (9): R54. doi:10.1186/gb-2003-4-9-r54. PMC 193654. PMID 12952533.
- ^ 완전한 파생은 여기를 참조하십시오.
- ^ Dirr H, Reinemer P, Huber R (March 1994). "X-ray crystal structures of cytosolic glutathione S-transferases. Implications for protein architecture, substrate recognition and catalytic function". European Journal of Biochemistry. 220 (3): 645–61. doi:10.1111/j.1432-1033.1994.tb18666.x. PMID 8143720.
- ^ Stone SR, Morrison JF (July 1988). "Dihydrofolate reductase from Escherichia coli: the kinetic mechanism with NADPH and reduced acetylpyridine adenine dinucleotide phosphate as substrates". Biochemistry. 27 (15): 5493–9. doi:10.1021/bi00415a016. PMID 3052577.
- ^ Fisher PA (1994). Enzymologic mechanism of replicative DNA polymerases in higher eukaryotes. Progress in Nucleic Acid Research and Molecular Biology. Vol. 47. pp. 371–97. doi:10.1016/S0079-6603(08)60257-3. ISBN 978-0-12-540047-3. PMID 8016325.
- ^ Akerman SE, Müller S (August 2003). "2-Cys peroxiredoxin PfTrx-Px1 is involved in the antioxidant defence of Plasmodium falciparum". Molecular and Biochemical Parasitology. 130 (2): 75–81. doi:10.1016/S0166-6851(03)00161-0. PMID 12946843.
- ^ Bravo IG, Barrallo S, Ferrero MA, Rodríguez-Aparicio LB, Martínez-Blanco H, Reglero A (September 2001). "Kinetic properties of the acylneuraminate cytidylyltransferase from Pasteurella haemolytica A2". The Biochemical Journal. 358 (Pt 3): 585–98. doi:10.1042/bj3580585. PMC 1222114. PMID 11577688.
- ^ Kraut J (1977). "Serine proteases: structure and mechanism of catalysis". Annual Review of Biochemistry. 46: 331–58. doi:10.1146/annurev.bi.46.070177.001555. PMID 332063.
- ^ Cornish-Bowden A (2012). Fundamentals of Enzyme Kinetics. Wiley-Blackwell.
Some enzymes are much more effective catalysts for one direction than the other. As a striking example, the limiting rates of the forward reaction catalyzed by methionine adenosyltransferase is about 105 greater than that for the reverse direction, even though the equilibrium constant is close to unity (page 59).
- ^ Srinivasan, Bharath (2021). "Explicit Treatment of Non Michaelis-Menten and Atypical Kinetics in Early Drug Discovery". ChemMedChem. 16 (6): 899–918. doi:10.1002/cmdc.202000791. PMID 33231926. S2CID 227157473.
- ^ a b Srinivasan, Bharath; Forouhar, Farhad; Shukla, Arpit; Sampangi, Chethana; Kulkarni, Sonia; Abashidze, Mariam; Seetharaman, Jayaraman; Lew, Scott; Mao, Lei; Acton, Thomas B.; Xiao, Rong (March 2014). "Allosteric regulation and substrate activation in cytosolic nucleotidase II from Legionella pneumophila". FEBS Journal. 281 (6): 1613–1628. doi:10.1111/febs.12727. PMC 3982195. PMID 24456211.
- ^ Ricard J, Cornish-Bowden A (July 1987). "Co-operative and allosteric enzymes: 20 years on". European Journal of Biochemistry. 166 (2): 255–72. doi:10.1111/j.1432-1033.1987.tb13510.x. PMID 3301336.
- ^ Ward WH, Fersht AR (July 1988). "Tyrosyl-tRNA synthetase acts as an asymmetric dimer in charging tRNA. A rationale for half-of-the-sites activity". Biochemistry. 27 (15): 5525–30. doi:10.1021/bi00415a021. PMID 3179266.
- ^ Helmstaedt K, Krappmann S, Braus GH (September 2001). "Allosteric regulation of catalytic activity: Escherichia coli aspartate transcarbamoylase versus yeast chorismate mutase". Microbiology and Molecular Biology Reviews. 65 (3): 404–21, table of contents. doi:10.1128/MMBR.65.3.404-421.2001. PMC 99034. PMID 11528003.
- ^ Schirmer T, Evans PR (January 1990). "Structural basis of the allosteric behaviour of phosphofructokinase". Nature. 343 (6254): 140–5. Bibcode:1990Natur.343..140S. doi:10.1038/343140a0. PMID 2136935. S2CID 4272821.
- ^ Hill AV (1910). "The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves". J. Physiol. 40: iv–vii.
- ^ Hartley BS, Kilby BA (February 1954). "The reaction of p-nitrophenyl esters with chymotrypsin and insulin". The Biochemical Journal. 56 (2): 288–97. doi:10.1042/bj0560288. PMC 1269615. PMID 13140189.
- ^ a b Fersht, Alan (1999). Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. San Francisco: W.H. Freeman. ISBN 978-0-7167-3268-6.
- ^ Bender ML, Begué-Cantón ML, Blakeley RL, Brubacher LJ, Feder J, Gunter CR, Kézdy FJ, Killheffer JV, Marshall TH, Miller CG, Roeske RW, Stoops JK (December 1966). "The determination of the concentration of hydrolytic enzyme solutions: alpha-chymotrypsin, trypsin, papain, elastase, subtilisin, and acetylcholinesterase". Journal of the American Chemical Society. 88 (24): 5890–913. doi:10.1021/ja00976a034. PMID 5980876.
- ^ Cleland WW (January 2005). "The use of isotope effects to determine enzyme mechanisms". Archives of Biochemistry and Biophysics. 433 (1): 2–12. doi:10.1016/j.abb.2004.08.027. PMID 15581561.
- ^ Northrop DB (1981). "The expression of isotope effects on enzyme-catalyzed reactions". Annual Review of Biochemistry. 50: 103–31. doi:10.1146/annurev.bi.50.070181.000535. PMID 7023356.
- ^ Baillie TA, Rettenmeier AW (1986). "Drug biotransformation: mechanistic studies with stable isotopes". Journal of Clinical Pharmacology. 26 (6): 448–51. doi:10.1002/j.1552-4604.1986.tb03556.x. PMID 3734135. S2CID 39193680.
- ^ Cleland WW (1982). "Use of isotope effects to elucidate enzyme mechanisms". CRC Critical Reviews in Biochemistry. 13 (4): 385–428. doi:10.3109/10409238209108715. PMID 6759038.
- ^ Christianson DW, Cox JD (1999). "Catalysis by metal-activated hydroxide in zinc and manganese metalloenzymes". Annual Review of Biochemistry. 68: 33–57. doi:10.1146/annurev.biochem.68.1.33. PMID 10872443.
- ^ Kraut DA, Carroll KS, Herschlag D (2003). "Challenges in enzyme mechanism and energetics". Annual Review of Biochemistry. 72: 517–71. doi:10.1146/annurev.biochem.72.121801.161617. PMID 12704087.
- ^ Walsh R, Martin E, Darvesh S (December 2011). "Limitations of conventional inhibitor classifications". Integrative Biology. 3 (12): 1197–201. doi:10.1039/c1ib00053e. PMID 22038120.
- ^ Cleland WW (February 1963). "The kinetics of enzyme-catalyzed reactions with two or more substrates or products. III. Prediction of initial velocity and inhibition patterns by inspection". Biochimica et Biophysica Acta. 67: 188–96. doi:10.1016/0006-3002(63)91816-x. PMID 14021669.
- ^ Walsh R, Martin E, Darvesh S (May 2007). "A versatile equation to describe reversible enzyme inhibition and activation kinetics: modeling beta-galactosidase and butyrylcholinesterase". Biochimica et Biophysica Acta (BBA) - General Subjects. 1770 (5): 733–46. doi:10.1016/j.bbagen.2007.01.001. PMID 17307293.
- ^ a b c Srinivasan B, Skolnick J (May 2015). "Insights into the slow-onset tight-binding inhibition of Escherichia coli dihydrofolate reductase: detailed mechanistic characterization of pyrrolo [3,2-f] quinazoline-1,3-diamine and its derivatives as novel tight-binding inhibitors". The FEBS Journal. 282 (10): 1922–38. doi:10.1111/febs.13244. PMC 4445455. PMID 25703118.
- ^ a b Srinivasan B, Tonddast-Navaei S, Skolnick J (October 2015). "Ligand binding studies, preliminary structure-activity relationship and detailed mechanistic characterization of 1-phenyl-6,6-dimethyl-1,3,5-triazine-2,4-diamine derivatives as inhibitors of Escherichia coli dihydrofolate reductase". European Journal of Medicinal Chemistry. 103: 600–14. doi:10.1016/j.ejmech.2015.08.021. PMC 4610388. PMID 26414808.
- ^ Srinivasan B, Rodrigues JV, Tonddast-Navaei S, Shakhnovich E, Skolnick J (July 2017). "Rational Design of Novel Allosteric Dihydrofolate Reductase Inhibitors Showing Antibacterial Effects on Drug-Resistant Escherichia coli Escape Variants". ACS Chemical Biology. 12 (7): 1848–1857. doi:10.1021/acschembio.7b00175. PMC 5819740. PMID 28525268.
- ^ Koshland DE (February 1958). "Application of a Theory of Enzyme Specificity to Protein Synthesis". Proceedings of the National Academy of Sciences of the United States of America. 44 (2): 98–104. Bibcode:1958PNAS...44...98K. doi:10.1073/pnas.44.2.98. PMC 335371. PMID 16590179.
- ^ Hammes GG (July 2002). "Multiple conformational changes in enzyme catalysis". Biochemistry. 41 (26): 8221–8. doi:10.1021/bi0260839. PMID 12081470.
- ^ Sutcliffe MJ, Scrutton NS (July 2002). "A new conceptual framework for enzyme catalysis. Hydrogen tunnelling coupled to enzyme dynamics in flavoprotein and quinoprotein enzymes". European Journal of Biochemistry. 269 (13): 3096–102. doi:10.1046/j.1432-1033.2002.03020.x. PMID 12084049.
- ^ Henri V (1902). "Theorie generale de l'action de quelques diastases". Compt. Rend. Acad. Sci. Paris. 135: 916–9.
- ^ Sørensen PL (1909). "Enzymstudien {II}. Über die Messung und Bedeutung der Wasserstoffionenkonzentration bei enzymatischen Prozessen" [Enzyme studies III: About the measurement and significance of the hydrogen ion concentration in enzymatic processes]. Biochem. Z. (in German). 21: 131–304.
- ^ 마이클 리스 L, Menten M(1913년)."다이 Kinetik Invertinwirkung der"[그 특성 Invertase 연대'의].Biochem.Z(독일어로).49:333–369., 마이클 리스 L, Menten 맥스, 존슨 KA, 구디 RS(2011년 10월)."원래 미카엘리스:1913년 Michaelis-Menten의 종이 번역 일정".생화학. 50(39):8264–9. doi:10.1021/bi201284u.PMC3381512.PMID 21888353.
- ^ Briggs GE, Haldane JB (1925). "A Note on the Kinetics of Enzyme Action". The Biochemical Journal. 19 (2): 338–9. doi:10.1042/bj0190338. PMC 1259181. PMID 16743508.
- ^ Flomenbom O, Velonia K, Loos D, Masuo S, Cotlet M, Engelborghs Y, Hofkens J, Rowan AE, Nolte RJ, Van der Auweraer M, de Schryver FC, Klafter J (February 2005). "Stretched exponential decay and correlations in the catalytic activity of fluctuating single lipase molecules". Proceedings of the National Academy of Sciences of the United States of America. 102 (7): 2368–72. Bibcode:2005PNAS..102.2368F. doi:10.1073/pnas.0409039102. PMC 548972. PMID 15695587.
- ^ English BP, Min W, van Oijen AM, Lee KT, Luo G, Sun H, Cherayil BJ, Kou SC, Xie XS (February 2006). "Ever-fluctuating single enzyme molecules: Michaelis-Menten equation revisited". Nature Chemical Biology. 2 (2): 87–94. doi:10.1038/nchembio759. PMID 16415859. S2CID 2201882.
- ^ Lu HP, Xun L, Xie XS (December 1998). "Single-molecule enzymatic dynamics". Science. 282 (5395): 1877–82. Bibcode:1998Sci...282.1877P. doi:10.1126/science.282.5395.1877. PMID 9836635.
- ^ Xue X, Liu F, Ou-Yang ZC (September 2006). "Single molecule Michaelis-Menten equation beyond quasistatic disorder". Physical Review E. 74 (3 Pt 1): 030902. arXiv:cond-mat/0604364. Bibcode:2006PhRvE..74c0902X. doi:10.1103/PhysRevE.74.030902. PMID 17025584. S2CID 41674948.
- ^ Bevc S, Konc J, Stojan J, Hodošček M, Penca M, Praprotnik M, Janežič D (2011). "ENZO: a web tool for derivation and evaluation of kinetic models of enzyme catalyzed reactions". PLOS ONE. 6 (7): e22265. Bibcode:2011PLoSO...622265B. doi:10.1371/journal.pone.0022265. PMC 3139599. PMID 21818304. ENZO 서버
추가 읽기
소개
- Cornish-Bowden, Athel (2012). Fundamentals of enzyme kinetics (4th ed.). Weinheim: Wiley-Blackwell. ISBN 978-3-527-33074-4.
- Stevens L, Price NC (1999). Fundamentals of enzymology: the cell and molecular biology of catalytic proteins. Oxford [Oxfordshire]: Oxford University Press. ISBN 978-0-19-850229-6.
- Bugg, Tim (2004). Introduction to Enzyme and Coenzyme Chemistry. Cambridge, MA: Blackwell Publishers. ISBN 978-1-4051-1452-3.
- Segel, Irwin H. (1993). Enzyme kinetics: behavior and analysis of rapid equilibrium and steady state enzyme systems. New York: Wiley. ISBN 978-0-471-30309-1.
고급
- Fersht, Alan (1999). Structure and mechanism in protein science: a guide to enzyme catalysis and protein folding. San Francisco: W.H. Freeman. ISBN 978-0-7167-3268-6.
- Schnell S, Maini PK (2004). "A century of enzyme kinetics: Reliability of the KM and vmax estimates". Comments on Theoretical Biology. 8 (2–3): 169–87. CiteSeerX 10.1.1.493.7178. doi:10.1080/08948550302453. Retrieved 22 September 2020.
- Walsh, Christopher (1979). Enzymatic reaction mechanisms. San Francisco: W. H. Freeman. ISBN 978-0-7167-0070-8.
- Cleland WW, Cook P (2007). Enzyme kinetics and mechanism. New York: Garland Science. ISBN 978-0-8153-4140-6.
외부 링크
- 효소 검사 애니메이션 — 검사 조건 조작 효과 표시
- MACiE — 효소 반응 메커니즘의 데이터베이스
- 효소 — expasis 효소 명명법
- ENZO — 효소 촉매 반응의 운동 모델을 쉽게 구성하고 신속하게 테스트하기 위한 웹 애플리케이션.
- ExCatDB — 효소 촉매 메커니즘의 데이터베이스
- BRENDA — 기질, 억제제 및 반응도를 제공하는 종합 효소 데이터베이스
- SABIO-RK — 대응 키네틱스
- Joseph Kraut's Research Group, 캘리포니아 대학교 샌디에이고 - 몇 가지 효소 반응 메커니즘의 애니메이션
- 효소 키네틱스의 상징성과 용어 — 효소 키네틱스의 개념과 용어에 대한 포괄적인 설명
- 효소 키네틱스에 대한 소개 — 효소 키네틱스에 대한 액세스 가능한 온라인 튜토리얼 세트
- 효소 운동학 애니메이션 튜토리얼 - 오디오가 포함된 애니메이션 튜토리얼







![{\displaystyle {\ce {ES ->[k_{cat}] E + P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/299f3433b9ca64a864deef13f572a0127a2d14e0)
![{\displaystyle v_{0}={\frac {V_{\max }[{\ce {S}}]}{K_{M}+[{\ce {S}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f2f1d1e9d417b925f380340d6d3581d4006672f)
![{\displaystyle {\begin{aligned}K_{M}\ &{\stackrel {\mathrm {def} }{=}}\ {\frac {k_{2}+k_{-1}}{k_{1}}}\approx K_{D}\\V_{\max }\ &{\stackrel {\mathrm {def} }{=}}\ k_{cat}{\ce {[E]}}_{tot}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1714252e04d803899ef6ad5b75c074d0f9ebc50c)
![{\displaystyle d{\ce {[ES]}}/{dt}\;{\overset {!}{=}}\;0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eea1ce2a30471bd05b46fe979bb4f12e365b4d5)
![{\displaystyle {\ce {[E]}}_{\text{tot}}={\ce {[E]}}+{\ce {[ES]}}\;{\overset {!}{=}}\;{\text{const}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c082974766078275f236f456e12426c4ea02fc8)

![{\displaystyle {\ce {[S]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5909e9989dfe9306325e8dab287928f3c984ee3)

![{\displaystyle [{\ce {S}}]/(K_{M}+[{\ce {S}}])\approx [{\ce {S}}]/K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d1befa5e00217f79ed63dc6ba5c6a15d78d5425)
![{\displaystyle {\ce {[E]_{\rm {tot}}\approx [E]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6ccda6e543afca4e4287f635c5f1a4931ca93e1)
![{\displaystyle v_{0}\approx {\frac {k_{cat}}{K_{M}}}{\ce {[E][S]}}\qquad \qquad {\text{if }}[{\ce {S}}]\ll K_{M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/596b2c4659de250ffbd0b65c085402f9fd16735d)

![[S]=[S]_{0}(1-k)^{{t}}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/93211e467eb88a4ed3ce4b1b8a64f3645c540709)
![[S]=[S]_{0}(1-v/[S]_{0})^{{t}}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc767ed4ec3fb17dbb2b342b438ca22f3a0c5e15)
![[S]=[S]_{0}(1-(V_{{\max }}[S]_{0}/(K_{M}+[S]_{0})/[S]_{0}))^{{t}}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/550cebc162d8baf678f05a64c8435882eba78bfb)
![{\frac {[S]}{K_{M}}}=W\left[F(t)\right]\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbfb88da686a3b0298417f08709f60c89538b35e)
![F(t) = \frac{[S]_0}{K_M} \exp\!\left(\frac{[S]_0}{K_M} - \frac{V_\max}{K_M}\,t \right) \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/39737501b38ca63037f8350456c777481706c602)
![{\frac {[S]}{K_{M}}}=W\left[F(t)\right]-{\frac {V_{\max }}{k_{{cat}}K_{M}}}\ {\frac {W\left[F(t)\right]}{1+W\left[F(t)\right]}}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/036e38cefdac7ce988899ea0d4b89f80c0b6e81d)
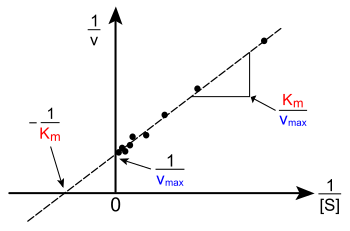
![{\frac {1}{v}}={\frac {K_{{M}}}{V_{{\max }}[{\mbox{S}}]}}+{\frac {1}{V_{\max }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f67c173c3e3e8c78da7dc5fa15c3b5ff299e4439)
![{\displaystyle {\ce {{E}+S<=>[k_{1}][k_{-1}]ES->[k_{2}]EI->[k_{3}]{E}+P}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cd1904bee27689d5df0933e40a4b01631243041)
![{\displaystyle v_{0}=k_{cat}{\frac {{\ce {[S] [E]_0}}}{K_{M}^{\prime }+{\ce {[S]}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d90d4c1b92e79705a9ecf0f8615982c0bc91f4a3)






![{\displaystyle {\ce {\overset {}{E->[{\ce {A \atop \downarrow }}]EA<=>E^{\ast }P->[{\ce {P \atop \uparrow }}]E^{\ast }->[{\ce {B \atop \downarrow }}]E^{\ast }B<=>EQ->[{\ce {Q \atop \uparrow }}]E}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9b768dbbd547267c22748f29590cb0a639375de)
![{\displaystyle {\ce {{E}+{S}<=>[k_{1}][k_{-1}]ES<=>[k_{2}][k_{-2}]{E}+{P}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe362b85b97b0614f6139dd0be2e8389a2c3b63e)


![{\displaystyle {\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {k_{1}k_{2}}{k_{-1}k_{-2}}}=K_{\rm {eq}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f0ca30bfb4f852fcc02a12f729bcbd3adc500d6)
![{\displaystyle [{\rm {S}}]\rightarrow \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3e69387ec816688807461db5902b440a6a65ed0)
![{\displaystyle [{\rm {P}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c498e9bfae3b2d0f1378c8a1a15031f4002279)
![{\displaystyle [{\rm {S}}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53ac89660d3f5c0ad06eac244190defc17cd7a61)
![{\displaystyle [{\rm {P}}]\rightarrow \infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/020c2fe953abd3c508b7bd3a6d97bb29225faeeb)
![{\displaystyle V_{\rm {max}}^{f}=k_{2}{\rm {[E]}}_{tot}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1834ca7ac4c486ffc3e1c89742f31c266797da98)
![{\displaystyle V_{\rm {max}}^{b}=-k_{-1}{\rm {[E]}}_{tot}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a09363446309c8c26702430b70bfec463a3b0134)


![{\displaystyle K_{\rm {eq}}={\frac {[{\rm {P}}]_{\rm {eq}}}{[{\rm {S}}]_{\rm {eq}}}}={\frac {V_{\rm {max}}^{f}/K_{M}^{S}}{V_{\rm {max}}^{b}/K_{M}^{P}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/621e1b38683241916244c9e90f5625f14f1f0088)





![{\displaystyle {\cfrac {V_{\max }}{1+{\cfrac {[I]}{K_{i}}}}}={\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{K_{i}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c58cef49731511f5011822f1e92d4da22814891)
![{\cfrac {V_{\max }}{\cfrac {[I]+K_{i}}{[I]+K_{i}-[I]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42e34b0927bf9484b8a664e022d3fd6ba0ad2326)
![{\displaystyle {\cfrac {V_{\max }}{\cfrac {1}{1-{\cfrac {[I]}{[I]+K_{i}}}}}}=V_{\max }-V_{\max }{\cfrac {[I]}{[I]+K_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4132fbd61b7474f8e3ef391f82d1d196a2a325ff)
![V_{\max }-\Delta V_{\max }{\cfrac {[I]}{[I]+K_{i}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90f5601fefd8114c165ac3dfb739e0642e62610c)
![{\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[I]}{[I]+K_{i}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c31b5f56aaeed122d1f8a67491c56d272686b6e)
![{\displaystyle V_{\max 1}-(V_{\max 1}-V_{\max 2}){\cfrac {[X]}{[X]+K_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bb687fca77a00dba879a00fb32b7ca1bc867973)
![{\displaystyle K_{m1}-(K_{m1}-K_{m2}){\cfrac {[X]}{[X]+K_{x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a298dbb441e88b96a618cc31df3aaebac17d85)


