Q–Q 그림

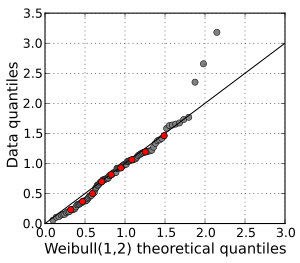
통계학에서 Q–Q 그림(quantile-quantile plot)은 확률도로, 분위수를 서로 표시하여 두 확률 분포를 비교하는 그래픽 방법입니다.^[1] 그림의 점 (x, y)는 첫 번째 분포(x 좌표)의 동일한 분위수에 대해 표시된 두 번째 분포(y 좌표)의 분위수 중 하나에 해당합니다. 매개 변수가 분위수 간격의 인덱스인 모수 곡선을 정의합니다.

비교되는 두 분포가 비슷하다면 Q–Q 그림의 점들은 대략 동일선 y = x 위에 놓이게 됩니다. 분포가 선형적으로 관련되어 있다면 Q–Q 그림의 점들은 대략적으로 선 위에 놓이지만 반드시 y = x 위에 있는 것은 아닙니다. Q–Q 그림은 위치 척도 분포의 모수를 추정하는 그래픽 수단으로도 사용할 수 있습니다.

Q–Q 그림은 분포의 모양을 비교하는 데 사용되며 위치, 척도 및 왜도와 같은 속성이 두 분포에서 유사하거나 다른지에 대한 그래픽 보기를 제공합니다. Q–Q 그림을 사용하여 데이터 수집 또는 이론적 분포를 비교할 수 있습니다. Q-Q 그림을 사용하여 두 표본의 데이터를 비교하는 것은 기본 분포를 비교하는 비모수적 접근 방식으로 볼 수 있습니다. Q–Q 그림은 일반적으로 표본의 히스토그램을 비교하는 것보다 더 진단적이지만 널리 알려져 있지 않습니다. Q–Q 그림은 일반적으로 데이터 집합을 이론 모형과 비교하는 데 사용됩니다.^[2][3] 이를 통해 수치 요약 통계량으로 줄이는 대신 그래픽으로 적합도를 평가할 수 있습니다. Q–Q 그림은 또한 두 이론적 분포를 서로 비교하는 데 사용됩니다.^[4] Q-Q 그림은 분포를 비교하기 때문에 산점도에서와 같이 값이 쌍으로 관측되거나 비교되는 두 그룹의 값의 수가 같을 필요가 없습니다.

"확률도"라는 용어는 구체적으로 Q–Q 그림을 가리키기도 하고, 보다 일반적인 유형의 그림을 가리키기도 하며, 덜 일반적으로 사용되는 P–P 그림을 가리키기도 합니다. 확률도 상관 계수 그림(PPCC plot)은 관측된 데이터와 적합 분포의 일치성을 측정하고 때로는 데이터에 분포를 적합시키는 수단으로 사용되는 Q–Q 그림의 아이디어에서 파생된 양입니다.

정의 및 구축

Q–Q 그림은 서로에 대한 두 분포의 분위수 또는 분위수의 추정치를 기반으로 한 그림입니다. 그림의 점 패턴은 두 분포를 비교하는 데 사용됩니다.

Q-Q 그림을 구성하는 주요 단계는 그림에 표시할 분위수를 계산하거나 추정하는 것입니다. Q-Q 그림에서 두 축 중 하나 또는 두 축이 연속 누적 분포 함수(CDF)를 갖는 이론적 분포를 기반으로 하는 경우 모든 분위수는 고유하게 정의되며 CDF를 반전하여 얻을 수 있습니다. 불연속 CDF를 사용한 이론적 확률 분포가 비교되는 두 분포 중 하나일 경우 분위수 중 일부가 정의되지 않을 수 있으므로 보간 분위수가 표시될 수 있습니다. Q-Q 그림이 데이터를 기반으로 하는 경우 사용되는 분위수 추정기가 여러 개 있습니다. 분위수를 추정하거나 보간해야 할 때 Q-Q 그림을 형성하는 규칙을 표시 위치라고 합니다.

간단한 경우는 동일한 크기의 데이터 세트가 두 개 있는 경우입니다. 이 경우 Q-Q 그림을 만들려면 각 집합을 순서대로 순서대로 정렬한 다음 쌍을 이루어 해당 값을 표시합니다. 더 복잡한 구성은 크기가 다른 두 데이터 세트를 비교하는 경우입니다. 이 경우 Q–Q 플롯을 구성하려면 동일한 기본 확률에 해당하는 분위수를 구성할 수 있도록 보간 분위수 추정치를 사용해야 합니다.

좀 더 추상적으로,^[4] 두 개의 누적 확률 분포 함수 F와 G가⁻¹ 관련된 분위 함수 F와⁻¹ G(CDF의 역함수는 분위 함수)와 함께 주어지면, Q-Q 그림은 q의 값 범위에 대해 G의 q 분위에 대해 F의 q 분위를 그립니다. 따라서 Q–Q 그림은 실제 평면 R의² 값으로 [0,1] 이상 지수화된 모수 곡선입니다.

해석

Q-Q 그림에 표시된 점은 왼쪽에서 오른쪽으로 볼 때 항상 감소하지 않습니다. 비교되는 두 분포가 동일한 경우 Q–Q 그림은 45° 선 y = x를 따릅니다. 두 분포 중 하나에서 값을 선형 변환한 후 일치하면 Q–Q 그림은 선을 따르지만 반드시 선 y = x를 따르지는 않습니다. Q–Q 그림의 일반적인 추세가 선 y = x보다 더 평평하다면, 가로축에 표시된 분포가 세로축에 표시된 분포보다 더 분산되어 있습니다. 반대로 Q–Q 그림의 일반적인 추세가 선 y = x보다 가파를 경우 세로축에 표시된 분포가 가로축에 표시된 분포보다 더 분산됩니다. Q-Q 그림은 종종 호 또는 "S" 모양으로 나타나 분포 중 하나가 다른 분포보다 더 치우쳐 있거나 분포 중 하나가 다른 분포보다 더 무거운 꼬리를 가지고 있음을 나타냅니다.

Q-Q 그림은 분위수를 기반으로 하지만 표준 Q-Q 그림에서는 Q-Q 그림의 어느 점이 주어진 분위수를 결정하는지 결정할 수 없습니다. 예를 들어, Q-Q 그림을 검사하여 비교되는 두 분포의 중위수를 결정할 수 없습니다. 일부 Q-Q 그림은 이와 같은 결정을 내릴 수 있는 10분위를 나타냅니다.

분위수 사이의 선형 회귀 분석의 절편 및 기울기를 통해 표본의 상대적 위치와 상대적 척도를 측정할 수 있습니다. 가로축에 표시된 분포의 중앙값이 0이면 회귀선의 절편은 위치 측도이고 기울기는 척도 측도입니다. 중앙값 사이의 거리는 Q-Q 그림에 반영된 상대적 위치의 또 다른 척도입니다. "확률도 상관 계수"(PPCC 그림)는 쌍을 이룬 표본 분위수 사이의 상관 계수입니다. 상관 계수가 하나에 가까울수록 분포가 서로의 이동 및 축척된 버전에 가까워집니다. 단일 형상 모수를 사용하는 분포의 경우 확률도 상관 계수 그림을 사용하여 형상 모수를 추정하는 방법을 제공합니다. 다른 유형의 분포를 비교하는 것처럼 형상 모수의 다른 값에 대한 상관 계수를 계산하고 가장 적합한 것을 사용합니다.

Q–Q 그림의 또 다른 일반적인 사용은 정규 확률도에서와 같이 표본의 분포를 표준 정규 분포 N(0,1)과 같은 이론적 분포와 비교하는 것입니다. 두 표본의 데이터를 비교하는 경우와 마찬가지로 데이터를 순서화한 다음(정식으로 순서 통계량을 계산합니다) 이론적 분포의 특정 분위수에 대해 그림을 그립니다.^[3]

위치 표시

이론적 분포에서 분위수를 선택하는 것은 상황과 목적에 따라 달라질 수 있습니다. 표본 크기 n이 주어지면 표본 분포가 실현하는 분위수이므로 k = 1, …, n에 대해 k/n입니다. 이들 중 마지막 n/n은 이론적 분포의 최대값인 100번째 백분위수에 해당하며, 때로는 무한합니다. 다른 선택은 (k - 0.5) / n을 사용하거나, k / (n + 1)을 사용하여 n개의 점과 두 개의 가장 바깥쪽 점과${\displaystyle }$[${\displaystyle 0,}$ 1${\displaystyle ]}$ ${\displaystyle [0,$ 1$]$ 간격의$$ 가장자리 사이에 동일한 거리가 있도록 간격을 두는 것입니다.^[6]

많은 다른 선택들이, 문맥과 관련된 이론이나 시뮬레이션에 기초하여, 형식적인 선택과 휴리스틱적인 선택 모두를 제안해 왔습니다. 다음 하위 섹션에서는 이 중 일부에 대해 설명합니다. 더 좁은 질문은 독일 탱크 문제로 알려진 최대값(인구 최대값 추정)을 선택하는 것인데, 이에 대해 유사한 "표본 최대값과 갭" 솔루션이 존재하며, 가장 간단하게 m + m/n - 1입니다. 이러한 간격 균일화의 보다 공식적인 적용은 매개변수의 최대 간격 추정에서 발생합니다.

균일 분포에 대한 주문 통계량의 기대 값

k / (n + 1) 접근 방식은 무작위로 그린 (n + 1) 값 중 마지막 값이 처음 n개의 무작위로 그린 값 중 k번째 작은 값을 초과하지 않을 확률에 따라 점을 표시하는 방식과 같습니다.^[7][8]

표준 정규 분포에 대한 주문 통계량의 기대 값

정규 확률도를 사용할 때 사용하는 분위수는 표준 정규 분포의 순서 통계량의 기대 값의 분위수인 랭크트입니다.

좀 더 일반적으로 샤피로-Wilk 검정은 주어진 분포의 차수 통계량의 기대값을 사용합니다. 결과 그림과 선은 (적합된 선의 절편 및 기울기로부터) 위치와 척도에 대한 일반화된 최소 제곱 추정치를 산출합니다.^[9] 정규 분포(위치와 척도는 각각 평균과 표준 편차로 추정됨)에는 그다지 중요하지 않지만 다른 많은 분포에서는 유용할 수 있습니다.

그러나 이를 위해서는 주문 통계량의 기대 값을 계산해야 하는데, 분포가 정규 분포가 아닌 경우에는 어려울 수 있습니다.

주문 통계량의 중위수

또는 균일 분포의 차수 통계와 분포의 분위 함수의 중위수 추정치를 기반으로 계산할 수 있는 차수 통계의 중위수 추정치를 사용할 수도 있습니다. 이는 Filliben(1975)에 의해 제안되었습니다.^[9]

이는 분위수 함수를 계산할 수 있는 모든 분포에 대해 쉽게 생성될 수 있지만, 반대로 위치와 척도의 결과 추정치는 더 이상 정확하게 최소 제곱 추정치가 아니지만 n개의 작은 경우에만 크게 다릅니다.

휴리스틱

몇 가지 다른 공식이 아핀 대칭 플롯 위치로 사용되거나 제안되었습니다. 이러한 공식은 0에서 1까지의 범위에 있는 a의 일부 값에 대해 (k - a) / (n + 1 - 2a) 형태를 가지며, 이는 k / (n + 1) 및 (k - 1) / (n - 1) 사이의 범위를 제공합니다.

수식은 다음과 같습니다.

• k / (n + 1)
• (k − 0.3) / (n + 0.4).^[10]
• (k − 0.3175) / (n + 0.365).^{[11][note 1]}
• (k − 0.326) / (n + 0.348).^[12]
• (k − ⅓) / (n + ⅓).^{[note 2]}
• (k − 0.375) / (n + 0.25).^{[note 3]}
• (k − 0.4) / (n + 0.2).^[13]
• (k − 0.44) / (n + 0.12).^{[note 4]}
• (k − 0.5) / n.^[15]
• (k − 0.567) / (n − 0.134).^[16]
• (k − 1) / (n − 1).^{[note 5]}

표본 크기가 큰 경우 n, 이러한 다양한 식 사이에는 거의 차이가 없습니다.

필리벤의 추정치

순서 통계량 중위수는 분포의 순서 통계량의 중위수입니다. 이들은 연속 균일 분포에 대한 분위수 함수 및 순서 통계량 중위수로 다음과 같이 표현할 수 있습니다.

${\displaystyle N(i)=G(U(i))}$

여기서 U(i)는 균일 차수 통계량 중위수이고 G는 원하는 분포에 대한 분위수 함수입니다. 분위수 함수는 누적 분포 함수(X가 어떤 값보다 작거나 같을 확률)의 역수입니다. 즉, 확률이 주어지면, 우리는 누적 분포 함수의 해당 분위수를 원합니다.

James J. Filliben은 균일 순서 통계량 중위수에 대해 다음 추정치를 사용합니다.^[17]

${\displaystyle m(i)={\begin{cases}1-0.5^{1/n}&i=1\\\\{\dfrac {i-0.3175}{n+0.365}}&i=2,3,\ldots ,n-1\\\\0.5^{1/n}&i=n.\end{case}}}$

이 추정치의 이유는 순서 통계량 중위수가 단순한 형태를 가지고 있지 않기 때문입니다.

소프트웨어

R 프로그래밍 언어는 Q-Q 그림, 즉 qqnorm 및 qqplot을 만드는 기능과 함께 제공됩니다. stats 꾸러미의 그 fastqq 패키지는 많은 수의 데이터 포인트에 대해 더 빠른 플로팅을 구현합니다.

참고 항목

• 경험적 분배함수
• 프로빗 분석은 1934년 Chester Ittner Bliss에 의해 개발되었습니다.

메모들

참고문헌

인용

원천

외부 링크

• 확률도
• QQ-플롯에 대한 대체 설명: http://www.stats.gla.ac.uk/steps/glossary/probability_distributions.html#qqplot