물질파
Matter wave| 에 대한 일련의 기사의 일부. |
| 양자역학 |
|---|
물질 파동은 파동-입자 이중성의 절반인 양자 역학 이론의 중심 부분입니다.모든 물질은 파동과 같은 행동을 보입니다.예를 들어, 전자의 빔은 빛의 빔이나 물파처럼 회절될 수 있습니다.
물질이 파동처럼 행동한다는 개념은 1924년 프랑스 물리학자 루이 드 브로이(/dˈbrɪ/)에 의해 제안되었고, 그래서 물질 파동은 드 브로이 파동이라고도 알려져 있습니다.
드 브로글리 파장은 플랑크 상수 h를 통과하는 운동량 p를 가진 입자와 관련된 파장 γ입니다.
물질의 파동과 같은 행동은 조지 패짓 톰슨과 알렉산더 리드의 투과 회절 [1]실험에 의해 처음으로 실험적으로 입증되었고, 전자를 사용한 데이비슨-게르머 [2][3]실험에서 독립적으로 입증되었습니다. 그리고 그것은 또한 다른 기본 입자, 중성 원자와 분자에 대해서도 확인되었습니다.
소개
배경
19세기 말, 빛은 맥스웰 방정식에 따라 전파되는 전자기장의 파동으로 구성되어 있다고 생각된 반면, 물질은 국부적인 입자로 구성되어 있다고 생각되었습니다(파장과 입자 이중성의 역사 참조).1900년에, 흑체 복사 이론을 조사하면서, 막스 플랑크가 진동하는 원자의 열 에너지가 이산적인 부분, [4]즉 양자로 나뉘어진다고 제안했을 때, 이 분열은 의문이 제기되었습니다.플랑크의 연구를 광전 효과와의 연관성을 포함한 여러 가지 방법으로 확장하면서, 알버트 아인슈타인은 1905년에 빛도 현재 광자라고 불리는 [5]양자에서 전파되고 흡수된다는 것을 제안했습니다.이 양자는 플랑크-아인슈타인 관계에 의해 주어진 에너지를 가질 것입니다.
드 브로이 가설

1923-1924년 파동 역학의 첫 기본 아이디어를 구상했을 때, 저는 아인슈타인이 1905년 빛 양자 이론에서 광자에 대해 도입한 파동의 공존과 분자 측면에 대해 모든 입자에 유효한 실제 물리적 합성을 수행하는 것을 목표로 이끌었습니다.
— de Broglie[11]
De Broglie는 1924년 그의 [12]박사 논문에서 빛이 파동과 입자와 같은 특성을 모두 가지고 있는 것처럼, 전자도 파동과 같은 특성을 가지고 있다고 제안했습니다.그의 이론은 "에너지의 각 부분과 적절한 질량0 mon에 대한 주기적인 현상을 연관시킬 수 있다는 가설에서 출발했습니다. hν00 = mc02.주파수 µ는0 물론 에너지 패킷의 나머지 프레임에서 측정해야 합니다.이 가설은 우리 [13][12]: 8 [14][15][16][17]이론의 기초입니다." (이 주파수를 콤프턴 주파수라고도 합니다.)
운동하는 물체와 동등한 파장을 찾기 위해, 드 브로글리는[18] 그 물체에 대한 특수 상대성 이론의 총 에너지를 h와 동일하게 설정했습니다.
(현대 물리학은 더 이상 이러한 형태의 총 에너지를 사용하지 않습니다. 에너지-운동량 관계가 더 유용하다는 것이 증명되었습니다.)드 브로이는 입자의 속도 v를 자유 공간에서의 파동군 속도로 확인했습니다.
(군 속도의 현대적 정의는 각주파수 λ와 파동수 k를 사용합니다.)미분을 에너지 방정식에 적용하고 상대론적 운동량을 식별함으로써:
그 후, 드 브로이는 플랑크 상수를 통해 전자와 관련된 파장 γ와 운동량 계수 p 사이의 관계에 대한 공식으로 도착했습니다.[19]
이것은 이론의 근본적인 관계입니다.
— Louis de Broglie, 1929 Nobel Lecture[20]
슈뢰딩거 파동 방정식
드 브로이의 아이디어에 이어, 물리학자 피터 데비는 입자가 파동처럼 행동한다면, 어떤 종류의 파동 방정식을 만족시켜야 한다고 즉석에서 언급했습니다.데비의 말에 영감을 받은 에르빈 슈뢰딩거는 전자에 대한 적절한 3차원 파동 방정식을 찾기로 결정했습니다.그는 윌리엄 로언 해밀턴의 역학과 광학 사이의 유사성(해밀턴의 광학-기계적 유사성 참조)에 의해 이끌려 광학의 0파장 한계가 기계적 시스템과 비슷하다는 관측에 암호화되었다.[21]
1926년 슈뢰딩거는 맥스웰 방정식의 물질 파동 유사체인 파동[22] 방정식을 발표하고 수소의 에너지 스펙트럼을 도출하는 데 사용했습니다.비상대론적 슈뢰딩거 방정식의 해 주파수는 입자의 나머지 질량에 해당하는 에너지가 비상대론적 슈뢰딩거 방정식의 일부가 아니기 때문에 콤프턴 주파수만큼 드 브로글리 파동과 다릅니다.슈뢰딩거 방정식은 공간의 각 점에 복소수를 할당하는 함수인 파동 함수의 시간 진화를 설명합니다.슈뢰딩거는 파동 함수의 계수 제곱을 전하 밀도로 해석하려고 했습니다.그러나 이러한 접근 방식은 [23][24][25]성공적이지 못했습니다.맥스 보른은 파동 함수의 계수 제곱이 대신 확률 밀도라고 제안했는데, 이는 현재 보른 [23]규칙으로 알려진 성공적인 제안입니다.

1927년, C. G. 다윈 (유명한 생물학자의 손자)은 몇 가지 이상화된 [26]시나리오에서 슈뢰딩거 방정식을 탐구했습니다.자유 공간에서 결합되지 않은 전자에 대해 그는 초기 가우스 파동 패킷을 가정하여 파동의 전파를 계산했습니다.다윈은 에속도 v로 이동하는 패킷의 x x가 다음과 같다는 것을 보여주었습니다.
실험적 확인
물질 파동은 전자에 대해 조지 패짓 톰슨과 알렉산더[1] 리드의 회절 실험과 데이비슨-저머 [2][3]실험에서 처음으로 실험적으로 확인되었습니다.
드 브로이 가설과 물질 파동의 존재는 다른 기본 입자, 중성 원자, 심지어 분자도 파동과 [27]유사한 것으로 확인되었습니다.
파동-입자 이중성을 직접 보여주는 첫 번째 전자파 간섭 패턴은 전자 바이프리즘[28][29](본질적으로 전자 현미경에 배치된 와이어)을 사용하고 회절 패턴을 구성하는 단일 전자를 측정했습니다.최근, 물리적인 구멍을 통해 전자를 사용한 유명한 이중 슬릿 실험의[30]: 260 근접 복사가 영화에 [31]상영되었습니다.
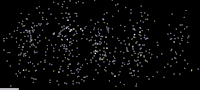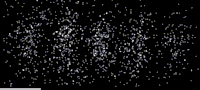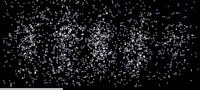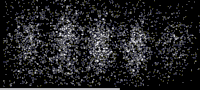
전자
1927년 벨 연구소에서 클린턴 데이비스와 레스터 저머는 결정질의 니켈 [2][3]표적을 향해 느리게 움직이는 전자를 발사했습니다.회절된 전자 강도를 측정했고, X선에 대해 브래그가 예측한 회절 패턴과 유사한 각도 의존성을 갖는 것으로 결정되었습니다.동시에 애버딘 대학의 조지 패짓 톰슨과 알렉산더 리드는 독립적으로 얇은 셀룰로이드 포일과 이후의 금속 필름에 전자를 발사하면서 비슷한 [1]해석이 가능한 고리를 관찰했습니다. (톰슨의 대학원생이었던 알렉산더 리드,첫 번째 실험을 수행했지만 오토바이 사고로[32] 곧 사망했으며 거의 언급되지 않습니다.)드 브로글리 가설이 받아들여지기 전에는 회절은 파동에 의해서만 나타나는 것으로 생각되었던 특성이었습니다.따라서, 물질에 의한 회절 효과의 존재는 [33]물질의 파동과 같은 성질을 보여주었습니다.물질 파동 해석은 슈뢰딩거 [22]방정식을 푼 한스 베테에 [34]의해 1928년에 견고한 기초 위에 놓였고, 이것이 어떻게 실험 결과를 설명할 수 있는지 보여주었습니다.그의 접근법은 현대 전자 회절 [35][36]접근법에서 사용되는 것과 유사합니다.
이것은 양자 역학의 발전에 있어서 중추적인 결과였습니다.광전 효과가 빛의 입자성을 보여주었듯이, 이 실험들은 물질의 파동성을 보여주었습니다.
중성자
약 1 MeV의 운동 에너지를 가진 원자로에서 생성된 중성자는 가벼운 원자에서 산란되면서 약 0.025 eV로 열화됩니다.결과 드 브로글리 파장(약 180pm)은 원자간 간격과 일치합니다.1944년, 어니스트 O. 아서 콤프턴의 박사 연구에서[37] 나온 X선 산란 배경을 가진 울란은 새로 작동하는 X-10 원자로에서 결정학에 열 중성자를 적용할 수 있는 잠재력을 인식했습니다.클리포드 G가 합류했습니다. 그들은[38] 1940년대 내내 중성자 회절을 개발했습니다.1970년대에 중성자 간섭계가 그것을 증명했습니다.[39]중성자 간섭계에서 파동-양성자 이중성과 관련된 중력의 작용.
아톰스
원자 물질 파동의 간섭은 1930년에 Immanu Estermann과 Otto Stern에 의해 처음 관찰되었는데, 이때 NaCl의 [40]표면에서 Na 빔이 회절되었습니다.원자의 짧은 드 브로이 파장은 정밀한 작은 장치를 허용하는 마이크로 리소그래피와 레이저 냉각으로 원자의 속도를 늦추고 드 브로이 [41]파장을 증가시키는 두 가지 기술적 돌파구가 관심을 되살릴 때까지 수년 동안 진행을 방해했습니다.
레이저 냉각의 발전으로 중성 원자를 나노켈빈 온도까지 냉각할 수 있게 되었습니다.이러한 온도에서 드 브로글리 파장은 마이크로미터 범위로 들어갑니다.원자의 브래그 회절과 램지 간섭법을 사용하여 차가운 나트륨 원자의 드 브로글리 파장을 명시적으로 측정한 결과 다른 방법으로 [42]측정한 온도와 일치하는 것으로 밝혀졌습니다.
분자
최근의 실험은 양자 역학적 효과를 겪기에는 너무 클 것으로 추정되는 분자와 심지어 거대 분자의 관계를 확인합니다.1999년, 비엔나의 한 연구팀은 [43]풀러렌만큼 큰 분자의 회절을 증명했습니다.연구원들은 가장 가능성이60 높은 C 속도의 드 브로글리 파장을 오후 2.5로 계산했습니다.더 최근의 실험들은 810개의 원자로 구성되고 10123Da의 [44]질량을 가진 분자들의 양자적 성질을 증명합니다. 2019년 현재, 이것은 25000Da의 [45]분자들로 밀려났습니다.
이러한 실험에서 이러한 간섭 패턴의 축적은 실시간으로 단일 분자 [46]민감도로 기록될 수 있습니다.큰 분자는 이미 매우 복잡하여 양자-고전적 인터페이스의 일부 측면, 즉 특정 비일관성 [47][48]메커니즘에 대한 실험적 접근을 제공합니다.
이동 물질 파동
파동은 고체 물체보다 속도에 대한 개념이 더 복잡합니다.가장 간단한 접근법은 자유 입자에 대한 평면 물질 파동의 측면에서 설명에 초점을 맞추는 것입니다. 즉, 파동 함수는 다음과 같습니다.
군속
드 브로이 가설에서, 입자의 속도는 물질 [50]: 214 파동의 그룹 속도와 같습니다.등방성 매질 또는 진공에서 파동의 그룹 속도는 다음과 같이 정의됩니다.
대안으로, 물질 파동에 상대론적 분산 관계를 사용합니다.
비등방성 매체의 경우 에너지-모멘트 형식을 대신 사용합니다.
그러나 (아래 참조), 위상 속도가 / = 2 / {\= = 이므로,
위상 속도
등방성 매체의 위상 속도는 다음과 같이 정의됩니다.
비등방성 매체의 경우,
에너지 및 운동량 산출에 상대론적 관계 사용
특수상대성이론
특수 상대성 이론의 두 공식을 사용합니다. 하나는 상대론적 질량 에너지이고 다른 하나는 상대론적 운동량입니다.
사벡터
4개의 벡터를 사용하여 드 브로글리 관계는 단일 방정식을 형성합니다.
일반 물질 파동
앞의 섹션에서는 특히 파형 기능이 평면파인 자유 입자에 대해 설명합니다.다른 물질 파동은 크게 세 가지 부류로 나눌 수 있는데, 단일 입자 물질 파동, 집단 물질 파동, 그리고 정지 파동입니다.
단입자 물질 파동
단일 입자 유형(예: 단일 전자 또는 중성자만)에 해당하는 물질 파동에 대한 보다 일반적인 설명은 다음과 유사한 형태를 가질 것입니다.
- 애쉬크로프트와 머민에서 설명한 대로 많은 밴드 구조의 기초를 형성하는 블로흐 파동은 [54][36]고체에 의한 고에너지 전자의 회절을 설명하는 데 사용되기도 합니다.
- 전자 소용돌이 [55]빔과 같은 각운동량을 가진 파동.
- 한 방향에서 파동 벡터의 성분이 복잡한 에바네센트 파동.이것들은 물질 파동이 반사될 때, 특히 방목 발생 회절에 일반적입니다.
집단 물질 파동
다른 종류의 물질 파동은 두 개 이상의 입자를 포함하기 때문에 집단 파동이라고 불리며 종종 준입자입니다.대부분 고체에서 발생합니다. 애쉬크로프트와 머민을 참조하십시오.예를 들어 다음과 같습니다.
- 고체에서, 전자 준입자는 고체의 다른 전자들과의 상호작용이 포함된 전자입니다.전자 준입자는 "일반"(기본 입자) 전자와 동일한 전하와 스핀을 가지며, 일반 전자와 마찬가지로 페르미온입니다.하지만, 그것의 유효 질량은 일반적인 [56]전자의 그것과 상당히 다를 수 있습니다.전기장 스크리닝의 결과로 전기장도 수정됩니다.
- 구멍은 상태에서 전자의 빈 공간으로 생각할 수 있는 준입자입니다;[56] 그것은 반도체의 원자가 대역에서 빈 상태의 맥락에서 가장 일반적으로 사용됩니다.구멍은 전자의 반대 전하를 가지고 있습니다.
- 폴라론은 전자가 근처 원자의 편광과 상호작용하는 준입자입니다.
- 엑시톤은 함께 결합된 전자와 구멍 쌍입니다.
- 쿠퍼 쌍은 두 개의 전자가 결합되어 있어서 단일 물질 파동처럼 작용합니다.
물질파

세 번째 부류는 파동 벡터, 파장을 가지며 시간에 따라 다르지만 그룹 속도 또는 확률 플럭스가 0인 물질 파동입니다.위의 표기법과 유사한 이들 중 가장 단순한 것은 다음과 같습니다.
물질파 대 전자파(빛)
슈뢰딩거는 해밀턴의 광학 기계적 유추를 적용하여 아원자[61]: xi 입자에 대한 파동 역학을 개발했습니다. 결과적으로 슈뢰딩거 방정식에 대한 파동 솔루션은 광파 광학의 결과와 많은 특성을 공유합니다.특히, 키르히호프의 회절 공식은 전자[30]: 745 광학과 원자 [62]광학에서 잘 작동합니다.드 브로글리 파장보다 전기장이 더 느리게 변화하는 한 근사는 잘 작동합니다.거시적 장치는 이 조건을 충족하지만 고체에서 느린 전자는 그렇지 않습니다.
운동 방정식을 넘어 물질 파동 광학의 다른 측면은 해당 광 광학 케이스와 다릅니다.
환경 조건에 대한 물질 파동의 민감도.전자기(빛) 회절의 많은 예는 많은 환경 조건에서 공기 중에서 발생합니다.분명히 가시광선은 공기 분자와 약하게 상호작용합니다.반대로 느린 전자와 분자와 같이 강하게 상호 작용하는 입자는 진공을 필요로 합니다. 물질 파동 특성은 낮은 가스 압력에도 노출되면 [63]빠르게 사라집니다.특수 장치를 사용하면 액체와 가스를 연구하는 데 고속 전자를 사용할 수 있습니다.중요한 예외인 중성자는 주로 원자핵과의 충돌에 의해 상호작용하기 때문에 [64]수백 피트 상공을 이동합니다.
분산.모든 주파수의 광파는 동일한 광속으로 이동하는 반면 물질의 파장은 주파수에 따라 크게 다릅니다.주파수(에너지에 비례)와 파동수 또는 속도(운동량에 비례) 사이의 관계를 분산 관계라고 합니다.진공 상태의 광파는 주파수 사이에 선형 분산 관계를 갖습니다. {\ = 물질파의 경우 관계는 비선형입니다.
일관성 광학 이론 접근법을 사용하는 회절 특징의 가시성은 양자 수준에서 밀도 행렬 [65][66]접근법과 동등한 빔 [30]일관성에 따라 달라집니다.빛과 마찬가지로, (전파 방향에 걸친) 횡단 일관성은 콜리메이션에 의해 증가할 수 있습니다.전자 광학 시스템은 안정화된 고전압을 사용하여 콜리메이트(병렬화) 렌즈 및 뾰족한 필라멘트 소스와 결합하여 좁은 에너지 확산을 제공하여 양호한 [67]일관성을 달성합니다.모든 주파수의 빛은 동일한 속도로 이동하기 때문에 종방향 및 시간적 일관성이 연결됩니다. 물질파에서는 독립적입니다.예를 들어 원자의 경우 속도(에너지) 선택은 세로 일관성을 제어하고 펄스 또는 절단은 시간 [62]: 154 일관성을 제어합니다.
광학적으로 형성된 물질 파동 물질의 광학적 조작은 물질 파동 광학에서 중요한 역할을 합니다: "유리가 광파와 [68]상호 작용하는 것처럼 광파는 물질 파동에 대해 굴절, 반사, 그리고 흡수 구조로 작용할 수 있습니다."레이저 광 운동량 전달은 물질 입자를 냉각시키고 [69]원자의 내부 흥분 상태를 변화시킬 수 있습니다.
다중 입자 실험 단일 입자 자유 공간 광학 방정식과 물질 파동 방정식은 동일하지만, 우연 실험과 같은 다중 입자 시스템은 그렇지 않습니다.[70]
물질파의 응용
다음 하위 섹션은 물질의 탐침 또는 기본 양자 특성으로 물질 파동의 응용을 설명하는 페이지에 대한 링크를 제공합니다.대부분의 경우, 이것은 처음에한{k \r를 갖는 이동 물질 파동을 생성하는 어떤 방법을 포함하고, 이를 사용하여 물질을 조사합니다.
아래 표에 표시된 것처럼 물질 파동의 질량은 6배 이상이고 에너지는 9배 이상이지만 파장은 모두 피코미터 범위에 있습니다. 이는 원자 공간과 비슷합니다.(원자 지름의 범위는 62 ~ 520 pm이고, 탄소-탄소 단일 결합의 일반적인 길이는 154 pm입니다.)더 긴 파장에 도달하려면 더 낮은 에너지에 도달하기 위해 레이저 냉각과 같은 특별한 기술이 필요합니다. 더 짧은 파장은 회절 효과를 [41]더 식별하기 어렵게 만듭니다.따라서 많은 응용 분야는 전자파, 특히 X선의 응용과 병행하여 재료 구조에 초점을 맞춥니다.빛과 달리 물질 파동 입자는 질량, 전하, 자기 모멘트 및 내부 구조를 가질 수 있어 새로운 도전과 기회를 제시합니다.
| 문제 | 덩어리 | 운동 에너지 | 파장 | 언급 |
|---|---|---|---|---|
| 전자 | 1/1823 Da | 54 eV | 167시 | 데이비슨-독일 실험 |
| 전자 | 1/1823 Da | 5×104 eV | 오후 5시 | 토노무라 외. |
| He 원자, H2 분자 | 4다 | 오후 50시 | 에스터만과[72] 스턴 | |
| 중성자 | 1다 | 0.025 eV | 오후 181시 | 울란과 슐[73] |
| 나트륨 원자 | 23 다 | 오후 20시 | 모스코위츠 [74]외. | |
| 헬륨 | 4다 | 0.065 eV | 오후 56시 | 그리센티 외.[75] |
| 나2 | 23 다 | 0.00017 eV | 오후 459시 | 채프먼 외.[76] |
| C60 플러렌 | 720 Da | 0.2 eV | 오후 5시 | 아른트 [43]외. |
| 플러렌70 | 841 다 | 0.2 eV | 오후 2시 | 브레즈거 외.[77] |
| 폴리펩타이드, 그라미시딘 A | 1860년 다 | 360fm | 샤예히 외.[78] | |
| 기능화된 올리고포르피린 | 25000 Da | 17 eV | 53 fm | 파인 외.[79] |
전자
전자 회절 패턴은 에너지 전자가 순서 있는 고체를 반사하거나 통과할 때 나타납니다. 패턴의 분석은 고체의 원자 배열 모델로 이어집니다.
전자 현미경을 사용하여 마이크론에서 원자 규모로 이미징, 전송, 스캔 및 낮은 에너지의 표면에 사용됩니다.
전자 에너지 손실 분광법에서 그들이 잃는 에너지의 측정은 물질의 화학과 전자 구조에 대한 정보를 제공합니다.전자 빔은 또한 나노 스케일에서 화학적 함량에 대한 정보를 생성할 수 있는 에너지 분산 분광학에서 특징적인 X선을 유도합니다.
양자 터널링은 고전적인 예측이 허용하는 것보다 적은 에너지로 정전장에서 금속으로부터 전자가 탈출하는 방법을 설명합니다: 물질 파동은 금속의 작업 기능 장벽을 관통합니다.
스캔 터널링 현미경은 양자 터널링을 활용하여 고체 표면의 맨 위 원자층을 이미지화합니다.
광학 홀로그래피의 전자 물질 파동 아날로그인 전자 홀로그래피는 박막의 전기장과 자기장을 조사합니다.
중성자
중성자 회절은 서로 다른 산란 단면과 자기에 대한 민감도를 통해 X선 회절을 보완합니다.
작은 각도의 중성자 산란은 빛 요소, 동위원소 및 자기 모멘트에 민감한 무질서한 시스템의 구조를 얻을 수 있는 방법을 제공합니다.
중성자 반사 측정은 박막의 구조를 측정하기 위한 중성자 회절 기술입니다.
중성 원자
광학 간섭계와 유사한 원자 간섭계는 서로 다른 경로를 따라 원자 물질 파동 사이의 위상 차이를 측정합니다.
원자 광학은 거울, 원자 초점 영역 판을 포함한 많은 광학 장치를 모방합니다.
헬륨 현미경 스캔은 He 원자파를 사용하여 고체 구조를 비파괴적으로 영상화합니다.
양자 반사는 물질 파동 행동을 사용하여 일부 원자 거울의 기초인 방목 각도 원자 반사를 설명합니다.
양자 비일관성 측정은 Rb 원자파 간섭에 의존합니다.
분자
큰 분자의 물질 파동 간섭에 의해 밝혀진 양자 중첩은 파동-입자 이중성과 양자 거시성의 [79][80]한계를 조사합니다.
물질파장 간섭계는 나노미터 정확도로 읽을 수 있는 분자 빔에 나노구조를 생성하므로 개별화된 [81]복잡한 분자의 과잉 또는 특성을 추론할 수 있는 매우 민감한 힘 측정에 사용됩니다.
참고 항목
레퍼런스
- ^ a b c Thomson, G. P.; Reid, A. (1927). "Diffraction of Cathode Rays by a Thin Film". Nature. 119 (3007): 890. Bibcode:1927Natur.119Q.890T. doi:10.1038/119890a0. ISSN 0028-0836. S2CID 4122313.
- ^ a b c Davisson, C.; Germer, L. H. (1927). "Diffraction of Electrons by a Crystal of Nickel". Physical Review. 30 (6): 705–740. Bibcode:1927PhRv...30..705D. doi:10.1103/physrev.30.705. ISSN 0031-899X.
- ^ a b c Davisson, C. J.; Germer, L. H. (1928). "Reflection of Electrons by a Crystal of Nickel". Proceedings of the National Academy of Sciences. 14 (4): 317–322. Bibcode:1928PNAS...14..317D. doi:10.1073/pnas.14.4.317. ISSN 0027-8424. PMC 1085484. PMID 16587341.
- ^ Kragh, Helge (1 December 2000). "Max Planck: the reluctant revolutionary". Physics World. Retrieved 19 May 2023.
- ^ Whittaker, Sir Edmund (1 January 1989). A History of the Theories of Aether and Electricity. Vol. 2. Courier Dover Publications. p. 87. ISBN 0-486-26126-3.
- ^ 아인슈타인, A. (1917)Zur Quant theor der Strahlung, Physicalische Zeitschrift 18:121-128번역 대상
- ^ Whittaker, Sir Edmund (1 January 1989). A History of the Theories of Aether and Electricity. Courier Dover Publications. p. 89. ISBN 0-486-26126-3.
- ^ Richardson, O. W.; Compton, Karl T. (17 May 1912). "The Photoelectric Effect". Science. American Association for the Advancement of Science (AAAS). 35 (907): 783–784. Bibcode:1912Sci....35..783R. doi:10.1126/science.35.907.783. ISSN 0036-8075. PMID 17792421.
- ^ 휴즈, A. L. "XXIII.일부 화합물의 광전 효과."런던, 에든버러, 더블린 철학 잡지 및 과학 저널 24.141 (1912): 380–390
- ^ Millikan, R. (1916). "A Direct Photoelectric Determination of Planck's "h"". Physical Review. 7 (3): 355–388. Bibcode:1916PhRv....7..355M. doi:10.1103/PhysRev.7.355.
- ^ de Broglie, Louis (1970). "The reinterpretation of wave mechanics". Foundations of Physics. 1 (1): 5–15. Bibcode:1970FoPh....1....5D. doi:10.1007/BF00708650. S2CID 122931010.
- ^ a b de Broglie, Louis Victor. "On the Theory of Quanta" (PDF). Foundation of Louis de Broglie (English translation by A.F. Kracklauer, 2004. ed.). Retrieved 25 February 2023.
- ^ de Broglie, L. (1923). "Waves and quanta". Nature. 112 (2815): 540. Bibcode:1923Natur.112..540D. doi:10.1038/112540a0. S2CID 4082518.
- ^ Medicus, H.A. (1974). "Fifty years of matter waves". Physics Today. 27 (2): 38–45. Bibcode:1974PhT....27b..38M. doi:10.1063/1.3128444.
- ^ 맥키넌, E. (1976). De Broglie의 논문: 비판적 회고, Am. J. Phys. 44: 1047–1055.
- ^ Espinosa, J.M. (1982). "Physical properties of de Broglie's phase waves". Am. J. Phys. 50 (4): 357–362. Bibcode:1982AmJPh..50..357E. doi:10.1119/1.12844.
- ^ Brown, H.R.; Martins (1984). "De Broglie's relativistic phase waves and wave groups". Am. J. Phys. 52 (12): 1130–1140. Bibcode:1984AmJPh..52.1130B. doi:10.1119/1.13743. Archived from the original on 29 July 2020. Retrieved 16 December 2019.
- ^ Whittaker, Sir Edmund (1 January 1989). A History of the Theories of Aether and Electricity. Vol. 2. Courier Dover Publications. p. 214. ISBN 0-486-26126-3.
- ^ McEvoy, J. P.; Zarate, Oscar (2004). Introducing Quantum Theory. Totem Books. pp. 110–114. ISBN 978-1-84046-577-8.
- ^ Louis de Broglie – 노벨 강의.NobelPrize.org .노벨상 봉사활동 AB 2023.2023년 6월 2일 금요일<https://www.nobelprize.org/prizes/physics/1929/broglie/lecture/ >
- ^ Schrödinger, E. (1984). Collected papers. Friedrich Vieweg und Sohn. ISBN 978-3-7001-0573-2. 첫 1926년 논문의 서론을 참조하십시오.
- ^ a b Schrödinger, E. (1926). "An Undulatory Theory of the Mechanics of Atoms and Molecules". Physical Review. 28 (6): 1049–1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/PhysRev.28.1049. ISSN 0031-899X.
- ^ a b Moore, W. J. (1992). Schrödinger: Life and Thought. Cambridge University Press. pp. 219–220. ISBN 978-0-521-43767-7.
- ^ Jammer, Max (1974). Philosophy of Quantum Mechanics: The interpretations of quantum mechanics in historical perspective. Wiley-Interscience. pp. 24–25. ISBN 978-0-471-43958-5.
- ^ Karam, Ricardo (June 2020). "Schrödinger's original struggles with a complex wave function". American Journal of Physics. 88 (6): 433–438. Bibcode:2020AmJPh..88..433K. doi:10.1119/10.0000852. ISSN 0002-9505. S2CID 219513834.
- ^ 다윈, 찰스 갈튼"파동역학에서의 자유로운 움직임"런던 왕립 학회의 의사록.시리즈 A, 수학적 및 물리적 특성의 논문 포함 117.776(1927): 258–293.
- ^ Arndt, Markus; Hornberger, Klaus (April 2014). "Testing the limits of quantum mechanical superpositions". Nature Physics. 10 (4): 271–277. doi:10.1038/nphys2863. ISSN 1745-2473.
- ^ 메리, P.G., G.F.미시롤리, G.포찌."전자 간섭 현상의 통계적 측면에 관하여."미국 물리학 저널 44: 306
- ^ Tonomura, A.; Endo, J.; Matsuda, T.; Kawasaki, T.; Ezawa, H. (1989). "Demonstration of single‐electron buildup of an interference pattern". American Journal of Physics. American Association of Physics Teachers (AAPT). 57 (2): 117–120. Bibcode:1989AmJPh..57..117T. doi:10.1119/1.16104. ISSN 0002-9505.
- ^ a b c Born, M.; Wolf, E. (1999). Principles of Optics. Cambridge University Press. ISBN 978-0-521-64222-4.
- ^ a b Bach, Roger; Pope, Damian; Liou, Sy-Hwang; Batelaan, Herman (13 March 2013). "Controlled double-slit electron diffraction". New Journal of Physics. IOP Publishing. 15 (3): 033018. arXiv:1210.6243. Bibcode:2013NJPh...15c3018B. doi:10.1088/1367-2630/15/3/033018. ISSN 1367-2630. S2CID 832961.
- ^ Navarro, Jaume (2010). "Electron diffraction chez Thomson: early responses to quantum physics in Britain". The British Journal for the History of Science. 43 (2): 245–275. doi:10.1017/S0007087410000026. ISSN 0007-0874. S2CID 171025814.
- ^ Mauro Dardo, 노벨상 수상자와 20세기 물리학, 캠브리지 대학 출판부 2004, 156–157페이지
- ^ Bethe, H. (1928). "Theorie der Beugung von Elektronen an Kristallen". Annalen der Physik (in German). 392 (17): 55–129. Bibcode:1928AnP...392...55B. doi:10.1002/andp.19283921704.
- ^ John M., Cowley (1995). Diffraction physics. Elsevier. ISBN 0-444-82218-6. OCLC 247191522.
- ^ a b Peng, L.-M.; Dudarev, S. L.; Whelan, M. J. (2011). High energy electron diffraction and microscopy. Oxford: Oxford University Press. ISBN 978-0-19-960224-7. OCLC 656767858.
- ^ Snell, A. H.; Wilkinson, M. K.; Koehler, W. C. (1984). "Ernest Omar Wollan". Physics Today. 37 (11): 120. Bibcode:1984PhT....37k.120S. doi:10.1063/1.2915947.
- ^ Shull, C. G. (1997). "Early Development of Neutron Scattering" (PDF). In Ekspong, G. (ed.). Nobel Lectures, Physics 1991–1995. World Scientific Publishing. pp. 145–154. Archived from the original (PDF) on 19 May 2017.
- ^ Colella, R.; Overhauser, A. W.; Werner, S. A. (1975). "Observation of Gravitationally Induced Quantum Interference" (PDF). Physical Review Letters. 34 (23): 1472–1474. Bibcode:1975PhRvL..34.1472C. doi:10.1103/PhysRevLett.34.1472.
- ^ Estermann, I.; Stern, Otto (1930). "Beugung von Molekularstrahlen". Z. Phys. 61 (1–2): 95. Bibcode:1930ZPhy...61...95E. doi:10.1007/bf01340293. S2CID 121757478.
- ^ a b Adams, C.S; Sigel, M; Mlynek, J (1994). "Atom optics". Physics Reports. Elsevier BV. 240 (3): 143–210. Bibcode:1994PhR...240..143A. doi:10.1016/0370-1573(94)90066-3. ISSN 0370-1573.
- ^ Pierre Cladé; Changhyun Ryu; Anand Ramanathan; Kristian Helmerson; William D. Phillips (2008). "Observation of a 2D Bose Gas: From thermal to quasi-condensate to superfluid". Physical Review Letters. 102 (17): 170401. arXiv:0805.3519. Bibcode:2009PhRvL.102q0401C. doi:10.1103/PhysRevLett.102.170401. PMID 19518764. S2CID 19465661.
- ^ a b Arndt, M.; O. Nairz; J. Voss-Andreae; C. Keller; G. van der Zouw; A. Zeilinger (14 October 1999). "Wave–particle duality of C60". Nature. 401 (6754): 680–682. Bibcode:1999Natur.401..680A. doi:10.1038/44348. PMID 18494170. S2CID 4424892.
- ^ Eibenberger, Sandra; Gerlich, Stefan; Arndt, Markus; Mayor, Marcel; Tüxen, Jens (14 August 2013). "Matter–wave interference of particles selected from a molecular library with masses exceeding 10000 amu". Physical Chemistry Chemical Physics. 15 (35): 14696–700. arXiv:1310.8343. Bibcode:2013PCCP...1514696E. doi:10.1039/c3cp51500a. ISSN 1463-9084. PMID 23900710. S2CID 3944699.
- ^ "2000 atoms in two places at once: A new record in quantum superposition". phys.org. Retrieved 25 September 2019.
- ^ Juffmann, Thomas; et al. (25 March 2012). "Real-time single-molecule imaging of quantum interference". Nature Nanotechnology. 7 (5): 297–300. arXiv:1402.1867. Bibcode:2012NatNa...7..297J. doi:10.1038/nnano.2012.34. PMID 22447163. S2CID 5918772.
- ^ Hornberger, Klaus; Stefan Uttenthaler; Björn Brezger; Lucia Hackermüller; Markus Arndt; Anton Zeilinger (2003). "Observation of Collisional Decoherence in Interferometry". Phys. Rev. Lett. 90 (16): 160401. arXiv:quant-ph/0303093. Bibcode:2003PhRvL..90p0401H. doi:10.1103/PhysRevLett.90.160401. PMID 12731960. S2CID 31057272.
- ^ Hackermüller, Lucia; Klaus Hornberger; Björn Brezger; Anton Zeilinger; Markus Arndt (2004). "Decoherence of matter waves by thermal emission of radiation". Nature. 427 (6976): 711–714. arXiv:quant-ph/0402146. Bibcode:2004Natur.427..711H. doi:10.1038/nature02276. PMID 14973478. S2CID 3482856.
- ^ Resnick, R.; Eisberg, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-471-87373-0.
- ^ a b c Whittaker, Sir Edmund (1 January 1989). A History of the Theories of Aether and Electricity. Vol. 2. Courier Dover Publications. p. 215. ISBN 0-486-26126-3.
- ^ Holden, Alan (1971). Stationary states. New York: Oxford University Press. ISBN 978-0-19-501497-6.
- ^ W.S.C. Williams(2002)특수 상대성 이론 소개, 테일러 & 프랜시스, 런던, ISBN 0-415-27761-2, 페이지 192.
- ^ a b Schiff, Leonard I. (1987). Quantum mechanics. International series in pure and applied physics (3. ed., 24. print ed.). New York: McGraw-Hill. ISBN 978-0-07-085643-1.
- ^ Metherell, A. J. (1972). Electron Microscopy in Materials Science. Commission of the European Communities. pp. 397–552.
- ^ Verbeeck, J.; Tian, H.; Schattschneider, P. (2010). "Production and application of electron vortex beams". Nature. 467 (7313): 301–304. Bibcode:2010Natur.467..301V. doi:10.1038/nature09366. ISSN 1476-4687. PMID 20844532. S2CID 2970408.
- ^ a b Efthimios Kaxiras (9 January 2003). Atomic and Electronic Structure of Solids. Cambridge University Press. pp. 65–69. ISBN 978-0-521-52339-4.
- ^ Jammer, Max (1989). The conceptual development of quantum mechanics. The history of modern physics (2nd ed.). Los Angeles (Calif.): Thomas publishers. ISBN 978-0-88318-617-6.
- ^ Mulliken, Robert S. (1932). "Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations". Physical Review. 41 (1): 49–71. Bibcode:1932PhRv...41...49M. doi:10.1103/PhysRev.41.49.
- ^ Griffiths, David J. (1995). Introduction to quantum mechanics. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0-13-124405-4.
- ^ Levine, Ira N. (2000). Quantum chemistry (5th ed.). Upper Saddle River, NJ: Prentice Hall. ISBN 978-0-13-685512-5.
- ^ Schrödinger, Erwin (2001). Collected papers on wave mechanics: together with his Four lectures on wave mechanics. Translated by Shearer, J. F.; Deans, Winifred Margaret (Third (augmented) edition, New York 1982 ed.). Providence, Rhode Island: AMS Chelsea Publishing, American Mathematical Society. ISBN 978-0-8218-3524-1.
- ^ a b Adams, C.S; Sigel, M; Mlynek, J (1 May 1994). "Atom optics". Physics Reports. 240 (3): 143–210. Bibcode:1994PhR...240..143A. doi:10.1016/0370-1573(94)90066-3.
- ^ Schlosshauer, Maximilian (1 October 2019). "Quantum decoherence". Physics Reports. 831: 1–57. arXiv:1911.06282. Bibcode:2019PhR...831....1S. doi:10.1016/j.physrep.2019.10.001. S2CID 208006050.
- ^ Pynn, Roger (1 July 1990). "Neutron Scattering – A Primer" (PDF). National Institute of Standards and Technology. Retrieved 24 June 2023.
- ^ Fano, U. (1957). "Description of States in Quantum Mechanics by Density Matrix and Operator Techniques". Reviews of Modern Physics. 29 (1): 74–93. doi:10.1103/RevModPhys.29.74. ISSN 0034-6861.
- ^ Hall, Brian C. (2013), "Systems and Subsystems, Multiple Particles", Quantum Theory for Mathematicians, New York, NY: Springer New York, vol. 267, pp. 419–440, doi:10.1007/978-1-4614-7116-5_19, ISBN 978-1-4614-7115-8, retrieved 13 August 2023
- ^ Hawkes, Peter W.; Hawkes, P. W. (1972). Electron optics and electron microscopy. London: Taylor & Francis. p. 117. ISBN 978-0-85066-056-2.
- ^ Cronin, Alexander D.; Schmiedmayer, Jörg; Pritchard, David E. (28 July 2009). "Optics and interferometry with atoms and molecules". Reviews of Modern Physics. 81 (3): 1051–1129. arXiv:0712.3703. Bibcode:2009RvMP...81.1051C. doi:10.1103/RevModPhys.81.1051. hdl:1721.1/52372. ISSN 0034-6861. S2CID 28009912.
- ^ Akbari, Kamran; Di Giulio, Valerio; García De Abajo, F. Javier (2022). "Optical manipulation of matter waves". Science Advances. 8 (42): eabq2659. arXiv:2203.07257. Bibcode:2022SciA....8.2659A. doi:10.1126/sciadv.abq2659. PMID 36260664.
- ^ Brukner, Časlav; Zeilinger, Anton (6 October 1997). "Nonequivalence between Stationary Matter Wave Optics and Stationary Light Optics". Physical Review Letters. 79 (14): 2599–2603. Bibcode:1997PhRvL..79.2599B. doi:10.1103/PhysRevLett.79.2599. ISSN 0031-9007.
- ^ Tonomura, Akira; Endo, J.; Matsuda, T.; Kawasaki, T.; Ezawa, H. (1989). "Demonstration of single‐electron buildup of an interference pattern". American Journal of Physics. 57 (2): 117–120. Bibcode:1989AmJPh..57..117T. doi:10.1119/1.16104.
- ^ Estermann, I.; Stern, O. (1 January 1930). "Beugung von Molekularstrahlen". Zeitschrift für Physik (in German). 61 (1): 95–125. doi:10.1007/BF01340293. ISSN 0044-3328.
- ^ Wollan, E. O.; Shull, C. G. (1948). "The Diffraction of Neutrons by Crystalline Powders". Physical Review. American Physical Society. 73 (8): 830–841. Bibcode:1948PhRv...73..830W. doi:10.1103/PhysRev.73.830. hdl:2027/mdp.39015086506584.
- ^ Moskowitz, Philip E.; Gould, Phillip L.; Atlas, Susan R.; Pritchard, David E. (1 August 1983). "Diffraction of an Atomic Beam by Standing-Wave Radiation". Physical Review Letters. 51 (5): 370–373. doi:10.1103/PhysRevLett.51.370.
- ^ Grisenti, R. E.; W. Schöllkopf; J. P. Toennies; J. R. Manson; T. A. Savas; Henry I. Smith (2000). "He-atom diffraction from nanostructure transmission gratings: The role of imperfections". Physical Review A. 61 (3): 033608. Bibcode:2000PhRvA..61c3608G. doi:10.1103/PhysRevA.61.033608.
- ^ Chapman, Michael S.; Christopher R. Ekstrom; Troy D. Hammond; Richard A. Rubenstein; Jörg Schmiedmayer; Stefan Wehinger; David E. Pritchard (1995). "Optics and interferometry with Na2 molecules". Physical Review Letters. 74 (24): 4783–4786. Bibcode:1995PhRvL..74.4783C. doi:10.1103/PhysRevLett.74.4783. PMID 10058598.
- ^ Brezger, B.; Hackermüller, L.; Uttenthaler, S.; Petschinka, J.; Arndt, M.; Zeilinger, A. (February 2002). "Matter–Wave Interferometer for Large Molecules" (reprint). Physical Review Letters. 88 (10): 100404. arXiv:quant-ph/0202158. Bibcode:2002PhRvL..88j0404B. doi:10.1103/PhysRevLett.88.100404. PMID 11909334. S2CID 19793304. Archived (PDF) from the original on 13 August 2007. Retrieved 30 April 2007.
- ^ Shayeghi, A.; Rieser, P.; Richter, G.; Sezer, U.; Rodewald, J. H.; Geyer, P.; Martinez, T. J.; Arndt, M. (19 March 2020). "Matter-wave interference of a native polypeptide". Nature Communications. 11 (1): 1447. doi:10.1038/s41467-020-15280-2. ISSN 2041-1723. PMC 7081299. PMID 32193414.
- ^ a b Fein, Yaakov Y.; Geyer, Philipp; Zwick, Patrick; Kiałka, Filip; Pedalino, Sebastian; Mayor, Marcel; Gerlich, Stefan; Arndt, Markus (December 2019). "Quantum superposition of molecules beyond 25 kDa". Nature Physics. 15 (12): 1242–1245. doi:10.1038/s41567-019-0663-9. ISSN 1745-2481.
- ^ Nimmrichter, Stefan; Hornberger, Klaus (18 April 2013). "Macroscopicity of Mechanical Quantum Superposition States". Physical Review Letters. 110 (16): 160403. doi:10.1103/PhysRevLett.110.160403.
- ^ Gerlich, Stefan; Fein, Yaakov Y.; Shayeghi, Armin; Köhler, Valentin; Mayor, Marcel; Arndt, Markus (2021), Friedrich, Bretislav; Schmidt-Böcking, Horst (eds.), "Otto Stern's Legacy in Quantum Optics: Matter Waves and Deflectometry", Molecular Beams in Physics and Chemistry: From Otto Stern's Pioneering Exploits to Present-Day Feats, Cham: Springer International Publishing, pp. 547–573, doi:10.1007/978-3-030-63963-1_24, ISBN 978-3-030-63963-1, retrieved 3 September 2023
진일보한 내용
- L. de Broglie, 양자 이론 연구 (양자 이론에 대한 연구), 논문 (파리), 1924; L. de Broglie, Ann. 물리학. (파리) 3, 22 (1925).A.F.에 의한 영어 번역 크라크라우어.
- 브로글리, 루이 드, 전자 노벨 강의의 파동성, 12, 1929.
- 티플러, 폴 A. 그리고 랄프 A.Llewellyn (2003).현대 물리학.4번째.뉴욕; W. H. 프리먼 앤드 컴퍼니ISBN 0-7167-4345-0. 페이지 203–4, 222–3, 236.
- Zumdahl, Steven S. (2005). Chemical Principles (5th ed.). Boston: Houghton Mifflin. ISBN 978-0-618-37206-5.
- 2009년 7월에 "원자와 분자에 대한 광학 및 간섭계"라는 광범위한 리뷰 기사가 등장했습니다. www.atomwave.org/rmparticle/RMPLAO.pdf ://https://web.archive.org/web/20110719220930/http
- 1953년 "막스 본이 에든버러 대학교의 자연철학 타이트 석좌교수직에서 은퇴할 때 제출한 과학 논문" (올리버와 보이드)
외부 링크
- Bowley, Roger. "de Broglie Waves". Sixty Symbols. Brady Haran for the University of Nottingham.








 이동하는 패킷의
이동하는 패킷의  다음과 같다는 것을 보여주었습니다.
다음과 같다는 것을 보여주었습니다.
 초기 위치의 불확실성입니다.이 위치 불확실성은
초기 위치의 불확실성입니다.이 위치 불확실성은 


 실제 공간의 위치이고
실제 공간의 위치이고 역 미터 단위의
역 미터 단위의 





 나머지 질량입니다.유도체를 적용하면 (비상대론적) 물질 파동군 속도를 얻을 수 있습니다.
나머지 질량입니다.유도체를 적용하면 (비상대론적) 물질 파동군 속도를 얻을 수 있습니다.







 입자의 질량 중심의 속도이며, 군 속도와 동일합니다.
입자의 질량 중심의 속도이며, 군 속도와 동일합니다. 






![{\displaystyle {\begin{aligned}E&=mc^{2}=\gamma m_{0}c^{2}\\[1ex]\mathbf {p} &=m\mathbf {v} =\gamma m_{0}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/053c1698b17f046a303b5d7423a80e81b2925184)
![{\displaystyle {\begin{aligned}&\lambda =\,\,{\frac {h}{\gamma m_{0}v}}\,=\,{\frac {h}{m_{0}v}}\,\,\,{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}\\[2.38ex]&f={\frac {\gamma \,m_{0}c^{2}}{h}}={\frac {m_{0}c^{2}}{h{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8992d4a8c16e09dbeec6ddac63ee3feb66a64a7)








 있고, 에너지는 파동 벡터의 함수로 더 일반적으로 쓰여졌습니다.에너지가 더 이상 파동 벡터 제곱에 항상 비례하지는 않지만 이전에 주어진 다양한 용어는 여전히 적용됩니다.일반적인 접근법은 일반적으로 다음과 같이 주어진 텐서
있고, 에너지는 파동 벡터의 함수로 더 일반적으로 쓰여졌습니다.에너지가 더 이상 파동 벡터 제곱에 항상 비례하지는 않지만 이전에 주어진 다양한 용어는 여전히 적용됩니다.일반적인 접근법은 일반적으로 다음과 같이 주어진 텐서 



 델로
델로 






