다변량 커널 밀도 추정

커널 밀도 추정은 밀도 추정을 위한 비모수 기법, 즉 확률밀도함수의 추정을 위한 기법으로, 통계학에서 근본적인 질문 중 하나이다. 통계적 특성이 개선된 히스토그램 밀도 추정의 일반화로 볼 수 있다. 히스토그램 외에 다른 유형의 밀도 추정기에는 파라메트릭, 스플라인, 파장 및 푸리에 시리즈가 포함된다. 커널 밀도 추정기는 1950년대와 1960년대에^[1]^[2] 일변량 데이터를 위한 과학 문헌에 처음 소개되었고 이후 널리 채택되었다. 다변량 데이터에 대한 유사 추정기가 다변량 통계에 중요한 추가가 될 것이라는 사실이 곧 인식되었다. 1990년대와 2000년대에 실시된 연구를 바탕으로 다변량 커널 밀도 추정은 단변량 커널 밀도에 버금가는 성숙 수준에 도달했다.^[3]

동기

우리는 히스토그램의 구성을 설명하기 위해 50개의 점의 합성 이바리테이트 데이터 세트를 사용한다. 이를 위해서는 앵커 포인트(히스토그램 그리드의 왼쪽 하단 모서리)를 선택해야 한다. 왼쪽 히스토그램의 경우(-1.5, -1.5): 오른쪽 히스토그램의 경우 앵커 포인트를 양방향(-1.625, -1.625)으로 0.125만큼 이동시킨다. 두 히스토그램 모두 빈 너비가 0.5이므로 어떤 차이도 앵커 포인트의 변경에 기인한다. 색상 코딩은 빈에 포함되는 데이터 포인트의 수를 나타낸다: 0=흰색, 1=팔색 노란색, 2=밝은 노란색, 3=주황색, 4=빨간색. 왼쪽 히스토그램은 위쪽 절반의 밀도가 아래쪽 절반보다 높음을 나타내는 반면, 오른쪽 히스토그램은 오른쪽 히스토그램의 경우로 나타나 히스토그램이 앵커 포인트의 위치에 매우 민감하다는 것을 확인시켜 준다.^[4]

2D 히스토그램 비교 왼쪽. 앵커 포인트가 있는 히스토그램(-1.5, -1.5) 오른쪽. 앵커 포인트가 있는 히스토그램(-1.625, -1.625). 두 히스토그램 모두 빈 너비가 0.5이므로 두 히스토그램의 외관 차이는 앵커 포인트의 배치로 인한 것이다.

이 앵커 포인트 배치 문제에 대한 한 가지 가능한 해결책은 히스토그램 바이닝 그리드를 완전히 제거하는 것이다. 아래 왼쪽 그림에서 커널(회색 선으로 표시됨)은 위의 50개 데이터 지점 각각에 중심화되어 있다. 이러한 커널을 합한 결과는 커널 밀도 추정치인 올바른 수치로 제시된다. 커널 밀도 추정치와 히스토그램의 가장 현저한 차이는 전자가 바이닝 그리드에 의해 유도된 예술성을 포함하지 않기 때문에 해석하기가 더 쉽다는 것이다. 색상 윤곽선은 빨간색 = 25%, 주황색 + 적색 = 50%, 노란색 + 주황색 + 적색 = 75% 등 각각의 확률 질량을 포함하는 가장 작은 영역에 해당하므로 단일 중앙 영역이 가장 높은 밀도를 가지고 있음을 나타낸다.

2D 커널 밀도 추정치 구축. 왼쪽. 개별 커널. 맞아. 커널 밀도 추정치.

밀도 추정의 목적은 데이터의 유한 표본을 취하여 데이터가 관찰되지 않는 곳을 포함하여 모든 곳에서 기본 확률 밀도 함수에 대해 추론하는 것이다. 커널 밀도 추정에서 각 데이터 점의 기여도는 한 점에서 그것을 둘러싼 공간의 영역으로 평활화된다. 개별적으로 평활화된 기여도를 종합하면 데이터의 구조와 그 밀도 함수에 대한 전체적인 그림을 볼 수 있다. 따라야 할 세부사항에서, 우리는 이 접근방식이 기본 밀도 함수의 합리적인 추정으로 이어진다는 것을 보여준다.

정의

앞의 그림은 커널 밀도 추정치를 그래픽으로 표현한 것이며, 현재 우리는 이를 정확하게 정의하고 있다. x₁, x₂, ..., x는_n 밀도함수 ƒ으로 기술된 공통분포에서 추출한 d-변수 랜덤 벡터의 표본이 되게 한다. 커널 밀도 추정치는 다음과 같이 정의된다.

{\f}_{\mathbf {H}}}(\mathbf {x} )={\frac {1}{n}\sum _{i=1}^{n_{n_}K_{}}}}}(\mathbf {x} -\mathbf {x} _{i}}}})

어디에

x = (x₁, x₂, …, x_d),^T x_i = (x_i1, x_i2, …, x_id),^T i = 1, 2, n은 d-벡터,
H는 대역폭(또는 평활) d×d 매트릭스로 대칭적이고 양수가 분명한 매트릭스.
K는 대칭 다변량 밀도인 커널 함수다.
$K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ x $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ ) $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ = $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ - $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ / $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ K $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ ( $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ - $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ / $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$ ) $K_{\mathbf {H}}}}(\mathbf {x} )= \mathbf {H$ ^{- $1/2$ }K $(\mathbf {H}$ ^- $1/2}\mathb {x}$ $K_{\mathbf {H} }(\mathbf {x} )=|\mathbf {H} |^{-1/2}K(\mathbf {H} ^{-1/2}\mathbf {x} )$

The choice of the kernel function K is not crucial to the accuracy of kernel density estimators, so we use the standard multivariate normal kernel throughout: ${\textstyle K_{\mathbf {H} }(\mathbf {x} )={(2\pi )^{-d/2}}\mathbf { H }$ $^{-1/2}}e^{-{\frac {1}{2}}\mathbf {x^{$ $T}} \mathbf{H^{-1} \mathbf {x$ 여기서 H는 공분산 행렬의 역할을 한다. 반면에 대역폭 매트릭스 H의 선택은 평활이 유도하는 양과 방향을 제어하기 때문에 정확도에 영향을 미치는 가장 중요한 단일 요인이다.^[5]^{: 36–39} 대역폭 매트릭스도 방향을 유도한다는 것은 1D 커널에 대해 방향이 정의되지 않기 때문에 단변량 아날로그로부터의 다변량 커널 밀도 추정 사이의 기본적인 차이점이다. 이것은 이 대역폭 매트릭스의 파라메타레이션 선택으로 이어진다. 세 가지 주요 파라메타 클래스(복잡성 순서에 따라)는 S로, 양의 스칼라 클래스는 ID 매트릭스를 곱한 S로, D는 주 대각선에 양의 입력이 있는 대각 행렬로, F는 대칭 양의 한정 행렬이다. S 클래스 커널은 모든 좌표 방향에 적용되는 평활의 양이 같으며, D 커널은 각 좌표에서 다른 양의 평활을 허용하며, F 커널은 평활의 임의 양과 방향을 허용한다. 역사적으로 S와 D 커널은 계산상의 이유로 가장 널리 퍼져있지만, 연구에 따르면 정확도의 중요한 이득은 보다 일반적인 F 클래스 커널을 사용하여 얻을 수 있다고 한다.^[6]^[7]

세 가지 주요 대역폭 매트릭스 파라메타레이션 클래스의 비교. 왼쪽, S양성 스칼라가 아이덴티티 매트릭스를 곱한다. 중앙. D 대각 행렬(주 대각선에 양수 항목 포함) 맞아, F 대칭 양정확정 행렬이야.

최적의 대역폭 매트릭스 선택

대역폭 매트릭스를 선택하는 데 가장 일반적으로 사용되는 최적성 기준은 MISE 또는 평균 통합 제곱 오차이다.

\operatorname {MISE}(\mathbf {H} )=\E}\!\좌측[\,\\int({f}_{\mathbf {H})}}}(\mathb {x})-f(\mathb {x})^{2},d\mathb {x}\mathb {x}\x}\x}\xf;\x}\x}\x}\우측근 {x}\x}\\x}\x}\x}\\\\\\\

이것은 일반적으로 폐쇄형 표현을 가지고 있지 않기 때문에, 그 점근법(AMISE)을 대리용으로 사용하는 것이 보통이다.

\operatorname {AMISE} (\mathbf {H} )=n^{-1} \mathbf {H}  ^{-1/2}R(K)+{\tfrac {1}{4}}m_{2}(K)^{2}(\operatorname {vec} ^{T}\mathbf {H} )\mathbf {\Psi } _{4}(\operatorname {vec} \mathbf {H} )

어디에

$R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ( $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ) $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ = $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ K $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ( $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ) $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ $R(K)=\int K(\mathbf {x} )^{2}\,d\mathbf {x}$ ${\$ K가 일반 커널일 때 R(K) = (4π)^−d/2인 경우
$\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ x $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ K $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ ( $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ ) d $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ = $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ ( $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ K ) $\int \mathbf {x} \mathbf {x} ^{T}K(\mathbf {x} )\,d\mathbf {x} =m_{2}(K)\mathbf {I} _{d}$ d ${\$ { $x} \mathbf {x} ^{T}$ K(\ $mathbf$ {x $} )\,d\$ mathbf { $x}$ = $m_{2}($ K)\ $mathbf$ { $I} _{$ d}, $_$ {d}, _},},},}, },},},},},

일반_d 커널의₂ 경우 m = 1을 갖는 d × d ID 매트릭스인 경우

Dƒ는² ƒ의 2차 부분파생상품의 d × d 헤시안 행렬이다.
$\mathbf {\Psi } _{4}=\int (\operatorname {vec} \,\operatorname {D} ^{2}f(\mathbf {x} ))(\operatorname {vec} ^{T}\operatorname {D} ^{2}f(\mathbf {x} ))\,d\mathbf {x}$ is a d² × d² matrix of integrated fourth order partial derivatives of ƒ
vec is the vector operator which stacks the columns of a matrix into a single vector e.g. ${\displaystyle \operatorname {vec} {\begin{bmatrix}a&c\\b&d\end{bmatrix}}={\begin{bmatrix}a&b&c&d\end{bmatrix}}^{T}.$ $}$

MISE에^[5]^{: 97} 대한 AMISE 근사치의 품질은 다음과 같다.

\operatorname {MISE}(\mathbf {H} )=\operatorname {AMISE}(\mathbf {H})+o(n^{-1} \mathbf {H} ^{-1} \mathbf {H} ^} ^} \tr}}}}

여기서 o는 일반적인 작은 o 표기법을 나타낸다. 경험적으로 이 문장은 AMISE가 표본 크기로서 MISE의 '좋은' 근사치임을 암시한다. n → ∞.

모든 합리적인 대역폭 선택기 H는 H = O(n^−2/(d+4))를 가지며, 여기서 빅 O 표기법이 요소별로 적용된다는 것을 알 수 있다. 이것을 MISE 공식으로 대체하면 최적의 MISE는 O(n^−4/(d+4))이다.^[5]^{: 99–100} 따라서 n → ∞로서 MISE → 0, 즉 커널 밀도 추정치는 평균 제곱으로 수렴되며 따라서 실제 밀도 f까지 확률로 수렴된다. 이러한 수렴 모드는 커널 방법이 합리적인 밀도 추정기로 이어진다는 동기부여 섹션의 문구를 확인하는 것이다. 최적의 대역폭 선택기는

\mathbf {H} _{\operatorname {AMISE} }=\operatorname {argmin} _{\mathbf {H} \in F}\\\operatorname {AMISE}(\mathbf {H}).

이 이상적인 선택기는 알 수 없는 밀도함수 ƒ을 포함하고 있기 때문에 직접 사용할 수 없다. 데이터 기반 대역폭 선택기의 다양한 다양성은 AMISE의 다른 추정기에서 발생한다. 우리는 실무에서 가장 광범위하게 적용되는 것으로 밝혀진 두 가지 등급의 선택기에 집중한다: 평활화된 교차 검증과 플러그인 선택기.

플러그인

AMISE의 플러그인(PI) 추정치는 추정기 ${\hat {\mathbf {\Psi } }}_{4}$ ${\hat {\mathbf {\Psi } }}_{4}$ ${\$ 에 의해 ψ을₄ 대체함으로써 형성된다.

\operatorname {PI} (\mathbf {H} )=n^{-1} \mathbf {H}  ^{-1/2}R(K)+{\tfrac {1}{4}}m_{2}(K)^{2}(\operatorname {vec} ^{T}\mathbf {H} ){\hat {\mathbf {\Psi } }}_{4}(\mathbf {G} )(\operatorname {vec} \,\mathbf {H} )

where ${\displaystyle {\hat {\mathbf {\Psi } }}_{4}(\mathbf {G} )=n^{-2}\sum _{i=1}^{n}\sum _{j=1}^{n}[(\operatorname {vec} \,\operatorname {D} ^{2})(\operatorname {vec} ^{T}\operatorname {D} ^{$ $2}]K_{\mathbf {G$ X $} _{i}-\mathbf {X}).$ Thus ${\hat {\mathbf {H} }}_{\operatorname {PI} }=\operatorname {argmin} _{\mathbf {H} \in F}\,\operatorname {PI} (\mathbf {H} )$ is the plug-in selector.^[8]^[9] 또한 이 참고문헌에는 파일럿 대역폭 매트릭스 G의 최적 추정에 관한 알고리즘이 포함되어 있으며, $H$ ${\hat {\mathbf {H} }}_{\operatorname {PI} }$ ${\$ 확률적으로_AMISE H에 ${\hat {\mathbf {H} }}_{\operatorname {PI} }$ 수렴하는 것을 확인할 수 있다.

평활 교차 검증

평활 교차 검증(SCV)은 더 큰 종류의 교차 검증 기법의 하위 집합이다. SCV Estimator가 두 번째 기간의 플러그인 Estimator와 다름

\operatorname {SCV} (\mathbf {H} )=n^{-1} \mathbf {H}  ^{-1/2}R(K)+n^{-2}\sum _{i=1}^{n}\sum _{j=1}^{n}(K_{2\mathbf {H} +2\mathbf {G} }-2K_{\mathbf {H} +2\mathbf {G} }+K_{2\mathbf {G} })(\mathbf {X} _{i}-\mathbf {X} _{j})

Thus ${\hat {\mathbf {H} }}_{\operatorname {SCV} }=\operatorname {argmin} _{\mathbf {H} \in F}\,\operatorname {SCV} (\mathbf {H} )$ is the SCV selector.^[9]^[10] 또한 이 참고문헌에는 파일럿 대역폭 매트릭스 G의 최적 추정에 관한 알고리즘이 포함되어 있으며 ${\hat {\mathbf {H} }}_{\operatorname {SCV} }$ ${\hat {\mathbf {H} }}_{\operatorname {SCV} }$ ${\hat {\mathbf {H} }}_{\operatorname {SCV} }$ ${\$ 확률적으로 H에_AMISE 수렴하는 ${\hat {\mathbf {H} }}_{\operatorname {SCV} }$ 것을 확립한다.

경험 법칙

Silverman's rule of thumb suggests using ${\sqrt {\mathbf {H} _{ii}}}=\left({\frac {4}{d+2}}\right)^{\frac {1}{d+4}}n^{\frac {-1}{d+4}}\sigma _{i}$ where $\sigma _{i}$ is the standard deviation of the ith variable and $\mathbf {H} _{ij}=0,i\neq j$ . Scott's rule is ${\sqrt {\mathbf {H} _{ii}}}=n^{\frac {-1}{d+4}}\sigma _{i}$ .

점근해석

최적의 대역폭 선택 섹션에서 MISE를 소개했다. 그것의 구조는 기대값과 밀도 추정기의^[5]^{: 97} 분산을 기반으로 한다.

\operatorname {E} {\hat {f}}(\mathbf {x} ;\mathbf {H} )=K_{\mathbf {H} }*f(\mathbf {x} )=f(\mathbf {x} )+{\frac {1}{2}}m_{2}(K)\operatorname {tr} (\mathbf {H} \operatorname {D} ^{2}f(\mathbf {x} ))+o(\operatorname {tr} \,\mathbf {H} )

여기서 *는 두 기능 사이의 콘볼루션 연산자 및

\operatorname {Var} {\hattbf {x};\mathbf {H}=n^{-1} \mathbf {H}=n-1} \mathbf {H}{x}^{-1}{-1} \mathbf {H}

이 두 가지 식이 잘 정의되기 위해서는 H의 모든 원소가 0이 되고 n⁻¹ H가 0이 되어 n이 무한이 되는 경향이 있음을 요구한다. 이 두 가지 조건을 가정하면, 기대값이 참 밀도인 경향이 있음을 알 수 있다. 즉, 커널 밀도 추정기가 무증상적으로 편향되지 않고, 분산이 0이 되는 경향이 있다는 것을 알 수 있다. 표준 평균 제곱 값 분해 사용

\operatorname {MSE} \,{\hat {f}}(\mathbf {x} ;\mathbf {H} )=\operatorname {Var} {\hat {f}}(\mathbf {x} ;\mathbf {H} )+[\operatorname {E} {\hat {f}}(\mathbf {x} ;\mathbf {H} )-f(\mathbf {x} )]^{2}

우리는 MSE가 0인 경향이 있다는 것을 가지고 있는데, 이는 커널 밀도 추정기가 (평균 제곱) 일관성이 있고 따라서 확률로 실제 밀도 f로 수렴된다는 것을 의미한다. MSE 0의 수렴 속도는 앞에서 언급한 MISE^−4/(d+4) 비율과 반드시 동일하므로, 밀도 추정기의 f의 포함률은 O_p(n^−2/(d+4))이며, 여기서_p O는 확률로 순서를 나타낸다. 이것은 포인트와 정합성을 확립한다. 기능적 포괄성은 MISE의 행동을 고려하여 유사하게 설정되며, 충분한 규칙성 하에서 통합은 융합율에 영향을 미치지 않는다는 점에 주목한다.

고려된 데이터 기반 대역폭 선택기의 경우 대상은 AMISE 대역폭 매트릭스다. 우리는 데이터 기반 선택기가 상대 속도_p O(n^−α), α > 0인 경우 AMISE 선택기로 수렴된다고 말한다.

{\displaystyle \operatorname {vc}({\hatbf {H}}}}) _{\operatorname {AMISE}}}=O(n^{-2\alpha }}}\operatorname {vc} \mathbf {H}{\operatorname {AMISE}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.

플러그인과 평활화된 교차 검증 선택기(단일 파일럿 대역폭 G)는 모두 O_p(n^−2/(d+6))의 상대적인 비율로 수렴되며, 즉 이러한 데이터 기반 선택기 모두 일관된 추정기라는 것이 확립되었다.

전체 대역폭 매트릭스를 사용한 밀도 추정

플러그인 대역폭 매트릭스를 사용한 기존 충실한 Geyser 데이터 커널 밀도 추정치.

R의 ks 패키지는^[12] 플러그인 및 평활 교차 검증 선택기를 구현한다(다른 것 중 가장 높음). 이 데이터 세트(R의 기본 분포에 포함)는 미국 옐로우스톤 국립공원에 있는 올드 프로스펙트 가이저의 분화 시간(분)과 다음 분화까지의 대기 시간(분)의 두 가지 측정값으로 272개의 레코드를 포함하고 있다.

코드 조각은 플러그인 대역폭 매트릭스 ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ = ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ [ ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ . ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ . ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ .510 0. ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ ]. ${\displaystyle {\hat {\\mathbf {H}}}}}}}{\\operatorname {PI}}}}={\begin}0.510\0.510$ &# $8.$ $882\end{bmatrix}.$ $}$ 다시 ${\hat {\mathbf {H} }}_{\operatorname {PI} }={\begin{bmatrix}0.052&0.510\\0.510&8.882\end{bmatrix}}.$ 말하지만, 색상 윤곽은 각각의 확률 질량을 포함하는 가장 작은 영역에 해당한다: 빨강 = 25%, 주황 + 빨강 = 50%, 노랑 + 주황 + 빨강 = 75%. SCV 선택기를 계산하려면 Hpi 로 대체되다 Hscv. 이 예는 대부분 플러그인 추정치와 비슷하기 때문에 여기에 표시되지 않는다.

도서관(ks) 자료(충실한) H <- 후피(x=충실한) 모자의 <- Kde(x=충실한, H=H) 음모를 꾸미다(모자의, 전시하다="filled.csv2) 포인트(충실한, 열매를 맺다=0.5, 꼬챙이질하다=16)

대각선 대역폭 매트릭스를 사용한 밀도 추정

합성 정규 혼합물 데이터에 대한 대각선 대역폭을 사용한 커널 밀도 추정치.

우리는 가우스의 혼합물(4π)−1 지수 함수의 밀도 추정(−.mw-parser-output .frac{white-space:nowrap}.mw-parser-output.frac.num,.mw-parser-output.frac .den{:80%;line-height:0;vertical-align:슈퍼 font-size}.mw-parser-output.frac .den{vertical-align:서브}.mw-parser-output .sr-only{생각한다.국경. 무작위로 생성된 포인트에서 0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1⁄2(x12+x22))+(4π)−1 exp(−1⁄2((x1-3.5)2+x22)),. 우리는 2차원 데이터를 위해 매트랩 루틴을 사용한다. 루틴은 2차 순서 가우스 커널을 위해 특별히 설계된 자동 대역폭 선택 방법이다.^[13] 그림은 자동으로 선택된 대역폭을 사용함으로써 발생하는 공동 밀도 추정치를 보여준다.

예제의 Matlab 스크립트

현재 디렉토리에 kde2d.m 함수를 다운로드하여 저장한 후 Matlab에 다음 명령을 입력하십시오.

  분명한 전부     % 합성 데이터 생성   자료=[랜드(500,2);       랜드(500,1)+3.5, 랜드(500,1);];   % 현재 디렉터리에 저장된 루틴 호출    [대역폭,밀도,X,Y]=kde2d(자료);   % 데이터 및 밀도 추정치 그림   등고선3(X,Y,밀도,50), 보유하다 에 관하여   음모를 꾸미다(자료(:,1),자료(:,2),'r.','마커사이즈',5)

대체 최적성 기준

MISE는 밀도 추정치와 실제 밀도함수 f 사이의 예상 통합 L 거리다₂. 주로 트랙터성 때문에 가장 널리 사용되며, 대부분의 소프트웨어는 MISE 기반 대역폭 선택기를 구현한다. MISE가 적절한 조치가 아닌 경우를 다루려고 하는 대안적 최적성 기준이 있다.^[3]^{: 34–37, 78} 등가 L₁ 측정값, 평균 통합 절대 오차 값은 다음과 같다.

{\displaystyle \operatorname {MIAE}(\mathbf {H} )=\E}\\int {\hat {f}_{\mathbf {H}}(\mathbf {x})-f(\mathbf {x} ) \d\mathbf {x}.}}.

그것의 수학적인 분석은 MISE보다 상당히 더 어렵다. 실제로, 그 이득은 크지 않은 것으로 보인다.^[14] L_∞ 표준은 평균 균일 절대 오차임

{\displaystyle \operatorname {MUAE}(\mathbf {H} )=\operatorname {E}\,\operatorname {sup} _{\mathbf {x}{f}{\hatbf {H}}(\mathbf {x})-f(\mathbf {x} ). .}.}.

잠깐 동안만 조사된 것.^[15] 우도 오차 기준에는 평균 Kullback-Leibler 분산을 기반으로 하는 기준이 포함된다.

\operatorname {MKL} (\mathbf {H} )=\int f(\mathbf {x} )\,\operatorname {log} [f(\mathbf {x} )]\,d\mathbf {x} -\operatorname {E} \int f(\mathbf {x} )\,\operatorname {log} [{\hat {f}}(\mathbf {x} ;\mathbf {H} )]\,d\mathbf {x}

그리고 Mean Hellinger 거리

\operatorname {MH} (\mathbf {H} )=\operatorname {E} \int ({\hat {f}}_{\mathbf {H} }(\mathbf {x} )^{1/2}-f(\mathbf {x} )^{1/2})^{2}\,d\mathbf {x} .

KL은 교차 검증 방법을 사용하여 추정할 수 있지만, KL 교차 검증 선택기는 경계 밀도 함수에 대해 일관성을 유지하더라도 차선 최적일 수 있다.^[16] MH 선택기는 문헌에서 간략하게 검토되었다.^[17]

이러한 모든 최적성 기준은 거리에 기초한 측정이며, 보다 직관적인 근접성 개념에 항상 부합하는 것은 아니므로, 이러한 우려에 대응하여 더 많은 시각적 기준이 개발되었다.^[18]

객관적이고 데이터 중심적인 커널 선택

필터 기능

I_{\vec {A}}({\vec {t}})

A

I_{\vec {A}}({\vec {t}})

→

I_{\vec {A}}({\vec {t}})

(

I_{\vec {A}}({\vec {t}})

→

I_{\vec {A}}({\vec {t}})

)

I_{\vec{A}({\vec {t})

의 시연

I_{\vec {A}}({\vec {t}})

The square of the empirical distribution function

{\hat {\varphi }} ^{2}

from N=10,000 samples of the ‘transition distribution’ discussed in Section 3.2 (and shown in Fig. 4), for

{\hat {\varphi }} ^{2}\geq 4(N-1)N^{-2}

. There 이 그림에는 두 가지 색채 구성이 있다. 중심에서 주로 어둡고 다색의 색상이 있는 'X자형' 영역은 가장 낮은 연속성 하이퍼볼륨(원점을 포함하는 영역)에

|{\hat {\varphi }}|^{2}

|{\hat {\varphi }}|^{2}

^

|{\hat {\varphi }}|^{2}

2

|{\hat {\varphi }}|^{2}

{\

displaystyle

{\

hat{\varphi }}^{2

}} 값에 해당하며, 오른쪽의 색상 막대는 이 영역의 색상에 적용된다. 첫 번째 연속 하이퍼볼륨에서 떨어진 연한 색상의 모노톤 영역은

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

4

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

(

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

-

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

)

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

-

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

{\

}\

geq

4(

N-1

)N

^{-2}}

의 추가 연속 하이퍼볼륨에 해당한다

|{\hat {\varphi }}|^{2}\geq 4(N-1)N^{-2}

이러한 지역의 색상은 임의적이며, 단지 인접한 지역을 서로 시각적으로 구별하는 역할을 한다.

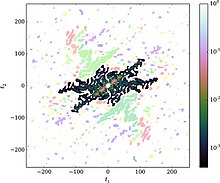
최근의 연구는 커널과 그 대역폭이 분배의 형태에 대해 어떠한 가정도 하지 않고 입력 데이터 자체에서 최적적이고 객관적으로 선택될 수 있다는 것을 보여주었다.^[19] 결과 커널 밀도 추정치는 모수 추정기에 기대되는 $n^{-1}$ $n^{-1}$ - 1 ${\$ n $^{-1}$ 에 근접한 속도로 샘플이 추가됨에 따라 실제 확률 분포로 빠르게 수렴된다.^[19]^[20]^[21] 이 커널 추정기는 일변량 검체와 다변량 검체에 모두 사용할 수 있다. The optimal kernel is defined in Fourier space—as the optimal damping function ${\hat {\psi _{h}}}({\vec {t}})$ (the Fourier transform of the kernel ${\hat {K}}({\vec {x}})$ )-- in terms of the Fourier transform of the data ${\hat {\varphi }}({\vec {t}})$ ${\hat {\varphi }}({\vec {t}})$ ${\displaystyle {\hat{\varphi$ ${\hat {\varphi }}({\vec {t}})$ 경험적 특성 함수 $({\vec{t}},$ 커널 밀도 추정 참조):

${\hat {\psi _{h}}}({\vec {t}})\equiv {\frac {N}{2(N-1)}}\left[1+{\sqrt {1-{\frac {4(N-1)}{N^{2} {\hat {\varphi }}({\vec {t}}) ^{2}}}}}I_{\vec{A}({\vec {t}})\오른쪽]$ ^[21]

${\f}(x)={\frac {1}{{{{\pi )^{d}}}\int{\hat {\\varphi }}}}}}{\vec{t}e^{-i{\vec{\cd}d}d{{x}d}d}}}}}}}}}}}}}{{{{{{{{{vec}d}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 N은 데이터 포인트의 수, d는 치수( $I_{\vec {A}}({\vec {t}})$ )의 수, $I_{\vec {A}}({\vec {t}})$ $I_{\vec {A}}({\vec {t}})$ → ( $I_{\vec {A}}({\vec {t}})$ t $I_{\vec {A}}({\vec {t}})$ → ) ${\displaystyle I_{\vec{A}({\vec{t}})$ 는 $I_{\vec {A}}({\vec {t}})$ '허용된 주파수'의 경우 1과 같고, 그렇지 않으면 0과 같은 필터다. 이 필터 기능을 정의하는 방법은 다양하며, 일변량 또는 다변량 샘플에 작용하는 간단한 것을 '최저 연속 하이퍼볼륨 필터'라고 하며, $I_{\vec {A}}({\vec {t}})$ A $I_{\vec {A}}({\vec {t}})$ → $I_{\vec {A}}({\vec {t}})$ → ) ${\displaystyle I_{\vec{A}({\vec{t}})$ 는 유일하게 허용되는 주파수가 surrooulou의 연속적인 부분집합으로 선택된다 $I_{\vec {A}}({\vec {t}})$ . $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ ^ $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ ( $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ → ) $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ ( $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ - 1 $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ ) $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ - $|{\hat {\varphi }}({\vec {t}})|^{2}\geq 4(N-1)N^{-2}$ ${\$ {\ $hat {\barphi }}}}{\vec{t}}^{2}\geq 4(N-1)N^{-2}}($ 이것과 기타 필터 기능에 대한 자세한 내용은 참조).

경험적 특성함수(ECF)의 직접 계산은 기본적으로 데이터 샘플의 직접 푸리에 변환을 수반하기 때문에 느리다는 점에 유의하십시오. 그러나 ECF는 (문제의 차원성에 따라) 여러 차례 계산 속도를 증가시키는 ^[20]^[21]불균일한 고속 푸리에 변환(nuFT) 방법을 사용하여 정확하게 추정할 수 있는 것으로 밝혀졌다. 이 목표 KDE 방법과 nuFT 기반 ECF 근사치의 조합은 문헌에서 fastKDE라고 언급되었다.^[21]

A demonstration of fastKDE relative to a sample PDF. (a) True PDF, (b) a good representation with fastKDE, and (c) a slightly blurry representation.

정규 분포의 비교 혼합: (a) 기초 PDF, (b) 1,000,000개 표본에 대한 패스트KDE 추정치 및 (c) 10,000개 표본에 대한 패스트KDE 추정치.

참고 항목

커널 밀도 추정 – 일변량 커널 밀도 추정
가변 커널 밀도 추정 – 가변 대역폭의 커널을 사용한 다변량 밀도 추정

참조

^ Rosenblatt, M. (1956). "Remarks on some nonparametric estimates of a density function". Annals of Mathematical Statistics. 27 (3): 832–837. doi:10.1214/aoms/1177728190.
^ Parzen, E. (1962). "On estimation of a probability density function and mode". Annals of Mathematical Statistics. 33 (3): 1065–1076. doi:10.1214/aoms/1177704472.
^ ^a ^b Simonoff, J.S. (1996). Smoothing Methods in Statistics. Springer. ISBN 978-0-387-94716-7.
^ Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC. pp. 7–11. ISBN 978-0-412-24620-3.
^ ^a ^b ^c ^d Wand, M.P; Jones, M.C. (1995). Kernel Smoothing. London: Chapman & Hall/CRC. ISBN 978-0-412-55270-0.
^ Wand, M.P.; Jones, M.C. (1993). "Comparison of smoothing parameterizations in bivariate kernel density estimation". Journal of the American Statistical Association. 88 (422): 520–528. doi:10.1080/01621459.1993.10476303. JSTOR 2290332.
^ Duong, T.; Hazelton, M.L. (2003). "Plug-in bandwidth matrices for bivariate kernel density estimation". Journal of Nonparametric Statistics. 15: 17–30. doi:10.1080/10485250306039.
^ Wand, M.P.; Jones, M.C. (1994). "Multivariate plug-in bandwidth selection". Computational Statistics. 9: 97–177.
^ ^a ^b ^c Duong, T.; Hazelton, M.L. (2005). "Cross validation bandwidth matrices for multivariate kernel density estimation". Scandinavian Journal of Statistics. 32 (3): 485–506. doi:10.1111/j.1467-9469.2005.00445.x.
^ Hall, P.; Marron, J.; Park, B. (1992). "Smoothed cross-validation". Probability Theory and Related Fields. 92: 1–20. doi:10.1007/BF01205233.
^ Duong, T.; Hazelton, M.L. (2005). "Convergence rates for unconstrained bandwidth matrix selectors in multivariate kernel density estimation". Journal of Multivariate Analysis. 93 (2): 417–433. doi:10.1016/j.jmva.2004.04.004.
^ Duong, T. (2007). "ks: Kernel density estimation and kernel discriminant analysis in R". Journal of Statistical Software. 21 (7). doi:10.18637/jss.v021.i07.
^ Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. (2010). "Kernel density estimation via diffusion". Annals of Statistics. 38 (5): 2916–2957. arXiv:1011.2602. doi:10.1214/10-AOS799.
^ Hall, P.; Wand, M.P. (1988). "Minimizing L₁ distance in nonparametric density estimation". Journal of Multivariate Analysis. 26: 59–88. doi:10.1016/0047-259X(88)90073-5.
^ Cao, R.; Cuevas, A.; Manteiga, W.G. (1994). "A comparative study of several smoothing methods in density estimation". Computational Statistics and Data Analysis. 17 (2): 153–176. doi:10.1016/0167-9473(92)00066-Z.
^ Hall, P. (1989). "On Kullback-Leibler loss and density estimation". Annals of Statistics. 15 (4): 589–605. doi:10.1214/aos/1176350606.
^ Ahmad, I.A.; Mugdadi, A.R. (2006). "Weighted Hellinger distance as an error criterion for bandwidth selection in kernel estimation". Journal of Nonparametric Statistics. 18 (2): 215–226. doi:10.1080/10485250600712008.
^ Marron, J.S.; Tsybakov, A. (1996). "Visual error criteria for qualitative smoothing". Journal of the American Statistical Association. 90 (430): 499–507. doi:10.2307/2291060. JSTOR 2291060.
^ ^a ^b Bernacchia, Alberto; Pigolotti, Simone (2011-06-01). "Self-consistent method for density estimation". Journal of the Royal Statistical Society, Series B. 73 (3): 407–422. arXiv:0908.3856. doi:10.1111/j.1467-9868.2011.00772.x. ISSN 1467-9868.
^ ^a ^b O’Brien, Travis A.; Collins, William D.; Rauscher, Sara A.; Ringler, Todd D. (2014-11-01). "Reducing the computational cost of the ECF using a nuFFT: A fast and objective probability density estimation method". Computational Statistics & Data Analysis. 79: 222–234. doi:10.1016/j.csda.2014.06.002.
^ ^a ^b ^c ^d ^e O’Brien, Travis A.; Kashinath, Karthik; Cavanaugh, Nicholas R.; Collins, William D.; O’Brien, John P. (2016). "A fast and objective multidimensional kernel density estimation method: fastKDE" (PDF). Computational Statistics & Data Analysis. 101: 148–160. doi:10.1016/j.csda.2016.02.014.

외부 링크

mvstat.net 다변량 커널 밀도 추정의 수학적 세부사항과 대역폭 선택기에 대한 동료 평가 자료 모음 mvstat.net 웹 페이지.
kde2d.m 이변량 커널 밀도 추정을 위한 Matlab 함수.
libagf 다변량, 가변 대역폭 커널 밀도 추정을 위한 C++ 라이브러리.
다변량, 가변 대역폭 커널 밀도 추정을 위한 Akde.m Matlab m 파일.
PyQt-Fit 패키지의 helit 및 pyqt_fit.kde 모듈은 다변량 커널 밀도 추정을 위한 Python 라이브러리다.

[1] Rosenblatt, M. (1956). "Remarks on some nonparametric estimates of a density function". Annals of Mathematical Statistics. 27 (3): 832–837. doi:10.1214/aoms/1177728190.

[2] Parzen, E. (1962). "On estimation of a probability density function and mode". Annals of Mathematical Statistics. 33 (3): 1065–1076. doi:10.1214/aoms/1177704472.

[simonoff1996-3] Simonoff, J.S. (1996). Smoothing Methods in Statistics. Springer. ISBN 978-0-387-94716-7.

[4] Silverman, B.W. (1986). Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC. pp. 7–11. ISBN 978-0-412-24620-3.

[WJ1995-5] Wand, M.P; Jones, M.C. (1995). Kernel Smoothing. London: Chapman & Hall/CRC. ISBN 978-0-412-55270-0.

[6] Wand, M.P.; Jones, M.C. (1993). "Comparison of smoothing parameterizations in bivariate kernel density estimation". Journal of the American Statistical Association. 88 (422): 520–528. doi:10.1080/01621459.1993.10476303. JSTOR 2290332.

[DH2003-7] Duong, T.; Hazelton, M.L. (2003). "Plug-in bandwidth matrices for bivariate kernel density estimation". Journal of Nonparametric Statistics. 15: 17–30. doi:10.1080/10485250306039.

[8] Wand, M.P.; Jones, M.C. (1994). "Multivariate plug-in bandwidth selection". Computational Statistics. 9: 97–177.

[DH2005-9] Duong, T.; Hazelton, M.L. (2005). "Cross validation bandwidth matrices for multivariate kernel density estimation". Scandinavian Journal of Statistics. 32 (3): 485–506. doi:10.1111/j.1467-9469.2005.00445.x.

[10] Hall, P.; Marron, J.; Park, B. (1992). "Smoothed cross-validation". Probability Theory and Related Fields. 92: 1–20. doi:10.1007/BF01205233.

[11] Duong, T.; Hazelton, M.L. (2005). "Convergence rates for unconstrained bandwidth matrix selectors in multivariate kernel density estimation". Journal of Multivariate Analysis. 93 (2): 417–433. doi:10.1016/j.jmva.2004.04.004.

[12] Duong, T. (2007). "ks: Kernel density estimation and kernel discriminant analysis in R". Journal of Statistical Software. 21 (7). doi:10.18637/jss.v021.i07.

[13] Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. (2010). "Kernel density estimation via diffusion". Annals of Statistics. 38 (5): 2916–2957. arXiv:1011.2602. doi:10.1214/10-AOS799.

[14] Hall, P.; Wand, M.P. (1988). "Minimizing L₁ distance in nonparametric density estimation". Journal of Multivariate Analysis. 26: 59–88. doi:10.1016/0047-259X(88)90073-5.

[15] Cao, R.; Cuevas, A.; Manteiga, W.G. (1994). "A comparative study of several smoothing methods in density estimation". Computational Statistics and Data Analysis. 17 (2): 153–176. doi:10.1016/0167-9473(92)00066-Z.

[16] Hall, P. (1989). "On Kullback-Leibler loss and density estimation". Annals of Statistics. 15 (4): 589–605. doi:10.1214/aos/1176350606.

[17] Ahmad, I.A.; Mugdadi, A.R. (2006). "Weighted Hellinger distance as an error criterion for bandwidth selection in kernel estimation". Journal of Nonparametric Statistics. 18 (2): 215–226. doi:10.1080/10485250600712008.

[18] Marron, J.S.; Tsybakov, A. (1996). "Visual error criteria for qualitative smoothing". Journal of the American Statistical Association. 90 (430): 499–507. doi:10.2307/2291060. JSTOR 2291060.

[:0-19] Bernacchia, Alberto; Pigolotti, Simone (2011-06-01). "Self-consistent method for density estimation". Journal of the Royal Statistical Society, Series B. 73 (3): 407–422. arXiv:0908.3856. doi:10.1111/j.1467-9868.2011.00772.x. ISSN 1467-9868.

[:1-20] O’Brien, Travis A.; Collins, William D.; Rauscher, Sara A.; Ringler, Todd D. (2014-11-01). "Reducing the computational cost of the ECF using a nuFFT: A fast and objective probability density estimation method". Computational Statistics & Data Analysis. 79: 222–234. doi:10.1016/j.csda.2014.06.002.

[:22-21] O’Brien, Travis A.; Kashinath, Karthik; Cavanaugh, Nicholas R.; Collins, William D.; O’Brien, John P. (2016). "A fast and objective multidimensional kernel density estimation method: fastKDE" (PDF). Computational Statistics & Data Analysis. 101: 148–160. doi:10.1016/j.csda.2016.02.014.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

Search