쇄도 내 상관 관계

클라스 내 상관 관계가 높은 데이터 집합을 표시하는 점 그림.같은 집단의 값도 비슷한 경향이 있다.

클라스 내 상관 관계가 낮은 데이터 집합을 표시하는 점 그림.같은 집단의 값이 비슷해지는 경향은 없다.

통계에서, 클라스 내 상관 계수 또는 클라스 내 상관 계수(ICC)^[1]는 그룹으로 구성된 단위에 대해 정량적 측정을 할 때 사용할 수 있는 기술 통계량이다.같은 집단의 단위가 얼마나 강하게 닮았는지를 기술한다.그것은 상관관계의 한 유형으로 간주되지만, 대부분의 다른 상관관계 측정과는 달리, 쌍체 관측으로 구성된 데이터가 아니라 그룹으로 구성된 데이터에서 작동한다.

쇄도 내 상관관계는 일정한 연관성(예: 완전한 형제자매)을 가진 개인이 정량적 특성(유전성 참조)에서 서로 닮은 정도를 정량화하기 위해 일반적으로 사용된다.또 다른 두드러진 적용은 동일한 양을 측정하는 서로 다른 관찰자가 수행한 정량적 측정의 일관성 또는 재현성에 대한 평가다.

초기 ICC 정의: 편향되지 않았지만 복잡한 공식

쌍체 측정의 사례에 초점을 맞춘 쇄도 내 상관관계에 대한 초기 연구와 제안할 첫 번째 ICC 통계는 클래스 간 상관관계(Pearson 상관관계)의 수정이었다.

n = 1, ..., N에 대해 N_n,2 쌍체 데이터 값(x_n,1, x)으로 구성된 데이터 세트를 고려하십시오. Ronald Fisher가^[3] 원래 제안한^[2] 철자 내 상관 관계 r은

r={\frac{1}{ns^{2}}\sum _{n=1}^{n}(x_{n,1}-{\bar{x})(x_{n,2}-{\x}),

어디에

{\bar}}={\frac {1}{2N}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}),

s^{2}={\frac {1}{2}N}}\왼쪽\{\sum _{n=1}^{n}(x_{n,1}-{\bar{x}})^{n=1}+\sum _{n=1}^{n}(x_{n,2}-{\bar {x})^{2}\right\}.

이 통계의 이후 버전에서는 s를² 계산하기 위한 분모의 자유도 2N -1과 r을 계산하기 위한 분모의 N -1을 사용했기 때문에 s는² 편향되지 않고, s가 알려지면 r이 편향되지 않게 된다.

이 ICC와 클래스 간(Pearson) 상관관계의 주요 차이점은 데이터가 평균과 분산을 추정하기 위해 풀링된다는 것이다.그 이유는 쇄도 내 상관관계가 필요한 설정에서 쌍을 정렬되지 않은 것으로 간주하기 때문이다.예를 들어, 우리가 쌍둥이의 유사성을 연구하고 있다면, 보통 쌍둥이에 속하는 두 개인에 대한 값을 주문할 수 있는 의미 있는 방법이 없다.클래스 간 상관관계와 마찬가지로, 쌍체 데이터에 대한 클라스 내 상관관계는 간격 [-1, +1]로 제한된다.

또한 두 개 이상의 값을 갖는 그룹이 있는 데이터 집합에 대해서도 클라스 내 상관관계가 정의된다.세 개의 값으로 구성된 그룹의 경우 다음과^[3] 같이 정의된다.

r={\frac {1}{3Ns^{2}}}\sum _{n=1}^{N}\left\{(x_{n,1}-{\bar {x}})(x_{n,2}-{\bar {x}})+(x_{n,1}-{\bar {x}})(x_{n,3}-{\bar {x}})+(x_{n,2}-{\bar {x}})(x_{n,3}-{\bar {x}})\right\},

어디에

{\bar{x}={\frac {1}{3}N}\sum _{n=1}^{N}(x_{n,1}+x_{n,2}+x_{n,3}),

s^{2}={\frac {1}{3}N}}\left\{\sum _{n=1}^{N}(x_{n,1}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,2}-{\bar {x}})^{2}+\sum _{n=1}^{N}(x_{n,3}-{\bar {x}})^{2}\right\}.

그룹당 항목 수가 증가함에 따라 이 표현에서 교차 제품 용어의 수 또한 증가하게 된다.다음과 같은 등가 형식을 계산하면 더 간단하다.

r={\frac {K}{K-1}\cdot {\frac{-1}\sum _{n=1}^{N}({\bar{x}-{n}-{x})^{2}}-{s^{1}{1}{K-1}}}}}

여기서 K는 그룹당 데이터 값의 수이며, ${\bar {x}}_{n}$ 의 ${\bar {x}}_{n}$ n ${\$ 은 ${\bar {x}}_{n}$ n 그룹의^th 표본 평균이다.^[3]이런 형태는 대개 해리스에게 귀속된다.^[4]왼쪽 항은 음수가 아니며, 따라서 클라스 내 상관관계가 충족되어야 한다.

r\geq {\frac {-1}{K-1}

대형 K의 경우, 이 ICC는 거의 다음과 같다.

{\frac{N^{-1}\sum _{n=1}^{N}({\bar {{x}_{n}-{\bar{x}})^{2}}:{s^{2}},}

그룹 간의 변동으로 인한 총 분산의 일부로 해석할 수 있다.로널드 피셔는 그의 고전적인 저서 "연구 노동자를 위한 통계적 방법"에서 철판 내 상관관계의 장 전체를 할애하고 있다.^[3]

완전한 소음인 모집단의 데이터에 대해, 피셔의 공식은 약 0(즉, 때로는 음수)으로 분포하는 ICC 값을 산출한다.이는 피셔가 공식을 편향되지 않도록 설계했기 때문에, 그 추정치는 때로는 과대평가되고 때로는 과소평가되기도 하기 때문이다.모집단의 작은 값 또는 0 기본 값의 경우 표본에서 계산된 ICC는 음수일 수 있다.

최신 ICC 정의: 단순한 공식이지만 양의 치우침

Ronald Fisher를 시작으로, 분산 분석(ANOVA)의 프레임워크 내에서, 그리고 더 최근에는 랜덤 효과 모델의 프레임워크에서 클라스 내 상관관계가 고려되었다.많은 ICC 추정기가 제안되었다.대부분의 추정기는 랜덤 효과 모형의 관점에서 정의될 수 있다.

Y_{ij}=\mu +\alpha _{j}+\varepsilon _{ij}

여기서 Y는_ij j 그룹의^th i 관측치^th, μ는 관측되지 않은 전체 평균, α는_j 그룹 j의 모든 값이 공유하는 관측되지 않은 무작위 효과, α는_ij 관측되지 않은 소음 용어다.^[5]식별할 모델에 대해 α와_j α는_ij 기대값 0을 가지며 서로 상관관계가 없는 것으로 가정한다.또한 α는_j 동일한 분포로 가정하고, α는_ij 동일한 분포로 가정한다.α의_j 분산을 α로²
_α 나타내고 α의_ij 분산을 α로²
_ε 나타낸다.

이 프레임워크의 모집단 ICC는 다음과 같다.^[6]

{\frac {\fract _{\frac _}^{2}}:{\probma _{\probma _{2}+\pretma _{\varepsilon }^{}}}}}}}.

이 프레임워크에서 ICC는 동일한 그룹의 두 관측치의 상관관계다.

[증거]

단방향 랜덤 효과 모형의 경우:

$Y_{ij}=\mu +\alpha _{i}+\epsilon _{ij}$

$\alpha _{i}\sim N(0,\sigma _{\alpha }^{2})$ , $\epsilon _{ij}\sim N(0,\sigma ^{2})$ , $\alpha _{i}$ s and $\epsilon _{ij}$ s independent and $\alpha _{i}$ s $\epsilon _{ij}$ $\epsilon _{ij}$ $\epsilon _{ij}$ ${\$ 로부터 $\epsilon _{{ij}}$ 독립적이다.

모든 관측치의 분산: $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ ) $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ = $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ 2 $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ + $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ ${\$ $nalpha$ ^{ $2}}:$ 같은 그룹 i에서 두 관측치의 공분산 $Var(Y_{ij})=\sigma ^{2}+\sigma _{\alpha }^{2}$ ( $j\neq k$ $j\neq k$ $j\neq k$ ${\displaysty$ j\na $j\na$ : $j\neq k$ ^[7]): )

${\begin{aigned}{\text{Cov}}(Y_{ij})Y_{ik}&={\text{Cov}}(\mu +\alpha _{ij},\mu +\alpha _{i}+\epsilon _{ik})\\&={\text{Cov}}(\alpha _{i}+\epsilon _{ij},\alpha _{i}+\epsilon _{ik})={\text{Cov}}(\alpha _{i},\alpha _{i})+2{\text{Cov}}(\alpha _{i},\epsilon _{ik})+{\text{Cov}}(\epsilon _{ij},\epsilon _{ik})\\&={\text{Cov}(\alpha _{i},\alpha _{i}={\text{Var})(\alpha _{i})\\&=\bma _{\buff}^{2}.\\end{aigned}$

여기에 공분산의 특성을 사용했었습니다.

종합해 보자: ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ j ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ , ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ k ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ) ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ = ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ( ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ j ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ , ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ k ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ) ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ( ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ) ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ a (Yi j ) ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ( ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ k ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ) ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ = ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ + ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ + ${\text{Cor}}(Y_{ij},Y_{ik})={\frac {{\text{Cov}}(Y_{ij},Y_{ik})}{\sqrt {Var(Y_{ij})Var(Y_{ik})}}}={\frac {\sigma _{\alpha }^{2}}{\sigma ^{2}+\sigma _{\alpha }^{2}}}$ 2 ${\$ $Y_{ik}={\frac {{\text{Cov}}(Y_{ij},$ $Y_{ik}}{\sqrt{Var(Y_{ij}}}}}}}}}}}}={\frac {\sigma _{\alpha }^{2}}:{{2}+\sigma _{\alpha }}}}:{\n2}}:}$

이 분산 분석 프레임워크의 장점은 그룹마다 데이터 값의 수가 다를 수 있다는 것이며, 이는 이전의 ICC 통계로 처리하기가 어렵다는 것이다.이 ICC는 항상 음수가 아니므로 "그룹 간" 총 분산의 비율로 해석할 수 있다.이 ICC는 공변량 효과를 허용하기 위해 일반화할 수 있으며, 이 경우 ICC는 공변량 조정 데이터 값의 클래스 내 유사성을 포착하는 것으로 해석된다.^[8]

이 식은 결코 음수일 수 없으며(Fisher의 원래 공식과는 달리) 따라서 ICC가 0인 모집단의 표본에서 표본 내 ICC는 모집단의 ICC보다 높을 것이다.

동일한 모집단 모수를 추정하는 모든 ICC 통계가 아닌 여러 가지 다른 ICC 통계가 제안되었다.동일한 데이터에 대해 현저하게 다른 결과를 산출할 수 있기 때문에 어떤 ICC 통계가 특정 용도에 적합한지에 대해 상당한 논쟁이 있었다.^[9]^[10]

Pearson의 상관 계수와의 관계

대수적 형태에서 피셔의 원래 ICC는 피어슨 상관 계수와 가장 유사한 ICC이다.두 통계량의 한 가지 주요 차이점은 ICC에서 데이터는 합동 평균과 표준 편차를 사용하여 중심화되고 크기가 조정되는 반면 Pearson 상관관계에서는 각 변수가 자체 평균과 표준 편차에 의해 중심화되고 크기가 조정된다는 것이다.ICC에 대한 이 풀링 스케일링은 모든 측정값이 동일하기 때문에 타당하다(다양한 그룹의 단위에서는 거의).예를 들어, 쌍체 데이터 집합에서 각 "쌍체"는 단일 단위(예: 각 개인에 대한 높이와 무게 측정)에 대해 서로 다른 두 단위(예: 일란성 쌍둥이의 쌍체에서 각 쌍둥이의 무게)에 대해 만들어진 단일 측정값으로, ICC는 피어슨의 상관 관계보다 더 자연스러운 측정값이다..

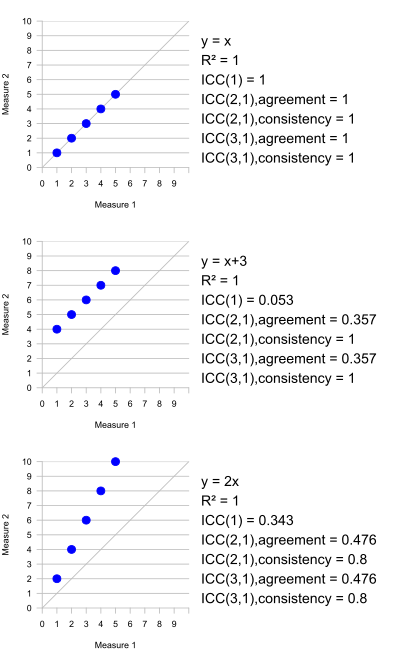
Pearson 상관관계의 중요한 특성은 비교 중인 두 변수에 대해 별도의 선형 변환을 적용하는 것이 불변하다는 것이다.따라서 X와 Y의 상관관계를 나타내는 경우, 예를 들어 Y = 2X + 1의 경우 X와 Y의 Pearson 상관관계는 1 - 완벽한 상관관계가 된다.그룹의 각 값에 적용되는 변환을 결정할 근거가 없기 때문에, 이 속성은 ICC에 대해 이치에 맞지 않는다.그러나 모든 그룹의 모든 데이터가 동일한 선형 변환을 받는다면 ICC는 변경되지 않는다.

관찰자 간의 적합성을 평가할 때 사용

ICC는 동일한 양을 측정하는 복수의 관측자가 수행한 측정의 일관성 또는 적합성을 평가하는 데 사용된다.^[11]예를 들어 여러 명의 의사들이 암 진행의 징후를 확인하기 위해 CT 스캔 결과의 점수를 매기라고 한다면, 우리는 그 점수가 서로 얼마나 일치하는지 물어볼 수 있다.만약 진실이 알려져 있다면(예를 들어, CT 스캔이 나중에 탐색 수술을 받은 환자들을 대상으로 한 것이라면), 일반적으로 주안점은 의사들의 점수가 진실과 얼마나 잘 일치하는지일 것이다.사실이 알려지지 않으면 점수 간의 유사성만 고려할 수 있다.이 문제의 중요한 측면은 서버 간 및 서버 내 변동성이 모두 있다는 것이다.서버 간 변동성은 관찰자 간의 체계적인 차이를 가리킨다. 예를 들어, 한 의사는 다른 의사보다 더 높은 위험 수준으로 환자를 일관성 있게 채점할 수 있다.서버 내 변동성은 체계적 차이의 일부가 아닌 특정 환자에 대한 특정 관찰자의 점수의 편차를 의미한다.

ICC는 교환 가능한 측정, 즉 그룹 내에서 측정을 정렬할 의미 있는 방법이 없는 그룹화된 데이터에 적용되도록 구성된다.관찰자 간의 적합성을 평가할 때 동일한 관찰자가 연구 중인 각 요소를 평가하면 관찰자 간의 체계적 차이가 존재할 가능성이 높으며, 이는 교환성의 개념과 상충된다.체계적 차이가 존재하는 상황에서 ICC를 사용한다면, 그 결과는 서버 내부와 서버 간 변동성의 복합적인 척도가 된다.교환성이 타당하게 유지된다고 가정할 수 있는 한 가지 상황은 혈액 검체라고 할 수 있는 시료를 여러 개의 지혈로 나누고 동일한 기기에서 지혈액을 별도로 측정하는 경우일 것이다.이 경우, 샘플 실행 순서가 존재하기 때문에 효과가 없는 한 교환성은 유지될 것이다.

클라스 내 상관 계수는 서버 내 및 서버 간 변동성의 복합체를 제공하므로 관찰자가 교환할 수 없을 때 결과를 해석하기 어려운 것으로 간주되기도 한다.코헨의 카파 통계량, 플라이스 카파, 일치성 상관 계수^[12] 등의 대체 척도가 비교환성 관측자 사이에 보다 적합한 합의 척도로 제시되었다.

소프트웨어 패키지의 계산

서버 간 일치성의 세 가지 시나리오에 적용되는 서로 다른 클래스의 상관 계수 정의.

ICC는 오픈 소스 소프트웨어 패키지 R에서 지원된다(패키지 싸이나 관개에서 "icc" 기능을 사용하거나 패키지 심리학에서 "ICC" 기능을 통해).rptR 패키지는 혼합 모델 프레임워크에서 가우스, 이항 및 포아송 분포 데이터에 대한 ICC 및 반복성 추정 방법을 제공한다.특히, 패키지는 조정된 ICC(즉, 다른 변수에 대한 제어)를 추정할 수 있고 파라메트릭 부트스트래핑과 잔차 순열에 기초한 유의성에 기반한 신뢰 구간을 계산할 수 있다.상용 소프트웨어도 ICC(예: Stata 또는 SPSS^[14])를 지원한다.

다양한 유형의 ICC [3] 웨이백 머신에 보관된 2009-03-03

슈루트 및 플라이스 협약	맥그로우와 웡 컨벤션	SPSS 및 Stata의 이름
ICC(1,1)	단방향 랜덤, 단일 점수 ICC(1)	단방향 랜덤, 단일 측정
ICC(2,1)	양방향 랜덤, 단일 점수 ICC(A,1)	이원 랜덤, 단일 측정, 절대 합의
ICC(3,1)	양방향 혼합, 단일 점수 ICC(C,1)	양방향 혼합, 단일 측정, 일관성
정의되지 않은	양방향 랜덤, 단일 점수 ICC(C,1)	양방향 랜덤, 단일 측정, 일관성
정의되지 않은	양방향 혼합, 단일 점수 ICC(A,1)	양방향 혼합, 단일 조치, 절대 합의
ICC(1,k)	일방향 랜덤, 평균 점수 ICC(k)	일방향 랜덤, 평균 측정값
ICC(2,k)	양방향 랜덤, 평균 점수 ICC(A,k)	이원 랜덤, 평균 측정, 절대 합의
ICC(3,k)	양방향 혼합 평균 점수 ICC(C,k)	양방향 혼합, 평균 측정, 일관성
정의되지 않은	양방향 랜덤, 평균 점수 ICC(C,k)	양방향 랜덤, 평균 측정, 일관성
정의되지 않은	양방향 혼합 평균 점수 ICC(A,k)	양방향 혼합, 평균 측정, 절대 합의

세 가지 모델은 다음과 같다.

단방향 랜덤 효과: 각 피사체는 랜덤하게 선택된 다른 k의 측정자 집합에 의해 측정된다.
이원 랜덤: k 레이터를 랜덤하게 선택한 다음, 각 피사체는 동일한 k 레이터 집합에 의해 측정된다.
양방향 혼합: k 고정 래터를 정의한다.각 피사체는 k 측정자에 의해 측정된다.

측정 횟수:

단일 측정: 실험에서 두 가지 이상의 측정을 수행하더라도 단일 레이터의 단일 측정이 수행되는 상황에 신뢰성이 적용된다.
평균 측정: 신뢰도는 각 과목에 대해 평균 측정자 수가 계산되는 상황에 적용된다.

일관성 또는 절대 합의:

절대적 합의: 두 측정자 간의 합의는 측정자 모두의 체계적 오류와 무작위 잔류 오류를 포함하여 관심의 대상이다.
일관성: 동일한 레이터에 의한 반복 측정의 맥락에서 레이터의 체계적 오류는 취소되고 무작위 잔류 오류만 유지된다.

일방향 랜덤 효과 모델에서는 일관성 ICC를 추정할 수 없으며, 이는 계수 간 및 잔차 분산을 분리할 방법이 없기 때문이다.

Liljequist 외 연구진(2019)이 사용하는 대안적 레시피와 함께 단일 측정 ICC에 대한 3가지 모델의 개요와 재분석을 제시했다.^[18]

해석

Cicchetti(1994)는 ^[19]카파 또는 ICC 사용자간 합의 조치에 대해 자주 인용되는 해석 지침을 다음과 같이 제공한다.

0.40 미만. 가난하다.
0.40에서 0.59 사이 - 공정.
0.60에서 0.74 사이—좋다.
0.75에서 1.00 사이—우수.

구씨와 리씨(2016년)가 각각 다른 가이드라인을 제시한다.^[20]

0.50 이하:빈곤함
0.50 ~ 0.75 사이: 중간
0.75 ~ 0.90: 양호
0.90 이상: 우수

참고 항목

참조

^ Koch GG (1982). "Intraclass correlation coefficient". In Samuel Kotz and Norman L. Johnson (ed.). Encyclopedia of Statistical Sciences. Vol. 4. New York: John Wiley & Sons. pp. 213–217.
^ Bartko JJ (August 1966). "The intraclass correlation coefficient as a measure of reliability". Psychological Reports. 19 (1): 3–11. doi:10.2466/pr0.1966.19.1.3. PMID 5942109. S2CID 145480729.
^ ^a ^b ^c ^d ^e Fisher RA (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.
^ Harris JA (October 1913). "On the Calculation of Intra-Class and Inter-Class Coefficients of Correlation from Class Moments when the Number of Possible Combinations is Large". Biometrika. 9 (3/4): 446–472. doi:10.1093/biomet/9.3-4.446. JSTOR 2331901.
^ Donner A, Koval JJ (March 1980). "The estimation of intraclass correlation in the analysis of family data". Biometrics. 36 (1): 19–25. doi:10.2307/2530491. JSTOR 2530491. PMID 7370372.
^ 아노바 모델에서 ICC가 두 가지 항목의 상관 관계임을 증명: ocram [1], 클래스 내 상관 계수 이해, URL(버전: 2012-12-05): [2]
^ dsxton(https://stats.stackexchange.com/users/78861/dsaxton), 랜덤 효과 모델:동일한 수준의 관측치에 공분산 $\sigma^2$?, URL(버전: 2016-03-22) 링크가 있음
^ Stanish W, Taylor N (1983). "Estimation of the Intraclass Correlation Coefficient for the Analysis of Covariance Model". The American Statistician. 37 (3): 221–224. doi:10.2307/2683375. JSTOR 2683375.
^
Müller R, Büttner P (December 1994). "A critical discussion of intraclass correlation coefficients". Statistics in Medicine. 13 (23–24): 2465–76. doi:10.1002/sim.4780132310. PMID 7701147. 참고 항목: 주석:
- Vargha P (1997). "Letter to the Editor". Statistics in Medicine. 16 (7): 821–823. doi:10.1002/(SICI)1097-0258(19970415)16:7<821::AID-SIM558>3.0.CO;2-B.
^
McGraw KO, Wong SP (1996). "Forming inferences about some intraclass correlation coefficients". Psychological Methods. 1: 30–46. doi:10.1037/1082-989X.1.1.30. 이 글에는 다음과 같은 몇 가지 오류가 있다.
- McGraw KO, Wong SP (1996). "Correction to McGraw and Wong (1996)". Psychological Methods. 1 (4): 390. doi:10.1037/1082-989x.1.4.390.
^ Shrout PE, Fleiss JL (March 1979). "Intraclass correlations: uses in assessing rater reliability". Psychological Bulletin. 86 (2): 420–8. doi:10.1037/0033-2909.86.2.420. PMID 18839484.
^ Nickerson CA (December 1997). "A Note on 'A Concordance Correlation Coefficient to Evaluate Reproducibility'". Biometrics. 53 (4): 1503–1507. doi:10.2307/2533516. JSTOR 2533516.
^ Stoffel MA, Nakagawa S, Schielzeth J (2017). "rptR: repeatability estimation and variance decomposition by generalized linear mixed-effects models". Methods in Ecology and Evolution. 8 (11): 1639–1644. doi:10.1111/2041-210x.12797. ISSN 2041-210X.
^ MacLennan RN (November 1993). "Interrater Reliability with SPSS for Windows 5.0". The American Statistician. 47 (4): 292–296. doi:10.2307/2685289. JSTOR 2685289.
^ McGraw KO, Wong SP (1996). "Forming Inferences About Some Intraclass Correlation Coefficients". Psychological Methods. 1 (1): 30–40. doi:10.1037/1082-989X.1.1.30.
^ Stata user's guide release 15 (PDF). College Station, Texas: Stata Press. 2017. pp. 1101–1123. ISBN 978-1-59718-249-2.
^ Howell DC. "Intra-class correlation coefficients" (PDF).
^ Liljequist D, Elfving B, Skavberg Roaldsen K (2019). "Intraclass correlation - A discussion and demonstration of basic features". PLOS ONE. 14 (7): e0219854. doi:10.1371/journal.pone.0219854. PMC 6645485. PMID 31329615.
^ Cicchetti DV (1994). "Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology". Psychological Assessment. 6 (4): 284–290. doi:10.1037/1040-3590.6.4.284.
^ Koo TK, Li MY (June 2016). "A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research". Journal of Chiropractic Medicine. 15 (2): 155–63. doi:10.1016/j.jcm.2016.02.012. PMC 4913118. PMID 27330520.

다른이들

철판내 상관 계수에 대한 두 지수 비교

외부 링크

[1] Koch GG (1982). "Intraclass correlation coefficient". In Samuel Kotz and Norman L. Johnson (ed.). Encyclopedia of Statistical Sciences. Vol. 4. New York: John Wiley & Sons. pp. 213–217.

[2] Bartko JJ (August 1966). "The intraclass correlation coefficient as a measure of reliability". Psychological Reports. 19 (1): 3–11. doi:10.2466/pr0.1966.19.1.3. PMID 5942109. S2CID 145480729.

[FisherR1954Statistical-3] Fisher RA (1954). Statistical Methods for Research Workers (Twelfth ed.). Edinburgh: Oliver and Boyd. ISBN 978-0-05-002170-5.

[4] Harris JA (October 1913). "On the Calculation of Intra-Class and Inter-Class Coefficients of Correlation from Class Moments when the Number of Possible Combinations is Large". Biometrika. 9 (3/4): 446–472. doi:10.1093/biomet/9.3-4.446. JSTOR 2331901.

[5] Donner A, Koval JJ (March 1980). "The estimation of intraclass correlation in the analysis of family data". Biometrics. 36 (1): 19–25. doi:10.2307/2530491. JSTOR 2530491. PMID 7370372.

[6] 아노바 모델에서 ICC가 두 가지 항목의 상관 관계임을 증명: ocram [1], 클래스 내 상관 계수 이해, URL(버전: 2012-12-05): [2]

[7] sxton(https://stats.stackexchange.com/users/78861/dsaxton), 랜덤 효과 모델:동일한 수준의 관측치에 공분산 $\sigma^2$?, URL(버전: 2016-03-22) 링크가 있음

[8] Stanish W, Taylor N (1983). "Estimation of the Intraclass Correlation Coefficient for the Analysis of Covariance Model". The American Statistician. 37 (3): 221–224. doi:10.2307/2683375. JSTOR 2683375.

[9] Müller R, Büttner P (December 1994). "A critical discussion of intraclass correlation coefficients". Statistics in Medicine. 13 (23–24): 2465–76. doi:10.1002/sim.4780132310. PMID 7701147. 참고 항목: 주석:
Vargha P (1997). "Letter to the Editor". Statistics in Medicine. 16 (7): 821–823. doi:10.1002/(SICI)1097-0258(19970415)16:7<821::AID-SIM558>3.0.CO;2-B.

[10] Vargha P (1997). "Letter to the Editor". Statistics in Medicine. 16 (7): 821–823. doi:10.1002/(SICI)1097-0258(19970415)16:7<821::AID-SIM558>3.0.CO;2-B.

[10] McGraw KO, Wong SP (1996). "Forming inferences about some intraclass correlation coefficients". Psychological Methods. 1: 30–46. doi:10.1037/1082-989X.1.1.30. 이 글에는 다음과 같은 몇 가지 오류가 있다.
McGraw KO, Wong SP (1996). "Correction to McGraw and Wong (1996)". Psychological Methods. 1 (4): 390. doi:10.1037/1082-989x.1.4.390.

[12] McGraw KO, Wong SP (1996). "Correction to McGraw and Wong (1996)". Psychological Methods. 1 (4): 390. doi:10.1037/1082-989x.1.4.390.

[11] Shrout PE, Fleiss JL (March 1979). "Intraclass correlations: uses in assessing rater reliability". Psychological Bulletin. 86 (2): 420–8. doi:10.1037/0033-2909.86.2.420. PMID 18839484.

[12] Nickerson CA (December 1997). "A Note on 'A Concordance Correlation Coefficient to Evaluate Reproducibility'". Biometrics. 53 (4): 1503–1507. doi:10.2307/2533516. JSTOR 2533516.

[13] Stoffel MA, Nakagawa S, Schielzeth J (2017). "rptR: repeatability estimation and variance decomposition by generalized linear mixed-effects models". Methods in Ecology and Evolution. 8 (11): 1639–1644. doi:10.1111/2041-210x.12797. ISSN 2041-210X.

[14] MacLennan RN (November 1993). "Interrater Reliability with SPSS for Windows 5.0". The American Statistician. 47 (4): 292–296. doi:10.2307/2685289. JSTOR 2685289.

[15] McGraw KO, Wong SP (1996). "Forming Inferences About Some Intraclass Correlation Coefficients". Psychological Methods. 1 (1): 30–40. doi:10.1037/1082-989X.1.1.30.

[16] Stata user's guide release 15 (PDF). College Station, Texas: Stata Press. 2017. pp. 1101–1123. ISBN 978-1-59718-249-2.

[17] Howell DC. "Intra-class correlation coefficients" (PDF).

[18] Liljequist D, Elfving B, Skavberg Roaldsen K (2019). "Intraclass correlation - A discussion and demonstration of basic features". PLOS ONE. 14 (7): e0219854. doi:10.1371/journal.pone.0219854. PMC 6645485. PMID 31329615.

[19] Cicchetti DV (1994). "Guidelines, criteria, and rules of thumb for evaluating normed and standardized assessment instruments in psychology". Psychological Assessment. 6 (4): 284–290. doi:10.1037/1040-3590.6.4.284.

[20] Koo TK, Li MY (June 2016). "A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research". Journal of Chiropractic Medicine. 15 (2): 155–63. doi:10.1016/j.jcm.2016.02.012. PMC 4913118. PMID 27330520.

[1]

[3]

[2]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[14]

[18]

[19]

[20]

Search