표준점수

통계학에서 표준 점수(standard score)는 원시 점수(즉, 관측값 또는 데이터 점)의 값이 관측 또는 측정 중인 것의 평균값보다 높거나 낮은 표준 편차의 수이다.평균 이상의 원시 점수는 표준 점수가 양인 반면 평균 이하의 점수는 표준 점수가 음입니다.

개별 원시 점수에서 모집단 평균을 뺀 다음 차이를 모집단 표준 편차로 나누어 계산합니다.원시 점수를 표준 점수로 변환하는 이 과정을 표준화 또는 정규화라고 합니다(그러나 "정규화"는 여러 유형의 비율을 나타낼 수 있습니다. 자세한 내용은 정규화를 참조하십시오).

표준 점수는 가장 일반적으로 z-점수라고 불리며, 두 용어는 이 기사에서 사용하는 것처럼 서로 교환하여 사용할 수 있습니다.사용되는 다른 동등한 용어로는 z 값, z 통계, 정상 점수, 표준화된 변수, 고에너지 물리학에서의 당김 등이 있습니다.^[1]^[2]

z 점수를 계산하려면 데이터 점이 속한 전체 모집단의 평균 및 표준 편차에 대한 지식이 필요합니다. 모집단의 관측치 표본만 있는 경우 표본 평균 및 표본 표준 편차를 사용하여 유사한 계산을 수행하면 t-통계량이 산출됩니다.

계산

모집단 평균과 모집단 표준 편차를 알고 있는 경우 원시 점수 x는 다음과^[3] 같이 표준 점수로 변환됩니다.

z={x-\mu \over \sigma }

여기서:

μ는 모집단의 평균입니다.

σ는 모집단의 표준 편차입니다.

z의 절대값은 원시 점수 x와 모집단 평균 사이의 거리를 표준 편차 단위로 나타냅니다. z는 원시 점수가 평균 미만일 때 음수이고, 위의 경우 양수입니다.

이 공식을 사용하여 z를 계산하려면 표본 평균이나 표본 편차가 아니라 모집단 평균과 모집단 표준 편차를 사용해야 합니다.그러나 모집단의 실제 평균과 표준 편차를 아는 것은 전체 모집단을 측정하는 표준화 검정과 같은 경우를 제외하고는 종종 비현실적인 예상입니다.

모집단 평균과 모집단 표준 편차를 알 수 없는 경우 표본 평균과 표본 표준 편차를 모집단 값의 추정치로 사용하여 표준 점수를 추정할 수 있습니다.^[4]^[5]^[6]^[7]

이 경우 z-score는 다음과 같습니다.

z={x-{\bar {x}} \over S

여기서:

{\bar {x}}

{\bar {x}}

{\bar {x}

은(는) 표본의 평균입니다.

S는 표본의 표준 편차입니다.

항상 명시되어야 하지만 모집단과 표본 통계량의 사용에 대한 구분은 종종 이루어지지 않습니다.어느 경우든 방정식의 분자와 분모는 같은 측정 단위를 가지므로 나눗셈을 통해 단위가 취소되고 z는 무차원으로 남게 됩니다.

적용들

Z-검정

z-score는 추정치가 아닌 모수가 알려진 모집단에 대한 학생 t-검정의 아날로그인 표준화 검정에서 z-검정에 자주 사용됩니다.전체 모집단을 아는 것은 매우 드문 일이기 때문에 t-검정이 훨씬 더 널리 사용됩니다.

예측간격

표준 점수는 예측 구간 계산에 사용할 수 있습니다.예측 구간 [L,U]는 하단 끝점 지정 L과 상단 끝점 지정 U로 구성되며, 미래 관측치 X가 높은 확률 γ $\gamma$ 인 구간에 놓이는 구간입니다 $\gamma$

P(L<X<U)=\gamma,

X의 표준 점수 Z에 대해서는 다음을 제공합니다.^[8]

P\left({\frac {L-\mu}{\sigma }}<Z<{\frac {U-\mu}}{\sigma }}\right)=\gamma.

다음과 같은 분위수를 결정함으로써

P\left(-z<Z\right)=\gamma

다음과 같습니다.

L=\mu -z\sigma,\U=\mu +z\sigma

공정관리

공정 제어 응용 프로그램에서 Z 값은 공정이 목표 외로 작동하는 정도에 대한 평가를 제공합니다.

ACT와 SAT의 여러 척도로 측정한 점수 비교

점수가 다른 척도로 측정되면 비교에 도움이 되도록 z 점수로 변환할 수 있습니다.Dietz 등은 ^[9](구) SAT와 ACT 고등학교 시험의 학생 점수를 비교하여 다음과 같은 예를 제시합니다.표는 SAT와 ACT의 총 점수에 대한 평균과 표준 편차를 보여줍니다.A 학생이 SAT에서 1800점을 받았고, B 학생이 ACT에서 24점을 받았다고 가정해 보겠습니다.어떤 학생이 다른 수험생들에 비해 더 좋은 성적을 보였습니까?

	앉았다	행동하다
의미하다	1500	21
표준편차	300	5

학생 A의 z 점수는 $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ = $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ - $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ σ = $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ = $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$ ${\displaystyle$ z = { $x-\mu \over \$ sigma } = {1800-1500 $\over 300$ } = $1}$ 입니다.

학생 B의 z 점수는 $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ = x $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ - $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ σ = $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ - $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ = $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$ ${\displaystyle$ z = { $x-\mu \over$ \sigma } = { $24-21 \over$ 5} = $0.6}$ 입니다.

A학생이 B학생보다 z점수가 높기 때문에 A학생이 B학생보다 다른 수험생에 비해 좋은 성적을 보였습니다.

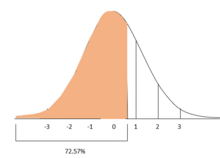
z-score 미만 관측치의 백분율

ACT 및 SAT 점수의 예를 계속하면, ACT 및 SAT 점수가 모두 정규 분포(대략적으로 정확함)라고 추가로 가정할 수 있는 경우, z 점수를 사용하여 학생 A와 B보다 낮은 점수를 받은 수험생의 비율을 계산할 수 있습니다.

클러스터 분석 및 다차원 확장

"다차원 스케일링 및 클러스터 분석과 같은 일부 다변량 기술의 경우 데이터의 단위 간 거리 개념이 상당한 관심과 중요성을 가지고 있는 경우가 많습니다.다변량 데이터 집합의 변수가 서로 다른 척도에 있을 때는 어떤 형태로든 표준화된 후의 거리를 계산하는 것이 더 합리적입니다."^[10]

주성분분석

주성분 분석에서 "다양한 척도 또는 범위가 매우 다른 공통 척도로 측정된 변수는 종종 표준화됩니다."^[11]

다중 회귀 분석에서 변수의 상대적 중요도: 표준화 회귀 계수

다중 회귀 분석 전에 변수를 표준화하는 것이 해석에 도움이 될 때도 있습니다.^[12](95쪽) 다음과 같이 기술합니다.

"표준화 회귀 기울기는 X와 Y를 표준화할 경우 회귀식의 기울기입니다 … X와 Y의 표준화는 각 관측치 집합에서 각각의 평균을 뺀 후 각각의 표준 편차로 나누는 방법으로 이루어집니다… 여러 X 변수가 사용되는 다중 회귀에서는,표준화된 회귀 계수는 각 X 변수의 상대적 기여도를 정량화합니다."

그러나, Kutner ^[13]등(p 278)은 다음과 같은 주의사항을 제공합니다: "… 표준화되든 아니든, 회귀 계수를 해석하는 것은 신중해야 합니다.그 이유는 예측 변수들이 서로 상관되어 있을 때, 회귀 계수들은 모형의 다른 예측 변수들에 의해 영향을 받기 때문입니다.표준화된 회귀 계수의 크기는 예측 변수들 간의 상관 관계의 유무뿐만 아니라 각 변수에 대한 관측치의 간격에도 영향을 받습니다.때로는 이러한 간격이 상당히 자의적일 수도 있습니다.따라서 표준화된 회귀 계수의 크기를 예측 변수의 비교 중요도를 반영하는 것으로 해석하는 것은 일반적으로 현명하지 않습니다."

수리통계학 표준화

수학 통계학에서 임의 변수 X는 $\operatorname {E} [X]$ 값 E ⁡ [ $\operatorname {E} [X]$ ] ${\displaystyle$ \ $operatorname$ { $E} [$ X]}을 $($ 를) 뺀 후 차이를 표준 편차 σ $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$ ( $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$ = $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$ ⁡ $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$ : ${\displaystyle$ \sigma ( $X)$ = {\ $sqrt {\operatorname {Var}}}:}$

Z= {X-\operator name {E} [X] \over \sigma(X)

고려 중인 랜덤 변수가 랜덤 표본 $\ X_{1},\dots ,X_{n}$ 의 표본 평균일 경우 $\ X_{1},\dots ,X_{n}$ X의 $\ X_{1},\dots ,X_{n}$ ${\$

{\bar {X}}={1 \overn}\sum _{i=1}^{n}X_{i}

그럼 표준화된 버전은

Z={\frac {{\bar {X}}-\operatorname {E}[{\bar {X}}}{\sigma(X)/{\sqrt {n}}}

티스코어

교육 평가에서 T-score는 표준 점수 Z가 이동되고 평균이 50이고 표준 편차가 10이 되도록 척도가 조정된 것입니다.^[14]^[15]^[16]그것은 일본어로 hensachi라고도 알려져 있는데, 여기서 그 개념은 훨씬 더 널리 알려져 있고 고등학교와 대학교 입학의 맥락에서 사용됩니다.

골밀도 측정에서 T-score는 건강한 30세 성인의 모집단과 비교한 측정의 표준점수이며, 통상적인 평균은 0이고 표준편차는 1입니다.^[17]

참고 항목

참고문헌

^ Mulders, Martijn; Zanderighi, Giulia, eds. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.
^ Gross, Eilam (2017-11-06). "Practical Statistics for High Energy Physics". CERN Yellow Reports: School Proceedings. 4/2017: 165–186. doi:10.23730/CYRSP-2017-004.165.
^ E. Kreyszig (1979). Advanced Engineering Mathematics (Fourth ed.). Wiley. p. 880, eq. 5. ISBN 0-471-02140-7.
^ Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (Fourth ed.), McGraw Hill, ISBN 978-0-07-148584-5
^ Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (Fifth ed.), Pearson / Prentice Hall, ISBN 978-0131877061
^ Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (Third ed.), McGraw Hill, ISBN 978-0071824118
^ Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (First ed.), Chapman & Hall / CRC Press, ISBN 978-1439873380
^ E. Kreyszig (1979). Advanced Engineering Mathematics (Fourth ed.). Wiley. p. 880, eq. 6. ISBN 0-471-02140-7.
^ Diez, David; Barr, Christopher; Çetinkaya-Rundel, Mine (2012), OpenIntro Statistics (Second ed.), openintro.org
^ Everitt, Brian; Hothorn, Torsten J (2011), An Introduction to Applied Multivariate Analysis with R, Springer, ISBN 978-1441996497
^ Johnson, Richard; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis, Pearson / Prentice Hall
^ Afifi, Abdelmonem; May, Susanne K.; Clark, Virginia A. (2012), Practical Multivariate Analysis (Fifth ed.), Chapman & Hall/CRC, ISBN 978-1439816806
^ Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (Fourth ed.), McGraw Hill, ISBN 978-0073014661
^ John Salvia; James Ysseldyke; Sara Witmer (29 January 2009). Assessment: In Special and Inclusive Education. Cengage Learning. pp. 43–. ISBN 978-0-547-13437-6.
^ Edward S. Neukrug; R. Charles Fawcett (1 January 2014). Essentials of Testing and Assessment: A Practical Guide for Counselors, Social Workers, and Psychologists. Cengage Learning. pp. 133–. ISBN 978-1-305-16183-2.
^ Randy W. Kamphaus (16 August 2005). Clinical Assessment of Child and Adolescent Intelligence. Springer. pp. 123–. ISBN 978-0-387-26299-4.
^ "Bone Mass Measurement: What the Numbers Mean". NIH Osteoporosis and Related Bone Diseases National Resource Center. National Institute of Health. Retrieved 5 August 2017.

추가열람

Carroll, Susan Rovezzi; Carroll, David J. (2002). Statistics Made Simple for School Leaders (illustrated ed.). Rowman & Littlefield. ISBN 978-0-8108-4322-6. Retrieved 7 June 2009.
Larsen, Richard J.; Marx, Morris L. (2000). An Introduction to Mathematical Statistics and Its Applications (Third ed.). p. 282. ISBN 0-13-922303-7.

외부 링크

z 점수와 Jim Reed의 정규 곡선 확률에 대한 대화형 플래시

[1] Mulders, Martijn; Zanderighi, Giulia, eds. (2017). 2015 European School of High-Energy Physics: Bansko, Bulgaria 02 - 15 Sep 2015. CERN Yellow Reports: School Proceedings. Geneva: CERN. ISBN 978-92-9083-472-4.

[2] Gross, Eilam (2017-11-06). "Practical Statistics for High Energy Physics". CERN Yellow Reports: School Proceedings. 4/2017: 165–186. doi:10.23730/CYRSP-2017-004.165.

[3] E. Kreyszig (1979). Advanced Engineering Mathematics (Fourth ed.). Wiley. p. 880, eq. 5. ISBN 0-471-02140-7.

[SpiegelStephens2008-4] Spiegel, Murray R.; Stephens, Larry J (2008), Schaum's Outlines Statistics (Fourth ed.), McGraw Hill, ISBN 978-0-07-148584-5

[Mendenhall2007-5] Mendenhall, William; Sincich, Terry (2007), Statistics for Engineering and the Sciences (Fifth ed.), Pearson / Prentice Hall, ISBN 978-0131877061

[GlantzSlinker2016-6] Glantz, Stanton A.; Slinker, Bryan K.; Neilands, Torsten B. (2016), Primer of Applied Regression & Analysis of Variance (Third ed.), McGraw Hill, ISBN 978-0071824118

[Aho2014-7] Aho, Ken A. (2014), Foundational and Applied Statistics for Biologists (First ed.), Chapman & Hall / CRC Press, ISBN 978-1439873380

[8] E. Kreyszig (1979). Advanced Engineering Mathematics (Fourth ed.). Wiley. p. 880, eq. 6. ISBN 0-471-02140-7.

[Diez2012-9] Diez, David; Barr, Christopher; Çetinkaya-Rundel, Mine (2012), OpenIntro Statistics (Second ed.), openintro.org

[EverittHothorn2011-10] Everitt, Brian; Hothorn, Torsten J (2011), An Introduction to Applied Multivariate Analysis with R, Springer, ISBN 978-1441996497

[JohnsonWichern2007-11] Johnson, Richard; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis, Pearson / Prentice Hall

[AfifiMayClark2012-12] Afifi, Abdelmonem; May, Susanne K.; Clark, Virginia A. (2012), Practical Multivariate Analysis (Fifth ed.), Chapman & Hall/CRC, ISBN 978-1439816806

[KutnerNachtsheim2004-13] Kutner, Michael; Nachtsheim, Christopher; Neter, John (204), Applied Linear Regression Models (Fourth ed.), McGraw Hill, ISBN 978-0073014661

[14] John Salvia; James Ysseldyke; Sara Witmer (29 January 2009). Assessment: In Special and Inclusive Education. Cengage Learning. pp. 43–. ISBN 978-0-547-13437-6.

[15] Edward S. Neukrug; R. Charles Fawcett (1 January 2014). Essentials of Testing and Assessment: A Practical Guide for Counselors, Social Workers, and Psychologists. Cengage Learning. pp. 133–. ISBN 978-1-305-16183-2.

[16] Randy W. Kamphaus (16 August 2005). Clinical Assessment of Child and Adolescent Intelligence. Springer. pp. 123–. ISBN 978-0-387-26299-4.

[17] "Bone Mass Measurement: What the Numbers Mean". NIH Osteoporosis and Related Bone Diseases National Resource Center. National Institute of Health. Retrieved 5 August 2017.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

Search