용어(논리)

수학 논리학에서, 용어는 수학적 대상을 나타내며, 공식은 수학적 사실을 나타냅니다.특히 항은 공식의 구성요소로 나타납니다.이것은 명사 구절은 사물을 가리키고 문장 전체가 사실을 가리키는 자연어와 유사하다.

1차 항은 상수 기호, 변수 및 함수 기호로부터 재귀적으로 구성된다.적절한 수의 용어에 술어 기호를 적용하여 형성된 식을 원자식이라고 하며, 해석에 따라 2가의 논리학에서 참 또는 거짓으로 평가합니다.예를 들어 $(x+1)*(x+1)$ ( $(x+1)*(x+1)$ + $(x+1)*(x+1)$ ) $(x+1)*(x+1)$ ( $(x+1)*(x+1)$ + $(x+1)*(x+1)$ $){ displaystyle$ ( x + 1 $)*$ ( $x$ + 1)}는 $(x+1)*(x+1)$ 상수 1, $변수$ x 및 이진 $+$ 함수 기호 $+$ { $displaystyle$ +} 및 $+$ ${\$ { $display$ * $*$ $(x+1)*(x+1)\geq 0$ 로 작성된 용어입니다.이것은 원자식 $x$ + $(x+1)*(x+1)\geq 0$ )의 일부입니다(x $+$ 1 $(x+1)*(x+1)\geq 0$ 0 $display$ style ( x $+ 1$ )h $x$ 의 실번호 값.

논리학 외에도, 용어는 보편 대수학, 재작성 체계에서 중요한 역할을 한다.

형식적 정의

항의 트리 구조(n((n+1)/2 및 n((n+1)/2)

변수 기호 집합 V, 상수 기호 집합 C 및 연산자 기호라고도 불리는 n-ary 함수 기호_n 집합 F가 주어지면 (일차 정렬되지 않은) 항 집합 T는 다음 특성을 가진 ^[1]최소 집합으로 재귀적으로 정의된다.

모든 변수 기호는 V t T,
모든 상수 기호는 C t T,
모든 n항₁ t, …, t 및_n 모든 n-ary 함수 기호 f δ_n F로부터 더 큰 항 f₁(t_n, ..., t)를 만들 수 있다.

직관적인 유사 문법 표기법을 사용하여 t ::= x c f(t₁, ..., t_n)로 쓰이기도 합니다.일반적으로 처음 몇 개의 함수 기호 집합_n F만 상주합니다.잘 알려진 예로는 단항 함수 기호 sin, cos θ₁ F 및 이진 함수 기호 +, -, θ, / θ₂ F가 있으며, 3진 연산은 상위 함수는 말할 것도 없고 덜 알려져 있습니다.많은 저자들은 상수 기호를 0-ary 함수₀ 기호 F로 간주하므로 특별한 구문 클래스가 필요하지 않습니다.

용어는 담화 영역의 수학적 대상을 나타낸다.상수 c는 그 도메인으로부터의 이름 있는 오브젝트를 나타내며 변수 x는 그 도메인내의 오브젝트에 걸쳐 있으며, n-ary 함수 f는 오브젝트의 n-tuples를 오브젝트에 매핑한다.예를 들어 n v V가 변수 기호, 1 c C가 상수 기호, 덧셈 F가₂ 이진 함수 기호인 경우 n t T, 1 t T 및 (따라서) add(n, 1) t T는 각각 제1항, 제2항 및 제3항 건물 규칙에 따라 각각 다르다.후자의 항은 일반적으로 infix 표기법과 보다 일반적인 연산자 기호 +를 사용하여 n+1로 작성됩니다.

용어 구조 대 표현

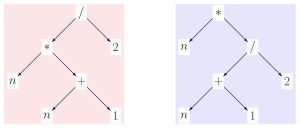
원래 논리학자들은 특정 건축 ^[2]규칙을 준수하는 문자열로 용어를 정의했습니다.하지만, 컴퓨터 공학에서 나무라는 개념이 인기를 끌었기 때문에, 나무라는 용어를 생각하는 것이 더 편리하다는 것이 밝혀졌다.예를 들어 "( $n ((n+1))/2$ ", $"(nn (n+$ 1)/ $2$ ") 및 ${\frac {n(n+1)}{2}}$ " ${\frac {n(n+1)}{2}}$ + ${\frac {n(n+1)}{2}}$ 1) ${\frac {n(n+1)}{2}}$ { $displaystyle {frac {n(n+1)}{2}}"$ 와 같은 몇 가지 개별 문자열은 동일한 용어를 나타내며 위 그림의 왼쪽 트리인 viz에 대응합니다.용어의 트리 구조를 종이 위의 그래픽 표현과 분리하면 괄호(구조가 아닌 표현일 뿐)와 보이지 않는 곱셈 연산자(표현이 아닌 구조에만 존재한다)도 쉽게 설명할 수 있다.

구조적 평등

두 용어가 같은 트리에 해당하는 경우 구조적으로, 문자 그대로 또는 구문적으로 동일하다고 합니다.예를 들어, 위 그림의 왼쪽과 오른쪽 트리는 구조적으로 불평등한 용어이지만, 합리적인 산술에서 항상 같은 값으로 평가되기 때문에 "의미적으로 동일한" 것으로 간주될 수 있습니다.구조적 평등은 기호의 의미에 대한 지식 없이 확인될 수 있지만, 의미적 평등은 확인할 수 없다.함수 /가 예를 들어 합리적이 아니라 절사 정수 나눗셈으로 해석되는 경우, n=2에서 왼쪽 항과 오른쪽 항은 각각 3과 2로 평가된다.구조적 대등항은 변수 이름에서 일치해야 합니다.

이와는 대조적으로, 용어 t는 전자의 모든 변수의 이름을 일관되게 바꾼 경우(즉, 일부 이름 바꾸기 대체에 대해 u = t for인 경우) u의 이름 바꾸기 또는 변형이라고 불린다.이 경우, 이름 바꾸기 치환 has는 역치환⁻¹ ,, t = uσ이므로⁻¹ u도 t의 이름 바꾸기이다.두 용어 모두 동일한 모듈 이름 변경이라고 합니다.많은 맥락에서, 예를 들어 덧셈을 위한 교환성 공리는 x+y=y+x 또는 a+b=b+a로 언급될 수 있다. 이러한 경우, 전체 공식은 이름이 바뀔 수 있지만, 임의의 하위 항은 일반적으로 ^{[note 1]}교환성의 유효한 버전이 아니다.^{[note 2]}

지반 항 및 선형 항

항 t의 변수 집합은 변수(t)로 표시됩니다.변수가 포함되지 않은 항을 기본 항이라고 하며, 변수가 여러 개 포함되어 있지 않은 항을 선형 항이라고 합니다.예를 들어, 2+2는 기저항이며, 따라서 선형항이며, xθ(n+1)는 선형항이며, nθ(n+1)는 비선형항이다.이러한 속성은 예를 들어 용어 개서 등에서 중요합니다.

함수 기호에 대한 시그니처가 주어지면, 모든 항의 집합이 자유항 대수를 형성합니다.모든 기본 항의 집합이 초기 항 대수를 형성합니다.

상수의 수를₀ f로, i-ary 함수 기호의 수를 f로_i 줄이면 다음 재귀 공식에 따라 최대 h 높이의 개별 접지 조건의 수 θ를_h 계산할 수 있습니다.

θ = f₀, 높이 0의 접지 항은 상수일 수 있으므로₀,
$\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ h $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ + 1 $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ = i = $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ ⋅ 0 ∞ $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ i $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ ⋅ 0 $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ ∞ $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ i $θ$ h i ⋅ h i = $\ sum _$ { i $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ = 0 }^{\infty $}f_{i}\cdot$ \ $theta _{i$ }{ $h}^{$ i $\theta _{h+1}=\sum _{i=0}^{\infty }f_{i}\cdot \theta _{h}^{i}$ 까지의 지반 항을 har-up을 사용하여 구할 수 있다.정수 및 함수 기호의 수가 유한한 경우 합계는 유한한 값을 가지며, 이는 보통 그렇습니다.

항에서 공식 작성

각 자연수 nθ1에 대한 n-ary 관계기호의_n 집합 R이 주어졌을 때 n항에는 n-ary 관계기호를 적용하여 (비정렬 1차) 원자식을 구한다.함수 심볼에 대해서는 통상 관계 심볼 집합_n R이 작은 n에 대해서만 비어 있지 않다.수학 논리학에서, 더 복잡한 공식은 논리적인 연결과 양자를 사용하는 원자 공식으로부터 만들어진다.예를 들어 R $(\$ 이 $\mathbb {R}$ 실수의 집합을 나타내면, δx: x $\mathbb {R}$ R $(\$ ⇒ $\mathbb {R}$ (x+1) 0 0은 복소수의 대수에서 true로 평가되는 수학식입니다.원자 공식은 완전히 그라운드 용어로 만들어지면 그라운드라고 불립니다. 주어진 함수 집합과 술어 기호 집합에서 합성할 수 있는 모든 그라운드 원자 공식은 이러한 기호 집합의 허브랜드 기저를 구성합니다.

조건이 있는 작업

검정 용어 a

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

(

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

(

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

+

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

)

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

( (

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

+

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

)

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

( (

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

3

){

displaystyle

{

a

* (

a

+ 1 ) * (

a

+

2 )

의 트리 구조.파란색 redex

{\frac {a*((a+1)*(a+2))}{1*(2*3)}}

x*(y*z)

x*(y*z)

(

x*(y*z)

x*(y*z)

z

){

style

x * ( y

* z

) }

용어는 트리 계층의 구조를 가지고 있기 때문에 각 노드에 위치 또는 경로를 할당할 수 있습니다. 즉, 계층에서 노드의 위치를 나타내는 자연수의 문자열입니다.빈 문자열(일반적으로 "로 표시됨)은 루트 노드에 할당됩니다.그림에서 검은색 용어 내의 위치 문자열은 빨간색으로 표시됩니다.
항 t의 각 위치 p에서 공통적으로 t로 $나타나는$ 고유 서브항이 시작된다.예를 들어 그림 중 검은 항의 위치 122에는 서브항 a+2가 그 근을 가진다."의 하위항" 관계는 일련의 용어에 대한 부분 순서이다. 각 용어가 그 자체의 하위항이기 때문에 반사적이다.
t항에서는 p위치에서의 서브항을 새로운 항 u로 치환하여 얻을 수 있는 항은 $일반적$ 으로 $p$ t[u]로 나타낸다.t $[u] p$ 라는 용어는 또한 용어 u와 용어 $유사$ 객체 t $[.]$ 의 일반화된 결합에서 비롯되었다고 볼 수 있다. 후자는 문맥 또는 구멍이 있는 용어(".; 그 위치는 p로 표시됨)라고 불리며, 여기서 u가 포함된다고 볼 수 있다.예를 들어 t가 그림에서 검은 용어인 경우 $t [b +1] 12$ 는 ${\frac {a*(b+1)}{1*(2*3)}}$ ( ${\frac {a*(b+1)}{1*(2*3)}}$ ${\frac {a*(b+1)}{1*(2*3)}}$ ) 1 " ${\frac {a*(b+1)}{1*(2*3)}}$ ( ${\frac {a*(b+1)}{1*(2*3)}}$ 3 ${\frac {a*(b+1)}{1*(2*3)}}$ ) { $display$ { $frac$ { $a$ * ( $b$ + 1 ) } { 1 * ( 2 * 3 ) ${\frac {a*(b+1)}{1*(2*3)}}$ ${\frac {a*(\;.\;)}{1*(2*3)}}$ 입니다. $후자 용어$ 는 b+1을 컨텍스트 ${\frac {a*(\;.\;)}{1*(2*3)}}$ ( ${\frac {a*(\;.\;)}{1*(2*3)}}$ 에 포함시킨 결과이기도 합니다 ${\frac {a*(\;.\;)}{1*(2*3)}}$ $\;}}}{1*(2*$ 3 ${\frac {a*(\;.\;)}{1*(2*3)}}$ 비공식적인 의미에서 인스턴스화와 임베딩의 연산은 서로 대화됩니다. 반면 전자는 용어의 하단에 함수 기호를 추가하고 후자는 맨 위에 함수를 추가합니다.포괄적 순서부여는 용어 및 양쪽에 추가되는 결과를 관련짓는다.
용어의 각 노드에 깊이(일부 저자에 의해 높이라고 함)를 할당할 수 있습니다. 즉, 루트로부터의 거리(가장자리 수)입니다.이 설정에서는 노드의 깊이는 항상 해당 위치 문자열의 길이와 동일합니다.그림에서 검은색 용어의 깊이 수준은 녹색으로 표시됩니다.
용어의 크기는 일반적으로 해당 용어의 노드 수 또는 용어의 서면 표현 길이와 동등하게 괄호 없이 기호를 세는 것을 나타냅니다.사진 속의 검은색과 파란색 용어의 크기는 각각 15와 5입니다.
항 u는 u의 치환 인스턴스가 구조적으로 t의 서브항과 같거나, t의 어떤 위치 p 및 어떤 치환 δ에 대해 $u$ $t$ = t이면 t항과 일치한다.이 경우 u, t, θ는 각각 패턴항, 서브젝트항, 매칭치환이라고 불린다.그림에서 파란색 패턴 $x*(y*z)$ x $x*(y*z)$ ( $x*(y*z)$ z $x*(y*z)$ ) { $displaystyle$ x * ( $y$ * $z$ ) }는 $x*(y*z)$ 위치 1의 검은색 피사체 용어와 일치하며 일치하는 치환 { $x a$ a, $y a$ a+1, $z a$ a $+2$ }는 검정색 치환에 바로 남겨진 파란색 변수로 나타납니다.직관적으로, 그 변수를 제외하고, 패턴은 주제에 포함되어야 한다. 패턴에서 변수가 여러 번 발생하는 경우, 대상의 각 위치에 동일한 하위 용어가 필요하다.
통일된 조건
용어 개서

관련 개념

분류된 용어

담화 영역이 기본적으로 다른 종류의 요소를 포함할 경우, 그에 따라 모든 용어의 집합을 분할하는 것이 유용하다.이를 위해 각 변수 및 상수 기호에는 정렬(종류라고도 함)이 할당되고 각 함수 기호에는 도메인 정렬 및 범위 정렬 선언이 할당됩니다.ih 서브텀의 정렬이 선언된 ih 도메인 종류의 f에 일치하는 경우에만 정렬된 서브텀₁ t, …, …로부터 정렬된 용어 f₁(t_n, …)를_n 구성할 수 있다.그러한 용어는 잘 정렬된 용어라고도 불리며, 다른 용어(즉, 정렬되지 않은 규칙만 준수함)는 잘못 정렬된 용어라고 불립니다.

예를 들어 벡터 공간에는 스칼라 숫자의 관련 필드가 있습니다.W와 N은 각각 벡터와 숫자의 종류를 나타내며, V와_N V는 각각 벡터와 숫자 변수의 집합이고_W, C와_N C는 각각 벡터와 숫자 상수의 집합이라고 하자_W. ${\vec {0}}\in C_{W}$ : 0 ${\vec {0}}\in C_{W}$ ${\vec {0}}\in C_{W}$ W {\ $displaystyle$ {\ $vec {0}}\in$ C_ ${$ W}} 및 $0 c N$ C, 벡터 덧셈인 스칼라 곱셈 및 내적을 + $+:W\times W\to W,*:W\times N\to W$ : $+:W\times W\to W,*:W\times N\to W$ × $+:W\times W\to W,*:W\times N\to W$ $+:W\times W\to W,*:W\times N\to W$ $+:W\times W\to W,*:W\times N\to W$ : $+:W\times W\to W,*:W\times N\to W$ W × $+:W\times W\to W,*:W\times N\to W$ 로 선언한다. $W\times$ W\ $to$ W, *: $\langle .,.\rangle :W\times W\to N$ $\times$ N $\to$ W $+:W\times W\to W,*:W\times N\to W$ $\langle .,.\rangle :W\times W\to N$ 및 $\langle .,.\rangle :W\times W\to N$ ., ., ., ., $\langle .,.\rangle :W\times W\to N$ ., ., ., ., ., ., . " : W × $\langle .,.\rangle :W\times W\to N$ $\displaystyle \scle$ . . . . . . . $rangle :$ $W\times$ W $\to$ N $\langle .,.\rangle :W\times W\to N$ 변수 ${\vec {v}},{\vec {w}}\in V_{W}$ v ${\vec {v}},{\vec {w}}\in V_{W}$ , ${\vec {v}},{\vec {w}}\in V_{W}$ ${\vec {v}},{\vec {w}}\in V_{W}$ ${\vec {v}},{\vec {w}}\in V_{W}$ W {\ $displaystyle$ {v $},$ {\ $vec {w}}\in$ V_ ${W}}$ ${\vec {v}},{\vec {w}}\in V_{W}$ a, $b v N$ V로 가정할 때, 용어 $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ ( $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ + 0 $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ ) $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ , w $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ ⟩ b $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ ⟩ $\langle ({\vec {v}}+{\vec {0}})*a,{\vec {w}}*b\rangle$ ⟩ \ $displaystyle$ \ l {\ $cv*}$ {0} { $c}$ {v} {c} {c} {v} {c} { $c}$ {c} {c} {c} {v} {v} {v} {c} {c} {c} {ve +는 두 번째 인수로 정렬 N의 용어를 받아들이지 않습니다). $a*{\vec {v}}$ v $→$ {\ $displaystyle$ a $*{\vec {v}}}$ 를 $a*{\vec {v}}$ $a*{\vec {v}}$ 용어로 만들려면 추가 선언 $*:N\times W\to W$ : $*:N\times W\to W$ × $*:N\times W\to W$ $*:N\times W\to W$ \ $displaystyle$ * : $N$ \ $times$ W \ $to$ W $*:N\times W\to W$ }가 $*:N\times W\to W$ 필요합니다.여러 선언이 있는 함수 기호를 오버로드라고 합니다.

여기서 설명하는 다중 정렬 프레임워크의 확장을 포함한 자세한 내용은 다중 정렬 로직을 참조하십시오.

람다항

한계 변수가 있는 항
표기법 예	바인드 변수	공짜 변수	로 써넣다 람다항
$limn \to 표준 x/ n$	n	x	limit(div(x,n))
$\sum _{i=1}^{n}i^{2}$	i	n	sum(1,n,θi. 검정력(i,2))
$\displaystyle \int _{a}^{b}\sin(k\cdot t)dt}$	t	a, b, k	적분(a, b, sin(kµt))

동기

표와 같은 수학적 표기법은 모두 표기법 범위 밖에 나타나지 않을 수 있는 로컬 변수 또는 바운드 변수를 도입하기 때문에 위에서 정의한 1차 항 체계에는 맞지 않습니다. 예를 $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ t $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ sin $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ ( $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ t ) $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ $t\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ \ $displaystyle$ t \ $cdot$ \ $cdot$ \ $int$ _ $b }$ \ $sin$ \ $cd t$ ; cd $t$ 반면, 자유라고 하는 다른 변수는 일반적인 1차 항 변수와 같이 동작합니다. 예를 $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ k $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ ( $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ t ) $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ $k\cdot \int _{a}^{b}\sin(k\cdot t)\;dt$ \ $displaystyle k\cdot$ \ $int _{a}^{b}\sin(k\cdot$ t $)\;dt$

이들 연산자는 모두 값 항이 아닌 함수를 인수 중 하나로 간주할 수 있습니다.예를 들어 lim 연산자는 시퀀스, 즉 양의 정수에서 예를 들어 실수에 대한 매핑에 적용된다.또 다른 예로 테이블에서 두 번째 예시를 구현하는 C 함수는 함수 포인터 인수를 가집니다(아래 상자 참조).

람다 항은 im, Ω, , 등에 대한 인수로 제공되는 익명 함수를 나타내기 위해 사용할 수 있습니다.

예를 들어, 아래 C 프로그램의 함수 제곱은 람다 항 δi. i.로² 익명으로 쓸 수 있다.그러면 일반합 연산자 δ는 하한값, 상한값 및 요약해야 할 함수를 갖는 삼원 함수 기호로 간주할 수 있다.후자의 인수로 인해 δ 연산자는 2차 함수 기호라고 불립니다.또 하나의 예로서 람다항 δn. x/n은 각각 x/1, x/2, x/3, ...에 매핑하는 함수, 즉 순서(x/1, x/2, x/3, ...)를 나타낸다.lim 연산자는 이러한 시퀀스를 취하여 한계치를 반환합니다(정의되어 있는 경우).

표의 맨 오른쪽 열은 각 수학적 표기 예제를 람다 용어로 표현하는 방법을 나타내며, 공통 infix 연산자를 접두사 형식으로 변환하기도 합니다.

인트 합(인트 lwb, 인트 업, 인트 기능하다(인트)) {    // 일반 합계 연산자 구현     인트 인식하다 = 0;     위해서 (인트 i=lwb; i<=>업; ++i)         인식하다 += 기능하다(i);     돌아가다 인식하다; }  인트 광장(인트 i) { 돌아가다 i*i; }            // 어나니머스 함수(lambda i. i*i)를 구현합니다.단, C에는 그 이름이 필요합니다.  #실패하다 <stdio.h> 인트 주된(무효) {     인트 n;     스캔("%d",&n);     인쇄물(%d\n", 합(1, n, 광장));        // 합계 제곱에 합계 연산자를 적용합니다.     돌아가다 0; }

정의.

「」를 참조해 주세요.

메모들

^ 원자 공식도 트리로 볼 수 있고, 이름 변경은 본질적으로 트리에 대한 개념이기 때문에 원자 공식(그리고 더 일반적으로, 수량자가 없는)은 용어와 유사한 방식으로 이름을 바꿀 수 있습니다.실제로 일부 저자는 (예를 들어 int, cf. #sorted terms가 아닌 bool 타입의) 무정량식을 용어로 간주한다.
^ 교환성 공리의 이름은 공리의 범용 폐쇄에 대한 알파 변환으로 볼 수 있습니다."x+y=y+x"는 실제로 "slambda, y: x+y=y+x"를 의미하며, 이는 "slambda, b: a+b=b+a"와 동의어이다. 아래의 #Lambda 항도 참조한다.
^ 즉, 시그니처(논리) 문서의 "다수 정렬된 시그니처" 섹션의 "기호 유형"입니다.

레퍼런스

Franz Baader; Tobias Nipkow (1999). Term Rewriting and All That. Cambridge University Press. pp. 1–2 and 34–35. ISBN 978-0-521-77920-3.

^ C.C. Chang; H. Jerome Keisler (1977). Model Theory. Studies in Logic and the Foundation of Mathematics. Vol. 73. North Holland.;여기서: 제1.3장
^ ; 여기: SectionHermes, Hans (1973). Introduction to Mathematical Logic. Springer London. ISBN 3540058192. ISSN 1431-4657..II.1.3

[3] 원자 공식도 트리로 볼 수 있고, 이름 변경은 본질적으로 트리에 대한 개념이기 때문에 원자 공식(그리고 더 일반적으로, 수량자가 없는)은 용어와 유사한 방식으로 이름을 바꿀 수 있습니다.실제로 일부 저자는 (예를 들어 int, cf. #sorted terms가 아닌 bool 타입의) 무정량식을 용어로 간주한다.

[4] 교환성 공리의 이름은 공리의 범용 폐쇄에 대한 알파 변환으로 볼 수 있습니다."x+y=y+x"는 실제로 "slambda, y: x+y=y+x"를 의미하며, 이는 "slambda, b: a+b=b+a"와 동의어이다. 아래의 #Lambda 항도 참조한다.

[5] 즉, 시그니처(논리) 문서의 "다수 정렬된 시그니처" 섹션의 "기호 유형"입니다.

[1] C.C. Chang; H. Jerome Keisler (1977). Model Theory. Studies in Logic and the Foundation of Mathematics. Vol. 73. North Holland.;여기서: 제1.3장

[2] ; 여기: SectionHermes, Hans (1973). Introduction to Mathematical Logic. Springer London. ISBN 3540058192. ISSN 1431-4657..II.1.3

[1]

[2]

[note 1]

[note 2]

Search

용어(논리)

네임스페이스

더

목차