다변화된 논리

이 글은 대부분의 독자들이 이해하기에는 너무 기술적인 것일 수도 있다. 기술 세부 정보를 삭제하지 않고 비전문가가 이해할 수 있도록 개선하십시오. (2013년 7월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

여러 가지 종류의 논리는 우주를 균일한 물체 집합으로 취급하지 않고 형식적인 프로그래밍의 유형과 유사한 방식으로 분할하려는 우리의 의도를 공식적으로 반영할 수 있다. 논리의 언어에서 기능적이고도 주장적인 "언론의 일부"는 구문적 수준에서도 우주의 이러한 유형적 분할을 반영한다: 치환과 논쟁 통과는 "구문"을 존중하면서 그에 따라서만 이루어질 수 있다.

위에서 언급한 의도를 공식화하는 방법에는 여러 가지가 있다. 다양한 종류의 논리는 그것을 충족시키는 정보의 모든 묶음이다. 대부분의 경우 다음과 같은 것이 주어진다.

• S종류의 한 벌
• 서명이란 개념의 적절한 일반화로서 그 종류와 함께 제공되는 추가 정보를 처리할 수 있다.

그 서명의 어떤 구조의 담론 영역은 모든 종류의 것 중 하나로 분리된다.

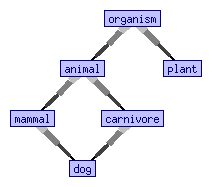
예

When reasoning about biological organisms, it is useful to distinguish two sorts: ${\displaystyle \mathrm {plant} }$ and ${\displaystyle \mathrm {animal} }$. While a function ${\displaystyle \mathrm {mother} \colon \mathrm {animal} \to \mathrm {animal} }$ makes 센스, 유사한 함수 $m{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{o}}$ t ${\displaystyle \mathrm{h}}$ ${\displaystyle \mathrm{e}}$ ${\displaystyle \mathrm{r}}$: p ${\displaystyle \mathrm{a}}$ ${\displaystyle \mathrm{n}}$ t${\displaystyle }$→ ${\displaystyle \mathrm{p}}$ a ${\displaystyle \mathrm{n}}$ ${\displaystyle \mathrm{t}}$ ${\$ {$matrm} \matrm {plant} \to \matrmatrm {plant} }$ }은(는) 일반적으로$$ 그렇지 않다. Many-sorted logic allows one to have terms like ${\displaystyle \mathrm {mother} (\mathrm {lassie} )}$, but to discard terms like ${\displaystyle \mathrm {mother} (\mathrm {my\_favorite\_oak} )}$ as syntactically ill-formed.

대수화

다변형 논리의 대수화는 칼리로와 곤살베스가 쓴 글에서 설명하는데,^[1] 다변형 논리에 추상 대수 논리를 일반화하지만 도입 자료로도 활용할 수 있다.

순서배합논리

많은 종류의 논리가 분리된 우주 세트를 갖기 위해서는 두 개의 구별되는 종류를 필요로 하는 반면에, 순서별 논리에서는 보통 ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}{s\mathrm{}}_{}}$ 2$${\$displaystyle s_{1$}}{{1$}\subseteq s_{2$}} 또는 유사한$$ 구문을 써서 다른 ${\displaystyle {종류}_{}}$의 $s{\displaystyle {}_{}}$ 1 ${\displaystyle {s\mathrm{}}_{}}$ 2${\$ s_${1$$}}}$의 하위조항을 선언할 수 있다$$$.$ 위의 생물학적 예에서, 선언하는 것이 바람직하다.

${\displaystyle \mathit{\text{개}}}$ ${\displaystyle \subseteq }$ ${\displaystyle \mathit{\text{육식동물}}}$ ${\$ {$dog}\dogeq {\textore$

${\displaystyle \mathit{\text{개}}}$ ${\displaystyle \subseteq }$ ${\displaystyle \mathit{\text{포유류}}}$ ${\$

${\$

${\$

${\displaystyle \mathit{\text{동물성}}}$ ${\displaystyle \subseteq \mathit{\text{생물}}}$ ${\$

${\displaystyle \mathit{\text{식물성}}\mathit{\text{유기체}}}$ ${\$

cf사진 등.

$s{\displaystyle }$ ${\$$displaystyle s}$의 용어가 필요한$$ 경우 s 하위 $집합$의$$용어가 대신 제공될 수 있다$$(리스코프 대체 원리). 예를 들어 함수 ${\displaystyle \mathit{\text{선언}}}$ 어미${\displaystyle :}$ ${\displaystyle \mathit{\text{동물}}}${ ${\displaystyle \mathit{\text{동물}}}$ ${\$ {$mother}$을(를) 가정:${\textit {lassie}\longrightarrow${\$textit {lassie}$및 상수 선언 ${\displaystyle \mathit{\text{래시}}}$:${\displaystyle \mathit{\text{개}}}$ ${\$ {$lassie}:$${\textit{dog$ $){\displaystyle{\textit{lassie}}$라는 용어는 완벽하게$$ 유효하며, 종류별 ${\displaystyle \mathit{\text{동물}}}$ ${\$ 개의 어머니가 개라는 정보를 차례대로 제공하기 위해 또 다른 선언 ${\displaystyle \mathit{\text{어미}}}$ 개 :${\displaystyle ⟶\mathit{\text{개}}}$ ${\$}$splaystyle {\textit{mair}:$${\textit{dog}\longrightarrow {\textit {dog}}$을(를) 발행할 수 있으며$$, 이를 프로그래밍 언어의 과부하와 유사한 함수 과부하라고 한다.

Order-sorted logic can be translated into unsorted logic, using a unary predicate ${\displaystyle p_{i}(x)}$ for each sort ${\displaystyle s_{i}}$, and an axiom ${\displaystyle \forall x(p_{i}(x)\rightarrow p_{j}(x))}$ for each subsort declaration ${\displaystyle s_i\subseteq s_j}$${\displaystyle s_{i}\vmseq s_{j$ 역접근법은 자동화된 정리 증명에서 성공적이었다: 1985년 크리스토프 발터는 당시 벤치마크 문제를 순서별 논리로 번역함으로써 해결할 수 있었고, 따라서 많은 단수 술어들이 분류로 변함에 따라 그 크기를 줄였다.^[2]

주문 정렬 논리를 절에 기초한 자동 정리 프로베어링에 통합하기 위해서는 ${\displaystyle {}_{}}$하는 주문 정렬 통일 알고리즘이 필요하며, 이 알고리즘은 다음과 같은 경우 두 ${\displaystyle {가지\mathrm{}}_{}}$ 선언된 s${\displaystyle {}_{}{1\mathrm{}}_{}}$,$$s 2 {\$displaystyle$$$s_${1$}, $s_{2$}}개의$$ ${\displaystyle {교차점\mathrm{}}_{}}$ s $1{\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}${\$displaystystyle$s_{1}\$cap s_{2$}}도 선언해야$$ 한다. ${\displaystyle x_{}}$$$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ ${\displaystyle x_{}}$$$ $2{\displaystyle {}_{}}$ ${\$ $s_{1$$}:{$2$\}\}:$ 각각 $s{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$ 식 x ${\displaystyle {1\mathrm{}}_{}\stackrel{}{}}$=${\displaystyle \stackrel{}{}}$? x ${\displaystyle {2\mathrm{}}_{}}$ ${\$$}}{=}\,x_{2$}}: 솔루션${\displaystyle }${${\displaystyle \mathrm{x1}{}_{}}$= x${\displaystyle ,}$ ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle 2{}_{}}$= ${\displaystyle \}}$ ${\displaystyle\{x_{1}=x,\;x_{2}=x\}}}}$이$($$가{\displaystyle )}$ 있으며$$, 여기서 x : ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$ x$:s_{$1}\$cap s_{$2$\}\}.$

스몰카는 파라메트릭 다형성을 허용하기 위해 순서 편중 논리를 일반화했다.^[3][4] 그의 틀에서 하위집단 선언은 복잡한 유형 표현으로 전파된다. 프로그래밍 예로서 파라메트릭 정렬 $($) {\$displaystyle {\textit}(X)}$을$($를) 선언할 수 ${\displaystyle \mathit{\text{있으며}}}$(X$$ {\$displaystyle$ X}이($가)$ C$$+++ 템플릿의 형식 매개 변수임$$), 하위 포트 선언에서 ${\displaystyle \mathit{\text{관계}}}$ ${\displaystyle \mathit{\text{목록}}}$$({\displaystystyle{int}\seteq {ft})$을 선언할 수 있다${\displaystyle .}$${\displaystyle \mathit{\text{t}}}$) ${\displaystyle \subseteq }$ $){\displaystyle {list}}({\textit{int})\\eq {\textit{list}}({\textit$ {$list})}}$은(는) 자동으로 유추되며$$, 이는 각 정수 목록도 플로트의 목록임을 의미한다.

슈미트-샤우프는 용어 선언을 허용하기 위해 주문-변형 논리를 일반화했다.^[5] As an example, assuming subsort declarations ${\displaystyle {\textit {even}}\subseteq {\textit {int}}}$ and ${\displaystyle {\textit {odd}}\subseteq {\textit {int}}}$, a term declaration like ${\displaystyle \forall i:{\textit {int}}.$$\;(i+i):$${\textit{even}}$은(는) 일반적인 과부하로 표현할 수 없는 정수 덧셈 속성을 선언할 수 있다$$.

참고 항목

• 범주형 논리학
• 다방면 1차 논리#다방면 논리

참조

다양한 논리에 대한 초기 논문은 다음과 같다.

• Wang, Hao (1952). "Logic of many-sorted theories". Journal of Symbolic Logic. 17 (2): 105–116. doi:10.2307/2266241. JSTOR 2266241., 저자의 계산, 논리, 철학에 수집되었다. 베이징 수필집: Science Press; Dordrecht: Kluwer Academy, 1990.
• Gilmore, P.C. (1958). "An addition to "Logic of many-sorted theories"" (PDF). Compositio Mathematica. 13: 277–281.
• A. Oberschelp (1962). "Untersuchungen zur mehrsortigen Quantorenlogik". Mathematische Annalen. 145 (4): 297–333. doi:10.1007/bf01396685. S2CID 123363080. Archived from the original on 2015-02-20. Retrieved 2013-09-11.
• F. Jeffry Pelletier (1972). "Sortal Quantification and Restricted Quantification" (PDF). Philosophical Studies. 23 (6): 400–404. doi:10.1007/bf00355532. S2CID 170303654.

외부 링크

• "다양한 논리" Calogero G. Zarba의 의사결정 과정에 대한 강의 노트 제1장