순위 투표

Ranked voting
타원형
이름
숫자
다양한 종류의 투표용지
정치 시리즈의 일부
선거 제도
Ballot box
1인승/메이저리스트
비례대표
혼합 시스템
  • 표현 유형별
  • 비보상 혼합 시스템
  • 보상 혼합 시스템
기타 시스템 및 관련 이론
  • 기타 시스템
icon 정치 포털

순위 투표(우선 투표 또는 순위 선택 투표라고도 함)는 유권자들이 각각의 투표용지에 첫 번째 또는 두 번째(또는 세 번째 등)의 순서로 후보(또는 옵션)를 순위를 매기는 투표 시스템을 말한다.이 순위의 목적은 첫 번째 선호도가 당선 불능으로 판명되거나 잉여 투표로 선출될 경우 유권자가 투표 이전 방식을 결정할 수 있도록 하는 것이다.

순위는 투표용지를 표시하는 방법, 선호도를 표로 정리하고 집계하는 방법, 의석을 채우는 방법에 따라 달라진다.순위 투표를 사용하는 선거 시스템은 승리자를 선택하기 위해 이용 가능한 많은 계수 방법 중 하나를 사용한다.또한 일부 순위 투표 시스템에서는, 공무원들이 유권자들에게 정해진 수의 후보, 때로는 그들 모두의 순위를 매길 것을 요구한다는 점에서, 순위 투표 제도들 사이에 차이가 있다; 다른 곳에서는, 시민들이 그들이 적합하다고 생각하는 만큼 많은 후보들의 순위를 매길 수도 있다.

순위 투표를 사용하여 단일 구성원을 선출하는 것은 보통 즉시 결선 투표입니다. 순위 투표를 사용하여 여러 구성원을 선출하는 것은 보통 단일 이전 투표이지만 다른 시스템이 될 수 있습니다.

복수 멤버 선거구 순위 투표(STV)는 호주, 아일랜드, 몰타, 영국(스코틀랜드 및 웨일스 의회)[1]의 전국 선거에서 사용되며, 단일 승자 투표는 미국 메인 주와[2] 알래스카[3] 주에서 온 국가 수준의 정치인을 선출하는 데 사용됩니다.순위 투표는 [4]슬로베니아와 나우루에서 사용됩니다.그것은 뉴질랜드의 [5]일부 지방선거에 사용된다.미국에서는 16개 주의 일부 시, 카운티 및 연방 예비선거와 5개 주의 해외 유권자가 연방 선거를 위해 사용합니다.

순위 투표 이력

윌리엄 로버트 웨어가 개발한 단일 의석 순위 선택 투표의 전형적인 개표 과정입니다.
주요 기사:선거제도와 사회선택론

순위 투표에 대한 최초의 언급은 13세기 말 라몬 룰의 글에서 찾을 수 있다.그의 뜻이 항상 명확하지는 않다.룰은 순위선택 투표가 아닌 양자대결 방식의 코프랜드 방식을 지지한 것으로 보인다.

15세기 초에, 그의 글은 쿠사의 니콜라스의 눈에 띄었다.하지만, 니콜라스는 그들에 의해 거의 영향을 받지 않고 독립적으로 현재 보르다 백작이라고 불리는 것을 발전시켰다.이 방법에서는 순위가 매겨진 투표용지를 사용합니다.룰과 니콜라스의 글은 20세기에 다시 나타나면서 사라졌습니다.

순위 투표에 대한 현대의 연구는 장 샤를 드 보다가 1781년에 그의 이름과 관련된 방법을 옹호하는 논문을 발표하면서 시작되었다.이 방법은 콘도르세 후작의 비판을 받았다.그는 집단적 선호도를 인식하는 방법을 개발했다.그는 Borda의 접근법이 항상 집단의 선호도를 확인하는 것은 아니라고 믿었다.그러나 그의 예는 여전히 논란이 되고 있다. 선거제도 비교 참조).[6]

이 주제에 대한 관심은 19세기에 Dane Carl André가 단일 양도 가능 투표(STV) 시스템을 개발하면서 되살아났다.그의 모국인 덴마크는 1855년에 STV 투표 제도를 도입했다.Thomas Hare는 1857년 영국에서 비슷한 시기에 STV를 재발명했습니다.

William Robert Ware는 1870년경 STV의 단일 승자 변형인 IRV를 제안했다.워어는 콘도셋이 이전에 언급했다는 것을 몰랐을 수도 있지만,[7][8] 단지 그것을 비난하기 위해서였을 뿐이다.

태즈메이니아는 1890년대 정부 선거에서 세계 최초로 순위 투표를 실시한 나라이다.지금까지 STV였습니다.그것은 1910년대부터 [9]호주에서 더 널리 쓰이게 되었다.

1920년대까지 아일랜드와 남아프리카공화국의 도시와 캐나다의 20개 도시, 미국의 거의 같은 수의 도시에서 순위투표가 실시되었다.이들 선거에서는 시장 및 기타 단일 공무원이 즉석결선투표를 통해 선출되었으며, STV를 통해 평의원이나 학교 이사회 등의 복수 공무원이 선출되었다.순위 투표는 1920년대에 시작된 아일랜드, 몰타, 캐나다(알베르타와 매니토바)의 정부 선거에서도 사용되었다.

선거 과정의 이론적 모델링은 던컨 [10]블랙의 1948년 논문으로 시작되었고, 이는 투표 기준의 일관성에 대한 케네스 애로우의 연구로 빠르게 이어졌다.그 주제는 일반적으로 경제학에 통합되는 사회적 선택 이론의 루브릭 아래에서 학계의 관심을 받아왔다.

순위 투표의 이론적 특성

Condorcet 기준

주요 기사: 컨디션 당첨자 기준

18세기에 콘도르세 후작에 의해 개발된 개념들 중 몇 가지는 여전히 그 주제에 중심적인 역할을 한다.

대부분의 유권자들이 다른 후보들보다 선호하는 후보가 있다면, 이 후보는 Condorcet 승자로 알려져 있다.Condorcet 승자가 있는 경우 항상 Condorcet 승자를 선출하는 투표 방법은 Condorcet 일관성 또는 Condorcet 기준을 충족하기 위해 (동등하게) 정의된다.이 속성을 가진 메서드를 Condorcet 메서드라고 합니다.

선거에서 Condorcet 승자가 없다고 가정해 보자.이 경우 Condorcet 사이클이 존재해야 합니다.이 사이클은 예를 들어 설명 가능합니다.세 명의 후보 A, B, C가 있으며, 10명의 투표자가 C–B–A, 10명의 투표자가 B–A–C, 10명의 투표자가 있다고 가정합니다.그렇다면 Condorcet 우승자는 없다.특히 A는 Condorcet 우승자가 될 수 없다는 것을 알 수 있습니다.유권자 중 2/3가 B를 A로 선택했다.단, 2⁄3은 B보다 C를 선호하기 때문에 B는 Condorcet 우승자가 될 수 없으며, 2⁄3은 C보다 A를 선호하기 때문에 C는 Condorcet 우승자가 될 수 없습니다.하지만 A는 Condorcet 우승자가 될 수 없습니다.따라서 Condorcet 수상자를 찾는 것은 우리를 한 명도 찾지 못한 채 동그랗게 만든다.

공간 모델

주요 기사:중위수 유권자 정리
IRVCopeland.png
공간 모델 다이어그램
투표용지 세어보세요
A~B~C 36
B–A–C 15
B–C–A 15
C–B–A 34

공간 모델은 던컨 블랙이 개발하고 앤서니 다운스가 확장한 선거 과정의 모델이다.모든 유권자와 모든 후보는 하나 이상의 차원을 가질 수 있는 의견의 공간에 있는 것으로 가정되며, 유권자들은 더 멀리 있는 후보보다 두 후보 중 가까운 쪽을 선호해야 한다.정치적 스펙트럼은 한 차원에서의 단순한 공간 모델이다.

이 다이어그램은 1차원의 단순한 공간 모델을 보여주며, 이 기사의 뒷부분에서 투표 방법을 보여준다.A의 지지자들은 A–B–C와 C에 투표하여 C–B–A에 투표하는 반면, B의 지지자들은 A와 C를 두 번째 우선으로 하는 것으로 동등하게 나뉜다.표시된 표에 따르면, 100명의 유권자가 있다면, 투표는 유권자와 후보자의 스펙트럼 내 위치에 따라 결정될 것입니다.

공간 모델은 유권자들의 의견을 시각화하는 자연스러운 방법이기 때문에 중요하다.그들은 또한 블랙 때문에 중앙 투표자 정리라는 중요한 정리로 이어진다.그것은 모든 1차원 모델과 고차원의 모든 대칭 모델을 포함한 광범위한 공간 모델의 경우 Condorcet 수상자가 존재하며 유권자 분포의 중앙값에 가장 가까운 후보가 될 것을 보장한다고 주장한다.

이 아이디어를 다이어그램에 적용한다고 가정해 보겠습니다.이 경우 Condorcet 당선자 B가 A보다 64%, C보다 66% 더 선호되고 Condorcet 당선자가 유권자 분포의 중앙값에 가장 가까운 후보임을 알 수 있다.

기타 정리

주요 기사:애로우의 불가능성 정리와 지바드의 정리

애로우의 불가능성 정리는 순위 투표에 더 비관적인 빛을 던진다.중간 투표자 정리는 많은 유권자 선호도에 대해 완벽하게 작동하는 투표 방법을 고안하는 것이 쉽다는 것을 말해주는 반면, 애로우의 정리는 모든 경우에 완벽하게 작동하는 기술을 개발하는 것은 불가능하다고 말한다.

애로우의 비관론인지 블랙의 낙관론인지 선거 행태가 더 정확하게 묘사되는지는 경험적으로 결정되어야 할 문제이다.Tideman과 Plassman의 [11]논문을 포함한 일부 연구는 중앙 유권자 정리를 만족시키는 유형의 단순한 공간 모델이 관찰된 유권자 행동과 밀접한 일치함을 시사한다.

또 다른 비관적인 결과인 지바드의 정리(앨런 지바드의)는 어떤 투표 시스템도 전술적 투표에 취약해야 한다고 주장한다.

보르다 카운트

주요 기사: Borda count
후보 스코어
A 87
B 130
C 83

Borda 카운트는 각 투표용지에 의해 부여되는 점수를 더함으로써 각 후보에게 점수를 할당합니다.후보자가 m명일 경우, 투표용지의 1위 후보자는 m–1점, 2위 후보자는 m–2점, 그리고 마지막 후보자가 아무것도 받지 않을 때까지 계속됩니다.제공된 예에서 B는 총 300점 중 130점으로 선출됩니다.

Borda 카운트는 구현이 간단하지만 Condorcet 기준을 충족하지 않습니다.당선 가능성이 없는 후보들의 공천에 따라 그 결과가 크게 좌우될 수 있다는 점에서 특히 약점이 있다.

기타 위치 시스템

이러한 방식으로 포인트를 부여하지만 다른 공식을 사용할 수 있는 투표 시스템은 위치 시스템입니다.여기서 점수 벡터(m – 1, m – 2, ...,0)는 Borda 카운트에 해당합니다. (1, 1⁄2, 1⁄3, ...,1/m )는 Dowdall 시스템을 정의하고 (1, 0, ...,0)은 포스트의 첫 번째에 해당합니다.

대체투표(즉석결선투표)

주요 기사:즉석 결선 투표
세어보세요
후보
 제1라운드 제2라운드 제3라운드
A(A-B 마크가 붙은 투표) 36 51 51
B (15표 B-A, 15표 B-C) 30 0 0
C(C-B 마크가 붙은 투표) 34 49 49

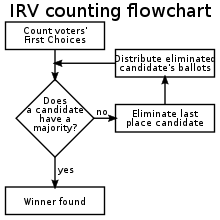
즉석결선투표(IRV)는 일련의 라운드에서 후보를 배제하고, 축소되는 후보군에 대한 개별 투표의 효과를 모방합니다.1차 투표는 투표로 이루어진다.첫 번째 개표에서 과반수 득표자가 없는 경우, 가장 적은 득표자를 특정하고(이 경우 B), 이후 라운드를 위해 개표에서 삭제한다.투표는 다음에 표시된 선호도에 따라 전송됩니다(있는 경우.이는 한 후보가 과반수 득표(우선 투표와 다른 후보로부터의 이전 투표의 조합)를 얻을 때까지 계속된다.

이 예에서는 2차 투표에서 A가 과반수를 획득하여 당선되었습니다.사실상 유권자들은 마지막 두 후보 사이의 선호도를 표현했다(더 일반적으로 m-1).A가 대다수 유권자의 선호이기 때문에 중단합니다.

제거 시스템은 정당 명부 PR과 같은 단순한 파생 통계 표에서 의석을 할당하는 것이 아니라 유권자의 개인 순위를 반영하기 위해 이전되는 각 표를 검토해야 한다.

IRV는 Condorcet 기준을 충족하지 않습니다.대부분의 순위 투표 시스템과 달리, IRV는 때때로 유권자의 가장 선호도가 낮은 후보 간에 동수 선호도를 허용하지 않습니다.

정당 순위에 적용되는[12] 단일 이전 투표의 [13]버전은 예비 투표로 2013년 독일 선거에 제안되었다.

단일 양도 가능 투표

100표 쿼터(드롭)로 선출되는 STV 선정 3의 예 26

세어보세요
후보
 제1라운드 제2라운드 제3라운드 제4라운드
A(A-B 마크가 붙은 투표) 26 선출된 선출된
B(B-E 마크가 붙은 투표) 18 26명 선출 선출된
C(C-D 마크가 붙은 투표) 17 17 17 마지막 자리를 채우는 마지막 남은 후보자로 선출되다
D(D-C 마크가 붙은 투표) 16 16 16 제거했다
E(E-B 마크가 붙은 투표) 15 15 제거했다
F(F-B 마크가 붙은 투표) 8 0 삭제 0
주요 기사:단일 양도 가능 투표

단일 이전 투표(STV)는 IRV의 복수 승자와 비례 버전입니다.IRV와 마찬가지로 STV에서 2차 선호는 예비투표입니다. 첫 번째 선호는 효과적으로 사용할 수 없을 때만 사용됩니다.STV에 따르면 각 유권자는 1표(백업 선호도 표시 가능)만 가지며, 선거인단의 투표는 처음에 가장 선호하는 후보에게 할당됩니다.쿼터에 도달하여 후보가 당선된 후(또는 당선된 경우) 유권자의 순서에 따라 잉여표가 당선자에서 나머지 후보(희망자)로 이동됩니다.그래도 의석을 채워야 한다면 후보들은 탈락하고 유권자들은 남은 후보들로 이동한다.STV의 형태에 따라 후보자를 배제하고 표심을 이전하는 방법이 다를 수 있습니다.

미니맥스

주요 기사:Minimax Condorcet법
두 번째
첫 번째
 A B C
A – 36:64 51:49
B 64:36 – 66:34
C 49:51 34:66 –

미니맥스 시스템은 결과 테이블을 구성하여 결과를 결정합니다.모든 개별 후보 쌍에 대한 입력은 첫 번째 후보가 두 번째 후보보다 얼마나 자주 선호되는지 보여줍니다.위의 공간 모델 섹션의 순위 표를 보면, 51명의 유권자가 C보다 A를 선호하고 49명이 반대의 선호도를 가지므로, (A, C) 항목은 '51:49'로 표시됩니다.각 행에서 첫 번째 후보(굵은 글씨로 표시)에 대해 가장 만족도가 낮은(즉, 최소) 결과를 식별한다.우승 후보는 선호도가 가장 낮고 선호도가 가장 높습니다(즉, 최대).이 예에서 승자는 B로, 가장 선호도가 낮은 결과가 승리입니다.반면 다른 후보자들의 가장 좋지 않은 결과는 약간 다른 손실이다.

투표용지 세트로 미니맥스 승자를 결정하는 것은 간단한 작업이다.이 방법은 Condorcet 기준을 충족하며 Condorcet 우승자가 있는 경우 Condorcet 우승자를 선출하고, 그렇지 않은 경우 Condorcet 우승자가 될 수 있는 후보를 선택하는 것으로 볼 수 있습니다(단순 메트릭으로).

라울법/코프랜드법

주요 기사:코프랜드법
후보 스코어
A 1
B 2
C 0

Copeland의 방법은 각 후보에게 미니맥스에 대해 위와 같이 결과 표에서 도출된 점수를 할당합니다.점수는 단순히 후보 열에서 유리한 결과의 수, 즉 특정 후보가 유권자 과반수보다 선호한 다른 후보의 수이다.가장 높은 점수를 받은 후보(이 경우 B)가 승리합니다.

Copeland의 방법은 Condorcet-consistent하고 직설적이지만 (Condorcet 수상자가 없는) 특정 유권자 선호 패턴에 대해서는 아무리 많은 유권자가 있어도 동점이 됩니다.따라서 지지자들은 일반적으로 동점자와의 연계를 권장한다.이 목적에 적합한 규칙에는 minimax, IRV 및 Borda 카운트가 포함됩니다.이 중 마지막 규칙은 Dasgupta-Maskin 메서드를 제공합니다.

기타 방법

  • Condorcet 완성은 Condorcet 우승자가 있는 경우 이를 선출하고, 그렇지 않은 경우 결과를 결정하는 별도의 절차에 따라 후퇴한다.Borda 카운트가 폴백이면 Black의 메서드, IRV를 사용하면 Tideman의 Condorcet-Hare가 됩니다.[15]
  • Bottom-Two-Runoff IRV 또는 BTR-IRV는 Condorcet-consistent이며 IRV에 대한 간단한 변경입니다.
  • Coombs의 방법은 IRV의 단순한 수정이다.각 라운드에서 탈락한 후보자는 가장 적은 1등 선택보다 가장 많은 꼴찌 선호도를 갖는다(따라서 예시의 첫 번째 라운드에서 B가 아닌 C가 탈락하고 B가 우승자가 된다).Coombs의 방법은 Condorcet-consistent는 아니지만 중앙 투표자 정리를 [16]충족한다.그것은 주로 유권자들의 꼴찌 선호도에 의존한다는 단점을 가지고 있는데, 이것은 그들의 첫 번째 자리보다 덜 신중하게 선택될 수 있다.
  • Baldwin과 Nanson의 방법은 Borda 카운트에 기초한 보다 복잡한 제거 규칙을 사용합니다.그들은 Condorcet-consistent입니다.
  • Kemeny-Young 방법은 복잡하지만 Condorcet-consistent입니다.
  • Smith의 방법은 후보 집합을 Smith 집합으로 줄인다. Smith 집합은 Condorcet 우승자가 있고 다른 경우 원래 집합보다 작은 단일 집합이다.일반적으로 IRV 및 미니맥스와[17] 함께 타이 브레이크와 함께 사용할 것을 권장합니다.그것은 계산적으로 간단하지만 대부분의 유권자들에게는 직관적이지 않다.
  • 예비투표는 IRV의 2라운드 버전이며, 보충투표는 예비투표가 제한된 형식입니다.
  • Bucklin의 방법은 여러 가지 형태로 존재하며, 그 중 일부는 Condorcet-consistent이다.
  • 순위 쌍법, 슐제법, 슐제 STV 및 분할 주기법은[18] 투표용지의 주기 구조 분석에 기초한 중간 계산 복잡도의 Condorcet-consistent한 방법이다.
  • 도그슨의 방법은 주로 루이스 캐롤이 고안한 것으로 유명하다.Condorcet-consistent이지만 계산상 복잡합니다.
  • 승인 규칙 확장

순위 투표 방식 비교

주요 기사:선거 제도 비교

비교의 가장 간단한 형태는 예를 들어 논증하는 것이다.이 기사의 예는 많은 사람들이 IRV의 약점이라고 생각하는 것을 보여준다.다른 예는 다른 방법에서 단언된 결함을 보여준다.

논리적 투표 기준은 사례의 주요 특징을 무한한 선거 공간으로 추정하는 것으로 생각할 수 있다.결과는 예측하기 어려운 경우가 많습니다.처음에는 합리적인 조치가 모순되고 그렇지 않으면 만족스러운 투표 방법을 거부합니다.

시뮬레이션된 선택을 사용하여 경험적 비교를 수행할 수 있다.유권자와 후보자의 인구는 공간적(또는 다른) 모델로 구성된다.유권자 분포의 중심에 가장 가까운 후보를 선출하는 빈도로 정의되는 각 투표 방법의 정확성은 무작위 시행을 통해 추정할 수 있다.콘도르세트 방식(및 Coombs 방식)은 최상의 결과를 제공하며, Borda 카운트가 그 뒤를 이으며, IRV는 어느 정도 뒤처져 있고, 무엇보다도 가장 과거가 나쁜 것이다.

투표 방법의 수학적 속성은 일반 유권자에 대한 이해와 같은 실용적인 특징과 균형을 이루어야 한다.

순위 투표의 단점

순위 투표는 유권자들이 사후 첫 투표보다 자신의 선호도를 더 정확하게 나타내는 후보를 선택할 수 있게 해준다.그러나 그것들은 더 [17]: §8.1 복잡하다.

단일양도투표에서 흔히 볼 수 있는 많은 후보들이 있다면, 많은 선호 투표 패턴은 유권자들만의 독특한 것이 될 것이고, 이는 유권자들이 부패나 협박의 맥락에서 자신을 식별하게 하여 [19][20]투표의 비밀성을 해칠 수 있다.예를 들어, 2002년 아일랜드 총선에서 더블린 북부 [21]선거구에 전자 투표가 발행되었습니다.

「 」를 참조해 주세요.

외부 링크

레퍼런스

  1. ^ Wiki: 영국의 정치
  2. ^ "Ranked Choice Voting in Maine". Maine State Legislature. Retrieved 21 October 2021.
  3. ^ "Alaska Better Elections Implementation". Alaska Division of Elections. Retrieved 21 October 2021.
  4. ^ Toplak, Jurij (2006). "The parliamentary election in Slovenia, October 2004". Electoral Studies. 25 (4): 825–831. doi:10.1016/j.electstud.2005.12.006.
  5. ^ "New Zealand Cities Voting to Implement Ranked Choice Voting".
  6. ^ George G. Szpiro, "Numbers Rule" (2010).
  7. ^ Nanson, E. J. (1882). "Methods of election: Ware's Method". Transactions and Proceedings of the Royal Society of Victoria. 19: 206. The method was, however, mentioned by Condorcet, but only to be condemned.
  8. ^ Condorcet, Jean-Antoine-Nicolas de Caritat (1788). On the Constitution and the Functions of Provincial Assemblies. Complete Works of Condorcet (in French). Vol. 13 (published 1804). p. 243. En effet, lorsqu'il y a plus de trois concurrents, le véritable vœu de la pluralité peut être pour un candidat qui n'ait eu aucune des voix dans le premier scrutin.
  9. ^ 호주 선거 시스템, 파렐과 맥칼리스터, 페이지 17
  10. ^ 던컨 블랙, "집단 의사결정의 원리에 대하여"(1948).
  11. ^ T. N. Tidman과 F.Plassman, "실제 선거에서의 투표-캐스팅 결과 모델링"(2012).
  12. ^ [https://www.landtag.ltsh.de/infothek/wahl18/umdrucke/1900/umdruck-18-1916.pdf 대체 II:Einführung einer Ersatzstimme(독일어)
  13. ^ 듀얼 레벨 투표란?
  14. ^ Riker, William Harrison (1982). Liberalism against populism: a confrontation between the theory of democracy and the theory of social choice. Waveland Pr. pp. 29–30. ISBN 0881333670. OCLC 316034736. Ordinal utility is a measure of preferences in terms of rank orders—that is, first, second, etc. ... Cardinal utility is a measure of preferences on a scale of cardinal numbers, such as the scale from zero to one or the scale from one to ten.
  15. ^ J. Green-Armyage, T. N. Tidman 및 R.코스먼, "투표 규칙의 통계적 평가"(2015).
  16. ^ B. 그로프만과 S. L. 펠드는 "만약 당신이 (즉각 결선투표를) 좋아한다면, 당신은 쿰스 규칙에 대해 알아야 한다." (2004)
  17. ^ a b R. B. 달링턴, "콘도르세트와 미니맥스 투표 시스템은 최고인가?" (v8, 2021).
  18. ^ W. H. H. Holiday와 E. Pacuit, "분할 주기: 클론으로부터 독립적이고 스포일러에 대한 면역이 있는 새로운 조건의 일관성 있는 투표 방법" (2021)
  19. ^ 선거 데이터베이스 2004년 2월 1일
  20. ^ 2004년 아일랜드 전자투표 위원회
  21. ^ 더블린 카운티 리턴 오피서 더블린 노스 투표표 작성(zip 파일)