스타인메츠 고체

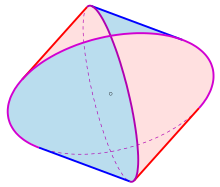
기하학에서 스타인메츠 고체는 직각으로 반지름이 같은 두세 개의 원통의 교차점으로서 얻은 고체체다. 두 실린더의 교차점 곡선은 각각 타원형이다.

두 실린더의 교차점은 자전거 실린더라고 불린다. 토폴로지로는 정사각형 호소헤드론에 해당한다. 세 개의 실린더가 교차하는 것을 3기통이라고 한다. 이등분된 자전거는 금고라고 불리는데,^[1] 건축에 있어서 망루형 금고는 이런 모양을 하고 있다.

슈타인메츠 고형물은 교차점의 부피를 결정하는 문제를 해결한 수학자 찰스 프로테우스 스타인메츠의 이름을 따서 명명되었다.^[2] 그러나 고대 그리스 세계의 아르키메데스,^[3][4] 고대 중국의 주총지,^[5] 이탈리아의 르네상스 초기에는 피에로 델라 프란체스카에 의해 같은 문제가 일찍이 해결되었다.^[3]

바이클린더

$반지름{\displaystyle }$ r ${\displaystyle r}$을(를) 가진 두 실린더에 의해 생성된$$ 자전거 실린더는

부피

${\displaystyle V={\frac {16}{3}r^{3}}}}$

그리고

표면 면적

${\displaystyle A}$= ${\displaystyle 16}$ ${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$^[1][6]

자전거의 상반부는 도미형 금고의 정사각형 케이스로, 횡단면이 폴리곤의 유사한 형태인 볼록형 폴리곤을 기반으로 한 돔형 고형이며, 둥근 프리즘의 부피와 표면적의 합리적인 배수로 도미형 금고의 부피와 표면적을 계산하는 유사한 공식은 보다 일반적인 의미를 갖는다.리의^[7]

볼륨 공식 증명

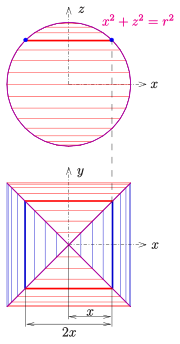
볼륨 공식을 도출하기 위해서는 구의 부피 계산에 공통적인 아이디어를 사용하는 것이 편리하다: 얇은 원통형 슬라이스 수집. 이 경우 얇은 조각은 사각형 큐보이드(도표 참조)이다. 이 되다

${\displaystyle V=\int _{-r}^{r}(2x)^{2}\mathrm {d} z=4\cdot \int _{-r}^{r}x^{2}\mathrm {d} z=4\cdot \int _{-r}^{r}(r^{2}-z^{2})\mathrm {d} z={\frac {16}{3}}r^{3}}$.

오른쪽 원형 원뿔의 부피와 구형의 반과 반지름과 높이가 같은 오른쪽 원형 원통의 부피와의 관계가 1 : 2 : 3이라는 것은 잘 알려져 있다. 자전거의 절반에 대해서도 이와 유사한 진술이 적용된다.

• The relations of the volumes of the inscribed square pyramid (${\displaystyle a=2r,h=r,V={\frac {4}{3}}r^{3}}$), the half bicylinder (${\displaystyle V={\frac {8}{3}}r^{3}}$) and the surrounding squared cuboid (${\displaystyle a=2r,h=r,V=4r^{3$$\}\}\}$은(는) 1 : 2 : 3이다.

다변량 미적분 사용

실린더의 방정식을 고려하십시오.

${\displaystyle x^{2}+z^{2}=r^{2}}$

${\displaystyle x^{2}+y^{2}}}=r^{2}}:$

볼륨은 다음과 같이 제공된다.

${\displaystyle V=\iint _{V}\mathrm {d} z\mathrm {d} y\mathrm {d} x}$

통합의 한계:

${\displaystyle -{\sqrt {r^{2}-x^{2}}\leqslant z\leqslant {\sqrt{2}-x^{2}}:$

${\displaystyle -{\sqrt {r^{2}-x^{2}}\leqslant y\leqslant {\sqrt{2}-x^{2}}:$

$(\displaystyle -r\leqslant x\leqslant r}$

대신 다음과 같은 혜택을 누리십시오.

${\displaystyle V=\int _{-r}^{r}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\int _{-{\sqrt {r^{2}-x^{2}}}}^{\sqrt {r^{2}-x^{2}}}\mathrm {d} z\mathrm {d} y\mathrm {d} x=8r^{3}-{\frac {8r^{3}}{3}}={\frac {16r^{3}}{3}}}$

면적 공식 증명

표면적은 두 개의 빨간색과 두 개의 파란색 원통형 생물체로 이루어져 있다. One red biangle is cut into halves by the y-z-plane and developed into the plane such that half circle (intersection with the y-z-plane) is developed onto the positive ${\displaystyle \xi }$-axis and the development of the biangle is bounded upwards by the sine arc ${\displaystyle \eta =r\sin$$\좌({\frac {\xi }{r}\오른쪽)\0\leq \xi \leq \pi r$ 따라서 이 개발의 영역은

${\displaystyle B=\int _{0}^{\pi r}r\sin \left({\frac {}}{r}\right)\mathrm {d}\xi =2r^{2}}$

총 표면적은 다음과 같다.

${\displaystyle A}$= ${\displaystyle 8\cdot }$ ${\displaystyle B}$= ${\displaystyle 16}$ ${\displaystyle {r\mathrm{}}^{}}$ 2 ${\$

볼륨 공식의 대체 증거

자전거의 부피(흰색)는 큐브(빨간색)에 싸서 얻을 수 있다. (기통 축과 평행) 자전거 기체를 교차하는 평면이 정사각형을 이루고 그 정육면과의 교차점은 더 큰 정사각형이다. 두 정사각형의 면적 차이는 4개의 작은 정사각형(파란색)과 같다. 비행기가 고형물을 통과하면서, 이 푸른 사각형들은 입방체 모서리에 이소셀 면들이 있는 사각형 피라미드를 묘사한다; 피라미드는 네 개의 입방체 가장자리의 중간 지점에 그들의 정점을 가지고 있다. 비행기를 자전거 전체로 이동시키는 것은 총 8개의 피라미드를 묘사한다.

• 

  구의 부피를 계산하는 주총지의 방법(카발리에리의 원리와 유사함)에는 자전거의 부피 계산이 포함된다.

• 

  큐브 단면을 가진 자전거 단면적의 관계

8개의 피라미드(파란색)의 부피를 뺀 큐브(빨간색)의 부피는 자전거(흰색)의 부피다. The volume of the 8 pyramids is: ${\displaystyle \textstyle 8\times {\frac {1}{3}}r^{2}\times r={\frac {8}{3}}r^{3}}$, and then we can calculate that the bicylinder volume is ${\displaystyle \textstyle (2r)^{3}-{\frac {8}{3}}r^{3}={\frac {16$$}{3}}r^{3}}}$

트리실린더

수직 교차 축이 있는 3개의 실린더의 교차점은 3개의 가장자리가 만나는 정점과 4개의 가장자리가 만나는 정점을 가진 고체의 표면을 생성한다. 정점 집합은 진드기 도데면체의 가장자리로 간주될 수 있다. 부피와 표면적을 결정하는 열쇠는 3개의 가장자리가 만나는 정점(s. diameter)과 6개의 곡면 피라미드(삼각형은 실린더 표면의 일부)를 가진 큐브에 의해 3기통 재샘플링될 수 있다는 관측이다. 곡선 삼각형의 부피와 표면적은 위의 자전거 기기에서와 유사한 고려사항으로 결정할 수 있다.^[1][6]

세발기통의 부피는

${\displaystyle V=8(2-{\sqrt{2}})r^{3}}$

그리고 표면적은

${\displaystyle A=24(2-{\sqrt{2}})r^{2}.}$

더 많은 실린더

4개의 실린더로, 4면체의 정점을 고체의 반대편에 있는 해당 지점에 연결하는 축으로, 부피는^[1][6]

${\displaystyle V_{4}=12\left(2{\sqrt{2}}-{\sqrt{6}\오른쪽)r^{3}\,}$

6개의 실린더가 있고, 축이 입방체 면의 대각선과 평행하며, 볼륨은 다음과 같다.^[1][6]

${\displaystyle V_{6}={\frac {16}{3}\좌측(3+2{\sqrt{3}-4}{\sqrt{2}}\오른쪽)r^{3},}$

참고 항목

• 운굴라

참조

외부 링크

• Google 3D 이미지갤러리에 있는 Steinmetz 솔리드 3D 모델