간격추정

구간 추정은 통계학에서 관심 모수의 가능한 값의 구간을 추정하기 위해 표본 데이터를 사용하는 것입니다. 이는 단일 값을 제공하는 점 추정과는 대조적입니다.^[1]

구간 추정의 가장 일반적인 형태는 신뢰 구간(빈수론적 방법)과 신뢰 구간(베이지안 방법)입니다.^[2] 덜 일반적인 형태에는 우도 구간, 기준 구간, 공차 구간 및 예측 구간이 포함됩니다. 비통계적 방법의 경우 퍼지 논리에서 구간 추정치를 추론할 수 있습니다.

구간추정유형

신뢰구간

신뢰 구간은 표본 데이터 집합(일반적으로 평균 또는 표준 편차)에서 관심 모수를 추정하는 데 사용됩니다. 신뢰 구간은 관심 모수가 하한 및 상한 내에 있다는 100 γ% 신뢰도를 나타냅니다. 신뢰 구간에 대한 일반적인 잘못된 인식은 데이터 집합이 한계 내에 있거나 위/아래에 있는 경우 100 γ%를 차지한다는 것이며, 이를 공차 구간이라고 합니다.

신뢰 구간을 구축하는 데 사용되는 방법은 여러 가지가 있습니다. 올바른 선택은 분석할 데이터에 따라 달라집니다. 알려진 분산이 있는 정규 분포의 경우 z-표를 사용하여 n개 측정 데이터 집합에서 표본 평균을 중심으로 100 γ%의 신뢰 수준을 얻을 수 있는 구간을 만듭니다. 이항 분포의 경우 Wald Approxate Method, Jeffrey 구간을 사용하여 신뢰 구간을 근사화할 수 있습니다. 그리고 클로퍼-피어슨 간격. 제프리 방법을 사용하여 포아송 분포에 대한 구간을 근사화할 수도 있습니다.^[3] 기본 분포를 알 수 없는 경우 부트스트래핑을 사용하여 데이터 집합의 중위수에 대한 경계를 만들 수 있습니다.

신뢰구간

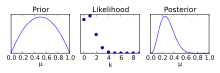
신뢰 구간은 신뢰 구간이 아닌 사전 가정, 베이즈 계수를 사용하여 가정을 수정하고 사후 분포를 결정해야 합니다. 사후 분포를 사용하면 추정치가 구간 내에 포함되어 있다고 100 γ% 확신할 수 있는 신뢰 구간과 달리 관심 매개 변수가 포함된 100 γ% 확률을 확인할 수 있습니다.

${\displaystyle Poster\ \alpha \ Likelihood\times Prior}$

이전의 가정은 구간을 구축하는 데 더 많은 데이터를 제공하는 데 도움이 되지만 신뢰 구간의 객관성은 제거됩니다. 사전은 사전에 이의를 제기하지 않으면 잘못된 예측으로 이어질 수 있는 경우 사후 정보를 제공하는 데 사용됩니다.^[5]

신뢰 구간의 경계는 신뢰 구간과 달리 가변적입니다. 올바른 상한 및 하한이 어디에 위치해야 하는지 결정하는 방법은 여러 가지가 있습니다. 구간의 경계를 조정하는 일반적인 방법에는 가장 높은 사후 밀도 구간(HPDI), 등미 구간 또는 평균 주변의 구간 중심을 선택하는 방법이 있습니다.

일반적이지 않은 양식

우도 기반

우도 함수의 원리를 이용하여 관심 모수를 추정합니다. 우도 기반 방법을 사용하면 지수, Weibull 및 로그 정규 평균에 대한 신뢰 구간을 찾을 수 있습니다. 또한, 우도 기반 접근법은 표준 편차에 대한 신뢰 구간을 제공할 수 있습니다. 우도 함수와 미래 확률 변수를 결합하여 예측 구간을 만들 수도 있습니다.

피듀시알

기준 추론은 데이터 세트를 활용하고 노이즈를 신중하게 제거하고 분포 추정기인 GFD(Generalized Fiducial Distribution)를 복구합니다. 베이즈 정리를 사용하지 않으면 신뢰 구간과 마찬가지로 사전 가정이 없습니다.

기준 추론은 덜 일반적인 형태의 통계적 추론입니다. 역확률 방법을 개발해 온 설립자 R.A. Fisher는 그 과정의 타당성에 대해 자신만의 질문을 가지고 있었습니다. 기준 추론은 20세기 초에 개발되었지만, 20세기 후반은 이 방법이 빈도주의 및 베이지안 접근법보다 열등하지만 통계적 추론에 대한 역사적 맥락에서 중요한 위치를 차지한다고 믿었습니다. 그러나 현대적인 접근 방식은 기준 간격을 GFI(Generalized Fiducial Inference)로 일반화하여 이산적이고 연속적인 데이터 세트를 추정하는 데 사용할 수 있습니다.

관용

공차 구간은 수집된 데이터 집합 모집단을 사용하여 공차 한계 내에서 100 γ% 값을 포함하는 구간을 구합니다. 공차 구간을 설명하는 데 일반적으로 사용되는 예로는 제조가 있습니다. 이러한 맥락에서 기존 제품 집합의 백분율을 평가하여 모집단의 백분율이 공차 한계 내에 포함되도록 합니다. 공차 구간을 생성할 때 한계를 상한 및 하한으로 표기할 수 있으며, $이$는 표본 평균 μ$${\$displaystyle \mu }$및 표본 표준 편차 s를 사용합니다.

${\displaystyle (l}$ b${\displaystyle {}_{}}$ ${\displaystyle u_{}}$ ${\displaystyle b{}_{}}$) = μ$$± k $2초$ {\displaystyle (l_{b},u_{${\displaystyle b}$}) =\mu \pm k_{2s} 양면 간격

양면 간격으로

그리고 허용오차가 임계값 이상 또는 미만으로만 요구되는 편면간격의 경우,

${\displaystyle l_{b}=\mu -k_{1}s}$

${\displaystyle u_{b}=\mu +k_{1}s}$

${\displaystyle {ki}_{}}$ ${\$는 구간 추정에서 분포와 변의 수, i에 따라 달라집니다$$. 정규 분포에서 ${\displaystyle {k2\mathrm{}}_{}}$ ${\$는 다음과 같이 표현할$$ 수 있습니다.

${\displaystyle k_{2}=z_{\alpha /2}{\sqrt {\frac {\nu(1+{\frac {1}{N}})}{\chi_{1-\alpha,\nu }^{2}}$

어디에,

${\displaystyle {}_{}^{}}$1 ${\displaystyle {-}_{}^{}}$ $α,$ ν 2$$${\displaystyle$ \chi _{1-\alpha,\nu }^{2}}는 확률 α {\displaystyle \alpha }에서${\displaystyle {}_{}^{}}$초과된 ν {\displaystyle \nu } 자유도를 사용하는 카이-제곱 분포의 임계값입니다.

${\displaystyle z_{}}$ ${\displaystyle {\alpha }_{}}$/ ${\displaystyle {2\mathrm{}}_{}}$ ${\$/ $2}}$는 정규 분포에서 얻은 임계값입니다.

예측

예측 구간은 미래의 표본들을 포함하는 구간을 어느 정도의 신뢰성, 즉 γ로 추정합니다. 예측 구간은 베이지안 상황과 빈도주의 상황 모두에 사용될 수 있습니다. 이러한 간격은 일반적으로 회귀 데이터 세트에서 사용되지만, 예측 간격은 이전 데이터의 실험적으로 통제된 매개변수를 넘어서는 외삽을 위해 사용되지 않는다는 점에 유의해야 합니다.^[8]

퍼지 논리

퍼지 논리는 인공 지능, 의료 결정 및 기타 분야의 의사 결정을 비이진 방식으로 처리하는 데 사용됩니다. 일반적으로 입력을 받아 퍼지 추론 시스템을 통해 매핑하고 출력 결정을 생성합니다. 이 프로세스에는 퍼지화, 퍼지 논리 규칙 평가 및 퍼지 해제가 포함됩니다. 퍼지 논리 규칙 평가를 볼 때, 멤버십 함수는 우리의 비이진 입력 정보를 유형 변수로 변환합니다. 이러한 멤버십 기능은 시스템의 불확실성을 예측하는 데 필수적입니다.

편면 대 양면

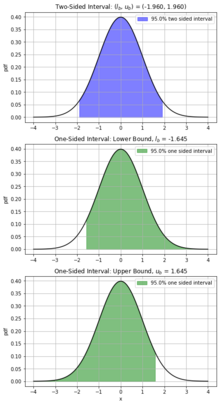
양면 간격은 하한$(l$ b $displaystyle$ l_{b}}) 및$$(u$$b${\displaystyle$ u_{b}})을 사용하여 신뢰 수준이 γ인 관심 매개 변수 θ를 추정합니다. 예로는 지리적 지역의 남성 평균 키 또는 제조업체에서 만든 특정 책상의 길이를 추정하는 것이 포함될 수 있습니다. 이러한 경우는 모수의 중심 값을 추정하는 경향이 있습니다. 이는 일반적으로 아래의 식과 유사한 형태로 제시됩니다.

${\displaystyle P(l_{b}<\theta <u_{b})=\ gamma }$

양면 구간과 구별되는 단측 구간은 관심 모수를 γ*100% 확률로 예측하는 최소 또는 최대 한계를 구성하기 위해 신뢰 수준, γ을 활용합니다. 일반적으로 추정치의 최소 한계 또는 최대 한계가 관심의 대상이 아닌 경우에는 일방적인 간격이 필요합니다. θ의 최소 예측값과 관련하여 더 이상 추정치의 상한을 찾을 필요가 없으므로 양면의 형태가 줄어듭니다.

${\displaystyle P(l_{b}<\Theta )=\ gamma }$

상한을 제거하고 신뢰도를 유지한 결과 하한(${\displaystyle {}_{}}$ ${\displaystyle b_{}}$ ${\$이 증가합니다. 마찬가지로 모수 추정치의 상한만 찾는 경우 상한이 줄어듭니다. 일방 간격은 재료 생산 품질 보증에서 흔히 볼 수 있는 것으로, 재료 강도의 예상 값인$$θ($Lb$ {\$displaystyle$l_{b}}) 이상이어야 하며, 어느 ${\displaystyle {정도}_{}}$의 신뢰도(100 γ%)가 있어야 합니다. 이 경우 제조업체는 너무 강한 제품을 생산하는 것에 관심이 없으며, 상한이 ${\displaystyle {없습니다}_{}}$(ub ${\$

사용 및 건물 견적 주의

모수의 유의성을 결정할 때는 데이터와 수집 방법을 이해하는 것이 가장 좋습니다. 데이터를 수집하기 전에 데이터의 불확실성이 통계적 편향이 아닌 표본 변동성이 되도록 실험을 계획해야 합니다.^[9] 실험 후 구간 추정치를 만드는 일반적인 첫 번째 단계는 다양한 그래픽 방법을 사용하여 그림을 그리는 것입니다. 이를 통해 데이터 집합에서 표본의 분포를 확인할 수 있습니다. 분포에 기초한 잘못된 가정으로 구간 경계를 생성하면 예측에 오류가 발생합니다.^[10]

구간 추정치가 보고되면 과학계 안팎에서 공통적으로 유지되는 해석이 있어야 합니다. 이와 관련하여 신뢰할 수 있는 간격은 일반 대중이^{[citation needed]} 가장 쉽게 이해할 수 있는 것으로 간주됩니다. 퍼지 논리에서 도출된 구간 추정치는 훨씬 더 많은 애플리케이션별 의미를 갖습니다.

일반적으로 발생하는 상황에서는 필요한 가정의 점검과 유효성에 따라 사용할 수 있는 표준 절차 세트가 있어야 합니다. 이는 신뢰 구간과 신뢰 구간 모두에 적용됩니다. 그러나 보다 새로운 상황에서는 구간 추정치를 어떻게 공식화할 수 있는지에 대한 지침이 있어야 합니다. 이와 관련하여 신뢰 구간과 신뢰 구간은 유사한 지위를 갖지만 두 가지 차이가 있습니다. 첫째, 신뢰 구간은 사전 정보를 쉽게 처리할 수 있는 반면 신뢰 구간은 처리할 수 없습니다. 둘째, 신뢰 구간은 신뢰 구간보다 더 유연하고 신뢰 구간보다 더 많은 상황에서 실용적으로 사용될 수 있습니다. 신뢰 구간이 비교에서 어려움을 겪는 한 영역은 비모수 모델을 다루는 것입니다.

구간 추정 절차의 성능을 테스트하는 방법이 있어야 합니다. 이와 같은 절차는 많은 경우 다양한 종류의 근사치를 포함하며 실제 절차의 성능이 주장하는 것에 근접하는지 확인할 필요가 있기 때문에 발생합니다. 확률적 시뮬레이션을 사용하면 신뢰 구간의 경우 이를 쉽게 만들 수 있지만 사전 정보를 적절하게 고려해야 하는 신뢰 구간의 경우 다소 문제가 있습니다. 신뢰할 수 있는 간격 검사는 사전 정보가 없는 상황에 대해 수행할 수 있지만 검사에는 절차의 장기 빈도 속성을 확인하는 것이 포함됩니다.

Severini는 신뢰 구간과 신뢰 구간이 유사한 결과를 도출하는 조건에 대해 논의하고 신뢰 구간의 커버리지 확률과 신뢰 구간과 관련된 사후 확률에 대해 논의합니다.^[11]

베이지안 통계에 대한 일반적인 접근법이자 정당화 방법인 의사결정 이론에서 구간 추정은 직접적인 관심사가 아닙니다. 결과는 구간 추정이 아닌 결정이므로 베이지안 의사결정 이론가들은 베이즈 작용을 사용합니다: 그들은 특정 구간이 아닌 전체 후방 분포에 대한 손실 함수의 예상 손실을 최소화합니다.

적용들

신뢰 구간의 적용은 불확실성을 다루는 다양한 문제를 해결하는 데 사용됩니다. Katz(1975)는 법적 절차에서 간격추정을 활용하기 위한 다양한 도전과 편익을 제안하고 있습니다.^[12] Altmen(1990)은 의학 연구에서 사용하기 위해 신뢰 구간의 사용과 이를 사용하기 위한 지침에 대해 논의합니다.^[13] 제조에서 제품 수명을 추정하는 구간 추정치를 찾거나 제품의 공차를 평가하는 경우도 일반적입니다. Meker와 Escova(1998)는 미래의 확률변수(예측구간) 예측을 포함하여 모수적 및 비모수적 추정하에서 신뢰성 데이터를 분석하는 방법을 제시하고 있습니다.

참고 항목

• 68–95–99.7 rule
• 알고리즘 추론
• 보장확률
• 추계통계
• 귀납법(철학)
• 오차한계
• 다중비교
• 통계철학
• 예측추론
• 베렌스 – 어부 문제 이것은 적용 가능한 통계 방법론의 이면에 있는 이론의 발전에 중요한 역할을 했습니다.

참고문헌

서지학

• 켄달, M.G. 그리고 스튜어트, A. (1973) 고급 통계학 이론. 2권: 추론과 관계 (제3판). 그리핀, 런던.

위의 20장에서는 신뢰 구간을 다루고, 21장에서는 기준 구간과 베이지안 구간을 다루며 세 가지 접근 방식을 비교하는 논의를 합니다. 이 작업은 현대의 계산 집약적인 방법론보다 앞서 있다는 점에 주목하십시오. 또한 21장에서는 베렌스-피셔 문제에 대해 논의합니다.

• 미커, W.Q., 한, G.J. 그리고 에스코바, LA. (2017년) 통계적 간격: 실무자 및 연구자를 위한 가이드(제2판). 존 와일리 & 선즈.

외부 링크

• 퍼지 수학 소개 https://web.archive.org/web/20061205114153/http ://blog.peltarion.com/2006/10/25/fuzzy-math-part-1-the-theory
• 퍼지 논리란? https://www.youtube.com/watch?v=__0nZuG4sTw